1. Introduction
Recently, artificial neural networks have been widely and successfully employed in solving classification and regression problems in finance and many other fields. One of their main advantages is that they are able to capture complex, non-linear interactions (see, e.g., [
1]). This is what other traditional financial economic tools often fail to handle (see, e.g., [
2,
3]). In this article, we are particularly interested in the potential of neural networks for forecasting financial crises with micro-, macroeconomic and financial factors. To create an early warning system based on neural networks for the stock market, many economic and financial factors which could be used as input data are available. On the other hand, the time frame on which such a model can be fitted is very limited. As a consequence, there is the risk of over-parameterization and unstable models. These problems are mentioned explicitly in [
4,
5]. As stock market investments are subject to high risk, and a huge amount of money might be at stake, the reliability and robustness of forecasting models are crucial features in early warning systems. To solve these problems, we develop an input variable selection method and we test this approach using a walk-forward testing procedure based on global and sequential estimations in an extending window. This procedure allows us to extract a large part of the information from the input data set, while we still avoid over-parameterized models.
With our results, we contribute to the literature on early warning systems for the stock market and to the literature on the application of neural networks in financial time series forecasts. Neural networks and deep learning models were successfully used in financial modeling for various tasks (see, e.g., [
1] or [
6] for an overview). The applications include the prediction of financial market movement directions (see [
7]), the construction of optimal portfolios (see [
8]) and trading strategies (see [
9]), predicting techniques for the equity premium (see [
2]) or exchange rates (see [
10,
11], as well as the quantification of enterprise risk (see [
12]) and the examination of risk management tools (see [
13]).
In the area of early warning systems for stock market crises, existing approaches include methods from machine learning and other areas. Among these are the pure identification of market crises based on Markov-switching models, as suggested by [
14]. Extensions incorporate input variables to receive an appropriate forecast (see, e.g., [
15]). Using the Akaike information criterion (AIC), [
15] selects a logistic regression model from a larger set of input factors to forecast stock market regimes. A comprehensive overview of various methods and publications for early warning systems can be found in [
5]. These approaches include machine learning, in particular neural networks. For example, [
16] presents a machine learning forecasting model for financial crises based on three input factors for the forecast. However, the choice of the input factors is not based on an objective method here.
As pointed out above and in the mentioned literature, we observe that neural networks are well-suited to detect and depict non-linear relations between input data and time series which shall be predicted. With this ability, the model is less subjective than a forecasting model with the structure being defined by a human expert. Unfortunately, as the examples show, achieving this objectivity is far more difficult when it comes to the selection of the input variables itself. An objective variable selection process for a regression model is presented in [
15]. One common technique to reduce input factors in neural network models is based on the output sensitivity (see e.g., [
17,
18]). The underlying idea is to remove input factors which do not contribute much to the output. However, this creates, in particular for financial data, the problem that variables which do not change much from one month to another, but which might provide valuable information over an economic cycle (such as key interest rates from central banks), or factors with a lower frequency of publication, could be disregarded.
Faced with the described challenges of the application of neural networks for financial time series analysis, we aim to demonstrate an efficient method of input factor reduction and a rigorous testing mechanism. By pruning variables that have less explanatory significance compared to others, we enable our neural network to avoid unfavorable local minima, mitigate over-parameterization, get closer to the globally optimal points, and return a more stable network (see, e.g., [
17,
19]). We begin by introducing the method for the determination of the financial crises for the S&P 500 index in
Section 2. Afterwards, we present the whole set of micro-, macroeconomic and financial input factors in
Section 3, to which we apply our input factor reduction method. The architecture of the neural networks we use and our input factor reduction method, are introduced in
Section 4. In
Section 5, we apply this method to select a subset of the input factors (from
Section 3) to forecast crisis states (as introduced in
Section 2). The chosen models are tested using a walk-forward testing of out-of-sample predictions in
Section 6. We conclude in
Section 7.
2. Determination of Financial Crises
Most current neural network approaches to financial prediction problems aim at predicting price movements, either from historical prices, or based on a set of variables (see [
4]). However, future market prices are difficult to predict from the history. Moreover, price predictions are not equal to investment decisions, indicating that translating price predictions into investment solutions requires an additional manual layer (see [
9] for more details). On the contrary, an accurate prediction of economic states based on the financial time series not only serves as a direct signal for the market participants, but can also be easily transmitted to investment strategies.
We follow a numerical and heuristic procedure proposed in [
20] to determine economic crisis states based on a stock index. This method is also used in [
21]. The authors of [
22] apply a different method and state that it leads to similar results as the method from [
20]. The parameters which we use as thresholds are also taken from [
20]. We found that the method is robust with respect to changes in the parameters of plus or minus 2%.
First, we divide the time series of all daily observations of the stock index (
) in blocks separated by days on which the respective stock index reaches a half-year high. A half-year is defined to be 120 days or 26 weeks. This set of all days reaching half-year highs, i.e., 26
week highs,
Second, we screen each period between two elements of
, i.e., the interval
, for a possible crisis. A crisis day between two
26-week-highs represents a minimum loss of
relative to the stock index at the beginning of this period. The set of
core crisis days in the interval
is correspondingly defined as:
There are two possible calculation results: or :
To determine the crisis period in this interval, we further define the starting and end days. We set the starting day of the crisis as the last day on which the 10% loss level relative to the stock index at
is reached, i.e.,
where
refers to the first day in the
i-th set of
core crisis dates.
For the end day of a crisis, we first denote
as the day of the lowest index value before the next 26 week high is reached, i.e.,
In normal cases, the end day of the crisis is , i.e., . However, if a stock market upswing after the lowest index value is followed by a new downturn, we extend the crisis period if the new downturn is at least 10% below the upswing’s highest value. The crisis is extended to the day of the lowest index value of the new downturn .
Two days are required for the determination of
, namely the latest possible starting day of the new 10% downturn,
, and consequently the latest possible end day of this downturn,
. These two days are defined as follows:
Then,
will be defined as:
We examine the data with Equations (
4)–(
7) for each crisis period to determine whether such exception exists and
is defined. If so,
. Otherwise, as mentioned before,
.
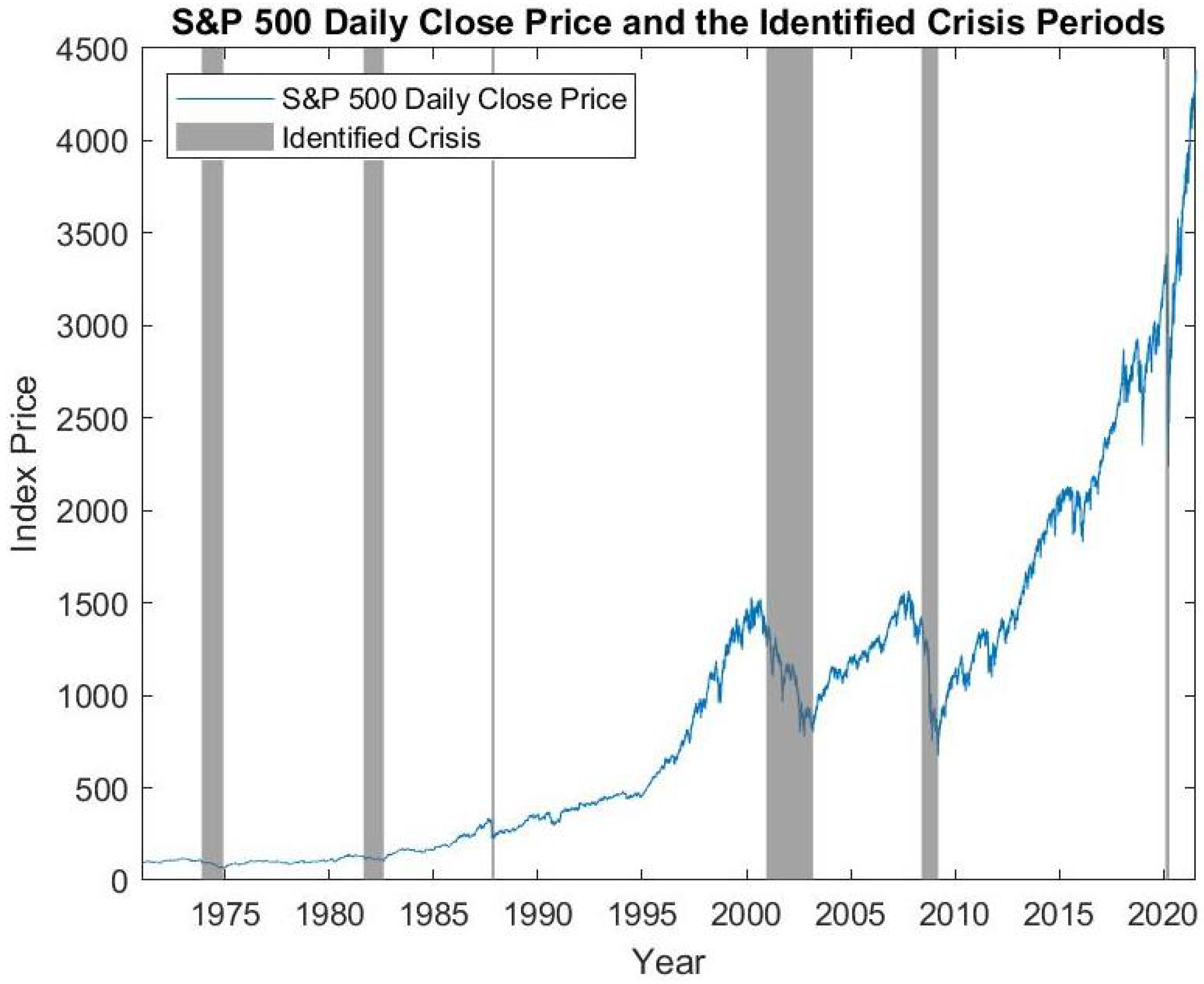
In our application, the examined index time series consists of the daily closing prices of the S&P 500 index from 1 January 1971 to 31 May 2021. The S&P 500 index and the determined crisis periods based on the described method are shown in
Figure 1. Specifically, six crisis periods are identified: 20 November 1973 to 6 December 1974 (1973 oil crisis), 24 August 1981 to 12 August 1982 (early 1980s recession), 15 October 1987 to 4 December 1987 (Black Monday), 12 December 2000 to 11 March 2003 (burst of the dot-com bubble), 21 May 2008 to9 March 2009 (global financial crisis) and 5 March 2020 to 23 March 2020 (COVID-19 crisis). The identified crisis periods match the crises recognized universally by economists and the public and are considered a reasonable representation of the true crisis periods.
We further transform the crisis days into a parameter for the determination of the crisis months, as many of the input factors we use to train our neural networks are published monthly. We define a month to be in crisis if at least half of the business days in this month are identified as crisis dates.
In the end, out of the 605 observed months, we identify 62 crisis months, which are: December 1973 to November 1974 (12 months), September 1981 to July 1982 (11 months), October 1987 to November 1987 (2 months), December 2000 to February 2003 (27 months), and June 2008 to February 2009 (9 months) and March 2020 (1 month). They represent 10.25% of the total observed months. Together with the remaining 543 non-crisis months, they constitute our targeted time series for the forecast.
3. The Economic and Financial Input Factors
Our aim is to build neural networks that use a set of input factors from different economic and financial categories to make one-month-ahead forecasts for the economic states. We achieve this by mapping the monthly data of the input factors to the economic states in the next month. Ideally, we obtain neural networks that can identify the hidden structure of the data as well as the underlying relationship between the factors and the economic states, which then provide reliable one-month-ahead forecasts when we include new data in the future.
Our original list, which contains 25 micro- and macroeconomic and financial factors, is an adapted version of the one used in [
15] covering the period from December 1970 to April 2021. Based on standard stationarity and correlation checks, we make a few adjustments to the data, e.g., using the relative change of a factor or differences between two factors instead of the original values. In the end, we develop the list comprised of 25 input factors shown in
Table 1. Last, but not least, to ensure efficient training, we take the
min-max standardized values of these series, which are scaled into the range between 0 and 1 (see [
23]).
5. Application of the Model Selection Procedure
We implement the described model selection process in this section and we test the results in
Section 6. A common split of the data set into a training, validation and test data set would not suit the nature of time series forecasting, for which one would naturally use all information available from the past to forecast one future period (see, e.g., [
30]). As it is our aim to present the best model with respect to all information available, rather than an outdated model, we train the models based on the whole data set (January 1971 until May 2021) for the input factor selection. Note that, with the limited number of data points (only 62 crisis months), a typical training/validation split would not be feasible. With the finally chosen model, we perform out-of-sample forecasts on a rolling basis in
Section 6. Using these forecasts, we ensure that the presented model provides good results out-of-sample. Therefore, this procedure is able to fulfill the purpose of the validation and testing. Each of the neural networks is trained for 500 epochs, where we use batch sizes of 32 samples. This means that we only take 32 randomly chosen time points into consideration at once when calculating the gradient of the loss function and subsequently the updates of the weights and biases. Repeating this procedure, while excluding the time points which were already used, one epoch is over when every time point has been considered. In the next epoch, we start the same process as before, beginning again with 32 random samples from the whole time series.
We apply the whole model selection and testing approach to two examples. In the first example, we start with an empty model, so we have
initially. We denote this model as
Model 1. In this example, we use the variable list from
Table 1 except for the term spread of the 5-year government bonds versus the federal funds rate, as this factor is highly correlated with the term spread of the 10-year government bonds versus the federal funds rate. Including highly correlated input variable in the process creates the risk that one of the factors gets a very good ranking and one of the factors gets a very bad ranking. If this happens for some seeds, but for other seeds in reverse order, there is the possibility that none of the factors is chosen as a final input factor though both factors individually would be very good. For completeness, we mention that this is not a problem in our case. As we see later, the term spread of the 10-year government bonds versus the federal funds rate is not represented in the final model. In the second example, we use the input factors determined by [
15] as a starting set
S. In this example, denoted as
Model 2, we do not exclude the term spread of the 5-year government bonds versus the federal funds rate as both term spreads are among the factors proposed by [
15]. The authors of [
15] argue that including both factors captures the concavity of the term structure rather than the steepness. However, adding the numerically calculated convexity of the term structure as an input factor could not improve the model in our case.
The order of the input factors with respect to their total rankings is determined based on model build-ups with 10 seeds in each of the two models. This can be seen in
Table 2 for Model 1 and in
Table 3 for Model 2. The associated gaps are also listed in the corresponding tables. As expected, the largest gaps appear at the top of the tables. This means that the corresponding factors are consistently on top of the list across the several seeds. In
Table 2, we can observe that the volatility is chosen as the most important factor by the models from almost all seeds with an average rank of 1.1. However, the high numbers above 20 for the last input factors show that these input factors were consistently regarded as less important. In total, the large variety of the total rankings shows that the random variable selection process exhibits good stability. Based on our criterion to choose the largest gap provided that at least six factors are included in the model, we choose
, i.e., the last variable which is included in the final model is the change in the federal government debt (GFDEBTN Change). Thus, our final model consists of nine input factors. Performing a principal component analysis, we discover that the first nine principal components explain 89.7% of the total variance in the data set. This gives us an indication that choosing nine variables enables us to capture the main characteristics of the data set well. The chosen input factors reflect various aspects of the financial market and the economy. The volatility (Volatility), the exchange rate (EURODOLLAR) and the federal funds rate (FEDFUNDS) capture different areas of the financial market, namely the stock market, international influences and the central bank policy. The product manufacturing index (PMI) reflects the current situation of companies, while the consumer sentiment index (UMSCENT), the personal savings rate (PSAVERT) and the housing starts (HOUST) incorporate the situation of the households. The unemployment rate (UNRATE) can be interpreted as a factor, in which information on consumers and companies is included. Finally, the change in the government debt (GFDEBTN Change) reflects governmental action. For Model 2, we observe that the first two gaps are given by 2.12 and 1.28 (see
Table 3). While the largest gap occurs after the first variable, we decide to cut the factors in this model after the second variable which is added (UMSCENT) for two reasons: first, such a large gap does not occur later anymore, second, the model has eight input factors in total, which makes it comparable to the model selected from
Table 2, which has nine input factors. Later, we use Model 2 primarily as a benchmark for Model 1. This means, we add two input factors in Model 2—the unemployment rate (UNRATE) and the consumer sentiment index (UMSCENT). While the model from [
15] consists largely of financial market indicators, these two additional factors add information on consumer sentiment (UMSCENT) and the unemployment rate which includes information on consumers and companies. In the following, we assess the quality of the out-of-sample predictions for these models. Model 1 represents our suggested input factor selection process. Model 2 serves as a benchmark as it represents a model which is largely chosen by another input factor selection process and is only extended by our approach.
6. Walk-Forward Forecasting and Testing
Walk-forward forecasting and testing examines the model on a rolling-forward basis (see, e.g., [
30]). This method utilizes the historical data up to the observed time point to fit the neural network at this time and tests the network’s forecasting performance (classification accuracy) comparing the forecasting result for the next time point with the corresponding crisis classification as determined in
Section 2. When the observation of the next time point becomes available, the same process is repeated with the same set of input factors and a data set containing one extra observation. As our point of observation moves forward in time, we continue to acquire more and more historical data to fit our most up-to-date neural networks, as well as more testing results from the new single tests. In the end, we investigate the testing results over time to analyze the performance of a series of neural networks, which reinforces the check on the suitability and effectiveness of the neural network series’ prescribed architecture and specifications.
Compared to fixed training/test splits, walk-forward testing suits the nature of a time series prediction better, but it requires us to train the neural network at each time point. Of course, the period for the walk-forward forecasting and testing should be set long enough to cover different market situations, such as calm periods and crises. We choose January 2000 as our starting point for the walk-forward forecasting and testing, meaning that the first model is trained with the data up to December 1999 (denoted by ) and with the data available at the end of December; the first forecast which we create is the one for January 2000. This division ensures that we have enough representations of both classes for training and for testing the predictions, as it grants 25 crisis months for the first model estimation and allows, in total, 37 crisis months for the subsequent testing up to the end of the final tests. Then, we obtain 257 successively estimated neural networks, each trained at time , and tested with the next available data at time , respectively. This means that each forecast is an out-of-sample prediction.
It is the core principle of walk-forward testing that, after each month, the model is adjusted to incorporate the newest information. On the other hand, the new information from adding only one month is very little compared to the rest of the information, as the older time points stay the same. Therefore, we should expect only a small change in the model from one month to another, while the change over a longer period can be substantial. To incorporate the characteristics of this data structure, we propose a modified walk-forward testing method that incorporates multiple global estimations as well as sequential estimations. We conduct global estimations once every 48 months and sequential estimations monthly between the global estimations. At each global estimation, we train the model for 750 epochs, where we use a batch size of 32 time points. At each sequential estimation, we train the model for 500 epochs. During the global estimations, the neural network is trained with neutral starting values for the parameters. Then, for the sequential estimations, we take the parameters of the previous model as starting values and we train the neural network based on the new input data set with the newest month added. After each globally-estimated neural network is rebuilt and retrained, sequential estimations follow until the next global estimation. The sequential estimations take advantage of the previous results and the fact that the input data set does not change much each month, whereas the global estimations prevent the model from being stuck in a local minimum, which might become more unfavorable as the data set grows.
Again, we use an ensembling method: all trainings and predictions are performed for 10 different seeds. As an output, we receive, for each neural network, numbers between 0 and 1, which can be interpreted as probabilities for a crisis. We define that an ensemble predicts a crisis if the average probability to be in the crisis state across all seeds is at least 50%. The results of the predictions are listed in
Table 4. We observe that Model 1 outperforms Model 2 with respect to all aspects. In particular, we see that Model 1 is good at predicting crisis states accurately, as only 3 of the 37 crisis months are missed. For an early warning system, the ability to predict times of crises is crucial. This is an aspect in which Model 1 very significantly outperforms Model 2, which detects only 56.8% of the crisis months. Model 1 succeeds here by recognizing 91.9% of the crisis months. On the other hand, the classification of non-crisis states, for which our model succeeds in 90.5% of the cases, does not suffer from its good crisis prediction properties. The strength of our model selection approach becomes even clearer when we compare the results to a walk-forward forecasting and testing approach for a model which uses the nine factors with the worst ranking from
Table 2. Such a model only predicts 19 of the 37 crisis months correctly (51.4%) and achieves a total accuracy of 72.8%.
Figure 3 and
Figure 4 show the average predicted probability over all seeds for each point in time. With the method from
Section 2, three crises have been identified after year 2000, which took place from December 2000 to February 2003, from June 2008 to February 2009 and in March 2020. We see that both models capture all of these crises. Moreover, we see that the models also detect the end of the crises in a timely manner. In addition, we can observe that both models also recognize smaller stock market setbacks which are not part of these crisis periods and that, during these setbacks, the probability for a crisis is not as high as during a major crisis. This is a remarkable feature as the models were neither directly selected nor directly trained with respect to setbacks outside major crisis periods. A possible reason for this behavior might be that patterns in financial markets are similar in times of setbacks and in crisis periods, but they are observed to a smaller extent in smaller setbacks. Comparing
Figure 3 and
Figure 4, we see that both models exhibit similar behavior, but Model 1 separates crisis times and non-crisis times in a more distinctive way.
In total, the walk-forward testing shows that our model-building process has successfully built neural networks that continuously make reliable out-of-sample forecasts of financial crises. It also demonstrates an improvement of performance compared to a traditional model selection method, represented by Model 2 in our example.
7. Conclusions
In this article, we explore the potential of neural networks for forecasting financial crises with micro-, macroeconomic and financial factors. In order to minimize the input dimension, we develop an input variable reduction method based on a successive selection procedure combined with a largest gap analysis.
We demonstrate the model-building process with the forecast of crises determined from the S&P 500 index. The walk-forward testing shows that our approach is able to create models which make reliable out-of-sample, one-month-ahead forecasts. We also observe that our model outperforms a model which consists largely of input factors taken from [
15]. Our procedure overcomes different shortcomings which are typically attributed to stock market early warning systems based on neural networks. Among these are the problems of over-fitting and unstable models, as described in [
2,
3]. Although, we do not need to select input factors based on expert knowledge, such as in [
16], their model and ours have in common that various segments of the financial markets are considered as an input to forecast a crisis. Furthermore, we present an alternative to a selection based on sensitivities (see [
17,
18]). Our approach suits financial input data sets that include variables with only minor changes from one period to another. but with larger effects over an economic cycle. The common strength of the input sensitivity approach and our approach, however, is that both procedures utilize a gap method to prune a whole set of variables at once.
With the research area on the applications of neural networks being so dynamic, several questions for further research emerge. Possible extensions of our input factor reduction approach to comprise more involved structures, such as recurrent neural networks, might be interesting. Furthermore, while we focus on forecasting financial crises, the question arises how our model can be used for specific tasks, such as risk and portfolio management and the construction of quantitative investment strategies.