Numerical Modeling and Experimental Investigation of Effective Elastic Properties of the 3D Printed Gyroid Infill
Abstract
:1. Introduction
2. Modeling and Finite Element Analysis
2.1. Gyroid Infill Geometry
2.2. Shell Element Discretization
2.3. Solid Element Discretization
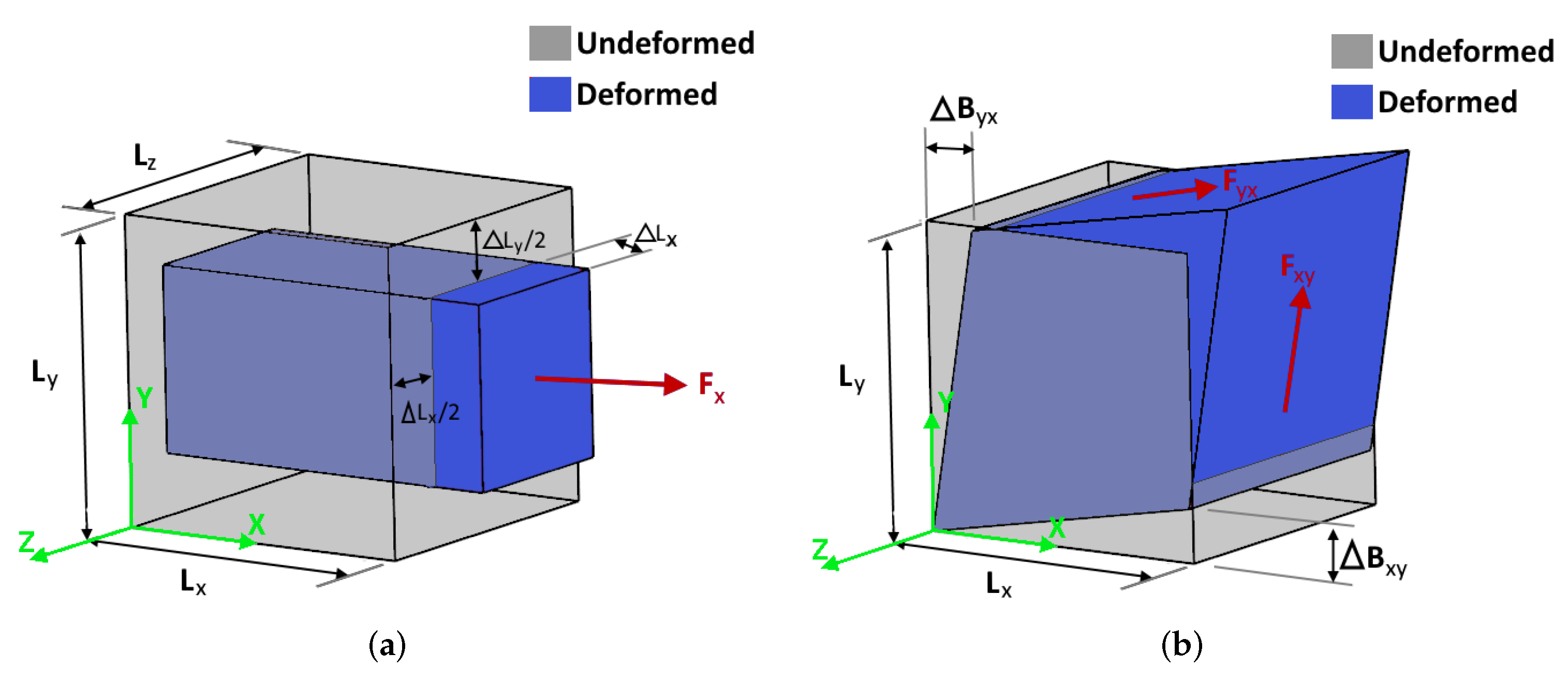
2.4. Periodic Boundary Conditions and Elastic Property Calculations
3. Compression Experiments
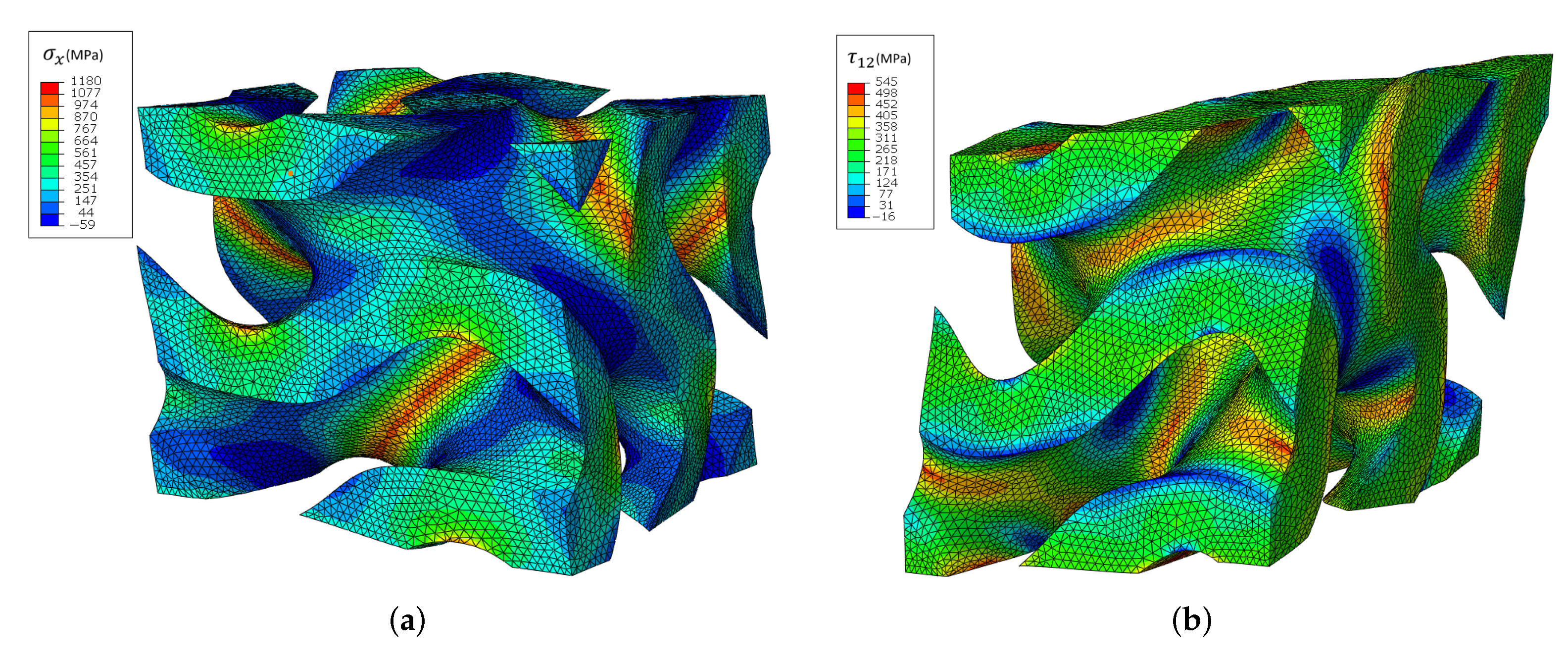
4. Results and Discussion
4.1. Mesh Convergence
4.2. Shell vs. Solid Models
4.3. Compression Results
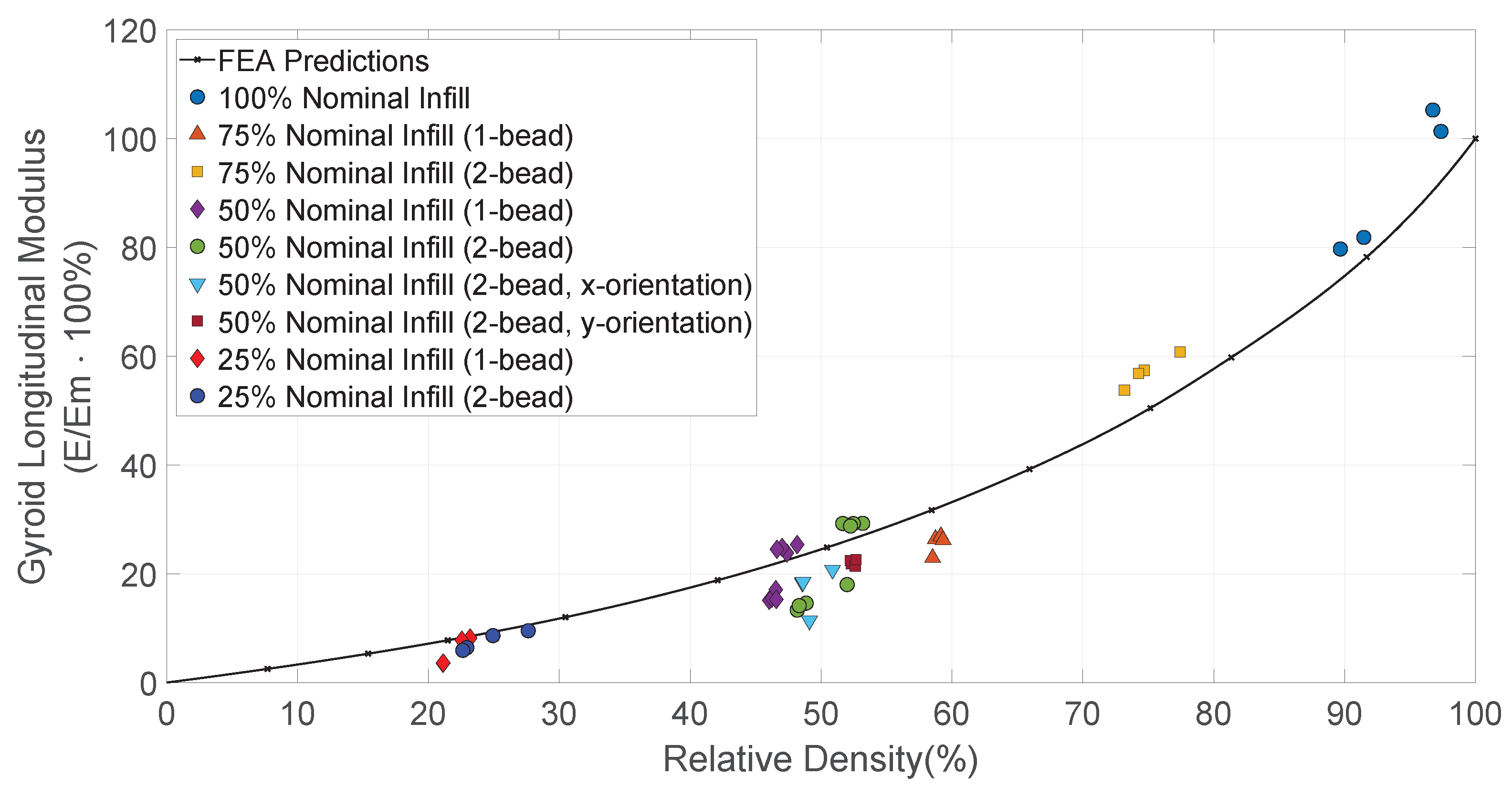
4.3.1. Longitudinal Modulus
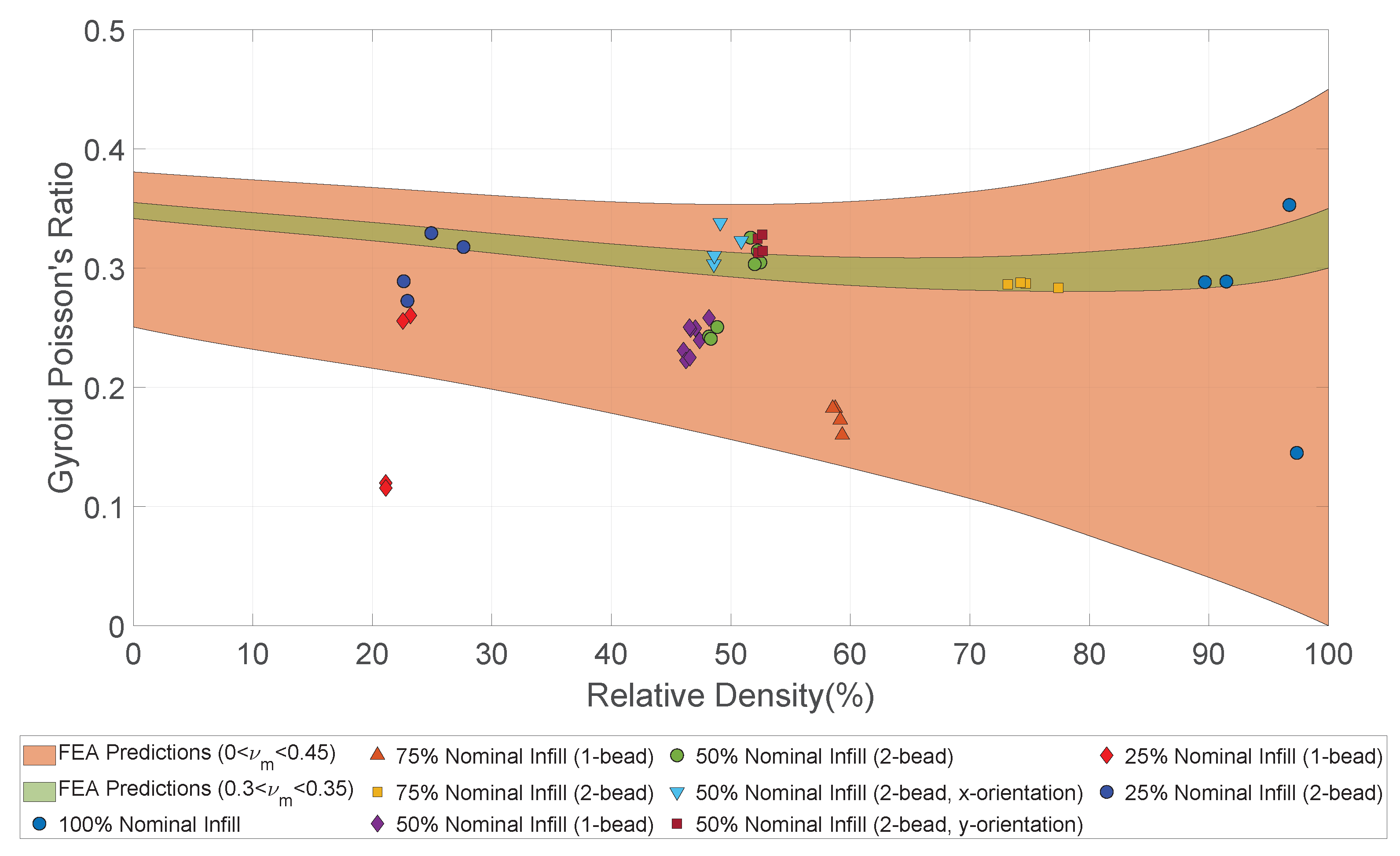
4.3.2. Poisson’s Ratio
4.4. Semi-Empirical Models
4.4.1. Longitudinal Modulus
4.4.2. Shear Modulus
4.4.3. Poisson’s Ratio
4.5. Degree of Anisotropy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | Additive Manufacturing |
| FEA | Finite Element Analysis |
| RVE | Representative Volume Element |
| DIC | Digital Image Correlation |
References
- Jiang, J.; Fu, Y.F. A short survey of sustainable material extrusion additive manufacturing. Aust. J. Mech. Eng. 2020, 1–10. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, Y. Path Planning Strategies to Optimize Accuracy, Quality, Build Time and Material Use in Additive Manufacturing: A Review. Micromachines 2020, 11, 633. [Google Scholar] [CrossRef]
- Lee, H.; Lim, C.H.J.; Low, M.J.; Tham, N.; Murukeshan, V.M.; Kim, Y.J. Lasers in additive manufacturing: A review. Int. J. Precis. Eng. Manuf. Green Technol. 2017, 4, 307–322. [Google Scholar] [CrossRef]
- Fu, Y.F.; Rolfe, B.; Chiu, L.N.; Wang, Y.; Huang, X.; Ghabraie, K. Parametric studies and manufacturability experiments on smooth self-supporting topologies. Virtual Phys. Prototyp. 2020, 15, 22–34. [Google Scholar] [CrossRef]
- Bikas, H.; Stavropoulos, P.; Chryssolouris, G. Additive manufacturing methods and modelling approaches: A critical review. Int. J. Adv. Manuf. Technol. 2016, 83, 389–405. [Google Scholar] [CrossRef] [Green Version]
- Khorasani, M.; Ghasemi, A.; Rolfe, B.; Gibson, I. Additive manufacturing a powerful tool for the aerospace industry. Rapid Prototyp. J. 2021, 28, 87–100. [Google Scholar] [CrossRef]
- Tan, C.; Zou, J.; Li, S.; Jamshidi, P.; Abena, A.; Forsey, A.; Moat, R.J.; Essa, K.; Wang, M.; Zhou, K.; et al. Additive manufacturing of bio-inspired multi-scale hierarchically strengthened lattice structures. Int. J. Mach. Tools Manuf. 2021, 167, 103764. [Google Scholar] [CrossRef]
- Kumar, M.; Sharma, V. Additive manufacturing techniques for the fabrication of tissue engineering scaffolds: A review. Rapid Prototyp. J. 2021, 27, 1230–1272. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.W.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer: Cham, Switzerland, 2021; Volume 17. [Google Scholar]
- Bhandari, S. Feasibility of Using 3D Printed Molds for Thermoforming Thermoplastic Composites. Master’s Thesis, University of Maine, Orono, ME, USA, 2016. [Google Scholar]
- Bhandari, S.; Lopez-Anido, R. Finite element modeling of 3D-printed part with cellular internal structure using homogenized properties. Prog. Addit. Manuf. 2019, 4, 143–154. [Google Scholar] [CrossRef]
- Bhandari, S.; Lopez-Anido, R. Finite element analysis of thermoplastic polymer extrusion 3D printed material for mechanical property prediction. Addit. Manuf. 2018, 22, 187–196. [Google Scholar] [CrossRef]
- 3D Metal Forge. Gyroid Infills for 3D Printing. Available online: https://3dmetalforge.com/en/gyroid-infills-for-3d-printing-2/ (accessed on 6 February 2020).
- Goldschmidt, B. The Best Cura Infill Pattern (For Your Needs). Available online: https://all3dp.com/2/cura-infill-patterns-all-you-need-to-know/ (accessed on 6 February 2020).
- Matt’s Hub. Introducing Gyroid Infill. Available online: https://mattshub.com/blog/2018/03/15/gyroid-infill (accessed on 6 February 2020).
- Li, D.; Dai, N.; Jiang, X.; Chen, X. Interior structural optimization based on the density-variable shape modeling of 3D printed objects. Int. J. Adv. Manuf. Technol. 2016, 83, 1627–1635. [Google Scholar] [CrossRef]
- Sundararajan, V.G. Topology Optimization for Additive Manufacturing of Customized Meso-Structures Using Homogenization and Parametric Smoothing Functions. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2010. [Google Scholar]
- Xie, Y.; Chen, X. Support-free interior carving for 3D printing. Vis. Inform. 2017, 1, 9–15. [Google Scholar] [CrossRef]
- Lu, L.; Chen, B.; Sharf, A.; Zhao, H.; Wei, Y.; Fan, Q.; Chen, X.; Savoye, Y.; Tu, C.; Cohen-Or, D. Build-to-last: Strength to Weight 3D Printed Objects. ACM Trans. Graph. 2014, 33, 1–10. [Google Scholar] [CrossRef]
- Clausen, A.; Aage, N.; Sigmund, O. Topology optimization of coated structures and material interface problems. Comput. Methods Appl. Mech. Eng. 2015, 290, 524–541. [Google Scholar] [CrossRef] [Green Version]
- Gaynor, A.T.; Meisel, N.A.; Williams, C.B.; Guest, J.K. Multiple-Material Topology Optimization of Compliant Mechanisms Created Via PolyJet Three-Dimensional Printing. J. Manuf. Sci. Eng. 2014, 136, 061015. [Google Scholar] [CrossRef] [Green Version]
- Riss, F.; Schilp, J.; Reinhart, G. Load-dependent optimization of honeycombs for sandwich components-new possibilities by using additive layer manufacturing. Phys. Procedia 2014, 56, 327–335. [Google Scholar] [CrossRef]
- Chu, J.; Engelbrecht, S.; Graf, G.; Rosen, D.W. A comparison of synthesis methods for cellular structures with application to additive manufacturing. Rapid Prototyp. J. 2010, 16, 275–283. [Google Scholar] [CrossRef] [Green Version]
- Schumacher, C.; Bickel, B.; Rys, J.; Marschner, S.; Daraio, C.; Gross, M. Microstructures to control elasticity in 3D printing. ACM Trans. Graph. 2015, 34, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wang, C.C.; Zhang, X.; Westermann, R. Self-supporting rhombic infill structures for additive manufacturing. Comput. Aided Des. 2016, 80, 32–42. [Google Scholar] [CrossRef]
- Brackett, D.; Ashcroft, I.; Hague, R. Topology optimization for additive manufacturing. Solid Free. Fabr. Symp. 2011. [Google Scholar] [CrossRef]
- McCaw, J.C.; Cuan-Urquizo, E. Mechanical characterization of 3D printed, non-planar lattice structures under quasi-static cyclic loading. Rapid Prototyp. J. 2020, 26, 707–717. [Google Scholar] [CrossRef]
- Tsouknidas, A.; Pantazopoulos, M.; Katsoulis, I.; Fasnakis, D.; Maropoulos, S.; Michailidis, N. Impact absorption capacity of 3D-printed components fabricated by fused deposition modelling. Mater. Des. 2016, 102, 41–44. [Google Scholar] [CrossRef]
- Lužanin, O.; Movrin, D.; Plan, M. Effect of Layer Thickness, Deposition Angle, and Infill on Maximum Flexural Force in Fdm-Built Specimens. J. Technol. Plast. 2014, 39, 49–58. [Google Scholar]
- Baich, L.; Manogharan, G.; Marie, H. Study of infill print design on production cost-time of 3D printed ABS parts. Int. J. Rapid Manuf. 2015, 5, 308–319. [Google Scholar] [CrossRef]
- Wang, W.; Wang, T.Y.; Yang, Z.; Liu, L.; Tong, X.; Tong, W.; Deng, J.; Chen, F.; Liu, X. Cost-effective printing of 3D objects with skin-frame structures. ACM Trans. Graph. 2013, 32, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Marschall, D.; Sindinger, S.L.; Rippl, H.; Bartosova, M.; Schagerl, M. Design, simulation, testing and application of laser-sintered conformal lattice structures on component level. Rapid Prototyp. J. 2021, 27, 43–57. [Google Scholar] [CrossRef]
- Shaikh, M.Q.; Graziosi, S.; Atre, S.V. Supportless printing of lattice structures by metal fused filament fabrication (MF3) of Ti-6Al-4V: Design and analysis. Rapid Prototyp. J. 2021, 27, 1408–1422. [Google Scholar] [CrossRef]
- Li, D.; Qin, R.; Chen, B.; Zhou, J. Analysis of mechanical properties of lattice structures with stochastic geometric defects in additive manufacturing. Mater. Sci. Eng. A 2021, 822, 141666. [Google Scholar] [CrossRef]
- Chan, Y.C.; Shintani, K.; Chen, W. Robust topology optimization of multi-material lattice structures under material and load uncertainties. Front. Mech. Eng. 2019, 14, 141–152. [Google Scholar] [CrossRef] [Green Version]
- Martínez, J.; Song, H.; Dumas, J.; Lefebvre, S. Orthotropic k-nearest foams for additive manufacturing. ACM Trans. Graph. 2017, 36, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Schoen, A.H. Infinite Periodic Minimal Surfaces without Self-Intersections; Technical Report; NASA: Washington, DC, USA, 1970. [Google Scholar]
- Zhang, B.; Mhapsekar, K.; Anand, S. Design of Variable-Density Structures for Additive Manufacturing Using Gyroid Lattices. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017; Volume 4. [Google Scholar]
- Sun, C.T.; Vaidya, R.S. Prediction of composite properties from a representative volume element. Compos. Sci. Technol. 1996, 56, 171–179. [Google Scholar] [CrossRef]
- Omairey, S.L.; Dunning, P.D.; Sriramula, S. Development of an ABAQUS plugin tool for periodic RVE homogenisation. Eng. Comput. 2019, 35, 567–577. [Google Scholar] [CrossRef] [Green Version]
- Theerakittayakorn, K.; Nanakorn, P. Periodic boundary conditions for unit cells of periodic cellular solids in the determination of effective properties using beam elements. In Proceedings of the 2013 World Congress on Advances in Structural Engineering and Mechanics (ASEM13), Jeju, Korea, 8–12 September 2013; pp. 3738–3748. [Google Scholar]
- Wu, W.; Owino, J.; Al-Ostaz, A.; Cai, L. Applying periodic boundary conditions in finite element analysis. In Proceedings of the SIMULIA Community Conference, Providence, Providence, RI, USA, 19–22 May 2014; pp. 707–719. [Google Scholar]
- Tyrus, J.; Gosz, M.; DeSantiago, E. A local finite element implementation for imposing periodic boundary conditions on composite micromechanical models. Int. J. Solids Struct. 2007, 44, 2972–2989. [Google Scholar] [CrossRef] [Green Version]
- ASTM D695-15; Standard Test Method for Compressive Properties of Rigid Plastics. American Society for Testing and Materials: West Conshohocken, PA, USA, 2015.
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Redenbach, C.; Shklyar, I.; Andrä, H. Laguerre tessellations for elastic stiffness simulations of closed foams with strongly varying cell sizes. Int. J. Eng. Sci. 2012, 50, 70–78. [Google Scholar] [CrossRef]
- Gibson, I.; Ashby, M.F. The mechanics of three-dimensional cellular materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 382, 43–59. [Google Scholar]
- El Ghezal, M.I.; Maalej, Y.; Doghri, I. Micromechanical models for porous and cellular materials in linear elasticity and viscoelasticity. Comput. Mater. Sci. 2013, 70, 51–70. [Google Scholar] [CrossRef]
- Gibson, L. Modelling the mechanical behavior of cellular materials. Mater. Sci. Eng. A 1989, 110, 1–36. [Google Scholar] [CrossRef]
- Gong, L.; Kyriakides, S.; Jang, W.Y. Compressive response of open-cell foams. Part I: Morphology and elastic properties. Int. J. Solids Struct. 2005, 42, 1355–1379. [Google Scholar] [CrossRef]
- Ahmadi, S.; Campoli, G.; Yavari, S.A.; Sajadi, B.; Wauthlé, R.; Schrooten, J.; Weinans, H.; Zadpoor, A. Mechanical behavior of regular open-cell porous biomaterials made of diamond lattice unit cells. J. Mech. Behav. Biomed. Mater. 2014, 34, 106–115. [Google Scholar] [CrossRef]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, USA, 1948. [Google Scholar]
- Chen, Z.; Xie, Y.M.; Wu, X.; Wang, Z.; Li, Q.; Zhou, S. On hybrid cellular materials based on triply periodic minimal surfaces with extreme mechanical properties. Mater. Des. 2019, 183, 108109. [Google Scholar] [CrossRef]








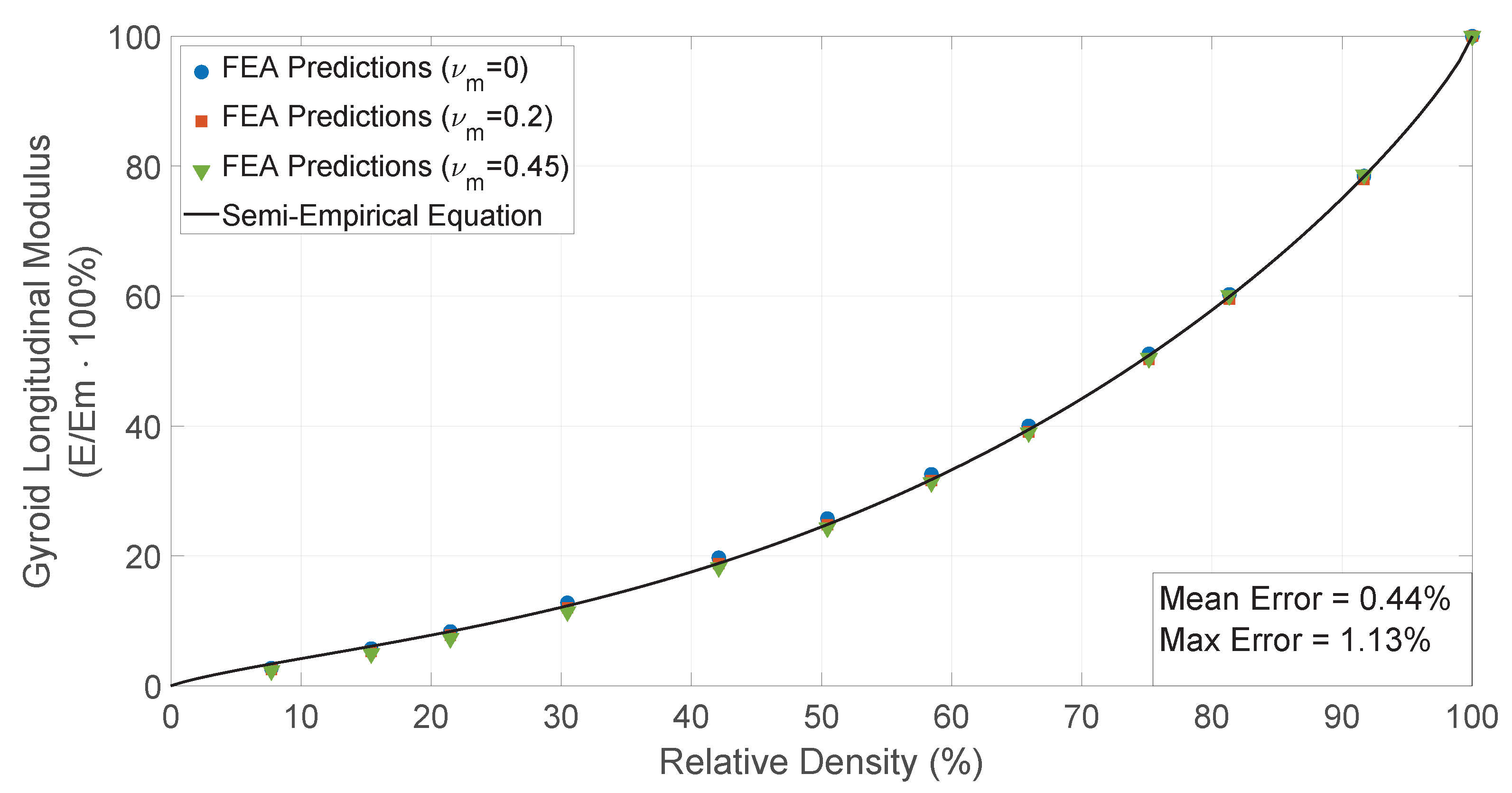

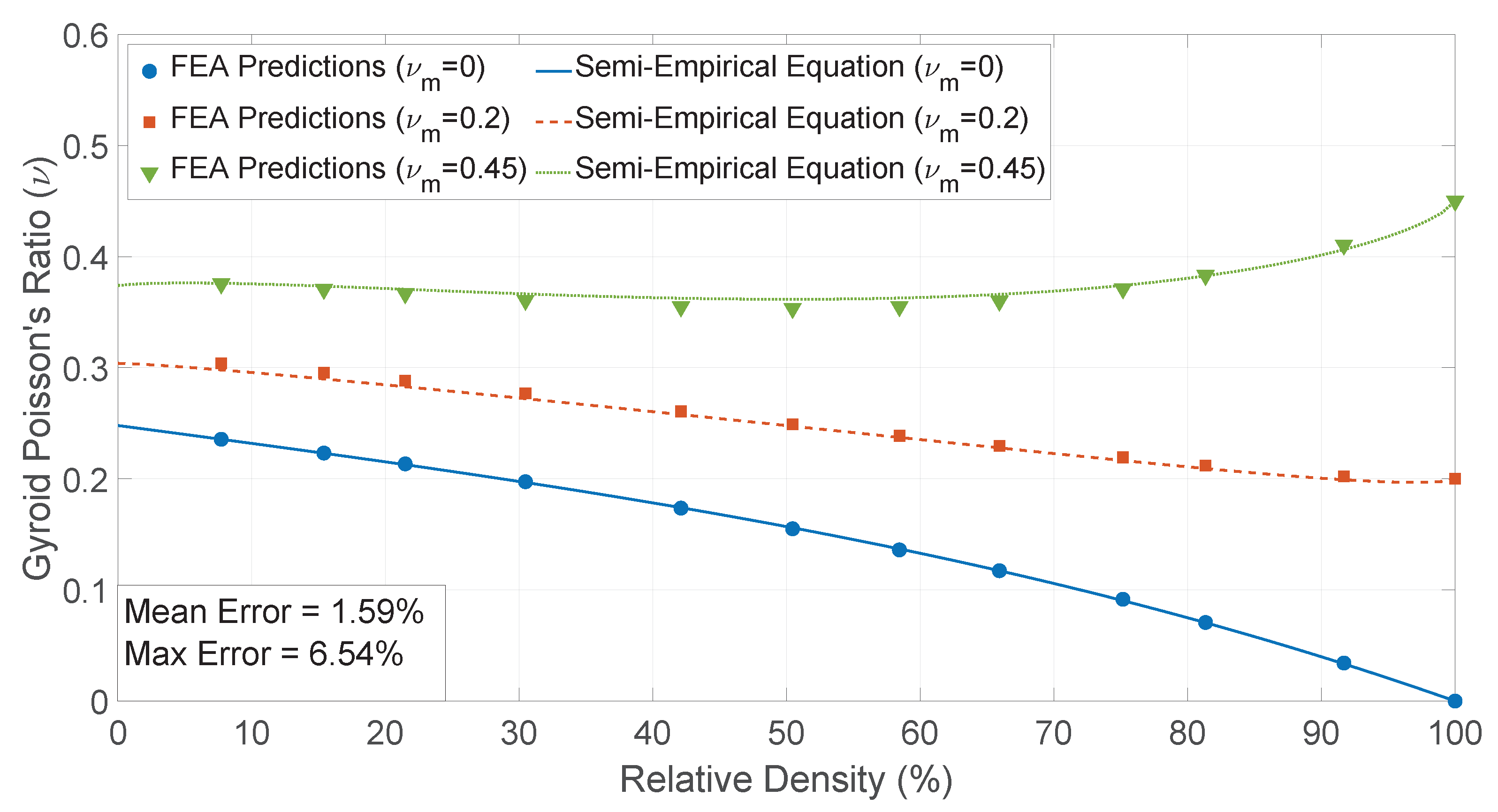
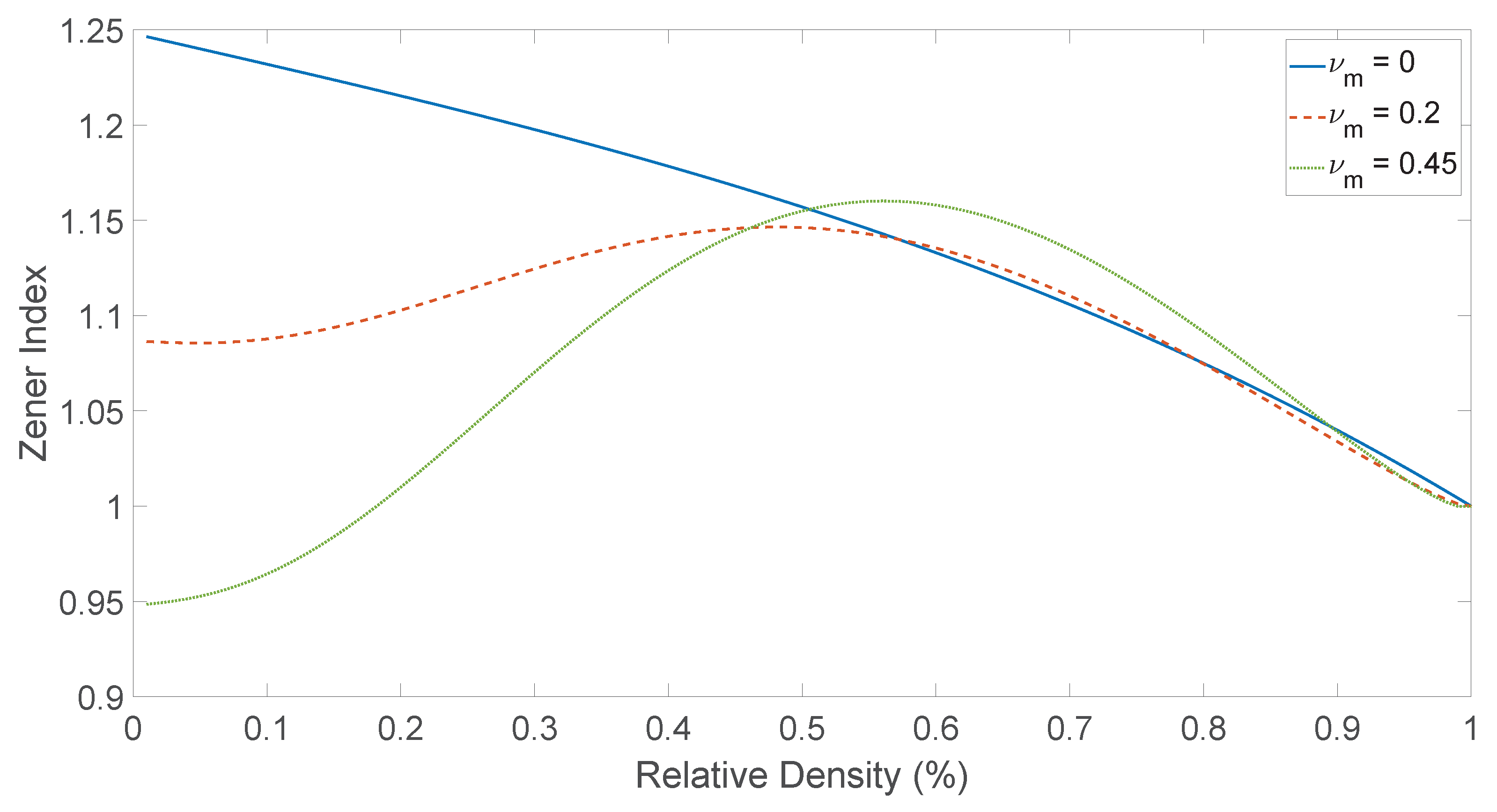
| Nominal Relative Density | Wall Thicknesses | Avg Relative Density (%) | Londitudinal Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| 100% | - | 94 | 2300 | 0.25 |
| 75% | Single-Bead | 59 | 639 | 0.18 |
| 75% | Double-Bead | 75 | 1420 | 0.28 |
| 50% | Single-Bead | 47 | 490 | 0.24 |
| 50% | Double-Bead | 51 | 520 | 0.30 |
| 25% | Single-Bead | 22 | 145 | 0.19 |
| 25% | Double-Bead | 25 | 191 | 0.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bean, P.; Lopez-Anido, R.A.; Vel, S. Numerical Modeling and Experimental Investigation of Effective Elastic Properties of the 3D Printed Gyroid Infill. Appl. Sci. 2022, 12, 2180. https://doi.org/10.3390/app12042180
Bean P, Lopez-Anido RA, Vel S. Numerical Modeling and Experimental Investigation of Effective Elastic Properties of the 3D Printed Gyroid Infill. Applied Sciences. 2022; 12(4):2180. https://doi.org/10.3390/app12042180
Chicago/Turabian StyleBean, Philip, Roberto A. Lopez-Anido, and Senthil Vel. 2022. "Numerical Modeling and Experimental Investigation of Effective Elastic Properties of the 3D Printed Gyroid Infill" Applied Sciences 12, no. 4: 2180. https://doi.org/10.3390/app12042180
APA StyleBean, P., Lopez-Anido, R. A., & Vel, S. (2022). Numerical Modeling and Experimental Investigation of Effective Elastic Properties of the 3D Printed Gyroid Infill. Applied Sciences, 12(4), 2180. https://doi.org/10.3390/app12042180







