Application of High-Order Compact Difference Schemes for Solving Partial Differential Equations with High-Order Derivatives
Abstract
1. Introduction
2. Compact Difference Schemes
- and and the 6th-order scheme is defined with the coefficients:
- with , the 8th-order scheme is obtained with the coefficients:
2.1. Truncation Error
- The 1st derivative approximation:
- The 3rd derivative approximation:
- The 5th derivative approximation:
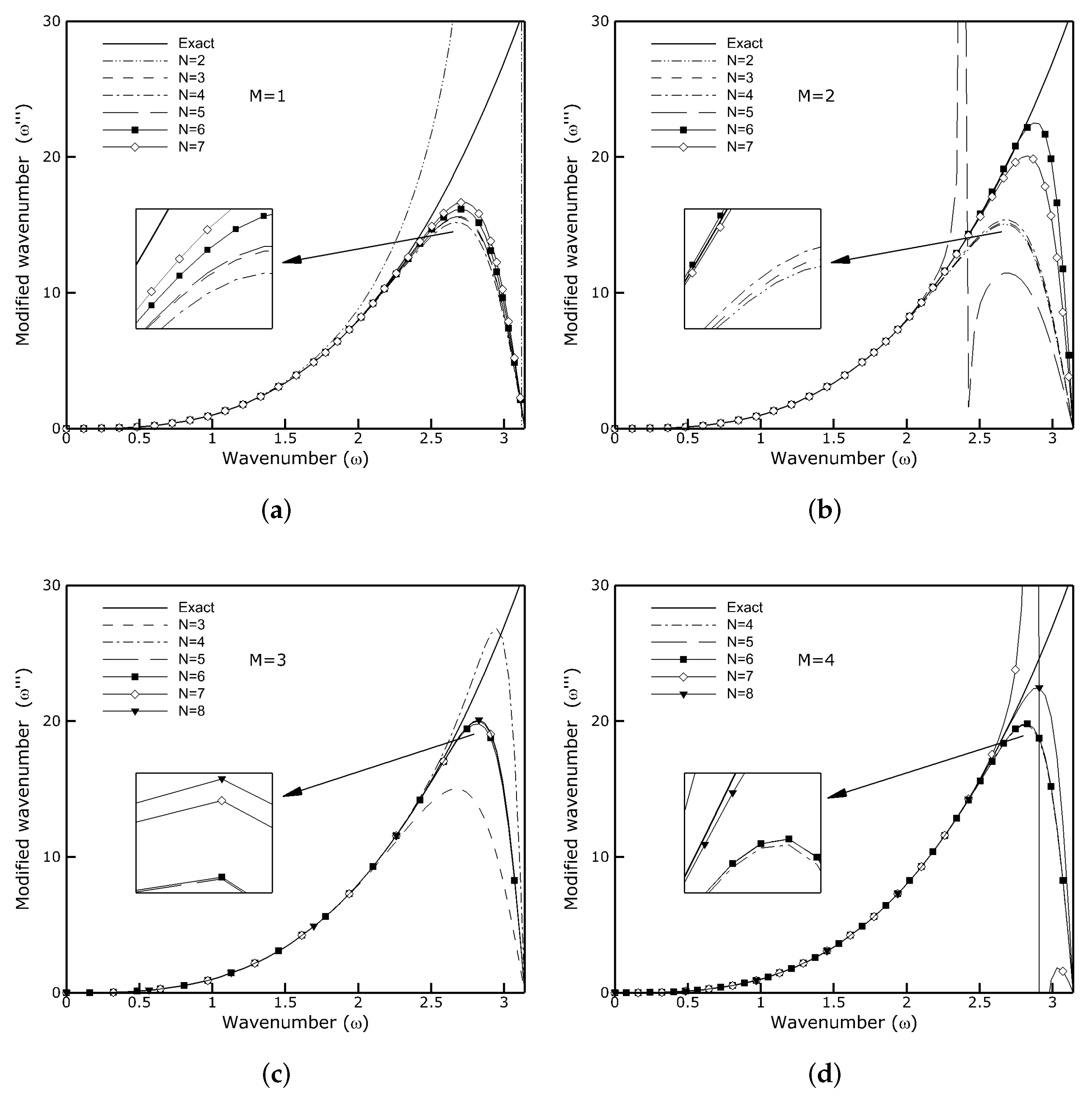
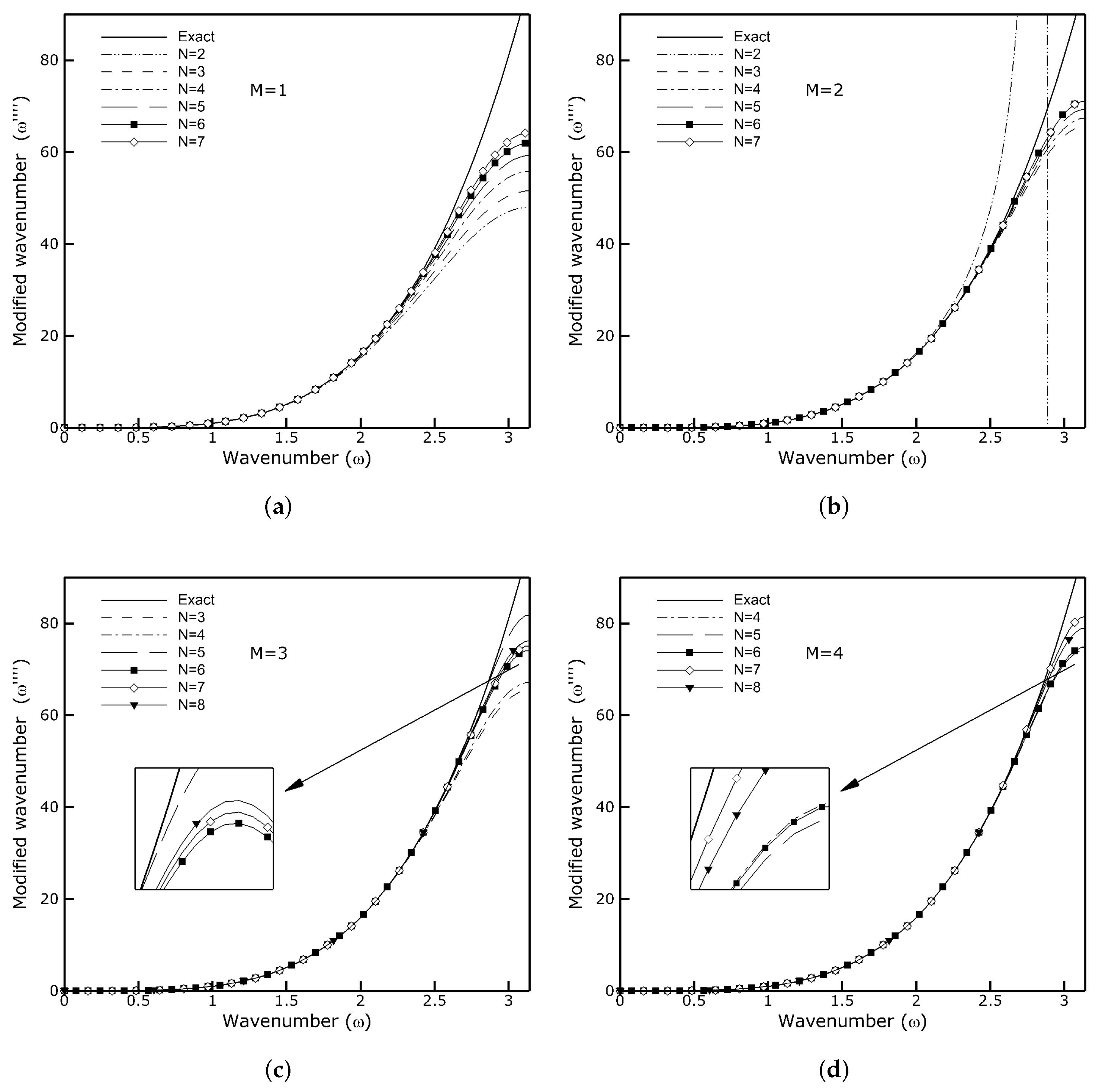
2.2. Fourier Analysis
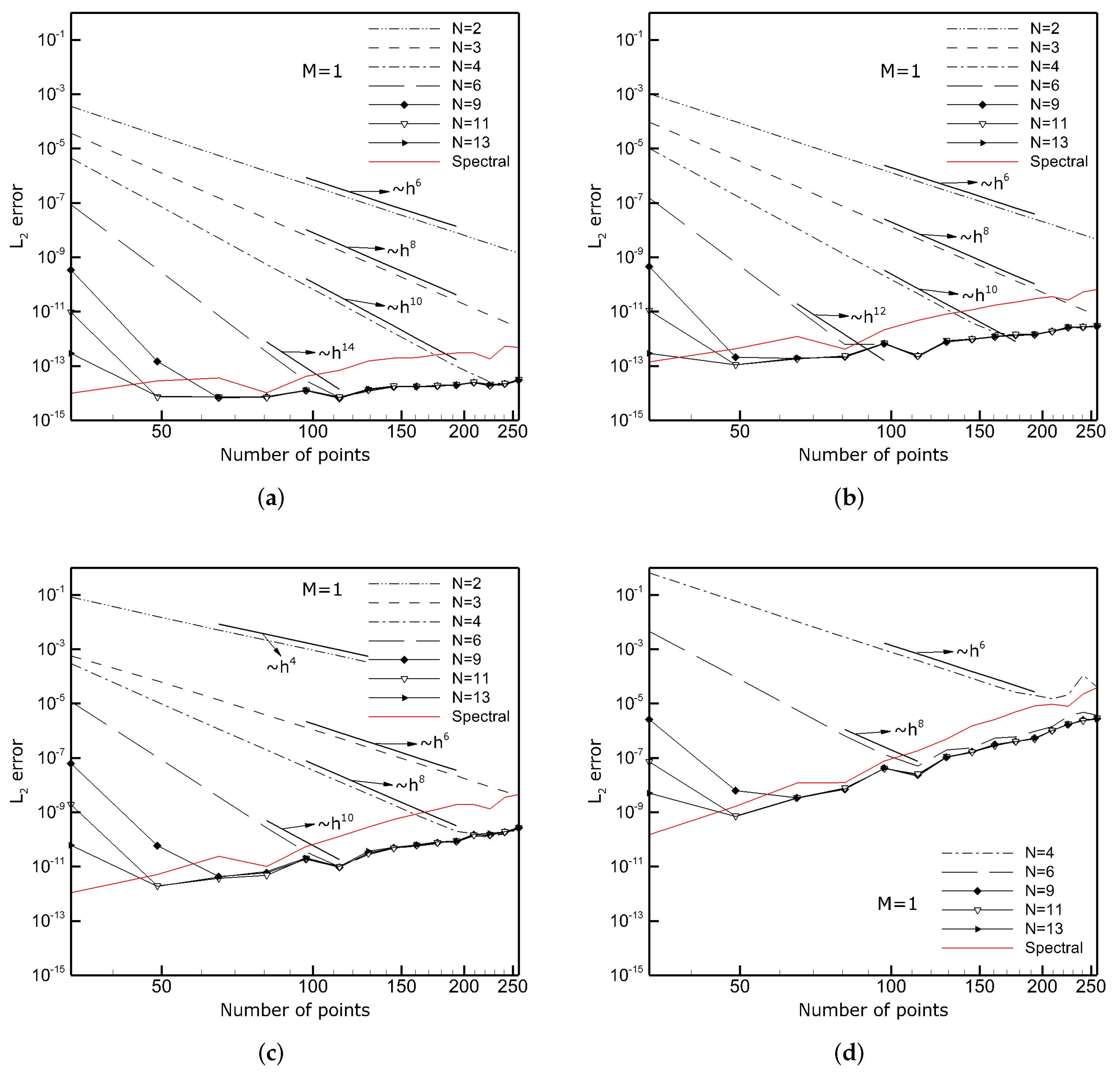
2.3. Test Computations
3. Results
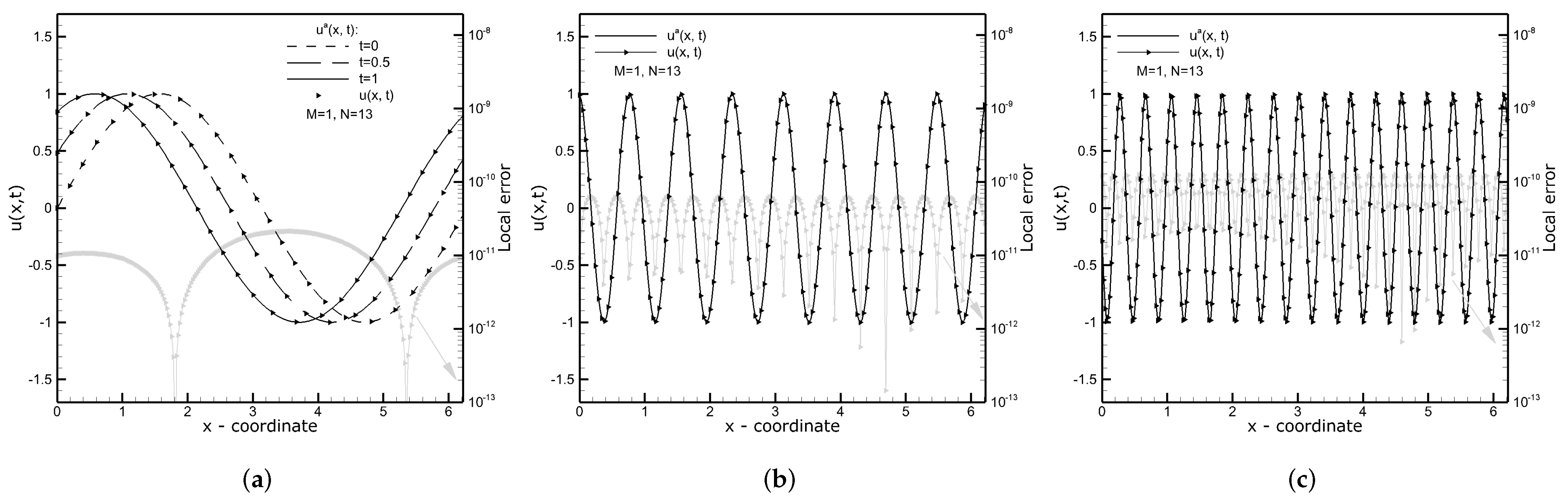
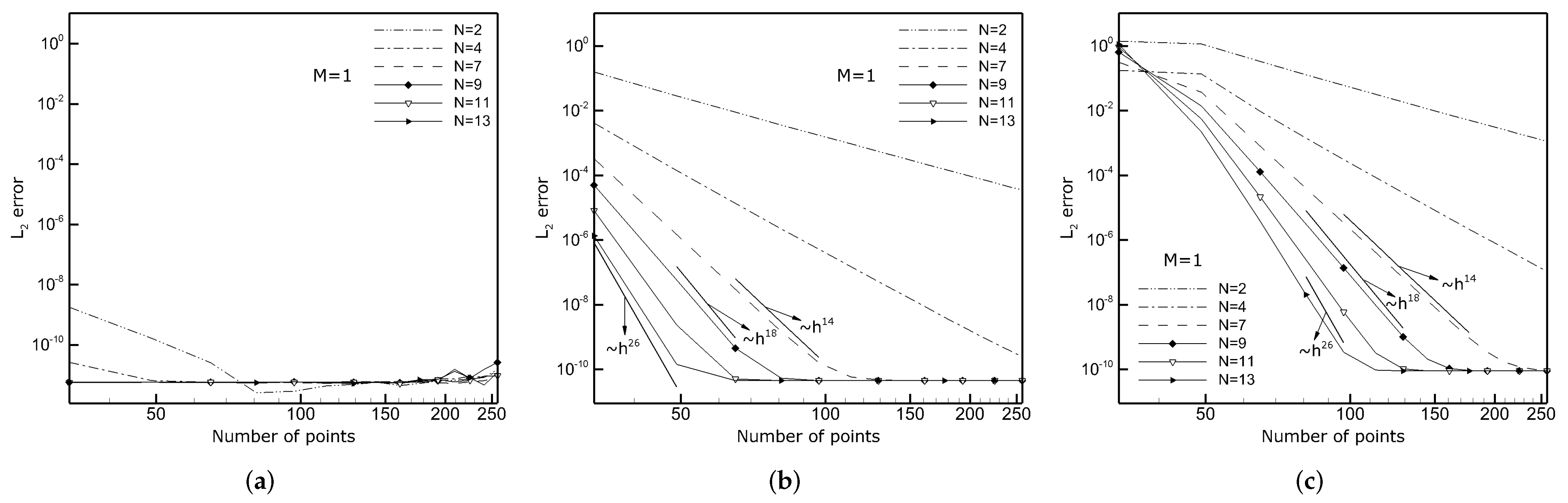
3.1. Third-Order Linear Dispersive Wave (LdW) Equation
3.2. Third-Order Korteweg–de Vries (KdV) Equation
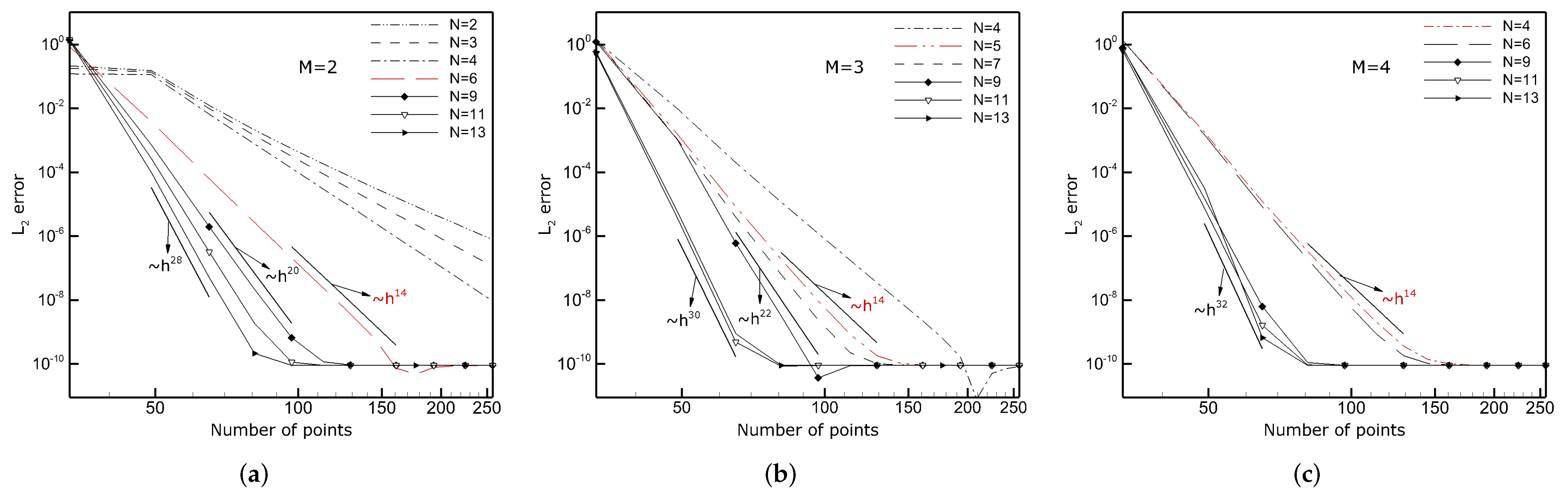
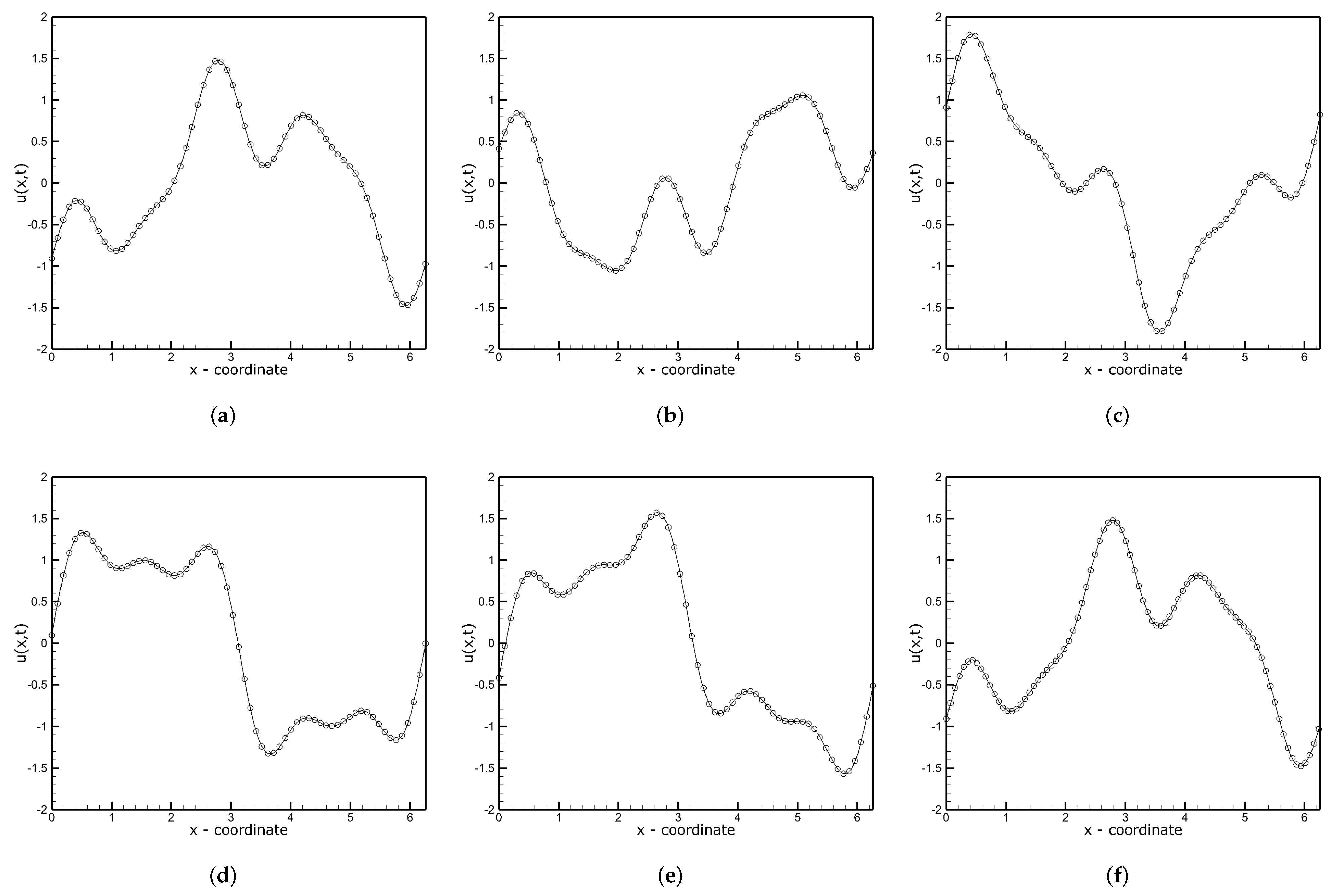
3.3. Fourth-Order Kuramoto–Sivashinsky (KS) Equation
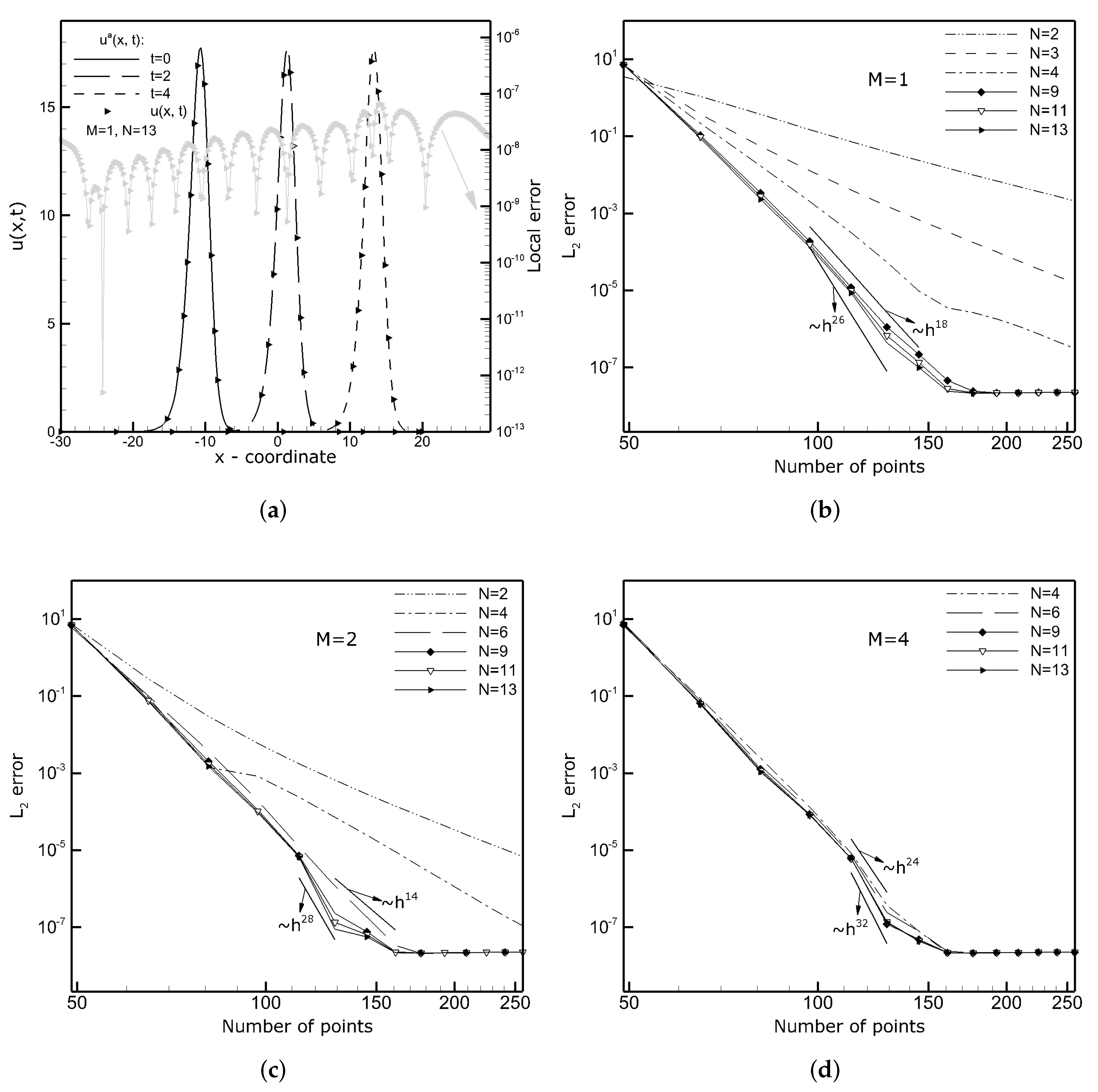
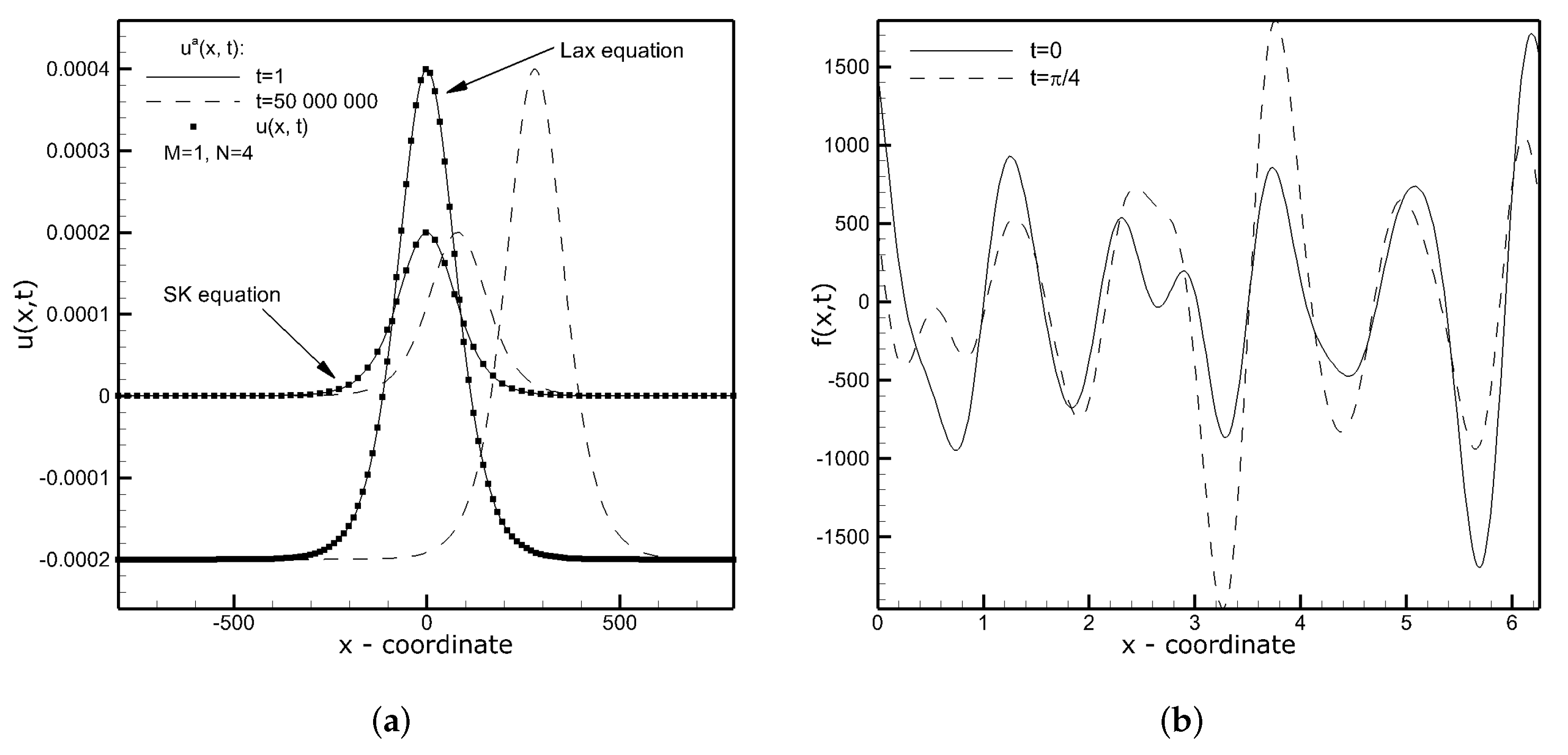
3.4. Fifth-Order Korteweg–de Vries (fKdV) Equations
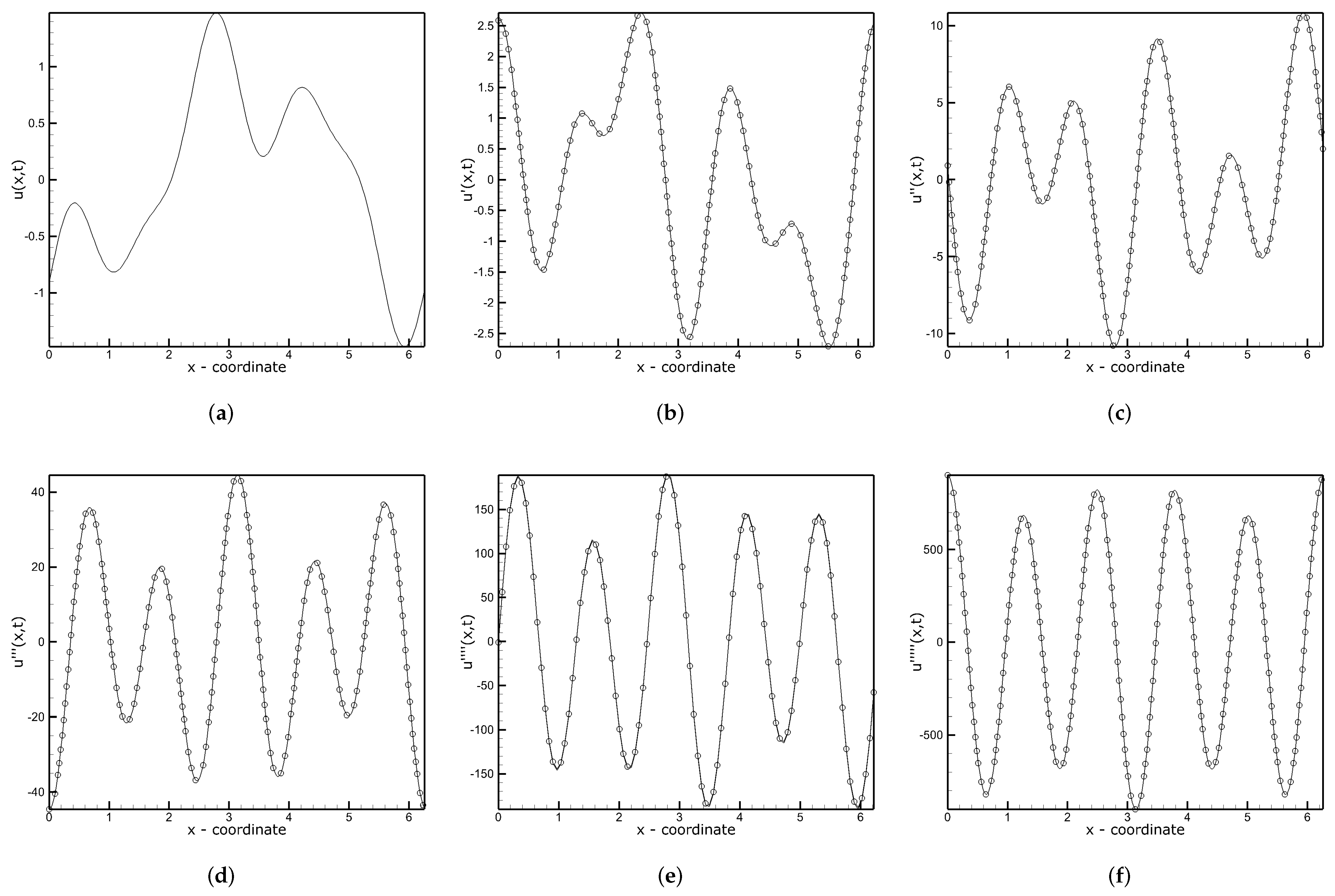
3.5. Fifth-Order Korteweg–de Vries (fKdV) Equation with a Manufactured Solution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kajishima, T.; Taira, K. Computational Fluid Dynamics: Incompressible Turbulent Flows; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Boutayeb, A.; Chetouani, A. A mini-review of numerical methods for high-order problems. Int. J. Comput. Math. 2007, 84, 563–579. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Gamet, L.; Ducros, F.; Nicoud, F.; Poinsot, T. Compact finite difference schemes on non-uniform meshes. Application to direct numerical simulations of compressible flows. Int. J. Numer. Methods Fluids 1999, 29, 159–191. [Google Scholar] [CrossRef]
- Boersma, B.J. A staggered compact finite difference formulation for the compressible Navier–Stokes equations. J. Comput. Phys. 2005, 208, 675–690. [Google Scholar] [CrossRef]
- Tyliszczak, A. A high-order compact difference algorithm for half-staggered grids for laminar and turbulent incompressible flows. J. Comput. Phys. 2014, 276, 438–467. [Google Scholar] [CrossRef]
- San, O.; Staples, A.E. High-order methods for decaying two-dimensional homogeneous isotropic turbulence. Comput. Fluids 2012, 63, 105–127. [Google Scholar] [CrossRef]
- San, O. A dynamic eddy-viscosity closure model for large eddy simulations of two-dimensional decaying turbulence. Int. J. Comput. Fluid Dyn. 2014, 28, 363–382. [Google Scholar] [CrossRef]
- Ekaterinaris, J.A. Implicit, High-Resolution, Compact Schemes for Gas Dynamics and Aeroacoustics. J. Comput. Phys. 1999, 156, 272–299. [Google Scholar] [CrossRef]
- Lee, D.-J.; Lee, I.C.; Kim, J.W.; Kim, Y.N. Computational aeroacoustics (CAA) Flow-Acoustic Feedback Problems. In Proceedings of the Conference: 6th KSME-JSME Thermal and Fluids Engineering Conference (TFEC6), Jeju, Korea, 20–23 March 2005. [Google Scholar]
- Zuo, Z.; Maekawa, H. Application of a High-Resolution Compact Finite Difference Method to Computational Aeroacoustics of Compressible Flows. In Proceedings of the ASME-JSME-KSME 2011 Joint Fluids Engineering Conference: Volume 1, Symposia—Parts A, B, C, and D, Hamamatsu, Japan, 24–29 July 2011. [Google Scholar]
- Tyliszczak, A. LES–CMC study of an excited hydrogen flame. Combust. Flame 2015, 162, 3864–3883. [Google Scholar] [CrossRef]
- Tyliszczak, A. High-order compact difference algorithm on half-staggered meshes for low Mach number flows. Comput. Fluids 2016, 127, 131–145. [Google Scholar] [CrossRef]
- Wawrzak, A.; Tyliszczak, A. Implicit LES study of spark parameters impact on ignition in a temporally evolving mixing layer between H2/N2 mixture and air. Int. J. Hydrogen Energy 2018, 43, 9815–9828. [Google Scholar] [CrossRef]
- Visbal, M.R.; Gaitonde, D.V. High-Order-Accurate Methods for Complex Unsteady Subsonic Flows. AIAA J. 1999, 37, 1231–1239. [Google Scholar] [CrossRef]
- Visbal, M.R.; Gaitonde, D.V. Very High-Order Spatially Implicit Schemes For Computational Acoustics On Curvilinear Meshes. J. Comput. Acoust. 2001, 9, 1259–1286. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Wang, B.; Xu, Y.; Chen, X. A new central compact finite difference scheme with high spectral resolution for acoustic wave equation. J. Comput. Phys. 2018, 366, 191–206. [Google Scholar] [CrossRef]
- Shang, J.S. High-Order Compact-Difference Schemes for Time-Dependent Maxwell Equations. J. Comput. Phys. 1999, 153, 312–333. [Google Scholar] [CrossRef]
- Hesthaven, J.S. High-order accurate methods in time-domain computational electromagnetics: A review. Adv. Imaging Electron Phys. 2003, 127, 59–123. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Boussinesq, J. Essai sur la Theorie des eaux Courantes Memoires Presentes par Divers Savants; Memoires Presentes par Divers Savants a l’Academie des Sciences de l’Institut National de France; Institut de France: Paris, France, 1877. [Google Scholar]
- Dai, H.-H. Exact Solutions of a Variable-Coefficient KdV Equation Arising in a Shallow Water. J. Phys. Soc. Jpn. 1999, 68, 1854–1858. [Google Scholar] [CrossRef]
- Costa, A.; Osborne, A.R.; Resio, D.T.; Alessio, S.; Chrivì, E.; Saggese, E.; Bellomo, K.; Long, C.E. Soliton Turbulence in Shallow Water Ocean Surface Waves. Phys. Rev. Lett. 2014, 113, 108501. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Seadawy, A.R.; Albarakati, W.A. Analytical wave solution for the generalized nonlinear seventh-order KdV dynamical equations arising in shallow water waves. Mod. Phys. Lett. B 2020, 34, 2050279. [Google Scholar] [CrossRef]
- Hunter, J.K.; Vanden-Broeck, J.-M. Solitary and periodic gravity—Capillary waves of finite amplitude. J. Fluid Mech. 1983, 134, 205. [Google Scholar] [CrossRef]
- Milewski, P.A. Three-dimensional localized solitary gravity-capillary waves. Commun. Math. Sci. 2005, 3, 89–99. [Google Scholar] [CrossRef]
- Biswas, H.A.; Rahman, A.; Das, T. An Investigation on Fiber Optical Soliton in Mathematical Physics and Its Application in Communication Engineering. Int. J. Res. Rev. Appl. Sci. 2011, 6, 268–276. [Google Scholar]
- Obregon, M.; Stepanyants, Y. Oblique magneto-acoustic solitons in a rotating plasma. Phys. Lett. A 1998, 249, 315–323. [Google Scholar] [CrossRef]
- Goswami, A.; Singh, J.; Kumar, D. Numerical simulation of fifth order KdV equations occurring in magneto-acoustic waves. Ain Shams Eng. J. 2018, 9, 2265–2273. [Google Scholar] [CrossRef]
- Sahu, B.; Roychoudhury, R. Exact solutions of cylindrical and spherical dust ion acoustic waves. Phys. Plasmas 2003, 10, 4162–4165. [Google Scholar] [CrossRef]
- Guo, M.; Fu, C.; Zhang, Y.; Liu, J.; Yang, H. Study of Ion-Acoustic Solitary Waves in a Magnetized Plasma Using the Three-Dimensional Time-Space Fractional Schamel-KdV Equation. Complexity 2018, 2018, 6852548. [Google Scholar] [CrossRef]
- Grant, A.K.; Rosner, J.L. Supersymmetric quantum mechanics and the Korteweg–de Vries hierarchy. J. Math. Phys. 1994, 35, 2142–2156. [Google Scholar] [CrossRef][Green Version]
- Zakharov, D.V.; Dyachenko, S.A.; Zakharov, V.E. Bounded Solutions of KdV and Non-Periodic One-Gap Potentials in Quantum Mechanics. Lett. Math. Phys. 2016, 106, 731–740. [Google Scholar] [CrossRef]
- Li, J.; Visbal, M.R. High-order Compact Schemes for Nonlinear Dispersive Waves. J. Sci. Comput. 2006, 26, 1–23. [Google Scholar] [CrossRef]
- Yan, J.; Shu, C.-W. A Local Discontinuous Galerkin Method for KdV Type Equations. SIAM J. Numer. Anal. 2002, 40, 769–791. [Google Scholar] [CrossRef]
- Wouwer, A.V.; Saucez, P.; Schiesser, W.E. (Eds.) Adaptive Method of Lines; Chapman and Hall/CRC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Djidjeli, K.; Price, W.G.; Twizell, E.H.; Wang, Y. Numerical methods for the solution of the third- and fifth-order dispersive Korteweg–de Vries equations. J. Comput. Appl. Math. 1995, 58, 307–336. [Google Scholar] [CrossRef]
- Li, J. High-order finite difference schemes for differential equations containing higher derivatives. Appl. Math. Comput. 2005, 171, 1157–1176. [Google Scholar] [CrossRef]
- Yan, J.; Shu, C.-W. Local Discontinuous Galerkin Method for Partial Differential Equations with Higher Order Derivatives. J. Sci. Comput. 2002, 17, 27–47. [Google Scholar] [CrossRef]
- Kuramoto, Y.; Tsuzuki, T. On the Formation of Dissipative Structures in Reaction-Diffusion Systems: Reductive Perturbation Approach. Prog. Theor. Phys. 1975, 54, 687–699. [Google Scholar] [CrossRef]
- Kuramoto, Y.; Tsuzuki, T. Persistent Propagation of Concentration Waves in Dissipative Media Far from Thermal Equilibrium. Prog. Theor. Phys. 1976, 55, 356–369. [Google Scholar] [CrossRef]
- Kuramoto, Y. Diffusion-Induced Chaos in Reaction Systems. Prog. Theor. Phys. Suppl. 1978, 64, 346–367. [Google Scholar] [CrossRef]
- Michelson, D.M.; Sivashinsky, G.I. Nonlinear analysis of hydrodynamic instability in laminar flames—II. Numerical experiments. Acta Astronaut. 1977, 4, 1207–1221. [Google Scholar] [CrossRef]
- Sivashinsky, G.I. Nonlinear analysis of hydrodynamic instability in laminar flames—I. Derivation of basic equations. Acta Astronaut. 1977, 4, 1177–1206. [Google Scholar] [CrossRef]
- Sivashinsky, G.I. On Flame Propagation Under Conditions of Stoichiometry. SIAM J. Appl. Math. 1980, 39, 67–82. [Google Scholar] [CrossRef]
- Chang, H. Evolution on a Falling Film. Annu. Rev. Fluid Mech. 1994, 26, 103–136. [Google Scholar] [CrossRef]
- Chang, H.-C.; Demekhin, E.A. Solitary Wave Formation and Dynamics on Falling Films. Adv. Appl. Mech. 1996, 32, 1–58. [Google Scholar]
- Hooper, A.P.; Grimshaw, R. Nonlinear instability at the interface between two viscous fluids. Phys. Fluids 1985, 28, 37–45. [Google Scholar] [CrossRef]
- Papageorgiou, D.T.; Maldarelli, C.; Rumschitzki, D.S. Nonlinear interfacial stability of core-annular film flows. Phys. Fluids A Fluid Dyn. 1990, 2, 340–352. [Google Scholar] [CrossRef]
- LaQuey, R.E.; Mahajan, S.M.; Rutherford, P.H.; Tang, W.M. Nonlinear Saturation of the Trapped-Ion Mode. Phys. Rev. Lett. 1975, 34, 391–394. [Google Scholar] [CrossRef]
- Carpenter, M.H.; Gottlieb, D.; Abarbanel, S. The stability of numerical boundary treatements for compact high-order finite-difference schemes. J. Comput. Phys. 1993, 108, 272–295. [Google Scholar] [CrossRef]
- Nordström, J.; Mattsson, K.; Swanson, C. Boundary conditions for a divergence free velocity-pressure formulation of the Navier-Stokes equations. J. Comput. Phys. 2007, 225, 874–890. [Google Scholar] [CrossRef]
- Svärd, M.; Nordström, J. Review of summation-by-parts schemes for initial-boundary-value problems. J. Comput. Phys. 2014, 268, 17–38. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Thomas, A., Jr. Spectral Methods in Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Bayliss, A.; Class, A.; Matkowsky, B.J. Roundoff Error in Computing Derivatives Using the Chebyshev Differentiation Matrix. J. Comput. Phys. 1995, 116, 380–383. [Google Scholar] [CrossRef]
- Benia, Y.; Scapellato, A. Existence of solution to Korteweg–de Vries equation in a non-parabolic domain. Nonlinear Anal. 2020, 195, 111758. [Google Scholar] [CrossRef]
- Xu, Y.; Shu, C.-W. Local discontinuous Galerkin methods for the Kuramoto–Sivashinsky equations and the Ito-type coupled KdV equations. Comput. Methods Appl. Mech. Eng. 2006, 195, 3430–3447. [Google Scholar] [CrossRef]
- Sawada, K.; Kotera, T. A Method for Finding N-Soliton Solutions of the K.d.V. Equation and K.d.V.-Like Equation. Prog. Theor. Phys. 1974, 51, 1355–1367. [Google Scholar] [CrossRef]
- Lax, P.D. Integrals of nonlinear equations of evolution and solitary waves. Commun. Pure Appl. Math. 1968, 21, 467–490. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. Solitons and periodic solutions for the fifth-order KdV equation. Appl. Math. Lett. 2006, 19, 1162–1167. [Google Scholar] [CrossRef]
- Bakodah, H.O. Modified Adomian Decomposition Method for the Generalized Fifth Order KdV Equations. Am. J. Comput. Math. 2013, 3, 53–58. [Google Scholar] [CrossRef]
- Ahmad, H.; Khan, T.A.; Yao, S.-W. An efficient approach for the numerical solution of fifth-order KdV equations. Open Math. 2020, 18, 738–748. [Google Scholar] [CrossRef]

| M = 1, N = 7 | M = 2, N = 6 | M = 3, N = 5 | M = 4, N = 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Grid | r | p | Error | p | Error | p | Error | p |
| 33 | - | - | - | - | ||||
| 49 | ||||||||
| 65 | ||||||||
| 81 | ||||||||
| 97 | ||||||||
| 113 | ||||||||
| 129 | ||||||||
| 145 | ||||||||
| 161 | ||||||||
| 177 | ||||||||
| 193 | ||||||||
| 209 | ||||||||
| 225 | ||||||||
| 241 | ||||||||
| 257 | ||||||||
| Time | M = 1, N = 7 | M = 2, N = 6 | M = 3, N = 5 | M = 4, N = 4 |
|---|---|---|---|---|
| 0 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caban, L.; Tyliszczak, A. Application of High-Order Compact Difference Schemes for Solving Partial Differential Equations with High-Order Derivatives. Appl. Sci. 2022, 12, 2203. https://doi.org/10.3390/app12042203
Caban L, Tyliszczak A. Application of High-Order Compact Difference Schemes for Solving Partial Differential Equations with High-Order Derivatives. Applied Sciences. 2022; 12(4):2203. https://doi.org/10.3390/app12042203
Chicago/Turabian StyleCaban, Lena, and Artur Tyliszczak. 2022. "Application of High-Order Compact Difference Schemes for Solving Partial Differential Equations with High-Order Derivatives" Applied Sciences 12, no. 4: 2203. https://doi.org/10.3390/app12042203
APA StyleCaban, L., & Tyliszczak, A. (2022). Application of High-Order Compact Difference Schemes for Solving Partial Differential Equations with High-Order Derivatives. Applied Sciences, 12(4), 2203. https://doi.org/10.3390/app12042203







