Reinforcement-Learning-Based Vibration Control for a Vehicle Semi-Active Suspension System via the PPO Approach

Abstract

The vehicle semi-active suspension system plays an important role in improving the driving safety and ride comfort by adjusting the coefficients of the damping and spring. The main contribution of this paper is the proposal of a PPO-based vibration control strategy for a vehicle semi-active suspension system, in which the designed reward function realizes the dynamic adjustment according to the road condition changes. More specifically, for the different suspension performances caused by different road conditions, the three performances of the suspension system, body acceleration, suspension deflection, and dynamic tire load, were taken as the state space of the PPO algorithm, and the reward value was set according to the numerical results of the passive suspension, so that the corresponding damping force was selected as the action space, and the weight matrix of the reward function was dynamically adjusted according to different road conditions, so that the agent could have a better improvement effect at different speeds and road conditions. In this paper, a quarter–car semi-active suspension model was analyzed and simulated, and numerical simulations were performed using stochastic road excitation for different classes of roads, vehicle models, and continuously changing road conditions. The simulation results showed that the body acceleration was reduced by 46.93% under the continuously changing road, which proved that the control strategy could effectively improve the performance of semi-active suspension by combining the dynamic changes of the road with the reward function.

1. Introduction

In the Nineteenth Century, the quality of people’s travel was greatly improved with the birth of the first automobile. The components of semi-active suspension systems, which mainly include shock absorbers, elastic elements, and dampers, play a key role in improving the smoothness, handling stability, and passenger comfort of a car.

An onboard sensor is used to extract the road information for the semi-active suspension system, through the adjustment of the damping coefficient to improve the smoothness and stability of the vehicle. At present, the control strategy of semi-active suspension has been extensively studied. A controller was proposed by [1] to characterize the inverse dynamics of magnetorheological dampers using a polynomial model. Rao et al. [2] proposed an improved sky-hook control (SHC) strategy to optimize the parameters by equating the control force of the feedback system with that obtained by a linear quadratic regulator (LQR). The paper [3] proved the conditions for the feedback controller in the ideal state using linear matrix inequalities (LMIs) and Liapunov functions that depend on the time lag distance. Based on variational optimal control theory, an open-loop variational feedback controller for semi-active control of a suspension system was proposed in [4]. A fuzzy controller and an adaptive fuzzy controller were developed in [5] to achieve road holding and passenger comfort on most road profiles. The article [6] developed an adaptive fuzzy sliding mode control method based on a bionic reference model, which takes into account the variation of the vehicle mass and is able to provide both finite-time convergence and energy-efficient performance. The article [7] developed a new dynamic model named the QSHM model based on quasi-static (QS) models and hysteretic multiplier (HM) factors. On the basis of the implementation of a new method of experiment-based modeling of magnetorheological hydrodynamics, several hysteresis multiplier factors were introduced. The article [8] developed a self-powered magnetic rheological (MR) damper to effectively control the vibration of a front-loaded washing machine. The damper consisted of a shear MR damping part and a generator with a permanent magnet and induction coil. The paper [9] proposed a new adaptive control method to deal with dead zones and time delay problems in actuators of vibration control systems. In addition, fuzzy neural networks were used to approximate unmodeled dynamics, and sliding mode controllers were designed to enhance the robustness of the system to uncertainty and robustness. Based on the Bolza–Meyer criterion, a new optimal control law related to sliding mode control was developed in [10]. The controller has gain adjustability, where the gain value can be greater than one. Most of the aforementioned methods are based on establishing an accurate mathematical model and proving the effectiveness of the proposed control strategy through a rigorous theory, which is computationally intensive and more difficult to implement in practice.

Since its introduction in 1954, reinforcement learning has been developed over the years with reformative advances in both theory and applications. In terms of theory, the deep Q-network (DQN) algorithm was proposed in [11], which solved the problem of the difficult convergence of training under off-policy by end-to-end training mode. The deep deterministic policy gradient (DDPG) algorithm was proposed in [12], which is based on the DQN, using a replay buffer and target network for updating, while using a neural network for function approximation. The paper [13] proposed the trust region policy optimization (TRPO) algorithm, which was improved for policy optimization and solves the problem of selecting the update step size during the policy update, which enables the policy update of the agent to be monotonically enhanced, but it also has the problem of high computational complexity. Compared with control strategies based on mathematical models, reinforcement learning can generate a large amount of data by interacting with the environment and find the best strategy from the sampled data, so it has been successfully applied in several application scenarios. In 2017, Alpha Go defeated Ke Jie by using reinforcement learning algorithms, which is the world’s top-ranked Go player, and since then, reinforcement learning has been known to the public [14] from the Wuzhen Go Summit. The paper [15] proposed a deep reinforcement learning framework in the MOBA game Honor of Kings, enabling the AI agent Tencent Solo to beat top human professional players in 1v1 games. In recent years, the PPO algorithm [16] based on the actor–critic algorithm uses an importance sample to transform the on-policy into the off-policy, which is conducive to fully reusing the sampled data, avoiding data waste and speeding up the learning rate, and the CLIP function is used to control the step size of the gradient update of the policy, so that the control strategy is monotonically improved without violent shaking. The PPO algorithm has been applied in several application scenarios. In paper [17], the PPO algorithm was applied to image caption generation; a single model was trained by fine-tuning the pre-trained X-Transformer, and good experimental results were obtained. The paper [18] utilized the proximal policy optimization (PPO) algorithm to construct a second-order intact agent for navigating through an obstacle field such that the angle-based formation was allowed to shrink while maintaining the shape, and the geometric centroid of the formation was constantly oriented toward the target. The PPO algorithm is suitable as a control strategy for semi-active suspensions because of its ability to continuously interact with the environment to achieve policy improvement and optimize monotonic enhancement through importance sampling, as well as due to its computational simplicity.

At present, the application of reinforcement learning in vehicle suspension control has attracted much attention and achieved a series of results in order to reduce the dependence on accurate mathematical models for the design of control strategies for suspension systems and to overcome the influence of its own uncertain parameters and the external environment on the control performance. The article [19] explored the application of batch reinforcement learning (BRL) to the problem of designing semi-active suspensions for optimal comfort. In the article [20], the performance of a nonlinear quarter-car active suspension system was investigated using a stochastic real-valued reinforcement learning control strategy. The article [21] developed a secure reinforcement learning framework that combines model-free learning with model-based safety supervision applied to active suspension systems. A model-free reinforcement learning algorithm was proposed based on a deterministic policy gradient and neural network approximation in [22], which learned the state feedback controller from the sampled data of the suspension system. Liu Ming et al. [23] used the deep deterministic policy gradient algorithm (DDPG) as the control strategy of a semi-active suspension system, which adaptively updates the learned reward value based on the control strategy based on the learned reward values and achieved good control results. The above results fully demonstrate that the use of reinforcement learning algorithms as the control strategy for a semi-active suspension system does not require a strict theoretical definition and accurate mathematical modeling, which can greatly reduce the amount of computation and simplify the complexity of the algorithm. It cannot be ignored that the performance of the vehicle suspension is related to vehicle driving comfort and driving safety, and the performance indicators should be different when facing different road conditions. However, existing successful designs do not sufficiently consider the integration of road information with vehicle driving status to guide the design of relevant strategies.

Motivated by integrating the road condition changes with the reward function, a PPO-based semi-active control strategy is proposed to improve the ride comfort and driving safety. The main contributions are listed as follows:

(1) The PPO algorithm was used as the control strategy of the semi-active suspension, and the body acceleration, suspension deflection, and dynamic tire load were selected as the state space to set the reward function of the PPO algorithm to optimize the performance of the semi-active suspension system;

(2) Combining the road variation with the reward function made it possible to improve the suspension performance by dynamically adjusting the weight matrix of the reward function for different levels of roads;

(3) The proposed control strategy was proven to be effective in improving the performance of the suspension by conducting simulations under different vehicle speeds, vehicle models, and road conditions.

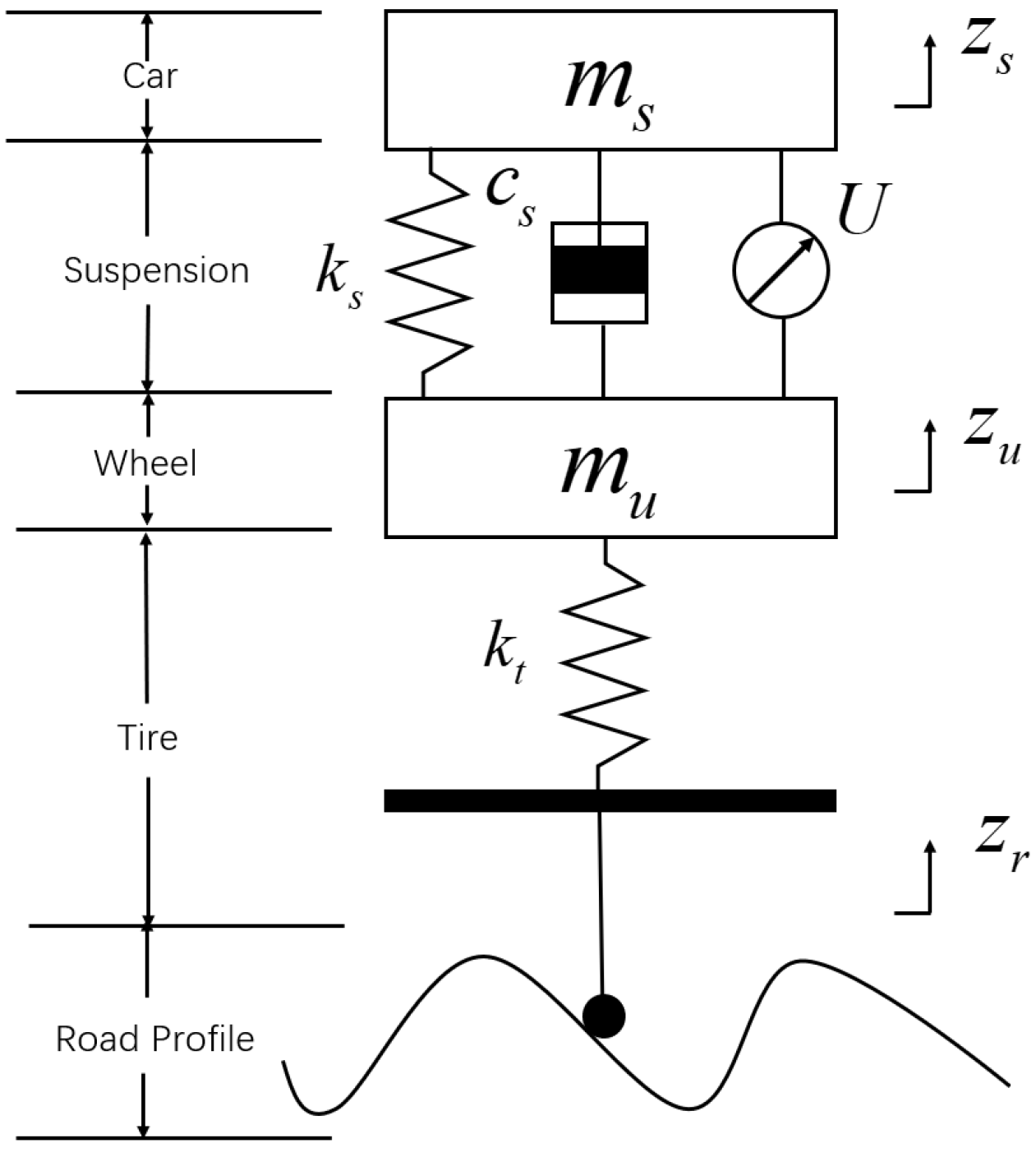
The rest of the paper is organized as follows: In Section 2, we give a systematic modeling of road disturbances and a two-degree-of-freedom (DOF) quarter semi-active suspension system model. Details of the implementation of a semi-active suspension system based on the proximal policy optimization (PPO) algorithm are given in the Section 3. The simulation experiments and results are given in Section 4. Finally, Section 5 gives a conclusion and future work.

2. System Modeling of Road Disturbance and Vehicle Suspension

2.1. Road Disturbance Model

The suspension performance of a vehicle is affected by many factors, including the roughness of the road. According to the international ISO 8608 standard [24], special index data $G_q\left(n\right)$ are used to describe the characteristics of the road, and the establishment of a frequency domain road model is mainly based on the actual measurement of the road information, including road unevenness. The road roughness can be divided into eight classes, as shown in

Table 1. Eight-level classification of road disturbance roughness.

Road Level	Road Unevenness Coefficient ${\mathit{G}}_{\mathit{q}}\left({\mathit{n}}_0\right)/10^{-6}{\mathbf{m}}^3{\mathit{n}}_0=0.1{\mathbf{m}}^{-1}$
	Lower Limit	Geometric Mean	Upper Limit
A	8	16	32
B	32	64	128
C	128	256	512
D	512	1024	2048
E	2048	4096	8192
F	8192	16,384	32,768
G	32,768	65,536	131,072
H	131,072	262,144	524,288

, which specifies the upper and lower limits and average values of the corresponding road spectrum for each road class.

The expression for road power spectral density $G_q\left(n\right)$ is as follows:

$$G_q\left(n\right)=G_q\left(n_0\right){\left(\frac{n}{n_0}\right)}^{-\omega },$$

(1)

where $G_q\left(n\right)$ is the road unevenness coefficient, which is the road power spectral density value at the reference spatial frequency. n is the spatial frequency, which is the reciprocal of the wavelength; $n_0$ is the reference spatial frequency, which is generally selected as $0.1{\mathrm{m}}^{-1}$; $\omega$ is the frequency index.

The corresponding time domain model of filtered white noise road unevenness is as follows [25]:

$${\dot{z}}_r=-2\pi f_{0}v{z}_r+2\pi n_0\sqrt{G_q\left(n_0\right)v}W,$$

(2)

where $z_r$ is the road input displacement, v is the vehicle speed, $f_0$ is the lower cutoff frequency, which is generally chosen as $0.01{\mathrm{m}}^{-1}$, and W is Gaussian white noise with a mean of zero and a sampling frequency of 10 Hz. Different levels of road will cause different amplitudes of vehicle vibration, which affect the suspension performance. In this paper, the PPO algorithm was used as the control strategy to improve the suspension performance for the change of suspension performance caused by road jitter.

2.2. Two-DOF Quarter Semi-Active Vehicle Suspension

The suspension system is affected by many factors, and correspondingly, there are models of suspension systems with complex and diverse degrees of freedom. The two-degree-of-freedom suspension is the most refined structure in the field of automotive suspensions, which can meet the basic requirements of vibration control studies for different levels of roads by intuitively responding to the vibration of a single tire. In this paper, by studying the control strategy of the 2-DOF suspension model, the advantages and disadvantages of the control method can be roughly judged, and the system structure and calculation are relatively simple, which is the basis for the study of the control system of the full vehicle [26]. The 2-DOF quarter semi-active suspension system model is shown in Figure 1.

$m_s$ is the sprung mass; $m_u$ is the unsprung mass; $k_s$ is the sprung stiffness; $k_t$ is the tire stiffness; $c_s$ is the damping coefficient of the suspension; U is the damping force of the semi-active suspension; $z_s$ is the sprung mass displacement; $z_u$ is the unsprung mass displacement; $z_r$ is the road input displacement.

According to the system model in Figure 1 and Newton’s second law, the following mechanical model equations of motion can be obtained:

$$\left\{\begin{array}{c}{\ddot{z}}_s=-\frac{k_s}{m_s}(z_s-z_u)-\frac{c_s}{m_s}({\dot{z}}_s-{\dot{z}}_u)+\frac{U}{m_s},\hfill \\ {\ddot{z}}_u=-\frac{k_s}{m_u}(z_u-z_s)+\frac{c_s}{m_u}({\dot{z}}_s-{\dot{z}}_u)-\frac{k_t}{m_u}(z_u-z_r)-\frac{U}{m_u},\hfill \end{array}\right.$$

(3)

where ${\ddot{z}}_s$ is the body acceleration as one of the suspension performance parameter, and the other two choose the suspension deflection $z_s-z_u$ and tire dynamic load $k_t(z_u-z_r)$, through dynamic adjustment of the three scale coefficients for multi-control objective optimization, so that the three control objectives can have a certain optimization effect at the same time.

3. Semi-Active Suspension Control Based on the PPO Algorithm

In this paper, the PPO algorithm was combined with a semi-active suspension, and the overall process is that the road information is collected by sensors and input into the suspension system model, while the control performance index of the current moment t is calculated and input into the actor network of the PPO algorithm as the state value; then, the corresponding actor value is selected as the output according to the probability density function in the policy network; a series of trajectories ${\tau }_i=\{s_i,a_i,r_i,s_{i+1}\}$ is stored in the memory space by repeatedly interacting with the environment; the value network is updated with importance sampling; the control strategy is continuously optimized according to the reward value obtained, and so on, until the control performance is no longer better and convergence is reached. The flowchart of the semi-active suspension control structure based on the PPO algorithm is shown in Figure 2.

3.1. State Space and Action Space

According to the above process, the road information is input into the suspension system by using sensors to obtain the corresponding suspension response performances. In this paper, the response indicators $\phi$ of the suspension system were selected as the body acceleration, suspension deflection, and tire dynamic load, and the three performance indicators were used as the state space S input for reinforcement learning; the action space A output is the damping force of the suspension system; considering the practical application of the suspension system, the range of the damping force was set to −500 N to 500 N. Figure 3 shows a change in the damping force of the semi-active suspension. The resulting response performance $\phi$ is input as the state space into the policy network of the PPO algorithm.

$$\phi =\left(\begin{array}{c}{\ddot{z}}_s\\ z_s-z_u\\ k_t(z_u-z_r)\end{array}\right).$$

(4)

3.2. PPO Algorithm Network Model

The proximal policy optimization (PPO) algorithm is an actor–critic-based reinforcement learning algorithm, which combines a value-based approach and a policy-based approach [27]. The architecture of the algorithm consists of two parts: the actor network part is based on the policy approach, which is used to optimize the policy model $\pi (s,a)$ by generating actions and interacting with the environment; the critic network part is based on the value approach, which is used to determine the merit of an action and select the next action accordingly to optimize the value function $Q(s,a)$. The network structure of the PPO algorithm is shown in Figure 4.

It contains four neural networks [28], which are the policy network, the target policy network, the value network, and the target value network. The network architectures of the policy network and the value network are the same as those of their corresponding target networks, and there are only differences in the network parameters. In the architecture of this control algorithm, the actor network obtains the control data based on the output state information of the suspension system, so as to obtain the action information damping force to optimize the entire algorithm. By adjusting different speeds and road bumps, the car’s body acceleration and suspension deflection at the current moment are affected, resulting in the next new state.

After a period of interaction between the agent and the environment, a series of trajectory data is generated, and the network parameters are updated by sampling the data stored in the memory network using a policy gradient. In the policy gradient (PG) [29] method, the goal is to learn a parameterized policy that determines a unique action or obtains a corresponding action probability density function directly from a selection in the state space. In the learning process, the strategy is optimized by calculating an estimate of the policy gradient, and the methods used are gradient up or gradient down depending on the expectation, respectively. The policy gradient function is shown in Equation (5):

$$\nabla {\overline{R}}_{\theta }=E_{(s_t,a_t)\sim {\pi }_{\theta }}[R(s_t,a_t)\nabla {log}_{{\pi }_{\theta }}(s_t,a_t)],$$

(5)

$$\begin{array}{c}{A}^{\pi ,\gamma }(s_t,a_t)=E_{s_{t+1}}[r_t+\gamma V^{\pi ,\gamma }\left(s_{t+1}\right)-V^{\pi ,\gamma }\left(s_t\right)]\hfill \\ =E_{s_{t+1}}[Q^{\pi ,\gamma }(s_t,a_t)-V^{\pi ,\gamma }\left(s_t\right)],\hfill \end{array}$$

(6)

where ${\pi }_{\theta }$ is a stochastic policy function and $R(s_t,a_t)$ is the reward value of the current state action pair. $V^{\pi ,\gamma }\left(s_t\right)$ is the state value function of the strategy $\pi$ at the current moment. $Q^{\pi ,\gamma }(s_t,a_t)$ is the action value function of the strategy $\pi$ at the current moment. $A^{\pi ,\gamma }(s_t,a_t)$ is an estimate of the advantage function at the moment t [30], containing a hyperparameter $\gamma$, which is usually obtained by estimating the advantage function based on the value of the reward function, and then, the policy gradient is estimated according to the parameter $\theta$ so as to optimize the policy with the policy gradient. If $A^{\pi ,\gamma }(s_t,a_t)>0$, this means that the current state action pair $(s_t,a_t)$ is able to obtain a higher reward than the baseline, and conversely, a lower reward is obtained.

3.3. Design If the Reward Function with Road Disturbances and Policy Update

The process of policy updating depends on the reward value of the agent’s state action pair to judge its goodness. The reward function in this paper was set for a semi-active suspension optimized for multiple objectives, which considered the vehicle acceleration on the human body, as well as the vehicle body more to improve the performance. Therefore, it is only necessary to ensure that the remaining two performance indicators have a certain improvement or some weakening within the acceptable range of the vehicle suspension performance. Considering different reward functions depending on the optimization task, we chose to make it as simple as possible to evaluate the efficiency of reinforcement learning optimization.

Therefore, in this paper, the performance metrics of the passive suspension for different road conditions were directly set up with a reward and punishment mechanism, giving a positive reward value if the performance improves and, conversely, giving a negative reward value. The reward function R was set by summing up the suspension performance $\phi$ caused by different road conditions $z_r$ and dynamically adjusting the weight matrix of the suspension performance according to different road conditions. For example, when the road is more rough and the safety requirement of the vehicle is greater, the weight coefficient corresponding to the tire load is increased. Therefore, the reward function is shown as follows:

$$z_r\to \phi ,$$

(7)

$$R=\sum _{t=0}^T{\phi }^{\mathrm{T}}A\phi ,$$

(8)

$$A=\left(\begin{array}{ccc}x& & \\ & y& \\ & & z\end{array}\right),$$

(9)

where A represents the weight matrix of each performance indicator, and the values of x, y, and z are dynamically adjusted according to different roads. For example, it was experimentally measured that when a light vehicle with a speed of 20 m/s is driving on a C-class road, the suspension response performance $\phi$ is better when $A=\left(\begin{array}{ccc}10^3& & \\ & 1.5& \\ & & 1\end{array}\right)$.

When using the reward function and the policy gradient method to update the network, the traditional on-policy policy was used, and the policy that interacts with the environment $\pi$ and the policy that needs to be updated ${\pi }^{\prime }$ were the same policy, the disadvantage being that the sampling efficiency was low and the data sampled each time could only be used for one policy update. Therefore, the PPO algorithm introduces another policy q to interact with the environment, and the empirical samples obtained from the interaction are placed in memory and can be used to update the policy p several times. According to Equation (10), it was proven that the purpose can be achieved by multiplying only one weighting factor $\frac{p\left(x\right)}{q\left(x\right)}$ on the basis of the original.

$$E_{x\sim p}\left[f\left(x\right)\right]\approx \frac{1}{N}\sum _{i=1}^{N}f\left(x_i\right)=\int f\left(x\right)p\left(x\right)dx=\int f\left(x\right)\frac{p\left(x\right)}{q\left(x\right)}q\left(x\right)dx=E_{x\sim q}[f\left(x\right)\frac{p\left(x\right)}{q\left(x\right)}],$$

(10)

$$J^{{\theta }^{\prime }}\left(\theta \right)=E_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}[\frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{\pi }_{{\theta }^{\prime }}\left(a_t\right|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)].$$

(11)

In Equation (11), $J^{{\theta }^{\prime }}\left(\theta \right)$ is the target function, p and q correspond to the specific policy distributions ${\pi }_{\theta }$ and ${\pi }_{{\theta }^{\prime }}$, respectively, and $A^{{\theta }^{\prime }}$ is the advantage function of the t moment, that is the gap between the score and the baseline obtained by the current strategy and the environment interaction. PPO uses importance sampling to change the previous on-policy policy into an off-policy policy [31], making the sampled data reusable and improving the learning efficiency. This was done by using two policy networks, one ${\pi }_{\theta }$ to interact with the environment and the other ${\pi }_{{\theta }^{\prime }}$ to update the network.

${\widehat{E}}_t[\cdots ]$ represents the expectation of a batch of samples, and the obtained expectation is approximately equal when the policy distribution of ${\pi }_{\theta }$ and ${\pi }_{{\theta }^{\prime }}$ is similar; otherwise, it will produce a large error. Therefore, PPO is constrained by a first-order optimization, converting Equation (11) to Equation (12) as shown in:

$$J^{{\theta }^{\prime }}\left(\theta \right)=min(\frac{{\pi }_{{\theta }^{\prime }}\left(a\right|s)}{{\pi }_{\theta }\left(a\right|s)}{A}^{{\pi }_{{\theta }^{\prime }}}(s,a),clip(\frac{{\pi }_{{\theta }^{\prime }}\left(a\right|s)}{{\pi }_{\theta }\left(a\right|s)},1-\epsilon ,1+\epsilon )A^{{\pi }_{{\theta }^{\prime }}}(s,a)),$$

(12)

where $\epsilon$ is the hyperparameter of the clip function, which is used to limit the magnitude of the update; the second half uses the clip function $clip(\frac{{\pi }_{{\theta }^{\prime }}\left(a\right|s)}{{\pi }_{\theta }\left(a\right|s)},1-\epsilon ,1+\epsilon )A^{{\pi }_{{\theta }^{\prime }}}(s,a)$ to limit ${\pi }_{\theta }$ and ${\pi }_{{\theta }^{\prime }}$ from being too different. This clip idea is that when $A>0$, this means that the current action produces a return estimate that is greater than the expected return of the baseline, so we update the strategy $\pi$ so that the probability of that action appearing is as high as possible, but to add a limit to this, that is it cannot be $1+\epsilon$-times higher than the original strategy. Similarly, if $A<0$, this means that the estimated return of the current action is less than the expected return of the baseline, so we made the probability of the action occurring, as low as possible, but not less than $1-\epsilon$-times the original strategy.

3.4. Semi-Active Suspension Control Based on the PPO Architecture

In view of the above ideas, the overall process of summarizing the algorithm is shown in

Table 2. Proximal policy optimization algorithm-semi-active suspension.

Procedure: PPO-semi-active suspension
The on-board sensor is used to collect road information in time for the semi-active suspension system to obtain the
suspension response performance $\phi$.
Randomly initialize the actor network and critic network with weights $\theta$ and $\omega$.
Initialize the actor target network and critic target network: ${\theta }^{\prime }\leftarrow \theta$, ${\omega }^{\prime }\leftarrow \omega$.
for $k=0,1,2,\cdots$do
Generate a set of trajectories ${\tau }_i=\{s_i,a_i,r_i,s_{i+1}\}$ by running policy ${\pi }_{{\theta }_k}$ in the environment.
Sample the data information in the memory network, and calculate the quality of the corresponding state action     pair $(s_i,a_i)$ according to the reward function R.
Compute the advantage function $A^{{\theta }^{\prime }}(s_t,a_t)=r(s_t,a_t)+\gamma V^{{\omega }_k}\left(s_{t+1}\right)-V^{{\omega }_k}\left(s_t\right)$ based on the current value function
$V_{{\omega }_k}$.
Update the policy parameter by maximizing the PPO-clip objective:
${\theta }_{k+1}=\underset{\theta }{argmax}\frac{1}{|{\tau }_k|T}{\displaystyle \sum _{t=0}^T}min(\frac{{\pi }_{{\theta }_k}\left(a_t\right|s_t)}{{\pi }_{\theta }\left(a_t\right|s_t)}{A}^{{\pi }_{{\theta }_k}}(s_t,a_t),clip(\frac{{\pi }_{{\theta }_k}\left(a_t\right|s_t)}{{\pi }_{\theta }\left(a_t\right|s_t)},1-\epsilon ,1+\epsilon )A^{{\pi }_{{\theta }_k}}(s_t,a_t)).$
Update the value parameter by minimizing the advantage function:
${\omega }_{k+1}=\underset{\omega }{argmin}\frac{1}{|{\tau }_k|T}{\displaystyle \sum _{t=0}^T}\alpha {(r(s_t,a_t)+\gamma V^{{\omega }_k}\left(s_{t+1}\right)-V^{{\omega }_k}\left(s_t\right))}^2.$
Soft update the target network parameters:
$\begin{array}{c}{\theta }^{\prime }\leftarrow \tau \theta +(1-\tau ){\theta }^{\prime },\hfill \\ {\omega }^{\prime }\leftarrow \tau \omega +(1-\tau ){\omega }^{\prime }.\hfill \end{array}$
end for

.

4. Simulation Results and Analysis

In this paper, MATLAB/SIMULINK was used to build a 1/4 semi-active suspension system model, in which the suspension parameters are shown in

Table 3. Parameters for the quarter semi-active suspension.

Parameters	Symbols	Unit	Light	Heavy
Sprung mass	$m_s$	(kg)	167.8	1465.4
Unsprung mass	$m_u$	(kg)	22.3	122.3
Sprung stiffness	$k_s$	(N/m)	11,530	11,530
Tire stiffness	$k_t$	(N/m)	115,300	315,300
Damping coefficient of suspension	$c_s$	(N*m/s)	278.4	4670.4

. The actor network and critic network of the PPO algorithm were neural networks with five and six hidden layers. The learning rate of the actor network ${\alpha }_A$ and the critic network ${\alpha }_C$ was set to 0.001 and 0.0001, respectively. The discount factor $\gamma$ was set to 0.98. The clipparameter $\epsilon$ was set to 0.2. The GAE parameter $\lambda$ was set to 0.9. The batch size was set to 64. The simulation time was set to 60 s. The specific hyperparameters were set as shown in

Table 4. Hyperparameters for the proximal policy optimization structure.

Hyperparameters	Symbols	Values
Actor learning rate	${\alpha }_A$	0.0002
Critic learning rate	${\alpha }_C$	0.001
Discount factor	$\gamma$	0.98
Clip parameter	$\epsilon$	0.2
GAE parameter	$\lambda$	0.9
Batch size		64
Time steps per batch		600

.

4.1. Simulation Experiments for Different Road Levels for a Light Vehicle

In order to verify the control performance and robustness of the semi-active suspension system based on the PPO algorithm, simulation comparison experiments were conducted for the passive suspension system, the semi-active suspension system based on fuzzy control, and the semi-active suspension system based on the PPO algorithm under the same conditions. Specifically, a vehicle speed of 20 m/s was simulated on the C-, D-, and E-class roads, respectively, and the road power spectrum is shown in Figure 5.

The simulation experimental results of the body acceleration, suspension deflection, and dynamic tire load on C-class and D-class roads at a vehicle speed of 20 m/s are shown in Figure 6 and Figure 7. For the ease of comparison, the percentages of the root mean square (RMS) values for the body acceleration, suspension deflection, and tire dynamic load of the passive suspension, the semi-active suspension system based on fuzzy control, and the PPO algorithm under the same conditions are given in

Table 5. The percentages of RMS values of the two semi-active suspensions for a light vehicle under the same conditions.

Road Level	Body Acceleration		Suspension Deflection		Tire Dynamic Load
	Fuzzy	PPO	Fuzzy	PPO	Fuzzy	PPO
C	26.4%	61.8%	6.1%	47.8%	−18%	28.8%
D	26.3%	59.1%	27%	45.5%	13.3%	28%
E	26.4%	59.3%	27.1%	46.5%	13.3%	28.8%

, and the corresponding root-mean-squared error (RMSE) values are given in

Table 6. The RMSE values of the two semi-active suspensions for a light vehicle under the same conditions.

Road Level	Body Acceleration			Suspension Deflection			Tire Dynamic Load
	Passive	Fuzzy	PPO	Passive	Fuzzy	PPO	Passive	Fuzzy	PPO
C	0.5896	0.4735	0.3492	0.1275	0.06218	0.05513	12.71	9.624	11.93
D	0.8338	0.6844	0.6614	0.1424	0.08794	0.07839	18.77	16.86	13.61
E	1.179	1.058	0.9787	0.1671	0.1244	0.1109	25.45	24.23	19.25

.

The simulation results showed that the body accelerations of the PPO-based semi-active suspension system and the fuzzy-based system were reduced by 59.1% and 26.3%, the suspension deflections were reduced by 45.5% and 27%, and the dynamic tire loads were reduced by 28% and 13.3%, compared with the passive suspension system under the D-class road.

4.2. Simulation Experiments for Different Road Levels for a Heavy Vehicle

In order to test the adaptability of the control strategy proposed in this paper to different vehicle models, simulation experiments were conducted for a heavy vehicle on B-, C-, and D-class roads by changing the vehicle speed to 15 m/s according to the actual situation, and the suspension parameters and road power spectrum are shown in Table 3 and Figure 5, respectively. Figure 8 shows the simulation results of the body acceleration on B- and C-class roads. The percentages of the RMS values of the body acceleration for the passive suspension and the semi-active suspension system based on the fuzzy and PPO algorithm under the same conditions are given in

Table 7. The percentages of the RMS values of the two semi-active suspensions for a heavy vehicle under the same conditions.

Percentage of Body Acceleration	B	C	D
Fuzzy	18.1%	3.8%	5%
PPO	44.4%	31.6%	10%

, and the corresponding RMSE values are given in

Table 8. The RMSE values of the two semi-active suspensions for a heavy vehicle under the same conditions.

Body Acceleration	B	C	D
Passive	0.218	0.3083	0.436
Fuzzy	0.1973	0.3023	0.425
PPO	0.1625	0.255	0.4147

. The experimental results showed that the PPO-based semi-active suspension system still had good performance under different vehicle models, vehicle speeds, and road conditions.

4.3. Simulation Experiments for a Continuously Changing Road Level

In order to verify the applicability of the proposed control strategy to the case of the road level changing randomly, simulation experiments were conducted for a light vehicle at a speed of 20 m/s with continuous changes in the road grade, and the road surface changes and body acceleration are shown in Figure 9 and Figure 10. As shown in Figure 9, the road changed from Class B to Class C, then to Class D, and finally, back to Class C. The duration of each section was 10 s, and the total simulation time was 40 s. According to the simulation experiment results in Figure 10, it was proven that the semi-active suspension system based on PPO still had good performance under the continuously changing roads, and the body acceleration value was reduced by 46.93%.

4.4. Number of Iterations and Computation Time

This paper used the PPO algorithm for training. The max episodes was set to 10,000. The max steps per episode was set to 600. The sampling time was 0.1 s. The time per iteration was 60 s. The mini batch size was set to 64. The convergence process of the algorithm is shown in Figure 11, which tended to converge at 90 episodes according to the figure, with a total time of about 1.2 h, and it took a short time from the beginning of the algorithm to search for good behavior to the final convergence, which was faster than the number of iterations of the particle swarm optimization (PSO) algorithm in the paper [32].

5. Conclusions and Future Work

In this paper, a semi-active suspension control strategy based on the Proximal Policy Optimization (PPO) algorithm was proposed. Firstly, the road unevenness information was collected in real time by the sensor, and the three performance indicators of the vehicle were obtained as the state input for reinforcement learning by establishing a 2-DOF quarter suspension semi-system model, then the control strategy was continuously optimized according to the corresponding reward and punishment functions and the prints of the weight matrix under different road conditions until the convergence state was reached. The simulation experiments showed that the proposed control strategy could improve the vehicle performance better than the passive suspension and fuzzy control.

However, the traditional reward function is not applicable in the face of complex and frequently changing roads, and the applicability of the control strategy involved to the full-vehicle suspension requires further exploration and research.