Quasi-Isotropic Hybrid Dielectric Resonator Antenna—Bow-Tie Patch with Harmonic Suppression
Abstract
:1. Introduction
2. Design of Proposed Quasi-Isotropic Hybrid Dielectric Resonator Antenna-Bow-Tie Patch with Harmonics Suppression
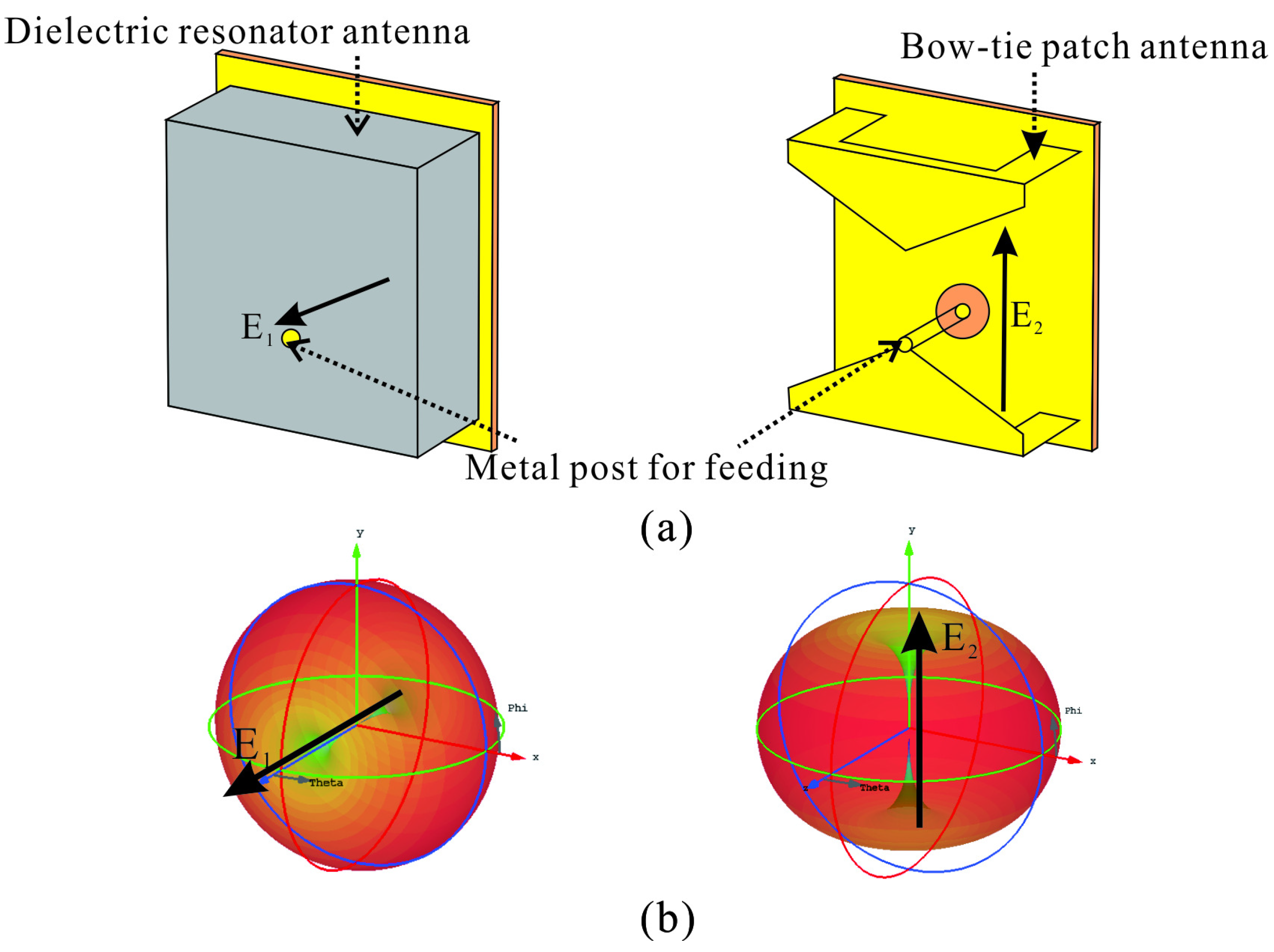
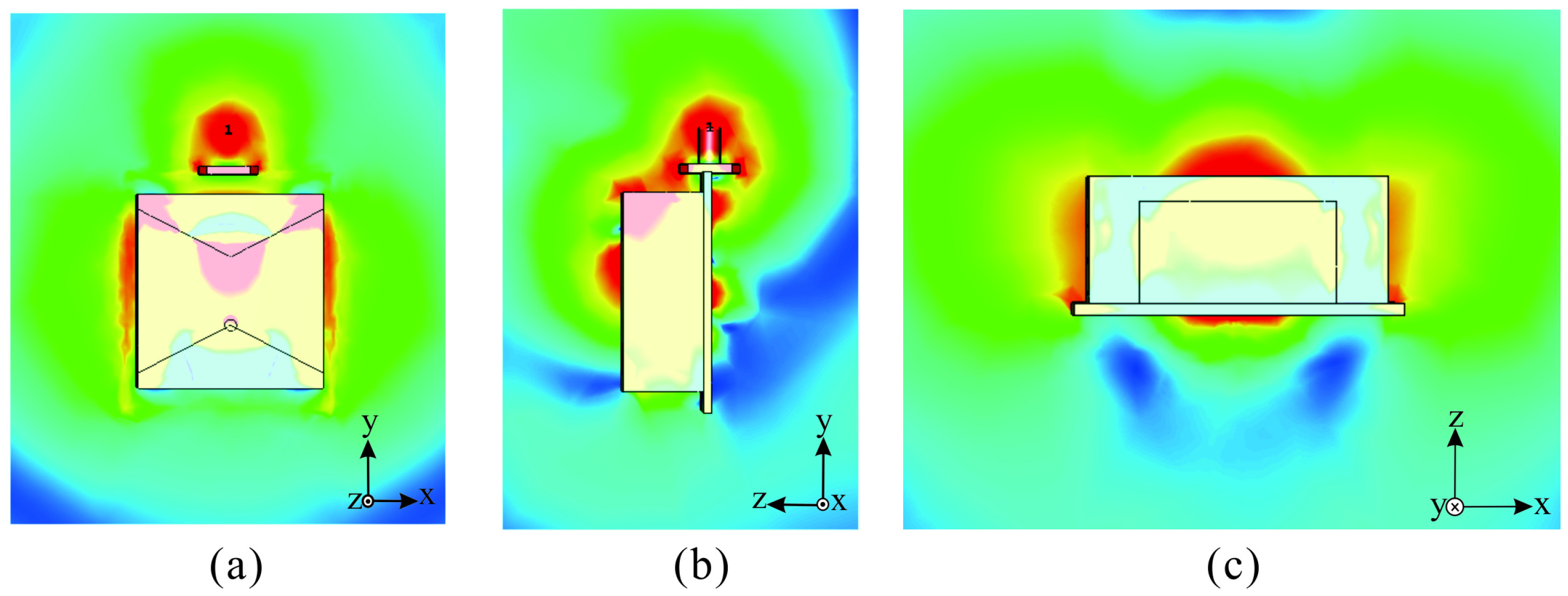
2.1. Design of Proposed Antenna Having a Quasi-Isotropic Pattern
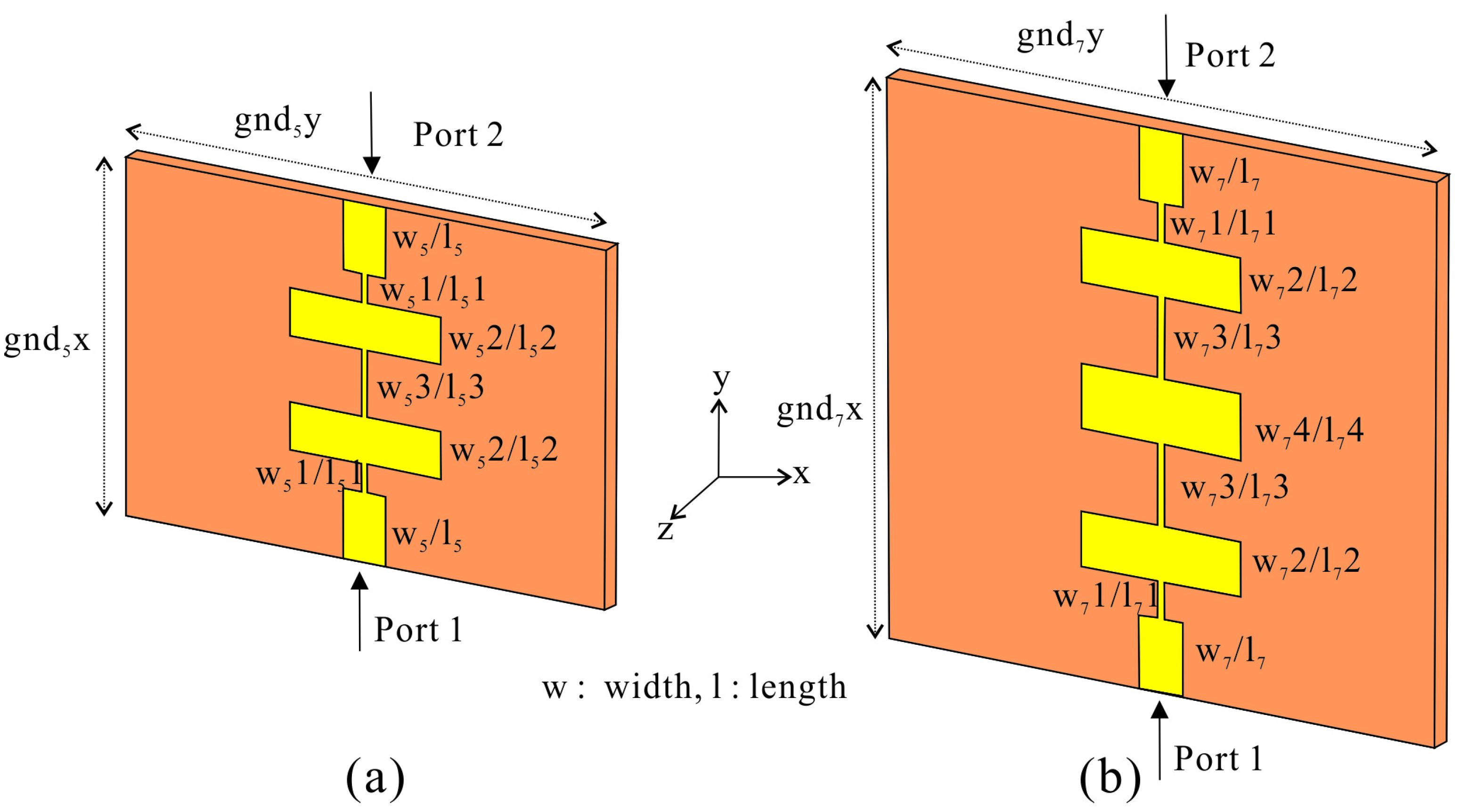
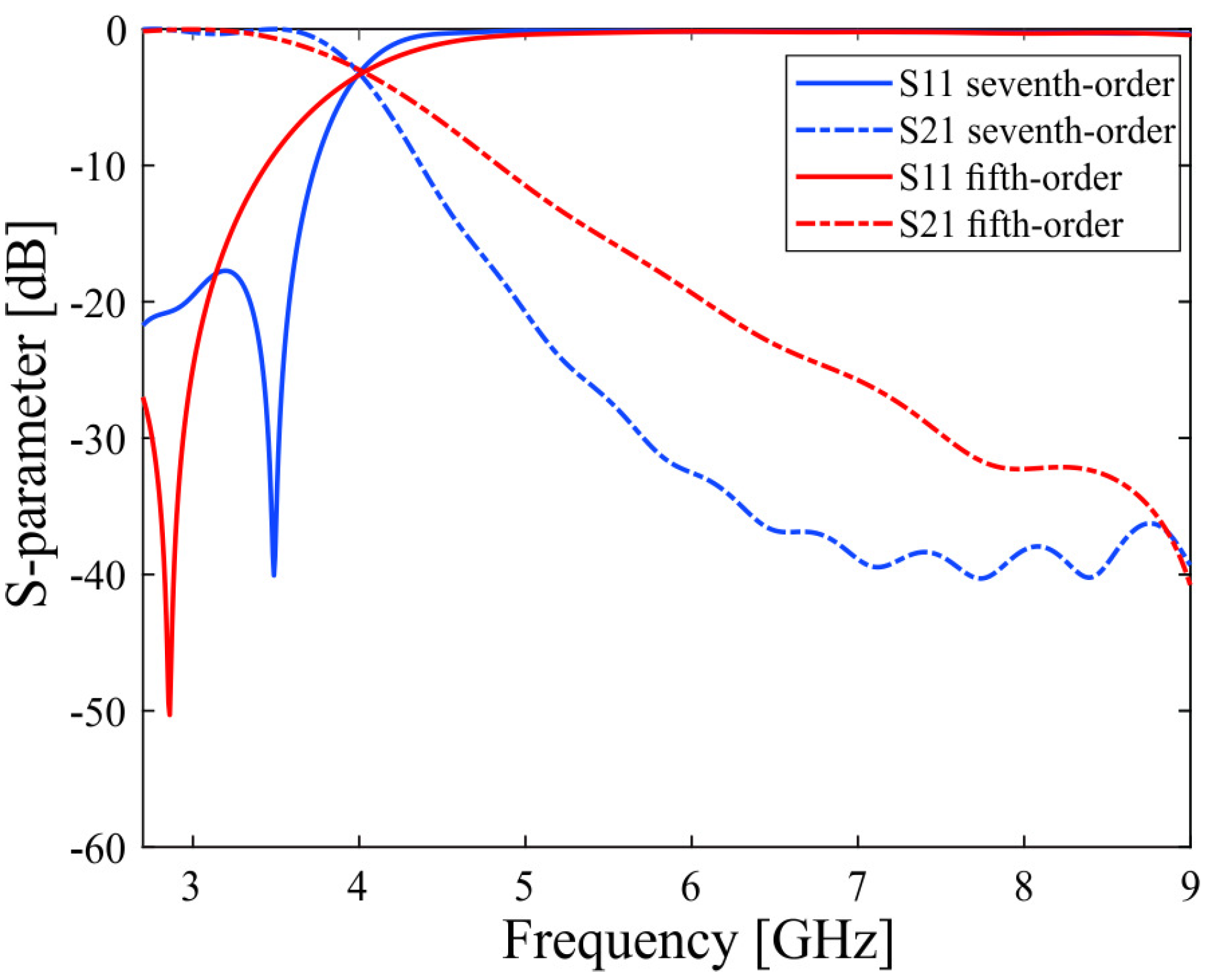
2.2. Design of the Filter for Harmonic Suppression
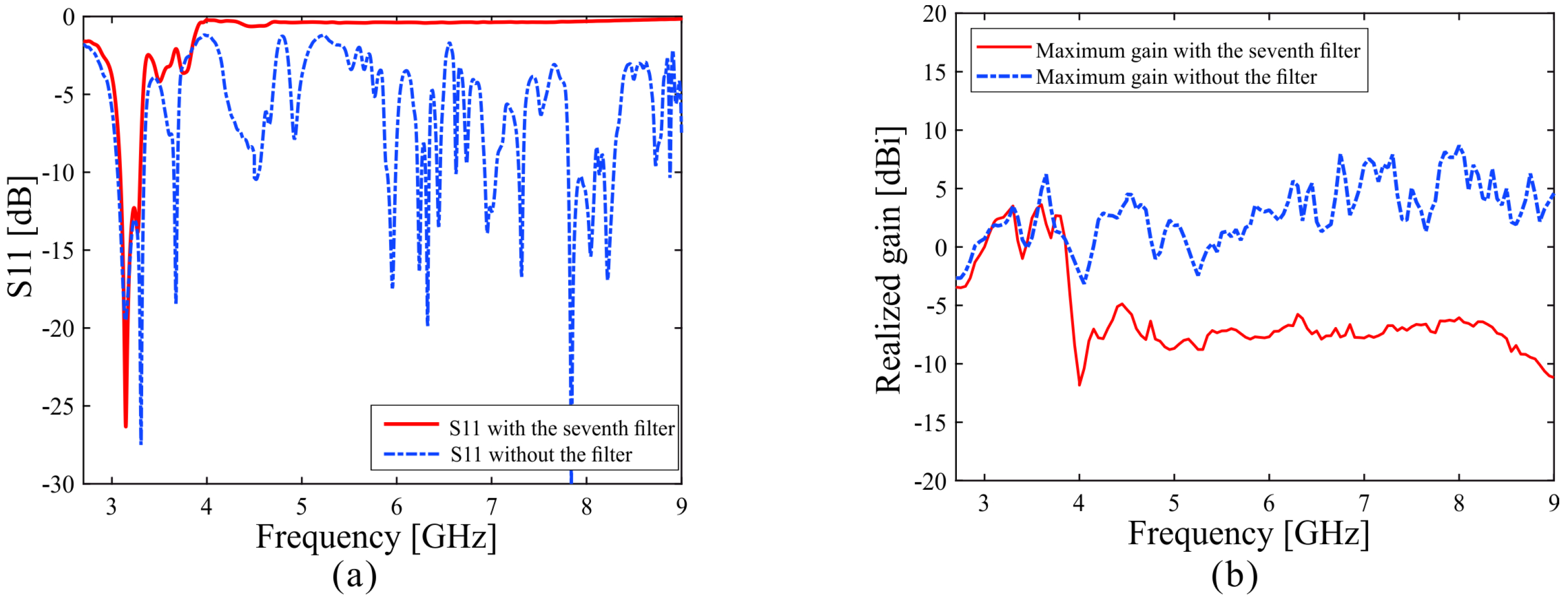
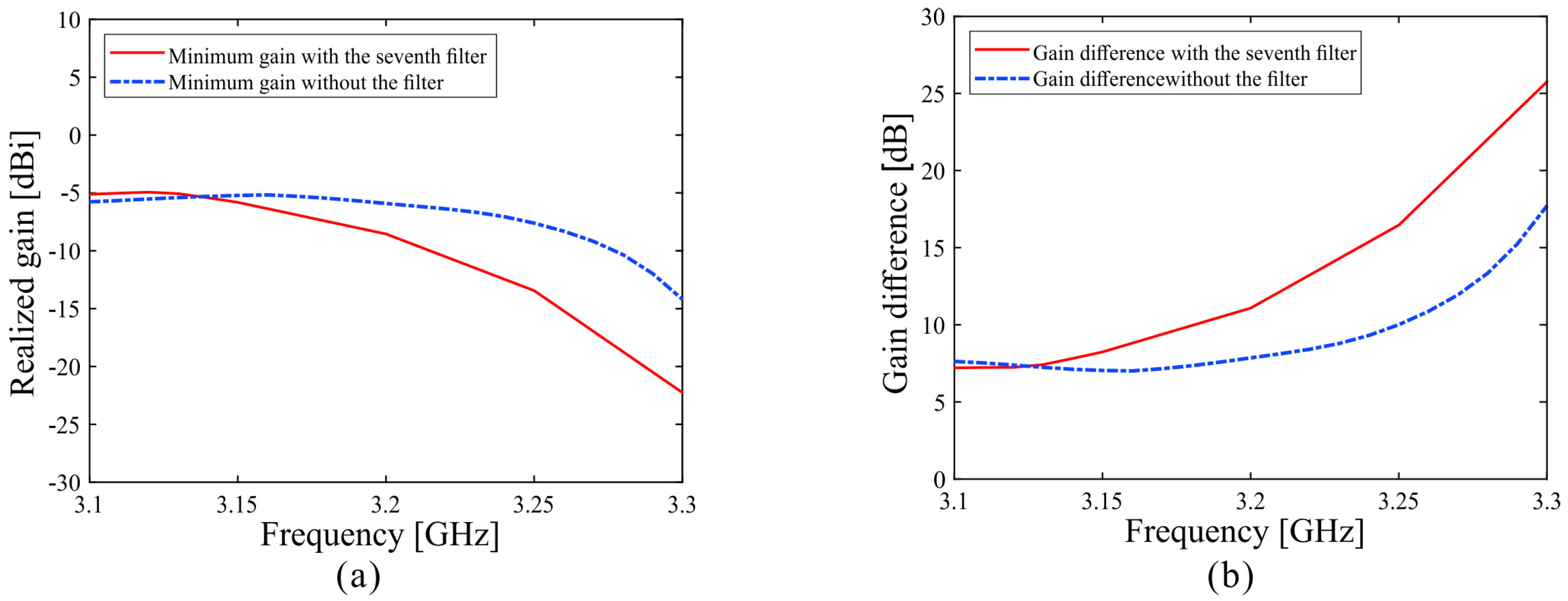
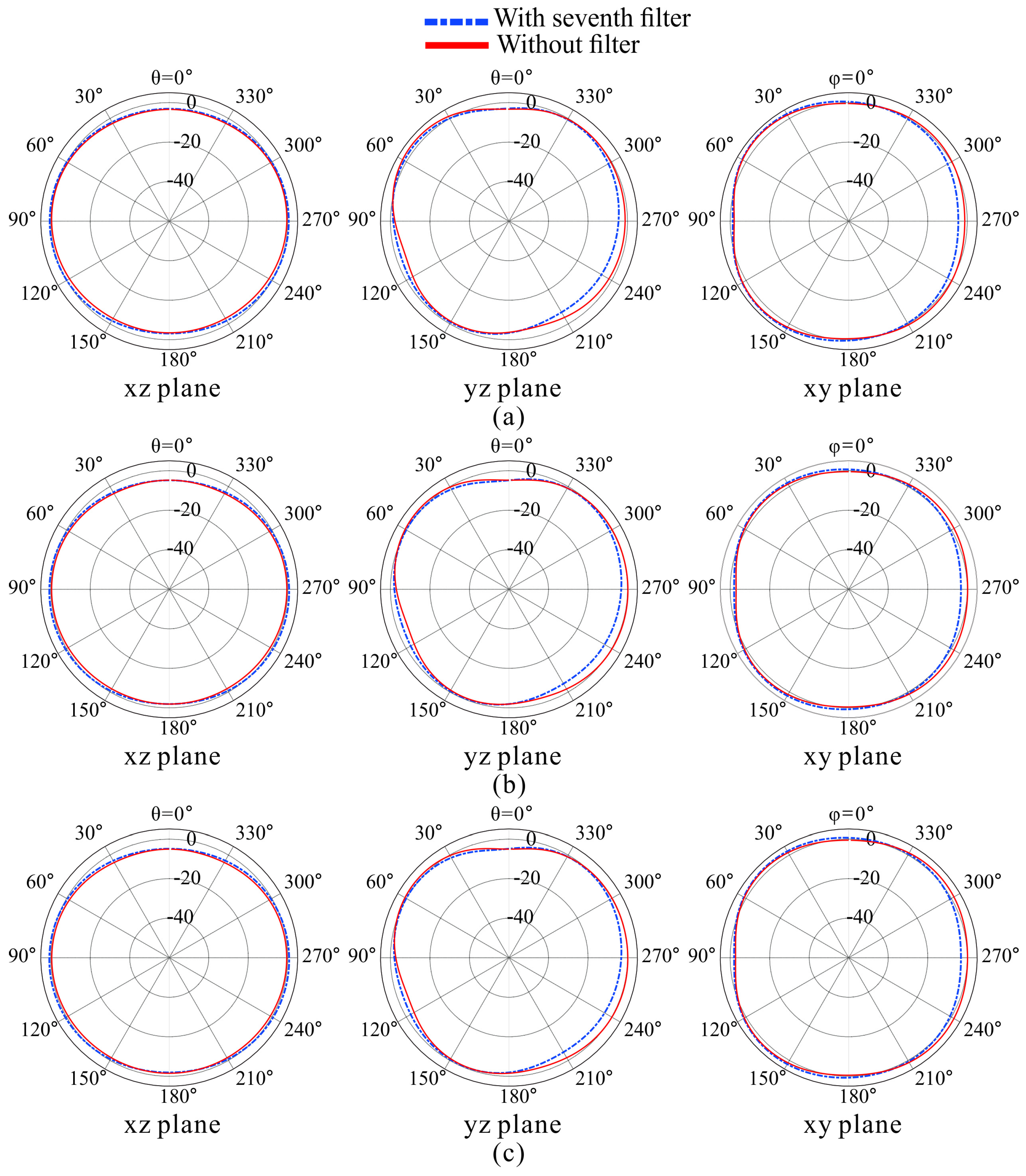
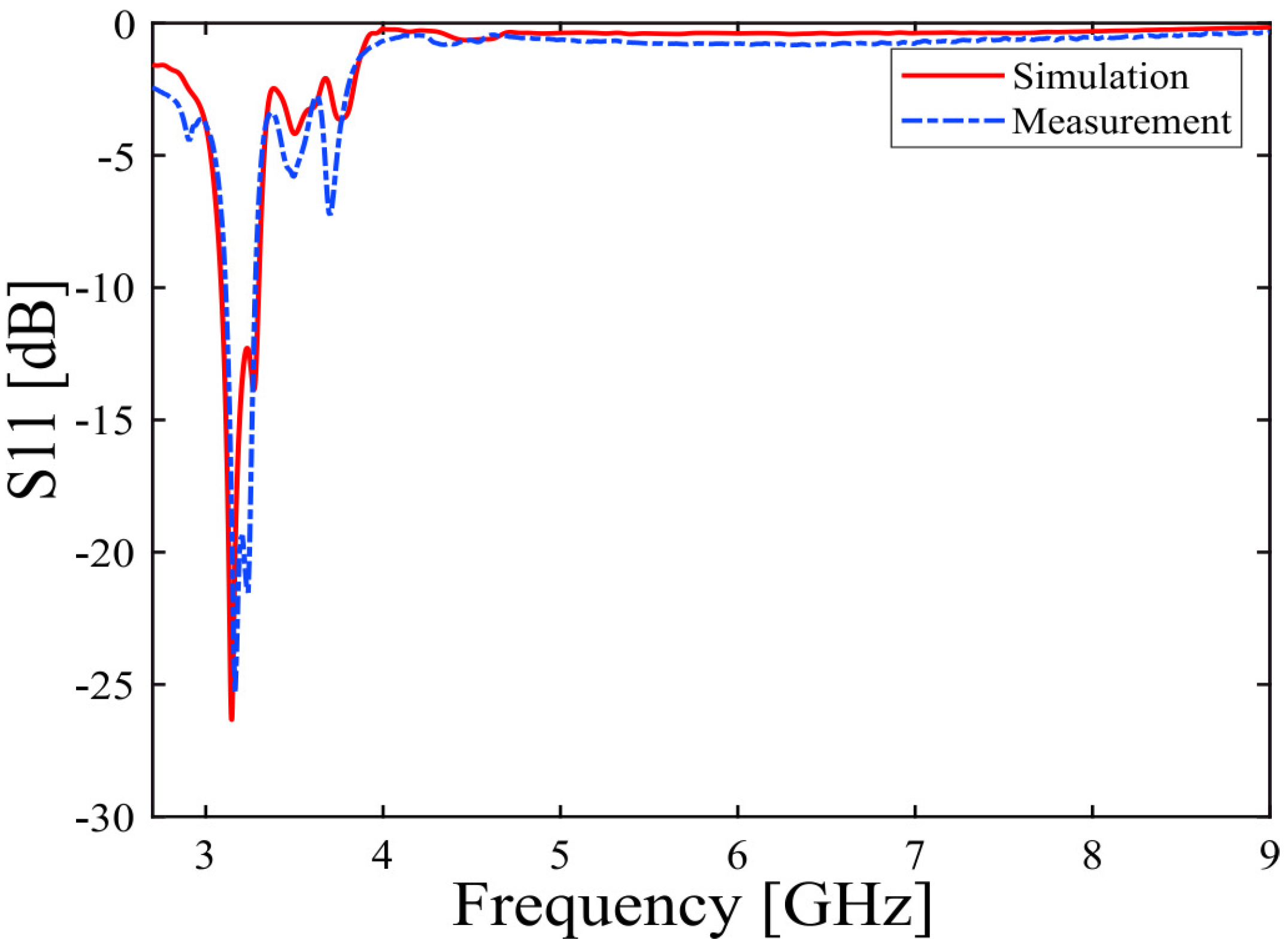
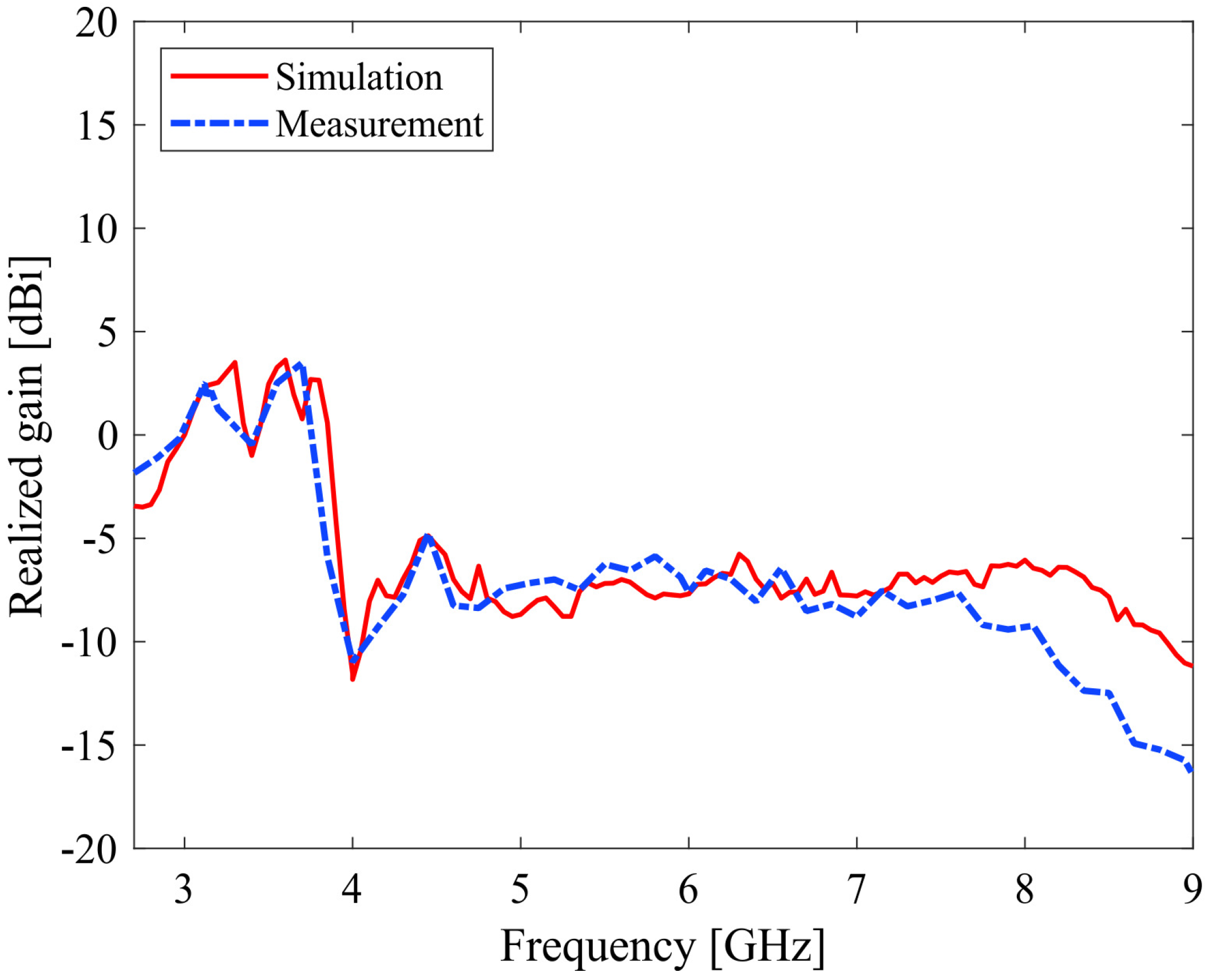
2.3. Simulated Result Analysis of the Proposed Antenna
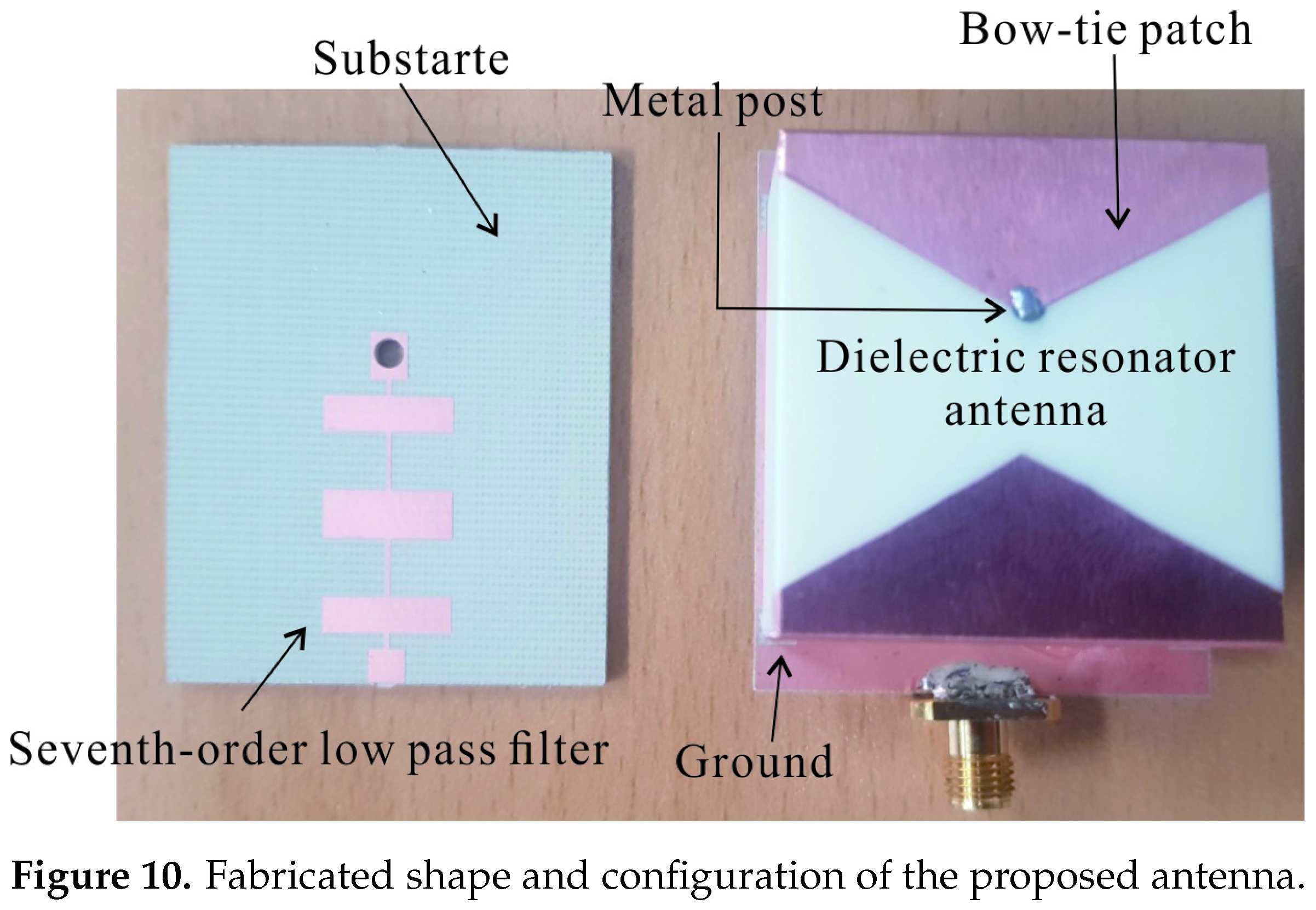
3. Fabrication and Measurement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liang, L.; Hum, S.V. A Low-Profile Antenna With Quasi-Isotropic Pattern for UHF RFID Applications. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 210–213. [Google Scholar] [CrossRef]
- Pan, G.; Li, Y.; Zhang, Z.; Feng, Z. Isotropic Radiation From a Compact Planar Antenna Using Two Crossed Dipoles. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1338–1341. [Google Scholar]
- Deng, C.; Li, Y.; Zhang, Z.; Feng, Z. A Wideband Isotropic Radiated Planar Antenna Using Sequential Rotated L-Shaped Monopoles. IEEE Trans. Antennas Propag. 2014, 62, 1461–1464. [Google Scholar] [CrossRef]
- Ryu, H.; Jung, G.; Ju, D.; Lim, S.; Woo, J. An Electrically Small Spherical UHF RFID Tag Antenna With Quasi-Isotropic Patterns for Wireless Sensor Networks. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 60–62. [Google Scholar] [CrossRef]
- Ouyang, J.; Pan, Y.M.; Zheng, S.Y.; Hu, P.F. An Electrically Small Planar Quasi-Isotropic Antenna. IEEE Antennas Wirel. Propag. Lett. 2018, 12, 303–306. [Google Scholar] [CrossRef]
- Kim, J.H.; Nam, S. A compact quasi-isotropic antenna based on folded split-ring resonators. IEEE Antennas Wirel. Propag. Lett. 2016, 16, 294–297. [Google Scholar] [CrossRef]
- Pan, Y.; Leung, K.W.; Lu, K. Compact Quasi-Isotropic Dielectric Resonator Antenna With Small Ground Plane. IEEE Trans. Antennas Propag. 2014, 62, 577–585. [Google Scholar] [CrossRef]
- Nguyen, N.; Ahmad, R.; Im, Y.; Shin, Y.; Park, S. A T-Shaped Wide-Slot Harmonic Suppression Antenna. IEEE Antennas Wirel. Propag. Lett. 2007, 6, 647–650. [Google Scholar] [CrossRef]
- Yun, J.; Trinh-Van, S.; Park, J.Y.; Yang, Y.; Lee, K.Y.; Hwang, K.C. Cavity-Backed Patch Filtenna for Harmonic Suppression. IEEE Access 2020, 8, 221580–221589. [Google Scholar] [CrossRef]
- Xiang, K.R.; Chen, F.C.; Tan, Q.; Chu, Q.X. Design of Novel Printed Filtering Dipole Antennas. IEEE Trans. Antennas Propag. 2021, 69, 2537–2545. [Google Scholar] [CrossRef]
- Mao, C.X.; Gao, S.; Wang, Y.; Sanz-Izquierdo, B.; Wang, Z.; Qin, F.; Chu, Q.X.; Li, J.; Wei, G.; Xu, J. Dual-Band Patch Antenna with Filtering Performance and Harmonic Suppression. IEEE Trans. Antennas Propag. 2016, 64, 4074–4077. [Google Scholar] [CrossRef]
- Ojaroudi, M.; Ghobadi, C.; Nourinia, J. Small Square Monopole Antenna With Inverted T-Shaped Notch in the Ground Plane for UWB Application. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 728–731. [Google Scholar] [CrossRef]
- Lee, W.; Hong, Y.K.; Choi, M.; Won, H.; Lee, J.; Park, S.O.; Bae, S.; Yoon, H.S. Ferrite-Cored Patch Antenna With Suppressed Harmonic Radiation. IEEE Trans. Antennas Propag. 2018, 66, 3154–3159. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, L.; Wu, Q.; Liu, N.; Wu, W. A Compact Microstrip-Fed Patch Antenna With Enhanced Bandwidth and Harmonic Suppression. IEEE Trans. Antennas Propag. 2016, 64, 5030–5037. [Google Scholar] [CrossRef]
- Liu, Z.X.; Zhu, L.; Liu, N.W. A Compact Omnidirectional Patch Antenna With Ultrawideband Harmonic Suppression. IEEE Trans. Antennas Propag. 2020, 68, 7640–7645. [Google Scholar] [CrossRef]
- Zang, Y.; Zhai, H.; Xi, L.; Li, L. A Compact Microstrip Antenna With Enhanced Bandwidth and Ultra-Wideband Harmonic Suppression. IEEE Trans. Antennas Propag. 2019, 67, 1969–1974. [Google Scholar] [CrossRef]
- Sung, Y.J.; Kim, M.; Kim, Y.S. Harmonics reduction with defected ground structure for a microstrip patch antenna. IEEE Antennas Wirel. Propag. Lett. 2003, 2, 111–113. [Google Scholar] [CrossRef]
- Ma, W. A Microstrip Patch Antenna Design with Harmonic Rejection Using Defected Ground Structure. In Proceedings of the 2019 IEEE MTT-S International Wireless Symposium (IWS), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar]
- Fan, J.; Lin, J.; Cai, J. Ultra-Wideband Harmonic Suppression of Microstrip Antennas Using Compact Defected Ground Structure. In Proceedings of the 2020 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), Online, 7–9 December 2020; pp. 1–3. [Google Scholar]
- Cameron, R.J.; Kudsia, C.M.; Mansour, R.R. Microwave Filters for Communication Systems: Fundamentals, Design, and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018. [Google Scholar]
- Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
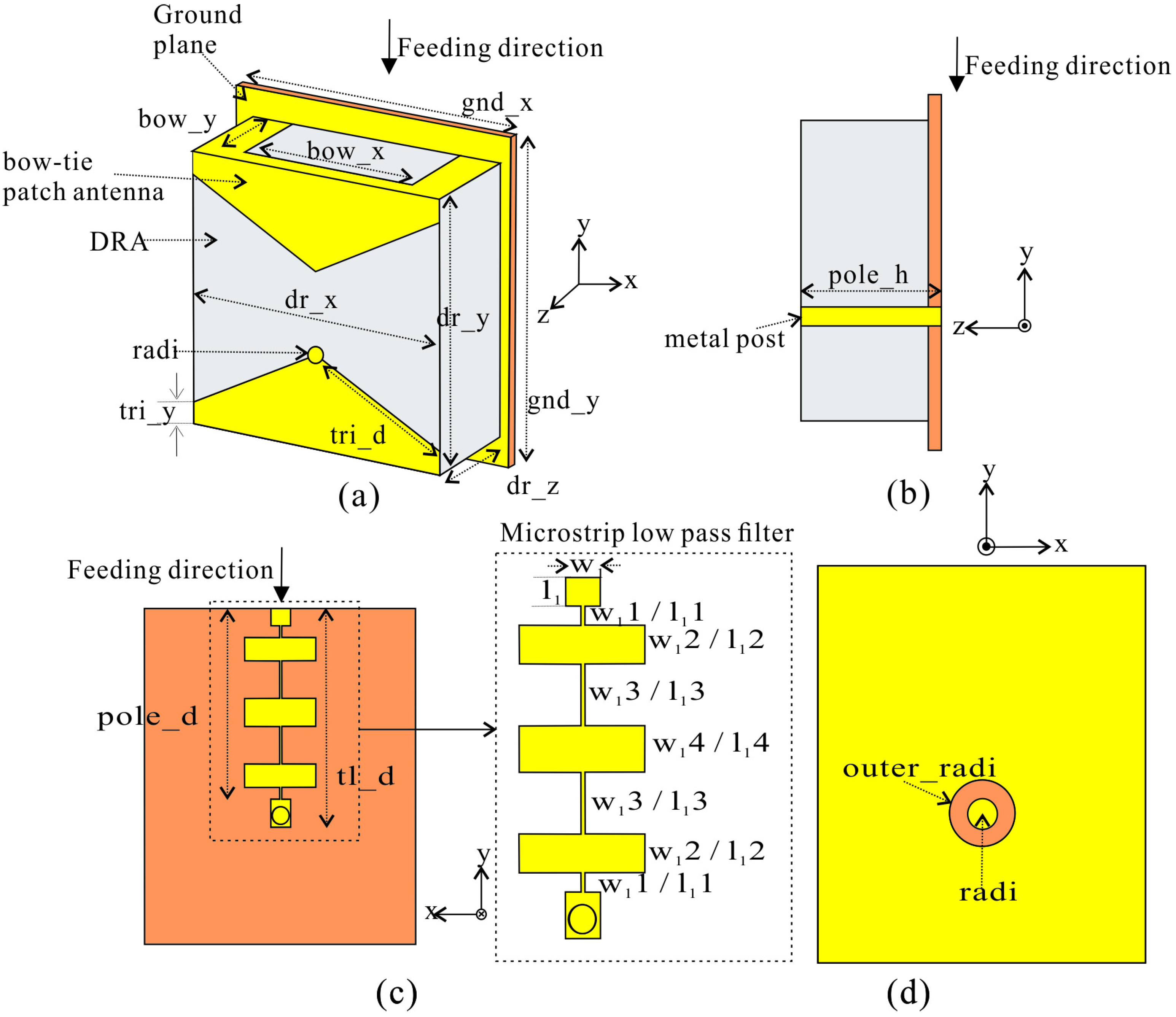



| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| gnd_x | 40.6 | tri_d | 22.29 | l | 1.5 |
| gnd_y | 49.4 | radi | 2.5 | w | 11.77 |
| dr_x | 39 | outer_radi | 8.28 | l | 3.30 |
| dr_y | 40.18 | pole_d | 28.19 | w | 0.425 |
| dr_z | 16.76 | pole_h | 18.28 | l | 5.40 |
| bow_x | 25 | w | 3.344 | w | 11.77 |
| bow_y | 14 | l | 3.29 | l | 4.5 |
| tri_y | 3.28 | w | 0.425 | l | 4.33 |
| g | g | g | g | g | g | g | g | g | |
|---|---|---|---|---|---|---|---|---|---|
| Fifth-order | 1 | 0.756 | 1.305 | 1.577 | 1.305 | 0.56 | 1 | ||
| Seventh-order | 1 | 0.797 | 1.392 | 1.748 | 1.633 | 1.748 | 1.392 | 0.797 | 1 |
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|---|---|
| w | 3.3 | l | 3.35 | w | 0.49 | l | 4.73 |
| l | 5 | w | 0.49 | l | 2.24 | w | 11.58 |
| w | 0.49 | l | 4.79 | w | 11.59 | l | 3.93 |
| l | 2.03 | w | 3.3 | l | 3.14 | ||
| w | 11.59 | l | 5 | w | 0.49 |
| Without a Filter | With the Seventh-Order Filter | |
|---|---|---|
| 3.1 GHz | 1.854 dBi | 2.092 dBi |
| 6 GHz (second harmonic) | 3.158 dBi | −7.689 dBi |
| 9 GHz (third harmonic) | 4.594 dBi | −11.18 dBi |
| Simulated Gain | Measured Gain | |||||
|---|---|---|---|---|---|---|
| 3.1 | 3.13 | 3.15 | 3.1 | 3.13 | 3.15 | |
| Frequency (GHz) | 3.1 | 3.13 | 3.15 | 3.1 | 3.13 | 3.15 |
| Maximum gain (dBi) | 2.080 | 2.358 | 2.428 | 2.145 | 1.908 | 2.282 |
| Minimum gain (dBi) | −4.254 | −5.061 | −5.812 | −6.396 | −7.449 | −8.798 |
| Gain difference (dB) | 6.334 | 7.419 | 8.240 | 8.541 | 9.357 | 11.080 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, T.; Lee, J.S.; Lee, D.G.; Kim, J.H.; Park, J.; Hwang, D.H.; Hwang, K.C. Quasi-Isotropic Hybrid Dielectric Resonator Antenna—Bow-Tie Patch with Harmonic Suppression. Appl. Sci. 2022, 12, 3842. https://doi.org/10.3390/app12083842
Jeong T, Lee JS, Lee DG, Kim JH, Park J, Hwang DH, Hwang KC. Quasi-Isotropic Hybrid Dielectric Resonator Antenna—Bow-Tie Patch with Harmonic Suppression. Applied Sciences. 2022; 12(8):3842. https://doi.org/10.3390/app12083842
Chicago/Turabian StyleJeong, Taeyong, Jong Seon Lee, Dong Geun Lee, Jun Hee Kim, Jinsu Park, Dong Hyee Hwang, and Keum Cheol Hwang. 2022. "Quasi-Isotropic Hybrid Dielectric Resonator Antenna—Bow-Tie Patch with Harmonic Suppression" Applied Sciences 12, no. 8: 3842. https://doi.org/10.3390/app12083842
APA StyleJeong, T., Lee, J. S., Lee, D. G., Kim, J. H., Park, J., Hwang, D. H., & Hwang, K. C. (2022). Quasi-Isotropic Hybrid Dielectric Resonator Antenna—Bow-Tie Patch with Harmonic Suppression. Applied Sciences, 12(8), 3842. https://doi.org/10.3390/app12083842









