Constitutive Modelling of Temperature-Dependent Behaviour of Soft Rocks with Fractional-Order Flow Rule
Abstract
:1. Introduction
2. Governing Equations
2.1. Fractional-Order Flow Rule
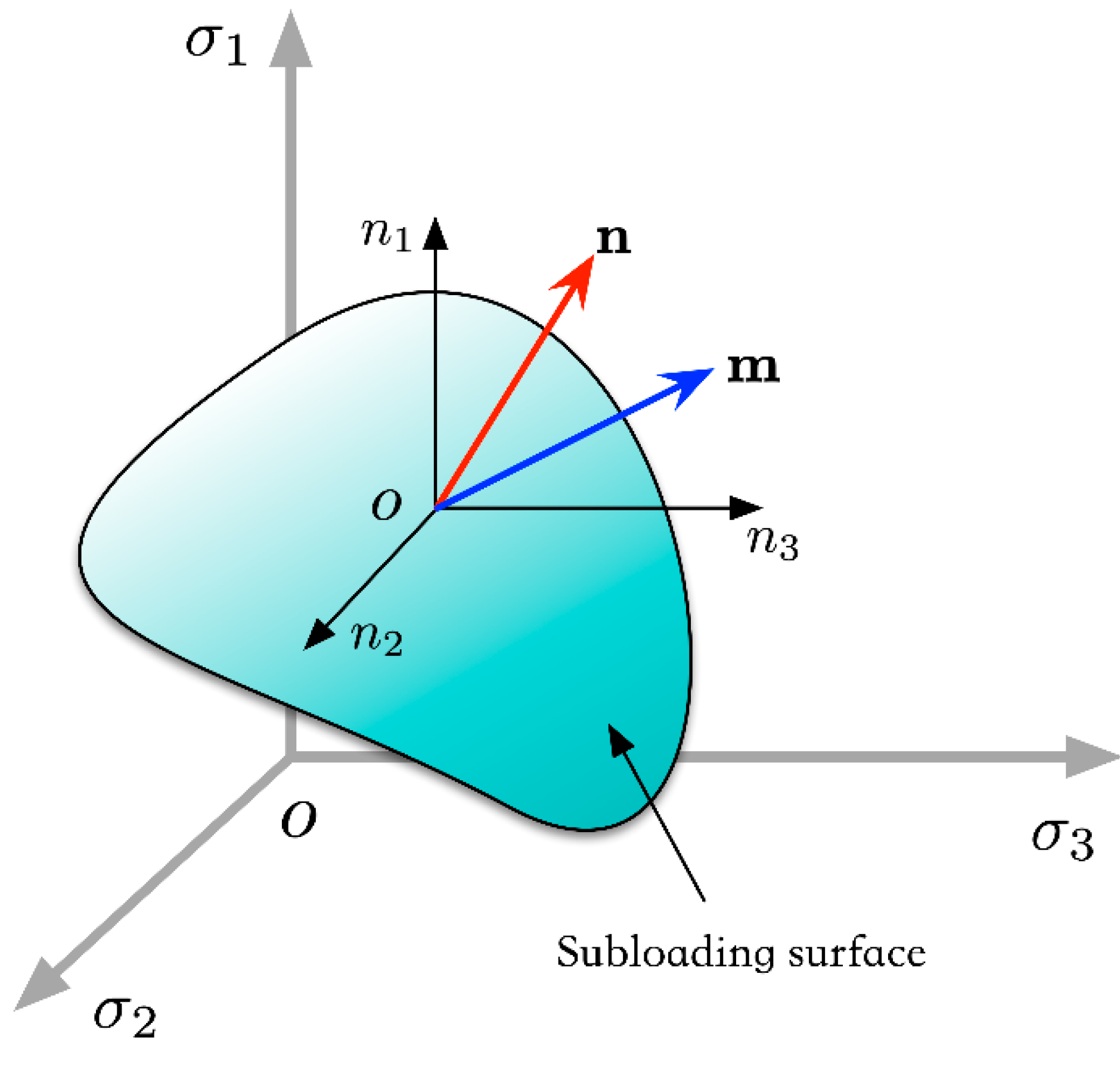
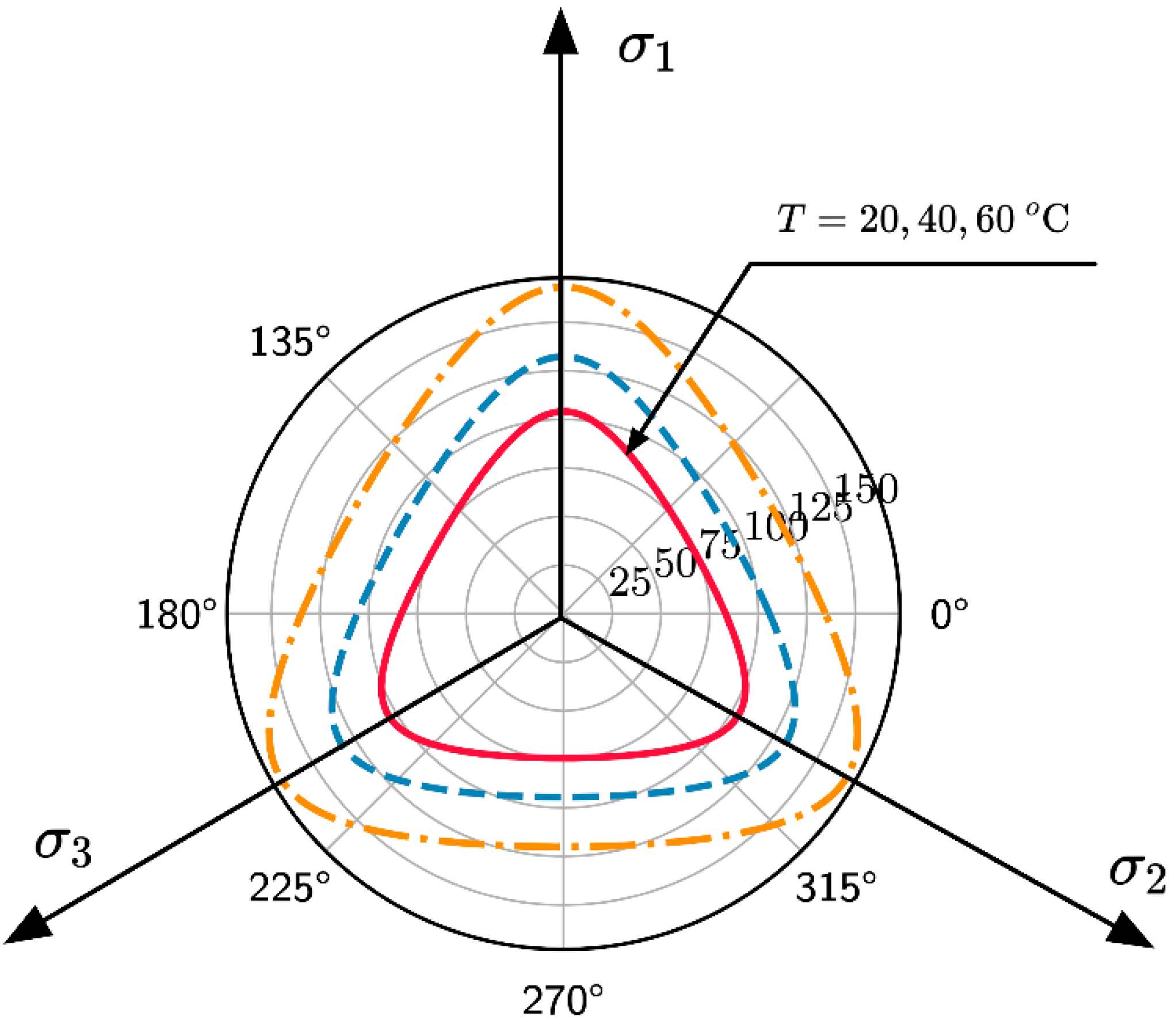
2.2. Temperature-Dependent Subloading Surface
2.3. Evolution of the Fractional-Order
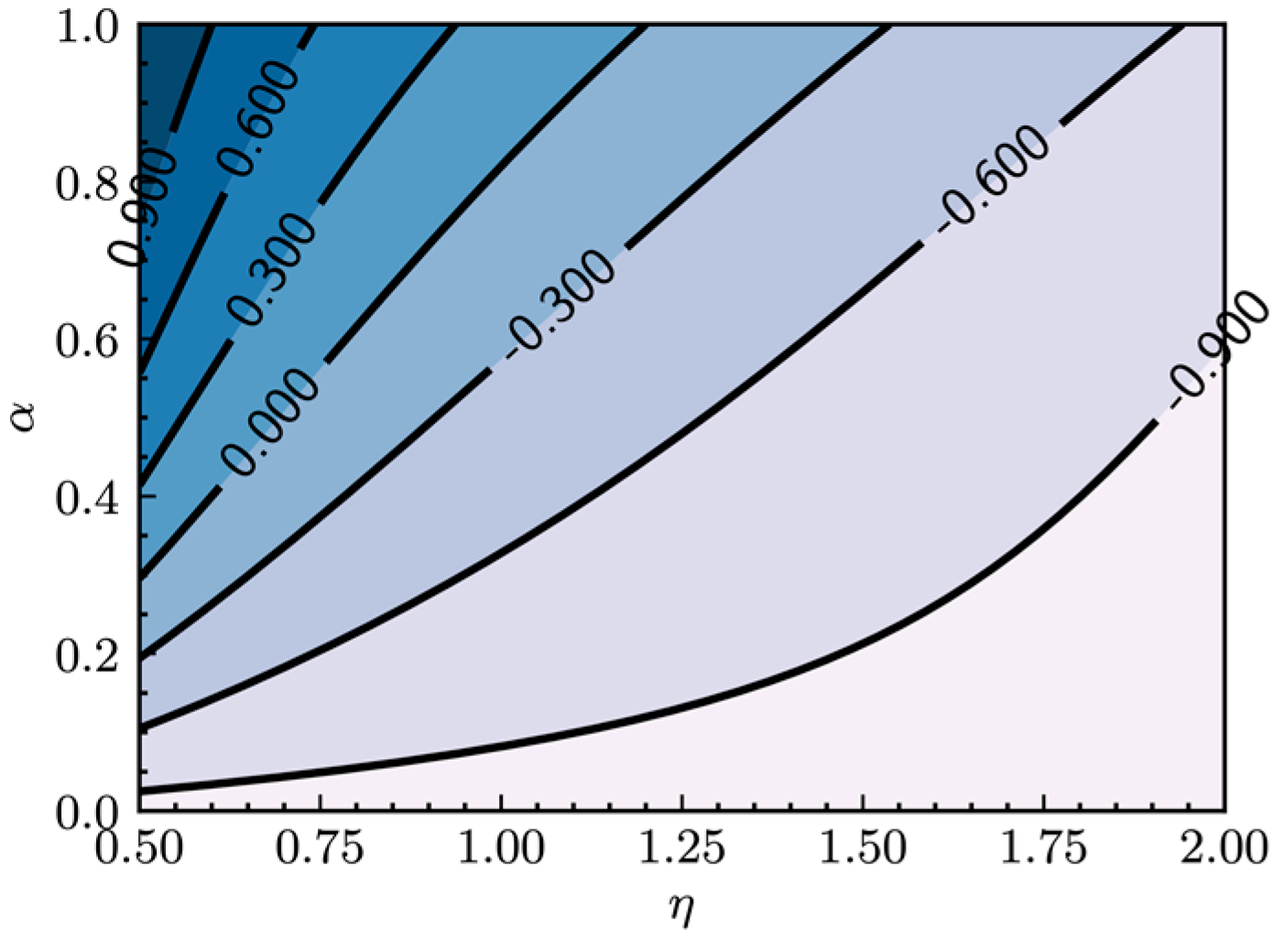
2.4. Incremental Stress–Strain Relation
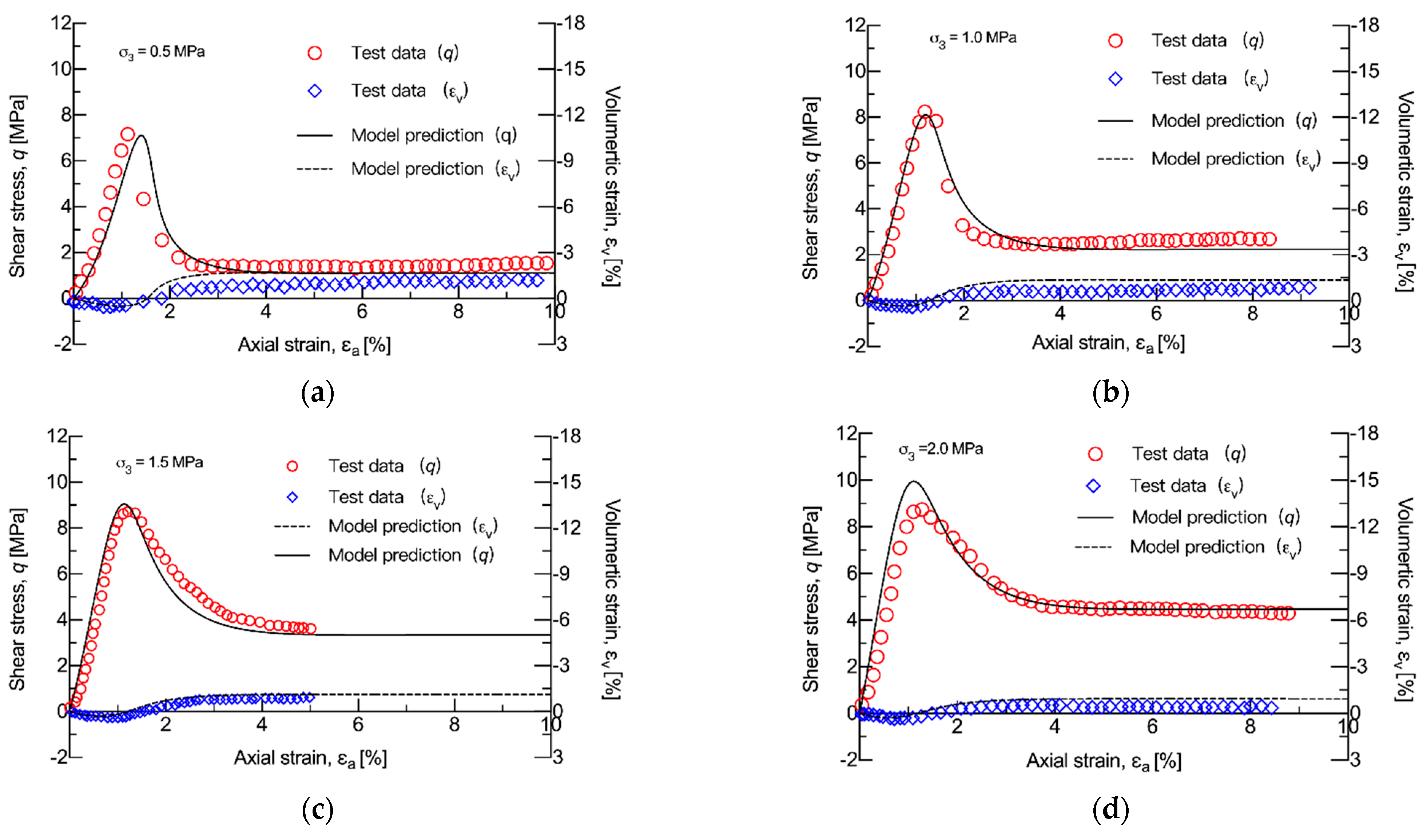
3. Model Verification
4. Conclusions
- (1)
- The concept of temperature-induced preconsolidated pressure with a new parameter, i.e., thermoelastic linear expansion coefficient, was adopted because of the temperature-induced elastic volumetric strain. A fractional-order flow rule is adopted in the proposed model with a new stress–dilatancy relation to account for the nonorthogonality between the plastic strain vectors and the yield surface. The fractional-order is assumed to be affected by the overconsolidated ratio and temperature.
- (2)
- The proposed model can predict the strain-softening and dilatancy features of soft rock specimens subjected to a wide range of temperatures. The peak strength of soft rock will be reduced by increasing the temperature, accompanied by a smaller tangent modulus and more significant dilation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miscevic, P.; Vlastelica, G. Impact of weathering on slope stability in soft rock mass. J. Rock Mech. Geotech. Eng. 2014, 6, 240–250. [Google Scholar] [CrossRef] [Green Version]
- Huang, F.; Wu, C.; Jang, B.; Hong, Y.; Guo, N.; Guo, W. Instability mechanism of shallow tunnel in soft rock subjected to surcharge loads. Tunn. Undergr. Space Technol. 2020, 99, 103350. [Google Scholar] [CrossRef]
- Xu, J.; Haque, A.; Gong, W.; Gamage, R.; Dai, G.; Zhang, Q.; Xu, F. Experimental Study on the Bearing Mechanisms of Rock-socketed Piles in Soft Rock Based on Micro X-ray CT Analysis. Rock Mech. Rock Eng. 2020, 53, 3395–3416. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, C.; Yang, Y.; Guo, Y.; Zhang, X. Analysis of Railway Ballasted Track Stiffness and Behavior with a Hybrid Discrete–Continuum Approach. Int. J. Geomech. 2021, 21, 04020268. [Google Scholar] [CrossRef]
- Xiong, Y.; Yang, Q.; Zhang, S.; Ye, G.; Liu, G.; Zheng, R.; Zhang, F. Thermo-elastoplastic Model for Soft Rock Considering Effects of Structure and Overconsolidation. Rock Mech. Rock Eng. 2018, 51, 3771–3784. [Google Scholar] [CrossRef]
- Kang, X.; Liao, H. A Bounding Surface Plasticity Model Considering Spacing Ratio for Overconsolidated Jointed Soft Rocks. Rock Mech. Rock Eng. 2020, 53, 59–69. [Google Scholar] [CrossRef]
- Kang, X.; Liao, H.; Leng, X. An enhanced bounding surface plasticity model for soft rock subjected to drained and undrained condition. Comput. Geotech. 2020, 127, 103742. [Google Scholar] [CrossRef]
- Romero, E.; Villar, M.; Lloret, A. Thermo-hydro-mechanical behaviour of two heavily overconsolidated clays. Eng. Geol. 2005, 81, 255–268. [Google Scholar] [CrossRef]
- Abuel-Naga, H.; Bergado, D.; Lim, B. 2007. Effect of temperature on shear strength and yielding behavior of soft bangkok clay. Soils Found. 2007, 47, 423–436. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Leng, W.; Zhang, F.; Xiong, Y. A simple thermo-elastoplastic model for geomaterials. Int. J. Plast. 2012, 34, 93–113. [Google Scholar] [CrossRef]
- Shang, X.; Wang, J.; Zhang, Z.; Gao, F. A three-parameter permeability model for the cracking process of fractured rocks under temperature change and external loading. Int. J. Rock Mech. Min. Sci. 2019, 123, 104106. [Google Scholar] [CrossRef]
- Hashiguchi, K. Subloading surface model in unconventional plasticity. Int. J. Solids Struct. 1989, 25, 917–945. [Google Scholar] [CrossRef]
- Anjiki, T.; Oka, M.; Hashiguchi, K. Complete implicit stress integration algorithm with extended subloading surface model for elastoplastic deformation analysis. Int. J. Numer. Methods Eng. 2020, 121, 945–966. [Google Scholar] [CrossRef]
- Islam, M.; Gnanendran, C. Non-Associated Flow Rule-Based Elasto-Viscoplastic Model for Clay. Geosciences 2020, 10, 227. [Google Scholar] [CrossRef]
- Liang, J.; Lu, D.; Du, X.; Ma, C.; Gao, Z.; Han, J. A 3D non-orthogonal elastoplastic constitutive model for transversely isotropic soil. Acta Geotech. 2022, 17, 19–36. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, Y. 2017. Fractional order plasticity model for granular soils subjected to monotonic triaxial compression. Int. J. Solids Struct. 2017, 118, 224–234. [Google Scholar] [CrossRef]
- Lu, D.; Liang, J.; Du, X.; Ma, C.; Gao, Z. Fractional elastoplastic constitutive model for soils based on a novel 3D fractional plastic flow rule. Comput. Geotech. 2019, 105, 277–290. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Sumelka, W.; Gao, Y. Advantages and limitations of an α-plasticity model for sand. Acta Geotech. 2020, 15, 1423–1437. [Google Scholar] [CrossRef]
- Almeida, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef] [Green Version]
- Lagioia, R.; Panteghini, A. On the existence of a unique class of yield and failure criteria comprising Tresca, von Mises, Drucker–Prager, Mohr–Coulomb, Galileo–Rankine, Matsuoka–Nakai and Lade–Duncan. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150713. [Google Scholar] [CrossRef]
- Roscoe, K.; Schofield, A.; Wroth, C. On The Yielding of Soils. Geotechnique 1958, 8, 22–53. [Google Scholar] [CrossRef]
- Been, K.; Jefferies, M.G. A state parameter for sands. Geotechnique 1985, 35, 99–112. [Google Scholar] [CrossRef]
- Ishihara, K.; Tatsuoka, F.; Yasuda, S. Undrained Deformation and Liquefaction of Sand under Cyclic Stresses. Soils Found. 1975, 15, 29–44. [Google Scholar] [CrossRef] [Green Version]
- Uchaipichat, A.; Khalili, N. Experimental investigation of thermo-hydro-mechanical behaviour of an unsaturated silt. Géotechnique 2009, 59, 339–353. [Google Scholar] [CrossRef]
- Bardet, J.P.; Choucair, W. A linearized integration technique for incremental constitutive equations. Int. J. Numer. Anal. Methods Geomech. 1991, 15, 1–19. [Google Scholar] [CrossRef]
- Janda, T.; Mašín, D. General method for simulating laboratory tests with constitutive models for geomechanics. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 304–312. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.-C.; Tong, C.-X.; Chang, X.; Zhang, S. Constitutive Modelling of Temperature-Dependent Behaviour of Soft Rocks with Fractional-Order Flow Rule. Appl. Sci. 2022, 12, 3875. https://doi.org/10.3390/app12083875
Li H-C, Tong C-X, Chang X, Zhang S. Constitutive Modelling of Temperature-Dependent Behaviour of Soft Rocks with Fractional-Order Flow Rule. Applied Sciences. 2022; 12(8):3875. https://doi.org/10.3390/app12083875
Chicago/Turabian StyleLi, Hai-Chao, Chen-Xi Tong, Xin Chang, and Sheng Zhang. 2022. "Constitutive Modelling of Temperature-Dependent Behaviour of Soft Rocks with Fractional-Order Flow Rule" Applied Sciences 12, no. 8: 3875. https://doi.org/10.3390/app12083875
APA StyleLi, H.-C., Tong, C.-X., Chang, X., & Zhang, S. (2022). Constitutive Modelling of Temperature-Dependent Behaviour of Soft Rocks with Fractional-Order Flow Rule. Applied Sciences, 12(8), 3875. https://doi.org/10.3390/app12083875






