Flexural Analysis Model of Externally Prestressed Steel-Concrete Composite Beam with Nonlinear Interfacial Connection
Abstract
:1. Introduction
2. Finite Element Formulations and Developed Procedure
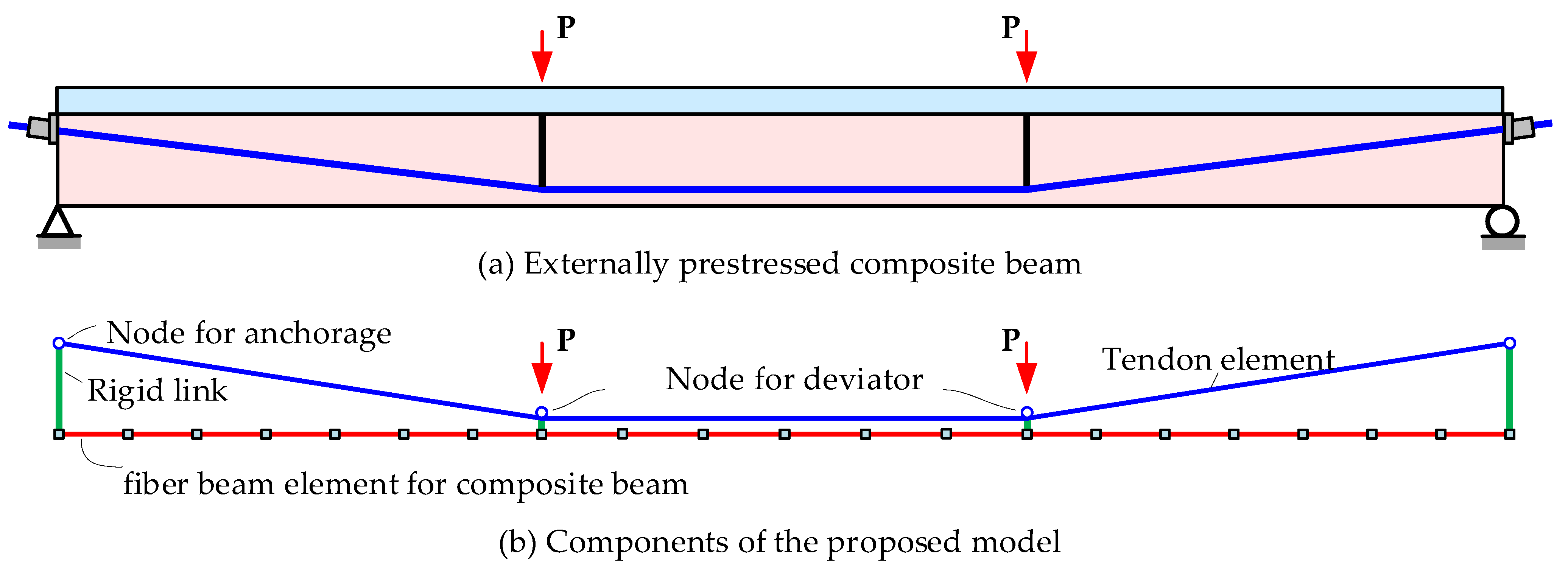
2.1. Schemes of the Proposed Model
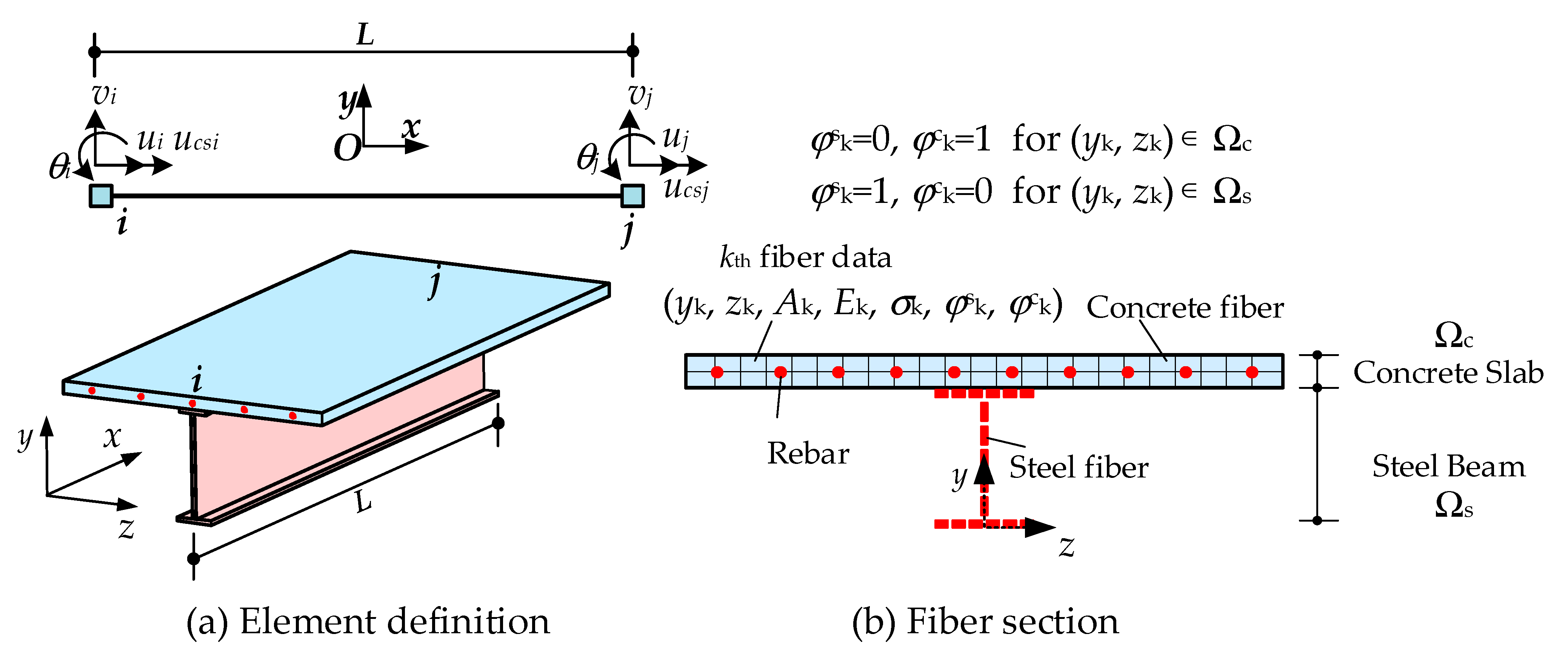
2.2. Fiber Beam Element Model with Nonlinear Interfacial Connection
2.3. Multi-Node Slipping Cable Element for External Tendon
2.4. Rigid Link between Beam and Tendon
2.5. Constitutive Model
- (1)
- Concrete constitutive model
- (2)
- Prestressing steel tendon constitutive model
- (3)
- Constitutive model for steel beam and reinforcements
- (4)
- Interfacial shear-slip model
2.6. Computational Procedure Development
2.7. Highlights of the Proposed Model
- (1)
- A new modeling method is proposed by introducing two relative slip DOFs into the ends of the fiber beam element. An 8-DOF fiber beam element was built for the composite beam with material, geometric and interfacial nonlinearity.
- (2)
- Taking the external tendon as the whole member, a multi-node slipping cable element is proposed with a complete stiffness and resistance matrix. Compared with the equivalent load method, the numerical convergence was improved and can be widely used for external tendons with different profiles.
- (3)
- The methods and framework of the element classes developed in OpenSees are presented.
3. Experimental Verification
3.1. Verification for the Nonlinear Interfacial Behaviors
3.2. Verification for the Case of Simply Supported EPCB
3.3. Verification for the Case of Continuous EPCB
4. Parametric Analysis
4.1. Effects of Deviator Spacing
4.2. Effects of External Tendon Effective Height
4.3. Effects of Interfacial Slip
5. Conclusions
- Interfacial slip effects are inevitable for steel-concrete composite beams during their service life, even when they are designed with full shear connections. The structural stiffness, capacity and failure modes are all affected. The proposed fiber beam element model considering interfacial slip effects can be used to predict the capacity, deformation and failure mode, which are all verified to agree well with the experimental results.
- Ignoring the friction at the deviators, the external tendon has equal traction along its whole length. The conventional truss element could not satisfy the strain-compatibility property in multiple segments, causing some overestimation of the stress increments and flexural capacity. The proposed slipping cable element is built considering the strain-compatibility property, which shows better agreement with the experimental results.
- The parameter analysis results reveal that the deviator spacing, external tendon effective height, interfacial shear capacity and loading type all affect the flexural capacity of EPCBs. An increase in the deviator spacing decreases the ultimate effective height of the external tendon, which then leads to a decrease in the flexural capacity. The increased external tendon effective height increases the ultimate stress increments and flexural capacity. With an increase in the interfacial shear capacity, the flexural capacity increases gradually but the stress increments and effective height of the tendon do not vary monotonously. The proposed model provides an effective method for predicting the flexural behaviors of EPCBs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, L.B.; Han, B.; Fan, L.; Li, X. Fatigue Damage of PBH Shear Connector of Steel-Concrete Composite Structure. Eng. Struct. 2020, 213, 110540. [Google Scholar] [CrossRef]
- El-Zohairy, A.; Salim, H.; Saucier, A. Steel-Concrete Composite Beams Strengthened with Externally Post-Tensioned Tendons under Fatigue. J. Bridge Eng. 2019, 24, 04019027. [Google Scholar] [CrossRef]
- Xu, J.; Sun, H.; Chen, W.; Guo, X. Experiment-Based Fatigue Behaviors and Damage Detection Study of Headed Shear Studs in Steel-Concrete Composite Beams. Appl. Sci. 2021, 11, 8297. [Google Scholar] [CrossRef]
- Kim, S.-H.; Park, J.-S.; Jung, W.-T.; Kim, T.-K.; Park, H.-B. Experimental Study on Strengthening Effect Analysis of a Deteriorated Bridge Using External Prestressing Method. Appl. Sci. 2021, 11, 2478. [Google Scholar] [CrossRef]
- Kim, S.-H.; Park, J.-S.; Jung, W.-T.; Kang, J.-Y. Strengthening Effect of the External Prestressing Method That Simulated a Deterioration Bridge. Appl. Sci. 2021, 11, 2553. [Google Scholar] [CrossRef]
- Alqam, M.; Alkhairi, F. Numerical and Analytical Behavior of Beams Prestressed with Unbonded Internal or External Steel Tendons: A State-of-the-Art Review. Arab. J. Sci. Eng. 2019, 44, 8149–8170. [Google Scholar] [CrossRef]
- Ayyub, B.M.; Sohn, Y.G.; Saadatmanesh, H. Prestressed Composite Girders under Positive Moment. J. Struct. Eng. 1990, 116, 2931–2951. [Google Scholar] [CrossRef]
- Chen, S.; Gu, P. Load Carrying Capacity of Composite Beams Prestressed with External Tendons under Positive Moment. J. Constr. Steel Res. 2005, 61, 515–530. [Google Scholar] [CrossRef]
- Chen, S.M. Experimental Study of Prestressed Steel-Concrete Composite Beams with External Tendons for Negative Moments. J. Constr. Steel Res. 2005, 61, 1613–1630. [Google Scholar] [CrossRef]
- Lorenc, W.; Kubica, E. Behavior of Composite Beams Prestressed with External Tendons: Experimental Study. J. Constr. Steel Res. 2006, 62, 1353–1366. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X.; Jia, Y. A Comparative Study of Continuous Steel-Concrete Composite Beams Prestressed with External Tendons: Experimental Investigation. J. Constr. Steel Res. 2009, 65, 1480–1489. [Google Scholar] [CrossRef]
- Chen, S.; Jia, Y.; Wang, X. Experimental Study of Moment Redistribution and Load Carrying Capacity of Externally Prestressed Continuous Composite Beams. Struct. Eng. Mech. 2009, 31, 605–619. [Google Scholar] [CrossRef]
- Nie, J.; Tao, M.; Cai, C.S.; Li, S. Deformation Analysis of Prestressed Continuous Steel-Concrete Composite Beams. J. Struct. Eng. 2009, 135, 1377–1389. [Google Scholar] [CrossRef]
- Sun, Q.; Yang, Y.; Fan, J.; Zhang, Y.; Bai, Y. Effect of Longitudinal Reinforcement and Prestressing on Stiffness of Composite Beams under Hogging Moments. J. Constr. Steel Res. 2014, 100, 1–11. [Google Scholar] [CrossRef]
- Hassanin, A.I.; Shabaan, H.F.; Elsheikh, A.I. Cyclic Loading Behavior on Strengthened Composite Beams Using External Post-Tensioning Tendons (Experimental Study). Structures 2021, 29, 1119–1136. [Google Scholar] [CrossRef]
- El-Sisi, A.A.; Hassanin, A.I.; Shabaan, H.F.; Elsheikh, A.I. Effect of External Post-Tensioning on Steel-Concrete Composite Beams with Partial Connection. Eng. Struct. 2021, 247, 113130. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Fu, W.; Du, H.; Sun, Q.; Zhang, Q. Experimental and Theoretical Study on Longitudinal Shear Behavior of Steel-Concrete Composite Beams. J. Constr. Steel Res. 2020, 171, 106144. [Google Scholar] [CrossRef]
- Wang, B.; Huang, Q.; Liu, X.; Li, W. Experimental Investigation of Steel-Concrete Composite Beams with Different Degrees of Shear Connection under Monotonic and Fatigue Loads. Adv. Struct. Eng. 2018, 21, 227–240. [Google Scholar] [CrossRef]
- Alsharari, F.; El-Zohairy, A.; Salim, H.; El-Din El-Sisi, A. Pre-Damage Effect on the Residual Behavior of Externally Post-Tensioned Fatigued Steel-Concrete Composite Beams. Structures 2021, 32, 578–587. [Google Scholar] [CrossRef]
- Nie, J.; Tao, M.; Cai, C.S.; Li, S. Analytical and Numerical Modeling of Prestressed Continuous Steel-Concrete Composite Beams. J. Struct. Eng.-ASCE 2011, 137, 1405–1418. [Google Scholar] [CrossRef]
- El-Zohairy, A.; Salim, H.; Shaaban, H.; Mustafa, S.; El-Shihy, A. Finite-Element Modeling of Externally Posttensioned Composite Beams. J. Bridge Eng. 2015, 20, 04015018. [Google Scholar] [CrossRef]
- El-Zohairy, A.; Salim, H. Parametric Study for Post-Tensioned Composite Beams with External Tendons. Adv. Struct. Eng. 2017, 20, 1433–1450. [Google Scholar] [CrossRef]
- da Rocha Almeida, M.M.; Clemente de Souza, A.S.; de Albuquerque, A.T.; Rossi, A. Parametric Analysis of Steel-Concrete Composite Beams Prestressed with External Tendons. J. Constr. Steel Res. 2022, 189, 107087. [Google Scholar] [CrossRef]
- Sanchez, B.d.S.; Tamayo, J.P.; Morsch, I.B.; Miranda, M.P. A Nonlinear Geometric Model for Pre-Stressed Steel-Concrete Composite Beams. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 233. [Google Scholar] [CrossRef]
- Alsharari, F.; El-Zohairy, A.; Salim, H.; El-Sisi, A.E.-D. Numerical Investigation of the Monotonic Behavior of Strengthened Steel-Concrete Composite Girders. Eng. Struct. 2021, 246, 113081. [Google Scholar] [CrossRef]
- Palomino Tamayo, J.L.; Franco, M.I.; Morsch, I.B.; Desir, J.M.; Wayar, A.M.M. Some Aspects of Numerical Modeling of Steel-Concrete Composite Beams with Prestressed Tendons. Lat. Am. J. Solids Struct. 2019, 16, e219. [Google Scholar] [CrossRef] [Green Version]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. Numerical Modeling of Externally Prestressed Steel-Concrete Composite Beams. J. Constr. Steel Res. 2016, 121, 229–236. [Google Scholar] [CrossRef]
- Lou, T.; Karavasilis, T.L. Numerical Assessment of the Nonlinear Behavior of Continuous Prestressed Steel-Concrete Composite Beams. Eng. Struct. 2019, 190, 116–127. [Google Scholar] [CrossRef]
- Lou, T.; Karavasilis, T.L. Numerical Evaluation of Prestressed Steel-Concrete Composite Girders with External FRP or Steel Tendons. J. Constr. Steel Res. 2019, 162, 105698. [Google Scholar] [CrossRef]
- Lou, T.; Karavasilis, T.L.; Chen, B. Assessment of Second-Order Effect in Externally Prestressed Steel-Concrete Composite Beams. J. Bridge Eng. 2021, 26, 04021024. [Google Scholar] [CrossRef]
- El-Zohairy, A.; Alsharari, F.; Salim, H. Analytical Model and Parametric Study for Externally Post-Tensioned Reinforced Concrete-Steel Composite Beams. Structures 2020, 27, 411–423. [Google Scholar] [CrossRef]
- Zhang, Q.; Jia, D.; Bao, Y.; Dong, S.; Cheng, Z.; Bu, Y. Flexural Behavior of Steel-Concrete Composite Beams Considering Interlayer Slip. J. Struct. Eng. 2019, 145, 04019084. [Google Scholar] [CrossRef]
- Dall’Asta, A.; Dezi, L.; Leoni, G. Failure Mechanisms of Externally Prestressed Composite Beams with Partial Shear Connection. Steel Compos. Struct. 2002, 2, 315–330. [Google Scholar] [CrossRef]
- Dall’Asta, A.; Zona, A. Finite Element Model for Externally Prestressed Composite Beams with Deformable Connection. J. Struct. Eng. 2005, 131, 706–714. [Google Scholar] [CrossRef]
- Zona, A.; Ragni, L.; Dall’Asta, A. Finite Element Formulation for Geometric and Material Nonlinear Analysis of Beams Prestressed with External Slipping Tendons. Finite Elem. Anal. Des. 2008, 44, 910–919. [Google Scholar] [CrossRef]
- Sousa, J.B.M., Jr.; Parente, E., Jr.; Lima, E.M.F.; Oliveira, M.V.X. Beam-Tendon Finite Elements for Post-Tensioned Steel-Concrete Composite Beams with Partial Interaction. J. Constr. Steel Res. 2019, 159, 147–160. [Google Scholar] [CrossRef]
- Mckenna, F.; Fenves, G. Opensees 2.5.0, Computer Software; UC Berkeley: Berkeley, CA, USA, 2015; Available online: http://opensees.berkeley.edu (accessed on 1 March 2020).
- CEB-FIP, Model Code 2010; Thomas Telford: Lausanne, Switzerland, 2010.
- Ollgaard, J.G.; Slutter, R.G.; Fisher, J.G. Shear Strength of Stud Shear Connections in Lightweight and Normal Weight Concrete. AISC Eng. J. 1971, 8, 55–64. [Google Scholar]



















| Components | Yield Strength (MPa) | Ultimate Strength (MPa) | Elastic Modulus (MPa) |
|---|---|---|---|
| Rebar φ6 | 440 | 524 | 2.23 × 105 |
| Steel Beam | 342 | 447 | 2.23 × 105 |
| Shear Studs | 488 | 552 | - |
| Specimen | Cubic Compressive Strength (MPa) | Prismatic Compressive Strength (MPa) | Elastic Modulus (MPa) |
|---|---|---|---|
| NCB-4 | 30.0 | 22.8 | 22,800 |
| NCB-5 | 29.4 | 22.3 | 22,300 |
| NCB-6 | 35.6 | 27.1 | 27,100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, W.; Chen, L.; Han, B.; Xie, H.; Sun, Y. Flexural Analysis Model of Externally Prestressed Steel-Concrete Composite Beam with Nonlinear Interfacial Connection. Appl. Sci. 2022, 12, 4699. https://doi.org/10.3390/app12094699
Yan W, Chen L, Han B, Xie H, Sun Y. Flexural Analysis Model of Externally Prestressed Steel-Concrete Composite Beam with Nonlinear Interfacial Connection. Applied Sciences. 2022; 12(9):4699. https://doi.org/10.3390/app12094699
Chicago/Turabian StyleYan, Wutong, Liangjiang Chen, Bing Han, Huibing Xie, and Yue Sun. 2022. "Flexural Analysis Model of Externally Prestressed Steel-Concrete Composite Beam with Nonlinear Interfacial Connection" Applied Sciences 12, no. 9: 4699. https://doi.org/10.3390/app12094699
APA StyleYan, W., Chen, L., Han, B., Xie, H., & Sun, Y. (2022). Flexural Analysis Model of Externally Prestressed Steel-Concrete Composite Beam with Nonlinear Interfacial Connection. Applied Sciences, 12(9), 4699. https://doi.org/10.3390/app12094699







