Development of Charging/Discharging Scheduling Algorithm for Economical and Energy-Efficient Operation of Multi-EV Charging Station
Abstract
:1. Introduction
- (1)
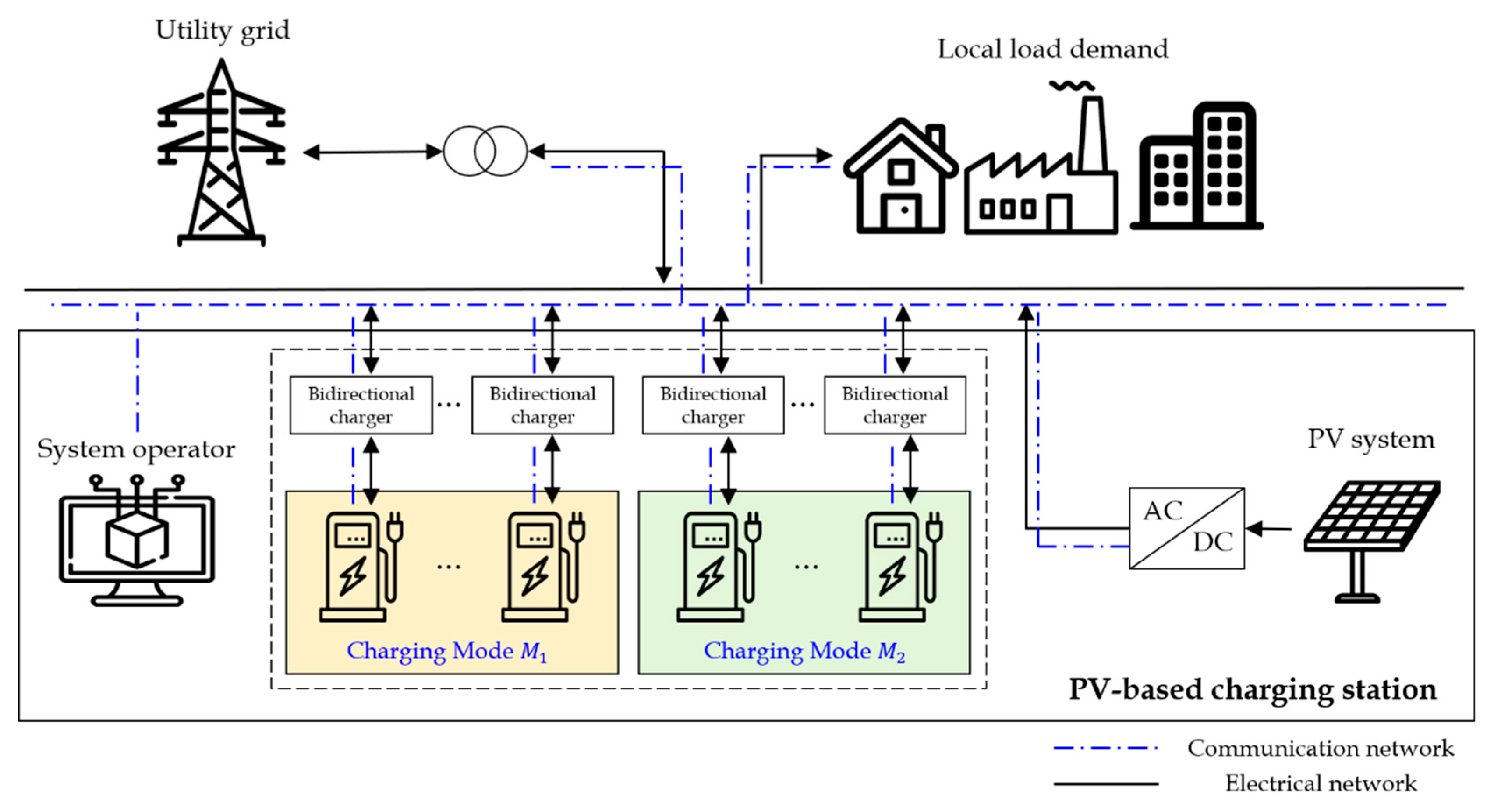
- A novel power management scheme for independent MG and EV fleets in the PV-based charging station is presented. The PV power produced from the PV-based charging station is used as a secondary source to satisfy the local load demand and charging demand of EVs, and it is consumed prior to grid power. With the proposed EV charging/discharging scheduling algorithm, discharging power from parked EVs is also be used to meet the local load demand and charging demand of EVs. In addition, the system operator of the PV-based charging station can decrease the operating cost by selling the produced PV power and discharging power of EVs to electric companies which are supplemented to the local load demand. For economical and energy-efficient power management of the PV-based charging station, a demand response (DR) program, SMP, and REC are considered.
- (2)
- The multi-EV charging/discharging scheduling algorithm with GRU network is proposed for economical and energy-efficient power management of parked EVs in the PV-based charging station. Parked EVs of the PV-based charging station are assigned to charging/discharging operation based on the maximum amount of discharging power of EVs determined by the future trends of local load demand and PV power production that are predicted by the GRU network. Compared with the power management scheme with conventional EV charging/discharging scheduling algorithm utilizing only the currently measured local load demand and PV power production, the power management scheme with the proposed EV charging/discharging scheduling algorithm considering the variation trends of local load demand and PV power production can further reduce the operating cost of the PV-based charging station. The proposed power management scheme is also compared with the conventional scheme using the EV charging scheduling algorithm not considering discharging of EVs. As a result of comparing the performance of the power management schemes presented in this paper, a substantial difference is observed in the aspect of operational efficiency and economic feasibility of the PV-based charging station
- (3)
- In the PV-based charging station, several EVs are connected to the charging system via individual EV charging connectors. Since the parked EVs are interconnected to the MG through the electricity network, some EVs can be charged by the utility grid, PV system, and discharging of other EVs, and some EVs can be discharged to supplement the local load demand and charging demand of EVs among EV charging/discharging candidates. In this study, driving pattern of EVs is considered according to distribution of arrival at home and workplace. The EV charging/discharging candidates are established based on each EV’s information such as predetermined parking time including margin time, current state of charge (SOC) value, and initiation of charging/discharging process. Using the proposed EV charging/discharging scheduling strategy, parked EVs of the PV-based charging station are utilized as ESSs in the MG.
- (4)
- In the proposed power management scheme, multi-objective optimization is applied for the power management of interdependent MG and EV fleets, which determines the coordinated power distribution of power sources and the charging/discharging operation of parked EVs. Multi-objective optimization for optimal power management of nanogrid is presented in [52]. Through the multi-objective optimization, the operating cost of the PV-based charging station and grid dependency of the MG is minimized, and the utilization of EV charging/discharging is maximized for economical and energy-efficient operation of the PV-based charging station. In addition, the collected information such as remaining parking time and the current SOC of EVs are considered to satisfy the charging requirements of parked EVs, and the operating SOC range and the initiation of charging/discharging process are reflected to prevent over-charging and over-discharging and improve battery health.
2. System Model Formulation
2.1. Overall System Architecture
2.2. Energy Supply/Demand Model of the PV-Based Charging Station
2.2.1. EV Model
2.2.2. PV Power Model
2.2.3. Grid Power Model
2.2.4. Local Load Demand Model
2.3. Electricity Rate (DR program, SMP, and REC)
2.4. Prediction of Local Load Demand and PV Power Production
3. Power Management Scheme of MG with EV Charging/Discharging Scheduling Algorithm
3.1. Proposed EV Charging/Discharging Scheduling Algorithm
3.2. Multi-Objective Optimization for Power Management of Interdependent MG and EV fleets
3.2.1. Constraints
3.2.2. Objective Functions
4. Simulation Results
4.1. Simulation Setup
4.2. Comparative Performance of Power Management Scheme based on the Newly Proposed EV Charging/Discharging Scheduling Algorithm
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| EV | Electric vehicle |
| MG | Microgrid |
| PEV | Plug-in electric vehicle |
| PHEV | Plug-in hybrid electric vehicle |
| FCV | Fuel cell vehicle |
| ESS | Energy storage system |
| V2B | Vehicle-to-building |
| V2H | Vehicle-to-home |
| V2G | Vehicle-to-grid |
| G2V | Grid-to-vehicle |
| DCQC | Direct current quick charging |
| RES | Renewable energy system |
| PV | Photovoltaic |
| BESS | Battery energy storage system |
| PSO | Particle swarm optimization |
| V2V | Vehicle-to-vehicle |
| SMP | System marginal price |
| REC | Renewable energy certificates |
| KPX | Korea Power Exchange |
| EVSE | Electric vehicle supply equipment |
| DL | Deep learning |
| CNN | Convolutional neural network |
| RNN | Recurrent neural network |
| LSTM | Long short-term memory |
| GRU | Gated recurrent unit |
| ANN | Artificial neural network |
| DR | Demand response |
| SOC | State of charge |
| PCC | Point of common coupling |
| MGCC | Microgrid central controller |
| KMA | Korea Meteorological Administration |
| KEPCO | Korea Electric Power Corporation |
| RPS | Renewable Portfolio Standard |
| RMSE | Root-mean-squared-error |
| TOU | Time-of-use |
| GA | Genetic algorithm |
References
- Ehsani, M.; Gao, Y.; Longo, S.; Ebrahimi, K.M. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Daina, N.; Sivakumar, A.; Polak, J.W. Electric vehicle charging choices: Modelling and implications for smart charging services. Transp. Res. Part C Emerg. Technol. 2017, 81, 36–56. [Google Scholar] [CrossRef]
- Vandael, S.; Claessens, B.; Hommelberg, M.; Holvoet, T.; Deconinck, G. A scalable three-step approach for demand side management of plug-in hybrid vehicles. IEEE Trans. Smart Grid 2012, 4, 720–728. [Google Scholar] [CrossRef]
- Dagdougui, H.; Ouammi, A.; Dessaint, L.A. Peak load reduction in a smart building integrating microgrid and V2B-based demand response scheme. IEEE Syst. J. 2018, 13, 3274–3282. [Google Scholar] [CrossRef]
- Freund, D.; Lützenberger, M.; Albayrak, S. Costs and gains of smart charging electric vehicles to provide regulation services. Procedia Comput. Sci. 2012, 10, 846–853. [Google Scholar] [CrossRef] [Green Version]
- Shin, H.; Baldick, R. Plug-in electric vehicle to home (V2H) operation under a grid outage. IEEE Trans. Smart Grid 2016, 8, 2032–2041. [Google Scholar] [CrossRef]
- Parvizimosaed, M.; Farmani, F.; Rahimi-Kian, A.; Monsef, H. A multi-objective optimization for energy management in a renewable micro-grid system: A data mining approach. J. Renew. Sustain. Energy 2014, 6, 023127. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; You, P.; Cai, L. Optimal charging scheduling by pricing for EV charging station with dual charging modes. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3386–3396. [Google Scholar] [CrossRef]
- Yudovina, E.; Michailidis, G. Socially optimal charging strategies for electric vehicles. IEEE Trans. Autom. Control 2014, 60, 837–842. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Deng, R.; Liang, H. Game-theoretic control of PHEV charging with power flow analysis. AIMS Energy 2016, 4, 379–396. [Google Scholar] [CrossRef]
- Chung, S.H.; Kwon, C. Multi-period planning for electric car charging station locations: A case of Korean Expressways. Eur. J. Oper. Res. 2015, 242, 677–687. [Google Scholar] [CrossRef]
- Lam, A.Y.; Leung, Y.-W.; Chu, X. Electric vehicle charging station placement: Formulation, complexity, and solutions. IEEE Trans. Smart Grid 2014, 5, 2846–2856. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, A.; Leibowicz, B.D.; Beagle, E.A.; Webber, M.E. As one falls, another rises? Residential peak load reduction through electricity rate structures. Sustain. Cities Soc. 2020, 60, 102191. [Google Scholar] [CrossRef]
- Dominguez, J.A.; Dante, A.W.; Agbossou, K.; Henao, N.; Campillo, J.; Cardenas, A.; Kelouwani, S. Optimal Charging Scheduling of Electric Vehicles based on Principal Component Analysis and Convex Optimization. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 935–940. [Google Scholar]
- McCarthy, D.; Wolfs, P. The HV system impacts of large scale electric vehicle deployments in a metropolitan area. In Proceedings of the 2010 20th Australasian Universities Power Engineering Conference, Christchurch, New Zealand, 5–8 December 2010; pp. 1–6. [Google Scholar]
- Putrus, G.; Suwanapingkarl, P.; Johnston, D.; Bentley, E.; Narayana, M. Impact of electric vehicles on power distribution networks. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 827–831. [Google Scholar]
- Di Silvestre, M.L.; Sanseverino, E.R.; Zizzo, G.; Graditi, G. An optimization approach for efficient management of EV parking lots with batteries recharging facilities. J. Ambient. Intell. Humaniz. Comput. 2013, 4, 641–649. [Google Scholar] [CrossRef]
- Hüls, J.; Remke, A. Coordinated charging strategies for plug-in electric vehicles to ensure a robust charging process. In Proceedings of the 10th EAI International Conference on Performance Evaluation Methodologies and Tools on 10th EAI International Conference on Performance Evaluation Methodologies and Tools, Taormina, Italy, 25–28 October 2016; pp. 19–22. [Google Scholar]
- Eldeeb, H.H.; Faddel, S.; Mohammed, O.A. Multi-objective optimization technique for the operation of grid tied PV powered EV charging station. Electr. Power Syst. Res. 2018, 164, 201–211. [Google Scholar] [CrossRef]
- Tulpule, P.J.; Marano, V.; Yurkovich, S.; Rizzoni, G. Economic and environmental impacts of a PV powered workplace parking garage charging station. Appl. Energy 2013, 108, 323–332. [Google Scholar] [CrossRef]
- Zhang, Q.; Tezuka, T.; Ishihara, K.N.; Mclellan, B.C. Integration of PV power into future low-carbon smart electricity systems with EV and HP in Kansai Area, Japan. Renew. Energy 2012, 44, 99–108. [Google Scholar] [CrossRef]
- Denholm, P.; Kuss, M.; Margolis, R.M. Co-benefits of large scale plug-in hybrid electric vehicle and solar PV deployment. J. Power Sources 2013, 236, 350–356. [Google Scholar] [CrossRef]
- Sehar, F.; Pipattanasomporn, M.; Rahman, S. Demand management to mitigate impacts of plug-in electric vehicle fast charge in buildings with renewables. Energy 2017, 120, 642–651. [Google Scholar] [CrossRef] [Green Version]
- Kempton, W.; Tomic, J.; Letendre, S.; Brooks, A.; Lipman, T. Vehicle-to-Grid Power: Battery, Hybrid, and Fuel Cell Vehicles as Resources for Distributed Electric Power in California; UC Davis Institute of Transportation Studies: Davis, CA, USA, 2001. [Google Scholar]
- Wang, Q.; Liu, X.; Du, J.; Kong, F. Smart charging for electric vehicles: A survey from the algorithmic perspective. IEEE Commun. Surv. Tutor. 2016, 18, 1500–1517. [Google Scholar] [CrossRef] [Green Version]
- Nunes, P.; Brito, M. Displacing natural gas with electric vehicles for grid stabilization. Energy 2017, 141, 87–96. [Google Scholar] [CrossRef]
- Marano, V.; Rizzoni, G. Energy and economic evaluation of PHEVs and their interaction with renewable energy sources and the power grid. In Proceedings of the 2008 IEEE International Conference on Vehicular Electronics and Safety, Columbus, OH, USA, 22–24 September 2008; pp. 84–89. [Google Scholar]
- Kempton, W.; Tomić, J. Vehicle-to-grid power implementation: From stabilizing the grid to supporting large-scale renewable energy. J. Power Sources 2005, 144, 280–294. [Google Scholar] [CrossRef]
- Aluisio, B.; Conserva, A.; Dicorato, M.; Forte, G.; Trovato, M. Optimal operation planning of V2G-equipped Microgrid in the presence of EV aggregator. Electr. Power Syst. Res. 2017, 152, 295–305. [Google Scholar] [CrossRef]
- Saber, A.Y.; Venayagamoorthy, G.K. Intelligent unit commitment with vehicle-to-grid—A cost-emission optimization. J. Power Sources 2010, 195, 898–911. [Google Scholar] [CrossRef]
- Habib, S.; Khan, M.M.; Abbas, F.; Tang, H. Assessment of electric vehicles concerning impacts, charging infrastructure with unidirectional and bidirectional chargers, and power flow comparisons. Int. J. Energy Res. 2018, 42, 3416–3441. [Google Scholar] [CrossRef]
- Lambert, G.; Lavoie, S.; Lecourtois, É.; Giumento, A.; Lagace, M.; Dupré, J.-L.; Patault, L.-A.; Boudjerida, N.; Zaghib, K.; Perreault, É. Bidirectional Charging System for Electric Vehicle. U.S. Patent 20170050529A1, 23 February 2017. [Google Scholar]
- Kaiser, A.; Nguyen, A.; Pham, R.; Granados, M.; Le, H.T. Efficient Interfacing Electric Vehicles with Grid using Bi-directional Smart Inverter. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; pp. 178–182. [Google Scholar]
- Zhang, R.; Cheng, X.; Yang, L. Stable matching based cooperative V2V charging mechanism for electric vehicles. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar]
- Wang, M.; Ismail, M.; Zhang, R.; Shen, X.S.; Serpedin, E.; Qaraqe, K. A semi-distributed V2V fast charging strategy based on price control. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 4550–4555. [Google Scholar]
- Lee, H.G.; Kim, G.-G.; Bhang, B.G.; Kim, D.K.; Park, N.; Ahn, H.-K. Design algorithm for optimum capacity of ESS connected with PVs under the RPS program. IEEE Access 2018, 6, 45899–45906. [Google Scholar] [CrossRef]
- Venayagamoorthy, G.K.; Mitra, P.; Corzine, K.; Huston, C. Real-time modeling of distributed plug-in vehicles for V2G transactions. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 3937–3941. [Google Scholar]
- Garg, S.; Kaur, K.; Ahmed, S.H.; Bradai, A.; Kaddoum, G.; Atiquzzaman, M. MobQoS: Mobility-aware and QoS-driven SDN framework for autonomous vehicles. IEEE Wirel. Commun. 2019, 26, 12–20. [Google Scholar] [CrossRef]
- Garg, S.; Kaur, K.; Kaddoum, G.; Ahmed, S.H.; Jayakody, D.N.K. SDN-based secure and privacy-preserving scheme for vehicular networks: A 5G perspective. IEEE Trans. Veh. Technol. 2019, 68, 8421–8434. [Google Scholar] [CrossRef]
- Ustun, T.S.; Ozansoy, C.R.; Zayegh, A. Implementing vehicle-to-grid (V2G) technology with IEC 61850-7-420. IEEE Trans. Smart Grid 2013, 4, 1180–1187. [Google Scholar] [CrossRef]
- He, Y.; Venkatesh, B.; Guan, L. Optimal scheduling for charging and discharging of electric vehicles. IEEE Trans. Smart Grid 2012, 3, 1095–1105. [Google Scholar] [CrossRef]
- Mahmud, K.; Town, G.E.; Morsalin, S.; Hossain, M. Integration of electric vehicles and management in the internet of energy. Renew. Sustain. Energy Rev. 2018, 82, 4179–4203. [Google Scholar] [CrossRef]
- Saltanovs, R.; Krivchenkov, A.; Krainyukov, A. Analysis of effective wireless communications for V2G applications and mobile objects. In Proceedings of the 2017 IEEE 58th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 12–13 October 2017; pp. 1–5. [Google Scholar]
- Schmutzler, J.; Wietfeld, C.; Andersen, C.A. Distributed energy resource management for electric vehicles using IEC 61850 and ISO/IEC 15118. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Korea, 9–12 October 2012; pp. 1457–1462. [Google Scholar]
- Carvallo, J.P.; Larsen, P.H.; Sanstad, A.H.; Goldman, C.A. Long term load forecasting accuracy in electric utility integrated resource planning. Energy Policy 2018, 119, 410–422. [Google Scholar] [CrossRef] [Green Version]
- Brownlee, J. Deep Learning for Time Series Forecasting: Predict the Future with MLPs, CNNs and LSTMs in Python; Machine Learning Mastery: Vermont, Australia, 2018. [Google Scholar]
- Wang, R.; Li, C.; Fu, W.; Tang, G. Deep learning method based on gated recurrent unit and variational mode decomposition for short-term wind power interval prediction. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3814–3827. [Google Scholar] [CrossRef] [PubMed]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Ke, K.; Hongbin, S.; Chengkang, Z.; Brown, C. Short-term electrical load forecasting method based on stacked auto-encoding and GRU neural network. Evol. Intell. 2019, 12, 385–394. [Google Scholar] [CrossRef]
- Rai, A.; Shrivastava, A.; Jana, K.C. A Robust Auto Encoder-Gated Recurrent Unit (AE-GRU) Based Deep Learning Approach for Short Term Solar Power Forecasting. Optik 2022, 252, 168515. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.; Jung, H.; Cho, J.; Hong, J.; Lee, S.; Har, D. Optimal power management for nanogrids based on technical information of electric appliances. Energy Build. 2019, 191, 174–186. [Google Scholar] [CrossRef]
- Moraes, C.; Har, D. Charging distributed sensor nodes exploiting clustering and energy trading. IEEE Sens. J. 2016, 17, 546–555. [Google Scholar] [CrossRef]
- Hwang, K.; Cho, J.; Park, J.; Har, D.; Ahn, S. Ferrite position identification system operating with wireless power transfer for intelligent train position detection. IEEE Trans. Intell. Transp. Syst. 2018, 20, 374–382. [Google Scholar] [CrossRef]
- Jiang, W.; Zhen, Y. A real-time EV charging scheduling for parking lots with PV system and energy store system. IEEE Access 2019, 7, 86184–86193. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of battery charger topologies, charging power levels, and infrastructure for plug-in electric and hybrid vehicles. IEEE Trans. Power Electron. 2012, 28, 2151–2169. [Google Scholar] [CrossRef]
- Darabi, Z.; Ferdowsi, M. Aggregated impact of plug-in hybrid electric vehicles on electricity demand profile. IEEE Trans. Sustain. Energy 2011, 2, 501–508. [Google Scholar] [CrossRef]
- Pasaoglu, G.; Fiorello, D.; Martino, A.; Scarcella, G.; Alemanno, A.; Zubaryeva, A.; Thiel, C. Driving and Parking Patterns of European Car Drivers—A Mobility Survey; European Commission Joint Research Centre: Luxembourg, 2012. [Google Scholar]
- Qdr, Q. Benefits of Demand Response in Electricity Markets and Recommendations for Achieving Them; US Department Energy: Washington, DC, USA, 2006.
- Moon, J.; Jung, T.Y. A critical review of Korea’s long-term contract for renewable energy auctions: The relationship between the import price of liquefied natural gas and system marginal price. Util. Policy 2020, 67, 101132. [Google Scholar] [CrossRef]
- Kim, T.; Vecchietti, L.F.; Choi, K.; Lee, S.; Har, D. Machine Learning for Advanced Wireless Sensor Networks: A Review. IEEE Sens. J. 2021, 21, 12379–12397. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep learning for household load forecasting—A novel pooling deep RNN. IEEE Trans. Smart Grid 2017, 9, 5271–5280. [Google Scholar] [CrossRef]
- Ni, P.; Li, Y.; Li, G.; Chang, V. Natural language understanding approaches based on joint task of intent detection and slot filling for IoT voice interaction. Neural Comput. Appl. 2020, 32, 16149–16166. [Google Scholar] [CrossRef]
- Borowy, B.S.; Salameh, Z.M. Optimum photovoltaic array size for a hybrid wind/PV system. IEEE Trans. Energy Convers. 1994, 9, 482–488. [Google Scholar] [CrossRef]
- Peterson, S.B.; Apt, J.; Whitacre, J. Lithium-ion battery cell degradation resulting from realistic vehicle and vehicle-to-grid utilization. J. Power Sources 2010, 195, 2385–2392. [Google Scholar] [CrossRef]
- Nengroo, S.H.; Ali, M.U.; Zafar, D.A.; Hussain, S.; Murtaza, T.; Alvi, M.J.; Raghavendra, K.V.G.; Kim, H.J. An Optimized Methodology for a Hybrid Photo-Voltaic and Energy Storage System Connected to a Low-Voltage Grid. Electronics 2019, 8, 176. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.-Y.; Zou, C.-M.; Wu, P. A task scheduling algorithm based on genetic algorithm and ant colony optimization in cloud computing. In Proceedings of the 2014 13th International Symposium on Distributed Computing and Applications to Business, Engineering and Science, Xi’an, China, 24–27 November 2014; pp. 68–72. [Google Scholar]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]












| Epoch | 1000 |
| Batch size | 200 |
| Learning rate | 0.005 |
| Gradient moving average | 0.9 |
| Dropout rate | 0.2 |
| Gradient threshold | 1 |
| Power Management Scheme | Operating Cost of PV-Based Charging Station |
|---|---|
| With proposed EV Ch/Dch scheduling | $−35.45 |
| With (conventional) EV Ch/Dch scheduling | $−27.51 |
| With (conventional) EV Ch scheduling | $−13.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, H.; Lee, S.; Nengroo, S.H.; Har, D. Development of Charging/Discharging Scheduling Algorithm for Economical and Energy-Efficient Operation of Multi-EV Charging Station. Appl. Sci. 2022, 12, 4786. https://doi.org/10.3390/app12094786
Jin H, Lee S, Nengroo SH, Har D. Development of Charging/Discharging Scheduling Algorithm for Economical and Energy-Efficient Operation of Multi-EV Charging Station. Applied Sciences. 2022; 12(9):4786. https://doi.org/10.3390/app12094786
Chicago/Turabian StyleJin, Hojun, Sangkeum Lee, Sarvar Hussain Nengroo, and Dongsoo Har. 2022. "Development of Charging/Discharging Scheduling Algorithm for Economical and Energy-Efficient Operation of Multi-EV Charging Station" Applied Sciences 12, no. 9: 4786. https://doi.org/10.3390/app12094786
APA StyleJin, H., Lee, S., Nengroo, S. H., & Har, D. (2022). Development of Charging/Discharging Scheduling Algorithm for Economical and Energy-Efficient Operation of Multi-EV Charging Station. Applied Sciences, 12(9), 4786. https://doi.org/10.3390/app12094786







