Solving Vehicle Routing Problems under Uncertainty and in Dynamic Scenarios: From Simheuristics to Agile Optimization
Abstract
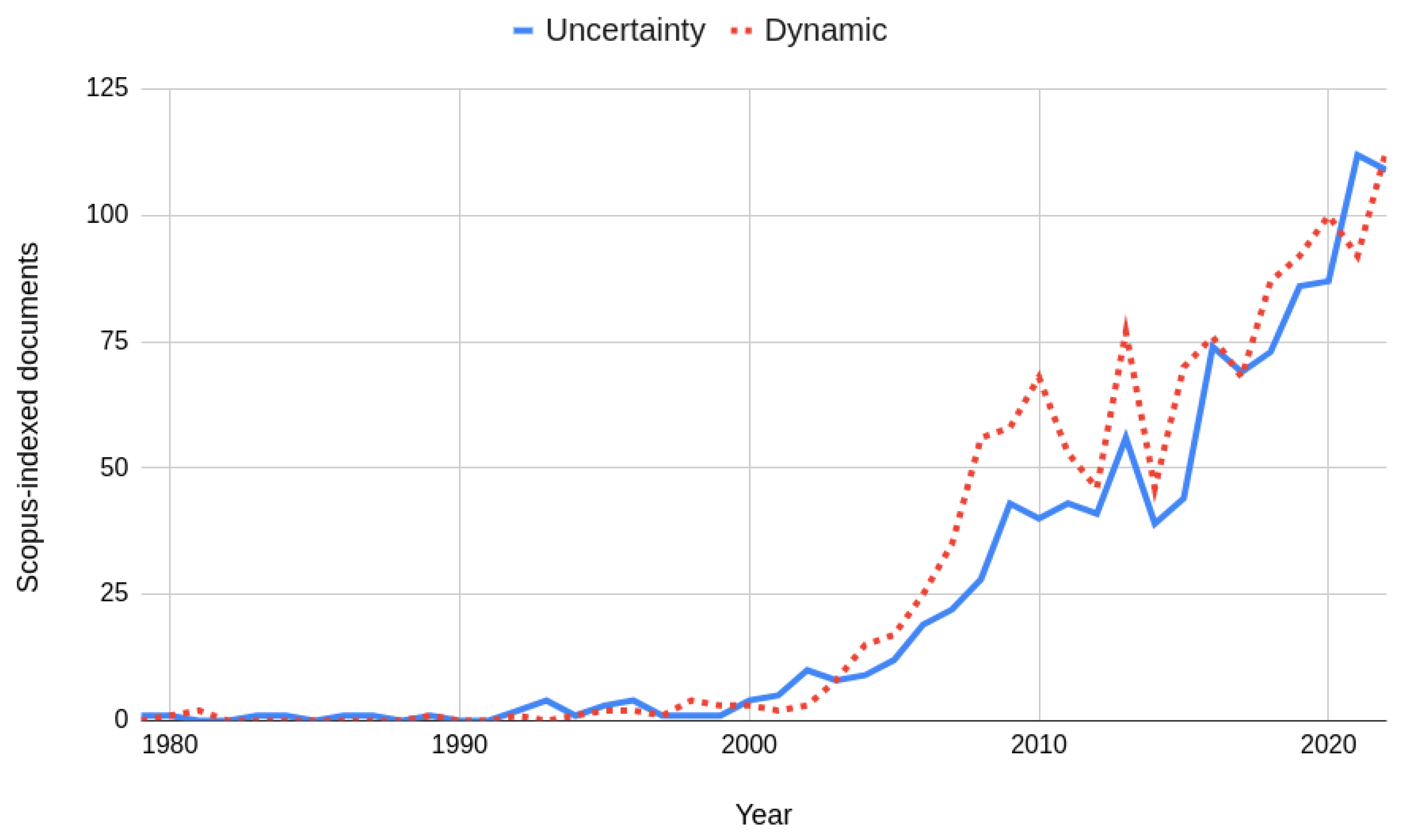
1. Introduction
2. Recent Trends in VRPs
- Minimization of pollutant emissions: The problem of minimizing pollutant emissions in routing, which is included in the green vehicle routing problem, was profiled in the period of 2005–2010. Even though the complete analysis is still in progress, this represents an essential challenge in current mobility paradigms [20]. This topic lies on the basis of the three typical sustainability dimensions of the VRP—the economic, environmental, and social dimensions—which are now omnipresent in the transportation and routing literature [21]. Usually, the environmental and social dimensions are considered key externalities associated with transportation [22].
- Consideration of social issues related to transportation: In the last decade, the social externalities due to transportation—e.g., congestion, pollutant emissions, noise, infrastructure wearing, etc.—have been revealed as critical in the way of designing sustainable modes of mobility [21,22,23]. These traits also assume a very dynamic behavior in mobility problems, which should be contemplated in VRP modeling.
- Greater importance of the urban scenarios: Knowing the importance of the previously mentioned sustainability dimensions, in recent years, it has become clear that the urban arena is the key location in which those dimensions present their critical facets [24]. Urban mobility problems need the support of agile procedures more and more [25].
- Greater importance of energetic objectives and constraints in the transportation programs: It is clear that most of the new challenges that transportation is going to face are going to be related to energy, not only for the use of more sustainable means of mobility, but also for the need to optimize consumption and production [28].
- Necessity of collaboration as a way of facing complex distribution processes: Collaborative and cooperative approaches are becoming quite common in goods and merchandise distribution [29]. They allow for good performance in the sustainability dimensions, as presented by Muñoz-Villamizar et al. [30]. Finally, the dynamic VRP was contemplated by Basso et al. [31].
- Greater occurrence of disruptions in urban and interurban mobility processes: This type of mobility incident is becoming extraordinarily common in real transportation, and there is a demand for quick answers, which represents the basis of the concept of ‘agile optimization’ [25].
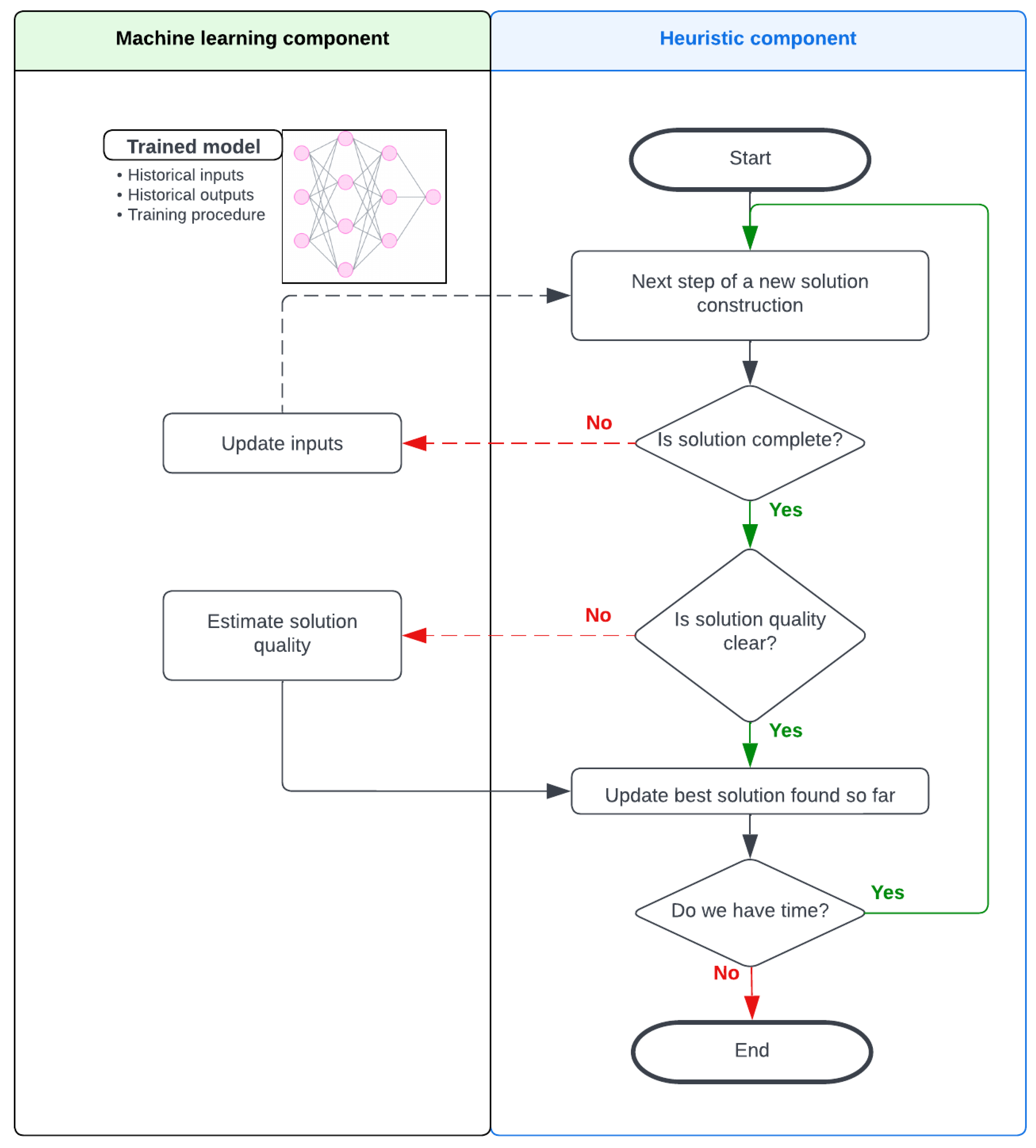
3. VRPs under Uncertainty
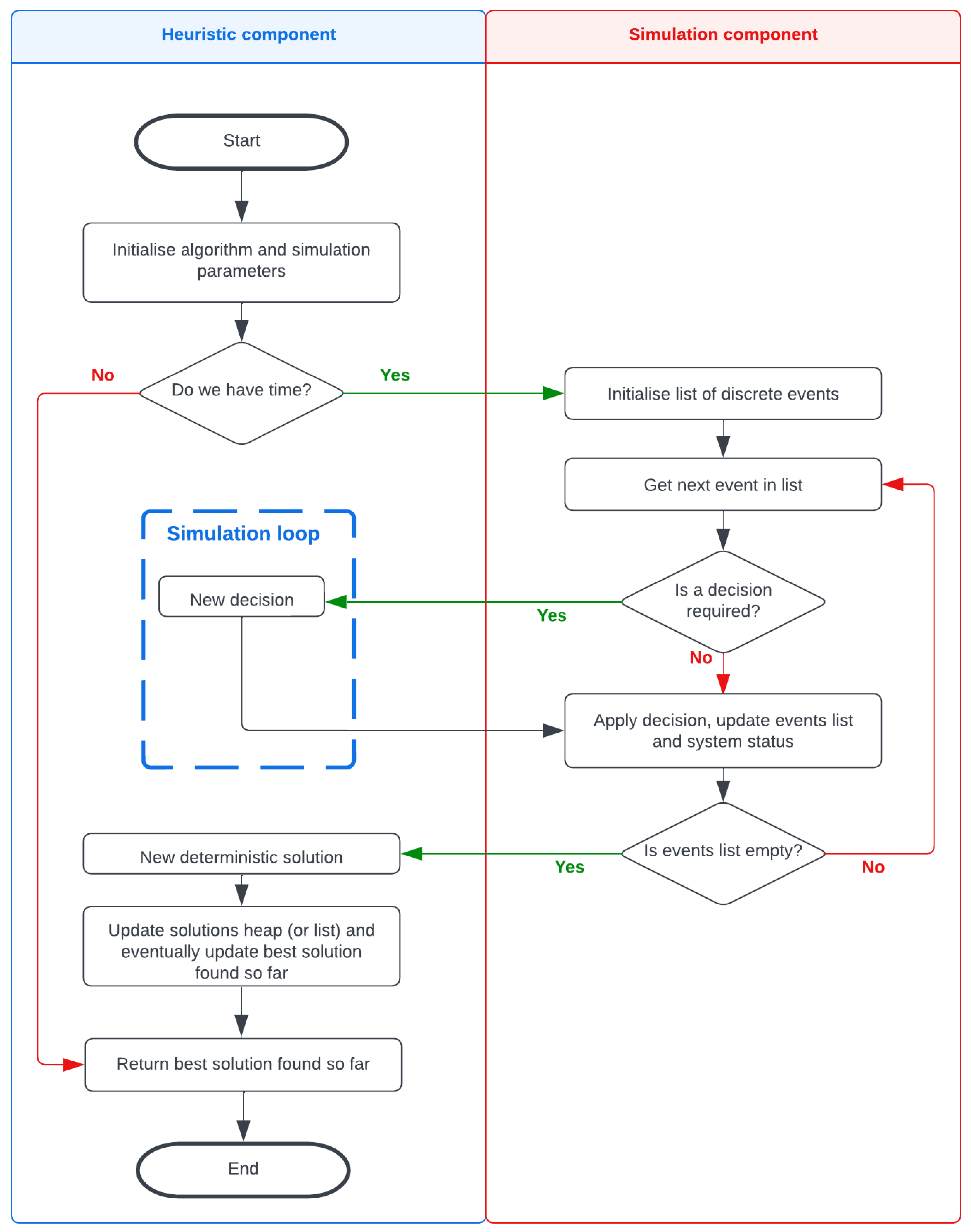
4. VRPs in Dynamic Environments
5. VRPs with Synchronization Issues
6. VRPs under Real-Time Constraints
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Toth, P.; Vigo, D. Vehicle Routing: Problems, Methods, and Applications; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
- Caceres-Cruz, J.; Arias, P.; Guimarans, D.; Riera, D.; Juan, A.A. Rich vehicle routing problem: Survey. ACM Comput. Surv. (CSUR) 2014, 47, 1–28. [Google Scholar] [CrossRef]
- Lahyani, R.; Khemakhem, M.; Semet, F. Rich vehicle routing problems: From a taxonomy to a definition. Eur. J. Oper. Res. 2015, 241, 1–14. [Google Scholar] [CrossRef]
- Oyola, J.; Arntzen, H.; Woodruff, D.L. The stochastic vehicle routing problem, a literature review, part I: Models. EURO J. Transp. Logist. 2018, 7, 193–221. [Google Scholar] [CrossRef]
- Pillac, V.; Gendreau, M.; Guéret, C.; Medaglia, A.L. A review of dynamic vehicle routing problems. Eur. J. Oper. Res. 2013, 225, 1–11. [Google Scholar] [CrossRef]
- Asghari, M.; Al-e, S.M.J.M. Green vehicle routing problem: A state-of-the-art review. Int. J. Prod. Econ. 2021, 231, 107899. [Google Scholar] [CrossRef]
- Drexl, M. Synchronization in vehicle routing—A survey of VRPs with multiple synchronization constraints. Transp. Sci. 2012, 46, 297–316. [Google Scholar] [CrossRef]
- Jozefowiez, N.; Semet, F.; Talbi, E.G. Multi-objective vehicle routing problems. Eur. J. Oper. Res. 2008, 189, 293–309. [Google Scholar] [CrossRef]
- Kucukoglu, I.; Dewil, R.; Cattrysse, D. The electric vehicle routing problem and its variations: A literature review. Comput. Ind. Eng. 2021, 161, 107650. [Google Scholar] [CrossRef]
- Mor, A.; Speranza, M.G. Vehicle routing problems over time: A survey. Ann. Oper. Res. 2022, 314, 255–275. [Google Scholar] [CrossRef]
- Hu, C.; Lu, J.; Liu, X.; Zhang, G. Robust vehicle routing problem with hard time windows under demand and travel time uncertainty. Comput. Oper. Res. 2018, 94, 139–153. [Google Scholar] [CrossRef]
- Pessoa, A.A.; Poss, M.; Sadykov, R.; Vanderbeck, F. Branch-cut-and-price for the robust capacitated vehicle routing problem with knapsack uncertainty. Oper. Res. 2021, 69, 739–754. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, S.; Wang, J.; Huang, M. A branch-and-price algorithm for the heterogeneous fleet green vehicle routing problem with time windows. Transp. Res. Part B Methodol. 2019, 122, 511–527. [Google Scholar] [CrossRef]
- Lee, C. An exact algorithm for the electric-vehicle routing problem with nonlinear charging time. J. Oper. Res. Soc. 2021, 72, 1461–1485. [Google Scholar] [CrossRef]
- Laporte, G. Fifty years of vehicle routing. Transp. Sci. 2009, 43, 408–416. [Google Scholar] [CrossRef]
- Lin, C.; Choy, K.L.; Ho, G.T.; Chung, S.H.; Lam, H. Survey of green vehicle routing problem: Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Braekers, K.; Ramaekers, K.; Van Nieuwenhuyse, I. The vehicle routing problem: State of the art classification and review. Comput. Ind. Eng. 2016, 99, 300–313. [Google Scholar] [CrossRef]
- Rios, B.H.O.; Xavier, E.C.; Miyazawa, F.K.; Amorim, P.; Curcio, E.; Santos, M.J. Recent dynamic vehicle routing problems: A survey. Comput. Ind. Eng. 2021, 160, 107604. [Google Scholar] [CrossRef]
- Fontaine, P.; Minner, S.; Schiffer, M. Smart and Sustainable City Logistics: Design, Consolidation, and Regulation. Eur. J. Oper. Res. 2022, in press. [Google Scholar] [CrossRef]
- Figliozzi, M.; Saenz, J.; Faulin, J. Minimization of urban freight distribution lifecycle CO2e emissions: Results from an optimization model and a real-world case study. Transp. Policy 2020, 86, 60–68. [Google Scholar] [CrossRef]
- Abdullahi, H.; Reyes-Rubiano, L.; Ouelhadj, D.; Faulin, J.; Juan, A.A. Modelling and multi-criteria analysis of the sustainability dimensions for the green vehicle routing problem. Eur. J. Oper. Res. 2021, 292, 143–154. [Google Scholar] [CrossRef]
- Sánchez-García, M.; Zouaghi, F.; Lera-López, F.; Faulin, J. An extended behavior model for explaining the willingness to pay to reduce the air pollution in road transportation. J. Clean. Prod. 2021, 314, 128134. [Google Scholar] [CrossRef]
- Lera-López, F.; Sánchez, M.; Faulin, J.; Cacciolatti, L. Rural environment stakeholders and policy making: Willingness to pay to reduce road transportation pollution impact in the Western Pyrenees. Transp. Res. Part D Transp. Environ. 2014, 32, 129–142. [Google Scholar] [CrossRef]
- Faulin, J.; Grasman, S.E.; Juan, A.A.; Hirsch, P. Sustainable transportation: Concepts and current practices. In Sustainable Transportation and Smart Logistics; Elsevier: Amsterdam, The Netherlands, 2019; pp. 3–23. [Google Scholar]
- Martins, L.d.C.; Hirsch, P.; Juan, A.A. Agile optimization of a two-echelon vehicle routing problem with pickup and delivery. Int. Trans. Oper. Res. 2021, 28, 201–221. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, N.; He, Z.; Jiang, B. Vehicle routing optimization for hazmat shipments considering catastrophe avoidance and failed edges. Transp. Res. Part E Logist. Transp. Rev. 2021, 150, 102337. [Google Scholar] [CrossRef]
- Reyes-Rubiano, L.; Voegl, J.; Rest, K.D.; Faulin, J.; Hirsch, P. Exploration of a disrupted road network after a disaster with an online routing algorithm. Spectrum 2021, 43, 289–326. [Google Scholar] [CrossRef]
- Ghorbanioskalaei, E.; Herrera, E.M.; Ammouriova, M.; Juan, A.A. On the Use of Agile Optimization for Efficient Energy Consumption in Smart Cities’s Transportation and Mobility. Future Transp. 2022, 2, 868–885. [Google Scholar] [CrossRef]
- Serrano-Hernandez, A.; Juan, A.A.; Faulin, J.; Perez-Bernabeu, E. Horizontal collaboration in freight transport: Concepts, benefits and environmental challenges. Sort 2017, 1, 393–414. [Google Scholar]
- Muñoz-Villamizar, A.; Quintero-Araújo, C.L.; Montoya-Torres, J.R.; Faulin, J. Short-and mid-term evaluation of the use of electric vehicles in urban freight transport collaborative networks: A case study. Int. J. Logist. Res. Appl. 2019, 22, 229–252. [Google Scholar] [CrossRef]
- Basso, F.; D’Amours, S.; Rönnqvist, M.; Weintraub, A. A survey on obstacles and difficulties of practical implementation of horizontal collaboration in logistics. Int. Trans. Oper. Res. 2019, 26, 775–793. [Google Scholar] [CrossRef]
- Amaran, S.; Sahinidis, N.V.; Sharda, B.; Bury, S.J. Simulation optimization: A review of algorithms and applications. Ann. Oper. Res. 2016, 240, 351–380. [Google Scholar] [CrossRef]
- Galvan, S.; Arias, J.; Lamos, H. A Simulation-Optimization Approach Based on EPSO for the Vehicle Routing Problem with Stochastic Demands. DYNA 2013, 80, 60–69. [Google Scholar]
- Figueira, G.; Almada-Lobo, B. Hybrid simulation–optimization methods: A taxonomy and discussion. Simul. Model. Pract. Theory 2014, 46, 118–134. [Google Scholar] [CrossRef]
- Chica, M.; Juan, A.A.; Bayliss, C.; Cordón, O.; Kelton, W.D. Why simheuristics? Benefits, limitations, and best practices when combining metaheuristics with simulation. SORT 2020, 44, 311–334. [Google Scholar] [CrossRef]
- Calvet, L.; Wang, D.; Juan, A.; Bové, L. Solving the multidepot vehicle routing problem with limited depot capacity and stochastic demands. Int. Trans. Oper. Res. 2019, 26, 458–484. [Google Scholar] [CrossRef]
- Guimarans, D.; Dominguez, O.; Panadero, J.; Juan, A.A. A simheuristic approach for the two-dimensional vehicle routing problem with stochastic travel times. Simul. Model. Pract. Theory 2018, 89, 1–14. [Google Scholar] [CrossRef]
- Latorre-Biel, J.I.; Ferone, D.; Juan, A.A.; Faulin, J. Combining simheuristics with Petri nets for solving the stochastic vehicle routing problem with correlated demands. Expert Syst. Appl. 2021, 168, 114240. [Google Scholar] [CrossRef]
- Reyes-Rubiano, L.; Ferone, D.; Juan, A.A.; Faulin, J. A simheuristic for routing electric vehicles with limited driving ranges and stochastic travel times. SORT 2019, 1, 3–24. [Google Scholar]
- Gruler, A.; Quintero-Araújo, C.L.; Calvet, L.; Juan, A.A. Waste collection under uncertainty: A simheuristic based on variable neighbourhood search. Eur. J. Ind. Eng. 2017, 11, 228–255. [Google Scholar] [CrossRef]
- Yazdani, M.; Kabirifar, K.; Frimpong, B.E.; Shariati, M.; Mirmozaffari, M.; Boskabadi, A. Improving construction and demolition waste collection service in an urban area using a simheuristic approach: A case study in Sydney, Australia. J. Clean. Prod. 2021, 280, 124138. [Google Scholar] [CrossRef]
- Gruler, A.; Panadero, J.; de Armas, J.; Moreno, J.A.; Juan, A.A. Combining variable neighborhood search with simulation for the inventory routing problem with stochastic demands and stock-outs. Comput. Ind. Eng. 2018, 123, 278–288. [Google Scholar] [CrossRef]
- Raba, D.; Estrada-Moreno, A.; Panadero, J.; Juan, A.A. A reactive simheuristic using online data for a real-life inventory routing problem with stochastic demands. Int. Trans. Oper. Res. 2020, 27, 2785–2816. [Google Scholar] [CrossRef]
- Onggo, B.S.; Panadero, J.; Corlu, C.G.; Juan, A.A. Agri-food supply chains with stochastic demands: A multi-period inventory routing problem with perishable products. Simul. Model. Pract. Theory 2019, 97, 101970. [Google Scholar] [CrossRef]
- Tordecilla, R.D.; Martins, L.d.C.; Panadero, J.; Copado, P.J.; Perez-Bernabeu, E.; Juan, A.A. Fuzzy simheuristics for optimizing transportation systems: Dealing with stochastic and fuzzy uncertainty. Appl. Sci. 2021, 11, 7950. [Google Scholar] [CrossRef]
- Bertolini, M.; Mezzogori, D.; Neroni, M.; Zammori, F. Machine Learning for industrial applications: A comprehensive literature review. Expert Syst. Appl. 2021, 175, 114820. [Google Scholar] [CrossRef]
- Sengupta, J.; Kubendran, R.; Neftci, E.; Andreou, A. High-speed, real-time, spike-based object tracking and path prediction on google edge TPU. In Proceedings of the 2020 2nd IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS), Genova, Italy, 31 August–2 September 2020; pp. 134–135. [Google Scholar]
- Calvet, L.; de Armas, J.; Masip, D.; Juan, A.A. Learnheuristics: Hybridizing metaheuristics with machine learning for optimization with dynamic inputs. Open Math. 2017, 15, 261–280. [Google Scholar] [CrossRef]
- Arnau, Q.; Juan, A.A.; Serra, I. On the use of learnheuristics in vehicle routing optimization problems with dynamic inputs. Algorithms 2018, 11, 208. [Google Scholar] [CrossRef]
- Calvet, L.; Ferrer, A.; Gomes, M.I.; Juan, A.A.; Masip, D. Combining statistical learning with metaheuristics for the multi-depot vehicle routing problem with market segmentation. Comput. Ind. Eng. 2016, 94, 93–104. [Google Scholar] [CrossRef]
- Bayliss, C.; Juan, A.A.; Currie, C.S.; Panadero, J. A learnheuristic approach for the team orienteering problem with aerial drone motion constraints. Appl. Soft Comput. 2020, 92, 106280. [Google Scholar] [CrossRef]
- Chankov, S.M.; Becker, T.; Windt, K. Towards definition of synchronization in logistics systems. Procedia CIRP 2014, 17, 594–599. [Google Scholar] [CrossRef]
- Castaneda, J.; Neroni, M.; Ammouriova, M.; Panadero, J.; Juan, A.A. Biased-Randomized Discrete-Event Heuristics for Dynamic Optimization with Time Dependencies and Synchronization. Algorithms 2022, 15, 289. [Google Scholar] [CrossRef]
- Kogler, C.; Rauch, P. Discrete event simulation of multimodal and unimodal transportation in the wood supply chain: A literature review. Silva Fenn. 2018, 52, 9984. [Google Scholar] [CrossRef]
- Bredström, D.; Rönnqvist, M. Combined vehicle routing and scheduling with temporal precedence and synchronization constraints. Eur. J. Oper. Res. 2008, 191, 19–31. [Google Scholar] [CrossRef]
- Afifi, S.; Dang, D.C.; Moukrim, A. Heuristic solutions for the vehicle routing problem with time windows and synchronized visits. Optim. Lett. 2016, 10, 511–525. [Google Scholar] [CrossRef]
- Guo, J.; Long, J.; Xu, X.; Yu, M.; Yuan, K. The vehicle routing problem of intercity ride-sharing between two cities. Transp. Res. Part B Methodol. 2022, 158, 113–139. [Google Scholar] [CrossRef]
- Bayliss, C.; Martins, L.d.C.; Juan, A.A. A two-phase local search with a discrete-event heuristic for the omnichannel vehicle routing problem. Comput. Ind. Eng. 2020, 148, 106695. [Google Scholar] [CrossRef]
- Fikar, C.; Juan, A.A.; Martinez, E.; Hirsch, P. A discrete-event driven metaheuristic for dynamic home service routing with synchronised trip sharing. Eur. J. Ind. Eng. 2016, 10, 323–340. [Google Scholar] [CrossRef]
- Boysen, N.; Briskorn, D.; Fedtke, S.; Schwerdfeger, S. Drone delivery from trucks: Drone scheduling for given truck routes. Networks 2018, 72, 506–527. [Google Scholar] [CrossRef]
- Das, D.N.; Sewani, R.; Wang, J.; Tiwari, M.K. Synchronized truck and drone routing in package delivery logistics. IEEE Trans. Intell. Transp. Syst. 2020, 22, 5772–5782. [Google Scholar] [CrossRef]
- Yetis, H.; Karakose, M. Collaborative Truck-Drone Routing Optimization Using Quantum-Inspired Genetic Algorithms. In Proceedings of the IEEE 2021 25th International Conference on Information Technology (IT), Zabljak, Montenegro, 16–20 February 2021; pp. 1–4. [Google Scholar]
- Deng, P.; Amirjamshidi, G.; Roorda, M. A vehicle routing problem with movement synchronization of drones, sidewalk robots, or foot-walkers. Transp. Res. Procedia 2020, 46, 29–36. [Google Scholar] [CrossRef]
- Grangier, P.; Gendreau, M.; Lehuédé, F.; Rousseau, L.M. An adaptive large neighborhood search for the two-echelon multiple-trip vehicle routing problem with satellite synchronization. Eur. J. Oper. Res. 2016, 254, 80–91. [Google Scholar] [CrossRef]
- Arnau, Q.; Barrena, E.; Panadero, J.; de la Torre, R.; Juan, A.A. A biased-randomized discrete-event heuristic for coordinated multi-vehicle container transport across interconnected networks. Eur. J. Oper. Res. 2022, 302, 348–362. [Google Scholar] [CrossRef]
- Hashemi Doulabi, H.; Pesant, G.; Rousseau, L.M. Vehicle routing problems with synchronized visits and stochastic travel and service times: Applications in healthcare. Transp. Sci. 2020, 54, 1053–1072. [Google Scholar] [CrossRef]
- Ghiani, G.; Guerriero, F.; Laporte, G.; Musmanno, R. Real-time vehicle routing: Solution concepts, algorithms and parallel computing strategies. Eur. J. Oper. Res. 2003, 151, 1–11. [Google Scholar] [CrossRef]
- Haghani, A.; Jung, S. A dynamic vehicle routing problem with time-dependent travel times. Comput. Oper. Res. 2005, 32, 2959–2986. [Google Scholar] [CrossRef]
- Hong, L. An improved LNS algorithm for real-time vehicle routing problem with time windows. Comput. Oper. Res. 2012, 39, 151–163. [Google Scholar] [CrossRef]
- Chen, H.K.; Hsueh, C.F.; Chang, M.S. The real-time time-dependent vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2006, 42, 383–408. [Google Scholar] [CrossRef]
- Ferrucci, F.; Bock, S.; Gendreau, M. A pro-active real-time control approach for dynamic vehicle routing problems dealing with the delivery of urgent goods. Eur. J. Oper. Res. 2013, 225, 130–141. [Google Scholar] [CrossRef]
- Barkaoui, M.; Gendreau, M. An adaptive evolutionary approach for real-time vehicle routing and dispatching. Comput. Oper. Res. 2013, 40, 1766–1776. [Google Scholar] [CrossRef]
- Azi, N.; Gendreau, M.; Potvin, J.Y. A dynamic vehicle routing problem with multiple delivery routes. Ann. Oper. Res. 2012, 199, 103–112. [Google Scholar] [CrossRef]
- Cardoso, P.J.; Schütz, G.; Mazayev, A.; Ey, E.; Corrêa, T. A solution for a real-time stochastic capacitated vehicle routing problem with time windows. Procedia Comput. Sci. 2015, 51, 2227–2236. [Google Scholar] [CrossRef]
- Martins, L.d.C.; Tarchi, D.; Juan, A.A.; Fusco, A. Agile optimization for a real-time facility location problem in Internet of Vehicles networks. Networks 2022, 79, 501–514. [Google Scholar] [CrossRef]
- Li, Y.; Peyman, M.; Panadero, J.; Juan, A.A.; Xhafa, F. IoT Analytics and Agile Optimization for Solving Dynamic Team Orienteering Problems with Mandatory Visits. Mathematics 2022, 10, 982. [Google Scholar] [CrossRef]
- Peyman, M.; Copado, P.J.; Tordecilla, R.D.; Martins, L.d.C.; Xhafa, F.; Juan, A.A. Edge Computing and IoT Analytics for Agile Optimization in Intelligent Transportation Systems. Energies 2021, 14, 6309. [Google Scholar] [CrossRef]



| Article | Problem | Real-Time Consideration | Objective | Approach |
|---|---|---|---|---|
| Haghani and Jung [68] | Pick-up or delivery Capacitated VRP with soft time windows. | Real-time service requests and real-time variations in travel times. | To minimize the total cost. | Genetic Algorithm. |
| Hong [69] | Dynamic VRP with hard time windows. | Real-time service requests. | To minimize the travel distance and number of vehicles. | Large Neighborhood Search. |
| Chen et al. [70] | Real-time time-dependent VRP with time windows. | Real-time travel times and service requests. | To determine optimal routes and departure times. | Heuristic. |
| Ferrucci et al. [71] | Dynamic VRP with soft time windows and urgent delivery of goods. | Real-time service requests. | To minimize the total customer inconveniences. | Tabu Search. |
| Barkaoui and Gendreau [72] | Dynamic VRP with time windows. | Real-time service requests. | To minimize the number of routes and the total traveled distance. | Evolutionary Genetic Algorithm. |
| Azi et al. [73] | Dynamic VRP with time windows. | Real-time service requests. | To maximize the total profit. | Adaptive Large Neighborhood Search. |
| Cardoso et al. [74] | Capacitated VRP with time windows. | Real-time service requests. | To minimize the number of vehicles and the total traveled distance. | Heuristic. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ammouriova, M.; Herrera, E.M.; Neroni, M.; Juan, A.A.; Faulin, J. Solving Vehicle Routing Problems under Uncertainty and in Dynamic Scenarios: From Simheuristics to Agile Optimization. Appl. Sci. 2023, 13, 101. https://doi.org/10.3390/app13010101
Ammouriova M, Herrera EM, Neroni M, Juan AA, Faulin J. Solving Vehicle Routing Problems under Uncertainty and in Dynamic Scenarios: From Simheuristics to Agile Optimization. Applied Sciences. 2023; 13(1):101. https://doi.org/10.3390/app13010101
Chicago/Turabian StyleAmmouriova, Majsa, Erika M. Herrera, Mattia Neroni, Angel A. Juan, and Javier Faulin. 2023. "Solving Vehicle Routing Problems under Uncertainty and in Dynamic Scenarios: From Simheuristics to Agile Optimization" Applied Sciences 13, no. 1: 101. https://doi.org/10.3390/app13010101
APA StyleAmmouriova, M., Herrera, E. M., Neroni, M., Juan, A. A., & Faulin, J. (2023). Solving Vehicle Routing Problems under Uncertainty and in Dynamic Scenarios: From Simheuristics to Agile Optimization. Applied Sciences, 13(1), 101. https://doi.org/10.3390/app13010101









