Peak Carbon Dioxide Emissions Strategy Based on the Gray Model between Carbon Emissions and Urban Spatial Expansion for a Built-Up Area
Abstract
1. Introduction
2. Areas and Research Methods
2.1. Background of the Study Area
2.2. Gray Relational Model
2.3. Urban Space Indicators
2.3.1. Land Expansion Intensity Index
2.3.2. Urban Morphology Indices
2.3.3. Urban Compactness
2.3.4. Urban Traffic Accessibility
3. Results
3.1. Urban Space Indicators Results
3.2. Measurement and Trend Prediction of Urban Carbon Emissions
3.2.1. Urban Carbon Emission Measurement
3.2.2. Prediction of Carbon Emission Trend
3.3. Gray Correlation Analysis Results
3.3.1. Correlation between Carbon Emissions and Urban Land Area
3.3.2. Carbon Emissions and the Correlation of Urban Spatial Extension
3.3.3. The CO2 Constraint Value
4. Discussion and Conclusions
4.1. Discussion
- (1)
- The correlation of the two indicators, the total carbon emissions and the per capita carbon emissions, to the area of each type of land use is extremely high, both above 0.9. It is also further confirmed that the growth of the urban population and land use is the main source of urban carbon emissions. Road traffic land itself does not produce significant carbon emissions, but the increase in residential land and commercial land caused by the improvement in road and transportation facilities is the main reason for the increase in carbon emissions.
- (2)
- Three spatial morphology indicators, namely, the shortest travel distance, urban compactness and morphology indices, are highly correlated with three emission indicators: carbon emissions, carbon-emission intensity and carbon emissions per unit of land use. Among them, the most correlated indicator is carbon-emission intensity and urban compactness, with a correlation coefficient of 0.858.
- (3)
- Changsha city has constraint target values for total carbon emissions, carbon-emission intensity, carbon emissions per capita and carbon emissions per unit of land until 2030. They are 87,291,300 t-CO2, 0.45 t-CO2/CNY104, 8.83 t-CO2/104 people and 9.12 million t-CO2/km2, respectively. The next revision of the Changsha Territorial Masterplan should control the urban construction land within 889.61 square kilometers. Residential, public-service, industrial and road lands should be controlled at approximately 231.3 km2, 143.88 km2, 150.17 km2 and 135.83 km2, respectively. The land expansion intensity, urban morphology index, urban compactness and shortest travel distance target values are 6.19, 32.04, 0.236 and 96086.76 km, respectively.
- (4)
- Considering the impact of COVID-19 on China’s GDP, the overall urban economy is in a downwards trend. Changsha’s GDP maintained a growth trend of 12.8% before 2019. Influenced by COVID-2019, the GDP growth rate in 2020, 2021 and 2022 decreased to 7.1%, 7.5% and 4.8%, respectively. Forecast for 2030, the GDP will decline to CNY 1900 billion. The economic downturn is likely to slow urban sprawl, so binding targets for carbon emissions will be adjusted accordingly.
4.2. Conclusions
- (1)
- Based on the gray correlation analysis of multiple factors, the calculation of the constraint control value of urban space expansion can provide policy guidance for the next round of spatial optimization of the city- and county-level land-space master plan and can also develop more precise constraint indicators to achieve the national 2030 carbon peak and carbon-neutral policy goals.
- (2)
- A coordinated development between urban land use and public transportation, particularly the promotion of rail transit to guide land development and reduce traffic trips, is the first strategy that needs to be considered for the reduction of carbon emissions.
- (3)
- The rapid urbanization and expansion of urban land is a necessity that continuously increases total carbon emissions and per capita carbon emissions. The goal of carbon peaking and carbon neutrality is not simply to limit urban expansion, nor is it simply to delineate urban spatial growth boundaries and control the total scale of construction lands. It should be more about the optimization of the urban space from the inside and change the urban development model from “incremental development” to “stock development” to reduce the disorderly expansion in favor of compact spatial development.
- (4)
- Although the gray system theoretical model introduced in this paper has high simulation accuracy, different types of gray models need to be selected for different types of data, and the quantitative relationship expression is more complex, so MATLAB software is needed to assist in analysis and research. Therefore, the correlation model of urban spatial expansion and carbon emissions is worth further deepening to select a more appropriate quantitative model to fit.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, Y.; Jin, G.; Deng, X.Z. Dynamic Interactive Effects of Urban Land–Use Efficiency, Industrial Transformation, and Carbon Emissions. J. Clean. Prod. 2020, 270, 122547. [Google Scholar] [CrossRef]
- Houghton, R.A. The Annual Net Flux of Carbon to the Atmosphere from Changes in Land Use 1850–1990. Chem. Phys. Meteorol. 1999, 51, 298–313. [Google Scholar]
- Wei, Y.R.; Chen, S.L. Spatial Correlation and Carbon Balance Zoning of Land Use Carbon Emissions in Fujian Province. Acta Ecol. Sin. 2021, 41, 5814–5824. [Google Scholar]
- Niu, Y.W.; Zhao, X.C.; Hu, Y.J. Spatial Variation of Carbon Emissions from County Land Use in Chang–Zhu–Tan Area Based on NPP–VIIRS Night Light. Acta Sci. Circumstantiae 2021, 41, 3847–3856. [Google Scholar]
- Xu, Z.; Li, C.; Niu, L. Decoupling Relationship between Land Mixed Use and Carbon Emissions in Hohhot–Baotou–Ordos–Yulin Urban Agglomeration. Res. Environ. Sci. 2022, 35, 299–308. [Google Scholar]
- Zhang, Y.; Jiang, B.; Zhao, Y.H.; Zhao, Y.; Zou, T.A.; Xue, R. Temporal and Spatial Pattern Changes and Influencing Factors of Land Use Carbon Emissions in the Three Provinces of Northeast China. Areal Res. Dev. 2022, 41, 150–156. [Google Scholar]
- Chang, Q.; Cai, W.M. A Study on the Coupling Relationship between Construction Land Scale and Carbon Emission Based on EKC Test and Tapio Model: A Case Study of Tianjin. J. Agric. Technol. 2022, 42, 56–61. [Google Scholar]
- Yan, C.; Hou, L.G. Study on Land Use Change and Carbon Emission in Shaanxi Province Based on Grey Theory. J. Xi’an Univ. Technol. 2021, 37, 25–31. [Google Scholar]
- Yang, X.; Xie, X.X. Kuznets Curve Empirical Analysis of Wuhan Construction Land Expansion and Carbon Emission Effect. J. Huazhong Agric. Univ. (Soc. Sci. Ed.) 2020, 04, 158–165. [Google Scholar]
- Zhang, R.Q.; Li, P.H.; Xu, L.P. Effects of Urbanization on Carbon Emission from Land Use in Xinjiang and Their Coupling Relationship. Acta Ecol. Sin. 2022, 42, 5226–5242. [Google Scholar]
- Wei, Y.; Jian, X.Y. Research evolution of Carbon Emissions from Land Use in Guizhou Province Based on Carbon Peak and Carbon Neutrality and the According Predictions. Ecol. Econ. 2022, 38, 108–114. [Google Scholar]
- Baumann, M.; Gasparri, I.; Mara, P.R.; Gregorio, G.P.; Patrick, G.; Patrick, H.; Tobias, K. Carbon Emissions from Agricultural Eexpansion and Intensification in the Chaco. Glob. Chang. Biol. 2016, 23, 1902–1916. [Google Scholar] [CrossRef] [PubMed]
- Leng, H.; Zhao, Y.R.; Yu, T.T. Impact of Land Use Change on Carbon Emissions in Small Towns and Its Optimization Strategy: A Case Study of Changxing County of Zhejiang Province. Mod. Urban Res. 2022, 6, 54–60, 66. [Google Scholar]
- Xiao, Y.; An, K.; Yang, Y. Forest Carbon Storage Trends along Altitudinal Gradients in Beijing, China. J. Resour. Ecol. 2014, 5, 148–156. [Google Scholar]
- Zhang, X.J.; Wang, C.X.; Miao, Y.; Wang, J.C.; Li, M.C. Study on the Impact of Urban Land Intensity on Carbon Emissions Based on Multi–source Data: A Case Study of Qingdao City. J. Xi’an Univ. Technol. 2022, 38, 1–10. [Google Scholar]
- Lv, Q.; Liu, H.B.; Wang, J.T.; Liu, H.; Shang, Y. Multiscale Analysis on Spatiotemporal Dynamics of Energy Consumption CO2 Emissions in China: Utilizing the Integrated of DMSP-OLS and NPP-VIIRS Nighttime Light Datasets. Sci. Total Environ. 2020, 703, 134394. [Google Scholar] [CrossRef]
- Shi, K.F.; Chen, Y.; Yu, B.F.; Xu, T.B.; Chen, Z.Q.; Liu, R.; Li, L.Y.; Wu, J.P. Modeling Spatiotemporal CO2 (carbon dioxide) Emission Dynamics in China from DMSP-OLS Nighttime Stable Light Data Using Panel Data Analysis. Appl. Energy 2016, 168, 523–533. [Google Scholar] [CrossRef]
- Glaeser, E.L.; Kahn, M.E. The Greenness of Cities: Carbon Dioxide Emissions and Urban Development. J. Urban Econ. 2010, 67, 404. [Google Scholar] [CrossRef]
- Mathy, S.; Fink, M.; Bibas, R. Rethinking the Role of Scenarios: Participatory Scripting of Low–Carbon Scenarios for France. J. Energy Policy. 2014, 77, 176–190. [Google Scholar] [CrossRef]
- Xi, F.M.; Liang, W.J.; Niu, M.F.; Wang, J.Y. Carbon Emissions and Low–Carbon Regulation Countermeasures of Land Use Change in the City and Town Concentrated Area of Central Liaoning Province, China. J. Appl. Ecol. 2016, 27, 577–584. [Google Scholar]
- Zhang, Z.L.; Zhu, J.Q.; Yang, X.L. Three-Dimensional Active Earth Pressures for Unsaturated Backfills with Cracks Considering Steady Seepage. Int. J. Geomech. 2023, 23, 04022270. [Google Scholar] [CrossRef]
- Zhou, L.Y. Study on the Influence of Urban Construction Land Expansion on Carbon Emission Based on VAR Model—A Case Study of Nanchang City. IOP Conf. Ser. Earth Environ. Sci. 2021, 769, 022–071. [Google Scholar] [CrossRef]
- Ishii, S.; Tabushi, S.; Aramaki, T.; Hanaki, K. Impact of Future Urban Form on the Potential to Reduce Greenhouse Gas Emissions from Residential, Commercial and Public Buildings in Utsunomiya, Japan. J. Energy Policy 2010, 38, 4888–4896. [Google Scholar] [CrossRef]
- Ou, J.P.; Liu, X.P.; Li, X.; Chen, Y.M. Quantifying the Relationship between Urban Forms and Carbon Emissions Using Panel Data Analysis. Landsc. Ecol. 2013, 28, 1889–1907. [Google Scholar] [CrossRef]
- Yi, Y.C.; Ma, S.S.; Guan, W.J.; Li, K. An Empirical Study on the Relationship between Urban Spatial Form and CO2 in Chinese Cities. Sustainability 2017, 9, 672. [Google Scholar] [CrossRef]
- Teng, F.; Wang, Y.J.; Wang, M.J.; Li, S.C.; Lin, Y.H.; Cai, H.F. Spatiotemporal Coupling Relationship between Urban Spatial Morphology and Carton Budget in Yangtze River Delta Urban Agglomeration. Acta Ecol. Sin. 2022, 42, 23. [Google Scholar]
- Wang, Z.Y.; Zhen, B.H.; Chen, Z.Z. Study of Correlation of Urban Space Shape and the Carbon Intensity: Based on Analysis of 35 Cities in China. Urban Stud. 2013, 20, 8–15. [Google Scholar]
- Shi, K.F.; Xu, T.; Li, Y.Q.; Chen, Z.Q.; Gong, W.K.; Wu, J.P.; Yu, B.L. Effects of Urban Forms on CO2 Emissions in China From A Multi–Perspective Analysis. J. Environ. Manag. 2020, 262, 110300. [Google Scholar] [CrossRef]
- Wang, M.S.; Marguerite, M.; Liu, X.J. Exploring the Relationship between Urban Forms and CO2 Emissions in 104 Chinese Cities. J. Urban Plan. Dev. 2017, 143, 04017014. [Google Scholar] [CrossRef]
- Ding, G.Q.; Guo, J.; Pueppke, S.G.; Yi, J.; Ou, M.H.; Ou, W.X.; Tao, Y. The Influence of Urban Form Compactness on CO2 Emissions and Its Threshold Effect: Evidence from Cities in China. J. Environ. Manag. 2022, 322, 116032. [Google Scholar] [CrossRef]
- Li, Z.; Wang, F.; Kang, T.T.; Wang, C.J.; Chen, X.D.; Miao, Z.; Zhang, L.; Ye, Y.Y.; Zhang, H. Exploring Differentiated Impacts of Socioeconomic Factors and Urban Forms on City–Level CO2 Emissions in China: Spatial Heterogeneity and Varying Importance Levels. Sustain. Cities Soc. 2022, 09, 104028. [Google Scholar] [CrossRef]
- Ye, H.; He, X.Y.; SONG, Y.; Li, X.H.; Zhang, G.Q.; Lin, T.; Xiao, L.S. A Sustainable Urban Form: The Challenges of Compactness From the Viewpoint of Energy Consumption and Carbon Emission. Energy Build. 2015, 93, 90–98. [Google Scholar] [CrossRef]
- Li, M.F.; Yun, G.L.; He, Y.R. Analysis on the Relationship between of Compactness of Urban Space and Carbon Intensity: A Case Study of Xiamen Island. J. Cent. South Univ. For. Technol. (Soc. Sci.) 2016, 10, 10–14. [Google Scholar]
- Yang, H.; Lu, X.H.; Kuang, B.; Hou, J. Spatial-Temporal Interaction and Driving Factors of Urban Compactness and Carbon Emission Intensity: A Case Study in Changsha-Zhuzhou-Xiangtan Urban Agglomeration. Resour. Environ. Yangtze Basin. 2021, 30, 2618–2629. [Google Scholar]
- Jeffrey, R.K.; Laube, F.B. Automobile Dependence in Cities: An International Comparison of Urban Transport and Land Use Patterns with Implications for Sustainability. J. Environ. Impact Assess. Rev. 1996, 16, 279–308. [Google Scholar]
- Reid, E. Is Los Angeles-Style Sprawl Desirable? J. Am. Plan. Assoc. 1997, 63, 107–126. [Google Scholar]
- Andong, R.F.; Sajor, E. Urban Sprawl, Public Transport, and Increasing CO2 Emissions: The Case of Metro Manila, Philippines. Environ. Dev. Sustain. 2017, 19, 99–123. [Google Scholar] [CrossRef]
- Pan, H.X. Urban Spatial Structure Towards Low Carbon: New Urban Transport and Land Use Model. Urban Stud. 2010, 17, 40–45. [Google Scholar]
- Waygood, E.O.D.; Chatterton, T.; Avineri, E. Comparing and Presenting City-Level Transportation CO Emissions Using GIS2. Transp. Res. Part D Transp. Environ. 2013, 24, 127–134. [Google Scholar] [CrossRef]
- Andrea, C.; Paolo, V. Spatial Structure and Carbon Dioxide (CO2) Emissions Due to Commuting: An Analysis of Italian Urban Areas. Reg. Stud. 2014, 48, 1993–2005. [Google Scholar]
- Sukarno, I.; Matsumoto, H.; Susanti, L. Transportation Energy Consumption and Emissions–a View from City of Indonesia. Future Cities Environ. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Zhao, T.T.; Horner, M.W.; John, S. A Geographic Approach to Sectoral Carbon Inventory: Examining the Balance between Consumption-Based Emissions and Land-Use Carbon Sequestration in Florida. Ann. Assoc. Am. Geogr. 2011, 101, 752–763. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, Y.; Jiang, X.H. Carbon Emission Measurement and Driving Factor Analysis of Transportation in Southwest China. J. Chongqing Univ. Technol. (Nat. Sci.) 2022, 36, 1–10. [Google Scholar]
- Alexander, R.; Christian, H.R.; Joachim, S. GHG Emissions in Daily Travel and Long-Distance Travel in Germany-Social and Spatial Correlates. Transp. Res. Part D Transp. Environ. 2016, 49, 25–43. [Google Scholar]
- William, P.A.; Pavlos, S.K.; Eric, J.M. Urban Form, Energy and the Environment: A Review of Issues, Evidence and Policy. Urban Stud. 1996, 33, 7–35. [Google Scholar]
- Christian, H.R.; Joachim, S. Land-Use and Transport Planning–A Field of Complex Cause-Impact Relationships. Thoughts on Transport Growth, Greenhouse Gas Emissions and the Built Environment. Transp. Policy 2019, 74, 127–137. [Google Scholar]
- GB 50137–2011; Code for Classification of Urban Land Use and Planning Standards of Development Land. China Architecture and Architecture Press: Beijing, China, 2010.
- Deng, J.L. The Grey Control System. Huazhong Univ. Sci. Technol. 1982, 10, 11–20. [Google Scholar]
- Luo, L.X. Progressive Optimization GM (1, 1) Model Based on Direct Modeling for Demand Forecast of Urban Construction Land and Its Empirical Research. Electron. J. Geotech. Eng. 2015, 20, 5023–5028. [Google Scholar]
- Xue, D.Q. Expanding Law and Restraining Mechanism about Urban Land: Taking Xi’an City as an Example. J. Nat. Resour. 2002, 17, 729–736. [Google Scholar]
- Boyce, R.R.; Clark, W.A.V. The Concept of Shape in Geography. Geogr. Rev. 1964, 54, 561–572. [Google Scholar] [CrossRef]
- Moellering, H.; Rayner, J.N. The Dual Axis Fourier Shape Analysis of Closed Cartographic Forms. J. Cartogr. J. 1982, 19, 53–59. [Google Scholar] [CrossRef]
- Thinh, N.X.; Arlt, G.; Heber, B. Evaluation of Urban Land-Use Structures with a View to Sustainable Development. Environ. Impact Assess. Rev. 2002, 22, 475–492. [Google Scholar] [CrossRef]
- Fong, W.K.; Matsumoto, H.; Lun, Y.F. Application of System Dynamics Model as Decision Making Tool in Urban Planning Process Toward Stabilizing Carbon Dioxide Emissions from Cities. Build. Environ. 2009, 44, 1528–1537. [Google Scholar] [CrossRef]
- Feng, Y.Y.; Chen, S.Q.; Zhang, L.X. System Dynamics Modeling for Urban Energy Consumption and CO2 Emissions: A Case Study of Beijing, China. Ecol. Model. 2013, 252, 44–52. [Google Scholar] [CrossRef]
- Liu, X.; Ma, S.F.; Tian, J.F.; Jia, N.; Li, G. A System Dynamics Approach to Scenario Analysis for Urban Passenger Transport Energy Consumption and CO2, Emissions: A Case Study of Beijing. Energy Policy 2015, 85, 253–270. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.Y.; Tang, Y.L.; Chen, Y.Y.; Zhou, X.; Bedra, K.B. Urban Sprawl and Carbon Emissions Effects in City Areas Based on System Dynamics: A Case Study of Changsha City. Appl. Sci. 2022, 12, 3244. [Google Scholar] [CrossRef]
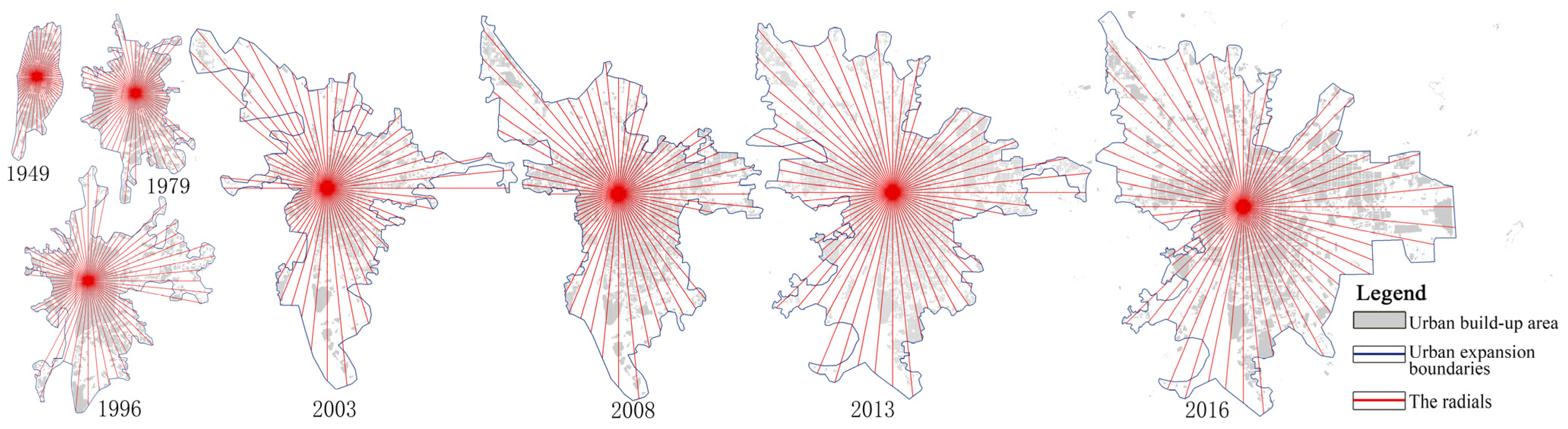



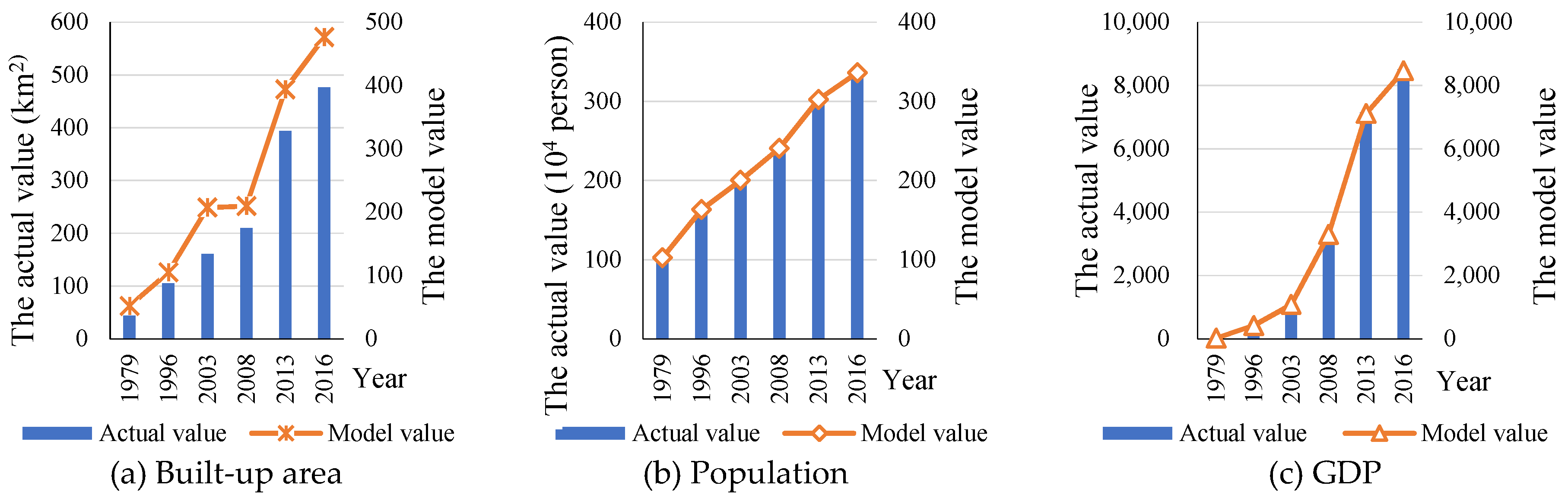
| Item | 1949 | 1979 | 1996 | 2003 | 2008 | 2013 | 2016 | |
|---|---|---|---|---|---|---|---|---|
| Population (104 person) | 38.35 | 99.28 | 160.38 | 196.38 | 237.06 | 299.25 | 336.25 | |
| GDP (CNY106) | 2.87 | 21.38 | 415.77 | 1077.22 | 3300.98 | 7153.13 | 8510.13 | |
| The built-up area (H, unit: sq. km) | 6.7 | 51.8 | 104.93 | 96.26 | 209.63 | 393.78 | 476.34 | |
| development land (unit: sq. km) | Residential land (R) | 1.92 | 11.02 | 25.38 | 30.95 | 69.95 | 134.79 | 155.32 |
| Commercial service land (A and B) | 1.26 | 13.33 | 26.97 | 37.02 | 43.98 | 73.4 | 66.58 | |
| Industrial land (M) | 1.52 | 12.5 | 21.9 | 27.1 | 30.6 | 66.5 | 94.56 | |
| Road and transportation land (S) | 0.8 | 2.97 | 9.59 | 20.58 | 31.76 | 37.67 | 52.87 | |
| Public green space (G) | 0.6 | 4.8 | 7.94 | 12.29 | 21.42 | 29.13 | 34.13 | |
| Year | IH | IR | IA&B | IM | IS | IG |
|---|---|---|---|---|---|---|
| 1949–1979 | 22.44 | 15.8 | 16.33 | 13.2 | 9.04 | 23.33 |
| 1979–1996 | 6.03 | 7.67 | 6.02 | 4.42 | 13.11 | 3.85 |
| 1996–2003 | 7.55 | 3.14 | 5.32 | 3.39 | 16.37 | 7.83 |
| 2003–2008 | 6.14 | 25.2 | 3.76 | 2.58 | 10.86 | 14.86 |
| 2008–2013 | 17.57 | 18.54 | 6 | 23.46 | 3.72 | 7.2 |
| 2003–2016 | 6.99 | 5.08 | 5.49 | 14.07 | 4.6 | 5.72 |
| Content | 1949 | 1979 | 1996 | 2003 | 2008 | 2013 | 2016 |
|---|---|---|---|---|---|---|---|
| Urban morphology indices (SBC) | 34.0 | 28.81 | 33.80 | 33.29 | 31.89 | 26.17 | 25.64 |
| Urban compactness (U) | 0.521 | 0.228 | 0.172 | 0.146 | 0.21 | 0.205 | 0.195 |
| Shortest travel distance (Z) | 607.12 | 1948.76 | 4740.335 | 15,463.21 | 29,804.45 | 53,102.61 | 71,254.58 |
| Content | Units | 1949 | 1979 | 1996 | 2003 | 2008 | 2013 | 2016 |
|---|---|---|---|---|---|---|---|---|
| Total carbon emissions (TCE) | t-CO2/104 | 1.73 | 5.88 | 5.21 | 6.96 | 12.32 | 17.88 | 18.13 |
| Per capita emissions (PCE) | 104 t-CO2/per. | 66.24 | 601.73 | 851.07 | 1392.75 | 2963.87 | 5404.60 | 6095.21 |
| Emission growth rate (EG) | % | / | 26.95 | 2.44 | 9.09 | 22.56 | 16.47 | 4.26 |
| Residential sub-model (FRes) | 104 t-CO2 | 6.42 | 25.32 | 50.95 | 132.37 | 208.77 | 347.48 | 410.2 |
| Commercial-service sub-model (FCom) | 5.02 | 52.24 | 65.89 | 240.39 | 471.61 | 784.93 | 1125.6 | |
| Industrial sub-model (FInd) | 42.35 | 472.27 | 587.47 | 641.26 | 1813.72 | 2147.59 | 2333.6 | |
| Transportation sub-model (FTra) | 12.52 | 51.96 | 146.81 | 378.79 | 469.81 | 2124.64 | 2225.8 | |
| Sequestration sub-model (FGa) | −695.95 | −609.3 | −592.44 | −552.02 | −427.69 | −343.41 | −231.54 | |
| Carbon-emission intensity (EI) | t-CO2/CNY104 | 23.08 | 28.14 | 2.05 | 1.29 | 0.9 | 0.76 | 0.72 |
| Emission per unit land (EPL) | 106 t-CO2/Km2 | 9.89 | 11.62 | 8.11 | 6.72 | 14.14 | 13.72 | 12.80 |
| Year | Carbon Emissions | |
|---|---|---|
| Base Scenario | COVID-19 Scenario | |
| 2017 | 6431.31 | 6824.57 |
| 2018 | 6903.27 | 7773.32 |
| 2019 | 7398.59 | 8393.766 |
| 2020 | 7917.81 | 9084.231 |
| 2021 | 8461.51 | 9571.036 |
| 2022 | 9030.24 | 10,070.21 |
| 2023 | 9624.56 | 10,581.52 |
| 2024 | 10,245.02 | 11,104.73 |
| 2025 | 10,892.20 | 11,550.77 |
| 2026 | 11,566.66 | 12,000.61 |
| 2027 | 12,268.95 | 12,453.83 |
| 2028 | 12,999.66 | 12,910.04 |
| 2029 | 13,759.34 | 13,375.11 |
| 2030 | 14,548.55 | 13,836.29 |
| Relational Grades | Correlation with Land Expansion Intensity | ||||
|---|---|---|---|---|---|
| R | A&B | M | S | G | |
| Total carbon emissions (TCE) | 0.999 | 0.938 | 0.967 | 0.962 | −0.984 |
| Per capita emissions (PCE) | 0.978 | 0.946 | 0.932 | 0.95 | −0.961 |
| Emission growth rate (EG) | 0.788 | 0.549 | 0.168 | −0.148 | 0.906 |
| Carbon-emission intensity (EI) | −0.621 | −0.844 | −0.634 | −0.723 | −0.613 |
| Emission per unit land (EPL) | 0.678 | 0.554 | 0.538 | 0.634 | 0.667 |
| Content | Urban Expansion Intensity(I) | Urban Morphology Indices (SBC) | Urban Compactness (U) | Shortest Travel Distance (Z) |
|---|---|---|---|---|
| TCE | / | −0.827 | −0.392 | 0.992 |
| PCE | / | −0.834 | −0.482 | 0.963 |
| EG | 0.669 | / | / | / |
| EI | / | 0.278 | 0.858 | −0.598 |
| EPL | / | 0.707 | −0.094 | 0.666 |
| Content | 2003 (Base Year) | 2016 (Current Situation) | 2030 (Target Year) | 2030 (COVID-19 Scenario) |
|---|---|---|---|---|
| GDP (CNY104) | 1077.22 | 8510.13 | ≥20,000 | ≥19,000 |
| Population (ten thousand people) | 196.38 | 336.25 | ≥889.61 | ≥830.44 |
| H (Km2) | 160.41 | 476.34 | ≤889.61 | ≤830.44 |
| Total carbon emissions (104 t-CO2) | 1392.75 | 6095.21 | ≤8729.13 | ≤8301.77 |
| Carbon emissions per capita (t-CO2/per) | 6.96 | 18.13 | ≤8.73 | ≤8.3 |
| Carbon-emission intensity (t-CO2/CNY104) | 1.29 | 0.72 | ≤0.45 | ≤0.48 |
| Carbon emission per unit land (t-CO2/hm) | 8.68 | 12.8 | ≤9.12 | ≤9.33 |
| Content | Built-Up Area | R | A&B | M | S | G |
|---|---|---|---|---|---|---|
| 2016 (current situation) | 476.34 | 155.32 | 66.58 | 94.56 | 52.87 | 34.13 |
| Percentage of land % | 100 | 32.61% | 13.98% | 19.85% | 11.10% | 7.17% |
| The relevance of carbon emissions | 0.990 | 0.999 | 0.938 | 0.967 | 0.962 | −0.984 |
| 2030 (target year) | 889.61 | 231.3 | 143.88 | 150.17 | 135.83 | 61.33 |
| Percentage of land % | 100 | 26.0% | 16.17% | 16.88% | 15.27% | 6.89% |
| EI correlation test results | −0.873 | −0.902 | −0.855 | −0.817 | −0.849 | −0.904 |
| Year | Urban Expansion Intensity (I) | Urban Morphology Indices (SBC) | Urban Compactness (U) | Shortest Travel Distance (Z) |
|---|---|---|---|---|
| 2016 (current situation) | 6.99 | 25.64 | 0.195 | 71,254.58 |
| 2030 (target year) | 6.19 | 32.04 | 0.236 | 96,086.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Xun, L.; Wang, Z.; Liu, H.; Huang, Y.; Bedra, K.B. Peak Carbon Dioxide Emissions Strategy Based on the Gray Model between Carbon Emissions and Urban Spatial Expansion for a Built-Up Area. Appl. Sci. 2023, 13, 187. https://doi.org/10.3390/app13010187
Liu L, Xun L, Wang Z, Liu H, Huang Y, Bedra KB. Peak Carbon Dioxide Emissions Strategy Based on the Gray Model between Carbon Emissions and Urban Spatial Expansion for a Built-Up Area. Applied Sciences. 2023; 13(1):187. https://doi.org/10.3390/app13010187
Chicago/Turabian StyleLiu, Luyun, Lingling Xun, Zhiyuan Wang, Huaiwan Liu, Yu Huang, and Komi Bernard Bedra. 2023. "Peak Carbon Dioxide Emissions Strategy Based on the Gray Model between Carbon Emissions and Urban Spatial Expansion for a Built-Up Area" Applied Sciences 13, no. 1: 187. https://doi.org/10.3390/app13010187
APA StyleLiu, L., Xun, L., Wang, Z., Liu, H., Huang, Y., & Bedra, K. B. (2023). Peak Carbon Dioxide Emissions Strategy Based on the Gray Model between Carbon Emissions and Urban Spatial Expansion for a Built-Up Area. Applied Sciences, 13(1), 187. https://doi.org/10.3390/app13010187






