Non-Magnetic Circulator Based on a Time-Varying Phase Modulator
Abstract
:1. Introduction
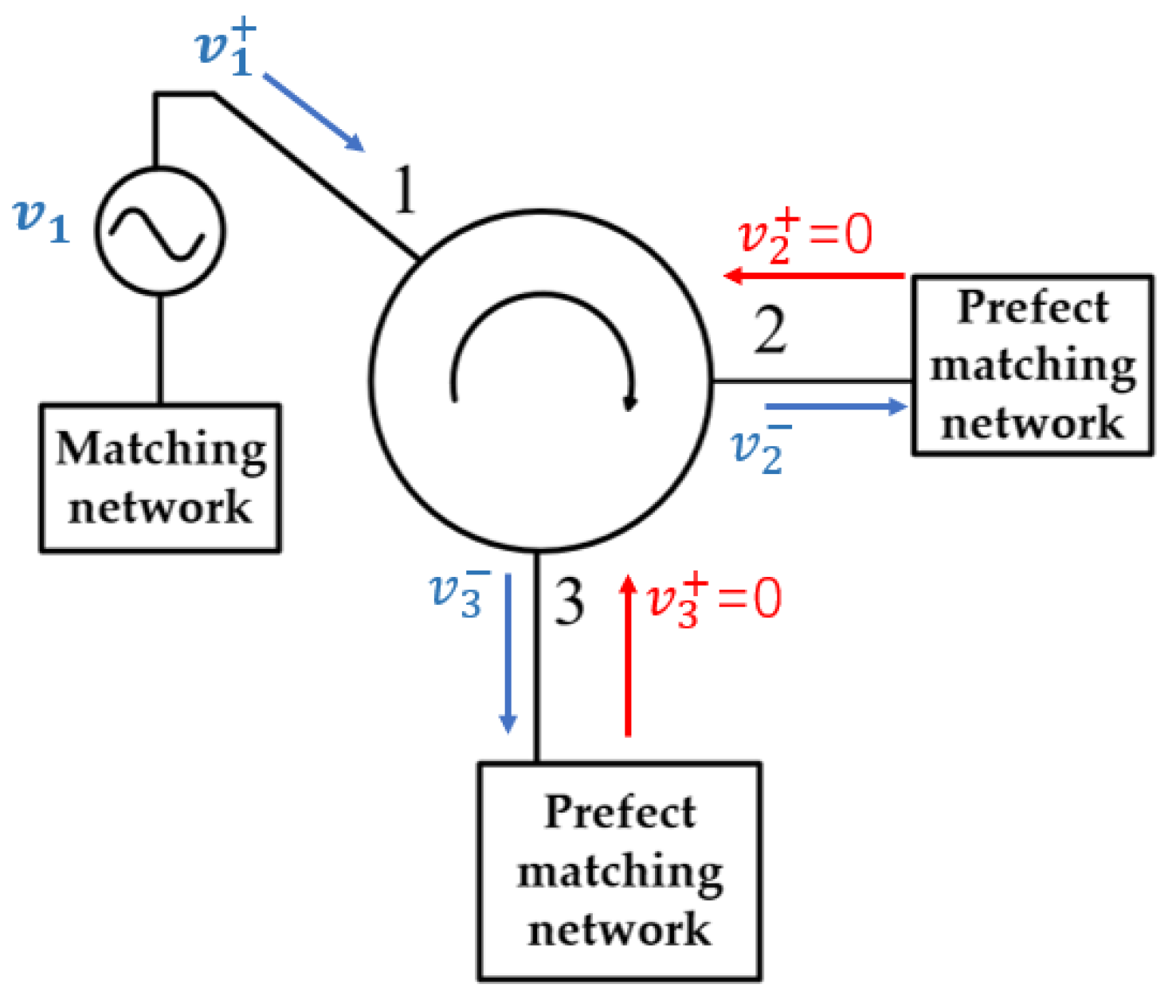
2. Gyrator Design
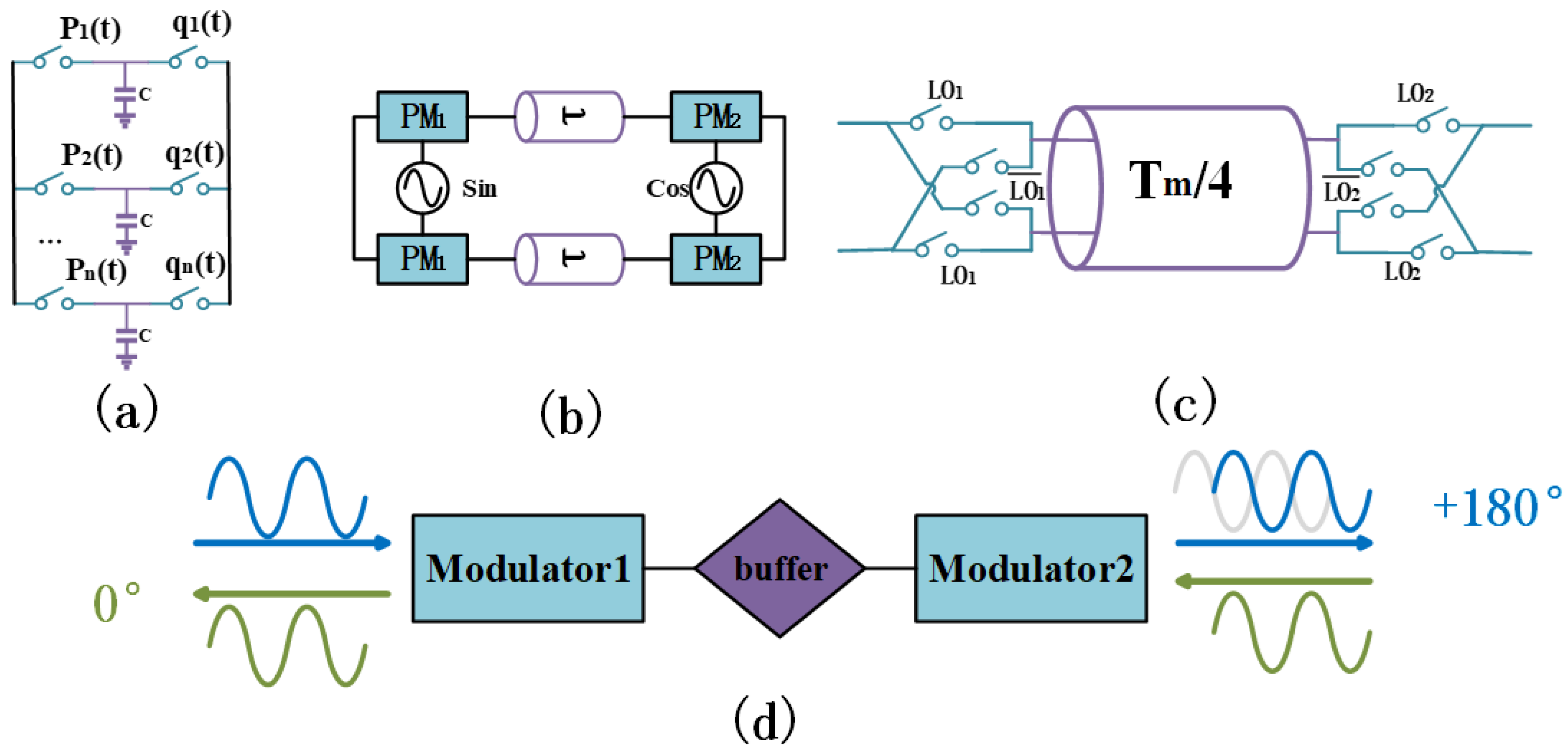
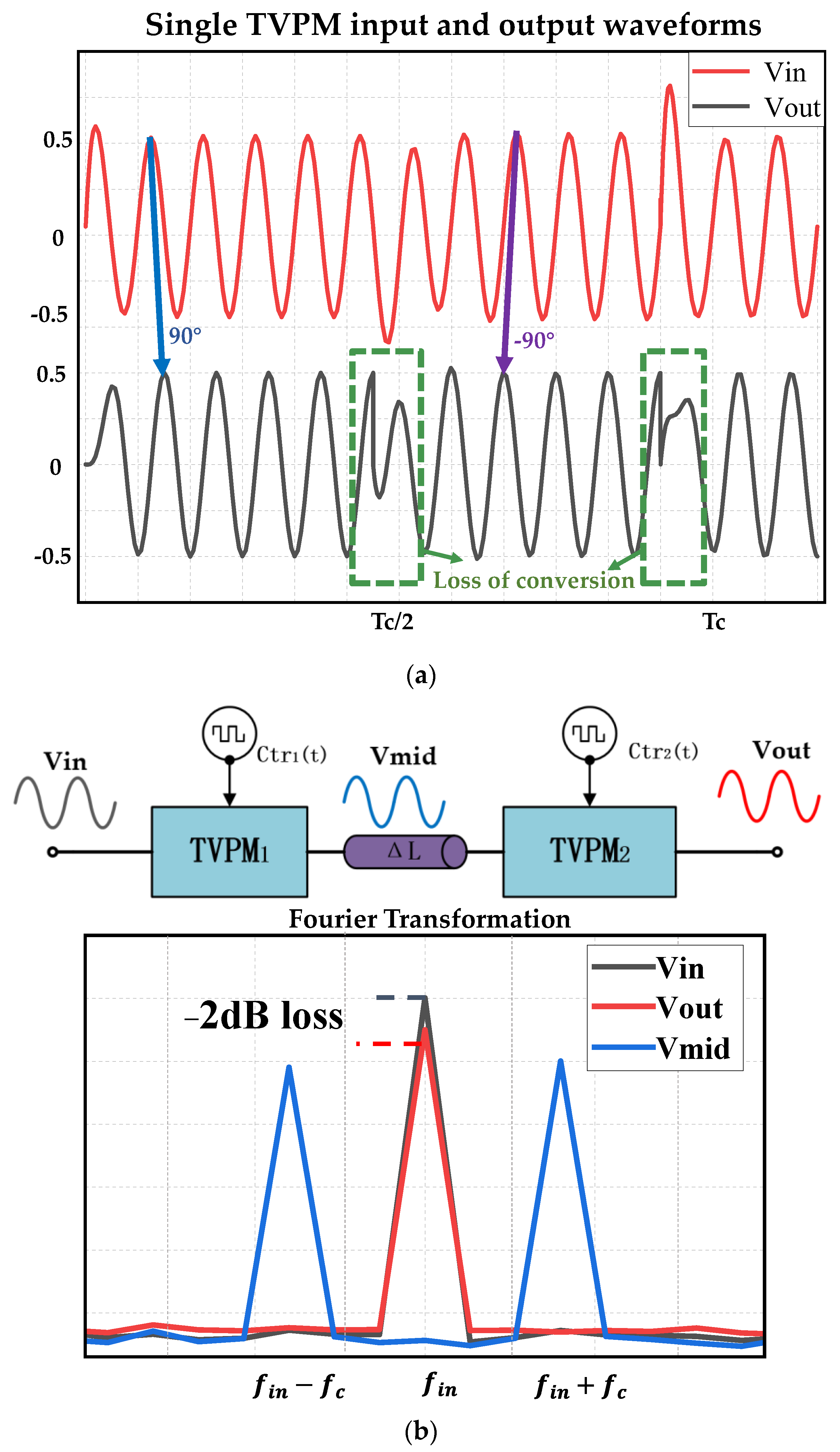
2.1. Time-Varying Phase Modulator (TVPM)
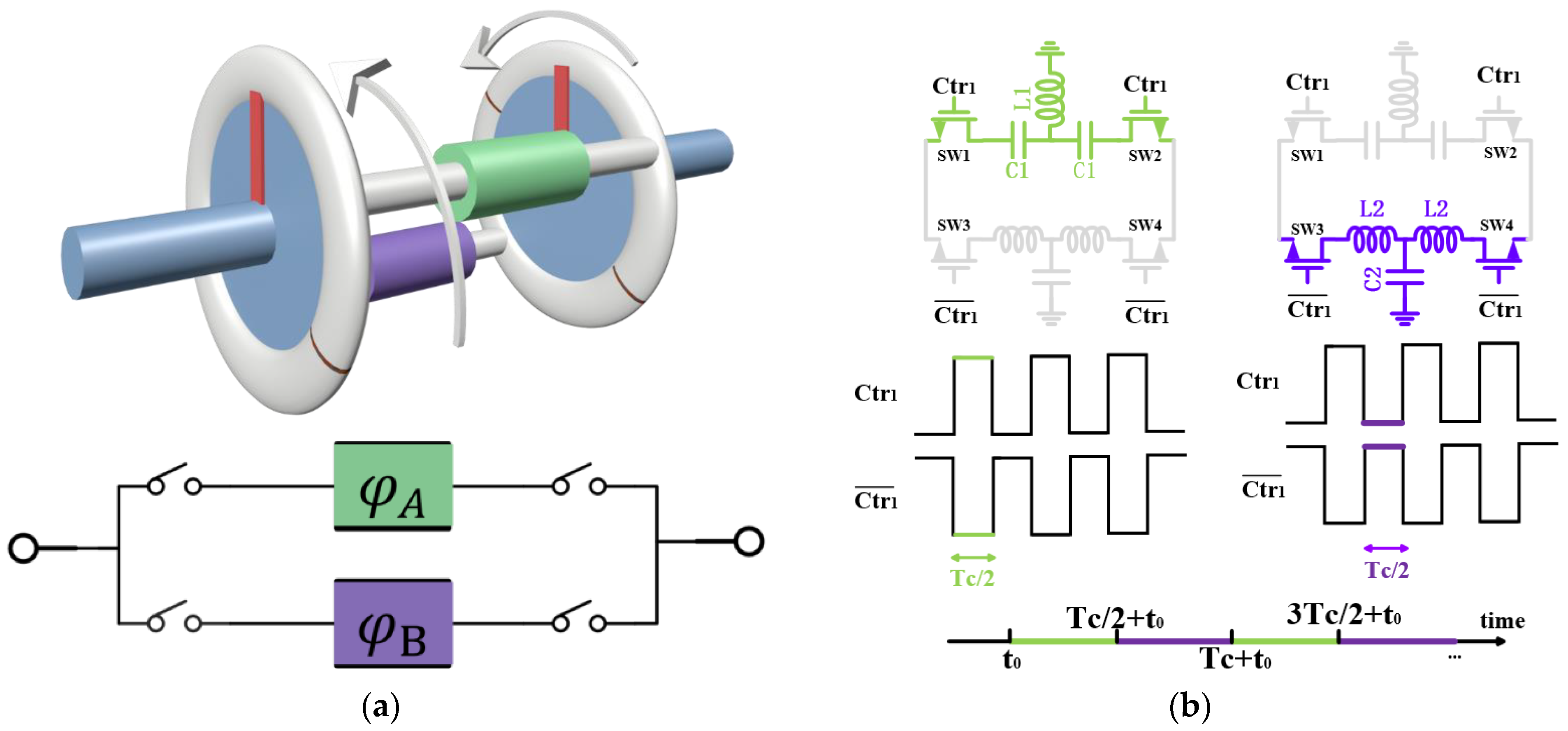
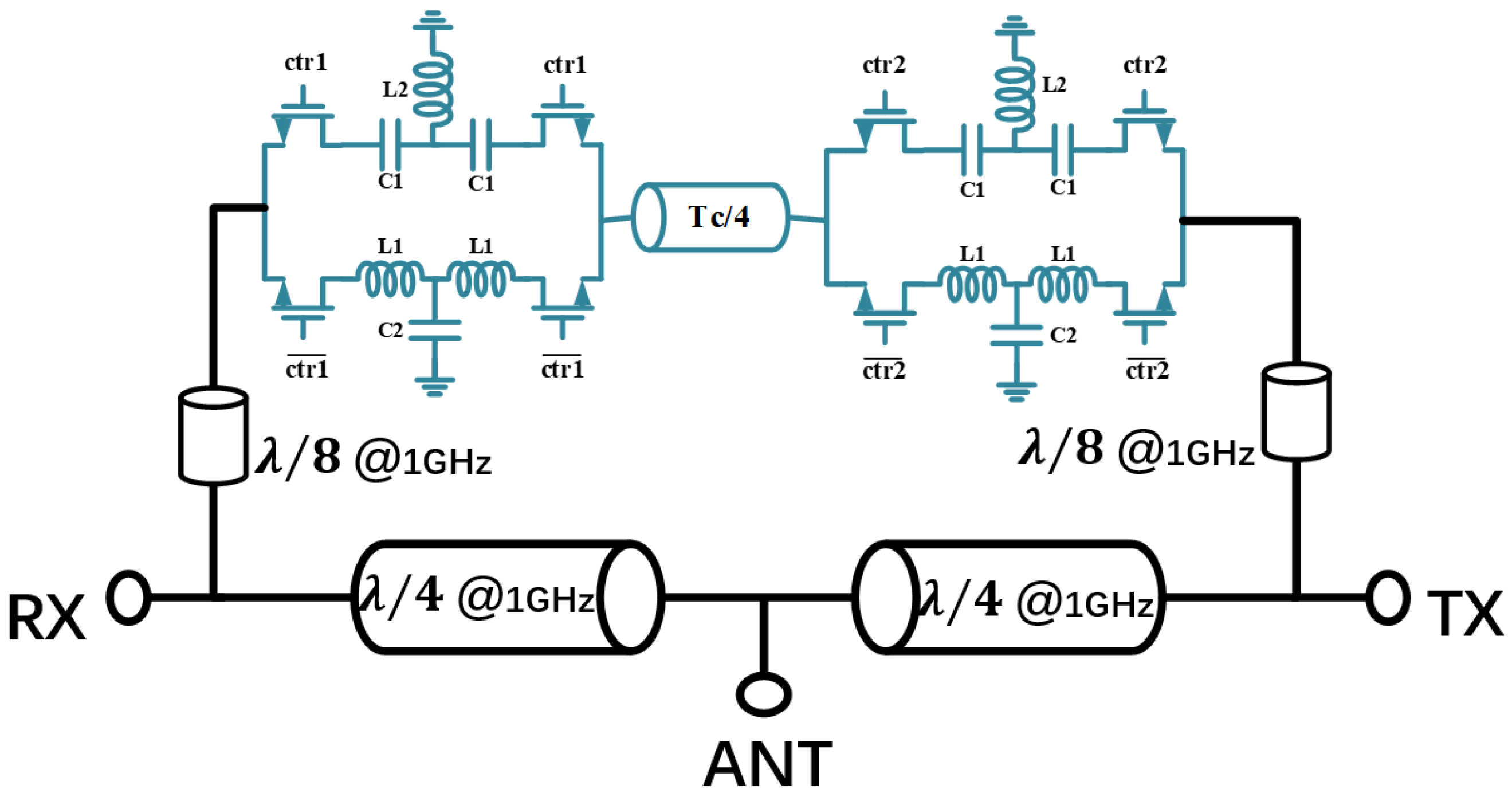
2.2. Circuit of Gyrator
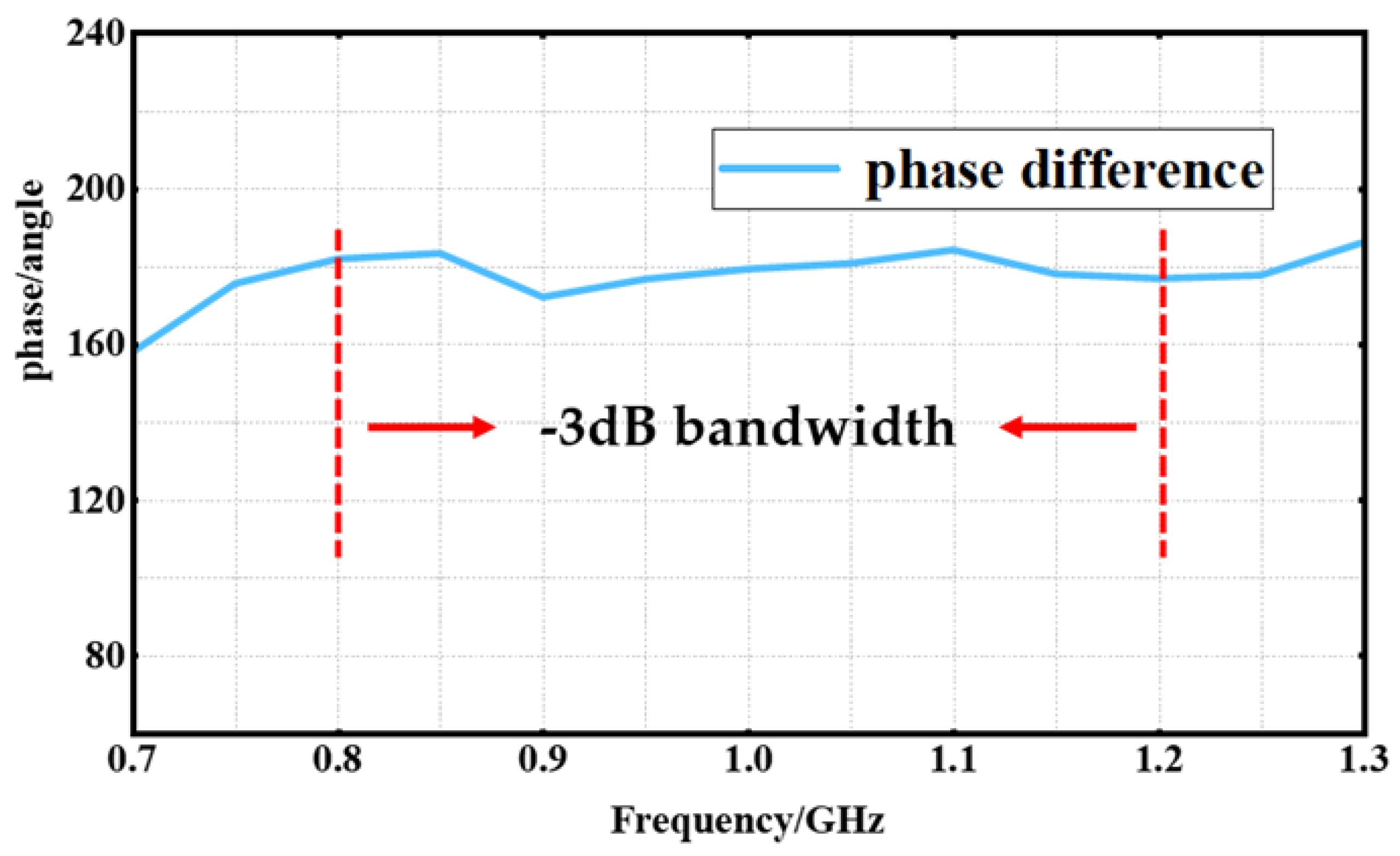
2.3. Conversion Loss
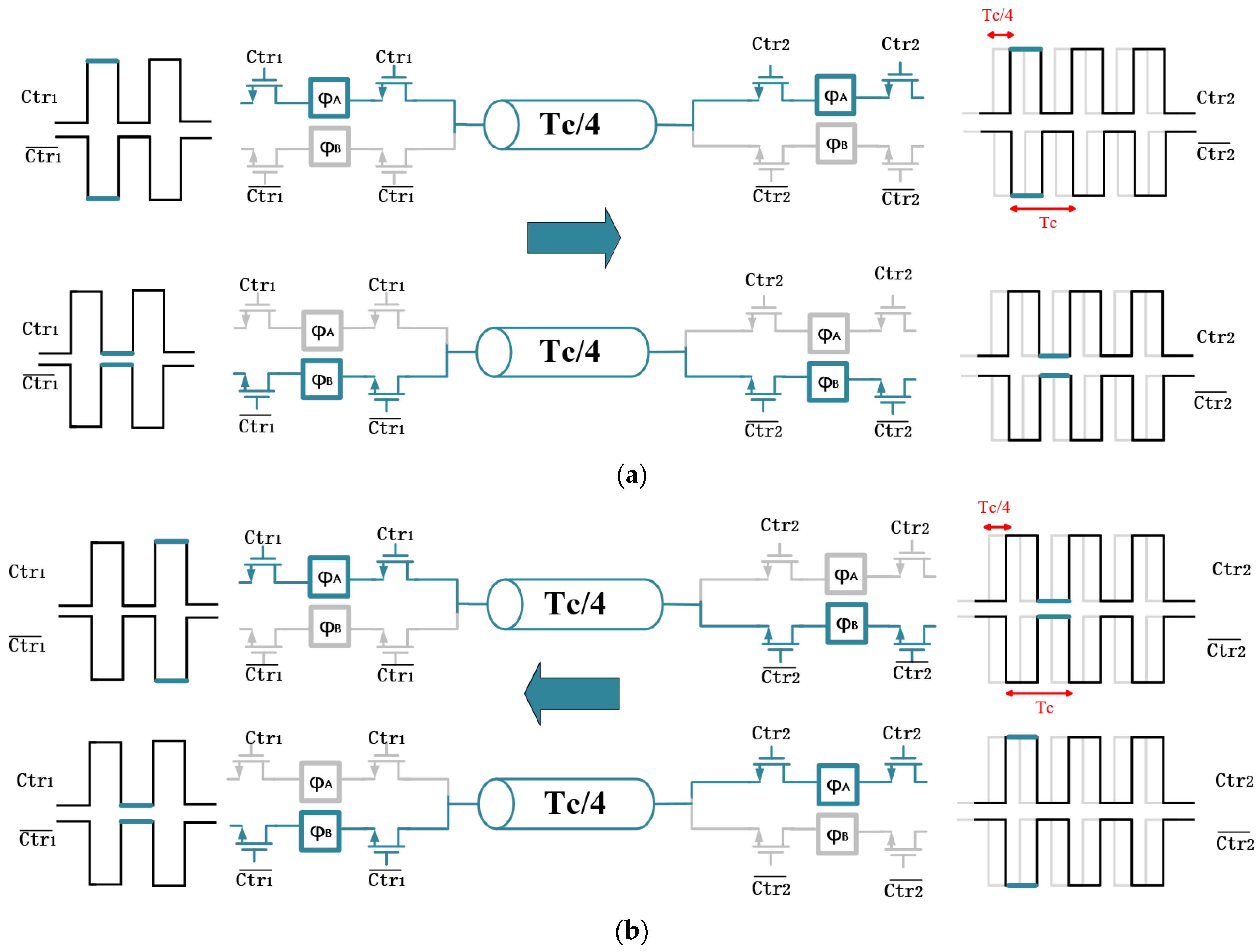
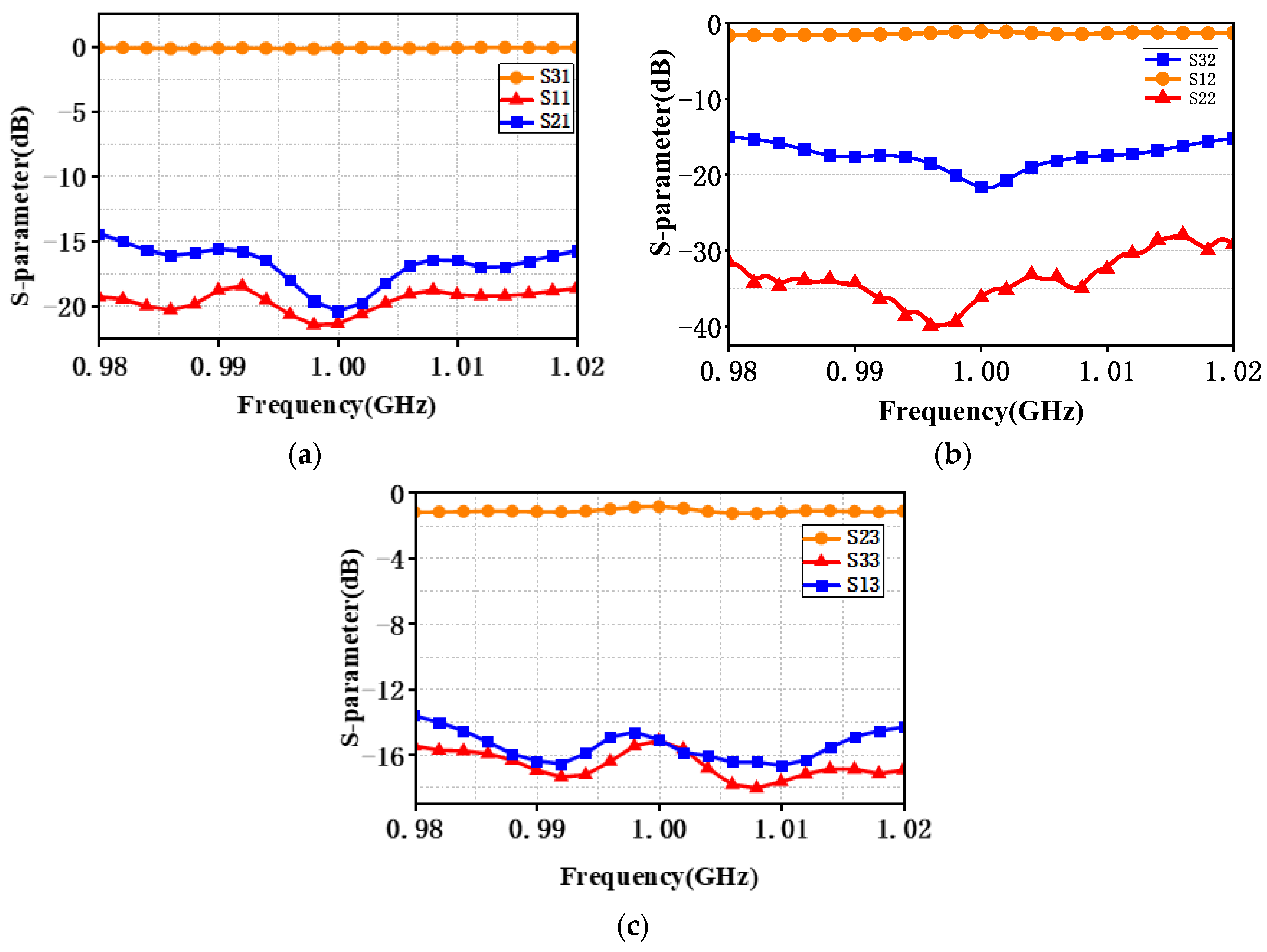
3. Circulator Implementation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jalas, D.; Petrov, A.; Eich, M.; Freude, W.; Fan, S.; Yu, Z.; Baets, R.; Popović, M.; Melloni, A.; Joannopoulos, J.D.; et al. What is? and what is not? an optical isolator. Nat. Photonics 2013, 7, 579–582. [Google Scholar] [CrossRef]
- Sabharwal, A.; Schniter, P.; Guo, D.; Bliss, D.W.; Rangarajan, S.; Wichman, R. In-Band Full-Duplex Wireless: Challenges and Opportunities. Sel. Areas Commun. IEEE J. 2014, 32, 1637–1652. [Google Scholar] [CrossRef] [Green Version]
- Giuseppe, T.; Ruzzene, M. Non-reciprocal elastic wave propagation in spatiotemporal periodic structures. New J. Phys. 2016, 18, 083047. [Google Scholar]
- Biedka, M.M.; Zhu, R.; Xu, Q.M.; Wang, Y.E. Ultra-wideband non-reciprocity through sequentially-switched delay lines. Sci. Rep. 2017, 7, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bi, L.; Hu, J.; Jiang, P.; Kim, D.; Dionne, G.; Kimerling, L.; Ross, C. On-chip optical isolation in monolithically integrated non-reciprocal optical resonators. Nat. Photonics 2011, 5, 1–5. [Google Scholar] [CrossRef]
- Zhou, J.; Chuang, T.-H.; Dinc, T.; Krishnaswamy, H. Integrated wideband self-interference cancellation in the RF domain for FDD and full-duplex wireless. IEEE J. Solid-State Circuits 2015, 50, 3015–3031. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 444–448. [Google Scholar]
- Zander, J.; Mähönen, P. Riding the data tsunami in the cloud: Myths and challenges in future wireless access. IEEE Commun. Mag. 2013, 51, 145–151. [Google Scholar] [CrossRef]
- Aleahmad, P.; Khajavikhan, M.; Christodoulides, D.; LiKamWa, P. Integrated multi-port circulators for unidirectional optical information transport. Sci. Rep. 2017, 7, 2129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Q.; Schmidt, B.; Pradhan, S.; Lipson, M. Micrometre-scale silicon electro-optic modulator. Nature 2005, 435, 325–327. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.E. Non-reciprocity with time-varying transmission lines (TVTLs). In Proceedings of the 2012 IEEE International Conference on Wireless Information Technology and Systems (ICWITS), Maui, HI, USA, 11–16 November 2012; pp. 1–4. [Google Scholar]
- Kadry, H.M.; Alhawari, M.; Sounas, D.L. Angular-Momentum Biased Circulator With Locally Generated Modulation. IEEE Trans. Microw. Theory Tech. 2020, 69, 551–565. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Experimental demonstration of a photonic Aharonov–Bohm effect at radio frequencies. Phys. Rev. B 2013, 87, 060301. [Google Scholar] [CrossRef]
- Poulton, C.G.; Pant, R.; Byrnes, A.; Fan, S.; Steel, M.J.; Eggleton, B.J. Design for broadband on-chip isolator using stimulated Brillouin scattering in dispersion-engineered chalcogenide waveguides. Opt. Express. 2012, 20, 2135–2156. [Google Scholar] [CrossRef] [PubMed]
- Reiskarimian, N.; Zhou, J.; Krishnaswamy, H. A CMOS Passive LPTV Nonmagnetic Circulator and Its Application in a Full-Duplex Receiver. IEEE J. Solid-state Circuits 2017, 5, 1–15. [Google Scholar] [CrossRef]
- Dinc, T.; Nagulu, A.; Krishnaswamy, H. A Millimeter-Wave Non-Magnetic Passive SOI CMOS Circulator Based on Spatio-Temporal Conductivity Modulation. IEEE J. Solid-State Circuits 2017, 52, 3276–3292. [Google Scholar] [CrossRef]
- Doerr, C.R.; Dupuis, N.; Zhang, L. Optical isolator using two tandem phase modulators. Opt. Lett. 2011, 36, 4293–4295. [Google Scholar] [CrossRef] [PubMed]
- Doerr, C.R.; Chen, L.; Vermeulen, D. Silicon photonics broadband modulation-based isolator. Optics Express 2014, 22, 4493. [Google Scholar] [CrossRef] [PubMed]
- Hogan, C.L. The ferromagnetic Faraday effect at microwave frequencies and its applications: The microwave gyrator. Bell Syst. Tech. J. 1952, 31, 1–31. [Google Scholar] [CrossRef]
- Regev, D.; Zolkov, E.; Ginzberg, N.; Weiss, R.; Cohen, E. The Role of Impedance Transparency of Non-Reciprocal 90° Phase Shifters in the Evolution of Electronic Circulators. In Proceedings of the 2021 IEEE Texas Symposium on Wireless and Microwave Circuits and Systems (WMCS), Virtual, 18–20 May 2021. [Google Scholar]
- Nagulu, A.; Krishnaswamy, H. Non-Magnetic CMOS Switched-Transmission-Line Circulators With High Power Handling and Antenna Balancing: Theory and Implementation. Solid State Circuits IEEE J. 2019, 54, 1288–1303. [Google Scholar] [CrossRef]



| τ | t1 |
|---|---|
| 0.25 | 0.25 |
| 0.25 | 0.75 |
| 0.75 | 0.25 |
| 0.75 | 0.75 |
| Reference | [19] 1 | [15] | [16] | This Work |
|---|---|---|---|---|
| Architecture | Magnetic ferrite | N-path filter | Conductivity mod. | TVPM |
| ANT port | Single end | Single end | Differential end | Single end |
| Frequency | 1 GHz | 0.75 GHz | 25 GHz | 1 GHz |
| BW(−3 dB) | 100 MHz | 40 MHz | Infinite 2 | 400 MHz |
| Insertion loss | −1 dB | −2 dB | −0.5 dB | −1.7 dB |
| C/M ratio 3 | N/A | 1 | 3 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.; Jiang, Y. Non-Magnetic Circulator Based on a Time-Varying Phase Modulator. Appl. Sci. 2023, 13, 512. https://doi.org/10.3390/app13010512
Jia X, Jiang Y. Non-Magnetic Circulator Based on a Time-Varying Phase Modulator. Applied Sciences. 2023; 13(1):512. https://doi.org/10.3390/app13010512
Chicago/Turabian StyleJia, Xiangjian, and Yanfeng Jiang. 2023. "Non-Magnetic Circulator Based on a Time-Varying Phase Modulator" Applied Sciences 13, no. 1: 512. https://doi.org/10.3390/app13010512
APA StyleJia, X., & Jiang, Y. (2023). Non-Magnetic Circulator Based on a Time-Varying Phase Modulator. Applied Sciences, 13(1), 512. https://doi.org/10.3390/app13010512







