Deformation Control of the Existing Medium-Low-Speed Maglev Metro Viaduct over a Double-Line Bored Tunnel
Abstract
:1. Introduction
2. Background
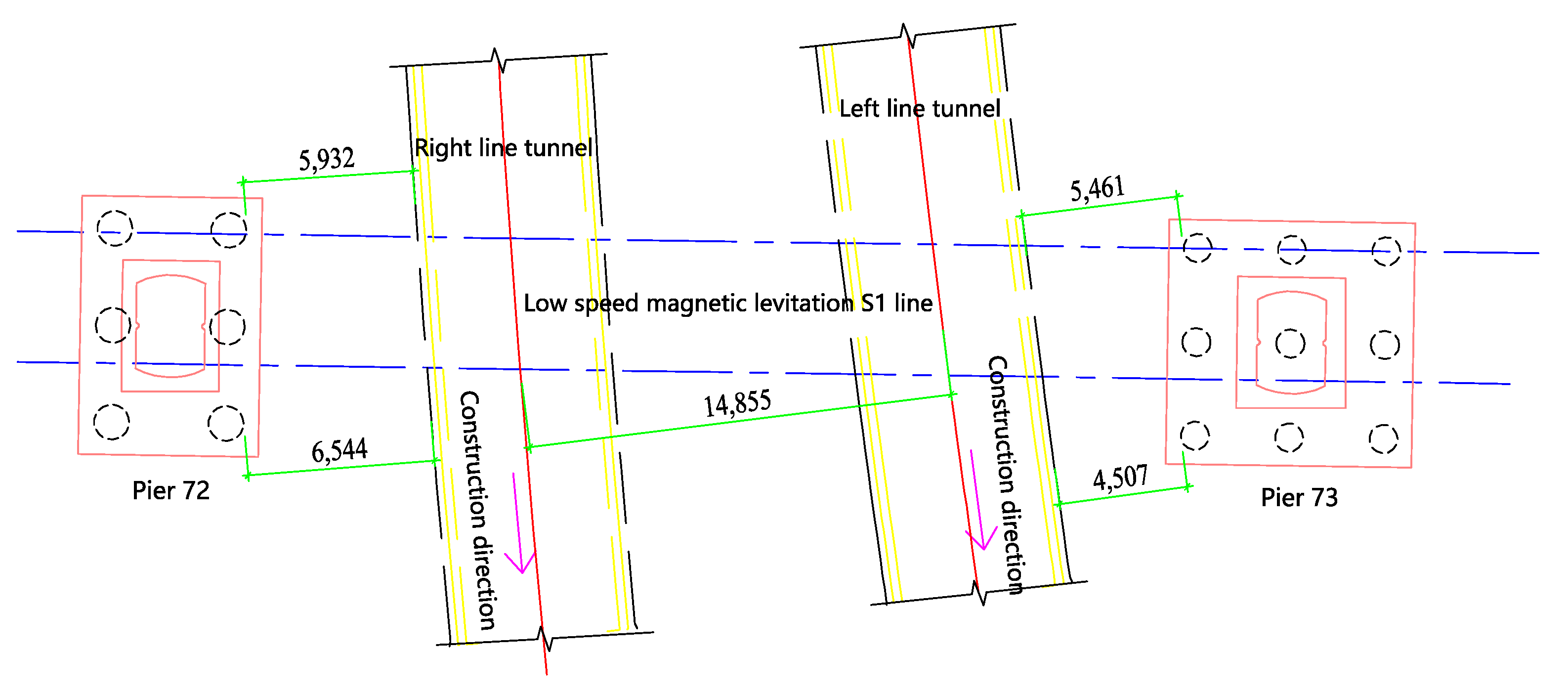
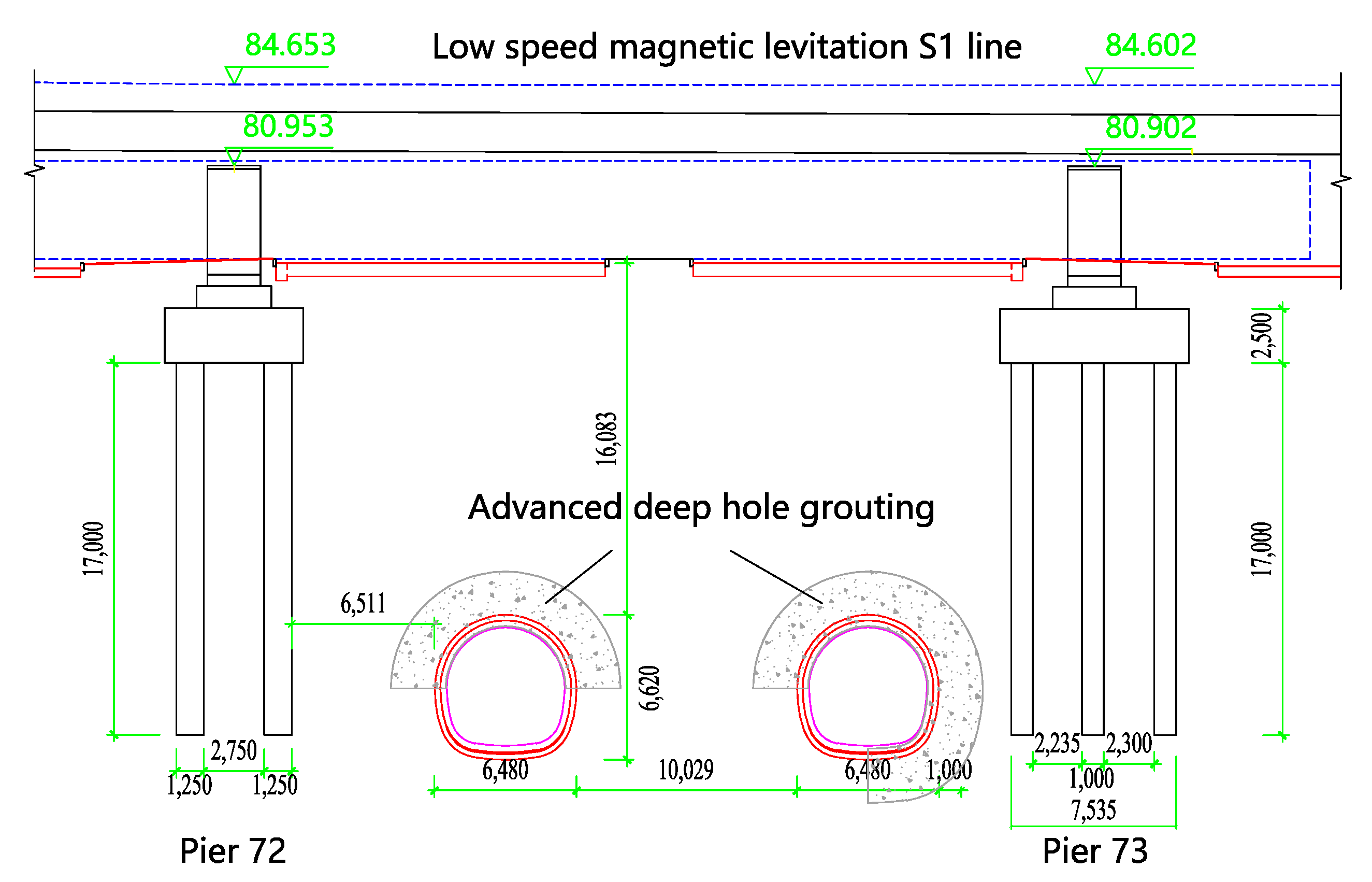
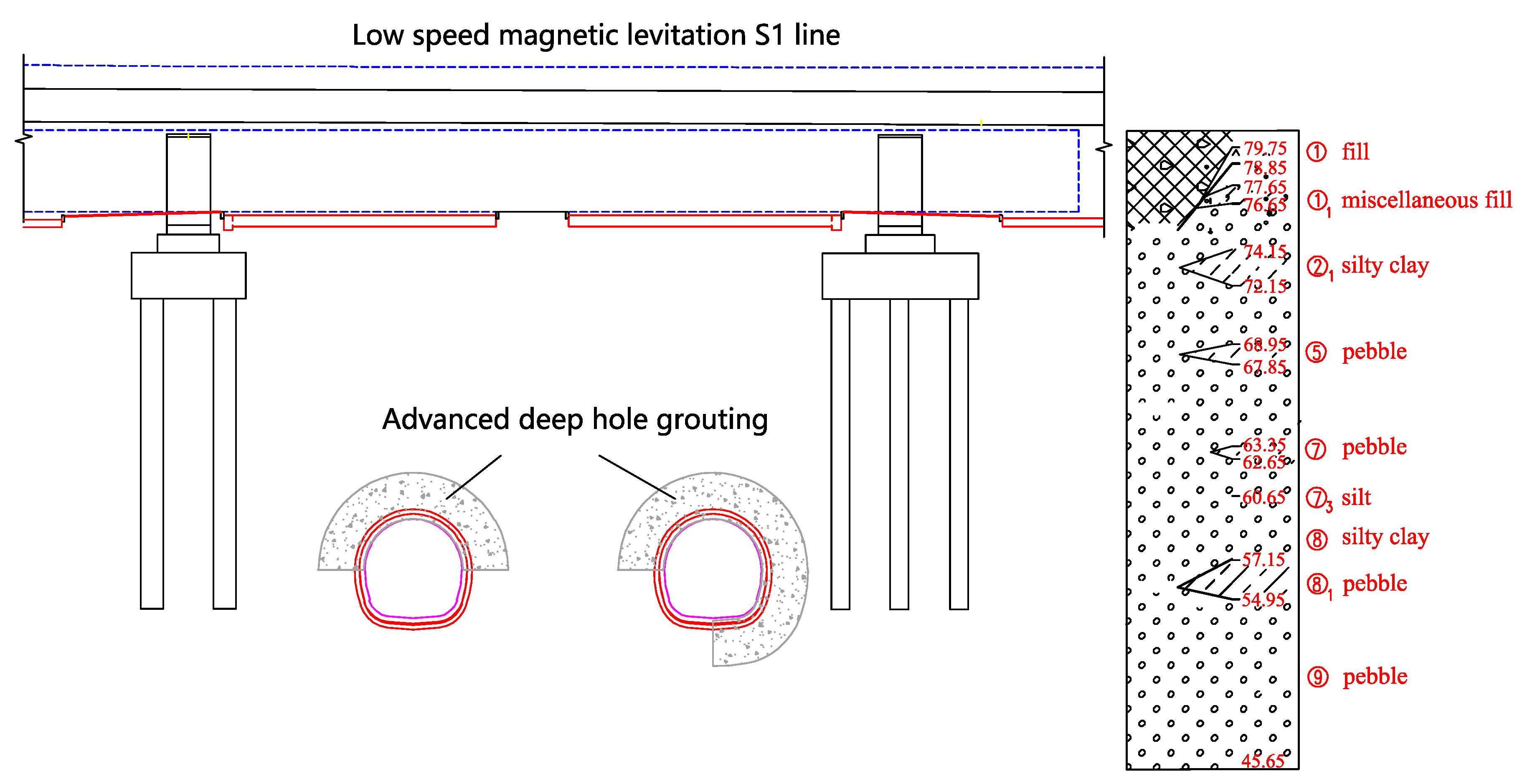
2.1. Project Overview
2.2. Deformation Control Measures for Double-Track Excavated Tunnel Passing under a Magnetic Suspension Viaduct
- (1)
- Deep-hole grouting is used in advance to reinforce the surrounding soil of the structure, and the cross-section is 2 m outside the initial support contour. The grouting slurry is a cement–water glass double slurry. The reinforced soil should have good uniformity and self-reliance, and the unconfined compressive strength of the reinforced soil should not be less than 0.8 MPa.
- (2)
- During the construction of the interval crossing bridge piles, the step method with a temporary inverted arch is adopted. The initial lining structure controls the excavation step of 0.5 m (the grid spacing is 0.5 m), and the temporary inverted arch is closed in time. The left and right lines of the tunnel are staggered 15 m, and the upper and lower steps are staggered 3 m.
- (3)
- Grouting behind the primary support is carried out in time during the construction of the primary support, and grouting behind the secondary lining is carried out in time during the construction of the secondary lining, so as to strictly control the grouting pressure and grouting amount and ensure the grouting effect.
- (4)
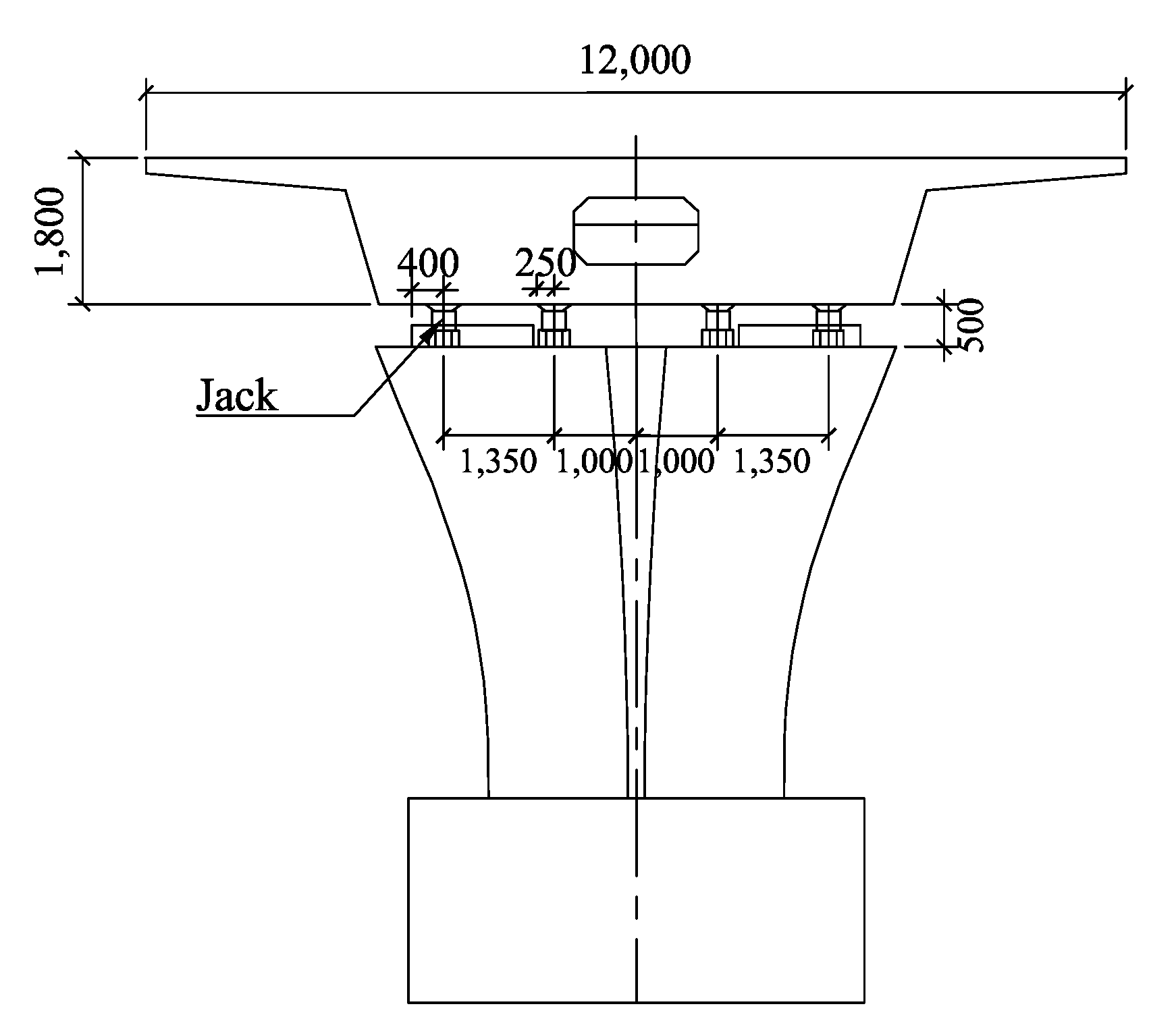
- The lifting scheme for the bridge superstructure is taken as a safety plan. During the construction period, jacks are arranged at the top of the pier to implement synchronous lifting. The jack arrangement is shown in Figure 4. Real-time monitoring is carried out during tunnel construction. Once the settlement of the main beam reaches 2 mm, the main beam is jacked up with a jack during the empty window period of the S1 line at night, and a height-adjusting steel plate is added between the bottom of the beam and the support to ensure that the deformation of the main beam structure does not exceed the limit.
2.3. Magnetic Levitation Rail Transit Control Standard
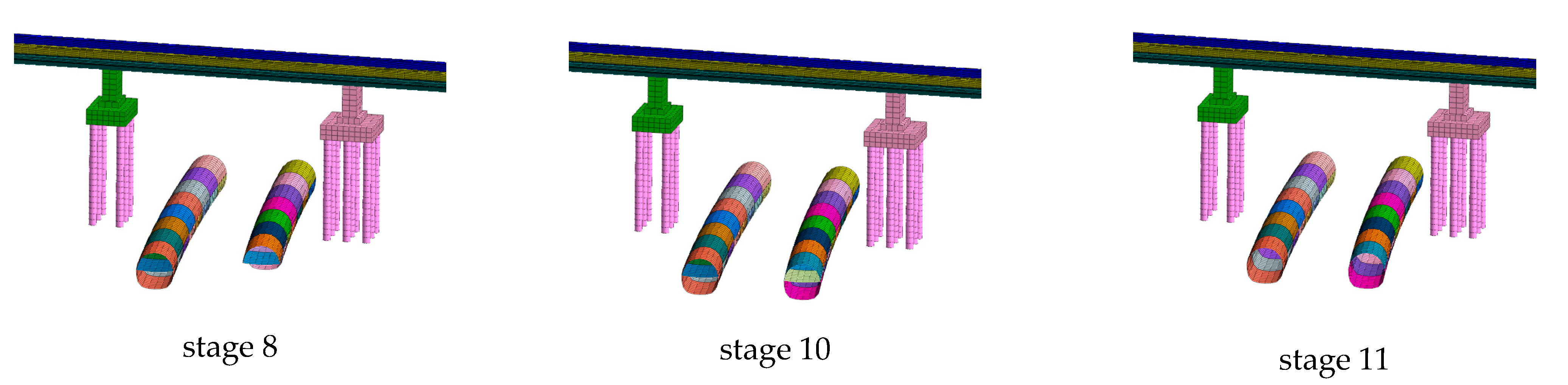
3. Numerical Calculation Model
4. Analysis of Calculation Results
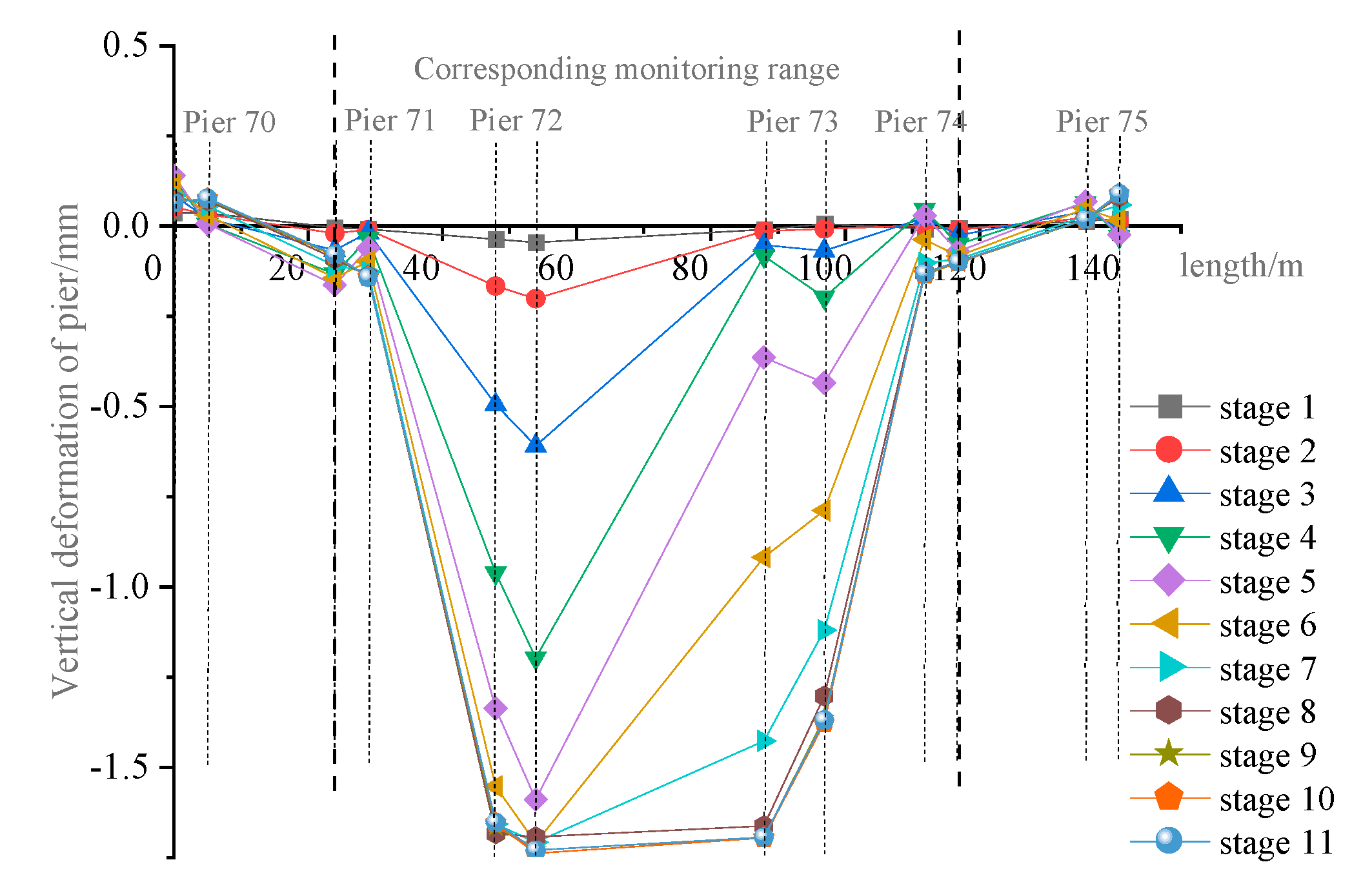
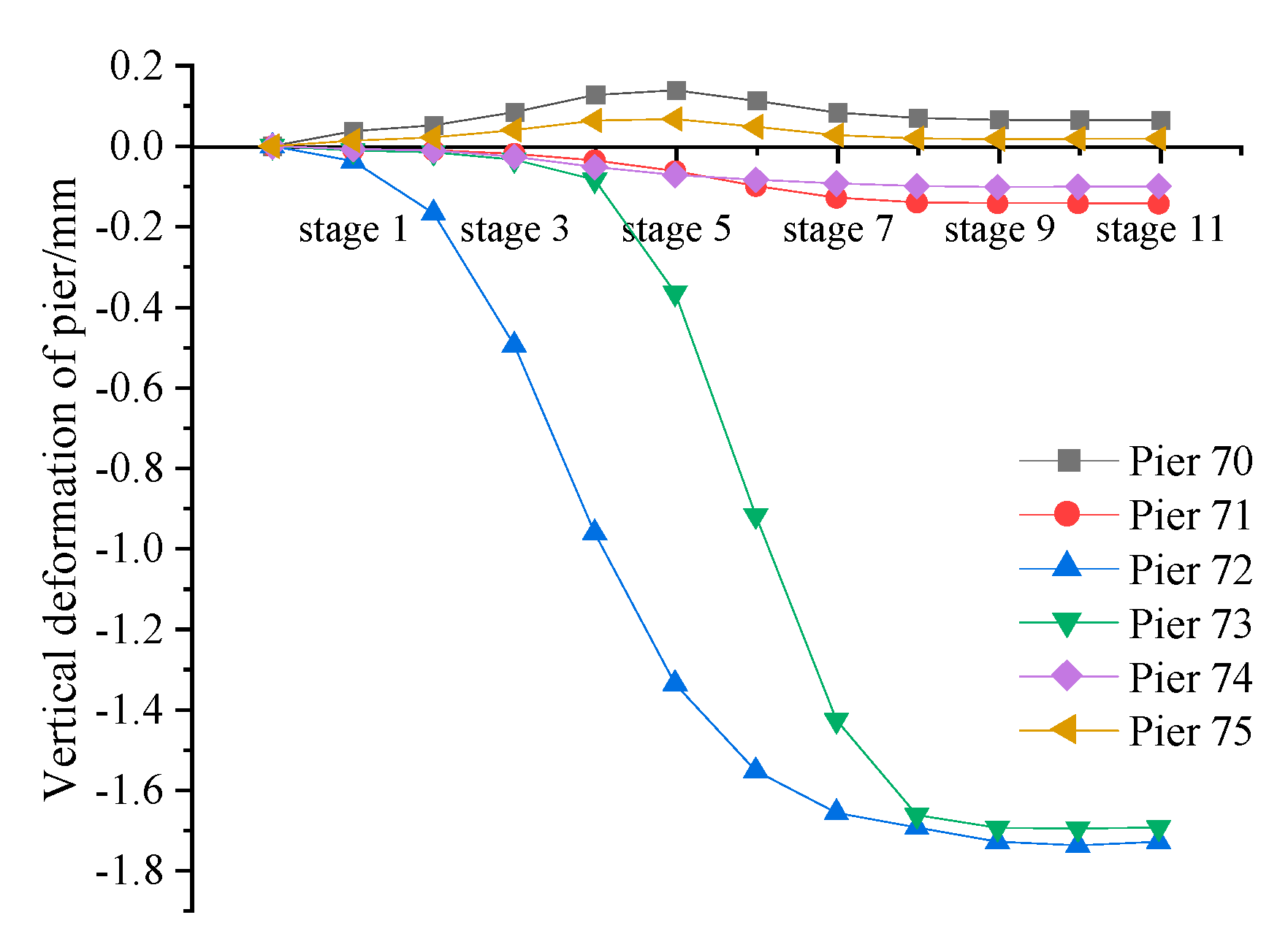
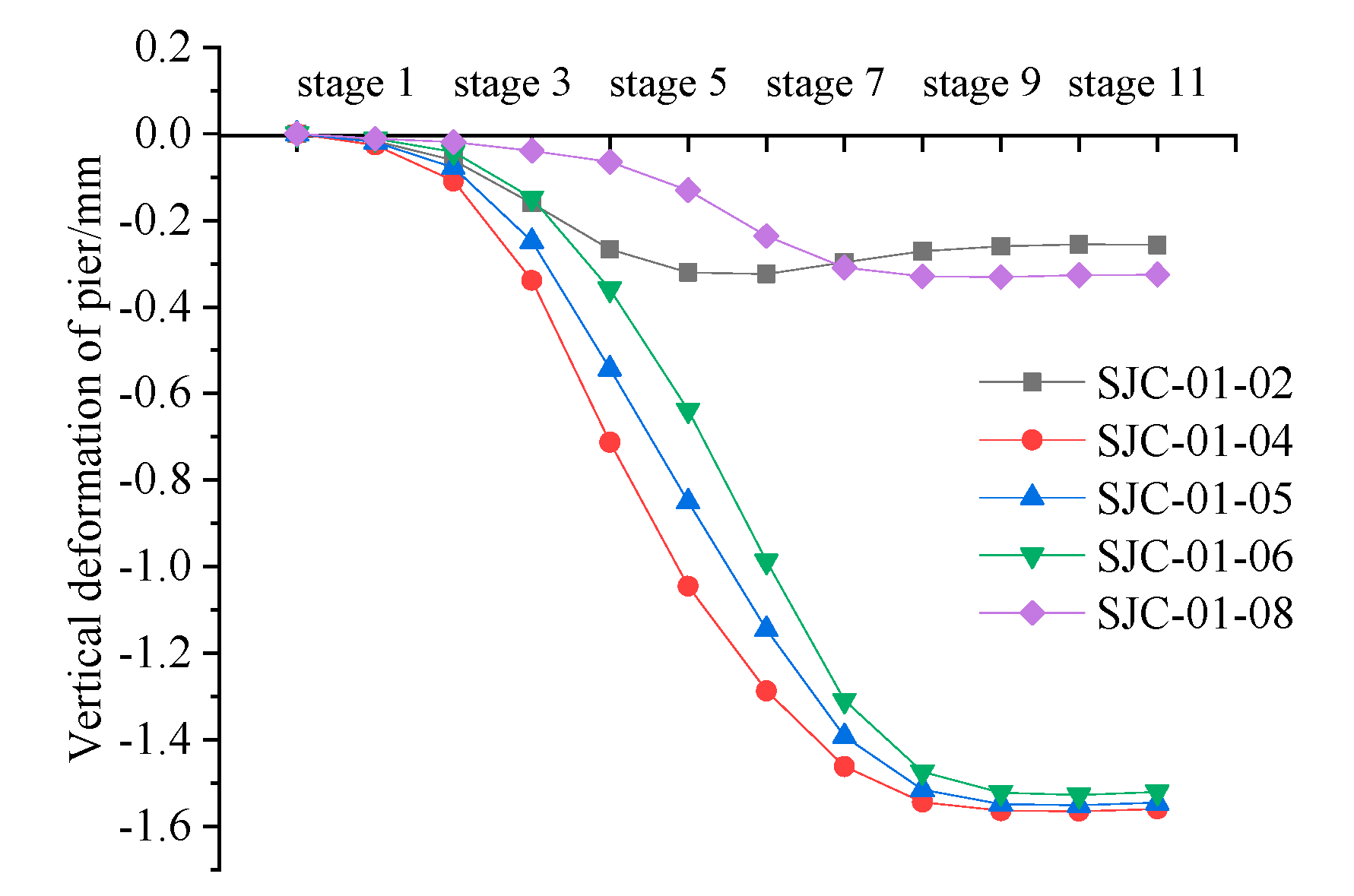
4.1. Deformation Analysis of Existing Bridge Piers
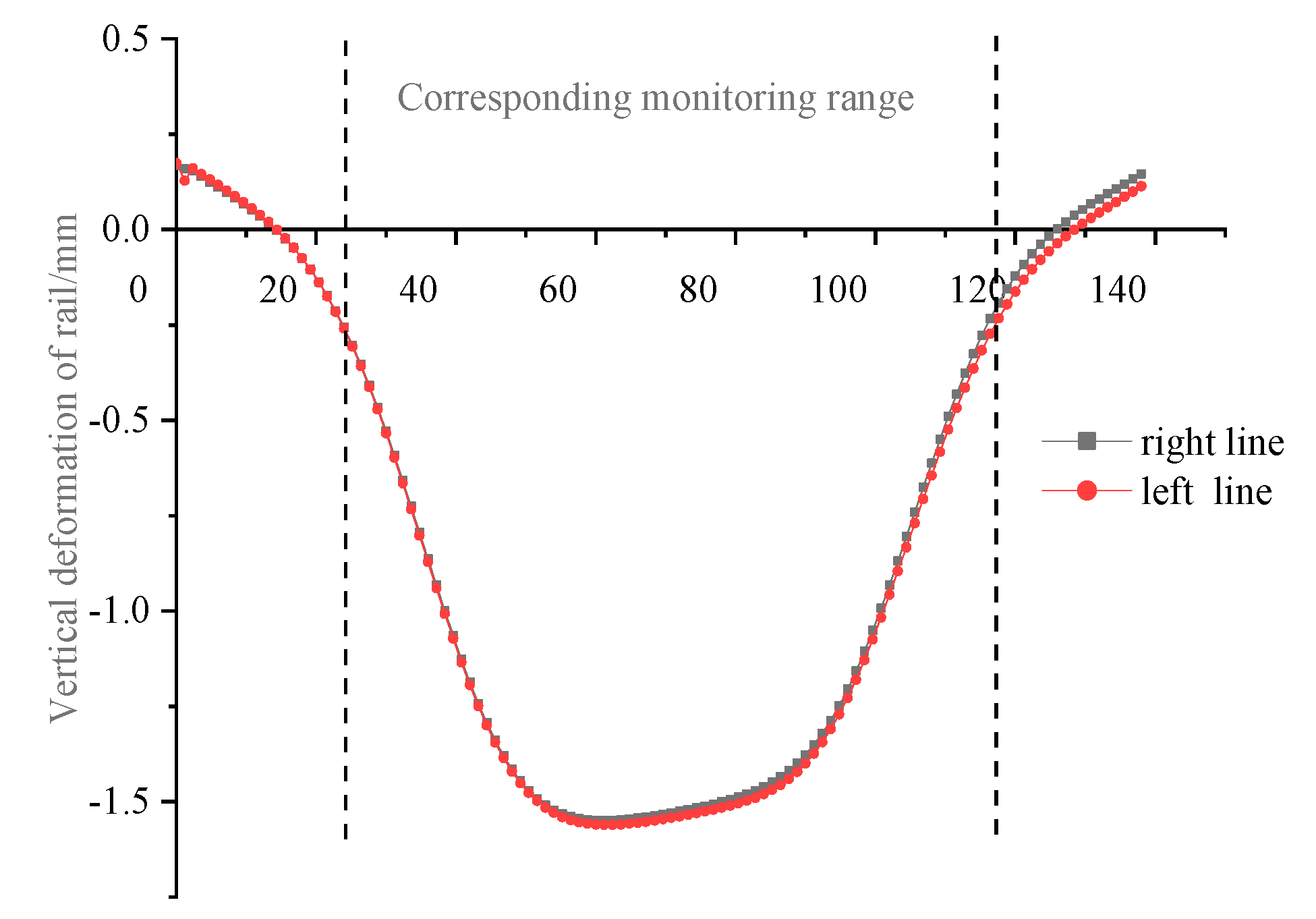
4.2. Track Structure Deformation Analysis
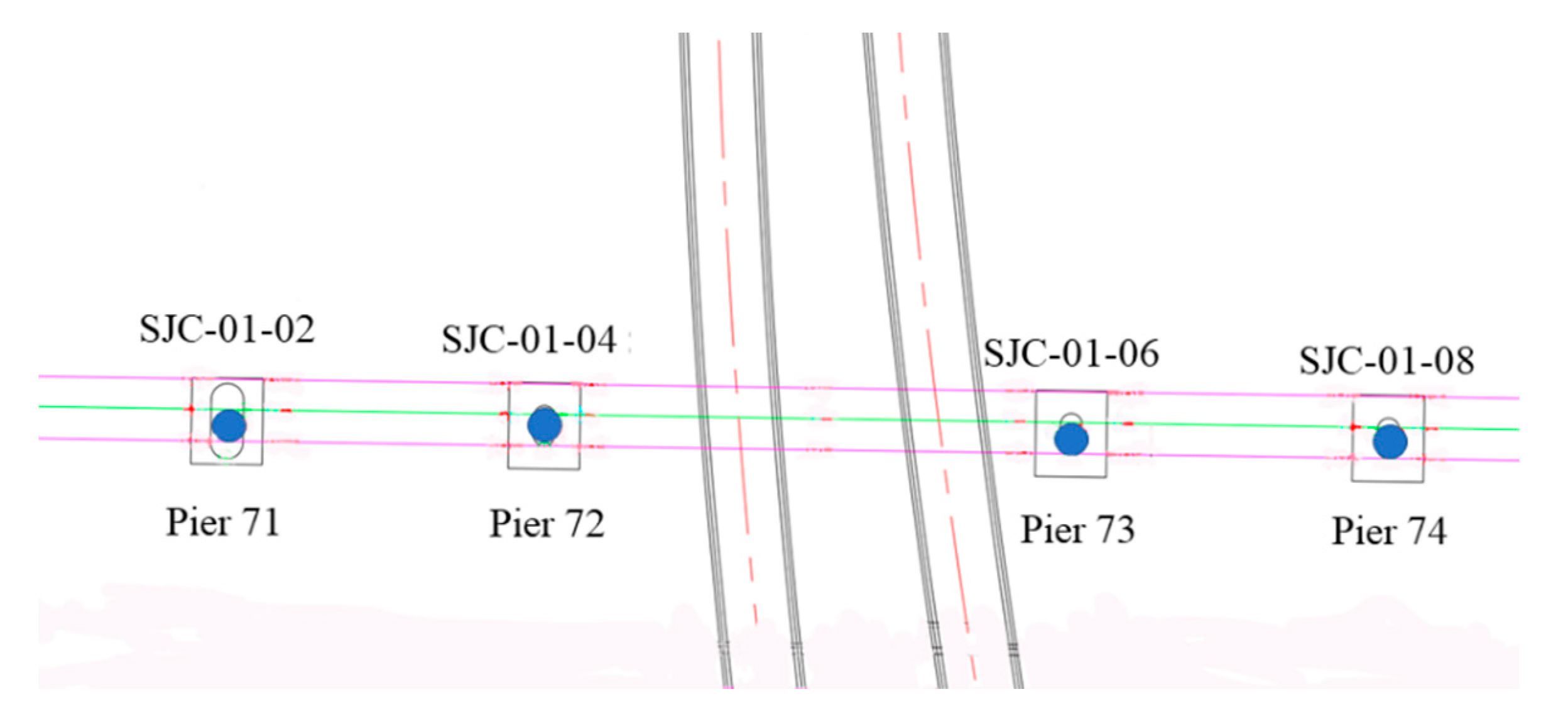
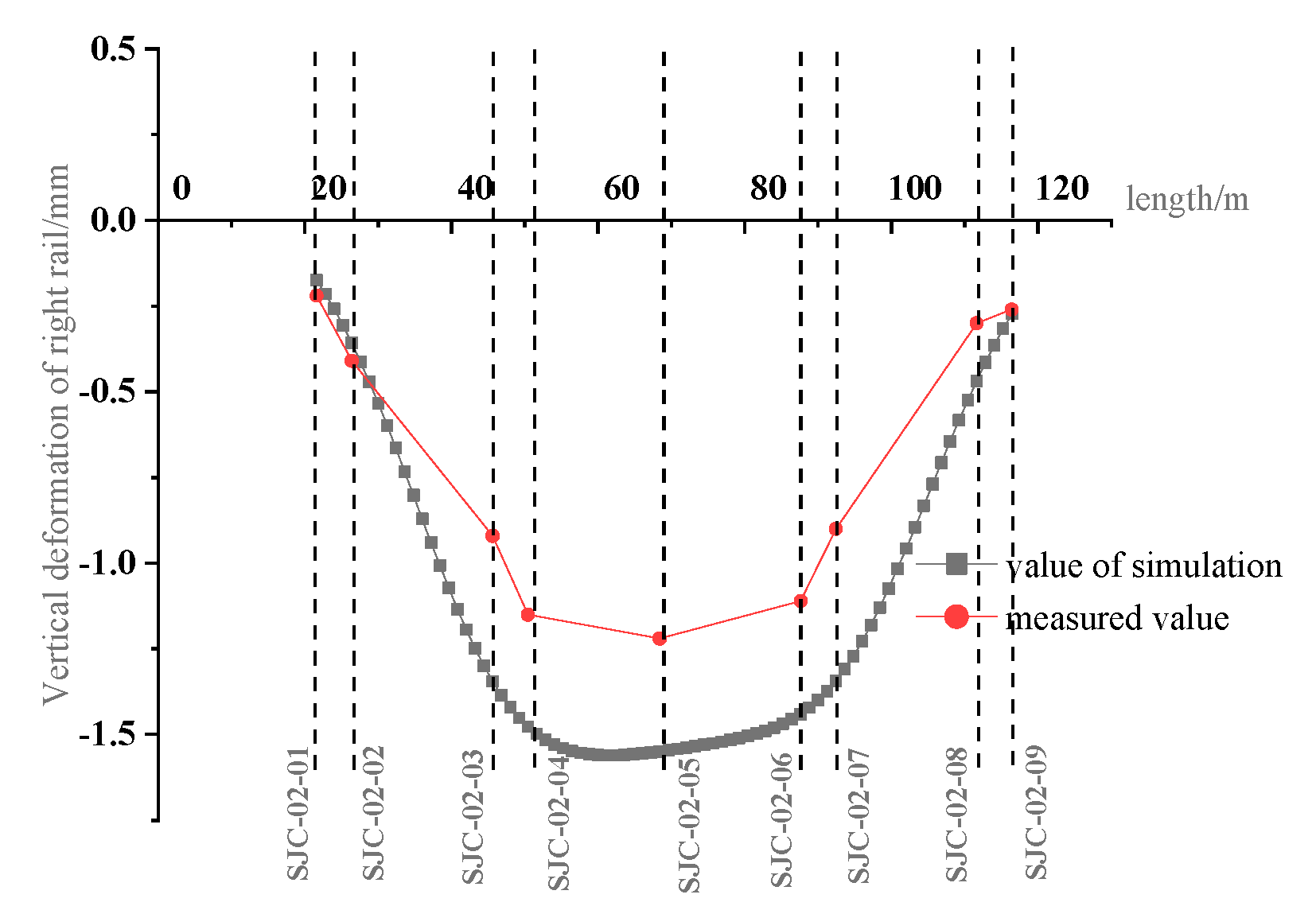
5. Field Measurement Analysis
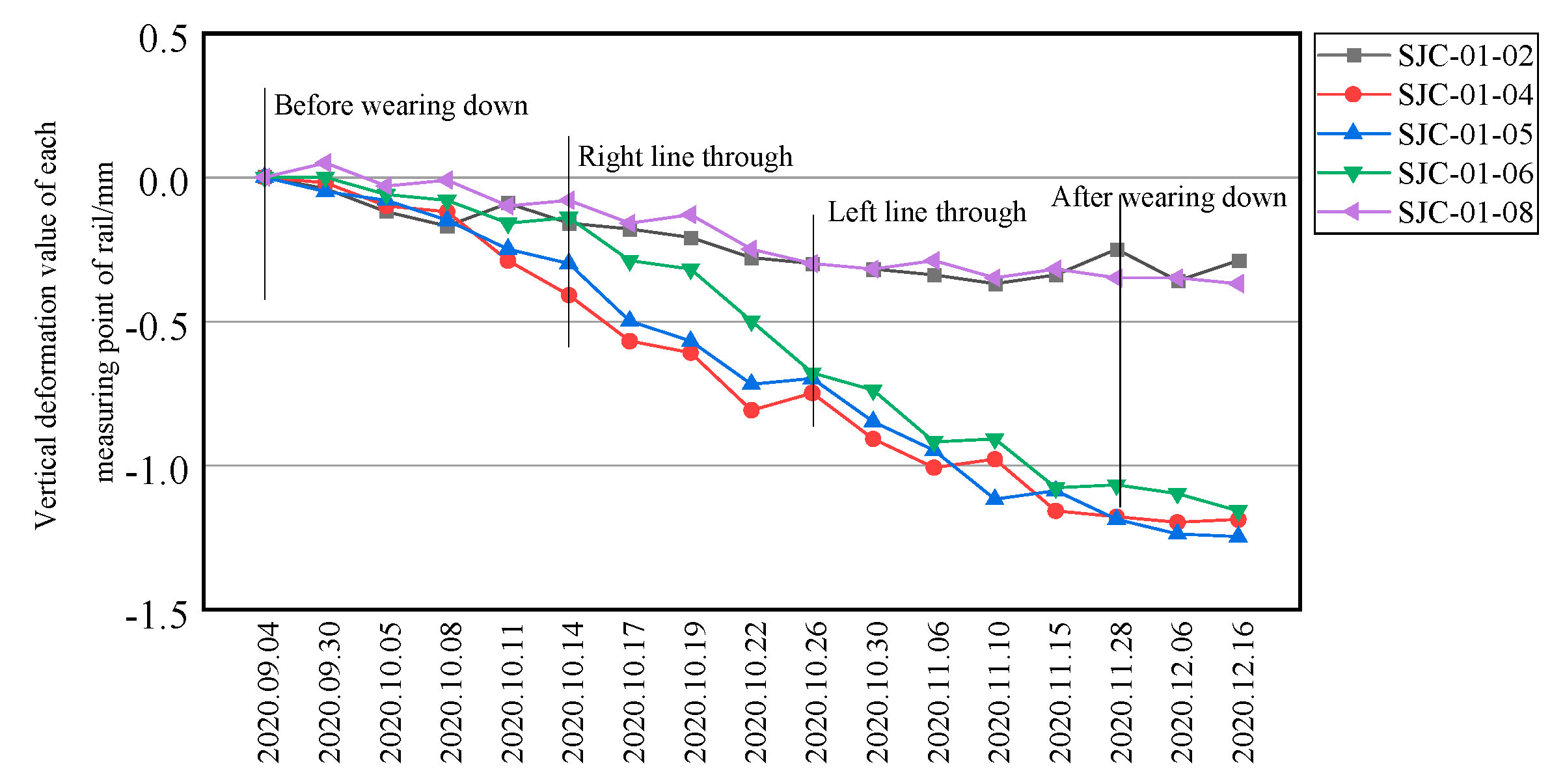
5.1. Existing Rail Deformation Measurement Analysis
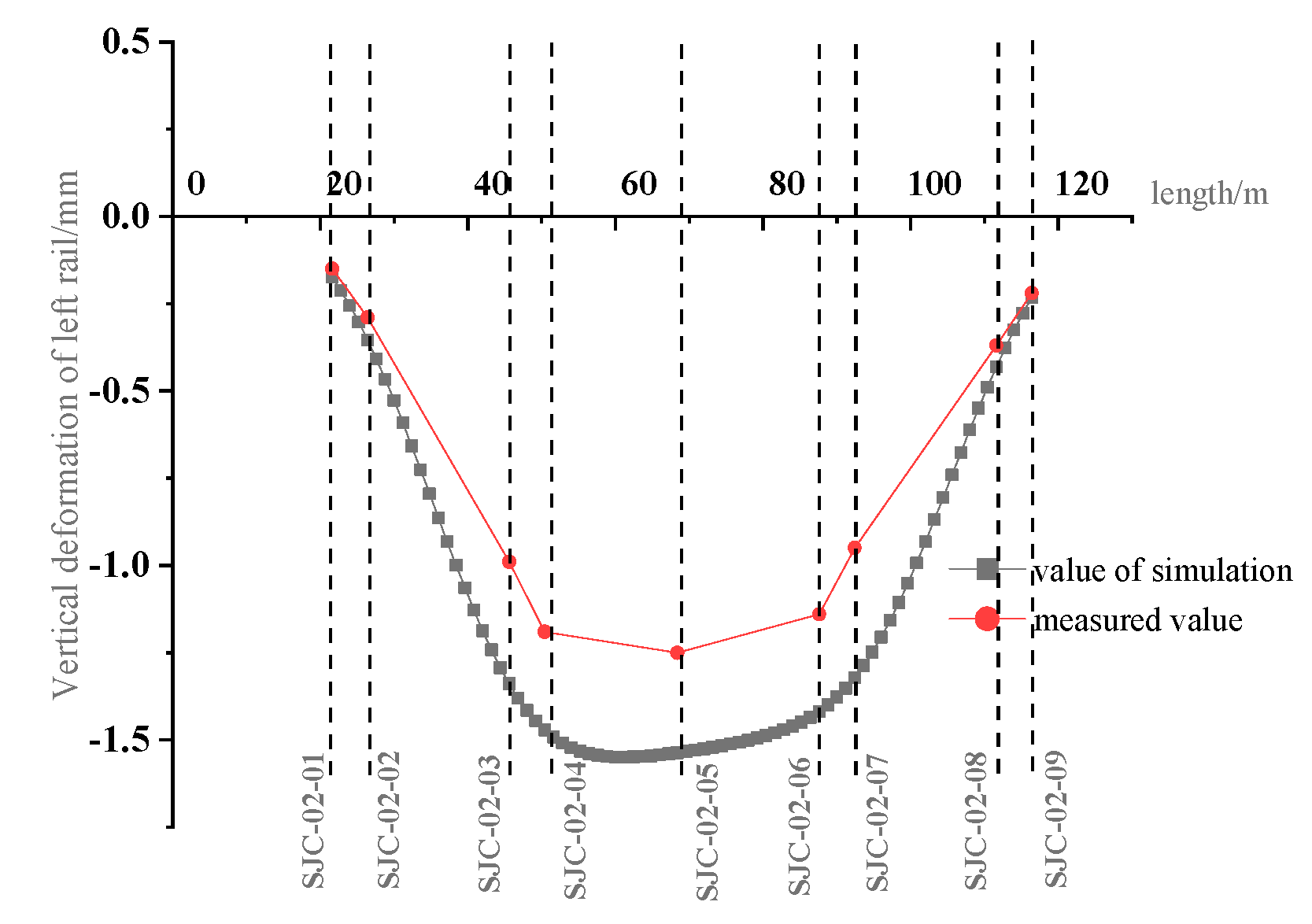
5.2. Comparison of Existing Rail Deformation Results
5.3. Comparison of Differential Deformation Results of Existing Rails
6. Conclusions
- (1)
- According to the particularity of the Maglev track structure, the main deformation control point of this project is the differential deformation of the magnetic levitation track. Considering the layout conditions of the field measuring points, the deformation difference between the Maglev rail panels can be monitored by measuring the rail joint and the dislocation of the F-shaped steel. The actual monitoring process data prove that the method is feasible.
- (2)
- The maximum deformation value of the pier adjacent to the tunnel crossing position is −1.73 mm and the maximum vertical deformation value of the magnetic levitation rail is −1.56 mm. It can be seen that the settlement deformation of the pier will be attenuated after passing through the pier, bearing, bridge, and track beam to the rail. Because the bridge is a continuous beam, the deformation curve of the rail is relatively flat, and there is no obvious differential settlement between the rails.
- (3)
- The measured maximum vertical deformation of the Maglev rail is −1.25 mm, which is slightly smaller than the numerical calculation. Due to the slow deformation curve, no obvious dislocation or differential deformation were found in the field rail joint and F-shaped steel during the monitoring process. The numerical simulation results of the existing magnetic levitation rail were basically consistent with the final vertical deformation trend of the field-measured data. Numerical simulation prediction combined with field measurement can better reflect the deformation trend of the existing structure.
- (4)
- In the project of the double-line tunnel crossing under the existing Maglev track viaduct, the deformation of the existing structure can be effectively controlled by using deep-hole grouting to reinforce the surrounding soil of the tunnel in advance. During the crossing process, jack lifting is used on the upper structure of the bridge as an emergency measure. This study can provide a reference for similar projects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zeng, D.Y.; Bai, D.F. Study on pile foundation measures for long distance lateral crossing of bridges in underground mining method tunnels. J. Railw. Eng. 2021, 38, 68–73+80. [Google Scholar]
- Lin, S.Y. Study on pile foundation replacement for underpass bridges in large span underground tunnels. Build. Struct. 2021, 51, 2128–2131. [Google Scholar]
- Huang, X.; Chen, X.; Yan, Q.X.; Song, L.Y.; Yang, T. Study on the mechanical behavior and parameters of pile foundation buttress replacement in underground tunnels underpassing bridges. Constr. Technol. 2017, 46, 67–70+85. [Google Scholar]
- Tang, X.Q. Design and construction of large axial force pile buttresses for underpass bridges in underground interval tunnels. Railw. Stand. Des. 2016, 60, 87–91. [Google Scholar]
- Li, K.; Gao, B. Study on the construction scheme of underground tunnel under small river and bridge. Geotechnics 2010, 31, 1509–1516. [Google Scholar]
- She, C.G.; Han, G.X. Research on construction parameters of metro shield tunnel when underpassing high-speed railway bridges in rock formations. Urban Rail Transit Res. 2015, 18, 90–93+99. [Google Scholar]
- Huang, Y.D. Pile foundation replacement of underground interval tunnel under existing bridge. Urban Rail Transit Res. 2012, 15, 100–103+107. [Google Scholar]
- Li, Y.; Yang, X.P.; Liu, T.J. Analysis of the influence of shield tunneling on the pile foundation of adjacent viaduct in Guangzhou. Railw. Build. 2012, 461, 74–78. [Google Scholar]
- Cui, G.Y.; Wang, M.N.; Lu, J.F.; Liu, J.S. Displacement control technology for construction of airport road tunnel underpassing viaduct adjacent to pile foundation. China Railw. Sci. 2011, 32, 68–73. [Google Scholar]
- Wang, G.F.; Sun, J.C.; Lu, L.H.; Li, G.; Dong, H.X.; Han, S. Research on active pre-support of shield tunnel under viaduct at close range. Mod. Tunn. Technol. 2017, 54, 195–202. [Google Scholar]
- Pan, J.S. Optimization and evaluation analysis of rail transit and high-speed Maglev close parallel scheme. Build. Technol. Dev. 2011, 38, 65–68. [Google Scholar]
- Liu, Z.G. Research on construction technology of shield crossing operating magnetic suspension foundation. Highway 2020, 65, 326–331. [Google Scholar]
- Zhang, X.F.; Zhang, T.; Lu, J. Data analysis of the deformation of the pipe jacking under the magnetic suspension section. Urban Constr. Theory Res. (Electron. Version) 2011. [Google Scholar]
- Guo, X.Z. Impact Analysis and Study on Protective Measures of Shield Tunnel Closely Undercrossing Guangzhou-Shenzhen Railway. Railw. Stand. Des. 2021, 65, 107–112+133. [Google Scholar]
- Peng, H.; Li, J.; Liang, Y.; Ma, W.H. Safety control for Large-diameter Shield Under-crossing the Viaduct of Airport Express. Urban Rapid Rail Transit 2016, 29, 42–46. [Google Scholar]
- Li, H.Y. Analysis of Settlement Control of Bridge Induced by Undercrossing of Four-line Overlapping Small-spacing Shield Tunnels. Tunn. Constr. 2020, 40, 343–349. [Google Scholar]
- Han, K. Numerical Study on Deformation of Bridge Pile Foundation Caused by Shield Tunnel Side Crossing. China Munic. Eng. 2021, 215, 106–109+129. [Google Scholar]
- Tullini, N.; Tralli, A.; Baraldi, D. Buckling of Timoshenko Beams in Frictionless Contact with an Elastic Half-Plane. J. Eng. Mech. 2013, 139, 824–831. [Google Scholar] [CrossRef]
- Gao, Q.; Lin, J.H.; Zhong, W.X.; Howson, W.P.; Williams, F.W. Isotropic layered soil-structure interaction caused by stationary random excitations. Int. J. Solids Struct. 2009, 46, 455–463. [Google Scholar] [CrossRef]
- Wu, H.Y. Research on shallow buried concealed excavation technology for large cross-sectional sections of underground interdistrict ferry lines. J. Railw. Eng. 2018, 35, 93–99. [Google Scholar]
- Yan, Q.X.; He, C.; Yao, Y.; Deng, G. Numerical simulation analysis of the effect of small conduit grouting for small clearances tunnel construction. Geotechnics 2004, 239–242. [Google Scholar]
- Zeng, X.G.; Zhao, S.P.; Yao, A.L.; Shi, X.S.; Wang, Q.Y.; Xv, S.S. Finite element analysis of the influence of small conduit grouting process on the stability of surrounding rock in small clear distance highway tunnels. J. Sichuan Univ. (Eng. Sci. Ed.) 2008, 1–6. [Google Scholar]
- Sun, Z.Y.; Zhang, D.L. A method for determining the ultimate roof thickness of submarine tunnels based on stratigraphic reinforcement. J. Civ. Eng. 2020, 53, 115–128. [Google Scholar]
- Wang, D.Y.; Qu, H.H.; Li, W.B. Influence of concealed excavation construction on surface deformation of large section underground twin tunnels under existing lines. J. Rock Mech. Eng. 2014, 33, 4075–4085. [Google Scholar]
- Deng, T.; Guan, Z.C.; Chen, K.L.; Liu, L.Y. Simplified calculation of jacking loads in active bridge pile foundation replacement. Geotechnics 2015, 36, 3259–3267. [Google Scholar]
- Su, J.; Zhang, D.L.; Yang, G.W.; Niu, X.K.; Zhao, J.T. Active compensation method for settlement of pile foundations of existing bridges under the influence of metro construction. Mod. Tunn. Technol. 2015, 52, 39–46. [Google Scholar]
- Huang, X.; Chen, X.; Yan, Q.X. Study on pile foundation replacement of underground interval tunnel under existing bridge. Railw. Stand. Des. 2016, 60, 89–93. [Google Scholar]
- Wang, J.N.; Niu, X.K.; Xue, Z.J.; Su, J. Research on active jacking monitoring system for underground crossing bridges. Sci. Technol. Eng. 2013, 13, 7903–7910. [Google Scholar]
- Yan, B.H.; Cao, W.; Lu, S.J.; Wang, K.J.; Yang, H.; Liu, H.J.; Shen, Q. Application of bridge jacking technology in underground near underpass bridges. Constr. Technol. 2012, 41, 42–46. [Google Scholar]
- CJJ/T262-2017; Code for Design of Medium and Low Speed Maglev Traffic. China Construction Industry Press: Beijing, China, 2017.
- Wang, R. Foundation design and settlement analysis of a near magnetic levitation and rail transit building. Build. Struct. 2021, 51, 1873–1878. [Google Scholar]
- Wei, Y.H. Simulation analysis and control of construction deformation of Beijing subway line 16 section tunnel undercrossing line 4. Railw. Build. 2020, 60, 75–78+115. [Google Scholar]
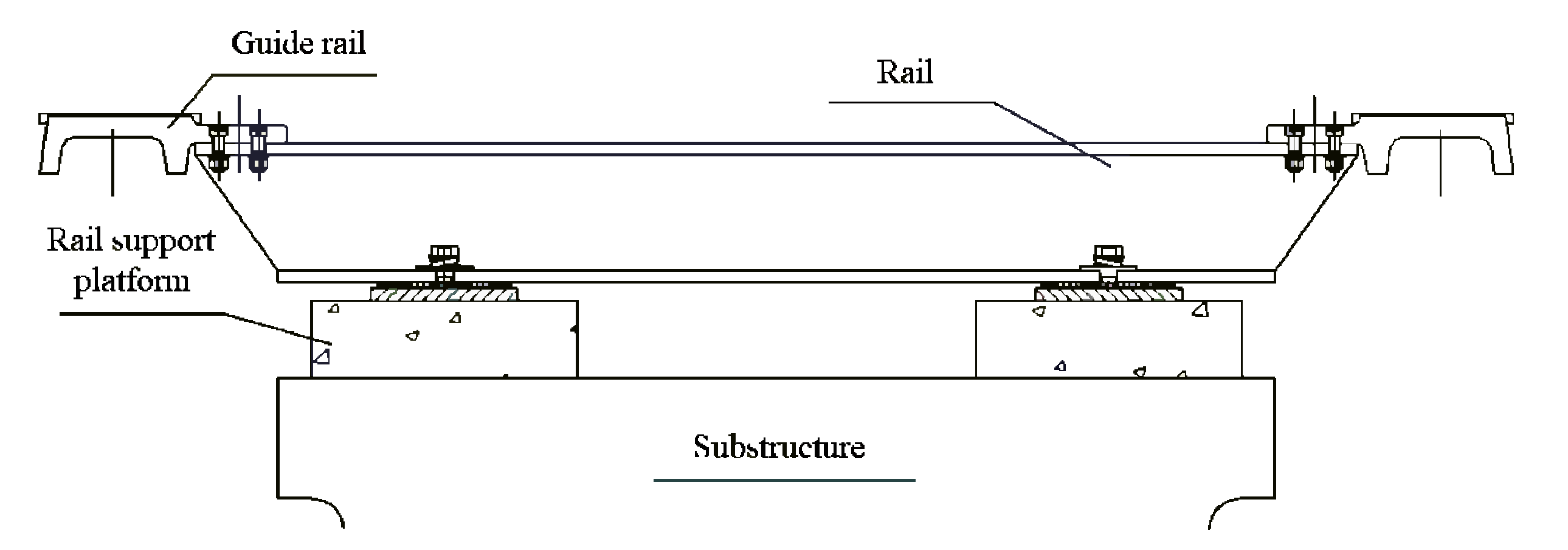


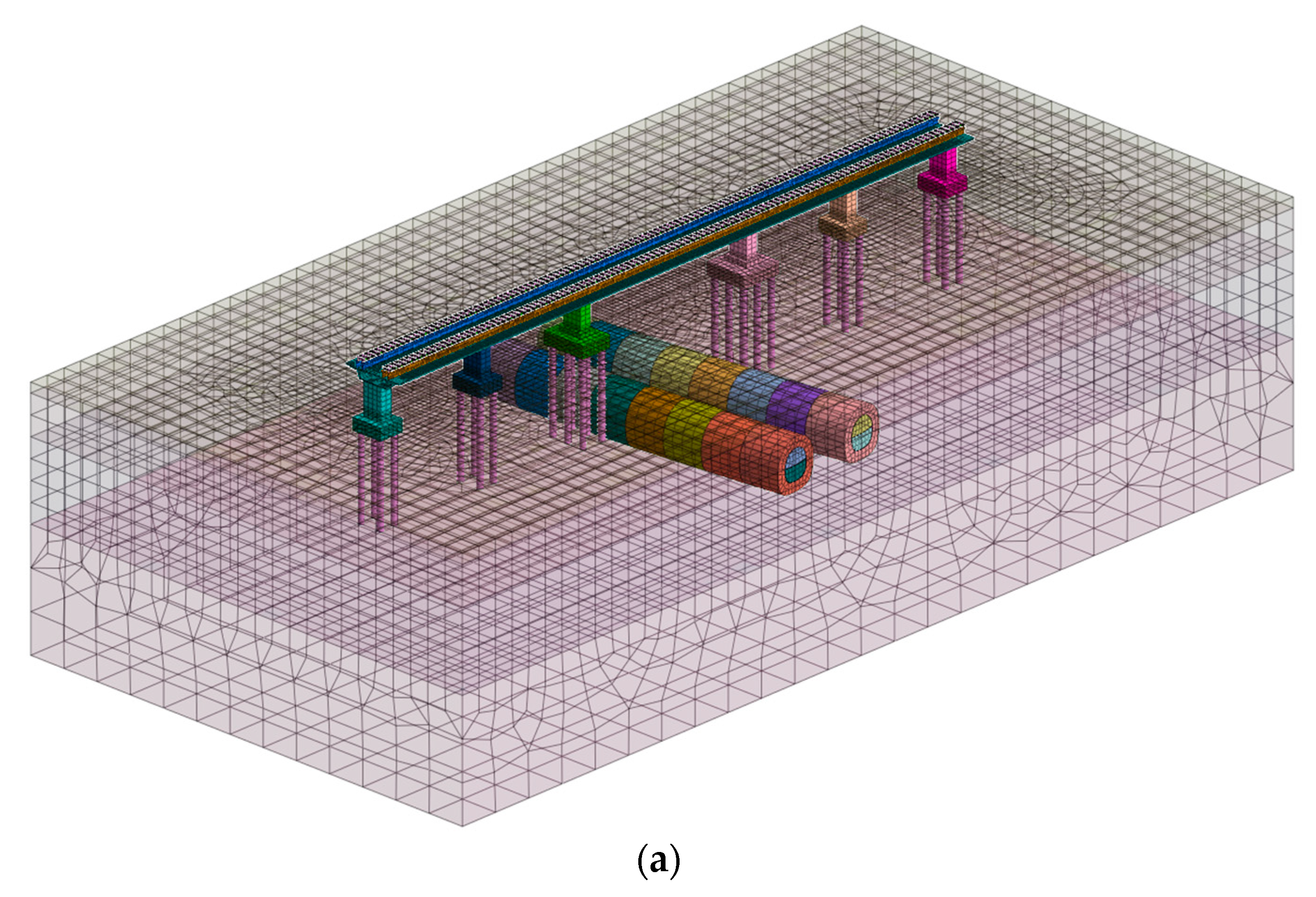
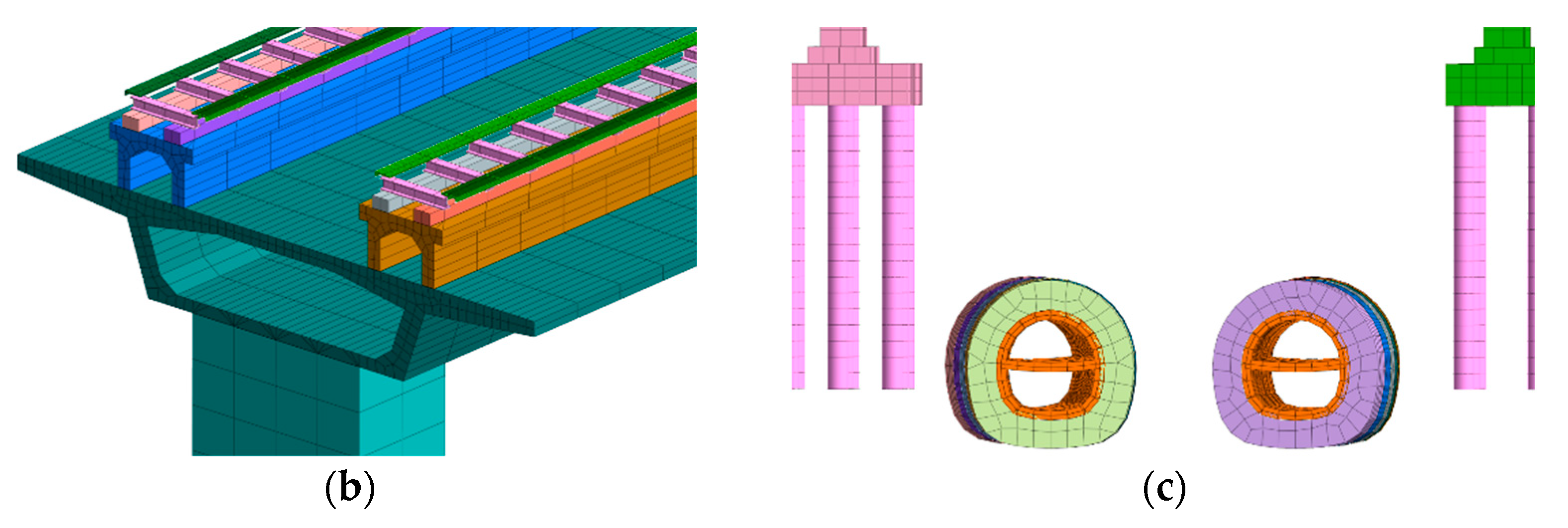
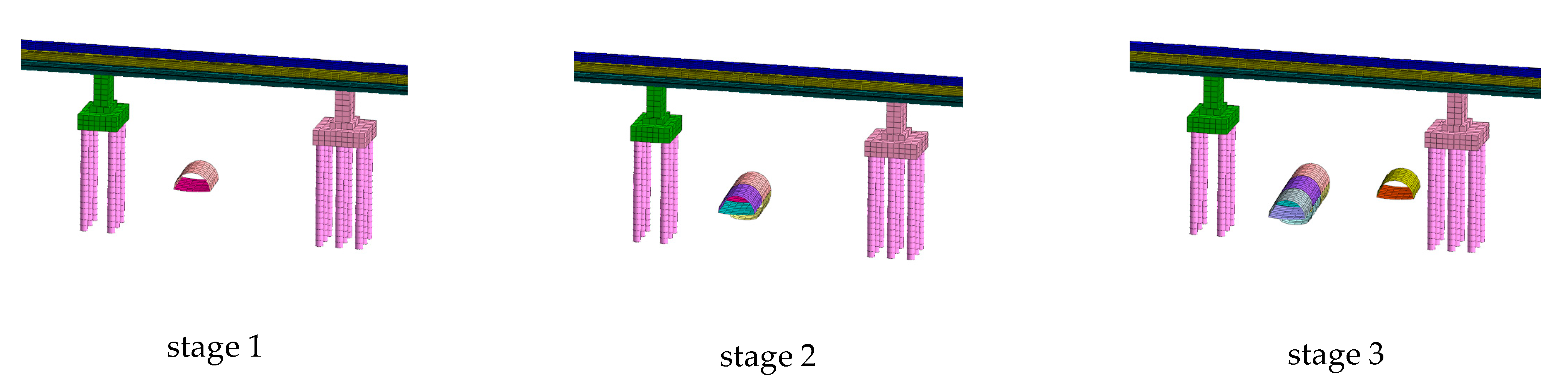




| Item | Threshold Value | Note |
|---|---|---|
| Rail alignment deviation | ±3 mm | Center distance between two tracks; the value under the condition of track-locking temperature. |
| Horizontal level deviation | ±3 mm | / |
| Vertical height deviation | ±3 mm | Front and rear height; measuring chord length 10 m. |
| Twist | ±1 mm | Measuring chord length 4 m. |
| Coplanarity of magnetic pole surface | ±1 mm | / |
| Rail-joint level | ±1 mm | The value under the condition of locked track temperature. |
| Control Index | Warning Value (mm) | Alarming Value (mm) | Controlled Value (mm) |
|---|---|---|---|
| Pier structure settlement | 1.4 | 1.6 | 2.0 |
| Differential settlement between piers | 1.4 | 1.6 | 2.0 |
| Differential deformation between Maglev rail panels | -- | -- | +/−1.0 |
| The up and down and left and right deviation of F-shaped steel frame | -- | -- | +/−1.0 |
| Material Type | /(kN/m−3) | E/MPa | C/kPa | /(°) | Poisson Ratio |
|---|---|---|---|---|---|
| Miscellaneous Fill | 17.0 | 12.0 | 10 | 5 | 0.30 |
| Pebble 5 | 21.0 | 140.0 | -- | 35 | 0.25 |
| Pebble 7 | 21.5 | 200.0 | -- | 40 | 0.25 |
| Pebble 9 | 21.5 | 300.0 | -- | 42 | 0.22 |
| Grouting Area | 22.0 | 300.0 | -- | 50 | 0.22 |
| Concrete C40 | 25.0 | 3.25 × 104 | -- | -- | 0.20 |
| Concrete C30 | 25.0 | 3.0 × 104 | -- | -- | 0.20 |
| Steel | 75.0 | 2.1 × 105 | -- | -- | 0.20 |
| Steps No. | Specification |
|---|---|
| 1 | Right line step excavation 8 m, apply upper primary lining and middle partition plate. |
| 2 | ① Right line step excavation 8 m, apply upper primary lining and middle partition plate; ② Right line lower bench excavation 8 m, Apply lower primary lining. |
| 3 | ① Right line step excavation 8 m, apply upper primary lining and middle partition plate; ② Right line lower bench excavation 8 m, apply lower primary lining; ③ Left line step excavation 8 m, apply upper primary lining and middle partition plate. |
| 4~10 | Left and right line synchronous excavation according to the upper and lower steps. |
| 11 | Complete all middle partition middle partition removal, complete all secondary lining. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, H.; Wu, Z.; Peng, X.; Xiao, X.; Li, Z. Deformation Control of the Existing Medium-Low-Speed Maglev Metro Viaduct over a Double-Line Bored Tunnel. Appl. Sci. 2023, 13, 6659. https://doi.org/10.3390/app13116659
Peng H, Wu Z, Peng X, Xiao X, Li Z. Deformation Control of the Existing Medium-Low-Speed Maglev Metro Viaduct over a Double-Line Bored Tunnel. Applied Sciences. 2023; 13(11):6659. https://doi.org/10.3390/app13116659
Chicago/Turabian StylePeng, Hua, Zikai Wu, Xv Peng, Xiaoqi Xiao, and Zichen Li. 2023. "Deformation Control of the Existing Medium-Low-Speed Maglev Metro Viaduct over a Double-Line Bored Tunnel" Applied Sciences 13, no. 11: 6659. https://doi.org/10.3390/app13116659
APA StylePeng, H., Wu, Z., Peng, X., Xiao, X., & Li, Z. (2023). Deformation Control of the Existing Medium-Low-Speed Maglev Metro Viaduct over a Double-Line Bored Tunnel. Applied Sciences, 13(11), 6659. https://doi.org/10.3390/app13116659






