Study on Seismic Reduction Measures of a Diaphragm Wall—Underground Structure System
Abstract
:1. Introduction
2. Underground Structure–Isolation Layer–Diaphragm Wall System
2.1. Time History Analysis
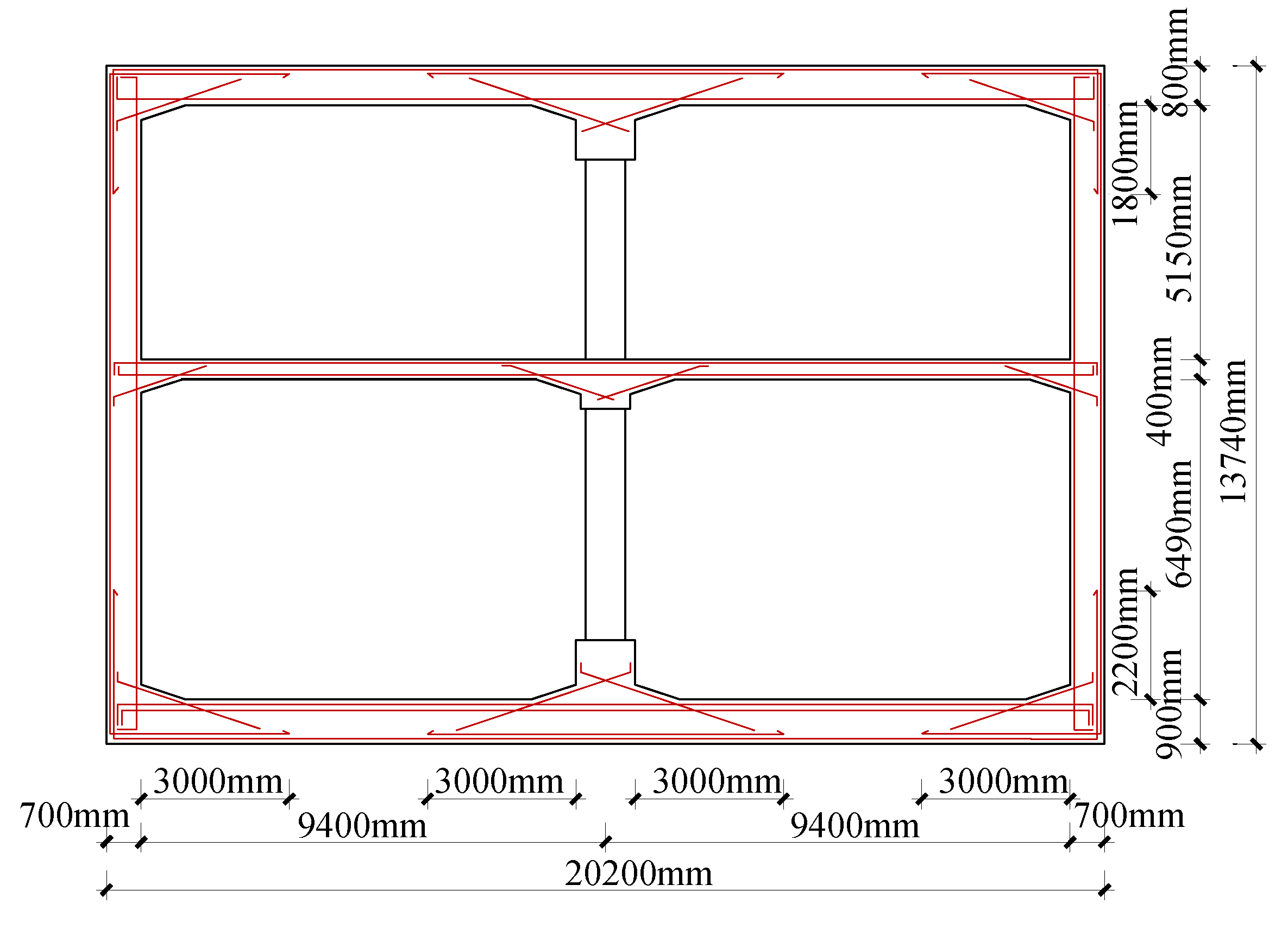
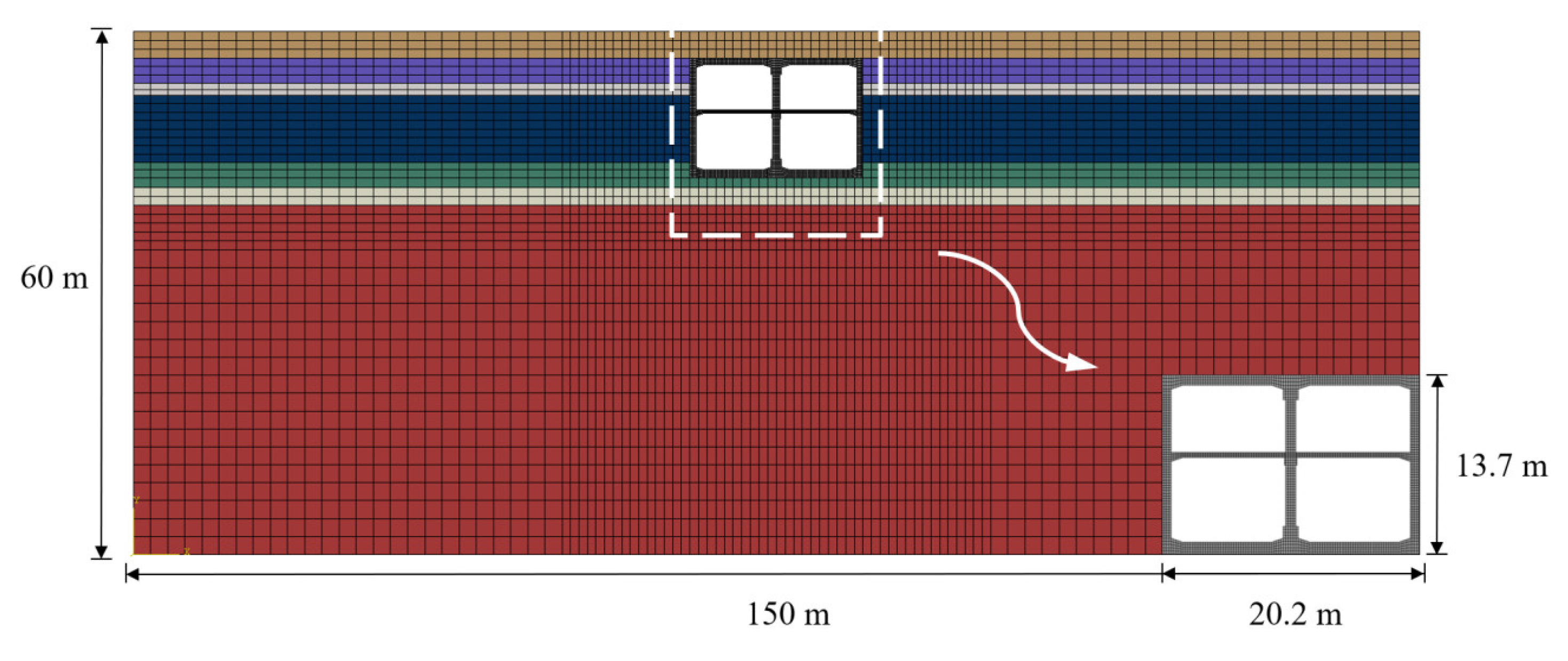
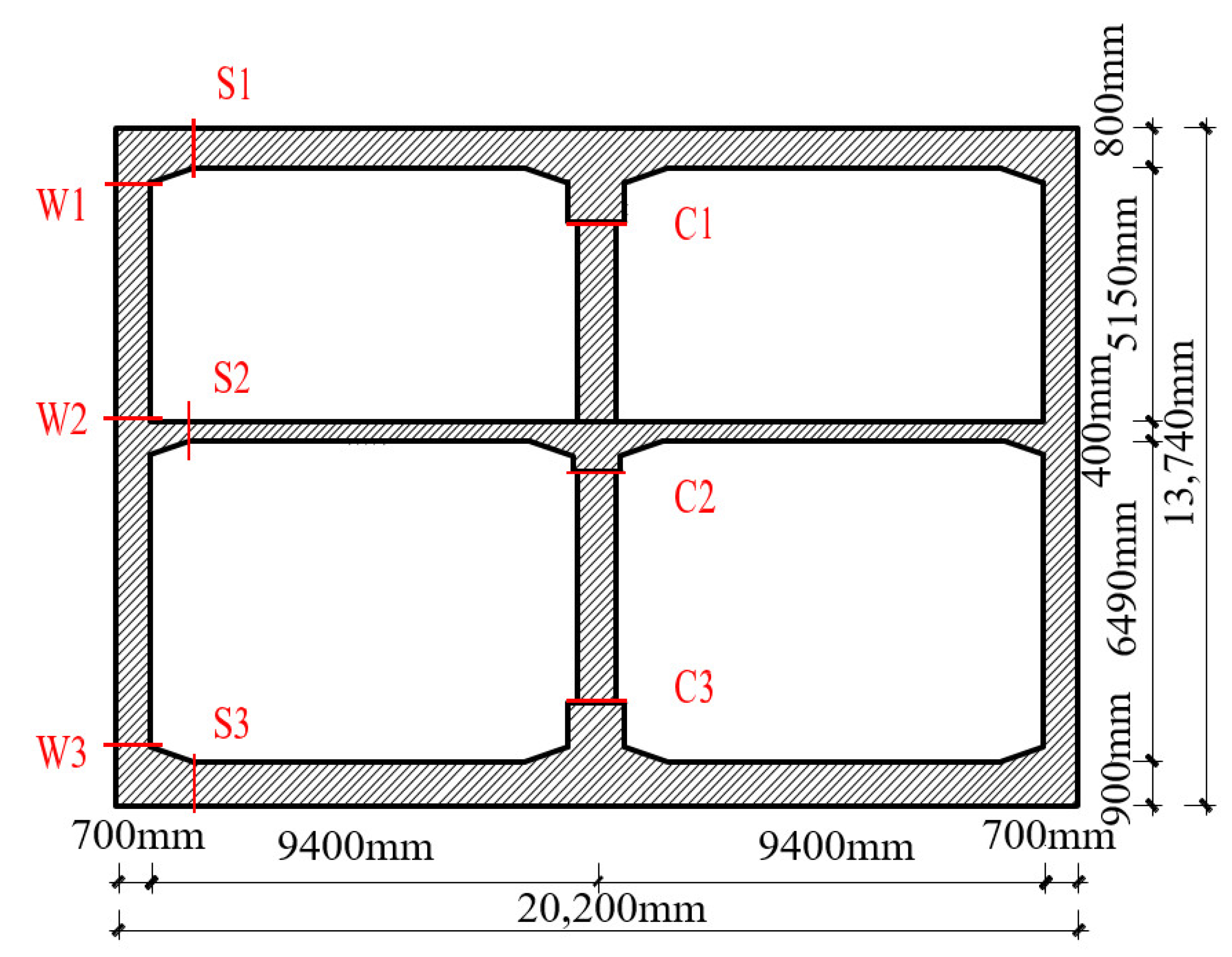
2.1.1. Model
2.1.2. Site Conditions
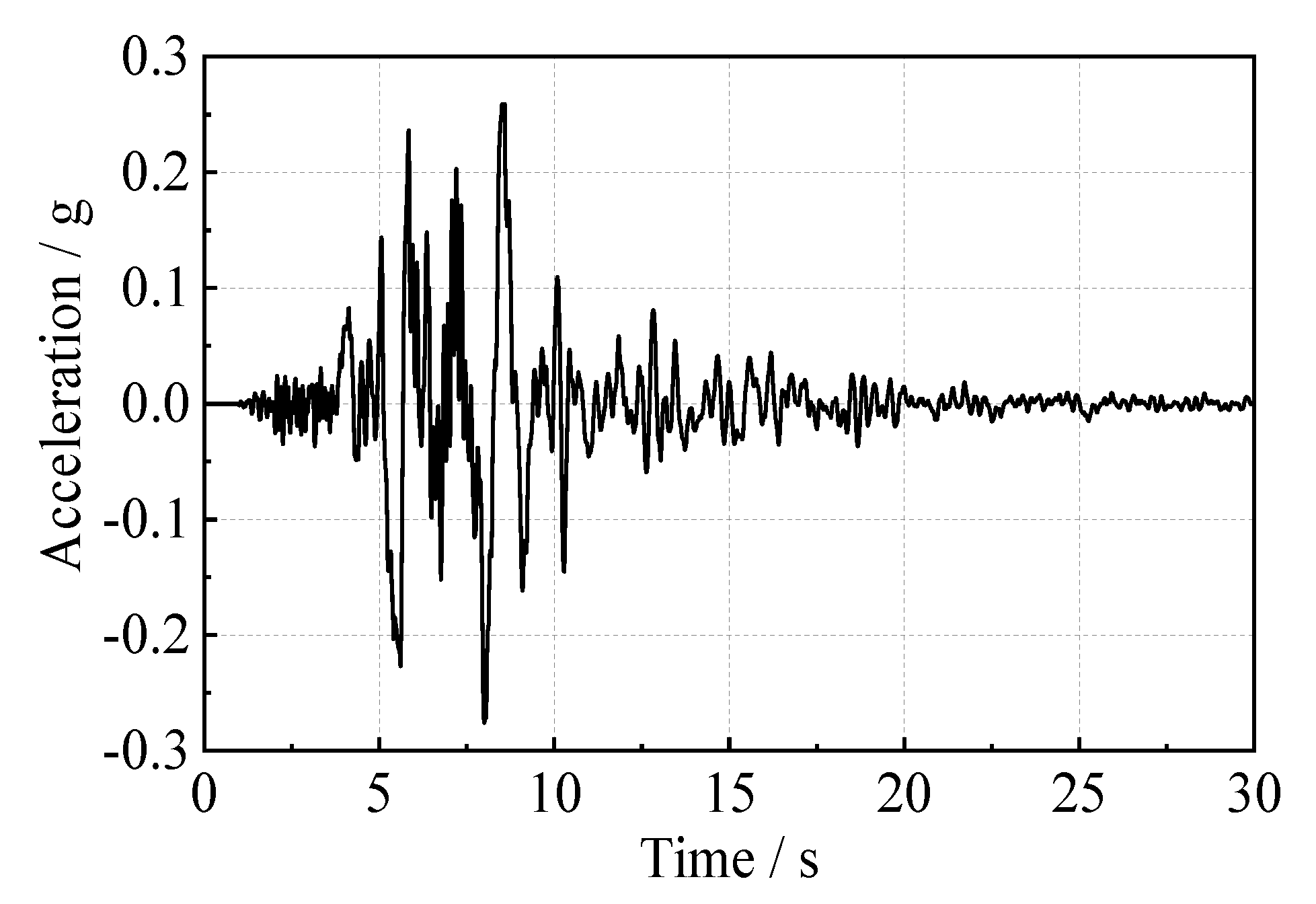
2.1.3. Ground Motion Input
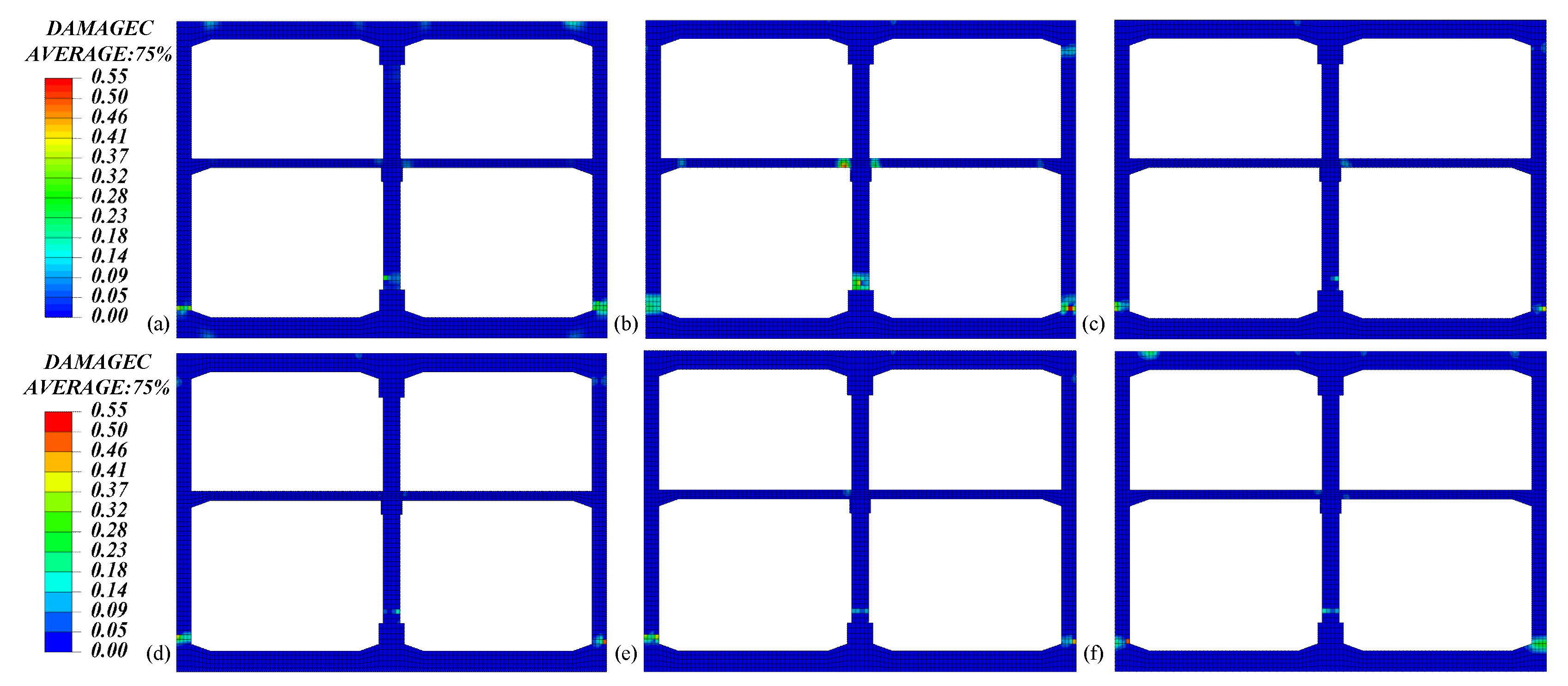
2.2. The Effect of Isolation Layer
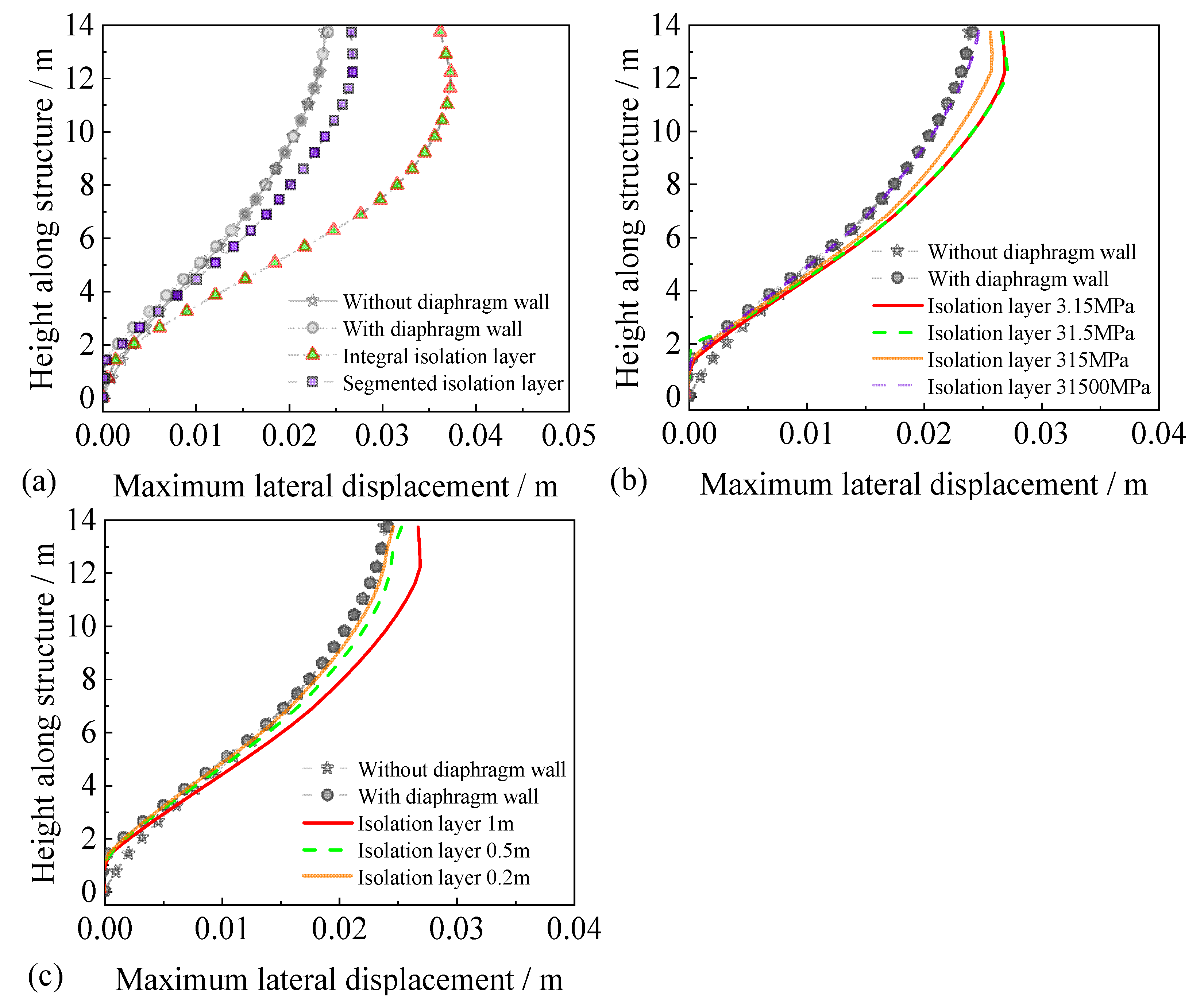
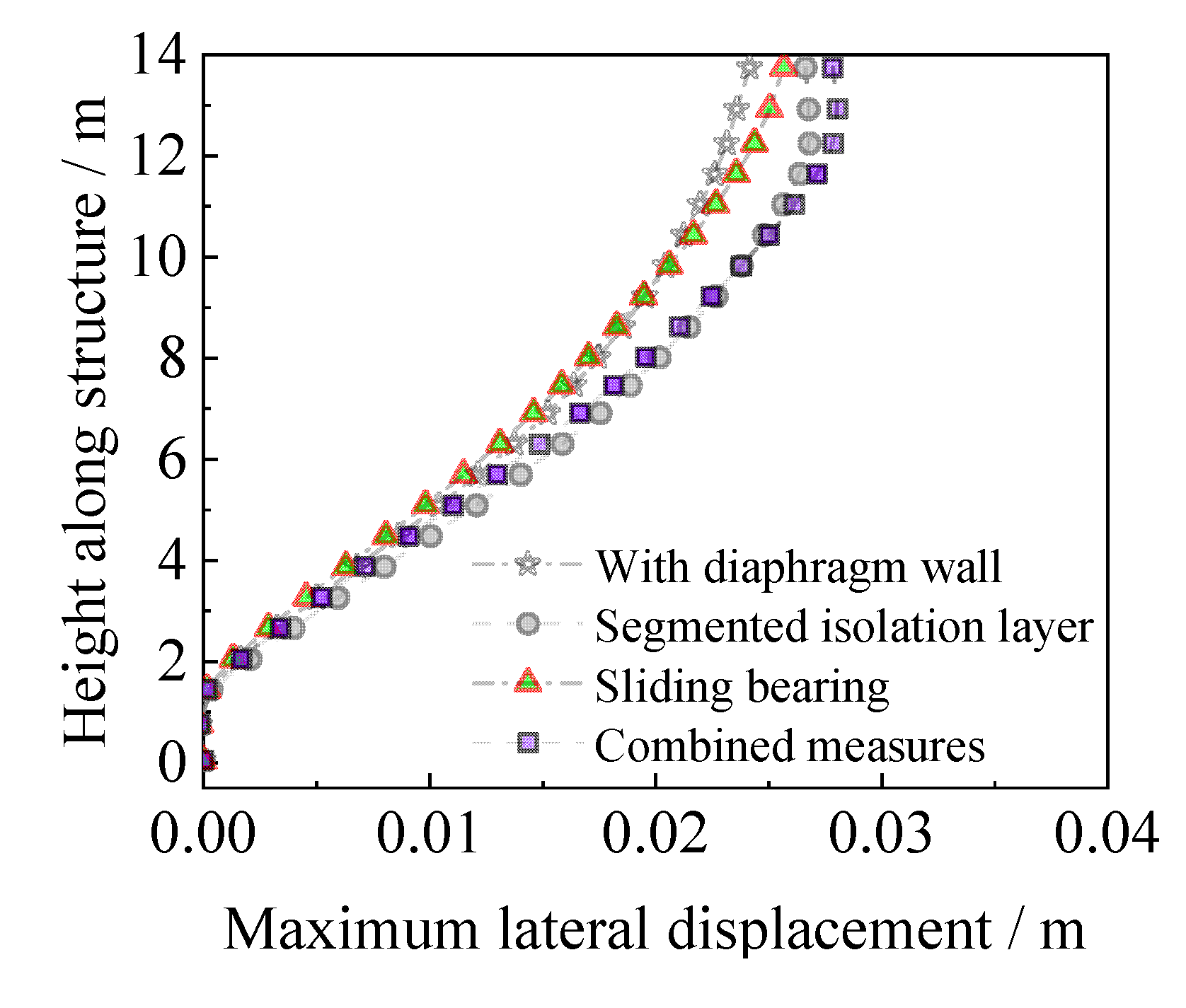
2.2.1. Deformation Analysis of Main Structure
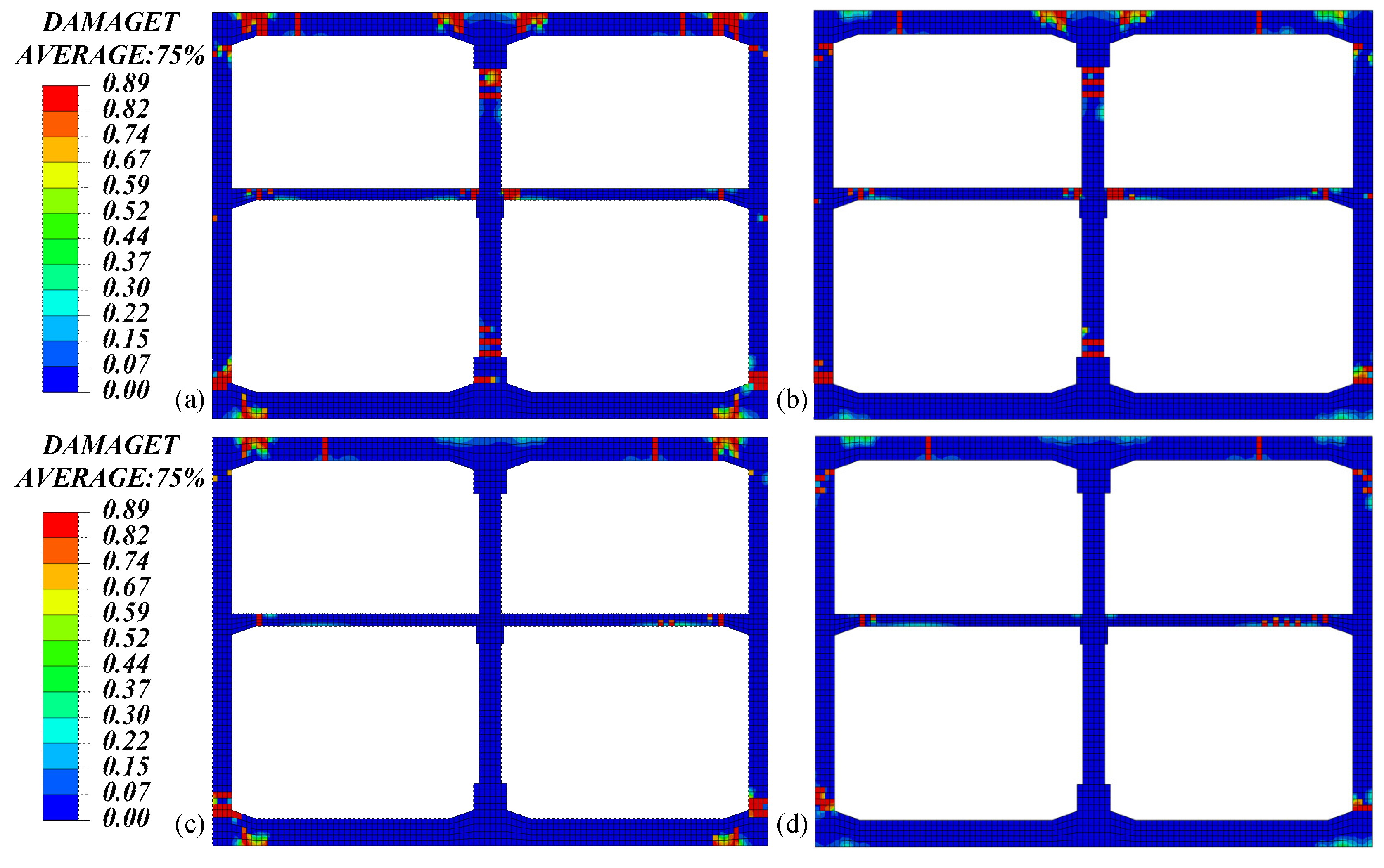
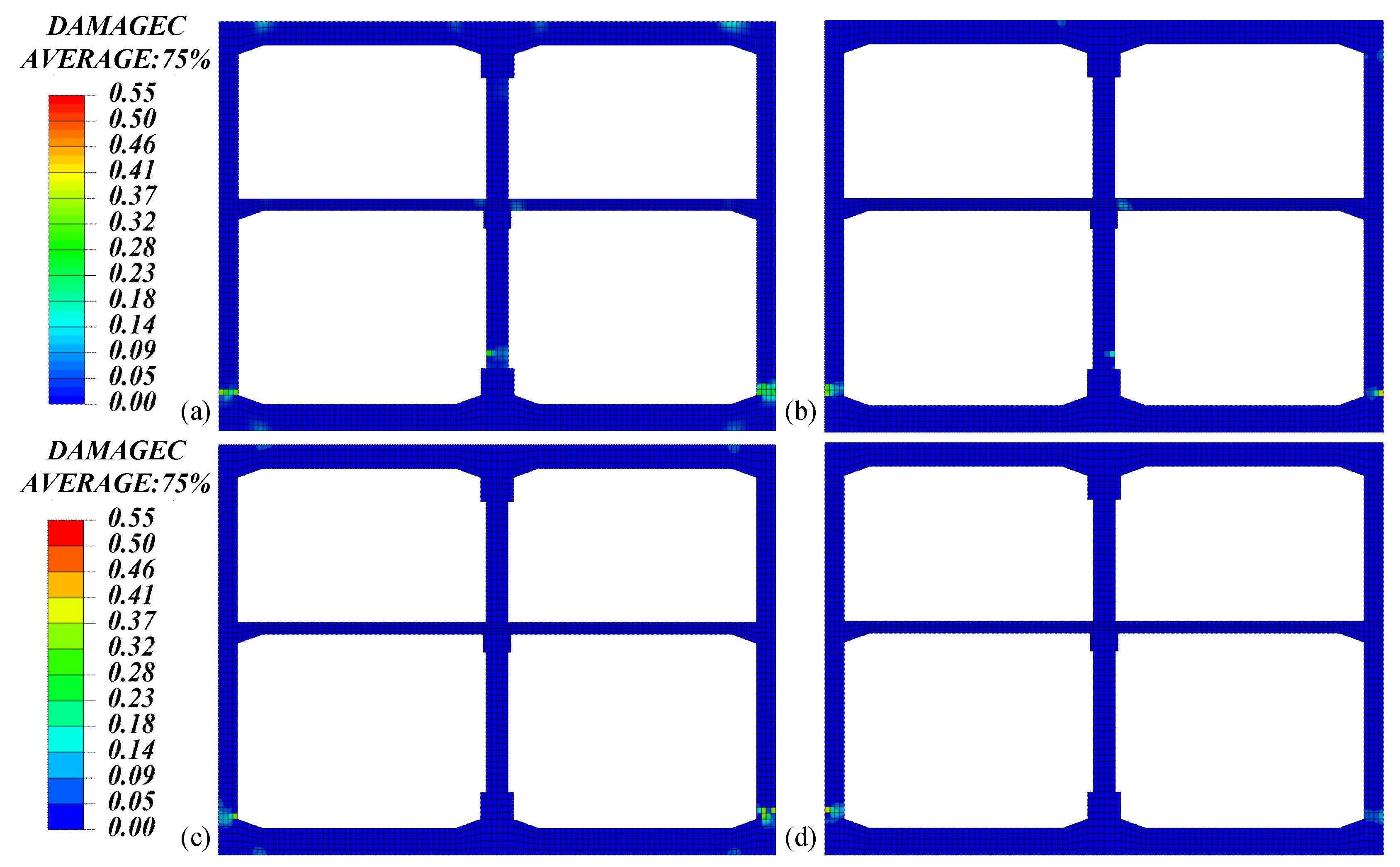
2.2.2. Damage Analysis of the Main Structure
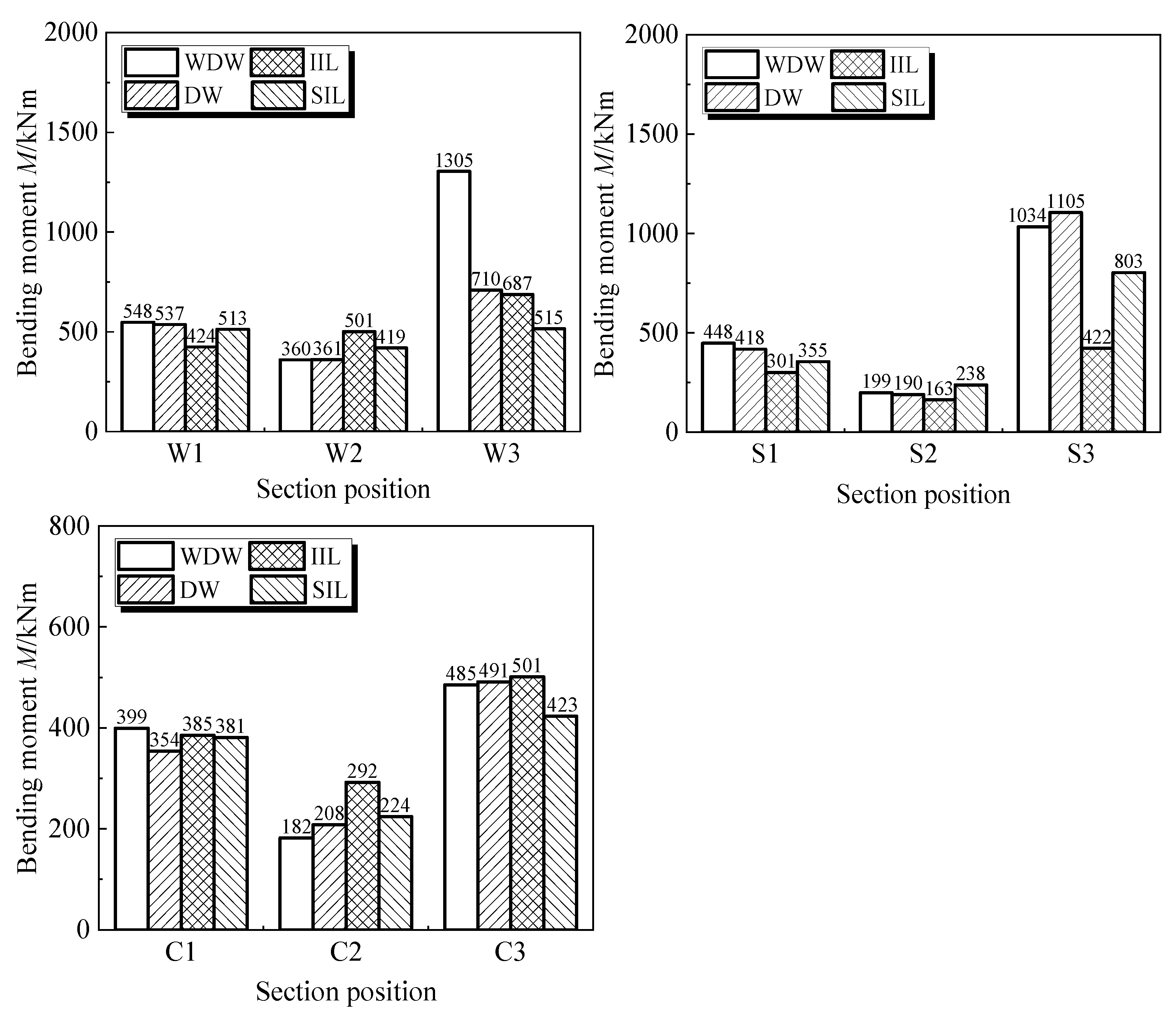
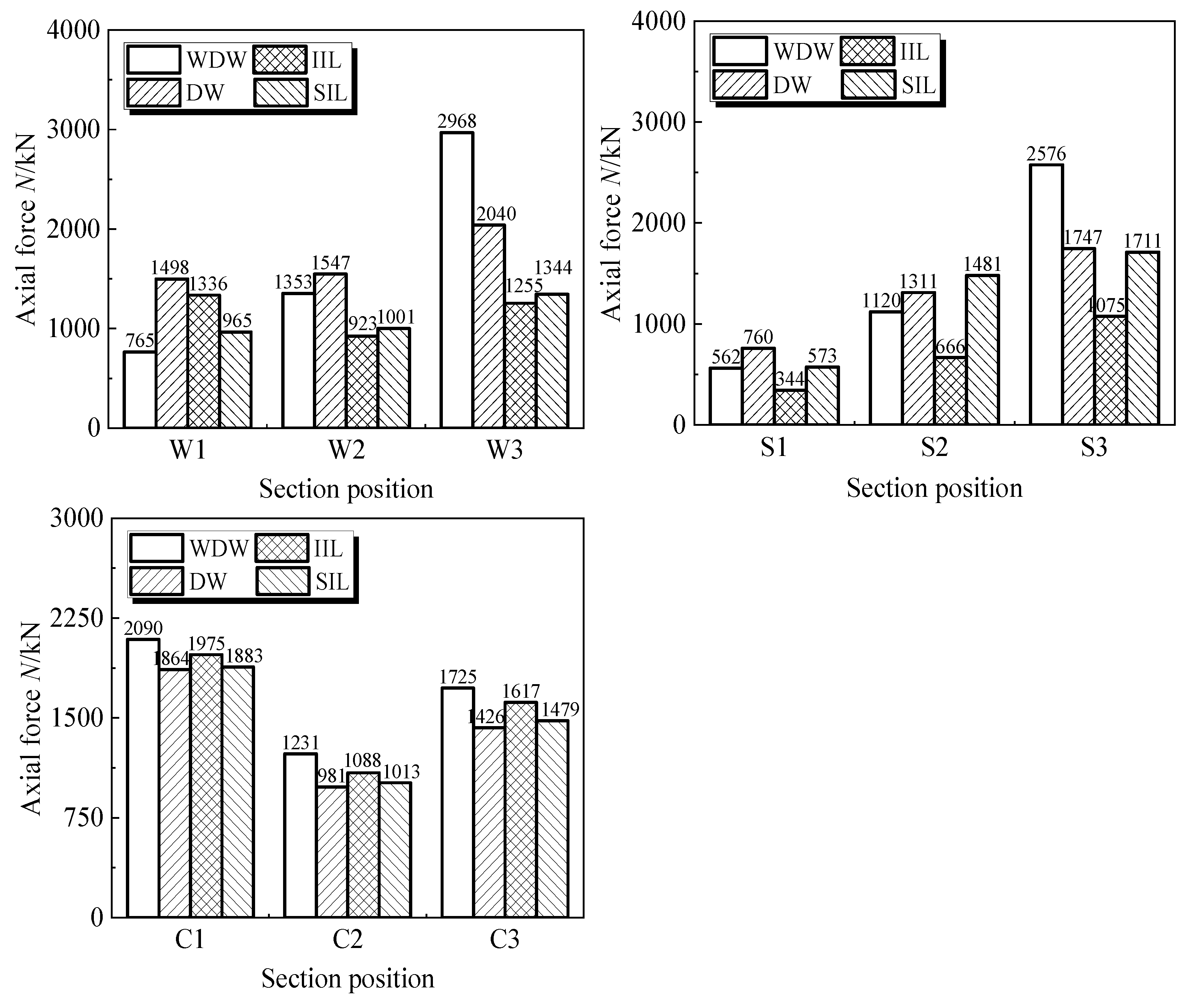
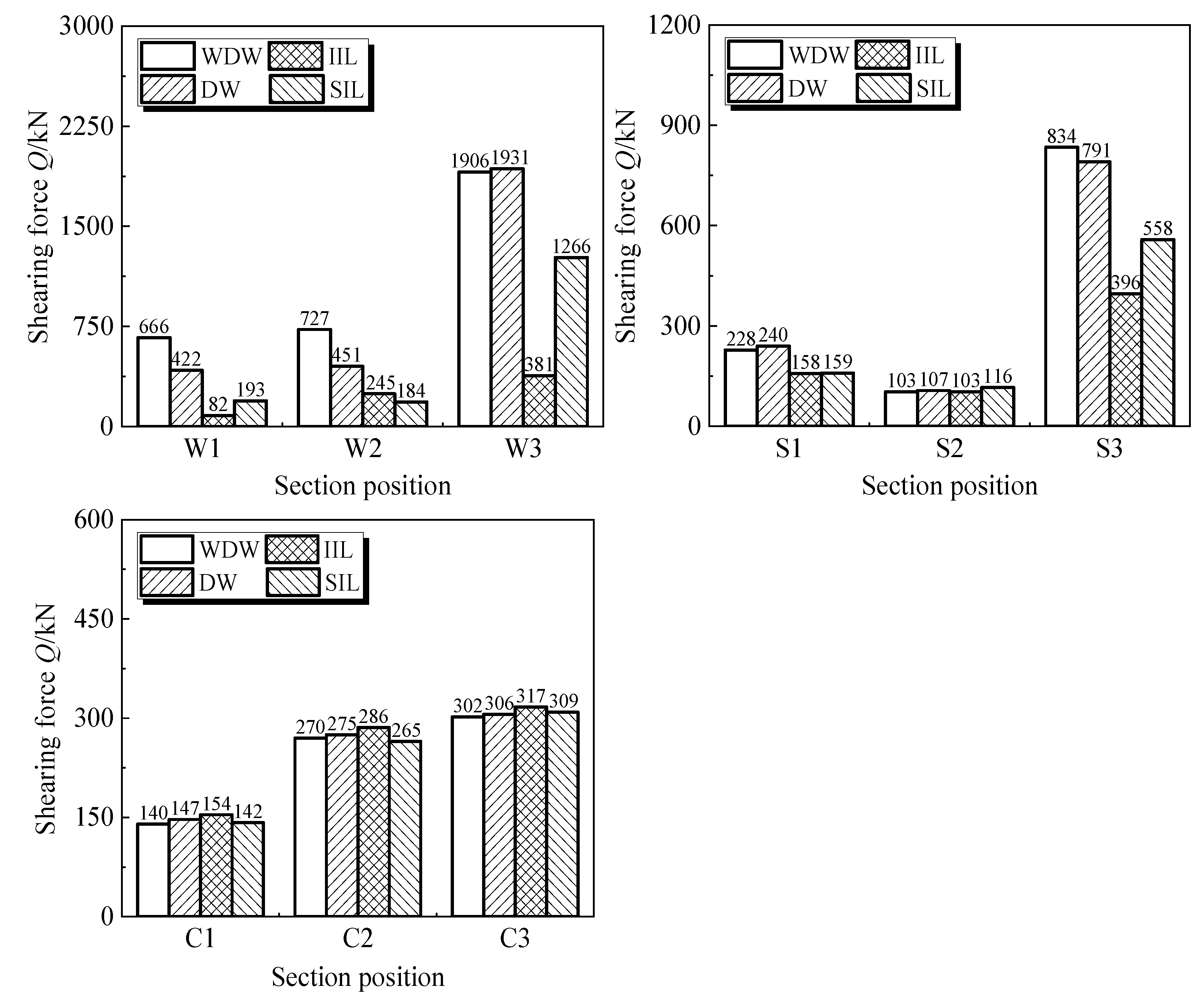
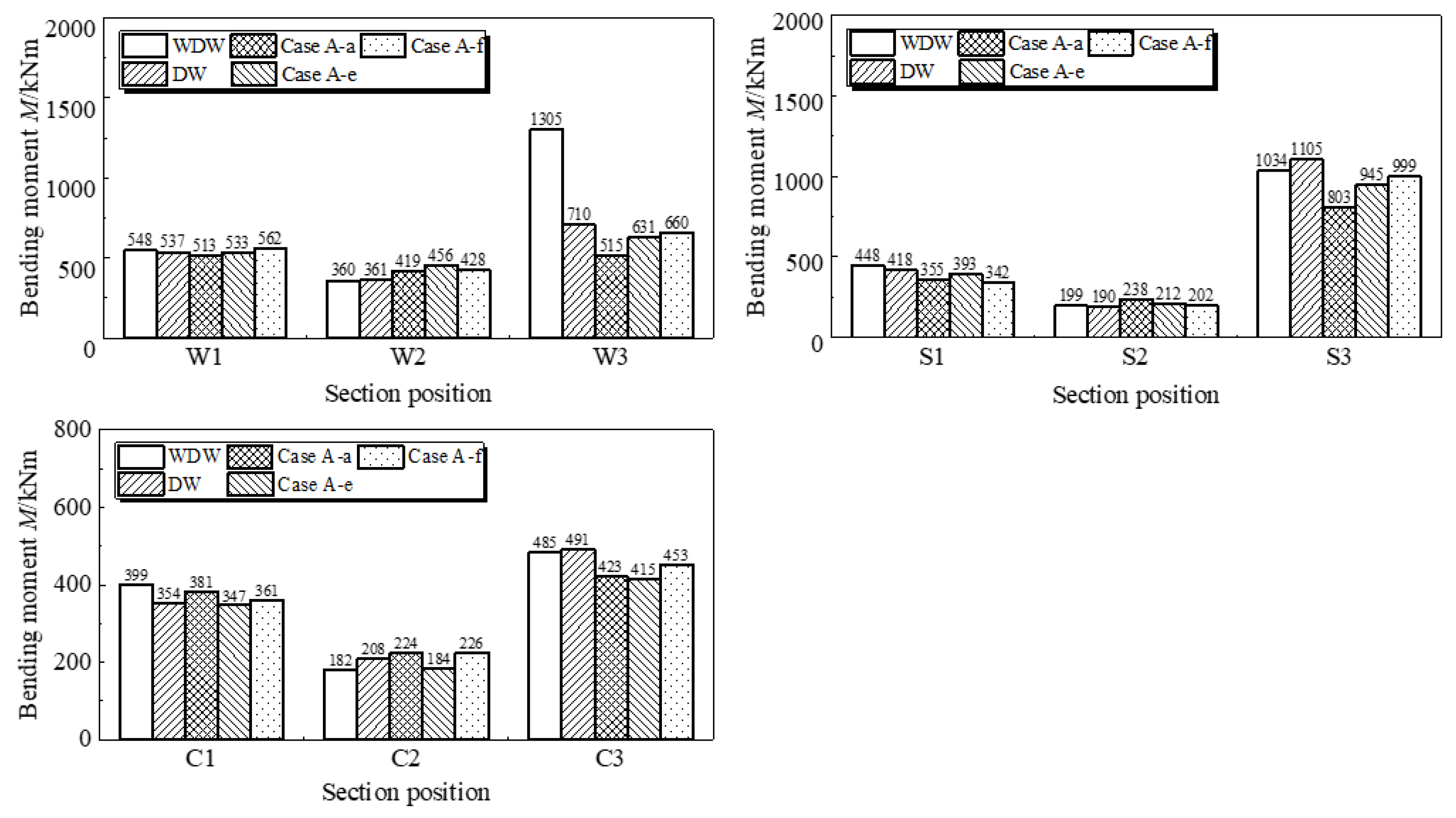
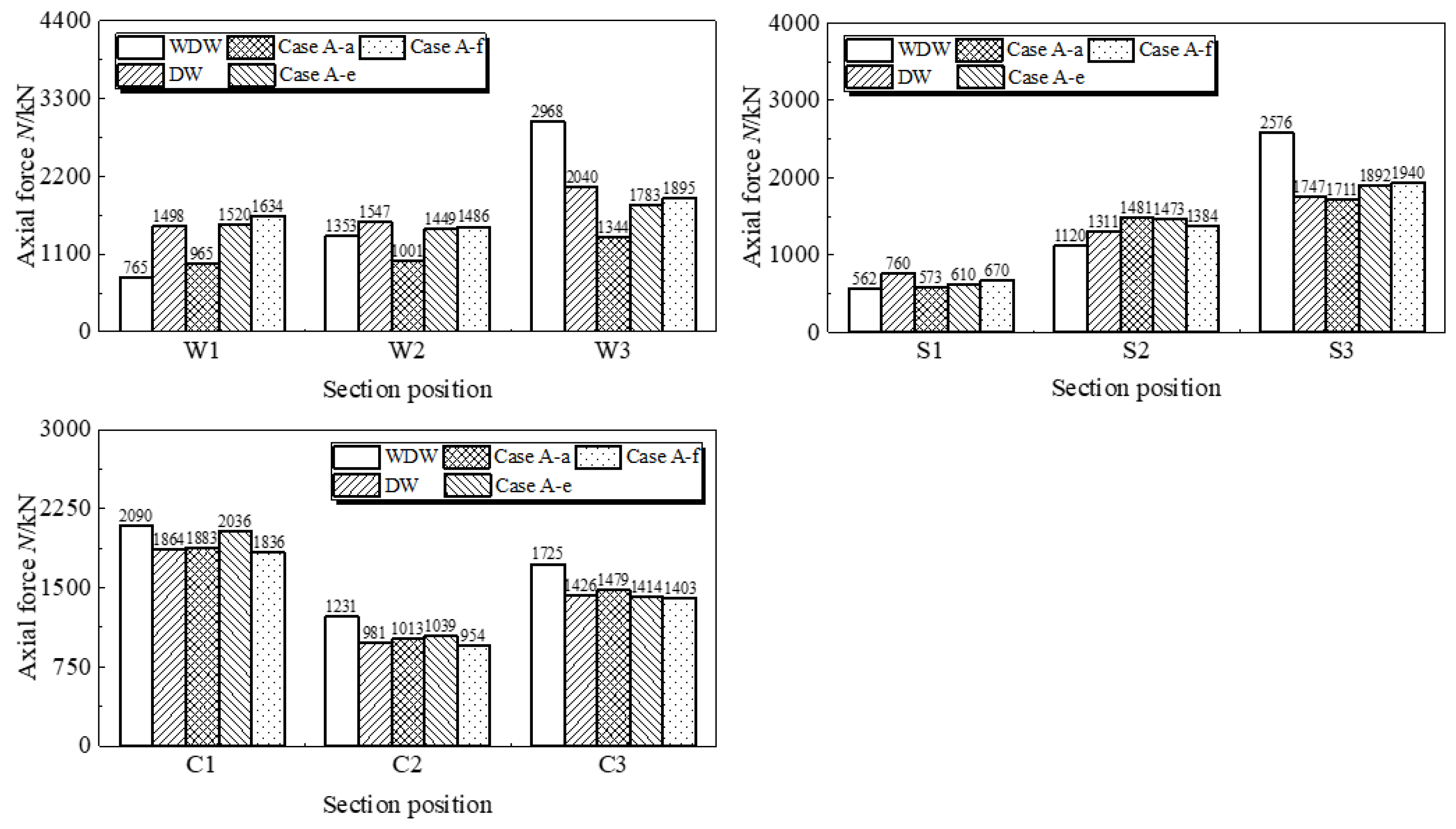
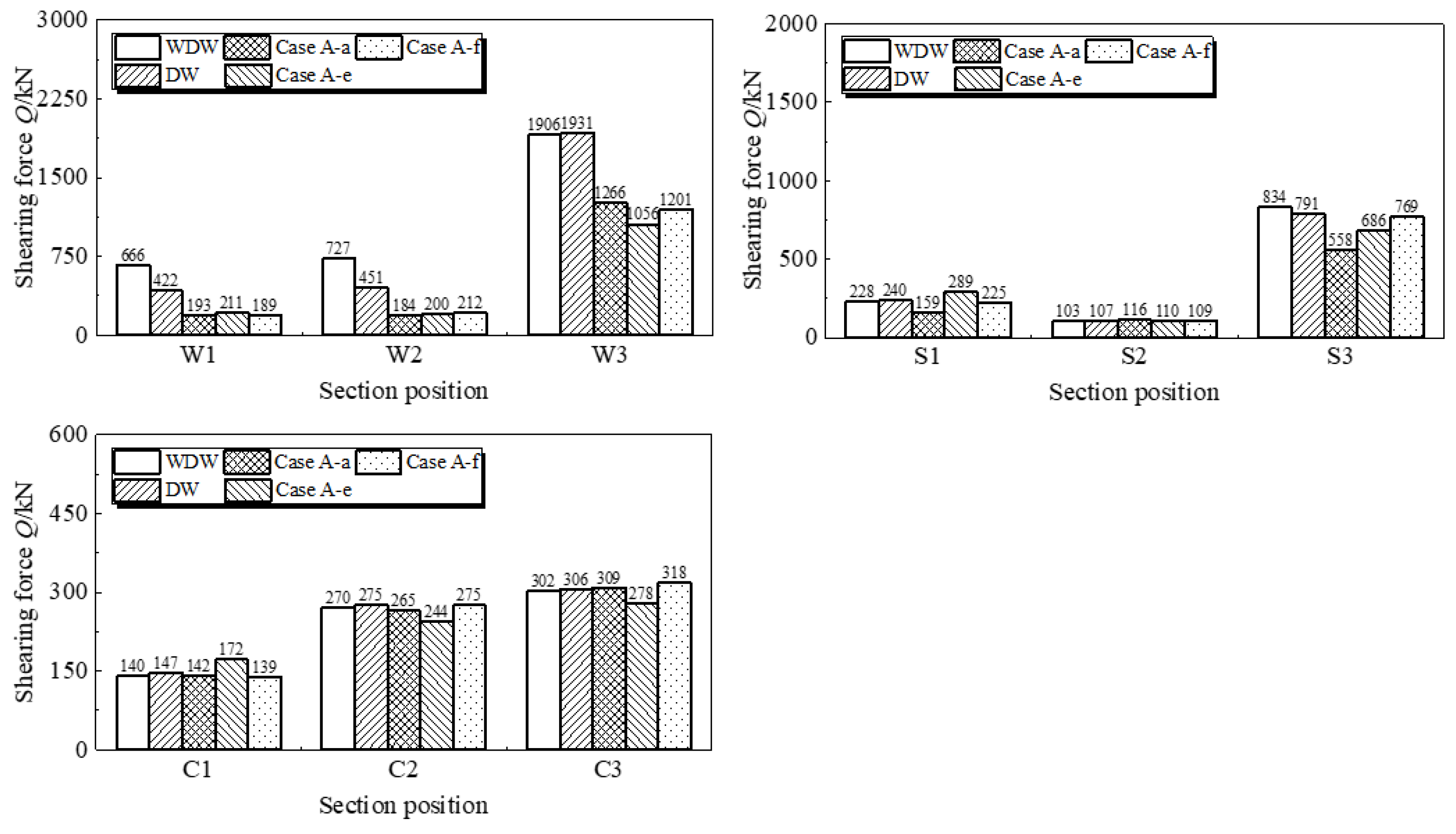
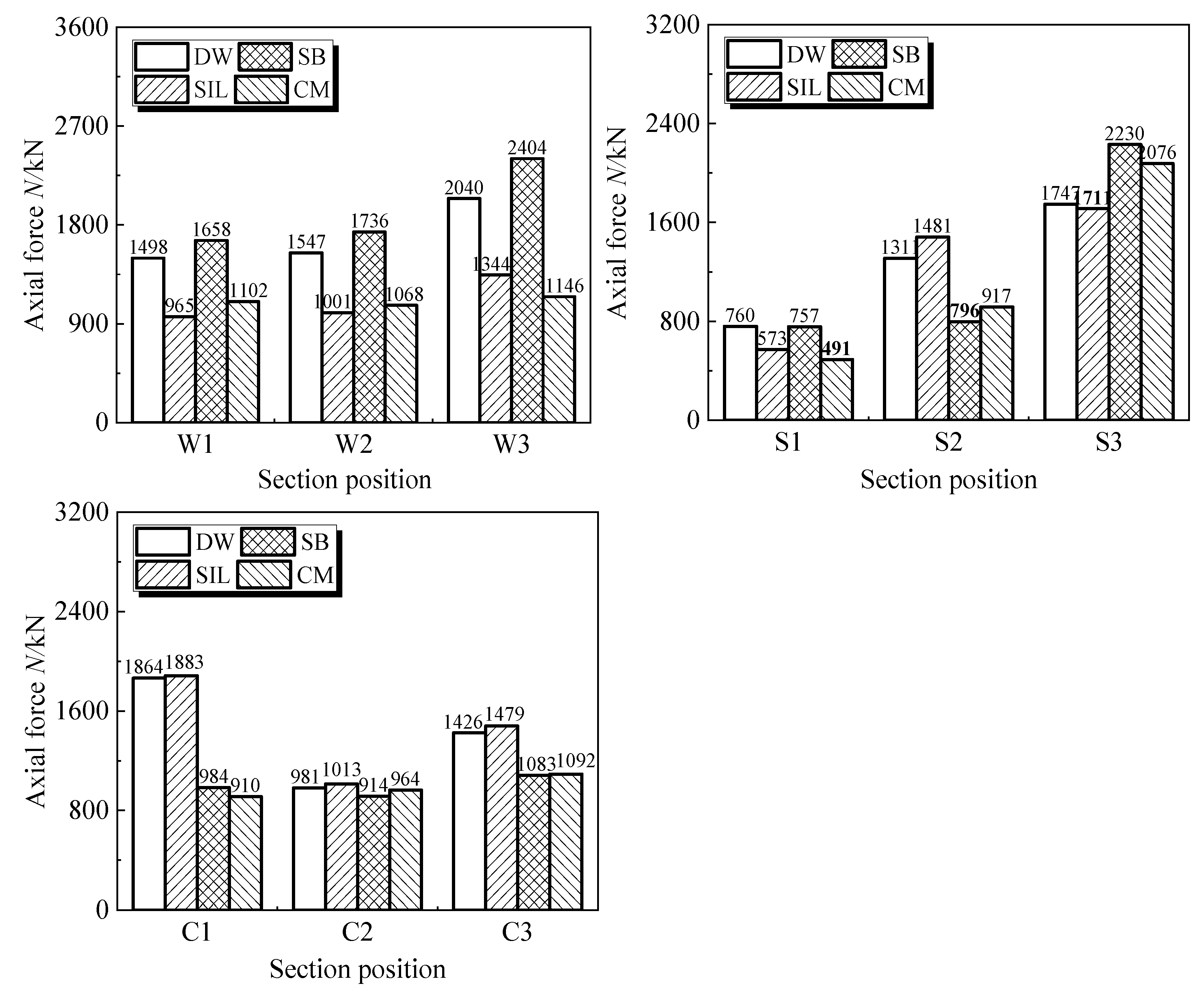
2.2.3. Internal Force Analysis of Key Sections
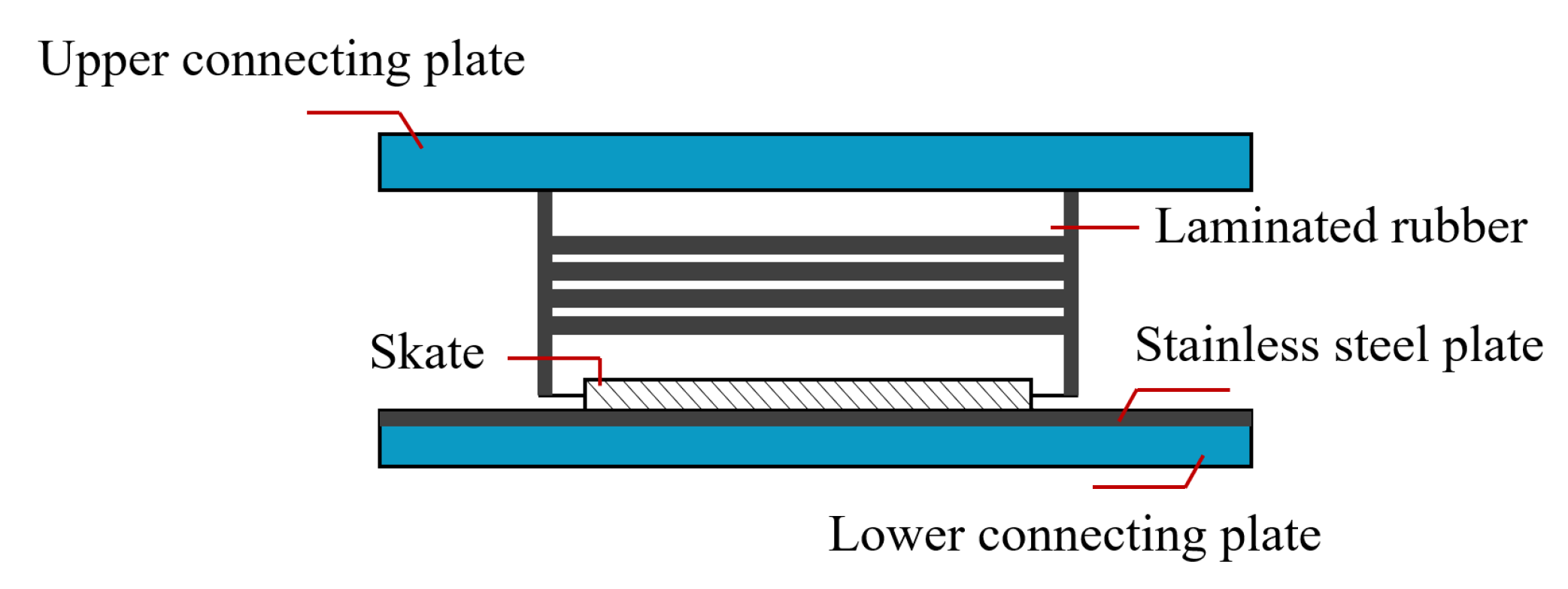
3. Combined Measures of the Sectional Interlayer and Column Top Sliding Support
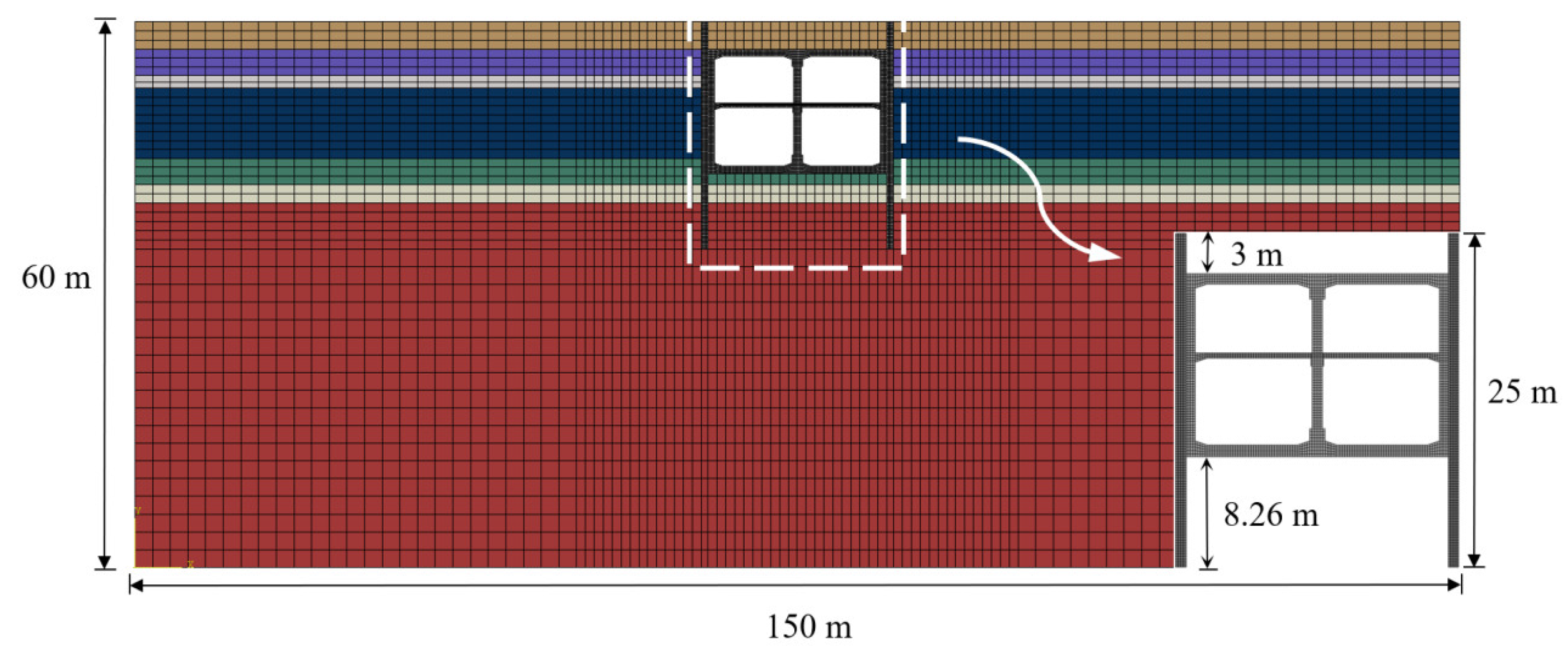
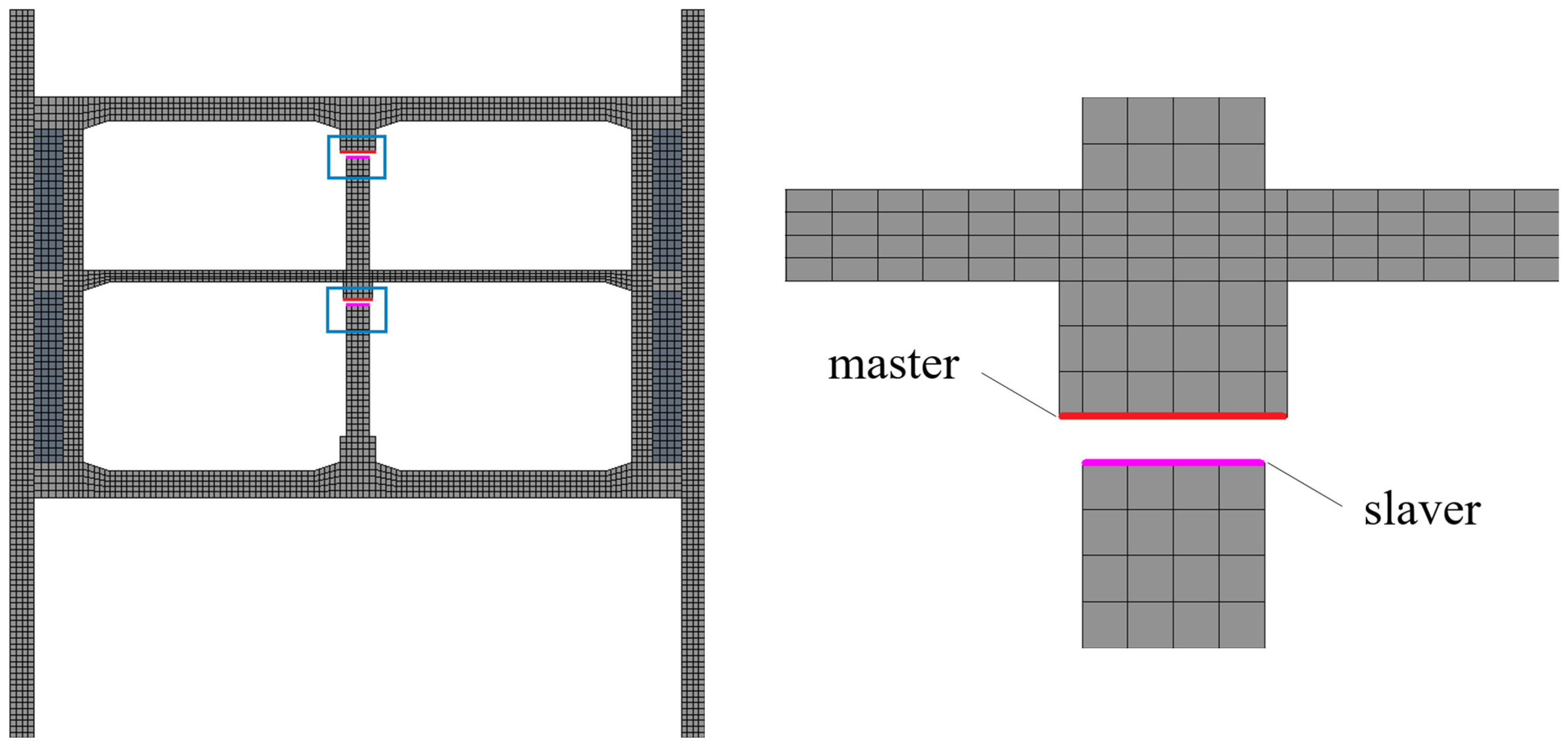
3.1. Finite Element Model
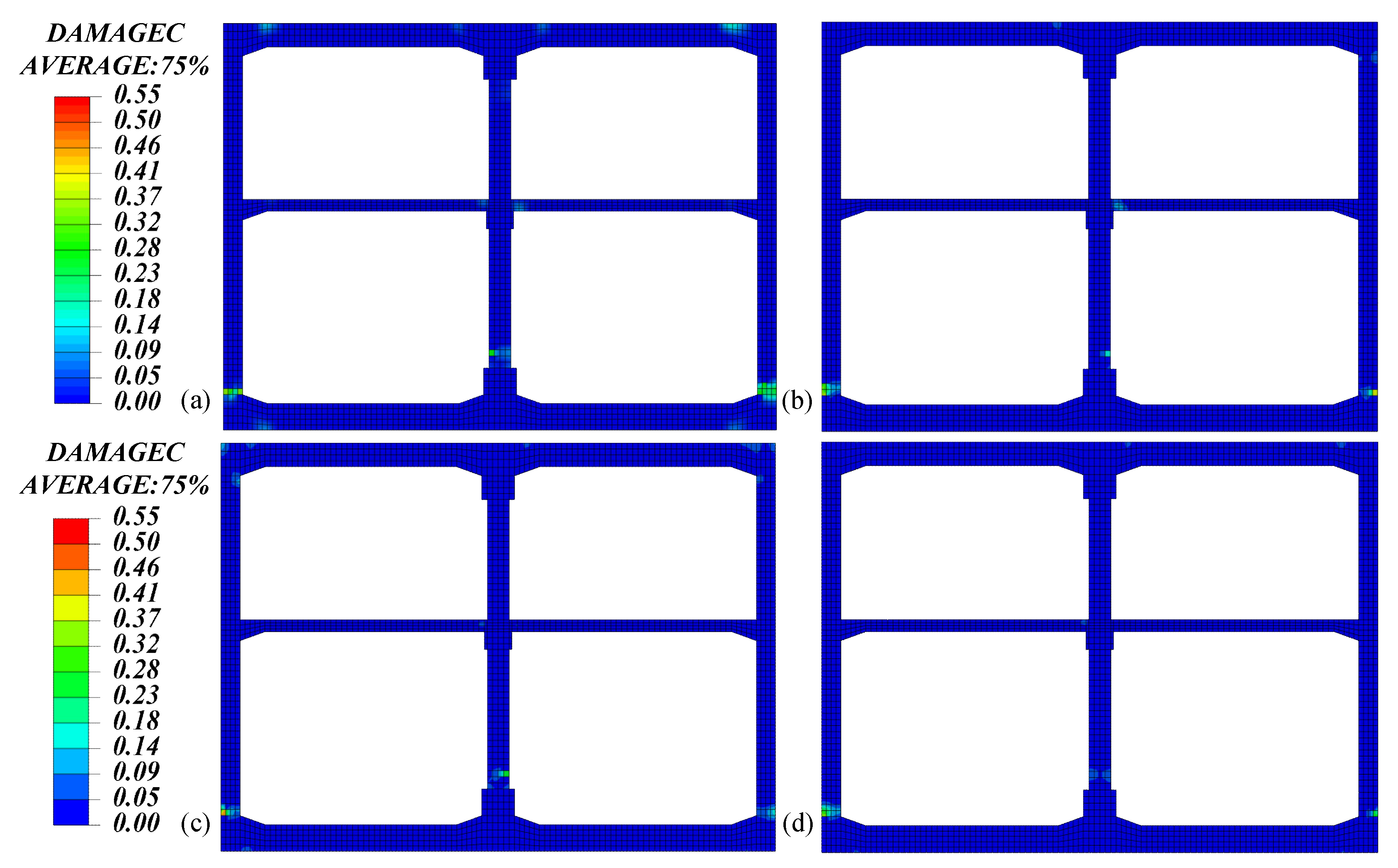
3.2. The Effect of Combined Measures
3.2.1. Deformation Analysis of the Main Structure
3.2.2. Damage Analysis of the Main Structure
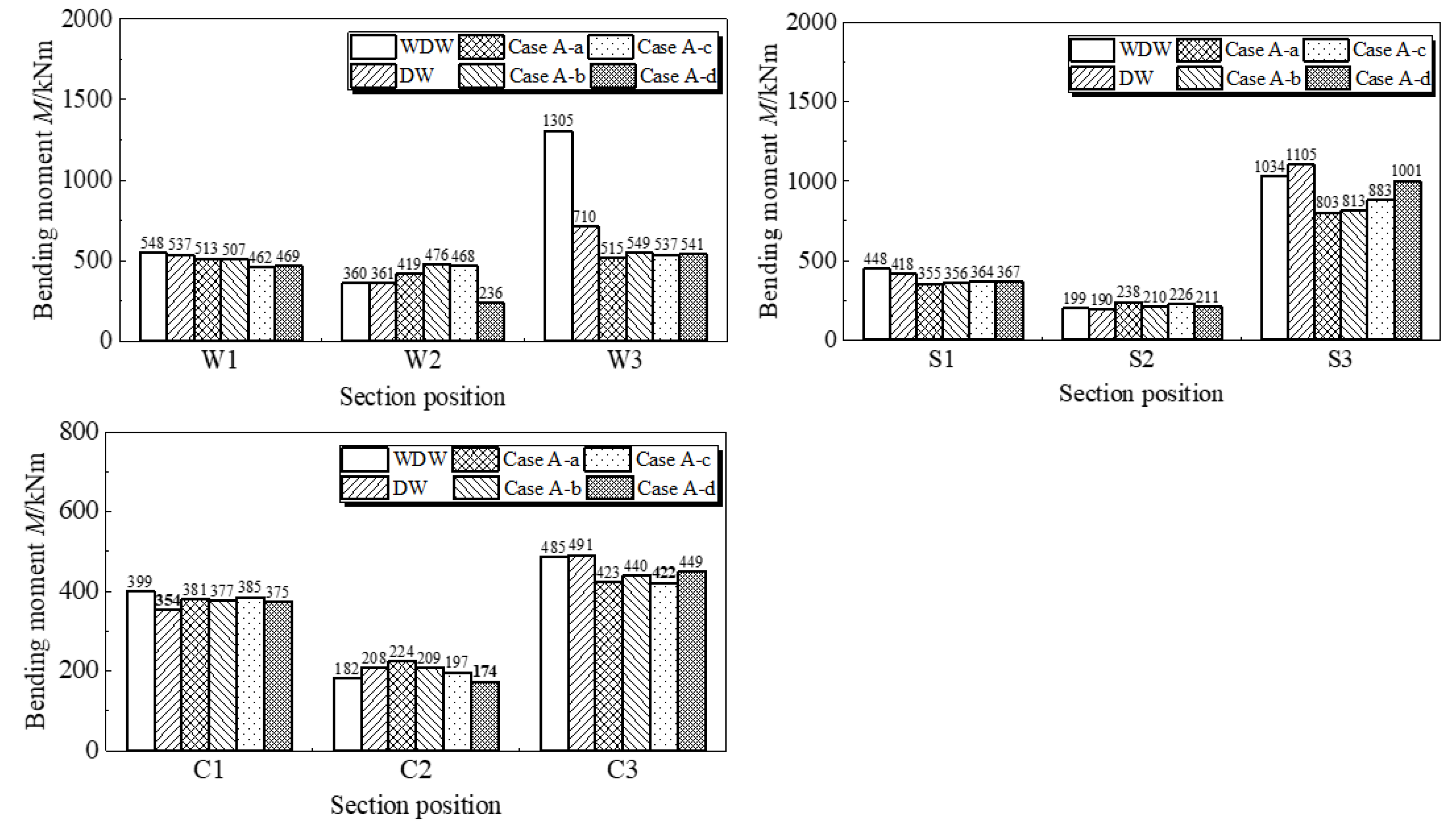
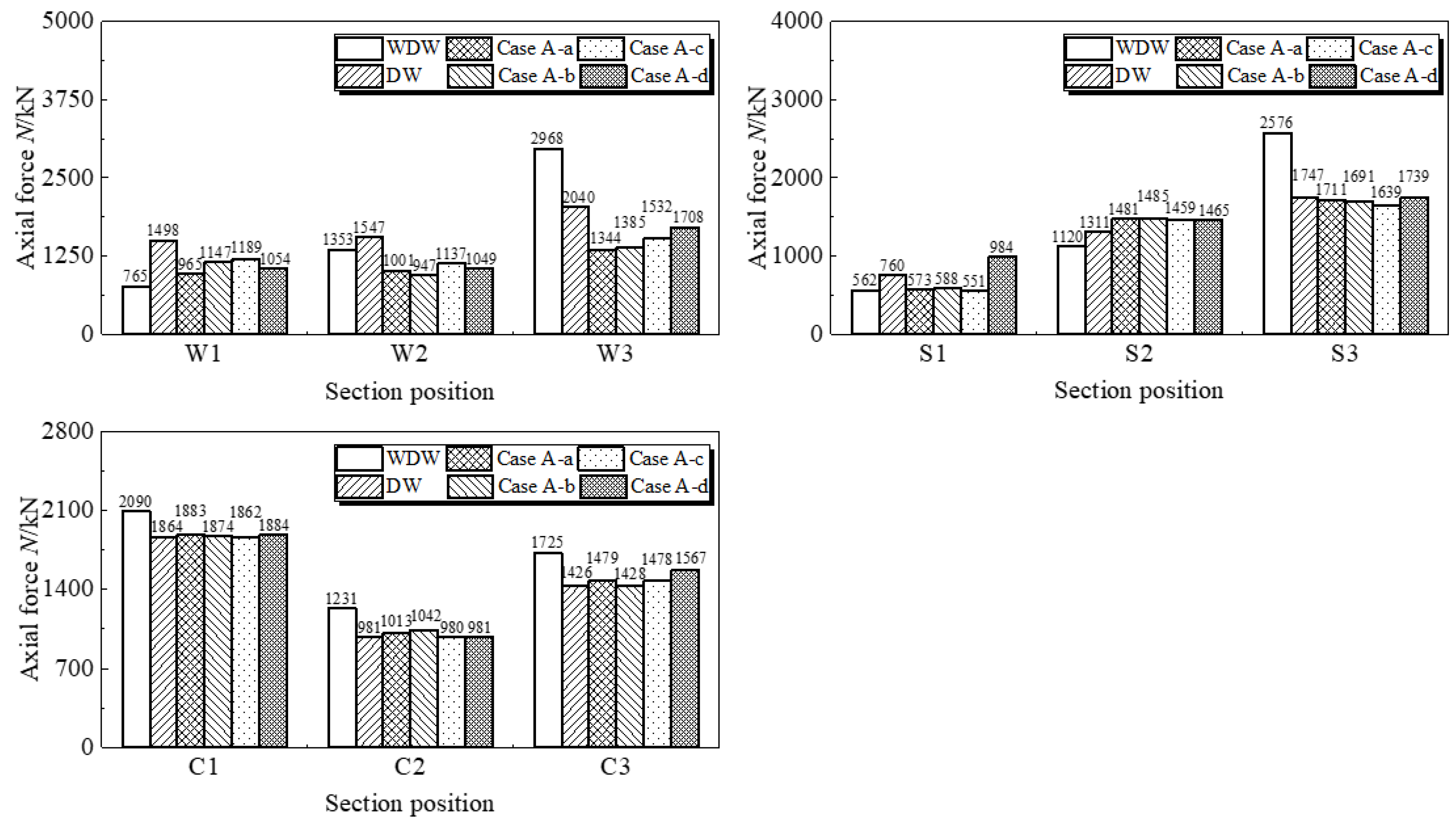
3.2.3. Internal Force Analysis of Key Sections
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zucca, M.; Valente, M. On the limitations of decoupled approach for the seismic behaviour evaluation of shallow multi-propped underground structures embedded in granular soils. Eng. Struct. 2020, 211, 110497. [Google Scholar] [CrossRef]
- Wang, J.N.; Ma, G.W.; Zhuang, H.Y.; Dou, Y.M.; Fu, J.S. Influence of diaphragm wall on seismic responses of large unequal-span subway station in liquefiable soils. Tunn. Undergr. Space Technol. 2019, 91, 102988. [Google Scholar] [CrossRef]
- Zhuang, H.Y.; Hu, Z.H.; Wang, X.J.; Chen, G.X. Seismic responses of a large underground structure in liquefied soils by FEM numerical modelling. Bull. Earthq. Eng. 2015, 13, 3645–3668. [Google Scholar] [CrossRef]
- Zhuang, H.Y.; Yang, J.; Chen, S.; Fu, J.S.; Chen, G.X. Seismic performance of underground subway station structure considering connection modes and diaphragm wall. Soil Dyn. Earthq. Eng. 2019, 127, 105842. [Google Scholar]
- Zhuang, H.Y.; Wang, R.; Shi, P.X.; Chen, G.X. Seismic response and damage analysis of underground structures considering the effect of concrete diaphragm wall. Soil Dyn. Earthq. Eng. 2019, 116, 278–288. [Google Scholar] [CrossRef]
- Yu, H.T.; Cai, C.; Yuan, Y.; Jia, M.C. Analytical solutions for Euler-Bernoulli Beam on Pasternak foundation subjected to arbitrary dynamic loads. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1125–1137. [Google Scholar] [CrossRef]
- John, C.; Zahrah, T.F. Aseismic design of underground structures. Tunn. Undergr. Space Technol. 1987, 2, 165–197. [Google Scholar] [CrossRef]
- Yu, H.T.; Yuan, Y.; Qiao, Z.Z.; Gu, Y.; Yang, Z.H.; Li, X.D. Seismic analysis of a long tunnel based on multi-scale method. Eng. Struct. 2013, 49, 572–587. [Google Scholar] [CrossRef]
- Li, P.; Song, E.X. Three-dimensional numerical analysis for the longitudinal seismic response of tunnels under an asynchronous wave input. Comput. Geotech. 2015, 63, 229–243. [Google Scholar] [CrossRef]
- Fabozzi, S.; Bilotta, E.; Yu, H.T.; Yuan, Y. Effects of the asynchronism of ground motion on the longitudinal behaviour of a circular tunnel. Tunn. Undergr. Space Technol. 2018, 82, 529–541. [Google Scholar] [CrossRef]
- Huang, J.Q.; Du, X.L.; Jin, L.; Zhao, M. Impact of incident angles of P waves on the dynamic responses of long lined tunnels. Earthq. Eng. Struct. Dyn. 2016, 45, 2435–2454. [Google Scholar] [CrossRef]
- Gao, Z.D.; Zhao, M.; Huang, J.Q.; Du, X.L. Three-dimensional nonlinear seismic response analysis of subway station crossing longitudinally inhomogeneous geology under obliquely incident P waves. Eng. Geol. 2021, 293, 106341. [Google Scholar] [CrossRef]
- Chen, J.; Shi, X.; Li, J. Shaking table test of utility tunnel under non-uniform earthquake wave excitation. Soil Dyn. Earthq. Eng. 2010, 30, 1400–1416. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Chen, W.; Bian, G.Q. Seismic performance upgrading for underground structures by introducing shear panel dampers. Adv. Struct. Eng. 2014, 17, 1343–1357. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Zhao, H.; Lou, M.L. Seismic performance and optimal design of framed underground structures with lead-rubber bearings. Struct. Eng. Mech. 2016, 58, 259–276. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Zhou, Y. Seismic performance of framed underground structures with self-centering energy-dissipation column base. Adv. Struct. Eng. 2019, 22, 2809–2822. [Google Scholar] [CrossRef]
- Ma, C.; Lu, D.C.; Du, X.L. Seismic performance upgrading for underground structures by introducing sliding isolation bearings. Tunn. Undergr. Space Technol. 2018, 74, 1–9. [Google Scholar] [CrossRef]
- Xu, Z.G.; Du, X.L.; Xu, C.S.; Han, R.B. Numerical analyses of seismic performance of underground and aboveground structures with friction pendulum bearings. Soil Dyn. Earthq. Eng. 2020, 130, 105967. [Google Scholar] [CrossRef]
- Liu, D.; Du, X.L.; El Naggar, H.M.; Xu, C.S.; Chen, Q. Seismic mitigation performance analysis of underground subway station with arc grooved roller bearings. Soil Dyn. Earthq. Eng. 2022, 153, 107082. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Miri, A.K. Seismic isolation effect of lined circular tunnels with damping treatments. Earthq. Eng. Eng. Vib. 2008, 7, 305–319. [Google Scholar] [CrossRef]
- Kiryu, S.; Murono, Y.; Morikawa, H. Seismic response of a cut-and-cover tunnel isolated by polymer material. Earthq. Eng. Struct. Dyn. 2012, 41, 2043–2057. [Google Scholar] [CrossRef]
- Martin, P.P.; Seed, H.B. One-dimensional dynamic ground response analyses. J. Geotech. Eng. Div. 1982, 108, 935–952. [Google Scholar] [CrossRef]
- Zhuang, H.Y.; Fu, J.S.; Chen, S.; Zhao, C.; Zhao, K.; Chen, G. Seismic performance analysis of subway underground station structures with sliding bearings installed at the top of columns. Tunn. Undergr. Eng. Disaster Prev. Control. 2019, 1, 57–67. (In Chinese) [Google Scholar]
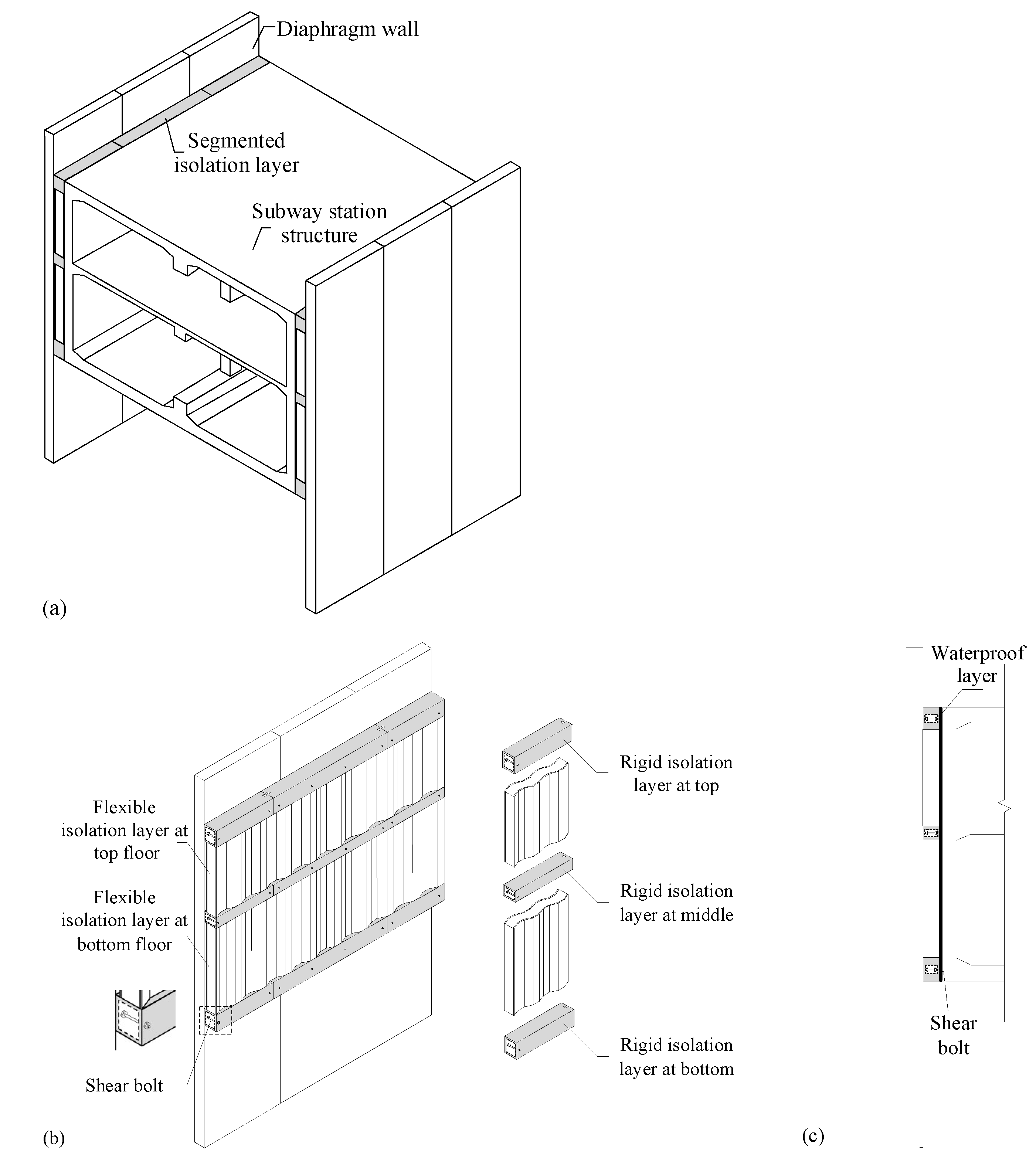
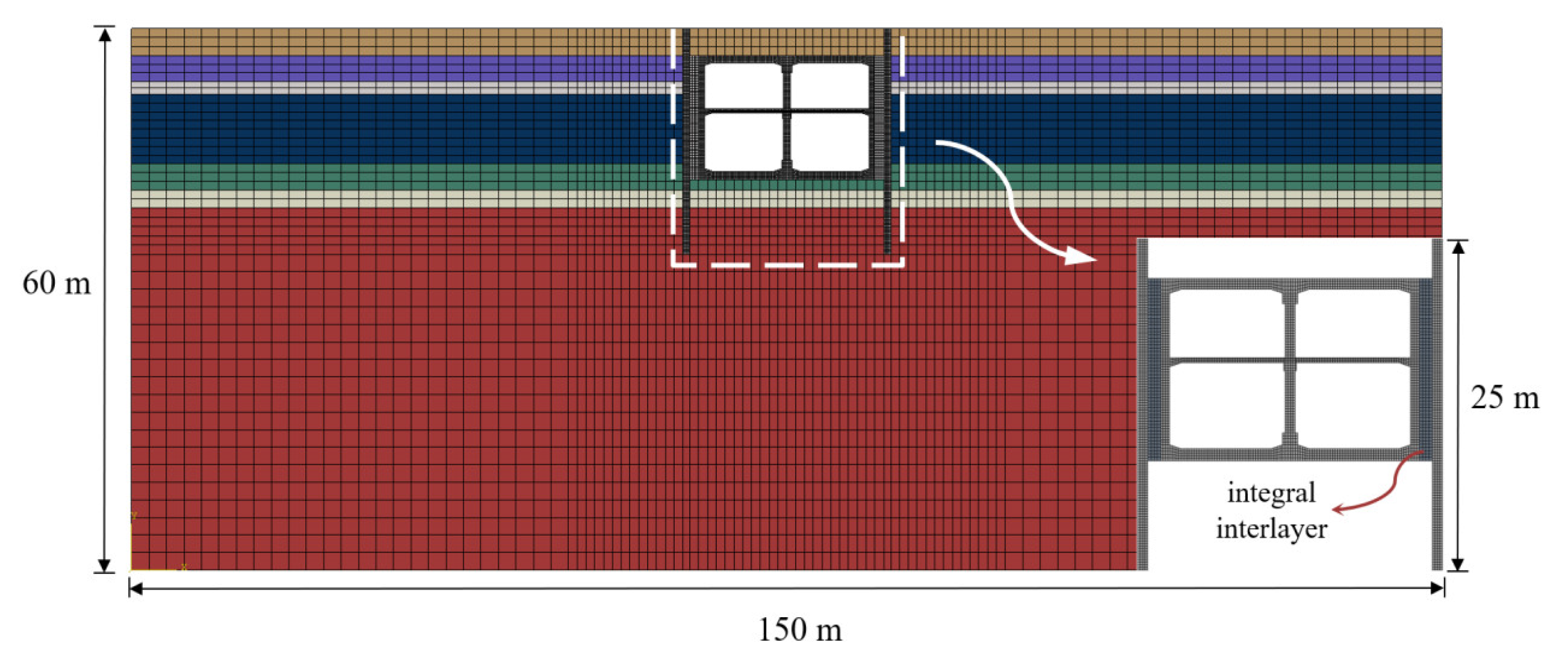
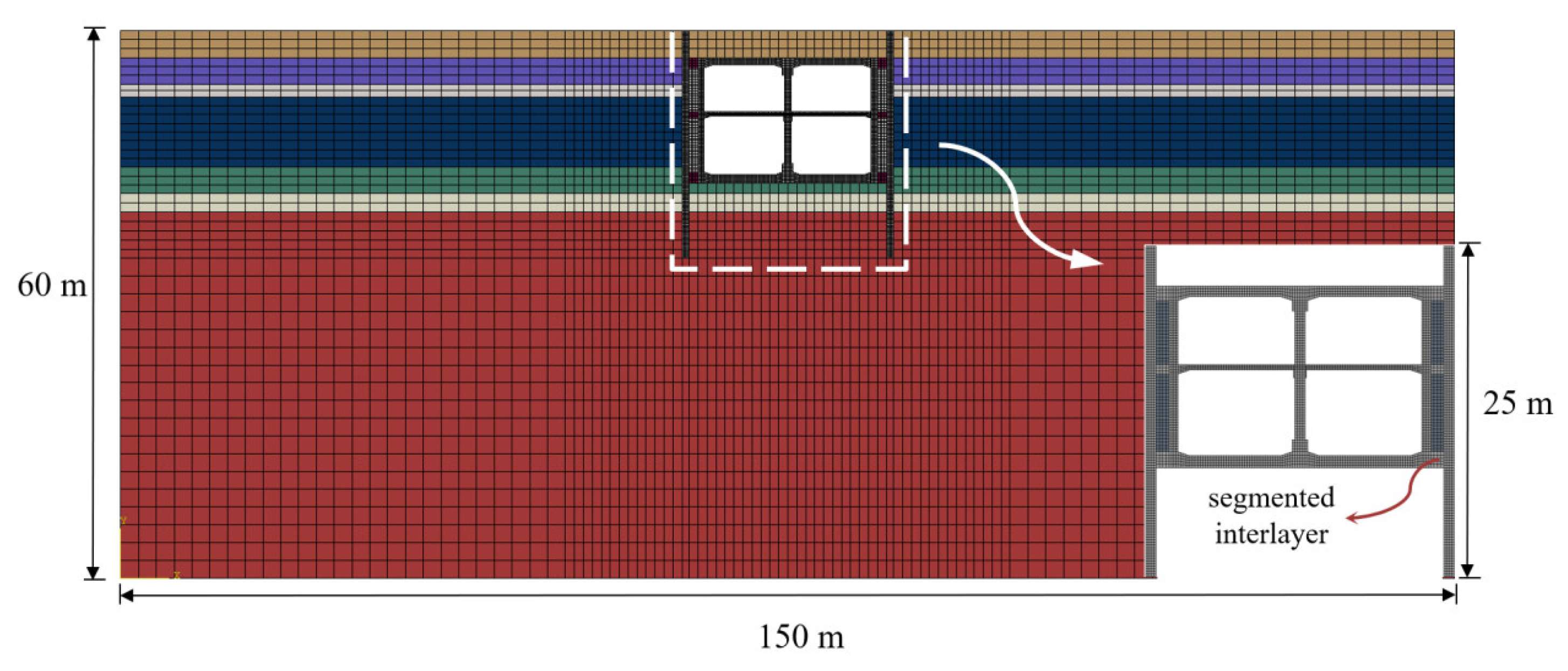





| Form of isolation layer | Stiffness and Thickness of Isolation Layer | |||||
| a | b | c | d | e | f | |
| EC35/10,000 | EC35/1000 | EC35/100 | EC35 | EC35/10,000 3.15 MPa | ||
| 3.15 MPa | 31.5 MPa | 315 MPa | 31,500 MPa | |||
| Thickness (1.0 m) | Thickness (0.5 m) | Thickness (0.2 m) | ||||
| Segmented isolation layer |  | |||||
| Layer Number | Soil Stratum | Unit Weight (kN/m3) | Elastic Modulus (MPa) | POISSON’S Ratio | Shear Wave Velocity (m/s) |
|---|---|---|---|---|---|
| 1 | Miscellaneous fill | 17.5 | 70.77 | 0.35 | 193 |
| 2 | Silty clay | 19.4 | 117.14 | 0.36 | 247 |
| 3 | Pebbles | 21.2 | 177.61 | 0.23 | 298 |
| 4 | Medium coarse sand | 20.3 | 149.45 | 0.29 | 279 |
| 5 | Pebbly silty clay | 19.7 | 169.7 | 0.31 | 295 |
| 6 | Silty clay | 19.4 | 183.79 | 0.36 | 307 |
| 7 | Clayey silt | 20.9 | 208.51 | 0.33 | 327 |
| Soil Stratum | A | B | γ0 (×104) |
|---|---|---|---|
| Miscellaneous fill | 1.2 | 0.4 | 1.69 |
| Silty clay | 1.2 | 0.47 | 5.8 |
| Pebbles | 1.25 | 0.31 | 8.99 |
| Sand | 1.15 | 0.33 | 5.36 |
| Silt | 1.05 | 0.49 | 5.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhao, M.; Huang, J.; Gao, Z. Study on Seismic Reduction Measures of a Diaphragm Wall—Underground Structure System. Appl. Sci. 2023, 13, 6910. https://doi.org/10.3390/app13126910
Zhang Q, Zhao M, Huang J, Gao Z. Study on Seismic Reduction Measures of a Diaphragm Wall—Underground Structure System. Applied Sciences. 2023; 13(12):6910. https://doi.org/10.3390/app13126910
Chicago/Turabian StyleZhang, Qi, Mi Zhao, Jingqi Huang, and Zhidong Gao. 2023. "Study on Seismic Reduction Measures of a Diaphragm Wall—Underground Structure System" Applied Sciences 13, no. 12: 6910. https://doi.org/10.3390/app13126910




