Are Protein Shape-Encoded Lowest-Frequency Motions a Key Phenotype Selected by Evolution?
Abstract
:1. From the Structure–Function Paradigm to Structure–Motion–Function
2. ENMs Overview and the Surprising Accuracy of Shape-Encoded Harmonic Motions
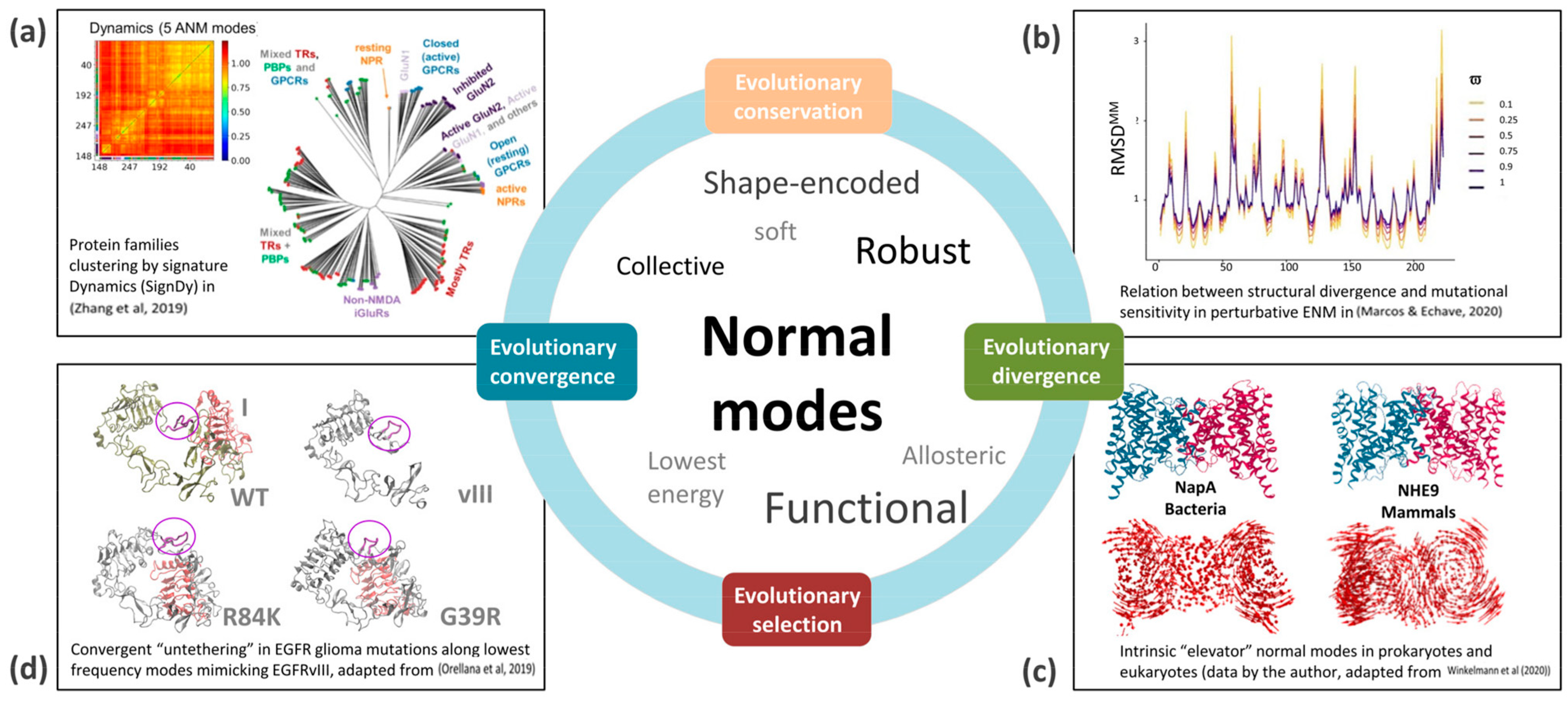
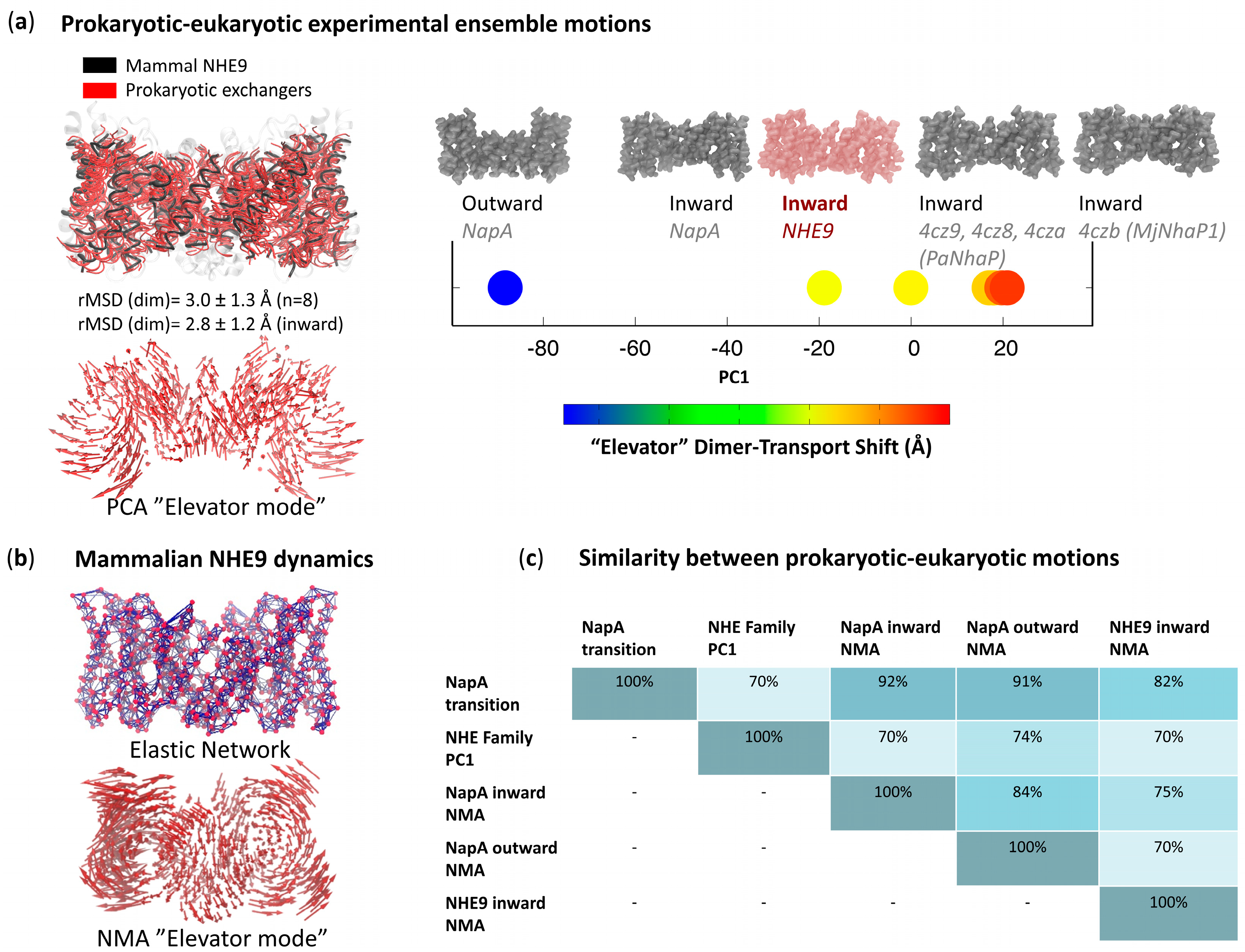
3. Lowest-Frequency Modes and Evolution
4. Examples of Evolutionary Conservation, Convergence and Divergence
Funding
Data Availability Statement
Conflicts of Interest
References
- Anfinsen, C.B.; Haber, E.; Sela, M.; White, F.H. The Kinetics of Formation of Native Ribonuclease during Oxidation of the Reduced Polypeptide Chain. Proc. Natl. Acad. Sci. USA 1961, 47, 1309–1314. [Google Scholar] [CrossRef] [PubMed]
- Daggett, V.; Fersht, A. The Present View of the Mechanism of Protein Folding. Nat. Rev. Mol. Cell Biol. 2003, 4, 497–502. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; McCammon, J.A. The Dynamics of Proteins. Sci. Am. 1986, 254, 42–51. [Google Scholar] [CrossRef] [PubMed]
- Frank, J. New Opportunities Created by Single-Particle Cryo-EM: The Mapping of Conformational Space. Biochemistry 2018, 57, 888. [Google Scholar] [CrossRef] [PubMed]
- James, L.C.; Tawfik, D.S. Conformational Diversity and Protein Evolution—A 60-Year-Old Hypothesis Revisited. Trends Biochem. Sci. 2003, 28, 361–368. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.; Kern, D. Dynamic Personalities of Proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef]
- Karplus, M.; Kuriyan, J. Molecular Dynamics and Protein Function. Proc. Natl. Acad. Sci. USA 2005, 102, 6679–6685. [Google Scholar] [CrossRef]
- Karplus, M.; McCammon, J.A. Molecular Dynamics Simulations of Biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef]
- Amaral, M.; Kokh, D.B.; Bomke, J.; Wegener, A.; Buchstaller, H.P.; Eggenweiler, H.M.; Matias, P.; Sirrenberg, C.; Wade, R.C.; Frech, M. Protein Conformational Flexibility Modulates Kinetics and Thermodynamics of Drug Binding. Nat. Commun. 2017, 8, 2276. [Google Scholar] [CrossRef]
- Tuffery, P.; Derreumaux, P. Flexibility and Binding Affinity in Protein–Ligand, Protein–Protein and Multi-Component Protein Interactions: Limitations of Current Computational Approaches. J. R. Soc. Interface 2012, 9, 20–33. [Google Scholar] [CrossRef]
- Teague, S.J. Implications of Protein Flexibility for Drug Discovery. Nat. Rev. Drug Discov. 2003, 2, 527–541. [Google Scholar] [CrossRef] [PubMed]
- Changeux, J.-P.; Edelstein, S. Conformational Selection or Induced-Fit? 50 Years of Debate Resolved. F1000 Biol. Rep. 2011, 3, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Csermely, P.; Palotai, R.; Nussinov, R. Induced Fit, Conformational Selection and Independent Dynamic Segments: An Extended View of Binding Events. Trends Biochem. Sci. 2010, 35, 539–546. [Google Scholar] [CrossRef]
- Thulasingam, M.; Orellana, L.; Nji, E.; Ahmad, S.; Rinaldo-Matthis, A.; Haeggström, J.Z. Crystal Structures of Human MGST2 Reveal Synchronized Conformational Changes Regulating Catalysis. Nat. Commun. 2021, 12, 5721. [Google Scholar] [CrossRef]
- Mhashal, A.R.; Romero-Rivera, A.; Mydy, L.S.; Cristobal, J.R.; Gulick, A.M.; Richard, J.P.; Kamerlin, S.C.L. Modeling the Role of a Flexible Loop and Active Site Side Chains in Hydride Transfer Catalyzed by Glycerol-3-Phosphate Dehydrogenase. ACS Catal. 2020, 10, 11253–11267. [Google Scholar] [CrossRef]
- Henzler-Wildman, K.A.; Thai, V.; Lei, M.; Ott, M.; Wolf-Watz, M.; Fenn, T.; Pozharski, E.; Wilson, M.A.; Petsko, G.A.; Karplus, M.; et al. Intrinsic Motions along an Enzymatic Reaction Trajectory. Nature 2007, 450, 838–844. [Google Scholar] [CrossRef] [PubMed]
- Babu, M.M.; Van Der Lee, R.; De Groot, N.S.; Gsponer, J. Intrinsically Disordered Proteins: Regulation and Disease. Curr. Opin. Struct. Biol. 2011, 21, 432–440. [Google Scholar] [CrossRef]
- Uversky, V.N. Intrinsically Disordered Proteins and Their “Mysterious” (Meta)Physics. Front. Phys. 2019, 7, 10. [Google Scholar] [CrossRef]
- Elber, R.; Karplus, M. Multiple Conformational States of Proteins: A Molecular Dynamics Analysis of Myoglobin. Science 1987, 235, 318–321. [Google Scholar] [CrossRef]
- Bahar, I.; Lezon, T.R.; Yang, L.-W.; Eyal, E. Global Dynamics of Proteins: Bridging between Structure and Function. Annu. Rev. Biophys. 2010, 39, 23–42. [Google Scholar] [CrossRef]
- Bastolla, U. Computing Protein Dynamics from Protein Structure with Elastic Network Models. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 488–503. [Google Scholar] [CrossRef]
- López-Blanco, J.R.; Chacón, P. New Generation of Elastic Network Models. Curr. Opin. Struct. Biol. 2016, 37, 46–53. [Google Scholar] [CrossRef] [PubMed]
- Sanejouand, Y.-H. Elastic Network Models: Theoretical and Empirical Foundations. Network 2011, 26, 601–616. [Google Scholar]
- Bonomi, M.; Vendruscolo, M. Determination of Protein Structural Ensembles Using Cryo-Electron Microscopy. Curr. Opin. Struct. Biol. 2019, 56, 37–450. [Google Scholar] [CrossRef] [PubMed]
- Krieger, J.M.; Sorzano, C.O.S.; Carazo, J.M.; Bahar, I. Protein Dynamics Developments for the Large Scale and CryoEM: Case Study of ProDy 2.0. Acta Cryst. D Struct. Biol. 2022, 78, 399–409. [Google Scholar] [CrossRef]
- Orellana, L. Large-Scale Conformational Changes and Protein Function: Breaking the in Silico Barrier. Front. Mol. Biosci. 2019, 6, 117. [Google Scholar] [CrossRef]
- Herzberg, G. Molecular Spectra and Molecular Structure; D. Van Nostrand Company, Inc.: Princeton, NJ, USA, 1945. [Google Scholar]
- Wilson, E.B.; Decius, J.C.; Cross, P.C. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Brooks, B. Harmonic Dynamics of Proteins: Normal Modes and Fluctuations in Bovine Pancreatic Trypsin Inhibitor. Proc. Natl. Acad. Sci. USA 1983, 80, 6571–6575. [Google Scholar] [CrossRef]
- Go, N.; Noguti, T.; Nishikawa, T. Dynamics of a Small Globular Protein in Terms of Low-Frequency Vibrational Modes. Proc. Natl. Acad. Sci. USA 1983, 80, 3696–3700. [Google Scholar] [CrossRef]
- Levitt, M.; Sander, C.; Stern, P.S. The normal modes of a protein: Native bovine pancreatic trypsin inhibitor. Int. J. Quantum Chem. 1983, 24, 181–199. [Google Scholar] [CrossRef]
- Noguti, T.; Gō, N. Collective Variable Description of Small-Amplitude Conformational Fluctuations in a Globular Protein. Nature 1982, 296, 776–778. [Google Scholar] [CrossRef]
- Tasumi, M.; Takeuchi, H.; Ataka, S.; Dwivedi, A.M.; Krimm, S. Normal Vibrations of Proteins: Glucagon. Biopolymers 1982, 21, 711–714. [Google Scholar] [CrossRef] [PubMed]
- Orozco, M.; Orellana, L.; Hospital, A.; Naganathan, A.N.; Emperador, A.; Carrillo, O.; Gelpí, J.L. Coarse-Grained Representation of Protein Flexibility. Foundations, Successes, and Shortcomings. Adv. Protein Chem. Struct. Biol. 2011, 85, 183–215. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J.; Gordon, M.; McCrum, N.G. Statistical Thermodynamics of Random Networks [and Discussion]. Proc. R. Soc. A Math. Phys. Eng. Sci. 1976, 351, 351–380. [Google Scholar] [CrossRef]
- Rouse, P.E. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys. 1953, 21, 1272. [Google Scholar] [CrossRef]
- Tirion, M. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. [Google Scholar] [CrossRef]
- Bahar, I.; Atilgan, A.R.; Erman, B. Direct Evaluation of Thermal Fluctuations in Proteins Using a Single-Parameter Harmonic Potential. Fold. Des. 1997, 2, 173–181. [Google Scholar] [CrossRef]
- Atilgan, A.R.; Durell, S.R.; Jernigan, R.L.; Demirel, M.C.; Keskin, O.; Bahar, I. Anisotropy of Fluctuation Dynamics of Proteins with an Elastic Network Model. Biophys. J. 2001, 80, 505–515. [Google Scholar] [CrossRef]
- Bauer, J.A.; Pavlovíc, J.; Bauerová-Hlinková, V. Normal Mode Analysis as a Routine Part of a Structural Investigation. Molecules 2019, 24, 3293. [Google Scholar] [CrossRef]
- Dobbins, S.E.; Lesk, V.I.; Sternberg, M.J.E. Insights into Protein Flexibility: The Relationship between Normal Modes and Conformational Change upon Protein-Protein Docking. Proc. Natl. Acad. Sci. USA 2008, 105, 10390–10395. [Google Scholar] [CrossRef]
- Petrone, P.; Pande, V.S. Can Conformational Change Be Described by Only a Few Normal Modes? Biophys. J. 2006, 90, 1583–1593. [Google Scholar] [CrossRef]
- Stein, A.; Rueda, M.; Panjkovich, A.; Orozco, M.; Aloy, P. A Systematic Study of the Energetics Involved in Structural Changes upon Association and Connectivity in Protein Interaction Networks. Structure 2011, 19, 881–889. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Song, G.; Jernigan, R.L. How Well Can We Understand Large-Scale Protein Motions Using Normal Modes of Elastic Network Models? Biophys. J. 2007, 93, 920–929. [Google Scholar] [CrossRef] [PubMed]
- Vu, H.T.; Zhang, Z.; Tehver, R.; Thirumalai, D. Plus and Minus Ends of Microtubules Respond Asymmetrically to Kinesin Binding by a Long-Range Directionally Driven Allosteric Mechanism. Sci. Adv. 2022, 8, eabn0856. [Google Scholar] [CrossRef] [PubMed]
- Kolan, D.; Fonar, G.; Samson, A.O. Elastic Network Normal Mode Dynamics Reveal the GPCR Activation Mechanism. Proteins Struct. Funct. Bioinform. 2014, 82, 579–586. [Google Scholar] [CrossRef]
- Bahar, I. On the Functional Significance of Soft Modes Predicted by Coarse-Grained Models for Membrane Proteins. J. Gen. Physiol. 2010, 135, 563–573. [Google Scholar] [CrossRef]
- Isin, B.; Rader, A.J.; Dhiman, H.K.; Klein-Seetharaman, J.; Bahar, I. Predisposition of the Dark State of Rhodopsin to Functional Changes in Structure. Proteins Struct. Funct. Bioinform. 2006, 65, 970–983. [Google Scholar] [CrossRef]
- Gerstein, M.; Krebs, W. A Database of Macromolecular Motions. Nucleic Acids Res. 1998, 26, 4280–4290. [Google Scholar] [CrossRef]
- Krebs, W.G.; Alexandrov, V.; Wilson, C.A.; Echols, N.; Yu, H.; Gerstein, M. Normal Mode Analysis of Macromolecular Motions in a Database Framework: Developing Mode Concentration as a Useful Classifying Statistic. Proteins 2002, 48, 682–695. [Google Scholar] [CrossRef]
- Tama, F.; Sanejouand, Y.H. Conformational Change of Proteins Arising from Normal Mode Calculations. Protein Eng. 2001, 14, 1–6. [Google Scholar] [CrossRef]
- Alexandrov, V. Normal Modes for Predicting Protein Motions: A Comprehensive Database Assessment and Associated Web Tool. Protein Sci. 2005, 14, 633–643. [Google Scholar] [CrossRef]
- Gur, M.; Zomot, E.; Bahar, I. Global Motions Exhibited by Proteins in Micro- to Milliseconds Simulations Concur with Anisotropic Network Model Predictions. J. Chem. Phys. 2013, 139, 121912. [Google Scholar] [CrossRef]
- Orellana, L.; Rueda, M.; Ferrer-Costa, C.; Lopez-Blanco, J.R.; Chacón, P.; Orozco, M. Approaching Elastic Network Models to Molecular Dynamics Flexibility. J. Chem. Theory Comput. 2010, 6, 2910–2923. [Google Scholar] [CrossRef] [PubMed]
- Orellana, L.; Yoluk, O.; Carrillo, O.; Orozco, M.; Lindahl, E. Prediction and Validation of Protein Intermediate States from Structurally Rich Ensembles and Coarse-Grained Simulations. Nat. Commun. 2016, 7, 12575. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Song, G.; Carriquiry, A.; Jernigan, R.L. Close Correspondence between the Motions from Principal Component Analysis of Multiple HIV-1 Protease Structures and Elastic Network Modes. Structure 2008, 16, 321–330. [Google Scholar] [CrossRef] [PubMed]
- Rueda, M.; Chacón, P.; Orozco, M. Thorough Validation of Protein Normal Mode Analysis: A Comparative Study with Essential Dynamics. Structure 2007, 15, 565–575. [Google Scholar] [CrossRef]
- Daidone, I.; Amadei, A. Essential Dynamics: Foundation and Applications. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 762–770. [Google Scholar] [CrossRef]
- Jollife, I.T.; Cadima, J. Principal Component Analysis: A Review and Recent Developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Kitao, A. Principal Component Analysis and Related Methods for Investigating the Dynamics of Biological Macromolecules. J 2022, 5, 298–317. [Google Scholar] [CrossRef]
- Rueda, M.; Ferrer-Costa, C.; Meyer, T.; Pérez, A.; Camps, J.; Hospital, A.; Gelpí, J.L.; Orozco, M. A Consensus View of Protein Dynamics. Proc. Natl. Acad. Sci. USA 2007, 104, 796–801. [Google Scholar] [CrossRef]
- Meyer, T.; D’Abramo, M.; Hospital, A.; Rueda, M.; Ferrer-Costa, C.; Pérez, A.; Carrillo, O.; Camps, J.; Fenollosa, C.; Repchevsky, D.; et al. MoDEL (Molecular Dynamics Extended Library): A Database of Atomistic Molecular Dynamics Trajectories. Structure 2010, 18, 1399–1409. [Google Scholar] [CrossRef]
- Ma, J. Usefulness and Limitations of Normal Mode Analysis in Modeling Dynamics of Biomolecular Complexes. Structure 2005, 13, 373–380. [Google Scholar] [CrossRef] [PubMed]
- Hubbard, J.H. The KAM Theorem. In Kolmogorov’s Heritage in Mathematics; Charpentier, É., Lesne, A., Nikolski, N.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 215–238. ISBN 978-3-540-36351-4. [Google Scholar]
- Kern, D.; Zuiderweg, E.R. The Role of Dynamics in Allosteric Regulation. Curr. Opin. Struct. Biol. 2003, 13, 748–757. [Google Scholar] [CrossRef] [PubMed]
- Goh, C.-S.; Milburn, D.; Gerstein, M. Conformational Changes Associated with Protein-Protein Interactions. Curr. Opin. Struct. Biol. 2004, 14, 104–109. [Google Scholar] [CrossRef]
- Hayward, S.; Kitao, A.; Go, N. Harmonic and Anharmonic Aspects in the Dynamics of BPTI: A Normal Mode Analysis and Principal Component Analysis. Protein Sci. A Publ. Protein Soc. 1994, 3, 936–943. [Google Scholar] [CrossRef] [PubMed]
- Hayward, S.; Kitao, A.; Go, N. Harmonicity and Anharmonicity in Protein Dynamics: A Normal Mode Analysis and Principal Component Analysis. Proteins 1995, 23, 177–186. [Google Scholar] [CrossRef]
- Dehouck, Y.; Bastolla, U. Why Are Large Conformational Changes Well Described by Harmonic Normal Modes? Biophys. J. 2021, 120, 5343–5354. [Google Scholar] [CrossRef]
- Kaynak, B.T.; Krieger, J.M.; Dudas, B.; Dahmani, Z.L.; Costa, M.G.S.; Balog, E.; Scott, A.L.; Doruker, P.; Perahia, D.; Bahar, I. Sampling of Protein Conformational Space Using Hybrid Simulations: A Critical Assessment of Recent Methods. Front. Mol. Biosci. 2022, 9, 832847. [Google Scholar] [CrossRef]
- Amadei, A.; Linssen, A.B.; Berendsen, H.J. Essential Dynamics of Proteins. Proteins 1993, 17, 412–425. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Li, H.; Krieger, J.M.; Bahar, I. Shared Signature Dynamics Tempered by Local Fluctuations Enables Fold Adaptability and Specificity. Mol. Biol. Evol. 2019, 36, 2053–2068. [Google Scholar] [CrossRef]
- Marcos, M.L.; Echave, J. The Variation among Sites of Protein Structure Divergence Is Shaped by Mutation and Scaled by Selection. Curr. Res. Struct. Biol. 2020, 2, 156–163. [Google Scholar] [CrossRef]
- Winkelmann, I.; Matsuoka, R.; Meier, P.F.; Shutin, D.; Zhang, C.; Orellana, L.; Sexton, R.; Landreh, M.; Robinson, C.V.; Beckstein, O.; et al. Structure and Elevator Mechanism of the Mammalian Sodium/Proton Exchanger NHE9. EMBO J. 2020, 39, 4541–4559. [Google Scholar] [CrossRef] [PubMed]
- Orellana, L.; Thorne, A.H.; Lema, R.; Gustavsson, J.; Parisian, A.D.; Hospital, A.; Cordeiro, T.N.; Bernadó, P.; Scott, A.M.; Brun-Heath, I.; et al. Oncogenic Mutations at the EGFR Ectodomain Structurally Converge to Remove a Steric Hindrance on a Kinase-Coupled Cryptic Epitope. Proc. Natl. Acad. Sci. USA 2019, 116, 10009–10018. [Google Scholar] [CrossRef]
- Muñoz, M.M.; Price, S.A. The Future Is Bright for Evolutionary Morphology and Biomechanics in the Era of Big Data. Integr. Comp. Biol. 2019, 59, 599–603. [Google Scholar] [CrossRef] [PubMed]
- Sikosek, T.; Chan, H.S. Biophysics of Protein Evolution and Evolutionary Protein Biophysics. J. R. Soc. Interface 2014, 11, 20140419. [Google Scholar] [CrossRef] [PubMed]
- Fuglebakk, E.; Tiwari, S.P.; Reuter, N. Comparing the Intrinsic Dynamics of Multiple Protein Structures Using Elastic Network Models. Biochim. Biophys. Acta—Gen. Subj. 2015, 1850, 911–922. [Google Scholar] [CrossRef] [PubMed]
- Bordin, N.; Sillitoe, I.; Lees, J.G.; Orengo, C. Tracing Evolution Through Protein Structures: Nature Captured in a Few Thousand Folds. Front. Mol. Biosci. 2021, 8, 668184. [Google Scholar] [CrossRef]
- Chothia, C.; Lesk, A.M. The Relation between the Divergence of Sequence and Structure in Proteins. EMBO J. 1986, 5, 823–826. [Google Scholar] [CrossRef]
- Kuhlman, B.; Baker, D. Native Protein Sequences Are Close to Optimal for Their Structures. Proc. Natl. Acad. Sci. USA 2000, 97, 10383–10388. [Google Scholar] [CrossRef]
- Koehl, P.; Levitt, M. Protein Topology and Stability Define the Space of Allowed Sequences. Proc. Natl. Acad. Sci. USA 2002, 99, 1280–1285. [Google Scholar] [CrossRef]
- Zheng, W.; Brooks, B.R.; Thirumalai, D. Low-Frequency Normal Modes That Describe Allosteric Transitions in Biological Nanomachines Are Robust to Sequence Variations. Proc. Natl. Acad. Sci. USA 2006, 103, 7664–7669. [Google Scholar] [CrossRef]
- Hensen, U.; Meyer, T.; Haas, J.; Rex, R.; Vriend, G.; Grubmüller, H. Exploring Protein Dynamics Space: The Dynasome as the Missing Link between Protein Structure and Function. PLoS ONE 2012, 7, e33931. [Google Scholar] [CrossRef] [PubMed]
- Narunsky, A.; Nepomnyachiy, S.; Ashkenazy, H.; Kolodny, R.; Ben-Tal, N. ConTemplate Suggests Possible Alternative Conformations for a Query Protein of Known Structure. Structure 2015, 23, 2162–2170. [Google Scholar] [CrossRef] [PubMed]
- Zsolyomi, F.; Ambrus, V.; Fuxreiter, M. Patterns of Dynamics Comprise a Conserved Evolutionary Trait. J. Mol. Biol. 2020, 432, 497–507. [Google Scholar] [CrossRef] [PubMed]
- Bastolla, U.; Dehouck, Y.; Echave, J. What Evolution Tells Us about Protein Physics, and Protein Physics Tells Us about Evolution. Curr. Opin. Struct. Biol. 2017, 42, 59–66. [Google Scholar] [CrossRef] [PubMed]
- Liberles, D.A.; Teichmann, S.A.; Bahar, I.; Bastolla, U.; Bloom, J.; Bornberg-Bauer, E.; Colwell, L.J.; De Koning, A.P.J.; Dokholyan, N.V.; Echave, J.; et al. The Interface of Protein Structure, Protein Biophysics, and Molecular Evolution. Protein Sci. 2012, 21, 769–785. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, S.P.; Reuter, N. Conservation of Intrinsic Dynamics in Proteins—What Have Computational Models Taught Us? Curr. Opin. Struct. Biol. 2018, 50, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Keskin, O.; Jernigan, R.L.; Bahar, I. Proteins with Similar Architecture Exhibit Similar Large-Scale Dynamic Behavior. Biophys. J. 2000, 78, 2093–2106. [Google Scholar] [CrossRef]
- Leo-Macias, A.; Lopez-Romero, P.; Lupyan, D.; Zerbino, D.; Ortiz, A.R. An Analysis of Core Deformations in Protein Superfamilies. Biophys. J. 2005, 88, 1291–1299. [Google Scholar] [CrossRef]
- Velázquez-Muriel, J.A.; Rueda, M.; Cuesta, I.; Pascual-Montano, A.; Orozco, M.; Carazo, J.-M. Comparison of Molecular Dynamics and Superfamily Spaces of Protein Domain Deformation. BMC Struct. Biol. 2009, 9, 6. [Google Scholar] [CrossRef]
- Leo-Macias, A.; Lopez-Romero, P.; Lupyan, D.; Zerbino, D.; Ortiz, A.R. Core Deformations in Protein Families: A Physical Perspective. Biophys. Chem. 2005, 115, 125–128. [Google Scholar] [CrossRef]
- Maguid, S.; Fernandez-Alberti, S.; Ferrelli, L.; Echave, J. Exploring the Common Dynamics of Homologous Proteins. Application to the Globin Family. Biophys. J. 2005, 89, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Maguid, S.; Fernández-Alberti, S.; Parisi, G.; Echave, J. Evolutionary Conservation of Protein Backbone Flexibility. J. Mol. Evol. 2006, 63, 448–457. [Google Scholar] [CrossRef] [PubMed]
- Skjaerven, L.; Yao, X.Q.; Scarabelli, G.; Grant, B.J. Integrating Protein Structural Dynamics and Evolutionary Analysis with Bio3D. BMC Bioinform. 2014, 15, 399. [Google Scholar] [CrossRef]
- Franzosa, E.A.; Xia, Y. Structural Determinants of Protein Evolution Are Context-Sensitive at the Residue Level. Mol. Biol. Evol. 2009, 26, 2387–2395. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.-T.; del Valle Marcos, M.L.; Hwang, J.-K.; Echave, J. A Mechanistic Stress Model of Protein Evolution Accounts for Site-Specific Evolutionary Rates and Their Relationship with Packing Density and Flexibility. BMC Evol. Biol. 2014, 14, 78. [Google Scholar] [CrossRef]
- Marsh, J.A.; Teichmann, S.A. Parallel Dynamics and Evolution: Protein Conformational Fluctuations and Assembly Reflect Evolutionary Changes in Sequence and Structure. BioEssays 2014, 36, 209–218. [Google Scholar] [CrossRef]
- Dong, Z.; Zhou, H.; Tao, P. Combining Protein Sequence, Structure, and Dynamics: A Novel Approach for Functional Evolution Analysis of PAS Domain Superfamily. Protein Sci. 2018, 27, 421–430. [Google Scholar] [CrossRef]
- Liu, Y.; Bahar, I. Sequence Evolution Correlates with Structural Dynamics. Mol. Biol. Evol. 2012, 29, 2253–2263. [Google Scholar] [CrossRef]
- Campitelli, P.; Modi, T.; Kumar, S.; Ozkan, S.B. The Role of Conformational Dynamics and Allostery in Modulating Protein Evolution. Annu. Rev. Biophys. 2020, 49, 267–288. [Google Scholar] [CrossRef]
- Nevin Gerek, Z.; Kumar, S.; Banu Ozkan, S. Structural Dynamics Flexibility Informs Function and Evolution at a Proteome Scale. Evol. Appl. 2013, 6, 423–433. [Google Scholar] [CrossRef]
- Sayılgan, J.F.; Haliloğlu, T.; Gönen, M. Protein Dynamics Analysis Reveals That Missense Mutations in Cancer-Related Genes Appear Frequently on Hinge-Neighboring Residues. Proteins Struct. Funct. Bioinform. 2019, 87, 512–519. [Google Scholar] [CrossRef] [PubMed]
- Ponzoni, L.; Bahar, I. Structural Dynamics Is a Determinant of the Functional Significance of Missense Variants. Proc. Natl. Acad. Sci. USA 2018, 115, 4164–4169. [Google Scholar] [CrossRef]
- Frappier, V.; Najmanovich, R.J. A Coarse-Grained Elastic Network Atom Contact Model and Its Use in the Simulation of Protein Dynamics and the Prediction of the Effect of Mutations. PLoS Comput. Biol. 2014, 10, e1003569. [Google Scholar] [CrossRef]
- Banerjee, A.; Bahar, I. Structural Dynamics Predominantly Determine the Adaptability of Proteins to Amino Acid Deletions. Int. J. Mol. Sci. 2023, 24, 8450. [Google Scholar] [CrossRef]
- Echave, J. Evolutionary Divergence of Protein Structure: The Linearly Forced Elastic Network Model. Chem. Phys. Lett. 2008, 457, 413–416. [Google Scholar] [CrossRef]
- Echave, J.; Fernández, F.M. A Perturbative View of Protein Structural Variation. Proteins Struct. Funct. Bioinform. 2010, 78, 173–180. [Google Scholar] [CrossRef]
- Echave, J. Why Are the Low-Energy Protein Normal Modes Evolutionarily Conserved? Pure Appl. Chem. 2012, 84, 1931–1937. [Google Scholar] [CrossRef]
- Tang, Q.-Y.; Kaneko, K. Dynamics-Evolution Correspondence in Protein Structures. Phys. Rev. Lett. 2021, 127, 098103. [Google Scholar] [CrossRef]
- Dos Santos, H.G.; Klett, J.; Méndez, R.; Bastolla, U. Characterizing Conformation Changes in Proteins through the Torsional Elastic Response. Biochim. Biophys. Acta 2013, 1834, 836–846. [Google Scholar] [CrossRef]
- Haliloglu, T.; Bahar, I. Adaptability of Protein Structures to Enable Functional Interactions and Evolutionary Implications. Curr. Opin. Struct. Biol. 2015, 35, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Doruker, P.; Kaynak, B.; Zhang, S.; Krieger, J.; Li, H.; Bahar, I. Intrinsic Dynamics Is Evolutionarily Optimized to Enable Allosteric Behavior. Curr. Opin. Struct. Biol. 2020, 62, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Jia, K.; Kilinc, M.; Jernigan, R.L. Functional Protein Dynamics Directly from Sequences. J. Phys. Chem. B 2023, 127, 1914–1921. [Google Scholar] [CrossRef] [PubMed]
- Nowell, P.C. The Clonal Evolution of Tumor Cell Populations. Science 1976, 194, 23–28. [Google Scholar] [CrossRef]
- Hedges, S.B.; Chen, H.; Kumar, S.; Wang, D.Y.; Thompson, A.S.; Watanabe, H. A Genomic Timescale for the Origin of Eukaryotes. BMC Evol. Biol. 2001, 1, 4. [Google Scholar] [CrossRef] [PubMed]
- Long, X.; Xue, H.; Wong, J.T.-F. Descent of Bacteria and Eukarya From an Archaeal Root of Life. Evol. Bioinform. Online 2020, 16, 1176934320908267. [Google Scholar] [CrossRef]
- Drew, D.; Boudker, O. Shared Molecular Mechanisms of Membrane Transporters. Annu. Rev. Biochem. 2016, 85, 543–572. [Google Scholar] [CrossRef] [PubMed]
- Qureshi, A.A.; Suades, A.; Matsuoka, R.; Brock, J.; McComas, S.E.; Nji, E.; Orellana, L.; Claesson, M.; Delemotte, L.; Drew, D. The Molecular Basis for Sugar Import in Malaria Parasites. Nature 2020, 578, 321–325. [Google Scholar] [CrossRef]
- Howard, R.J. Elephants in the Dark: Insights and Incongruities in Pentameric Ligand-Gated Ion Channel Models. J. Mol. Biol. 2021, 433, 167128. [Google Scholar] [CrossRef]
- Mhashal, A.R.; Yoluk, O.; Orellana, L. Exploring the Conformational Impact of Novel Glycine Receptor Mutations through Coarse-Grained Analysis and Atomistic Simulations. Front. Mol. Biosci. 2022, 9, 890851. [Google Scholar] [CrossRef]
- Ponzoni, L.; Peñaherrera, D.A.; Oltvai, Z.N.; Bahar, I. Rhapsody: Predicting the Pathogenicity of Human Missense Variants. Bioinformatics 2020, 36, 3084–3092. [Google Scholar] [CrossRef]
- Orellana, L. Convergence of EGFR Glioblastoma Mutations: Evolution and Allostery Rationalizing Targeted Therapy. Mol. Cell. Oncol. 2019, 6, e1630798. [Google Scholar] [CrossRef] [PubMed]
- Orellana, L.; Hospital, A.; Orozco, M. Oncogenic Mutations of the EGF-Receptor Ectodomain Reveal an Unexpected Mechanism for Ligand-Independent Activation. bioRxiv 2014. [Google Scholar] [CrossRef]
- Uribe, M.L.; Marrocco, I.; Yarden, Y. EGFR in Cancer: Signaling Mechanisms, Drugs, and Acquired Resistance. Cancers 2021, 13, 2748. [Google Scholar] [CrossRef] [PubMed]
- Lai, J.; Jin, J.; Kubelka, J.; Liberles, D.A. A Phylogenetic Analysis of Normal Modes Evolution in Enzymes and Its Relationship to Enzyme Function. J. Mol. Biol. 2012, 422, 442–459. [Google Scholar] [CrossRef]
- Petrovic, D.; Risso, V.A.; Kamerlin, S.C.L.; Sanchez-Ruiz, J.M. Conformational Dynamics and Enzyme Evolution. J. R. Soc. Interface 2018, 15, 20180330. [Google Scholar] [CrossRef]
- Narayanan, C.; Bernard, D.N.; Bafna, K.; Gagné, D.; Chennubhotla, C.S.; Doucet, N.; Agarwal, P.K. Conservation of Dynamics Associated with Biological Function in an Enzyme Superfamily. Structure 2018, 26, 426–436.e3. [Google Scholar] [CrossRef]
- Ramanathan, A.; Agarwal, P.K. Evolutionarily Conserved Linkage between Enzyme Fold, Flexibility, and Catalysis. PLoS Biol. 2011, 9, e1001193. [Google Scholar] [CrossRef]
- Carnevale, V.; Raugei, S.; Micheletti, C.; Carloni, P. Convergent Dynamics in the Protease Enzymatic Superfamily. J. Am. Chem. Soc. 2006, 128, 9766–9772. [Google Scholar] [CrossRef]
- Campbell, E.C.; Correy, G.J.; Mabbitt, P.D.; Buckle, A.M.; Tokuriki, N.; Jackson, C.J. Laboratory Evolution of Protein Conformational Dynamics. Curr. Opin. Struct. Biol. 2018, 50, 49–57. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly Accurate Protein Structure Prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Lin, Z.; Akin, H.; Rao, R.; Hie, B.; Zhu, Z.; Lu, W.; Smetanin, N.; Verkuil, R.; Kabeli, O.; Shmueli, Y.; et al. Evolutionary-Scale Prediction of Atomic-Level Protein Structure with a Language Model. Science 2023, 379, 1123–1130. [Google Scholar] [CrossRef] [PubMed]
- Mayr, E. The Objects of Selection. Proc. Natl. Acad. Sci. USA 1997, 94, 2091–2094. [Google Scholar] [CrossRef] [PubMed]
| Identity | Similarity | TM-Score | |
|---|---|---|---|
| NHE9—NapA | 22% | 42% | 0.82 |
| Overlap NHE9—NapA NMA | 75% | ||
| Overlap NHE9—NapA X-ray transition | 82% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orellana, L. Are Protein Shape-Encoded Lowest-Frequency Motions a Key Phenotype Selected by Evolution? Appl. Sci. 2023, 13, 6756. https://doi.org/10.3390/app13116756
Orellana L. Are Protein Shape-Encoded Lowest-Frequency Motions a Key Phenotype Selected by Evolution? Applied Sciences. 2023; 13(11):6756. https://doi.org/10.3390/app13116756
Chicago/Turabian StyleOrellana, Laura. 2023. "Are Protein Shape-Encoded Lowest-Frequency Motions a Key Phenotype Selected by Evolution?" Applied Sciences 13, no. 11: 6756. https://doi.org/10.3390/app13116756
APA StyleOrellana, L. (2023). Are Protein Shape-Encoded Lowest-Frequency Motions a Key Phenotype Selected by Evolution? Applied Sciences, 13(11), 6756. https://doi.org/10.3390/app13116756






