Case Study on the Effect of Delay-Time Differences between Columns during Blasting Demolition of RC Structures with a Small Height-to-Width Ratio
Abstract
:1. Introduction
2. Project Overview
3. Numerical Simulation Analysis of Demolition by Blasting
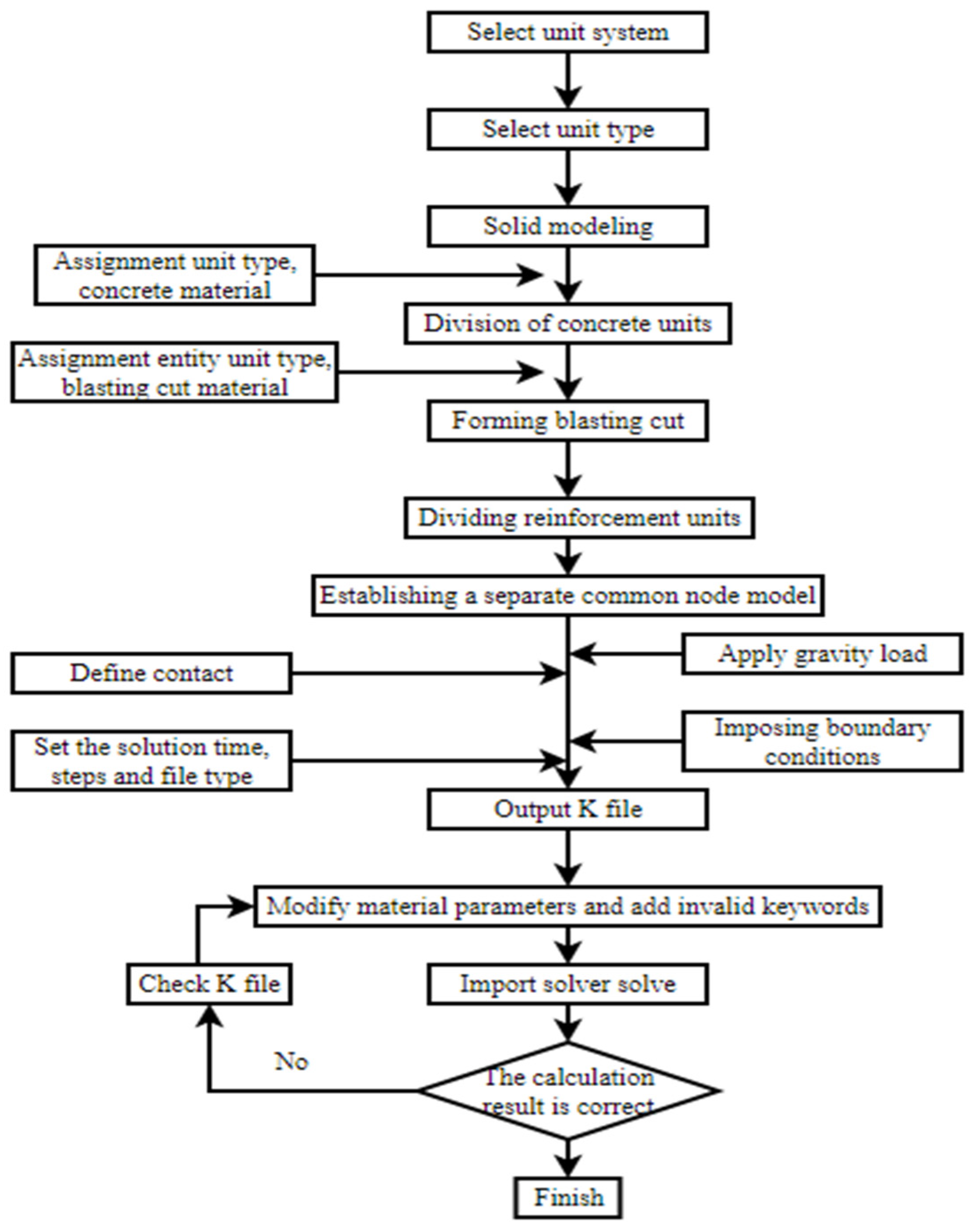
3.1. Structural Modeling Analysis
3.2. Collapse Process Comparison
3.3. Recoil Distance and Burst Stack Comparison
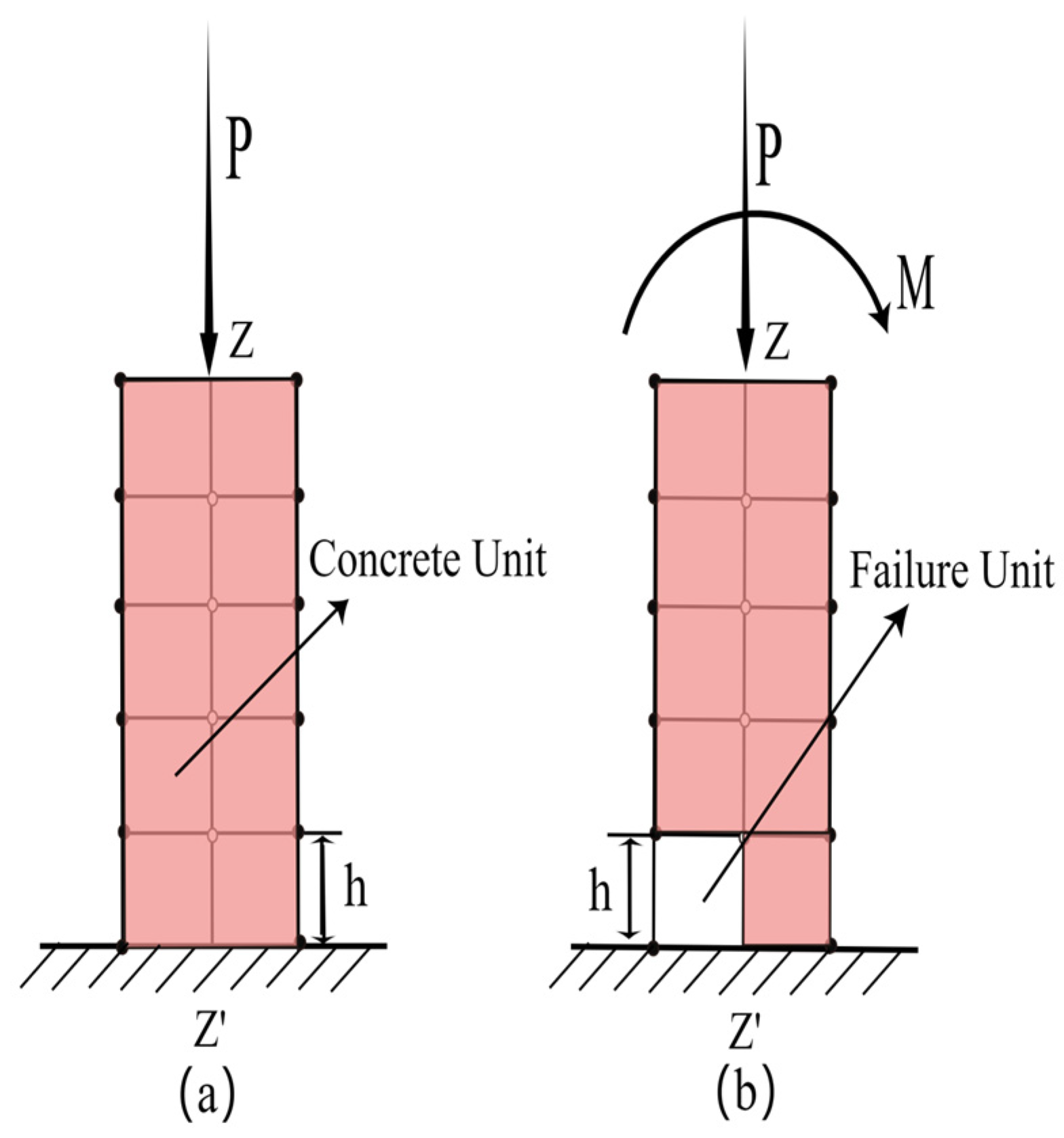
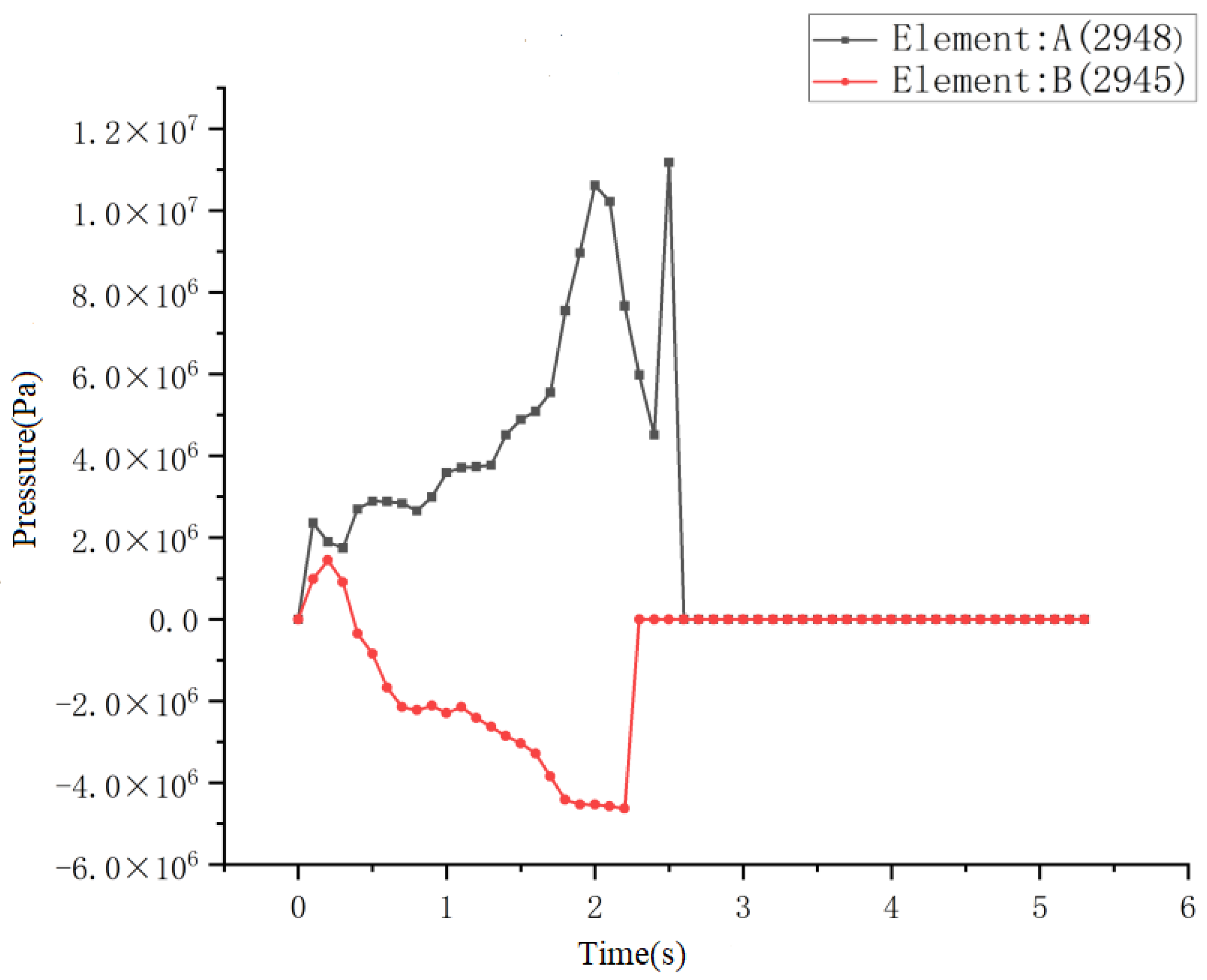
3.4. Force Analysis of Concrete in the Support Area
4. Results and Discussion
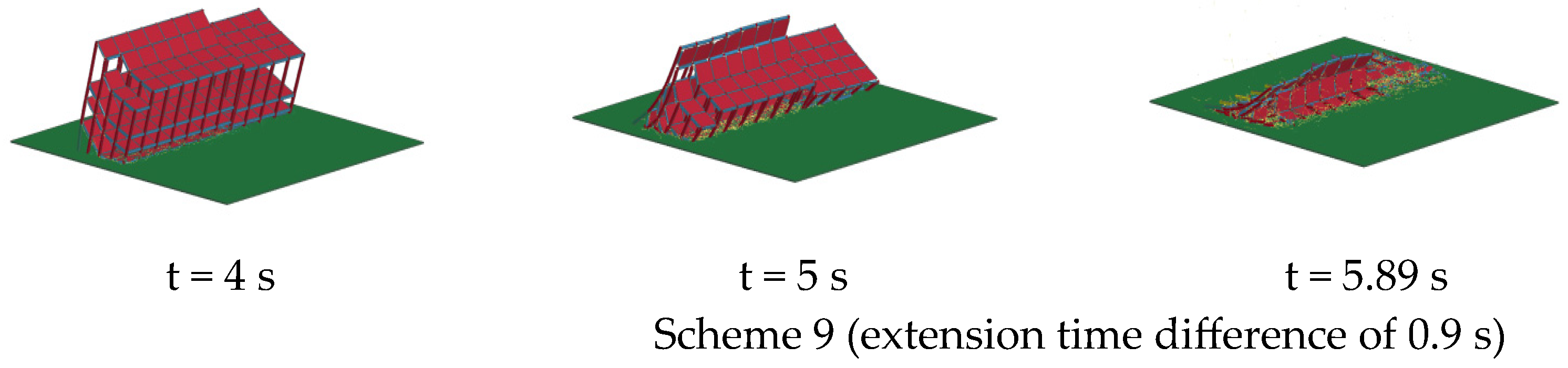
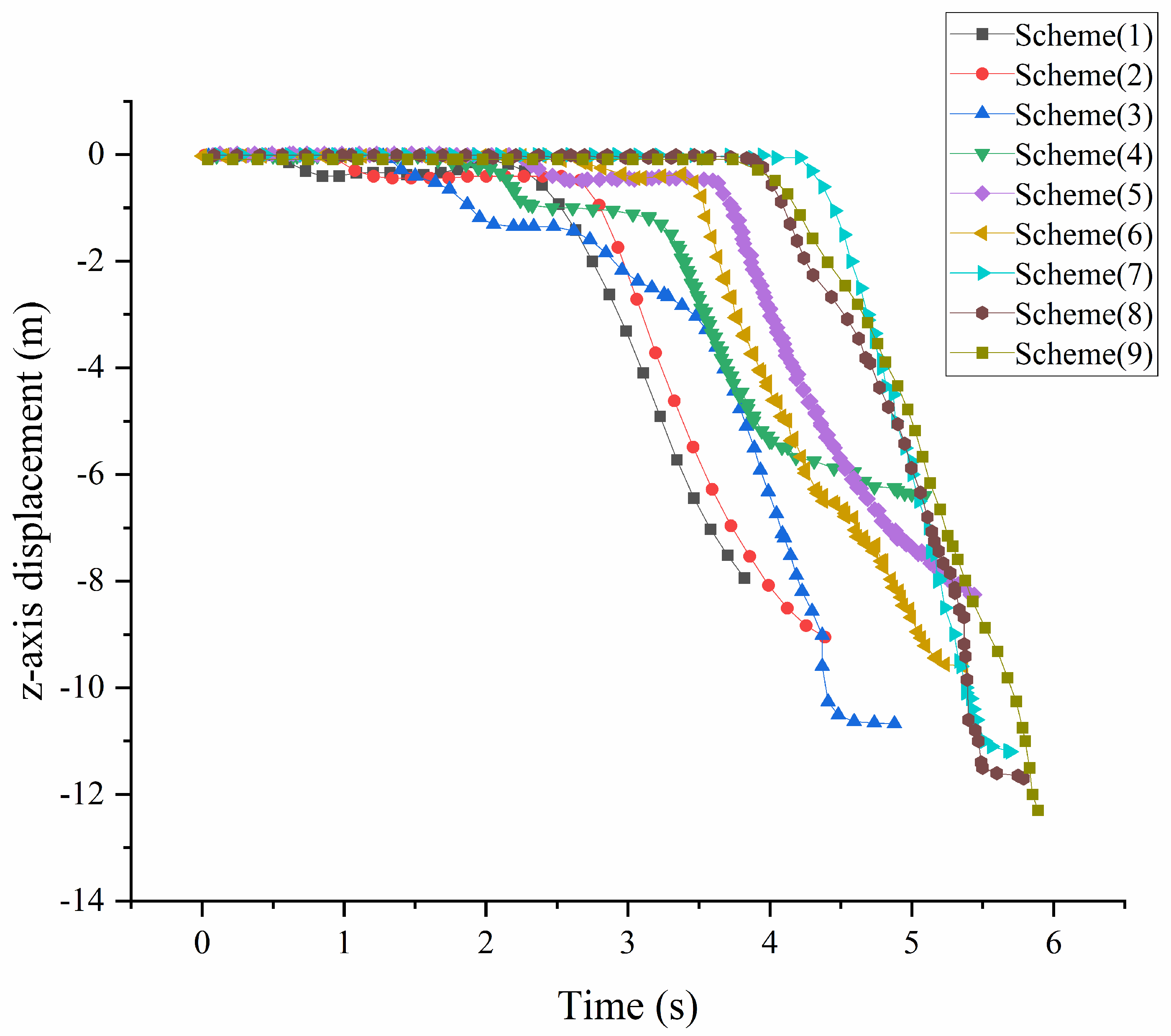
4.1. Effect of Different Extension Time Differences on the Collapse Process
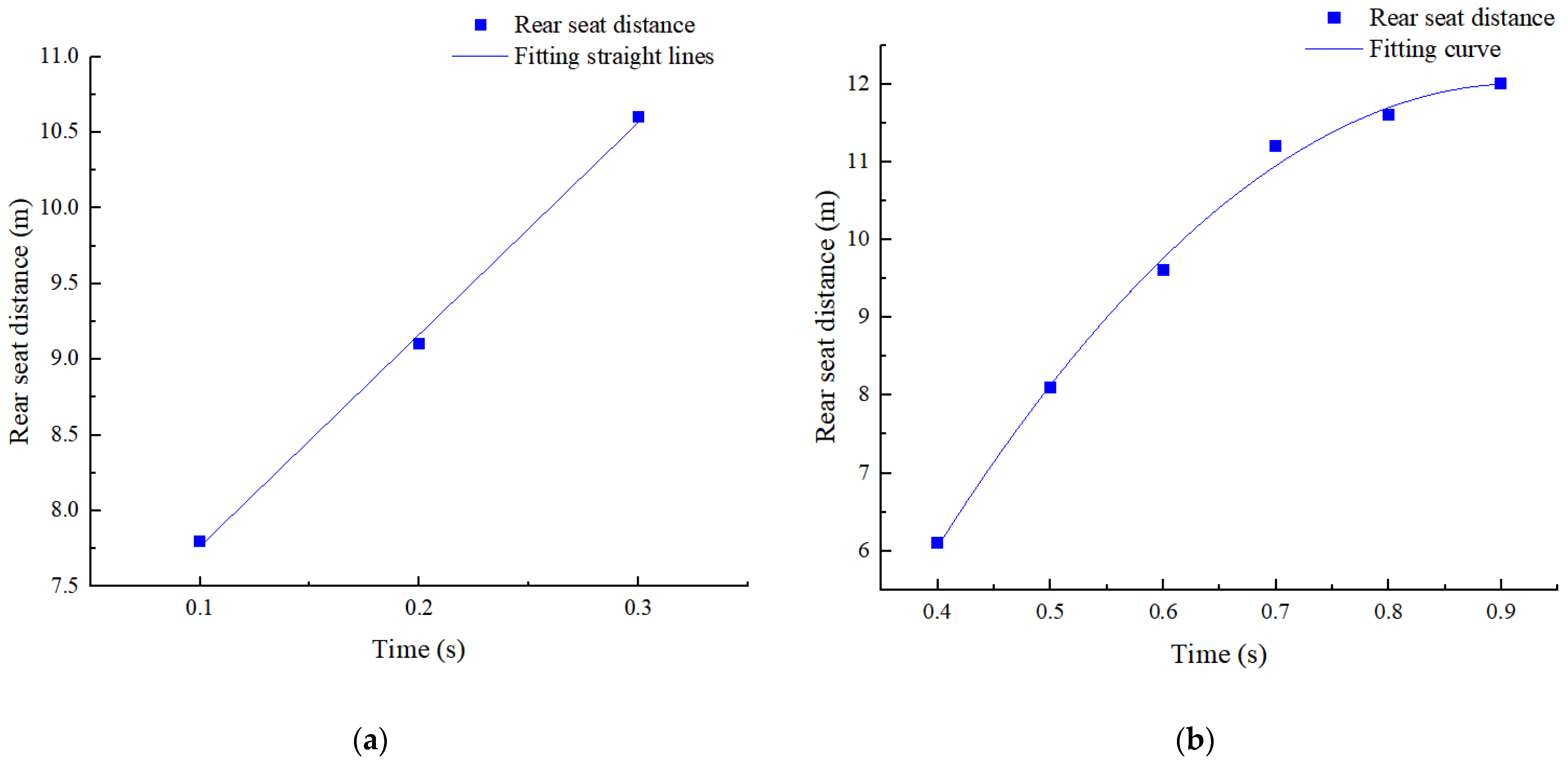
4.2. Effect of Different Extension Time Differences on the Recoil Distance
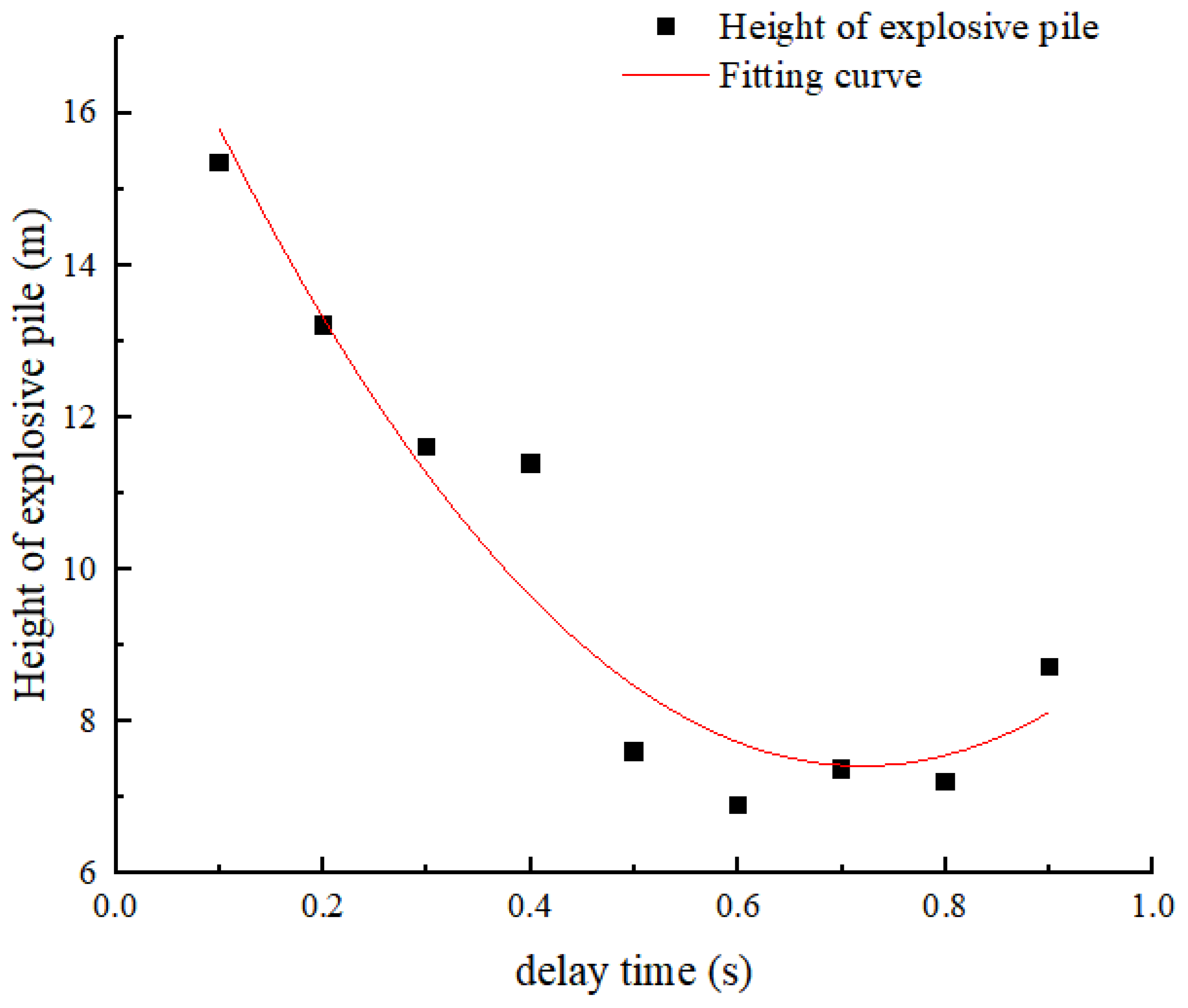
4.3. Effect of Different Extension Time Differences on the Height of the Burst Pile
4.4. Optimal Solution Selection for Intercolumn Delay-Time Differences
5. Conclusions
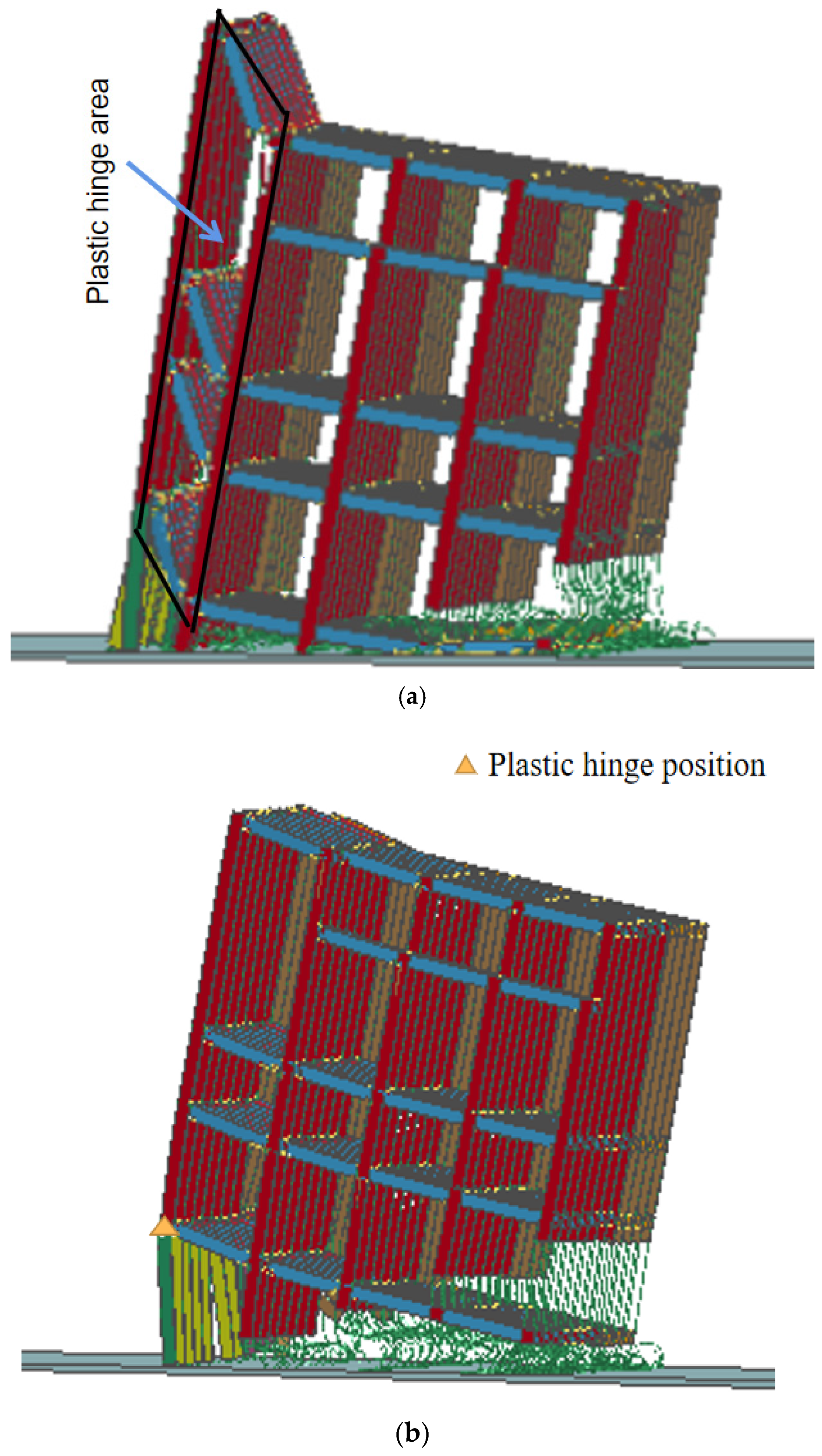
- The structural plastic hinge is formed at the end of the latter span beam at a time difference of 0.1~0.3 s, moves down to the top of the rear row of the first-floor columns at a time difference of 0.4~0.8 s, and finally moves to the end of each span beam at a time difference of 0.9 s. The position of the structural orientation axis is influenced by the position of the plastic hinge, which is located at the bottom of the rear column at time differences of 0.1~0.3 s and 0.9 s, and is in the same position as the plastic hinge at time differences of 0.4~0.8 s. The blasting effect is better when the plastic hinge of the structure is formed at the top of the rear layer of the columns;
- The recoil distance shows a linear growth trend of at the time difference of 0.1~0.3 s, plunges between 0.3~0.4 s, and shows a parabolic growth trend of at 0.4~0.9 s. For the small-aspect-ratio structure, the recoil distance is smaller at the time difference of 0.4~0.5 s for the extension;
- The height of the burst pile is , which represents a parabolic growth pattern. In a time difference between 0.5 s to 0.8 s, the height of the burst pile is relatively low;
- For small-aspect-ratio reinforced concrete structures, a reasonable range for the intercolumn delay-time difference is 400~500 ms, and the optimal solution is 400 ms. The actual selected blasting solution has an intercolumn extension time difference of 500 ms, which is consistent with the numerical simulation results.
- Reinforced concrete structures were studied using the separated common node model. Thus, the differences in the mechanical properties of concrete and two steel materials are observed. However, the distribution of the vertical reinforcement and hoop reinforcement makes it difficult to maintain consistency with the actual project. Therefore, a more suitable model for the study of concrete material properties will require further research;
- The ground is assumed to be a rigid body that does not allow for the analysis of the building’s grounding vibrations caused by blast demolitions. In future simulations, the ground can be modelled as a suitable elastoplastic material;
- A blast incision is formed by forcing the concrete units to fail directly, which does not reflect the damage and vibration to the surrounding structure when explosives are detonated inside the concrete. Therefore, the research and development on blasting materials using finite element software can be further strengthened.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aslam, M.S.; Huang, B.; Cui, L. Review of construction and demolition waste management in China and USA. J. Environ. Manag. 2020, 264, 110445. [Google Scholar] [CrossRef] [PubMed]
- Chu, H.; Xu, P.; Ye, H. Collapse process and load-bearing process of reinforced concrete chimney during blasting demolition. Vib. Shock 2015, 34, 183–186+198. [Google Scholar]
- Ming, Y.; Dai, Q.; Zhao, M. Cause analysis and disposal of explosive demolition failure of two 45 m high cooling tower. Blasting 2016, 33, 118–123. [Google Scholar]
- Laszlo, R.; Radeanu, C.; Ilici, S.; Grecea, M.; Levente, M. Technical and safety aspects at the demolition by blasting works of a cooling tower with a high of 72.00 m. MATEC Web Conf. 2020, 305, 72. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, J.; Li, J.; Kong, F.; Fan, J. Analysis of Vibration Attenuation and Energy Consumption of Blasting Demolition Chimney: A Case Study. Teh. Vjesn.-Tech. Gaz. 2020, 27, 826–834. [Google Scholar]
- Bažant, Z.P.; Verdure, M. Mechanics of Progressive Collapse: Learning from World Trade Center and Building Demolitions. J. Eng. Mech. 2007, 133, 308–319. [Google Scholar] [CrossRef]
- Sun, J.; Jia, Y.; Yao, Y.; Xie, X. Experimental investigation of stress transients of blasted RC columns in the blasting demolition of buildings. Eng. Struct. 2020, 210, 110417. [Google Scholar] [CrossRef]
- Wang, S.; Gong, M. Numerical Simulation Study on Blasting Demolition of 84 m Tall Building. IOP Conf. Ser. Earth Environ. Sci. 2019, 252, 022145. [Google Scholar] [CrossRef]
- Isobe, D.; Jiang, R. Explosive demolition planning of building structures using key element index. J. Build. Eng. 2022, 59, 104935. [Google Scholar] [CrossRef]
- Sun, J.; Jia, Y.; Xie, X.; Yao, Y. Design criteria for the folding implosion of high-rise RC buildings. Eng. Struct. 2021, 233, 111933. [Google Scholar] [CrossRef]
- Kangda, M.Z.; Bakre, S. The Effect of LRB Parameters on Structural Responses for Blast and Seismic Loads. Arab. J. Sci. Eng. 2018, 43, 1761–1776. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, H.; Wang, J.; Tian, N. Finite element analyses of constitutive models performance in the simulation of blast-induced rock cracks. Comput. Geotech. 2021, 135, 104172. [Google Scholar] [CrossRef]
- Jia, H.; Tian, S. Research and Application of a Reinforced Concrete Simplified Model. Adv. Civ. Eng. 2021, 2021, 8861831. [Google Scholar] [CrossRef]
- Min, G.; Fukuda, D.; Cho, S. 3D Numerical Analysis Method for Simulating Collapse Behavior of RC Structures by Hybrid FEM/DEM. Appl. Sci. 2022, 12, 3073. [Google Scholar] [CrossRef]
- Yan, B.; Liu, M.; Meng, Q.; Li, Y.; Deng, S.; Liu, T. Study on the Vibration Variation of Rock Slope Based on Numerical Simulation and Fitting Analysis. Appl. Sci. 2022, 12, 4208. [Google Scholar] [CrossRef]
- Zhai, X.; Wu, S.; Li, H.; Wang, K.; Wang, W.; Song, X. Experimental and numerical investigation on dynamic behaviors of the concrete wall in underground coal mine with hydraulic blasting demolition. J. Vibroeng. 2017, 19, 2043–2062. [Google Scholar] [CrossRef] [Green Version]
- Chai, Y.; Luo, N.; Zhang, H.; Duan, Y.; Sun, W.; Dong, J. Application of controlled blasting demolition technology in ultra-high coaxial thin-walled steel inner cylinder reinforced concrete chimney. Case Stud. Constr. Mater. 2023, 18, e01936. [Google Scholar]
- Zhou, X. Simulation Calculation of the Collapse Process of High-Rise Steel Structure Energy-Forming Cutting Blasting Demolition. Wirel. Commun. Mob. Comput. 2022, 2022, 3735006. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, Z.; Yao, E.; Liu, M.; Rao, Y. Investigation and Control of the Blasting-Induced Ground Vibration under Cold Condition. Shock Vib. 2021, 2021, 6660729. [Google Scholar] [CrossRef]
- Singh, C.P.; Agrawal, H.; Mishra, A.K. A study on influence of blast-induced ground vibration in dragline bench blasting using signature hole analysis. Arab. J. Geosci. 2020, 13, 522. [Google Scholar] [CrossRef]
- Song, W.; He, P. Safety regulations for blasting (GB 6722-2014) Released. Eng. Blasting 2015, 21, 62. [Google Scholar]
- Yue, H.Z.; Yu, C.; Li, H.B.; Zhou, C.B.; Chen, S.H.; Shao, Z.S. The Effect of Blast-Hole Arrangement, Delay Time, and Decoupling Charge on Rock Damage and Vibration Attenuation in Multihole Blasting. Shock Vib. 2022, 2022, 2110160. [Google Scholar] [CrossRef]
- Cai, R.; Li, Y.; Zhang, C.; Cao, H.; Qi, H.; Mao, J. Size effect on reinforced concrete slabs under direct contact explosion. Eng. Struct. 2022, 252, 113656. [Google Scholar] [CrossRef]
- Fouad, M.; Fayed, M.N.; Hamdy, G.A.; Abdelrahman, A. Effect of Blast Loading on Seismically Detailed RC Columns and Buildings. Civ. Eng. J. 2021, 7, 1406–1425. [Google Scholar] [CrossRef]
- Peerasak, A.; Kazunori, F.; Piti, S. Feasibility Study on Novel Blasting Technique Using Linear-Shaped Charges to Cut Reinforcing Steel Bars in Reinforced Concrete Members. Pract. Period. Struct. Des. Constr. 2023, 28, 04023013. [Google Scholar]
- Song, Z.; Ke, M.; Liu, X. Identifying Delay Time of Detonator for a Millisecond Blasting. Adv. Civ. Eng. 2021, 2021, 5592696. [Google Scholar]
- Ji, C.; Gao, F.; Li, X.; Yu, Y.; Cheng, L. Numerical analysis of vibration-isolating effect of vibration-isolating slot under buried pipe subjected to millisecond blasting. Vibroeng. Procedia 2018, 21, 32–37. [Google Scholar] [CrossRef] [Green Version]
- Gao, B.; Wu, J.; Zhao, R.; Feng, X.; Wang, Z. Residual seismic resistance of CFDST columns after a close-in explosion: Experimental study. Structures 2023, 48, 1082–1101. [Google Scholar] [CrossRef]
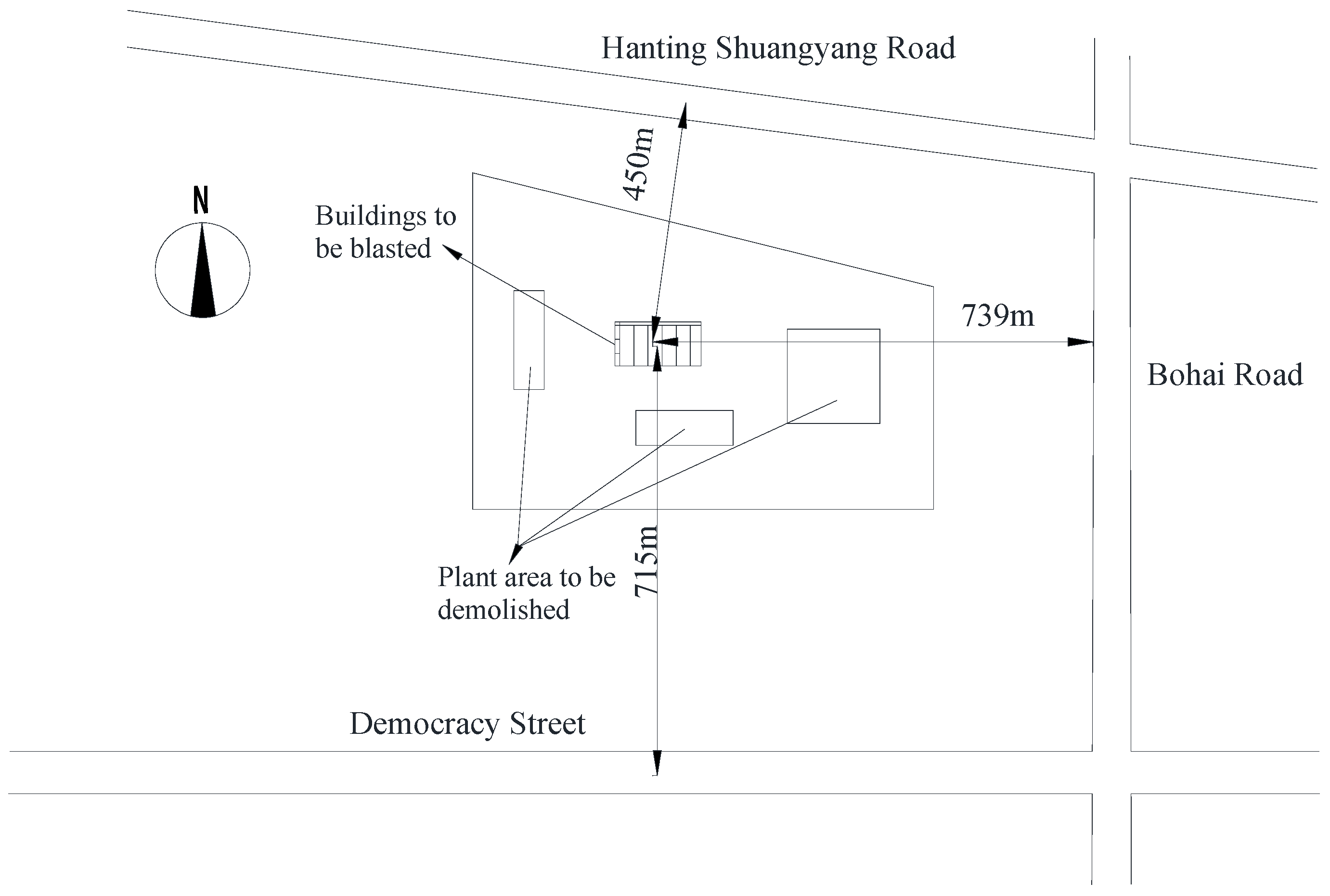
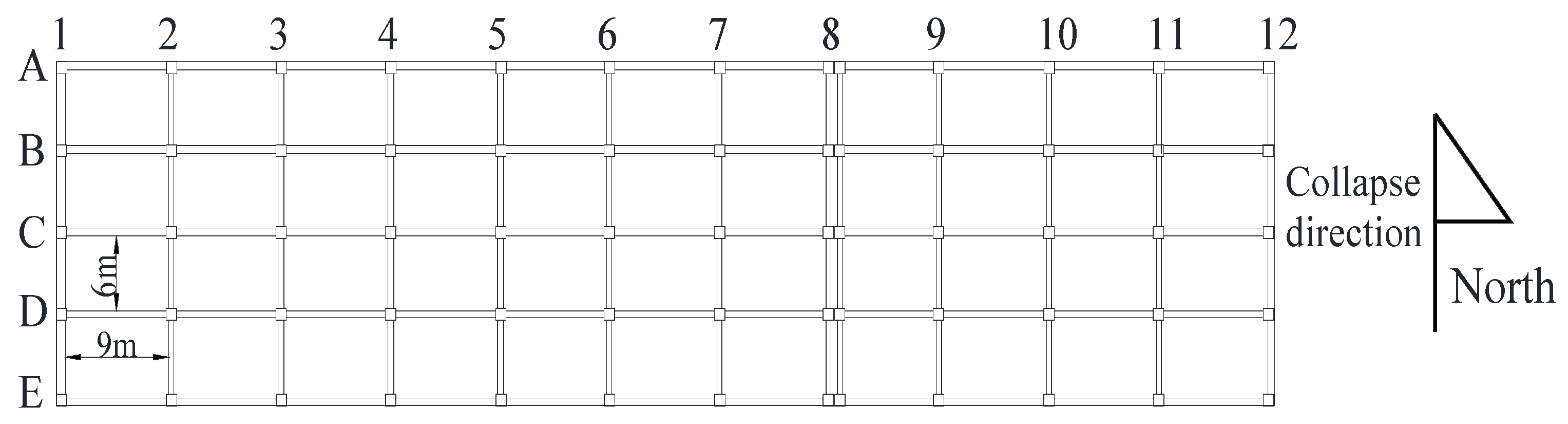
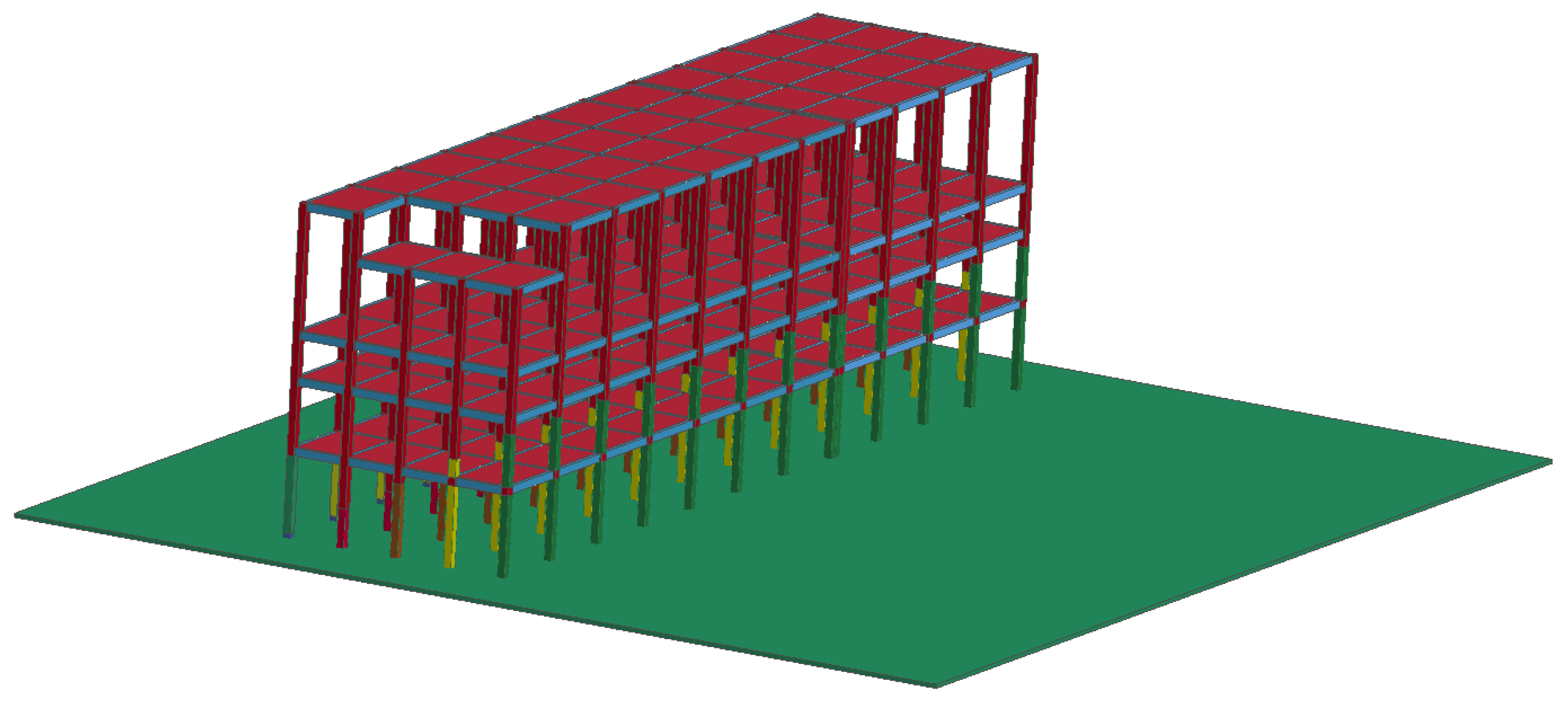




| Structure Properties | Total Length/m | Width /m | Total Height/m | Number of Floors | Spacing between Each Row in the North-South Direction/m | East-West Pillar Spacing/m |
|---|---|---|---|---|---|---|
| Numerical value | 100 | 25 | 34.4 | 4 | 6 | 9 |
| Name | Density | Modulus of Elasticity/GPa | Poisson’s Ratio | Stretching Limit/MPa |
|---|---|---|---|---|
| Reinforcing Steel | 7850 | 210 | 0.3 | 320 |
| Beams and Columns | 2500 | 35 | 0.18 | 5.8 |
| Board | 3400 | 35 | 0.18 | 5.6 |
| Analysis Type | Data Results | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Delayed time difference (s) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| Recoil distance (m) | 7.8 | 9.1 | 10.6 | 6.4 | 8.1 | 9.6 | 11.2 | 11.6 | 12.0 |
| Analysis Type | Data Results | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Delayed time difference (s) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| Burst height (m) | 15.35 | 13.21 | 11.62 | 11.40 | 7.60 | 6.89 | 7.37 | 7.21 | 8.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Kou, Y.; Yan, T.; Sun, H.; Li, S. Case Study on the Effect of Delay-Time Differences between Columns during Blasting Demolition of RC Structures with a Small Height-to-Width Ratio. Appl. Sci. 2023, 13, 6765. https://doi.org/10.3390/app13116765
Gao W, Kou Y, Yan T, Sun H, Li S. Case Study on the Effect of Delay-Time Differences between Columns during Blasting Demolition of RC Structures with a Small Height-to-Width Ratio. Applied Sciences. 2023; 13(11):6765. https://doi.org/10.3390/app13116765
Chicago/Turabian StyleGao, Wenle, Yuming Kou, Tongqing Yan, Hong Sun, and Saijiang Li. 2023. "Case Study on the Effect of Delay-Time Differences between Columns during Blasting Demolition of RC Structures with a Small Height-to-Width Ratio" Applied Sciences 13, no. 11: 6765. https://doi.org/10.3390/app13116765
APA StyleGao, W., Kou, Y., Yan, T., Sun, H., & Li, S. (2023). Case Study on the Effect of Delay-Time Differences between Columns during Blasting Demolition of RC Structures with a Small Height-to-Width Ratio. Applied Sciences, 13(11), 6765. https://doi.org/10.3390/app13116765





