Application of a Structured Training Plan on Different-Length Microcycles in Soccer—Internal and External Load Analysis between Training Weeks and Games
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Weeks Format
2.3. Training Plan
2.4. Data Collection
2.5. Statistical Analysis
3. Results
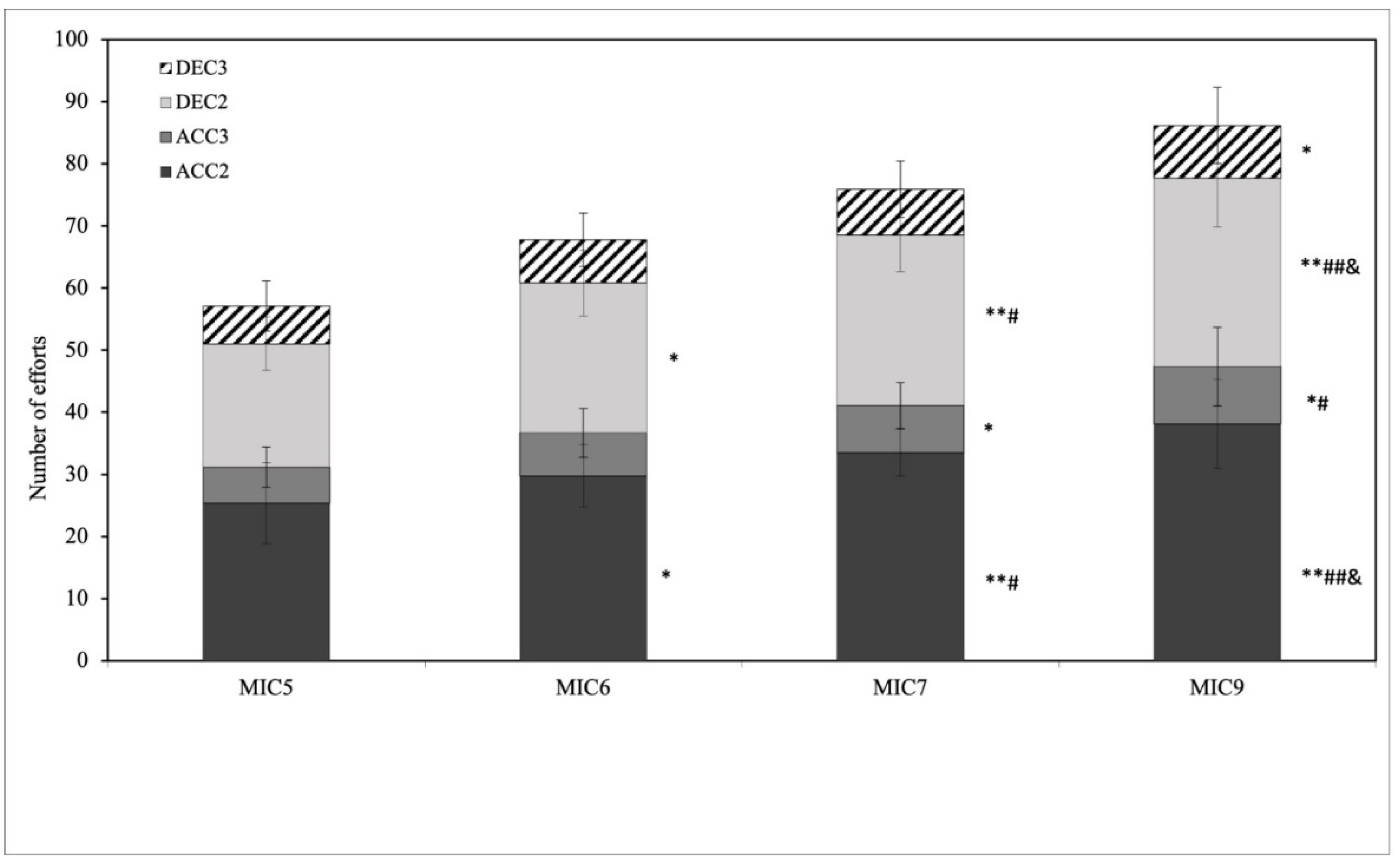
3.1. Weekly Average Load
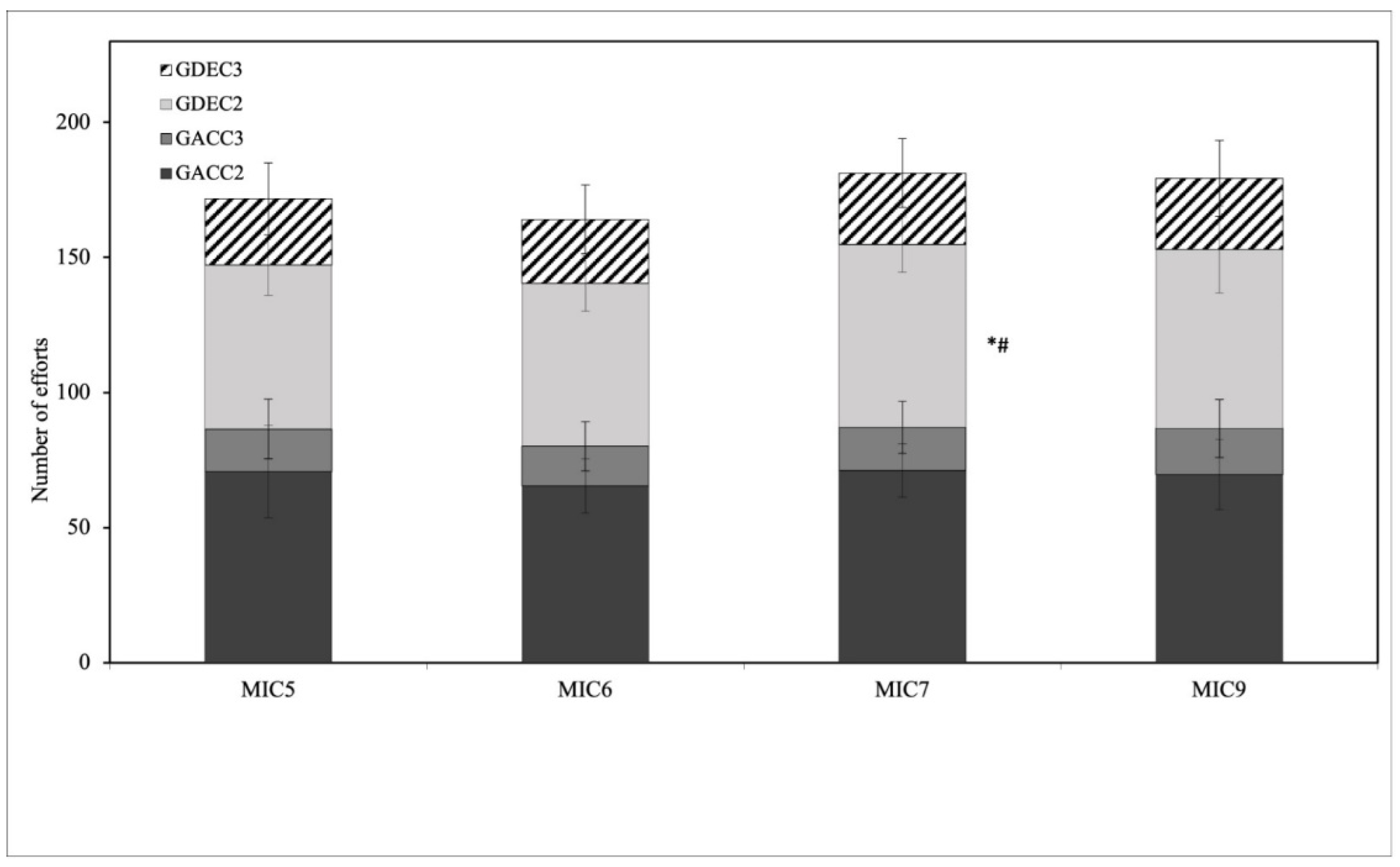
3.2. Games Average Load
4. Discussion
4.1. Microcycles Load Differences
4.2. Games’ Load Differences
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Delaney, J.A.; Thornton, H.R.; Rowell, A.E.; Dascombe, B.J.; Aughey, R.J.; Duthie, G.M. Modelling the decrement in running intensity within professional soccer players. Sci. Med. Footb. 2018, 2, 86–92. [Google Scholar] [CrossRef]
- Oliva-Lozano, J.M.; Fortes, V.; Muyor, J.M. The first, second, and third most demanding passages of play in professional soccer: A longitudinal study. Biol. Sport 2020, 38, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Gabbett, T.J. The training—Injury prevention paradox: Should athletes be training smarter and harder? Br. J. Sports Med. 2016, 50, 273–280. [Google Scholar] [CrossRef] [PubMed]
- Martín-García, A.; Díaz, A.G.; Bradley, P.S.; Morera, F.; Casamichana, D. Quantification of a professional football team’s external load using a microcycle structure. J. Strength Cond. Res. 2018, 32, 3511–3518. [Google Scholar] [CrossRef]
- Wallace, L.; Slattery, K.; Coutts, A.J. A comparison of methods for quantifying training load: Relationships between modelled and actual training responses. Eur. J. Appl. Physiol. 2014, 114, 11–20. [Google Scholar] [CrossRef]
- Scott, B.R.; Lockie, R.G.; Knight, T.J.; Clark, A.C.; de Jonge, X.A.J. A comparison of methods to quantify the in-season training load of professional soccer players. Int. J. Sports Physiol. Perform. 2013, 8, 195–202. [Google Scholar] [CrossRef]
- Impellizzeri, F.M.; Rampinini, E.; Marcora, S.M. Physiological assessment of aerobic training in soccer. J. Sport Sci. 2005, 23, 583–592. [Google Scholar] [CrossRef]
- Hooper, S.L.; Mackinnon, L.T. Monitoring overtraining in athletes: Recommendations. Sports Med. 1995, 20, 321–327. [Google Scholar] [CrossRef]
- Foster, C.A.R.L. Monitoring training in athletes with reference to overtraining syndrome. Med. Sci. Sports Exerc. 1998, 30, 1164–1168. [Google Scholar] [CrossRef]
- Haddad, M.; Chaouachi, A.; Wong, D.P.; Castagna, C.; Hambli, M.; Hue, O.; Chamari, K. Influence of fatigue, stress, muscle soreness and sleep on perceived exertion during submaximal effort. Physiol. Behav. 2013, 119, 185–189. [Google Scholar] [CrossRef]
- Clemente, F.M.; Mendes, B.; Nikolaidis, P.T.; Calvete, F.; Carriço, S.; Owen, A.L. Internal training load and its longitudinal relationship with seasonal player wellness in elite professional soccer. Physiol. Behav. 2017, 179, 262–267. [Google Scholar] [CrossRef]
- Oliveira, R.; Brito, J.P.; Loureiro, N.; Padinha, V.; Ferreira, B.; Mendes, B. Does the distribution of the weekly training load account for the match results of elite professional soccer players? Physiol. Behav. 2020, 225, 113118. [Google Scholar] [CrossRef]
- Oliva-Lozano, J.M.; Gómez-Carmona, C.D.; Rojas-Valverde, D.; Fortes, V.; Pino-Ortega, J. Effect of training day, match, and length of the microcycle on the worst-case scenarios in professional soccer players. Res. Sports Med. 2022, 30, 425–438. [Google Scholar] [CrossRef] [PubMed]
- Stevens, T.G.; de Ruiter, C.J.; Twisk, J.W.; Savelsbergh, G.J.; Beek, P.J. Quantification of in-season training load relative to match load in professional Dutch Eredivisie football players. Sci. Med. Footb. 2017, 1, 117–125. [Google Scholar] [CrossRef]
- Clemente, F.M.; Owen, A.; Serra-Olivares, J.; Nikolaidis, P.T.; Van Der Linden, C.M.; Mendes, B. Characterization of the weekly external load profile of professional soccer teams from Portugal and the Netherlands. J. Hum. Kinet. 2019, 66, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Kelly, D.M.; Strudwick, A.J.; Atkinson, G.; Drust, B.; Gregson, W. Quantification of training and match-load distribution across a season in elite English Premier League soccer players. Sci. Med. Footb. 2020, 4, 59–67. [Google Scholar] [CrossRef]
- Malone, J.J.; Di Michele, R.; Morgans, R.; Burgess, D.; Morton, J.P.; Drust, B. Seasonal training-load quantification in elite English premier league soccer players. Int. J. Sports Physiol. Perform. 2015, 10, 489–497. [Google Scholar] [CrossRef] [PubMed]
- Owen, A.L.; Lago-Peñas, C.; Gómez, M.Á.; Mendes, B.; Dellal, A. Analysis of a training mesocycle and positional quantification in elite European soccer players. Int. J. Sports Sci. Coach. 2017, 12, 665–676. [Google Scholar] [CrossRef]
- Fessi, M.S.; Zarrouk, N.; Di Salvo, V.; Filetti, C.; Barker, A.R.; Moalla, W. Effects of tapering on physical match activities in professional soccer players. J. Sports Sci. 2016, 34, 2189–2194. [Google Scholar] [CrossRef]
- Chmura, P.; Andrzejewski, M.; Konefał, M.; Mroczek, D.; Rokita, A.; Chmura, J. Analysis of motor activities of professional soccer players during the 2014 World Cup in Brazil. J. Hum. Kinet. 2017, 56, 187–195. [Google Scholar] [CrossRef] [PubMed]
- Martín-García, A.; Casamichana, D.; Díaz, A.G.; Cos, F.; Gabbett, T.J. Positional differences in the most demanding passages of play in football competition. J. Sports Sci. Med. 2018, 17, 563. [Google Scholar]
- Oliva-Lozano, J.M.; Martín-Fuentes, I.; Fortes, V.; Muyor, J.M. Differences in worst-case scenarios calculated by fixed length and rolling average methods in professional soccer match-play. Biol. Sport 2021, 38, 325–331. [Google Scholar] [CrossRef]
- Oliva-Lozano, J.M.; Muyor, J.M.; Fortes, V.; McLaren, S.J. Decomposing the variability of match physical performance in professional soccer: Implications for monitoring individuals. Eur. J. Sport Sci. 2021, 21, 1588–1596. [Google Scholar] [CrossRef] [PubMed]
- Oliva-Lozano, J.M.; Rojas-Valverde, D.; Gómez-Carmona, C.D.; Fortes, V.; Pino-Ortega, J. Impact of contextual variables on the representative external load profile of Spanish professional soccer match-play: A full season study. Eur. J. Sport Sci. 2021, 21, 497–506. [Google Scholar] [CrossRef]
- Curtis, R.M.; Huggins, R.A.; Benjamin, C.L.; Sekiguchi, Y.; Adams, W.M.; Arent, S.M.; Jain, R.; Miller, S.J.; Walker, A.J.; Casa, D.J. Contextual factors influencing external and internal training loads in collegiate men’s soccer. J. Strength Cond. Res. 2020, 34, 374–381. [Google Scholar] [CrossRef] [PubMed]
- Castillo, D.; Raya-González, J.; Weston, M.; Yanci, J. Distribution of external load during acquisition training sessions and match play of a professional soccer team. J. Strength Cond. Res. 2021, 35, 3453–3458. [Google Scholar] [CrossRef]
- Anderson, L.; Orme, P.; Di Michele, R.; Close, G.L.; Morgans, R.; Drust, B.; Morton, J.P. Quantification of training load during one-, two-and three-game week schedules in professional soccer players from the English Premier League: Implications for carbohydrate periodisation. J. Sports Sci. 2016, 34, 1250–1259. [Google Scholar] [CrossRef]
- Clemente, F.M.; Rabbani, A.; Conte, D.; Castillo, D.; Afonso, J.; Truman Clark, C.C.; Nikolaidis, P.T.; Rosemann, T.; Knechtle, B. Training/match external load ratios in professional soccer players: A full-season study. Int. J. Environ. Res. Public Health 2019, 16, 3057. [Google Scholar] [CrossRef]
- Modric, T.; Versic, S.; Sekulic, D. Relations of the weekly external training load indicators and running performances in professional soccer matches. Sport Mont. 2021, 19, 31–37. [Google Scholar]
- Turner, A.N.; Stewart, P.F. Strength and conditioning for soccer players. Strength Cond. J. 2014, 6, 1–13. [Google Scholar] [CrossRef]
- Akenhead, R.; Harley, J.A.; Tweddle, S.P. Examining the external training load of an English Premier League football team with special reference to acceleration. J. Strength Cond. Res. 2016, 30, 2424–2432. [Google Scholar] [CrossRef]
- Sarmento, H.; Clemente, F.M.; Harper, L.D.; Costa, I.T.D.; Owen, A.; Figueiredo, A.J. Small sided games in soccer–a systematic review. Int. J. Perf. Anal. Sport 2018, 18, 693–749. [Google Scholar] [CrossRef]
- Dellal, A.; Owen, A.; Wong, D.P.; Krustrup, P.; van Exsel, M.; Mallo, J. Technical and physical demands of small vs. large sided games in relation to playing position in elite soccer. Hum. Mov. Sci. 2012, 31, 957–969. [Google Scholar] [CrossRef] [PubMed]
- Fradua, L.; Zubillaga, A.; Caro, Ó.; Iván Fernández-García, Á.; Ruiz-Ruiz, C.; Tenga, A. Designing small-sided games for training tactical aspects in soccer: Extrapolating pitch sizes from full-size professional matches. J. Sport Sci. 2013, 31, 573–581. [Google Scholar] [CrossRef]
- Olthof, S.B.; Frencken, W.G.; Lemmink, K.A. A match-derived relative pitch area facilitates the tactical representativeness of small-sided games for the official soccer match. J. Strength Cond. Res. 2019, 33, 523. [Google Scholar] [CrossRef] [PubMed]
- Riboli, A.; Coratella, G.; Rampichini, S.; Cé, E.; Esposito, F. Area per player in small-sided games to replicate the external load and estimated physiological match demands in elite soccer players. PLoS ONE 2020, 15, e0229194. [Google Scholar] [CrossRef] [PubMed]
- Chena, M.; Morcillo, J.A.; Rodríguez-Hernández, M.L.; Zapardiel, J.C.; Owen, A.; Lozano, D. The Effect of Weekly Training Load across a Competitive Microcycle on Contextual Variables in Professional Soccer. Int. J. Environ. Res. Public Health 2021, 18, 5091. [Google Scholar] [CrossRef]
- Lago-Peñas, C.; Rey, E.; Lago-Ballesteros, J.; Casáis, L.; Domínguez, E. The influence of a congested calendar on physical performance in elite soccer. J. Strength Cond. Res. 2011, 25, 2111–2117. [Google Scholar] [CrossRef]
- Jeong, T.S.; Reilly, T.; Morton, J.; Bae, S.W.; Drust, B. Quantification of the physiological loading of one week of “pre-season” and one week of “in-season” training in professional soccer players. J. Sports Sci. 2011, 29, 1161–1166. [Google Scholar] [CrossRef]
- Oliveira, R.; Brito, J.P.; Martins, A.; Mendes, B.; Marinho, D.A.; Ferraz, R.; Marques, M.C. In-season internal and external training load quantification of an elite European soccer team. PLoS ONE 2019, 14, e0209393. [Google Scholar] [CrossRef]
- Moreira, A.; Kempton, T.; Aoki, M.S.; Sirotic, A.C.; Coutts, A.J. The impact of 3 different-length between-matches microcycles on training loads in professional rugby league players. Int. J. Sports Physiol. Perform. 2015, 10, 767–773. [Google Scholar] [CrossRef] [PubMed]
- Osgnach, C.; Poser, S.; Bernardini, R.; Rinaldo, R.; Di Prampero, P.E. Energy cost and metabolic power in elite soccer: A new match analysis approach. Med. Sci. Sports Exerc. 2010, 42, 170–178. [Google Scholar] [CrossRef] [PubMed]






| MIC5—Day off 1st Day | |||||
|---|---|---|---|---|---|
| MD + 2 | MD − 2 | MD − 1 | |||
| Running, mobility exercises, 10′ | Dynamic warm up, 10′ | Dynamic warm up, 10′ | |||
| Passing drills or rondo, 15′ | Passing drills or small rondo, 20′ | Coordination, acceleration, reaction drills, 10′ | |||
| Tactical content, 10′ | Tactical content, 20′ | Tactical content, 20′ | |||
| Tactical game 10v10 + 2 GK in reduced space (100–120 m2/player), 10′ | Tactical game 10v10 + 2 GK in reduced space (150–180 m2/player), 10′ | Tactical game 10v10 + 2 GK in reduced space (110—140 m2/player), 15′ | |||
| MIC6—Day off 1st day | |||||
| MD + 2 | MD − 3 | MD − 2 | MD − 1 | ||
| Running, mobility exercises, 10′ | Dynamic warm up, coordination drills, 20′ | Dynamic warm up, 10′ | Dynamic warm up, 10′ | ||
| Passing drills or rondo, 15′ | Passing drills or small rondo, 20′ | Passing drills or small rondo, 20′ | Coordination, acceleration, reaction drills, 10′ | ||
| Tactical content, 10′ | Tactical content, 20′ | Tactical content, 20′ | Tactical content, 20′ | ||
| Tactical game 10v10 + 2 GK in reduced space (100–120 m2/player), 10′ | Physical content: small side games 3v3 – 5v5 + GK (110–120 m2/player), 20′ | Tactical game 10v10 + 2 GK in reduced space (150–180 m2/player), 10′ | Tactical game 10v10 + 2 GK in reduced space (110–140 m2/player), 15′ | ||
| MIC7—Day off 1st day | |||||
| MD + 2 | MD − 4 | MD − 3 | MD − 2 | MD − 1 | |
| Running, mobility exercises, 10′ | Resistance training in the gym (power, emphasized on speed or max load) | Dynamic warm up, coordination drills, 20′ | Dynamic warm up, 10′ | Dynamic warm up, 10′ | |
| Passing drills or rondo, 15′ | Dynamic activation, coordination drills, 10′ | Passing drills or small rondo, 20′ | Passing drills or small rondo, 20′ | Coordination, acceleration, reaction drills, 10′ | |
| Tactical content, 10′ | Maximal speed drills, 10′ | Tactical content or game, medium space (135–160 m2/player) | Tactical content, 20′ | Tactical content, 20′ | |
| Tactical game 10v10 + 2 GK in reduced space (100–120 m2/player), 10′ | Tactical content: large space, usually transition drills or game (195–260 m2/player), 20′ | Physical content: small side games 3v3 – 5v5 + GK (110–120 m2/player), 20′ | Tactical game 10v10 + 2 GK in reduced space (150–180 m2/player), 10′ | Tactical game 10v10 + 2 GK in reduced space (110–140 m2/player), 15′ | |
| Large side game 10v10 +2 GK (195–260 m2/player), 15′ | |||||
| MIC9—Day off 1st and 2nd Day | |||||
| MD − 6 | MD − 5 | MD − 4 | MD − 3 | MD − 2 | MD − 1 |
| Running, mobility exercises, 10′ | Resistance training in the gym (power, emphasized on speed or max load) | Running, mobility exercises, 10′ | Dynamic warm up, coordination drills, 20′ | Dynamic warm up, 10′ | Dynamic warm up, 10′ |
| Passing drills or rondo, 20′ | Dynamic activation, coordination drills, 10′ | Passing drills or rondo, 10′ | Passing drills or small rondo, 20′ | Passing drills or small rondo, 20′ | Coordination, acceleration, reaction drills, 10′ |
| Tactical content, 15′ | Maximal speed drills, 10′ | Tactical content or game 10v10 + 2 GK in reduced space (100–120 m2/player), 20′ | Tactical content or game, medium space (135–160 m2/player) | Tactical content, 20′ | Tactical content, 20′ |
| Tactical game 10v10 + 2 GK in reduced space (100–120 m2/player), 15′ | Tactical content: large space, usually transition drills or game (195–260 m2/player), 20′ | Physical content: small side games 3v3–5v5 + GK (110–120 m2/player), 20′ | Tactical game 10v10 + 2 GK in reduced space (150–180 m2/player), 10′ | Tactical game 10v10 + 2 GK in reduced space (110–140 m2/player), 15′ | |
| Large side game 10v10 + 2 GK (195–260 m2/player), 15′ | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vardakis, L.; Michailidis, Y.; Topalidis, P.; Zelenitsas, C.; Mandroukas, A.; Gissis, I.; Christoulas, K.; Mavrommatis, G.; Metaxas, T. Application of a Structured Training Plan on Different-Length Microcycles in Soccer—Internal and External Load Analysis between Training Weeks and Games. Appl. Sci. 2023, 13, 6935. https://doi.org/10.3390/app13126935
Vardakis L, Michailidis Y, Topalidis P, Zelenitsas C, Mandroukas A, Gissis I, Christoulas K, Mavrommatis G, Metaxas T. Application of a Structured Training Plan on Different-Length Microcycles in Soccer—Internal and External Load Analysis between Training Weeks and Games. Applied Sciences. 2023; 13(12):6935. https://doi.org/10.3390/app13126935
Chicago/Turabian StyleVardakis, Lazaros, Yiannis Michailidis, Panagiotis Topalidis, Charalambos Zelenitsas, Athanasios Mandroukas, Ioannis Gissis, Kosmas Christoulas, George Mavrommatis, and Thomas Metaxas. 2023. "Application of a Structured Training Plan on Different-Length Microcycles in Soccer—Internal and External Load Analysis between Training Weeks and Games" Applied Sciences 13, no. 12: 6935. https://doi.org/10.3390/app13126935
APA StyleVardakis, L., Michailidis, Y., Topalidis, P., Zelenitsas, C., Mandroukas, A., Gissis, I., Christoulas, K., Mavrommatis, G., & Metaxas, T. (2023). Application of a Structured Training Plan on Different-Length Microcycles in Soccer—Internal and External Load Analysis between Training Weeks and Games. Applied Sciences, 13(12), 6935. https://doi.org/10.3390/app13126935








