1. Introduction
The steel–concrete composite structure has the outstanding advantages of high strength, convenient construction, and good overall performance, which can ensure the synergistic bearing of concrete and steel under reasonable combination and connection [
1]. Among them, the steel–concrete composite beam utilizes the compressive properties of concrete and the tensile properties of steel, which is a high-performance flexural load-bearing component and widely used in floor structures [
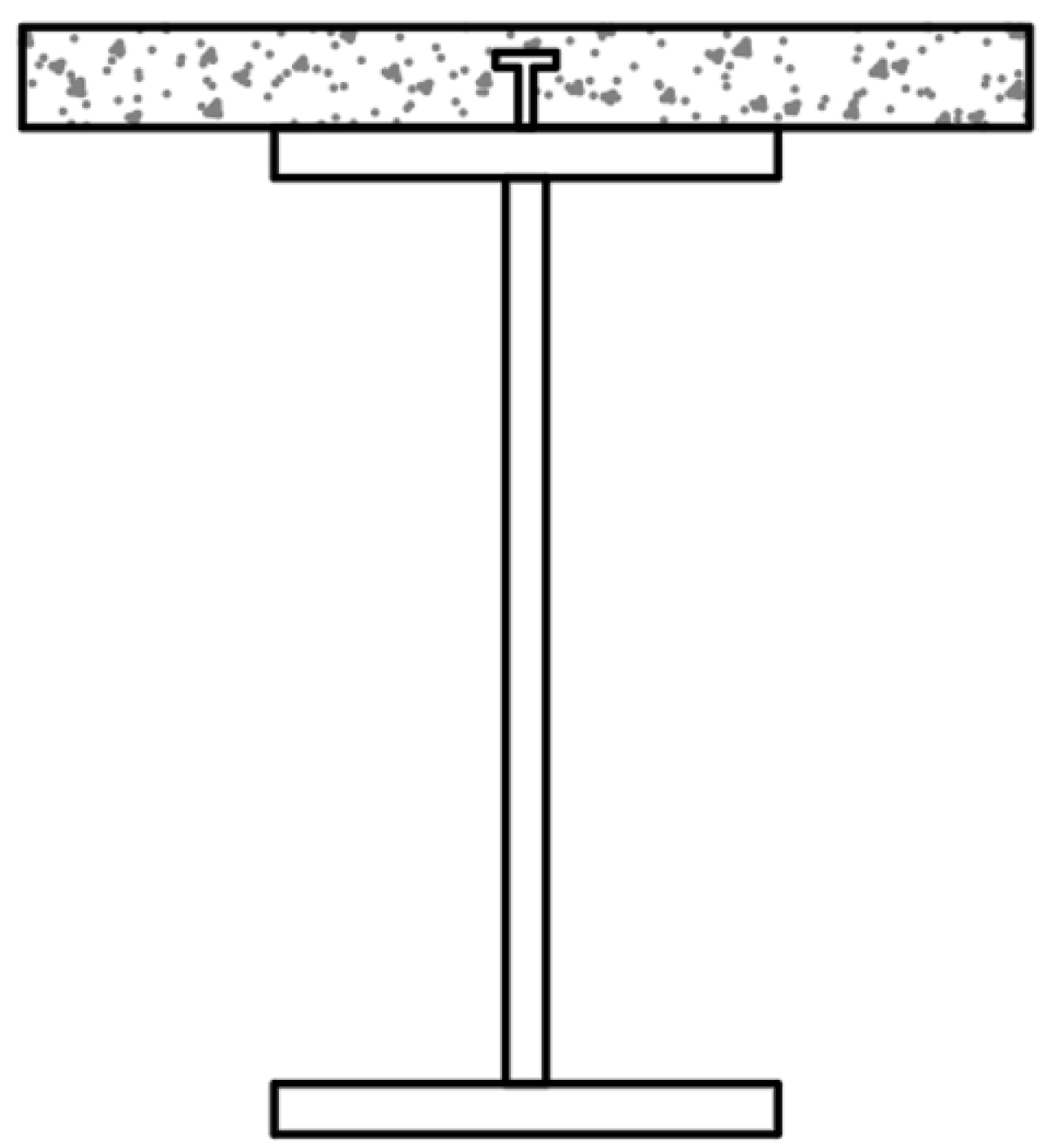
2]. The traditional steel–concrete composite beam is a T-shaped composite beam formed by placing a concrete slab on the upper flange of a steel beam or a concrete slab on the lower flange of a steel beam to form a composite flat beam, which can usually be divided into two forms of steel sections outside or inside the concrete, as shown in
Figure 1. Among them, the steel beam is exposed in the T-shaped composite beam, which requires fireproof and anti-corrosion treatment, and the out-of-plane stability of the steel beam is not guaranteed when its cross-section is high, so extra out-of-plane support is added. In addition, although the T-shaped combination beam has better performance in bearing capacity, the large cross-sectional height of the component causes the overall height of the building to increase, resulting in an increase in construction cost.
In order to reduce the aforementioned defects, the combination flat beam places the precast concrete slab on the lower flange of the steel beam, connects the precast base plate with the steel beam as a whole through the cast-in-place layer, and wraps most of the area of the steel beam with concrete, as shown in
Figure 2. Choi [
3] proposed a new type of wide and large-span steel–concrete composite beam that can be used to reduce the height of the structure. The experimental results showed that as the steel thickness increased by 3 mm, the bending strength of the wide composite steel beam increased by about 20%. In related studies, Lee [
4] conducted a flexural analysis of I-beam laminated plate composite beams and established a computational model for I-beam composite beams under vertical loads based on the theory of shear deformation beams. Yang [
5] proposed a new type of composite flat beam composed of a wide flange section and laminated plate. The plane section assumption of the composite beam was verified by two concentrated forces loading on the specimen, and the calculation method of flexural bearing capacity was proposed. Cao [
6] proposed a flat steel–concrete composite beam and tested its flexural performance. Through the traditional composite beam calculation theory, a simplified calculation model suitable for the bending stiffness and ultimate bending capacity of the model was proposed. Wang [
7] established the analysis theory of steel–concrete composite beams considering interface slip and shear deformation in steel and deduced the calculation formulas of the ultimate flexural capacity of simply supported composite beams under uniform load and concentrated load in mid-span, respectively. Luo [
8] studied the shear lag effect of steel–concrete composite beams under bending moment and proposed a method to predict the cracking site effect of steel–concrete composite beams. The effectiveness of the method was verified by experimental data. In summary, it can be seen that the flexural bearing capacity of the composite flat beam is mainly related to the effective plate width, the height of the composite flat beam, the beam spacing, and the thickness of the flange plate. The composite flat beam structure has reasonable structure, excellent bearing performance, and certain cost advantages. However, the integrity of the concrete composite plates on both sides is limited due to the form of the web, which is a certain restriction on the layout of the pipeline.
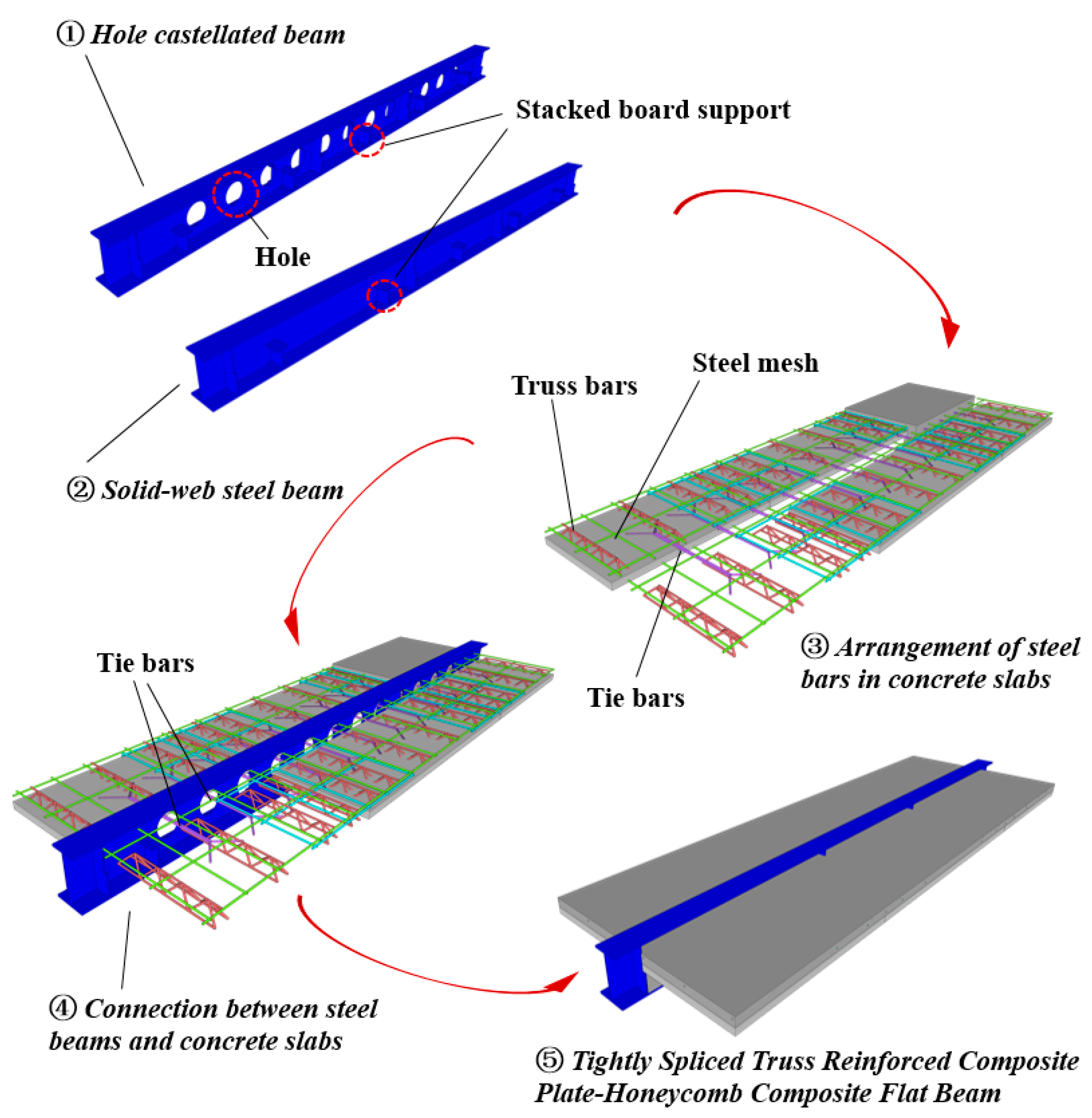
The honeycomb beam as the steel component in the combined beam provides a strong condition for solving the connection of the composite plate on both sides of the steel beam. Honeycomb beams are treated with holes in the beam webs to enhance the efficiency of steel utilization in the load-bearing process and to reduce the amount of steel used for cost control purposes [
9]. The failure mode of composite flat beams is influenced by the combination form, with significant differences in failure modes, and has higher bending stiffness, bending moment bearing capacity, and ductility bearing capacity [
6]. In addition, the honeycomb holes in the web of the steel beam can be used to pass through the layout of various pipelines as well as the internal reinforcement of the floor slab, which is conducive to the combined application with concrete slabs. Related studies have shown that the main factors affecting the load bearing of honeycomb beams include the honeycomb cavity rate, the shape of the openings, and the width-to-thickness ratio of the slab [
10,
11]. Deng [
12] investigated the variation of the critical load of local buckling of the web of I-beams with different hole–height ratios and number of holes, with and without transverse stiffening ribs and with and without web openings. On the basis of this, Serror [
13] supplemented to investigate the effects of parameters such as width-to-thickness ratio, opening shape, distance from the first opening to the end, hole size, and steel grade on the elastic and inelastic critical buckling stresses of honeycomb beams. Taufiq [
14] investigated the optimum diameter and opening spacing of components at different spans. Chang [
15] analyzed the effect of opening shape and expansion ratio on honeycomb beams by conducting four-point bending tests with octagonal hole honeycomb beams and studied the rise in the bearing capacity of honeycomb beams as the expansion ratio increased on the surface. Mehetre [
16] found that the moment bearing capacity of honeycomb beams with round holes increased by 20.78% and deflection decreased by 11.51% compared to honeycomb beams with hexagonal openings due to avoiding the stress concentration phenomenon at the corners. Velrajkumar [
17] investigated the flexural performance of hexagonal honeycomb beams using a combination of experimental and finite element methods, taking into account the effect of the location of the honeycomb hole openings. In addition, there are effects of beam length, section grade, and cross-section size on the buckling ultimate load and buckling mode of honeycomb steel beams [
18,
19,
20]. Du [
21] studied the influence of concrete strength on the load deflection, flexural bearing capacity, and ductility of high-speed steel–concrete composite beams. The simplified plastic method overestimated the ultimate flexural strength of high-speed steel–concrete composite beams, while nonlinear methods based on material constitutive models can accurately predict the bearing capacity of materials. In summary, the current research has conducted an in-depth analysis of the expansion ratio, span–height ratio, plate width–thickness ratio, and effective width of concrete flange plate, etc. Numerous experimental studies have been carried out for flexural load capacity, stiffness, buckling of honeycomb beams and their combination beams, and the corresponding design calculation equations for honeycomb beams and their combination beams have been proposed. However, there is limited research on the application of honeycomb beams to concrete composite floors.
The truss steel composited plate is a prefabricated steel truss formed by welding the lower part of the bent steel bars with the upper and lower longitudinal bars in the slab in the laminated layer and then tied to the upper layer of the reinforcing steel and cast-in-place concrete to form a concrete slab with overall stress [
22]. Many webs of truss reinforcement are interspersed in the laminated layer and the cast-in-place layer, which facilitates a tight connection between the two layers of concrete. Due to the configuration of truss reinforcement in the precast base slab, the stiffness of the base slab is increased, so that it can bear greater construction loads during construction and reduce the deformation of the slab due to self-weight and construction loads before the hardening of the cast-in-place layer [
23,
24]. The reinforced truss precast concrete slab is shown in
Figure 3. In order to solve the problem of traditional precast composited plates with reinforcement bars protruding from the sides, which affects the production and construction efficiency, the researchers propose to adopt the construction process of composited plates with tightly spliced joints to achieve standardized and automated production of composited plates and efficient construction. Ye [
25] studied the flexural performance of composited plates with different splice forms and found that the load-carrying capacity of the plate depends on the splice section, while the splice reinforcement can control the development of cracks along the superimposed surface and improve the shear resistance of the specimen. Ding [
26] studied the load-bearing mechanism and flexural performance of the slabs in terms of deformation, load-bearing capacity, and damage mode through static load tests on four types of reinforced concrete floor slabs, which showed that the stiffness of the close-packed composited plate was slightly lower than that of the cast-in-place slab, but the damage pattern was basically the same as that of the cast-in-place slab, and the strength of the close-packed composited plate could be improved by closing the reinforcement ring. The anchoring length of the transverse reinforcement at the bottom of the post-pouring zone has a significant impact on the shear performance of the composite concrete slab, especially when the anchoring length decreases to the critical value, and the ultimate bearing capacity and ductility of the test specimen decrease. In addition, the thickness of the composited plate, the depth of the splice recess, the reinforcement rate of the splice reinforcement, and the lap length of the splice reinforcement have obvious effects on the bearing capacity of the composited plate. The form of load transfer of dense splice is different from that of post-cast strip splice and monolithic cast-in-place slab, but the load-carrying capacity of the splice can be effectively ensured by enhancing additional reinforcement at the splice and encrypting reinforcement trusses so that it presents the force characteristics of the two-way slab.
This study proposes to arrange a truss-reinforced composite plate at the lower part of the upper flange of the honeycomb beam and strengthen the connection between the two through reasonable methods to form a new type of honeycomb composite flat beam structure. As the concrete slab is located within the height range of the steel beam, it maximizes the net height of the floor slab. In addition, laminated plates can limit the out-of-plane deformation of steel beams, thereby obtaining better stability and deformation capacity than ordinary T-shaped composite beams. On the basis of experimental research on the flexural bearing capacity of five composite flat beams, this article conducts numerical simulation analysis. Based on the analysis of failure modes and bearing capacity characteristics, the influence law of the honeycomb web on bearing capacity is established, and a simplified calculation method for this type of composite flat beam is proposed. Finally, design suggestions for honeycomb composite flat beams are proposed.
4. Theoretical Analysis and Design Method
4.1. The Basic Assumptions
The holes in the web of honeycomb composite flat beam led to its local weakening, which changes the longitudinal and vertical continuity of the section of steel web, forming a special kind of variable section beam, resulting in the calculation of the bearing capacity of the composite beam in the process of stressing becomes complicated. The honeycomb composite flat beam cross-sectional combination form is different from the common T-shaped composite beam, and the design formula of the T-shaped composite beam cannot be applied directly. The honeycomb composite flat beam component is formed by a honeycomb steel beam and concrete flange plate together, but the honeycomb composite flat beam can refer to the design calculation method of solid web steel composite flat beam in the calculation process because the concrete flange plate is located on both sides of the web, and the honeycomb hole is basically filled intact. The following assumptions should be met when calculating the flexural load-carrying capacity of the honeycomb composite flat beam:
- (1)
Honeycomb beam holes, stiffening ribs, and H-beam shear connection keys can ensure that the connection between steel and concrete resists sufficient longitudinal shear to form a synergistic force-bearing whole.
- (2)
The concrete in the tensile zone withdraws from the work after cracking, and the concrete tensile stress is much smaller than its compressive stress, so the concrete in the tensile zone is not involved in the force analysis. Since the concrete flange plate below the bottom part of the concrete is basically in tension, its enhancement of the combined flat beam flexural bearing capacity is not considered.
- (3)
Since the cross-sectional area of the reinforcement in the concrete flange slab is much smaller than the cross-sectional area of the steel beam, the enhancement effect of the reinforcement on the flexural bearing capacity of the combined flat beam specimen is not considered.
- (4)
The steel and reinforcement exhibit ideal elasticity and can reach the strength design value when in tension or compression.
- (5)
The cross-section of the honeycomb composite flat beam specimen can maintain the plane state during the load-bearing process, i.e., the assumption of flat section is satisfied, without considering the uneven distribution of stresses in the concrete flange.
- (6)
Since the concrete is located on both sides of the steel beam to have a stabilizing effect on it, and the steel beam section grade is S1, the overall buckling or local buckling of the specimen is not considered.
- (7)
The effect of the shear connection keys of H-beams on the lower flange of the honeycomb beam and the stiffening ribs is not considered.
- (8)
The concrete flange plate is treated as a whole.
- (9)
In the bending process of the specimen, the concrete compressive part of the stress is actually not rectangular distribution, but for the sake of calculation simplicity, this paper adopts the equivalent rectangular stress method to convert the concrete irregular compressive stress into rectangular stress equivalently. The magnitude of the equivalent rectangular stress should be equal to the magnitude of the actual stress, and the location of the point of action of the joint force should also be the same, then the height of the equivalent compressive zone of concrete , the equivalent compressive stress value is .
Where is the ratio of the height of the rectangular stress compression zone and the height of the plastic neutral axis of the combined flat beam section from the top surface of the concrete flange , is the distance of the plastic neutral axis of the combined flat beam section from the top surface of the steel beam, is the distance of the top surface of the concrete flange from the top surface of the steel beam, and the coefficient is the ratio of the equivalent stress value of the concrete in the compression zone to the design value of the concrete axial compressive strength.
4.2. Calculate the Ultimate Bending Capacity by Using Double T-Section Method
4.2.1. Cross-Section Type
In this paper, the equivalent rectangular stress method is used to equate the height of the theoretical compression zone of the concrete flange plate to the actual compression height of the concrete flange plate, so that it can better calculate the location of the plastic neutral axis of the cross-section of the honeycomb composite flat beam specimen. Since the honeycomb composite flat beam specimen is weakest at the honeycomb hole section, the ultimate flexural load capacity of the composite flat beam is calculated mainly by using the honeycomb hole section as the control section in this section. The combined flat beam is divided into two T-shaped sections above and below the honeycomb hole and the concrete flange plate for calculation, referred to as the double T-shaped steel method. Referring to the classification standard of the cross-section in a T-shaped reinforced concrete beam, the combined flat beam can be divided into two categories according to the position of the neutral axis: the first category of cross-section when the neutral axis is located within the thickness of concrete flange plate; the second category of cross-section when the neutral axis is located below the bottom surface of concrete flange plate. One type of cross-section can be distinguished according to the position of the plastic neutral axis relative to the honeycomb hole,
cross-section when the plastic neutral axis is located at the web above the honeycomb hole, and
cross-section when the plastic neutral axis is located within the height of the honeycomb hole opening, as shown in
Figure 19.
When the plastic neutral axis is located at the web above the honeycomb aperture when the section belongs to the
class of sections:
when the plastic neutral axis is located below the concrete flange slab, the section is a Class II section:
Among them:
, , , —The widths of the plates of the upper flange, lower flange, and web of the steel beam as well as the concrete flange plate;
, , , —Plate thicknesses of the upper flange, lower flange, and web of the steel beam as well as the concrete flange plate;
h—Height of the cross-section of the honeycomb combined flat beam;
—Honeycomb hole diameter;
—The yield stress of the steel section;
—Peak concrete stress.
When none of the specimen sections satisfy Equations (4) and (5), the plastic neutral axis of the combined flat beam section is located within the opening of the honeycomb hole and is a type section.
4.2.2. Bearing Capacity Calculation Formula
Due to the relative position between the plastic neutral axis of the composite specimen and the plastic neutral axis of the honeycomb beam, there are differences in the stress characteristics of the composite specimen. For example, the neutral axis of the composite specimen is located at position a, and the plastic neutral axis of the honeycomb steel beam is located at position d as shown in
Figure 19a. The equivalent stress distribution of the composite specimen is shown in
Figure 19b.
According to the cross-sectional tensile equilibrium equation of the combined flat beam specimen [
27,
28], Equation (6), the distance of the cross-sectional plastic neutral axis from the top of the combined flat beam can be found at
.
The cross-sectional equivalent force method decomposes the cross-sectional bending moment of the combined flat beam into two parts: the flexural load capacity of the steel beam around its own plastic neutral axis and the concrete equivalent compression zone combined force on the equivalent steel beam tension zone combined force after taking distance.
where
is the resistance distance of the shaped section of the honeycomb steel beam around its own plastic neutral axis. From Equation (9), the distance between the plastic neutral axis of the honeycomb steel beam and the top of the beam can be found at
:
From Equation (10), the distance
y between the combined force in the compression zone of the concrete to the combined force in the tension zone of the steel beam after equivalence is found:
where
is the equivalent combined force distance of the honeycomb beam in tension from the plastic neutral axis of the combined section.
Similarly, when the plastic neutral axis of the composite specimen is located at position b in
Figure 19, and the plastic neutral axis of the honeycomb steel beam is located at position d in
Figure 19, its bending capacity is:
When the plastic neutral axis of the composite specimen is located at position c in
Figure 19, and the plastic neutral axis of the honeycomb steel beam is located at position d in
Figure 19, its bending capacity is:
4.3. Simplified Calculation of Ultimate Bending Capacity
Using the equivalent rectangular stress method of double T-beams in the above section, the calculation is based on the section where the honeycomb hole is located. Although the flexural load capacity of the weakest section can be calculated, the calculation decomposes the cross-section of the combined flat beam into the upper and lower parts of unconnected T-beams and concrete flange plate and does not consider the role of the web at the longitudinal solid web of the honeycomb beam, which leads to conservative calculation results. This method also requires the identification of the relative relationship between the plastic neutral axis of the combined beam and the honeycomb hole before calculation, which makes the calculation process a bit tedious. Therefore, this section simplifies the formula for calculating the flexural load capacity of the honeycomb composite flat beam specimen on the basis of the equivalent rectangular stress method.
Under the condition that the previous assumptions hold, the effect of honeycomb holes on the calculation is ignored first, the formula for calculating the flexural load capacity of the solid web combination flat beam is derived, and the fitting function of the honeycomb hole–height ratio and the load capacity reduction coefficient fitted by the integrated finite element calculation results are derived for the flexural load capacity of the honeycomb combination beam.
In
Figure 20, a′, b′, and c′ represent the plastic neutral axis positions at different positions. When the neutral axis of the composite specimen is located at position a’ and the plastic neutral axis of the honeycomb steel beam is located at position c’, the section stress distribution of the first type of solid web composite beam is shown in
Figure 20b. Similarly, when the neutral axis of the composite specimen is located at position b’ and the plastic neutral axis of the honeycomb steel beam is located at position c’, the section stress distribution of the second type of solid web composite beam is shown in
Figure 20c.
According to the cross-sectional tensile equilibrium equation of the combined flat beam specimen, i.e., Equation (15), the distance of the cross-sectional plastic neutral axis from the top of the combined flat beam can be found at
.
The cross-sectional equivalent method decomposes the cross-sectional bending moment of the combined flat beam into two parts: the bending capacity of the steel beam around its own plastic neutral axis and the concrete equivalent compression zone combined force on the equivalent steel beam tension zone combined force after taking distance. Substitute Equations (7) and (15) into Equation (8) to find out the flexural load-carrying capacity of solid web type combined flat beam. Where y is the distance from the concrete compressive zone combined force to the steel beam tensile zone combined force, which can be found by the following formula:
The bending capacity of the solid web combined flat beam is calculated as shown in Equation (17):
When the plastic neutral axis is located below the bottom plate of the concrete flange plate, the stress diagram shown in
Figure 20c is used.
According to the cross-sectional tensile equilibrium equation of the combined flat beam specimen, i.e., Equation (18), the distance between the plastic neutral axis of the cross-section and the top of the combined flat beam can be found at
yc.
Substitute Equations (8), (16) and (18) into Equation (7) to find the bending capacity of the solid web type combined flat beam:
After finding out the above two types of solid web type combined flat beam specimen flexural load bearing capacity, in order to consider the honeycomb hole on the honeycomb combined flat beam flexural load bearing capacity reduction effect, in this introduction of the finite element calculation results of the honeycomb combined flat beam flexural load bearing capacity reduction coefficient with the function of the honeycomb hole–height ratio, then the honeycomb combined flat beam specimen ultimate flexural load bearing capacity calculation formula is as follows:
4.4. Verification of Ultimate Bending Capacity Calculation
In order to verify the applicability of the formula and simplified calculation formula for calculating the ultimate bending bearing capacity of specimens using the double T-shaped steel method, the bending bearing capacity of honeycomb composite flat beams under different section heights and hole–height ratios was explored by comparing the finite element model calculation results in the previous text.
Table 5 presents the results and comparative analysis data of three different calculation methods, including the double T-shaped steel calculation method (DT method), web reduction calculation method (RWP method), and finite element method (FE method).
The ultimate bending bearing capacity of the specimen calculated by the equivalent stress method is less than the finite element simulation value, indicating that the calculation of the bending bearing capacity of the specimen according to the formula given in this chapter is conservative and has sufficient safety. The main reasons why the calculated value of the formula is less than that of the finite element method are: (1) The formula ignores the tensile strength of concrete and the reinforcement in the concrete flange plate for the improvement of the bending bearing capacity of the specimen; (2) When calculating the formula, the effect of the H-shaped steel shear connection key and stiffener in the composite specimen was not considered. The H-shaped steel shear connection key and stiffener appear relative compression with the concrete during bending, which suppresses the deformation of the specimen and improves the flexural bearing capacity of the specimen. The error of formula A is basically between 17% and 20%, while the error of the RWP method is basically between 7% and 12%, indicating that the accuracy of the simplified calculation formula is higher than that of the double T-shaped steel method calculation formula.
When calculating using the double T-shaped steel method, the connection effect of the web plate at the honeycomb steel beam web plate pier on the upper and lower T-shaped steel sections was not considered. The contribution of the upper and lower separated T-shaped steel to the bearing capacity of the composite flat beam was calculated separately, and the formula calculation value was generally lower than the finite element simulation result. From
Table 5, it can be seen that the error of the DT method increases with the increase in the honeycomb hole–height ratio. When the hole–height ratio is 0, the formula calculation error is only 11.50%, which is significantly reduced compared to other hole–height ratio errors. The calculation results of the DT method for solid web composite flat beams are significantly better than those of honeycomb composite flat beams, and this formula takes into account the weakening effect of honeycomb holes too conservatively. The RWP method shows a relatively stable error in the formula calculation value when the cross-sectional height of the composite flat beam remains constant, but the error tends to decrease with the increase in the cross-sectional height of the honeycomb composite flat beam. It shows that the calculation of the bending bearing capacity of specimens with the same section height and different hole–height ratios has relatively stable results, but there is still about a 10% safety margin relative to the finite element method.
In summary, both the DT method and RWP method proposed for the bending bearing capacity of honeycomb composite flat beams can effectively calculate the bending bearing capacity of specimens, and the formula calculation values are generally smaller than the finite element simulation values, leaving a certain safety margin for specimen design. The RWP method simplifies the calculation process by using the reduction factor of the hole–height ratio on the basis of the solid web steel composite flat beam. Compared with the results of the finite element method, the RWP method has a smaller relative error and is more stable.
4.5. Design Suggestion Method of Honeycomb Composite Flat Beam
(1) In the process of bending, the steel components may have local buckling of the cross-sectional plates, which may cause early damage to the specimens and reduce the strength and stiffness of the combined flat beam specimens, thus affecting the bearing capacity and deformation capacity of the combined flat beam. It is recommended to fill the honeycomb holes and set up supporting stiffening ribs at the support and upper flange of the beam where the load is concentrated by a large, fixed load. When the web width-to-thickness ratio of the honeycomb beam is greater than 80 , transverse stiffening ribs should be provided at places with high local stress.
(2) The load location has a certain influence on the critical load of the steel beam. The floor load of the honeycomb composite flat beam proposed in this paper is transferred to the lower flange of the steel beam through the floor slab and to the H-beam anti-kinematic connection key, and this load transfer path can reduce the beam torsion as well as prevent beam instability. At the same time, since the concrete flange plate is located on both sides of the honeycomb beam web and basically fills the honeycomb holes, it provides effective lateral support to the honeycomb steel beam, so it is not necessary to verify the overall stability of the honeycomb composite beam when the overall stability of the honeycomb steel beam meets the requirements. The overall stability of the honeycomb beam element can be calculated by discounting the overall stability of the solid web flexural element by the corresponding formula, and the discount factor is related to the span-to-height ratio, the opening rate, and the hole density of the beam [
29]. Therefore, the honeycomb steel beam can be subjected to the overall stability test according to the following equation:
where:
—The maximum bending moment acting around the strong axis;
—The overall stability coefficient of the beam;
—Section modulus of the bridge section of the cellular beam;
—Standard values of steel strength;
—Cellular hole discount factor, , which can be approximated as 1.1;
—The span-to-height ratio of the beam;
—Opening rate;
—Hole density.
(3) The component strength of the honeycomb combination flat beam and other load-bearing limit states are generally designed using the plastic design method, that is, using Equations (7), (14), (15) or Equation (20) ultimate flexural load-bearing capacity calculation formula proposed in this chapter, with a certain safety factor. The honeycomb combined flat beam directly subjected to power should adopt the elastic design method, and the load should be combined according to the short-term effect.
(4) The calculation of the deflection of cellular combination beams is mainly divided into the estimation method, comparison method, and finite element method, where the estimation method is based on the calculation of the deflection of web-type combination flat beams by introducing an increase factor for the corresponding calculation. The calculation of deflection of solid web combination beams in China’s steel structure code is based on the standard combination of loads and the larger calculated deflection of quasi-permanent combination, and the combination beam subject to positive moment only should have its stiffness discounted accordingly:
where:
E—Modulus of elasticity of the steel;
—Composite beam commutation section moment of inertia;
—Stiffness reduction factor.
According to the relevant literature, the deflection calculation value of the cellular composite flat beam is obtained by appropriately scaling up the deflection calculation value on the basis of the solid web composite flat beam.
where:
fsm—The bending deflection of a solid web combined flat beam of equal section;
η—The deflection increase factor, when the expansion ratio is less than 1.5 and can be taken according to the value of
Table 6.
(5) The connection between the honeycomb steel beam and the concrete flange slab is mainly realized through the honeycomb holes, the slab bearing reinforcement through the honeycomb holes, the post-inserted tie bars, and the H-beam shear connection keys. From the test results, it can be seen that the solid web-type composite flat beam only relies on the bond stress of concrete to a steel beam, and the shear connection key of the H-beam may produce the damage state of the concrete flange plate detached from the steel beam during bending. The equally spaced honeycomb holes and the reinforcement and concrete through the honeycomb holes connect the two sides of the flange plate, which makes it have better integrity and can meet the requirements of its anti-slip in the normal use stage. Therefore, the H-beam shear connection key provides shear strength on the one hand and lies in supporting the composited plate on the other hand, making the construction process simpler. For the post-inserted tie bars according to the honeycomb hole arrangement, it is appropriate to meet the requirements of C6@200, and the anchorage length of the two ends extending into the end of the laminated plate using 135° bend hooks can be 0.6 times the basic anchorage length ξab, the inner diameter of the bent hook is not less than 4d, and the length of the straight section after bending is not less than 5d.
(6) For the honeycomb combination flat beam with higher fire protection requirements, the exposed steel beam part should be designed for fire protection in accordance with the requirements of structure type, working environment, and fire resistance time limit, such as using fireproof paint. Steel beams within the contact range of steel beams and concrete should not be coated to prevent slippage and misalignment between concrete and steel beams. Steel structure corrosion should be based on the importance of the building, corrosive environment, and other factors to determine a reasonable anti-corrosion design life can use anti-corrosion coatings, zinc or aluminum, and other metal protective layers, cathodic protection measures, the use of weathering steel, and other measures for corrosion. For the parts that endanger personal safety and maintenance difficulties, important load-bearing structures should be strengthened to protect them.