Applicability of Human Thermophysiological Model for Prediction of Thermal Strain in PPE
Abstract
:1. Introduction
2. Materials and Methods
- TF: impermeable chemical protective clothing Tychem F ® DuPontTM, with protective mask CM-6, cotton underwear with long sleeves and legs, cotton gloves + rubber gloves, and work boots + CBRN overboots;
- OPCH: fully encapsulated suit OPCH90PO by Ecoprotect with a self-contained breathing apparatus (SCBA) Auer Maxx, cotton underwear with long sleeves and legs, cotton gloves under rubber gloves, rubber boots;
- FOP: Air-permeable filtration NBC suit FOP96 by B.O.I.S. with protective mask CM-6, boots + CBRN overboots, bamboo underwear with long sleeves and legs, and cotton gloves + rubber gloves;
- TP: Air-permeable firefighter suit Tiger Plus by DEVA either with helmet without respiratory protection or with helmet + SCBA Auer Maxx, bamboo T-shirt, and firefighter gloves and boots.
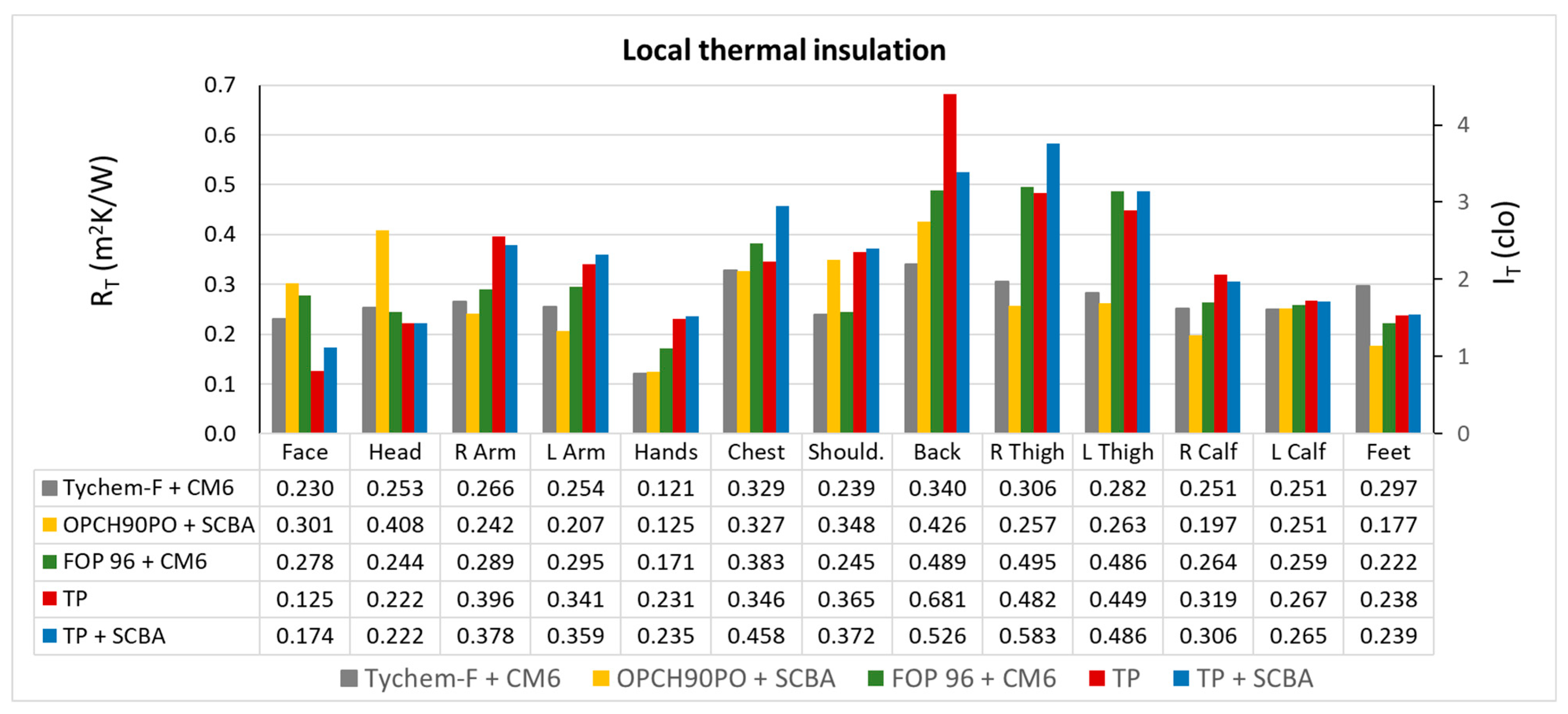
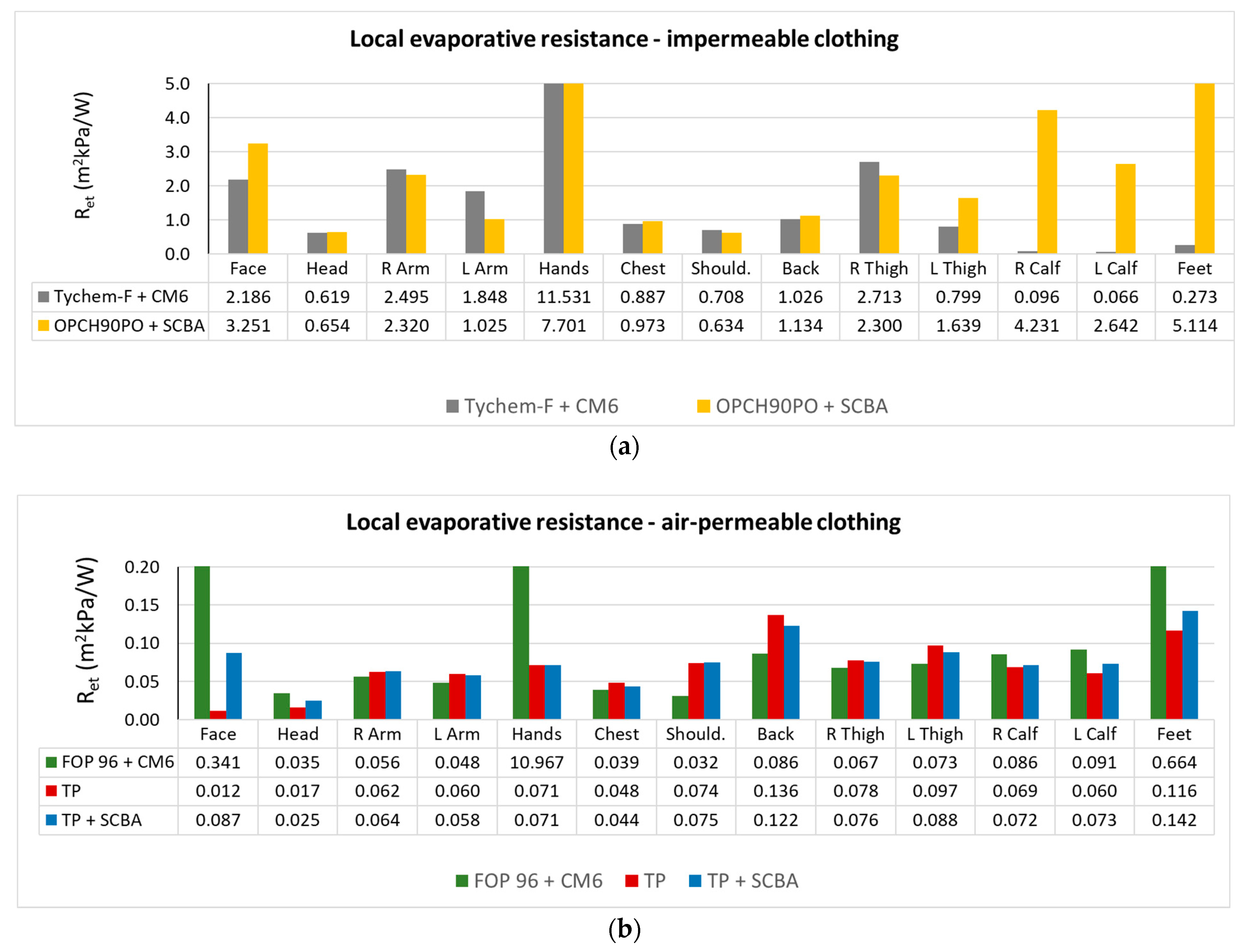
2.1. Thermal Insulation Characteristics of the Clothing
- IT—Total thermal insulation including the air boundary layer of the measured garment (m2·K·W−1);
- TS—Average manikin surface temperature (°C);
- Ta—Air temperature in the climatic chamber (°C);
- AM—Total body surface area of the manikin (m2);
- Hc—Total thermal energy delivered to the manikin (W).
- IT,i—Local thermal insulation including the air boundary layer of the measured garment (m2·K·W−1);
- TS,i—Local manikin surface temperature (°C);
- AM,i—Surface area of the individual zones of the manikin’s body (m2);
- Hc,i—Local thermal energy delivered to a given zone on the manikin (W).
- ReT—Total evaporative resistance (kPa·m2·W−1);
- Δpiso—The difference between the saturated vapor pressure at the manikin surface and the ambient vapor pressure (kPa);
- He—Amount of evaporative losses from the manikin surface (W);
- AS—Sweating surface of the manikin (m2).
- im—Static clothing permeability index (-);
- LR—Lewis constant (LR = 16.5 K·kPa−1).
2.2. Testing of the Thermal Strain in Climatic Chamber
- Parameters of the probands: (a) 6 men (age: 29–53 years, height: 170–187 cm, weight: 69–92 kg, BMI: 20.2–29.4 (2 normal, 4 Overweight Class I), fitness level based on VO2max value: from very poor (4 men, the worst 27.8 mL·min−1·kg−1 for a man of age 29 years) to good (2 men, the best 37.3 mL·min−1·kg−1 for a man of age 55 years)); (b) women (age 28–49 years, height: 158–176 cm, weight 56–71 kg, BMI: 20.3 to 26.1 (5 normal, 1 Overweight Class I), fitness level based on VO2max value: from poor (1 woman, 28.4 mL·min−1·kg−1 for a woman of age 28 years) to good (5 women, the best 33.6 mL·min−1·kg−1 for a woman of age 36 years)).
- Conditions in the climatic chamber: (a) −10 °C and 25–35% rel. humidity (RH), (b) 5 °C and 20–30% RH, (c) 25 °C and 20–30% RH, (d) 35 °C and 15–25% RH; air flow always 0.2 m/s, walking on ergometer (4 km/h, inclination 10%) in mode of 5 min acclimatization in the climatic chamber + max. 4 cycles of 20 min walking + 10 min rest, i.e., 125 min in total.
- Max time achieved—reasons for termination of the test: (a) reaching the end of the test with standard test time limit 125 min, or (b) reaching the heart rate limit (HRlim = 220 − age), or (c) reaching the body core temperature/rectal temperature limit (Tre,lim = 38.5 °C), or (d) proband’s own request (headache, unbearably hot, nausea, breathing problems, etc.).
- Monitored values: heart rate (HR in BPM = beats per minute), body core temperature = measured rectal temperature (Tre) in (°C), skin temperature (Tsk) (°C), and sweat production in (g·m−2·h−1).
- Physiological parameter measurement systems: Viridia (HR, Tre), Almemo (Tsk).
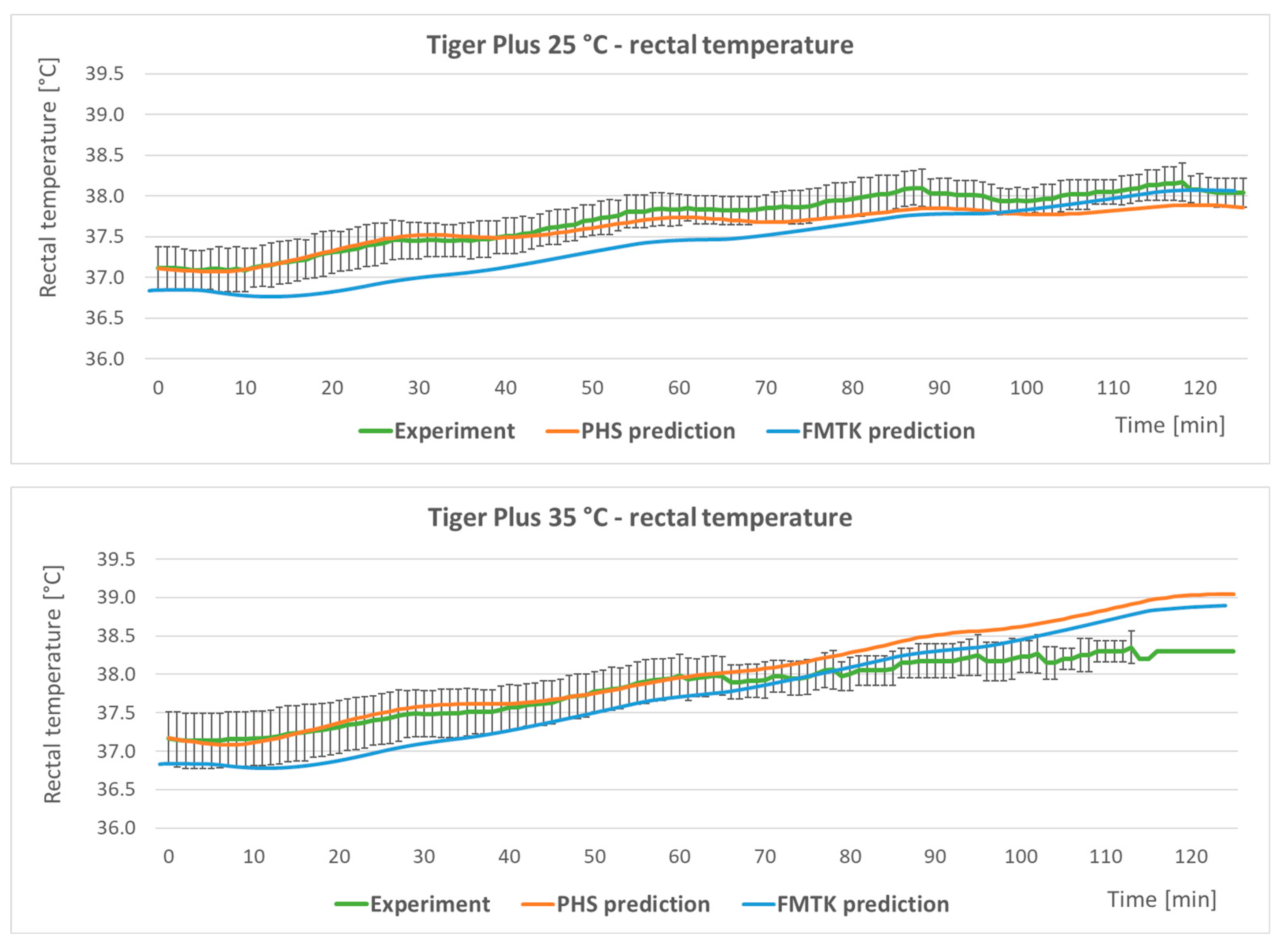
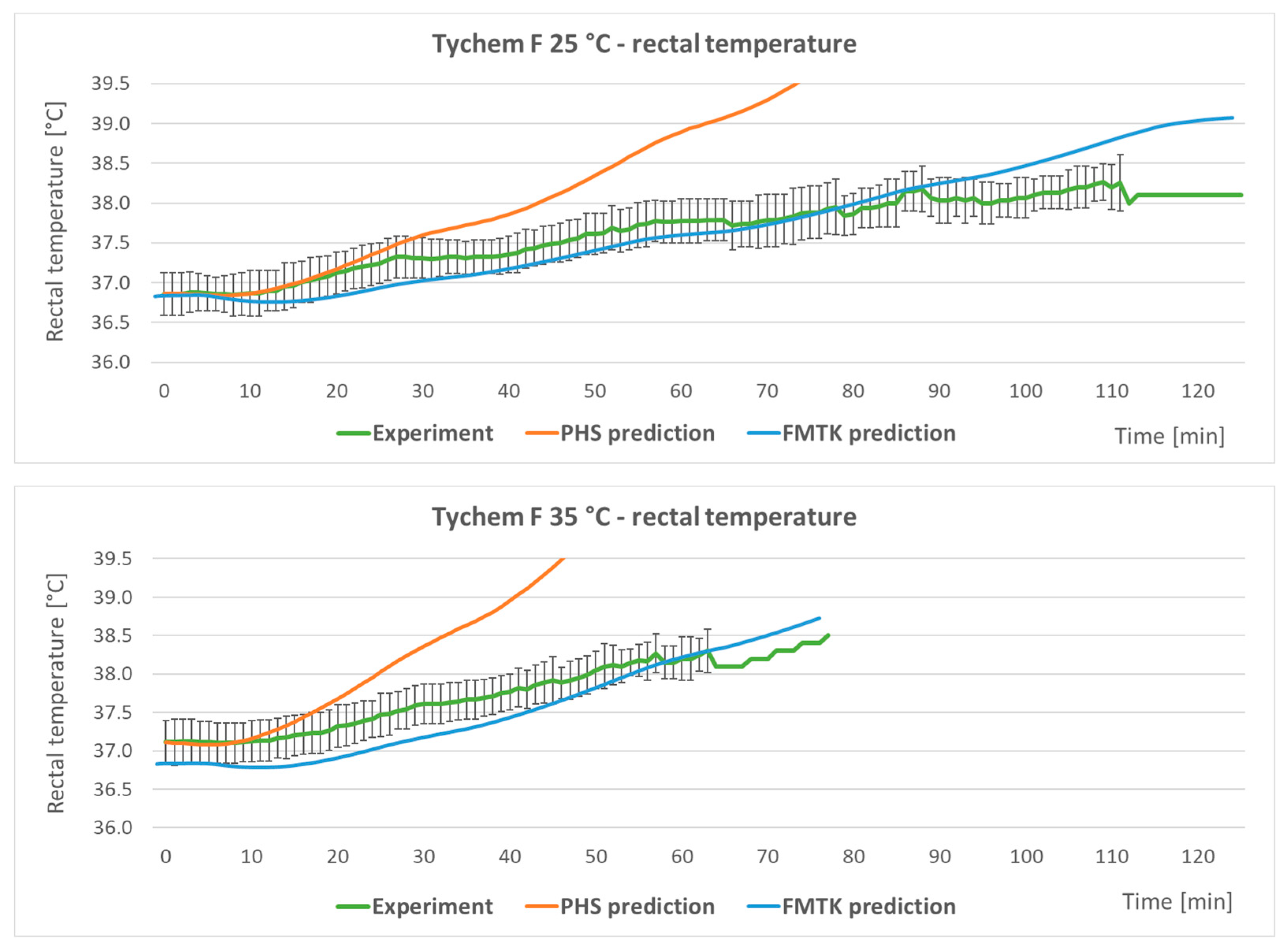
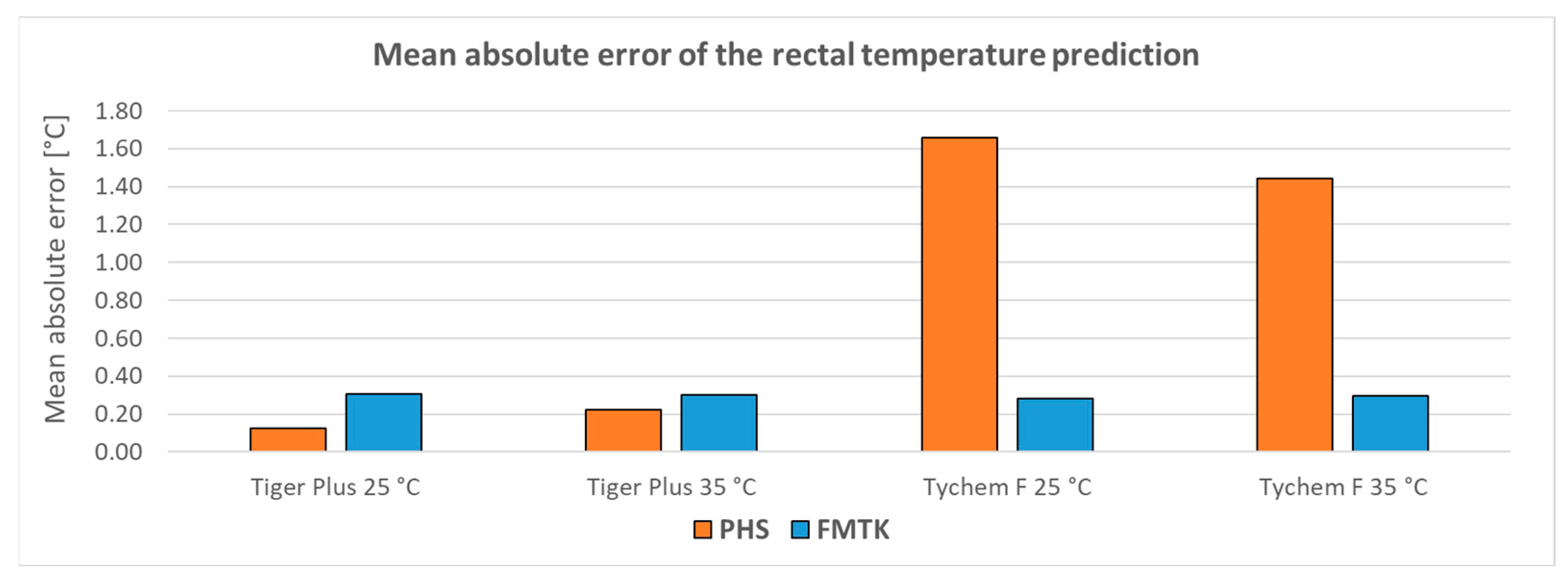
2.3. Verification of Usability of the Thermophysiological PHS and FMTK Models
- The predicted heat strain (PHS) model is described in the ISO standard 7933 [19] and is intended for the prediction of body core temperature, mean skin temperature, and intensity of sweating. The PHS is a simpler and less time-consuming model in comparison with the FMTK model below. The validity range of the PHS model is shown in Table 1 [19,30].
- The FIALA-based model of thermal comfort (FMTK) [15,20] is based on the calculation of heat exchange in the body with respect to the individual anthropometric data of the user, external climatic conditions, thermal insulating properties of the protective ensemble, and expected intensity of physical activity. The FMTK model works as a dynamic model, i.e., it consists of a system of partial differential equations of heat transfer in human tissues. The FMTK model is based on the numerical solution of heat transfer in the human body with a resolution of 19 human body segments and provides a prediction of the mean skin temperature, rectal temperature, and local skin temperatures. The validity range of the model is shown in Table 1 [15,20].
- MAE—Mean absolute error;
- n—Number of measurements;
- xi—Measured values;
- yi—Simulated values.
- MAPE—Mean absolute percentage error;
- n—Number of measurements;
- xi—Measured values;
- yi—Predicted values.
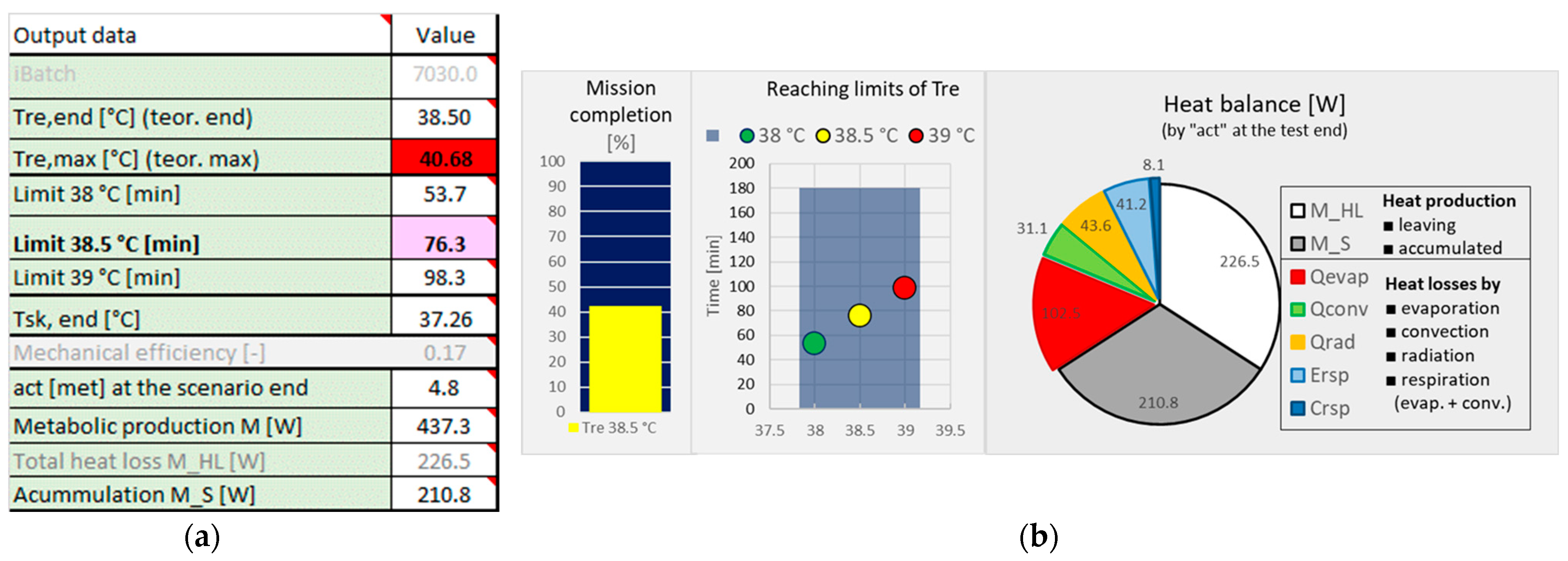
2.4. Creating of the Predictor of Thermal Stress Tool
3. Results
3.1. Thermal Insulation Characteristics of Protective Ensembles
3.2. Testing of the Physiological Strain in Climatic Chamber
3.3. Validation of PHS and FMTK Thermophysiological Models
3.4. Creating of Predictor of Thermal Stress Tool
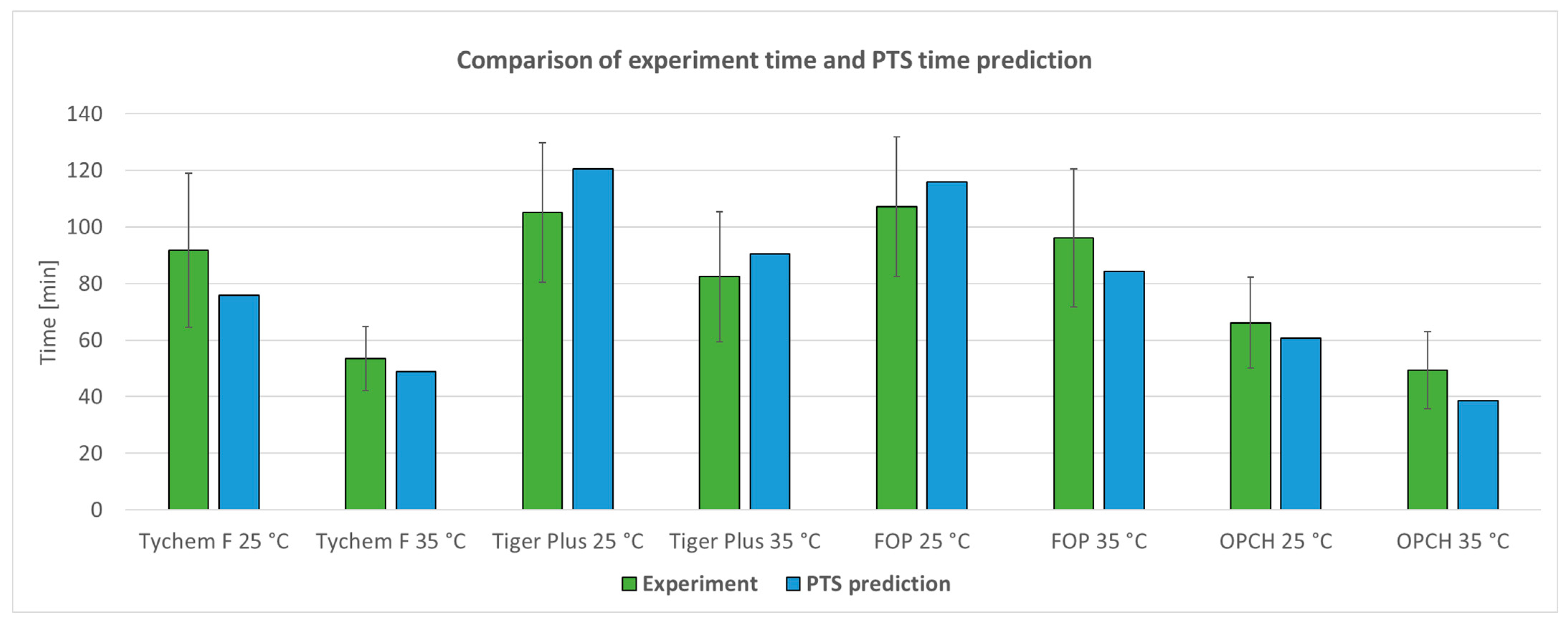
3.5. Validation of the PTS Tool Using Real Tests in Climatic Chamber
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghiyasa, S.; Nabizadeh, H.; Jazari, M.; Soltanzadeh, A.; Heidari, H.; Fardi, A.; Movahed, E. The Effect of Personal Protective Equipment on Thermal Stress: An Experimental Study on Firefighters. Work 2020, 67, 141–147. [Google Scholar] [CrossRef] [PubMed]
- Davey, S.L.; Lee, B.J.; Robbins, T.; Randeva, H.; Thake, C.D. Heat Stress and PPE during COVID-19: Impact on Healthcare Workers’ Performance, Safety and Well-Being in NHS Settings. J. Hosp. Infect. 2020, 108, 185–188. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liu, J.; Kim, M.K.; Zhou, S.; Du, Y. Experimental Investigation on Thermal Comfort of COVID-19 Nucleic Acid Sampling Staff in Hot and Humid Environment: A Pilot Study of University Students. Appl. Sci. 2021, 11, 11492. [Google Scholar] [CrossRef]
- Goldman, R.F. Heat Stress in Industrial Protective Encapsulating Garments. In Protecting Personnel at Hazardous Waste Sites; Elsevier: Amsterdam, The Netherlands, 2000; pp. 295–355. [Google Scholar] [CrossRef]
- Havenith, G.; den Hartog, E.; Martini, S. Heat Stress in Chemical Protective Clothing: Porosity and Vapour Resistance. Ergonomics 2011, 54, 497–507. [Google Scholar] [CrossRef] [PubMed]
- Morrisey, M.; Wang, F. Air and water perfusion-based cooling systems (PCSs) to protect against heat stress in protective clothing. In Protective Clothing: Managing Thermal Stress, 1st ed.; Wang, F., Gao, C., Eds.; Woodhead Publishing: Sawston, UK, 2014; Chapter 12; pp. 296–315. [Google Scholar]
- Gao, C. Phase-change material (PCMs) for warming or cooling in protective clothing. In Protective Clothing: Managing Thermal Stress, 1st ed.; Wang, F., Gao, C., Eds.; Woodhead Publishing: Sawston, UK, 2014; Chapter 9; pp. 227–248. [Google Scholar]
- Kim, E. Shape-memory alloys (SMAs) for warming or cooling in protective clothing. In Protective Clothing: Managing Thermal Stress, 1st ed.; Wang, F., Gao, C., Eds.; Woodhead Publishing: Sawston, UK, 2014; Chapter 10; pp. 250–280. [Google Scholar]
- Kuklane, K.; Toma, R.; Lucas, R.A.I. Insulation and Evaporative Resistance of Clothing for Sugarcane Harvesters and Chemical Sprayers, and Their Application in PHS Model-Based Exposure Predictions. Int. J. Environ. Res. Public Health 2020, 17, 3074. [Google Scholar] [CrossRef]
- Havenith, G.; Fiala, D. Thermal Indices and Thermophysiological Modeling for Heat Stress. Compr. Physiol. 2016, 6, 255–302. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Wissler, E.H. A Mathematical Model of the Human Thermal System. Bull. Math. Biophys. 1964, 26, 147–166. [Google Scholar] [CrossRef]
- Stolwijk, J.A.J. A Mathematical Model of Physiological Temperature Regulation in Man; NASA: Washington, DC, USA, 1971.
- Gagge, A.P.; Fobelets, A.P.; Berglund, L.G. A Standard Predictive Index of Human Response to the Thermal Environment. ASHRAE Trans. 1986, 92, 709–731. [Google Scholar]
- Fiala, D. Dynamic Simulation of Human Heat Transfer and Thermal Comfort. Ph.D. Thesis, De Montfort University, Leicester, UK, 1998. [Google Scholar]
- Fiala, D.; Lomas, K.J.; Stoher, M. A Computer Model of Human Thermoregulation for a Wide Range of Environmental Conditions: The Passive System. J. Appl. Physiol. 1999, 87, 1957–1972. [Google Scholar] [CrossRef]
- Schellen, L.; Loomans, M.G.L.C.; Kingma, B.R.M.; de Wit, M.H.; Frijns, A.J.H.; van Marken Lichtenbelt, W.D. The Use of a Thermophysiological Model in the Built Environment to Predict Thermal Sensation. Build. Environ. 2013, 59, 10–22. [Google Scholar] [CrossRef]
- Katić, K.; Li, R.; Zeiler, W. Thermophysiological Models and Their Applications: A Review. Build. Environ. 2016, 106, 286–300. [Google Scholar] [CrossRef] [Green Version]
- EN ISO 7933:2004; Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Heat Stress Using Calculation of the Predicted Heat Strain. International Organization for Standardization: Geneva, Switzerland, 2004.
- Pokorný, J.; Fišer, J.; Fojtlín, M.; Kopečková, B.; Toma, R.; Slabotínský, J.; Jícha, M. Verification of Fiala-Based Human Thermophysiological Model and Its Application to Protective Clothing under High Metabolic Rates. Build. Environ. 2017, 126, 13–26. [Google Scholar] [CrossRef]
- Psikuta, A.; Fiala, D.; Laschewski, G.; Jendritzky, G.; Richards, M.; Błażejczyk, K.; Mekjavič, I.; Rintamäki, H.; de Dear, R.; Havenith, G. Validation of the Fiala Multi-Node Thermophysiological Model for UTCI Application. Int. J. Biometeorol. 2012, 56, 443–460. [Google Scholar] [CrossRef] [Green Version]
- Martínez, N.; Psikuta, A.; Kuklane, K.; Quesada, J.I.P.; de Anda, R.M.C.O.; Soriano, P.P.; Palmer, R.S.; Corberán, J.M.; Rossi, R.M.; Annaheim, S. Validation of the Thermophysiological Model by Fiala for Prediction of Local Skin Temperatures. Int. J. Biometeorol. 2016, 60, 1969–1982. [Google Scholar] [CrossRef]
- Bröde, P.; Fiala, D.; Błażejczyk, K.; Holmér, I.; Jendritzky, G.; Kampmann, B.; Tinz, B.; Havenith, G. Deriving the Operational Procedure for the Universal Thermal Climate Index (UTCI). Int. J. Biometeorol. 2012, 56, 481–494. [Google Scholar] [CrossRef] [Green Version]
- Kopeckova, B.; Pokorny, J.; Lunerova, K.; Fiser, J.; Jicha, M. Case Study Comparing Fiala-Based Thermophysiological Model and PHS Index with Experimental Data to Predict Heat Strain in Normal and Protective Clothing. J. Meas. Eng. 2021, 9, 36–47. [Google Scholar] [CrossRef]
- Potter, A.W.; Looney, D.P.; Santee, W.R.; Gonzalez, J.A.; Welles, A.P.; Srinivasan, S.; Castellani, M.P.; Rioux, T.P.; Hansen, E.O.; Xu, X. Validation of New Method for Predicting Human Skin Temperatures during Cold Exposure: The Cold Weather Ensemble Decision Aid (CoWEDA). Inf. Med. Unlocked 2020, 18, 100301. [Google Scholar] [CrossRef]
- EN ISO 15831:2004; Clothing—Physiological Effects—Measurement of Thermal Insulation by Means of a Thermal Manikin. International Organization for Standardization: Geneva, Switzerland, 2004.
- Toma, R.; Kuklane, K.; Fojtlín, M.; Fišer, J.; Jícha, M. Using a Thermal Manikin to Determine Evaporative Resistance and Thermal Insulation—A Comparison of Methods. J. Ind. Text. 2021, 50, 1493–1515. [Google Scholar] [CrossRef]
- ISO 9920:2007; Ergonomics of the Thermal Environment—Estimation of Thermal Insulation and Water Vapour Resistance of a Clothing Ensemble. International Organization for Standardization: Geneva, Switzerland, 2007.
- Fojtlín, M.; Fišer, J.; Jícha, M. Determination of Convective and Radiative Heat Transfer Coefficients using 34-zones Thermal Manikin: Uncertainty and Reproducibility Evaluation. Exp. Fluid Sci. 2016, 77, 257–264. [Google Scholar] [CrossRef]
- Malchaire, J.; Piette, A.; Kampmann, B.; Mehnert, P.; Gebhardt, H.; Havenith, G.; Den Hartog, E.; Holmer, I.; Parsons, K.; Alfano, G.; et al. Development and Validation of the Predicted Heat Strain Model. Ann. Occup. Hyg. 2001, 45, 123–135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ainsworth, B.E.; Haskell, W.L.; Herrmann, S.D.; Meckes, N.; Bassett, D.R.; Tudor-Locke, C.; Greer, J.L.; Vezina, J.; Whitt-Glover, M.C.; Leon, A.S. 2011 Compendium of Physical Activities. Med. Sci. Sport. Exerc. 2011, 43, 1575–1581. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Threshold Limit Values (TLVs®); Biological Exposure Indices (BEIs®). American Conference of Governmental Industrial Hygienists; ACGIH: Cincinnati, OH, USA, 2017. [Google Scholar]
- O’Brien, C.; Blanchard, L.A.; Cadarette, B.S.; Endrusick, T.L.; Xu, X.; Berglund, L.G.; Sawka, M.N.; Hoyt, R.W. Methods for Evaluating Protective Clothing Relative to Heat and Cold Stress: Thermal Manikin, Biomedical Modeling and Human Testing. J. Occup. Environ. Hyg. 2011, 8, 588–599. [Google Scholar] [CrossRef]
- Miller, V.S.; Bates, G.P. The Thermal Work limit is a Simple Reliable Heat Index for the Protection of Workers in Thermally Stressful Environments. J. Occup. Environ. Hyg. 2021, 18, 430–435. [Google Scholar] [CrossRef]
- Flouris, A.D.; Ioannou, L.G.; Dinas, P.C.; Mantzios, K.; Gkiata, P.; Gkikas, G.; Vliora, M.; Amorim, T.; Tsoutsoubi, L.; Kapnia, A. Assessment of Occupational Heat Stain and Mitigation Strategies in Qatar; Report No. FL/2019/13; International Labour Organization: Doha, Qatar, 2019. [Google Scholar]
- Herstein, J.J.; Abdoulaye, A.A.; Jelden, K.C.; Le, A.B.; Beam, E.L.; Gibbs, S.G.; Hewlett, A.L.; Vasa, A.; Boulter, K.C.; Stentz, T.L.; et al. A pilot study of Core Body Temperatures in Health Workers Wearing Personal Protective Equipment in High-level Isolation Unit. Occup. Environ. Hyg. 2021, 18, 430–435. [Google Scholar] [CrossRef]
- Nielsen, B.; Hales, J.R.S.; Strange, S.; Christensen, N.J.; Warberg, J.; Saltin, B. Human Circulatory and Thermoregulatory Adaptations with Heat Acclimation and Exercise in a Hot, Dry Environment. J. Physiol. 1993, 460, 467–485. [Google Scholar] [CrossRef]




| Parameter | PHS | FMTK | ||
|---|---|---|---|---|
| Min | Max | Min | Max | |
| Ta (°C) | 15 | 50 | 5 | 48 |
| pa (kPa) | 0 | 4.5 | ||
| Trad–Ta (°C) | 0 | 60 | ||
| va (m·s−1) | 0 | 3 | ||
| M (W) | 100 | 450 | 46 | 522 |
| Icl (clo) | 0.1 | 1.0 | 0.01 | 1.08 |
| Input * | Variations | v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ta (°C) | 9 | −10 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 45 |
| RH (%) | 3 | 0 | 0.5 | 1 | ||||||
| v (m/s) | 2 | 0.05 | 1 or M/3.5 | |||||||
| M (met) | 6 | 1 | 2.2 | 3.5 | 4.8 | 6.5 | 8.5 | |||
| Ensemble | 6 | Underwear | FOP + mask | TP | TP + SCBA | TF + mask | OPCH + SCBA | |||
| Work regime | 6 | 1 | 2 | 3 | 4 | 5 | 6 | |||
| Scenarios | 11,664 |
| No. | Variant |
|---|---|
| 1 | Easy access + 1 h work (83 min in total) |
| 2 | Difficult access + 1 h work (83 min in total) |
| 3 | Easy access + 2.6 h work (180 min in total) |
| 4 | Difficult access + 2.6 h work (180 min in total) |
| 5 | Constant (uninterrupted) work 3 h (180 min in total) |
| 6 | Intermittent activity: 20 min work + 10 min rest (repeated, 180 min in total) |
| TF + CM-6 | OPCH + SCBA | FOP + CM-6 | TP | TP + SCBA | |
|---|---|---|---|---|---|
| Total thermal insulation of clothing IT (clo) | |||||
| (a) | 1.66 | 1.55 | 1.95 | 2.06 | 2.19 |
| (b) | 1.73 | 1.73 | 2.12 | - | 2.23 |
| Evaporation resistance ReT (kPa·m2/W) | |||||
| (a) | 0.301 | 1.098 | 0.059 | 0.052 | 0.057 |
| (b) | - | - | 0.063 | - | 0.069 |
| Static clothing permeability index im (-) | |||||
| (a) | 0.05 | 0.01 | 0.31 | 0.36 | 0.36 |
| (b) | - | - | 0.31 | - | 0.30 |
| Ta [°C] | TF + CM-6 | OPCH + SCBA | FOP + CM-6 | TP | TP + SCBA |
|---|---|---|---|---|---|
| −10 Time Tre,0 Tre,max |  n = 9 |  n = 1 |  n = 4 |  n = 4 | 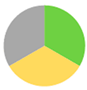 n = 3 |
| 102 ± 26 min 37.2 ± 0.33 (°C) | 65 min 37.0 °C | 125 ± 0 min 37.0 ± 0.25 (°C) | 125 ± 0 min 37.2 ± 0.27 (°C) | 82 ± 37 min 37.0 ± 0.26 (°C) | |
| 37.9 ± 0.33 (°C) | 38.0 °C | 37.7 ± 0.42 (°C) | 38.0 ± 0.38 (°C) | 37.5 ± 0.20 (°C) | |
| 5 Time Tre,0 Tre,max |  n = 3 |  n = 6 |  n = 4 |  n = 5 | 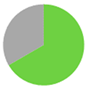 n = 3 |
| 125 ± 0 min 37.2 ± 0.03 (°C) | 86 ± 22 min 37.2 ± 0.12 (°C) | 125 ± 0 min 37.0 ± 0.25 (°C) | 125 ± 0 min 37.2 ± 0.15 (°C) | 105 ± 35 min 37.0 ± 0.06 (°C) | |
| 37.8 ± 0.23 (°C) | 37.6 ± 0.26 (°C) | 37.7 ± 0.42 (°C) | 37.8 ± 0.20 (°C) | 37.7 ± 0.21 (°C) | |
| 25 Time Tre,0 Tre,max | 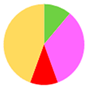 n = 9 | 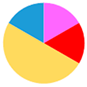 n = 6 |  n = 11 |  n = 12 |  n = 8 |
| 92 ± 27 min 36.9 ± 0.27 (°C) | 66 ± 16 min 37.2 ± 0.25 (°C) | 107 ± 25 min 37.2 ± 0.33 (°C) | 105 ± 25 min 37.1 ± 0.24 (°C) | 65 ± 19 min 37.1 ± 0.21 (°C) | |
| 38.2 ± 0.30 (°C) | 38.2 ± 0.18 (°C) | 38.1 ± 0.30 (°C) | 38.1 ± 0.26 (°C) | 37.9 ± 0.37 (°C) | |
| 35 Time Tre,0 Tre,max |  n = 9 |  n = 7 |  n = 8 |  n = 11 |  n = 8 |
| 53 ± 11 min 37.1 ± 0.28 (°C) | 49 ± 14 min 36.2 ± 0.18 (°C) | 96 ± 24 min 37.2 ± 0.28 (°C) | 82 ± 23 min 37.1 ± 0.35 (°C) | 62 ± 18 min 37.0 ± 0.29 (°C) | |
| 38.3 ± 0.26 (°C) | 38.0 ± 0.37 (°C) | 38.2 ± 0.35 (°C) | 38.2 ± 0.26 (°C) | 37.6 ± 0.26 (°C) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lunerová, K.; Řehák Kopečková, B.; Pokorný, J.; Mašín, M.; Kaiser, D.; Fialová, V.; Fišer, J. Applicability of Human Thermophysiological Model for Prediction of Thermal Strain in PPE. Appl. Sci. 2023, 13, 7170. https://doi.org/10.3390/app13127170
Lunerová K, Řehák Kopečková B, Pokorný J, Mašín M, Kaiser D, Fialová V, Fišer J. Applicability of Human Thermophysiological Model for Prediction of Thermal Strain in PPE. Applied Sciences. 2023; 13(12):7170. https://doi.org/10.3390/app13127170
Chicago/Turabian StyleLunerová, Kamila, Barbora Řehák Kopečková, Jan Pokorný, Michal Mašín, David Kaiser, Vladimíra Fialová, and Jan Fišer. 2023. "Applicability of Human Thermophysiological Model for Prediction of Thermal Strain in PPE" Applied Sciences 13, no. 12: 7170. https://doi.org/10.3390/app13127170
APA StyleLunerová, K., Řehák Kopečková, B., Pokorný, J., Mašín, M., Kaiser, D., Fialová, V., & Fišer, J. (2023). Applicability of Human Thermophysiological Model for Prediction of Thermal Strain in PPE. Applied Sciences, 13(12), 7170. https://doi.org/10.3390/app13127170






