Prediction of Reinforcement Connection Loads in Geosynthetic Reinforced Segmental Retaining Walls Using Response Surface Method
Abstract
:1. Introduction
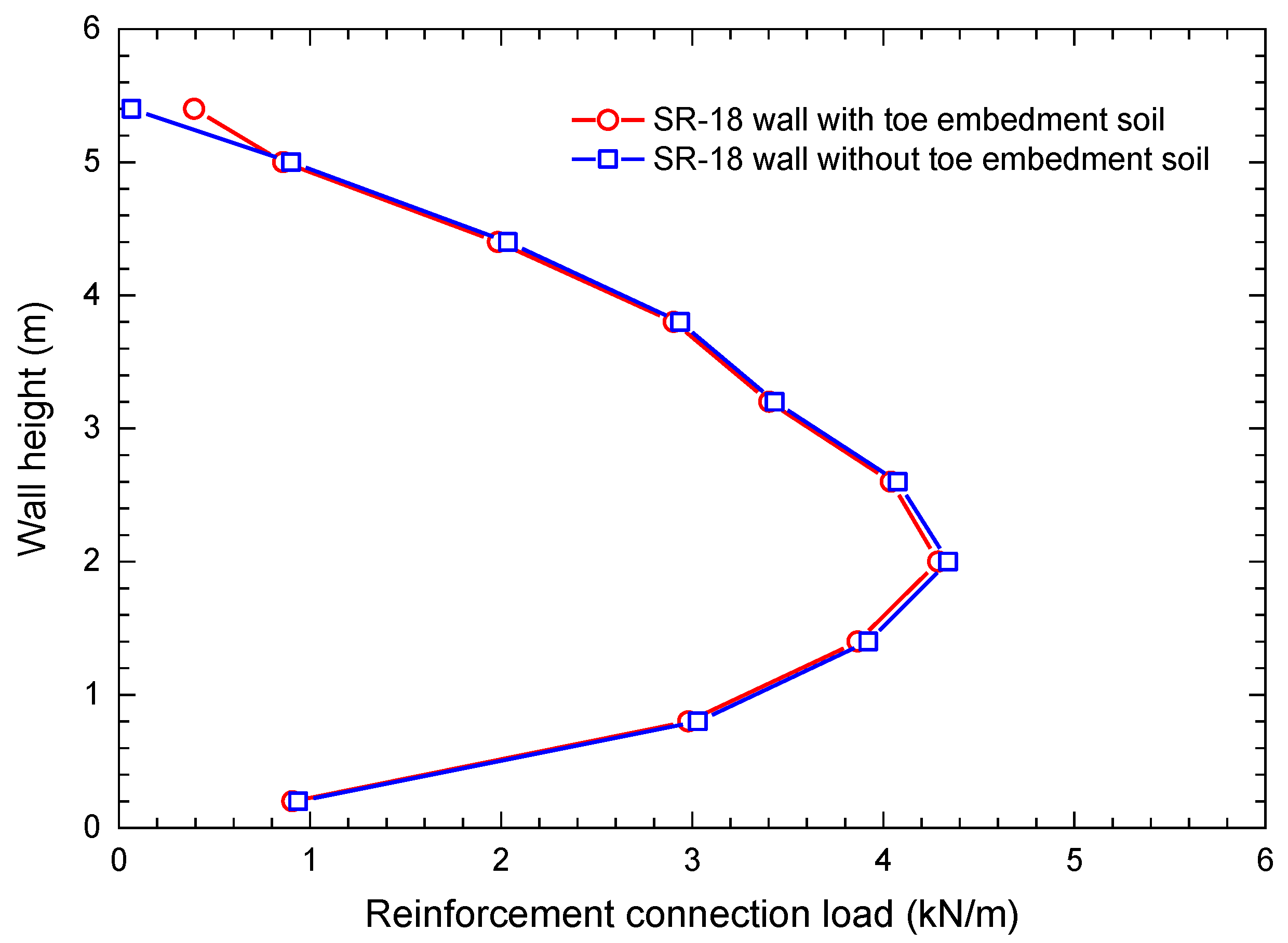
2. Numerical Model Validation
2.1. Numerical Model
2.2. Material Constitutive Model and Parameters
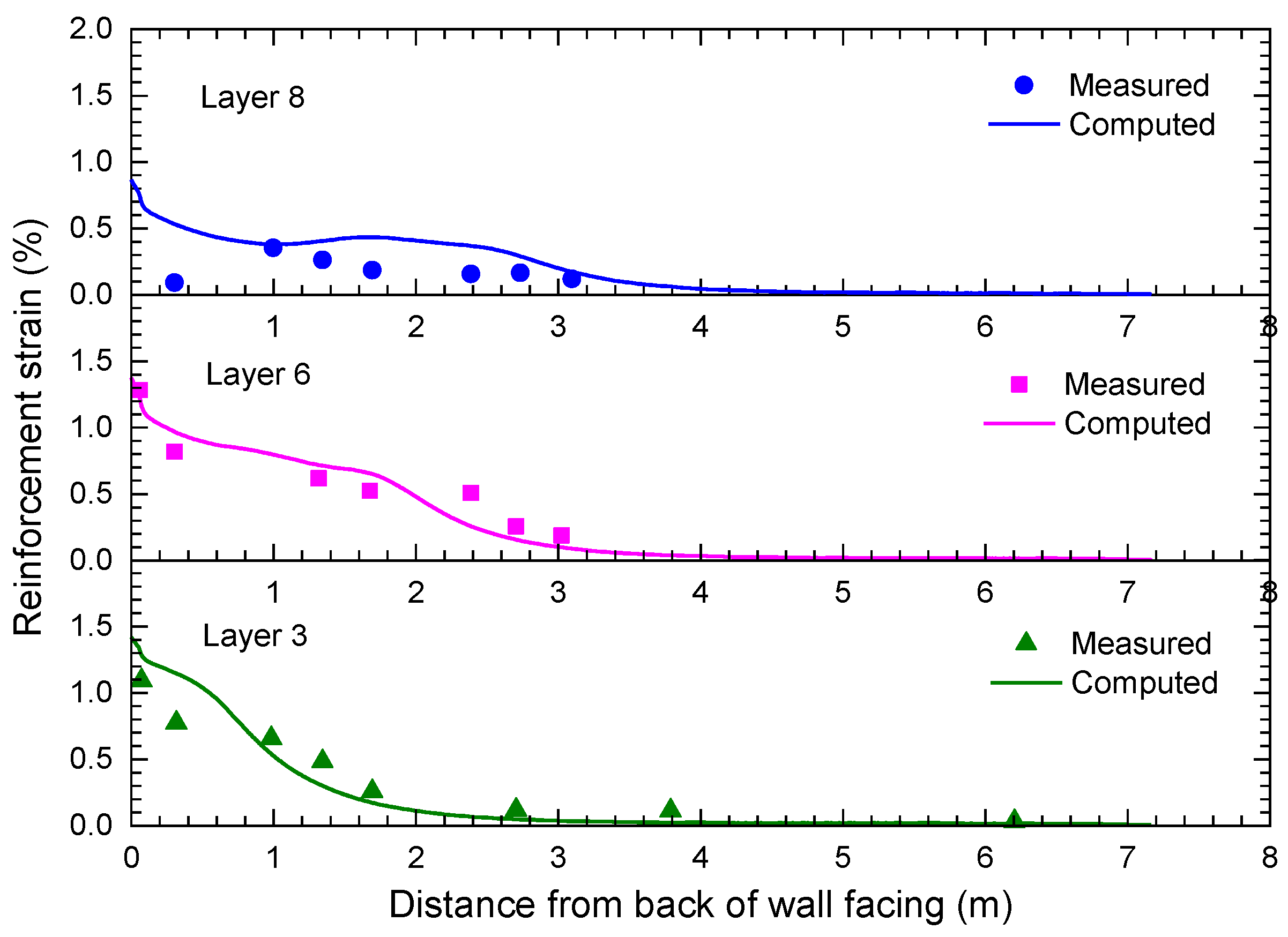
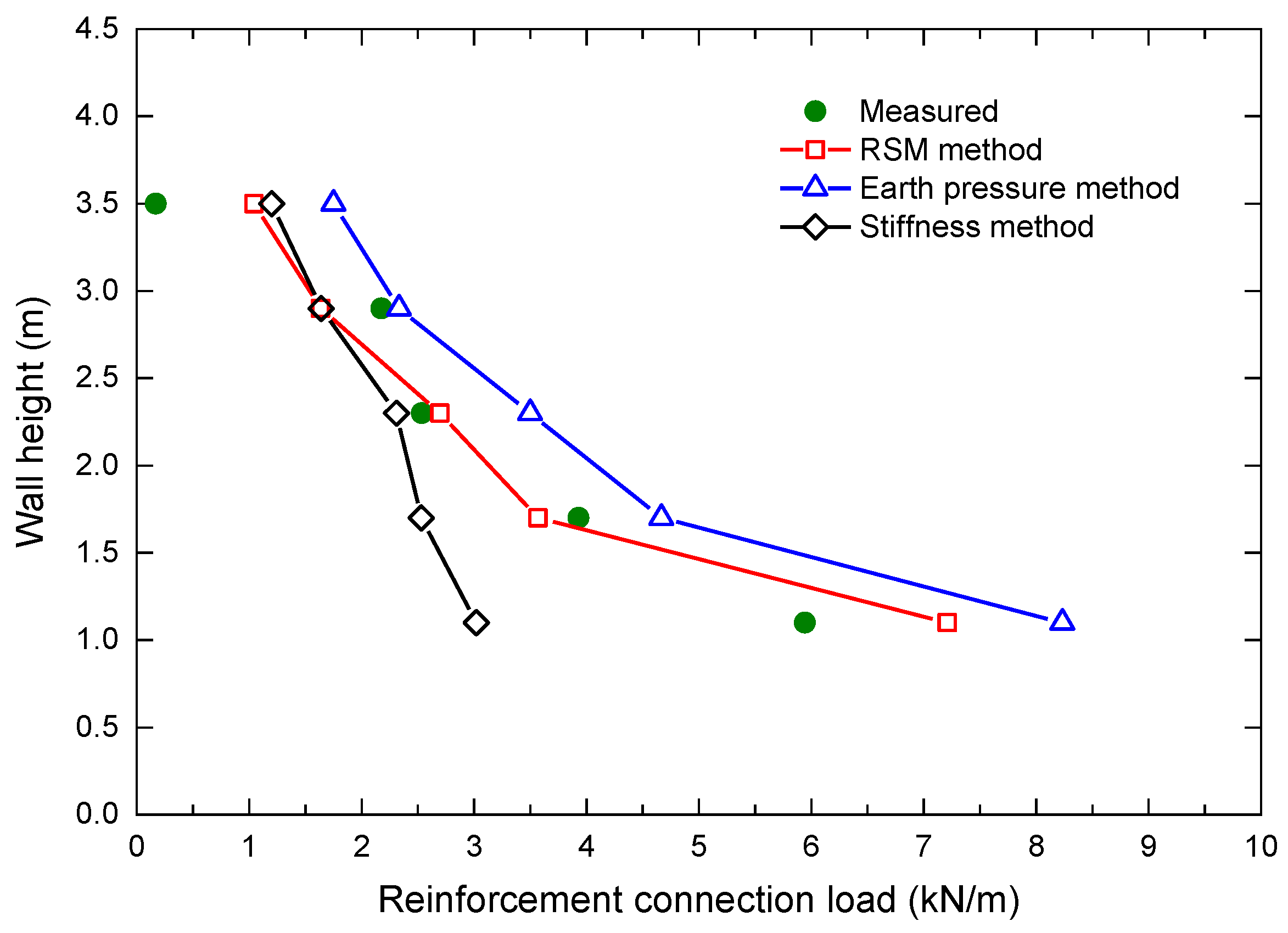
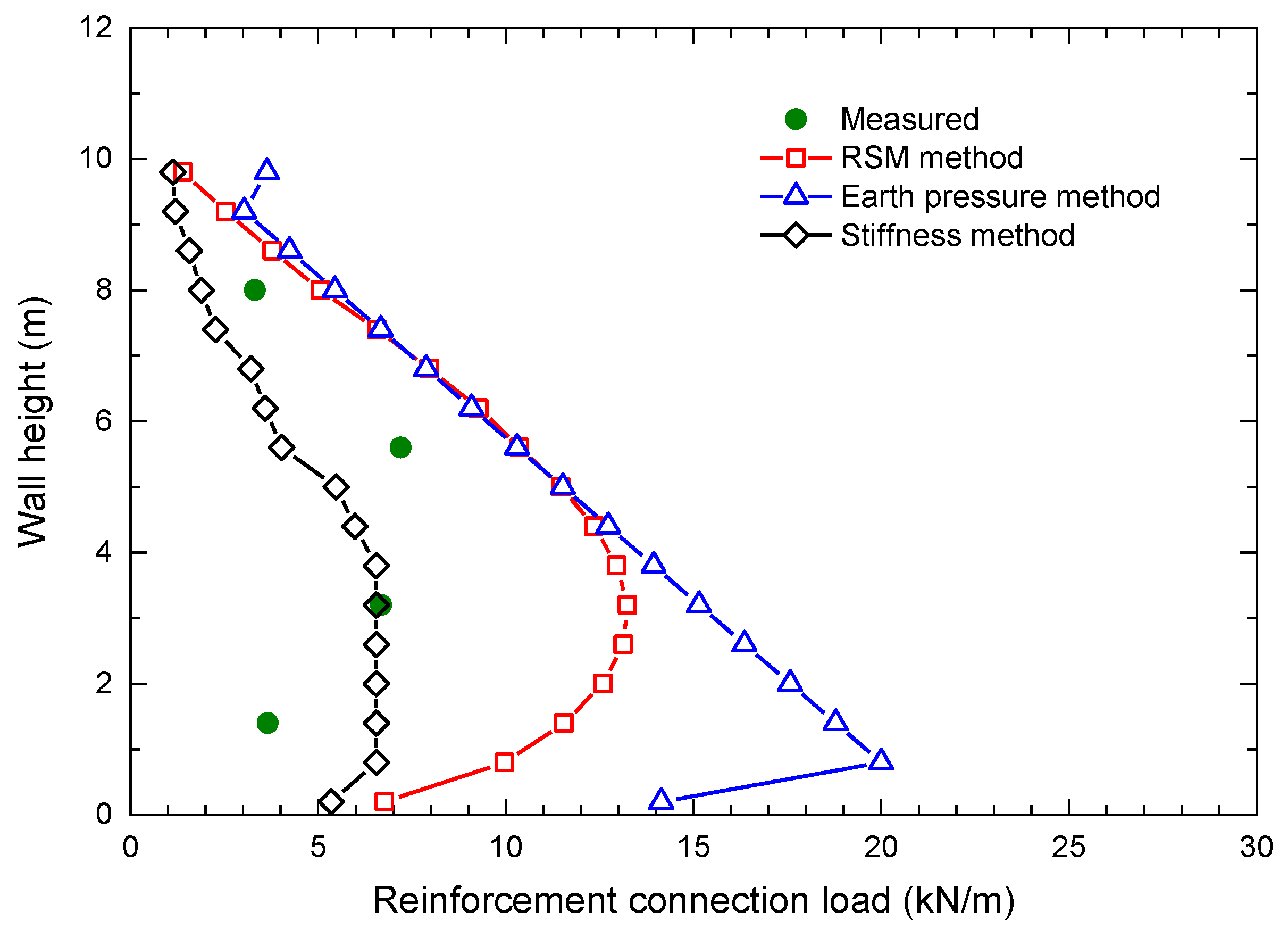
2.3. Validation Results
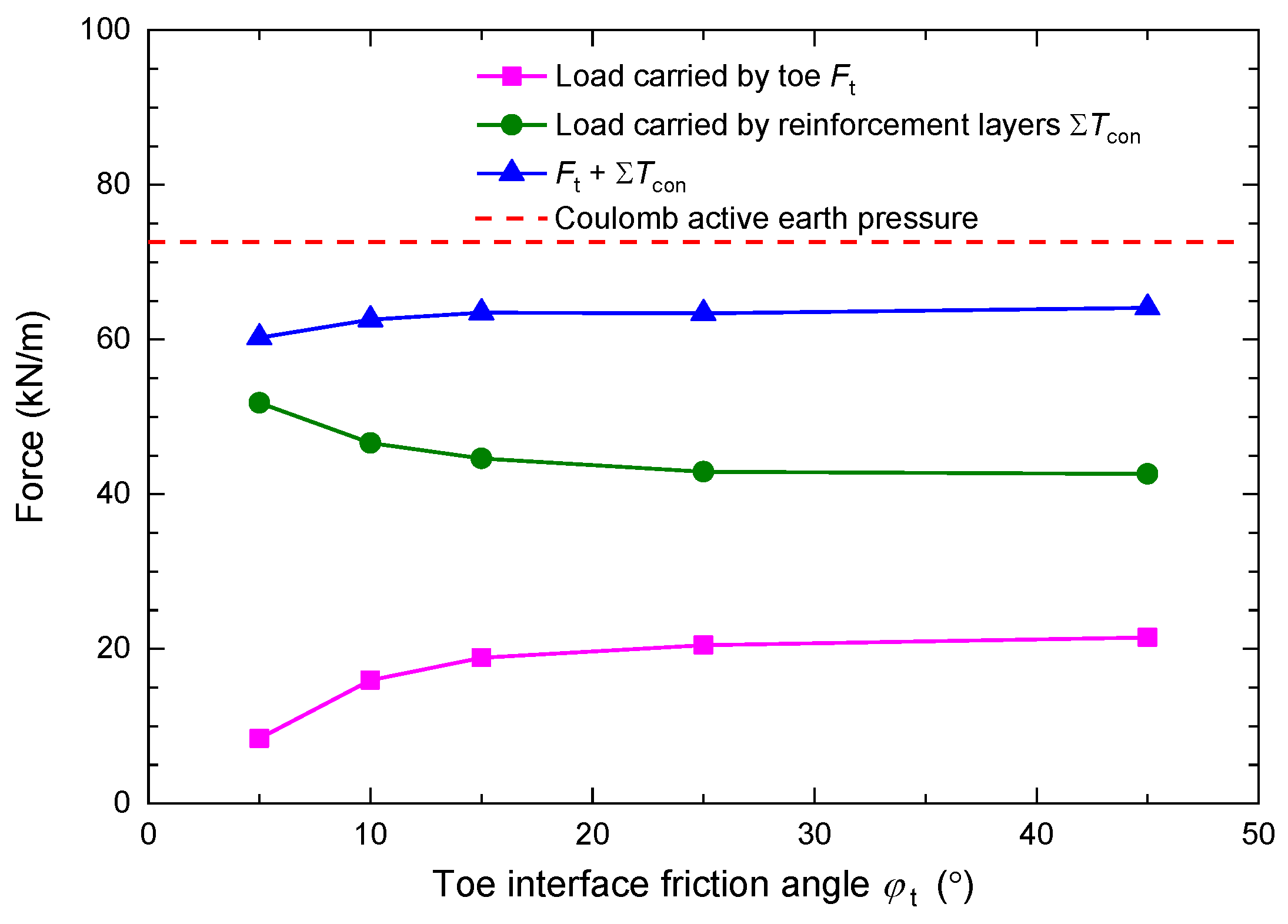
3. Toe Load Analysis
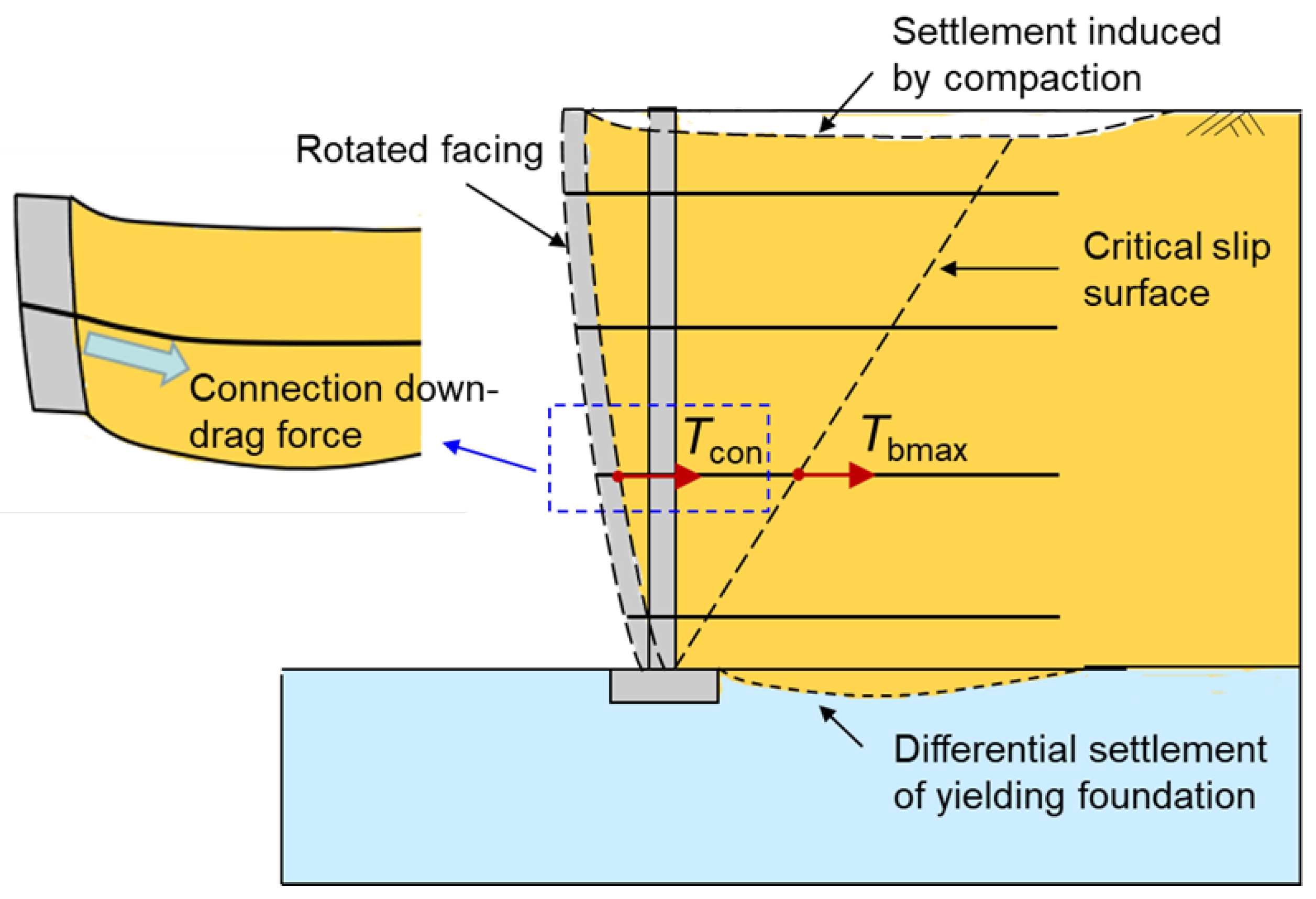
3.1. Mechanical Model of the GRS Segmental Wall
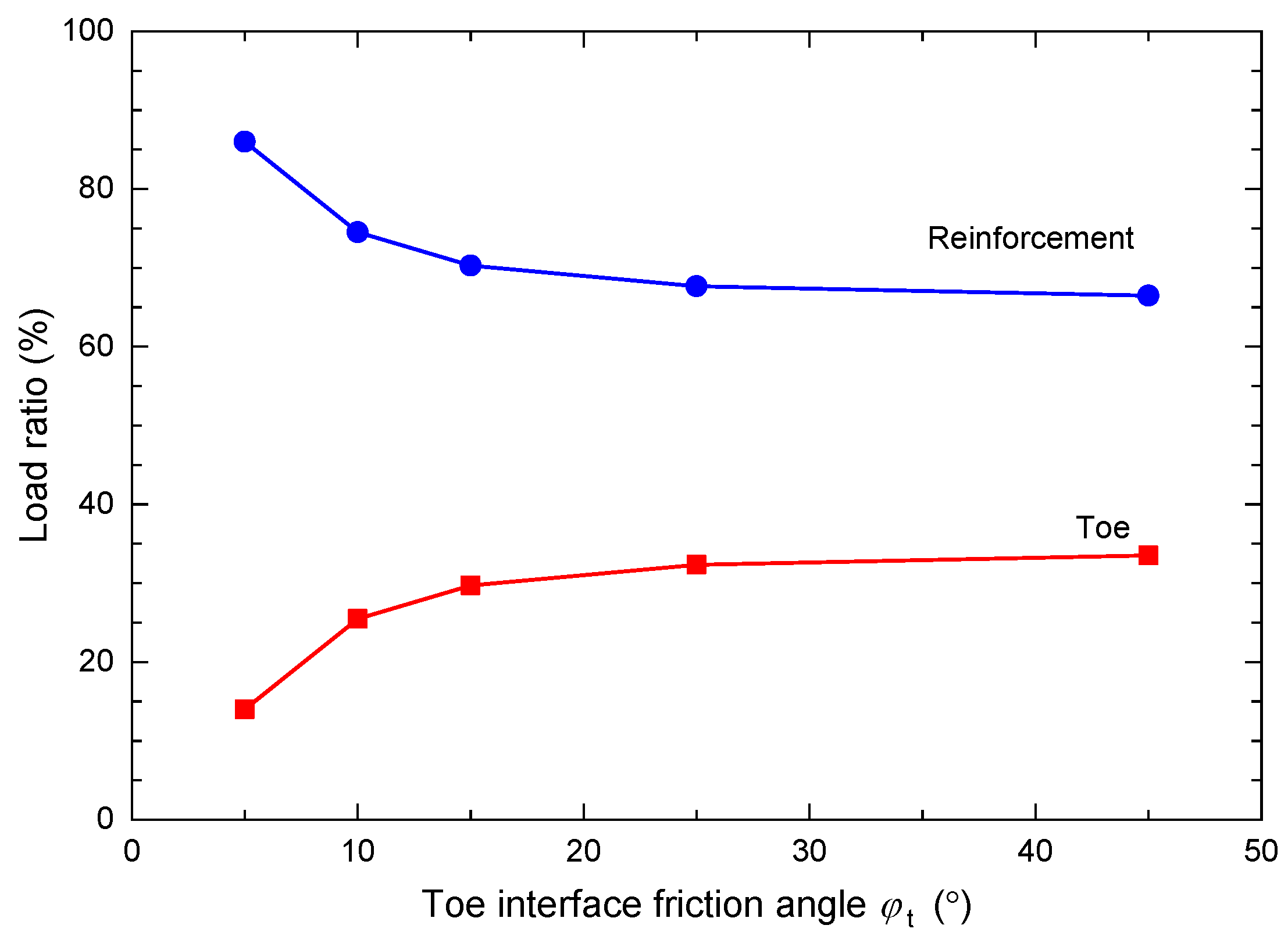
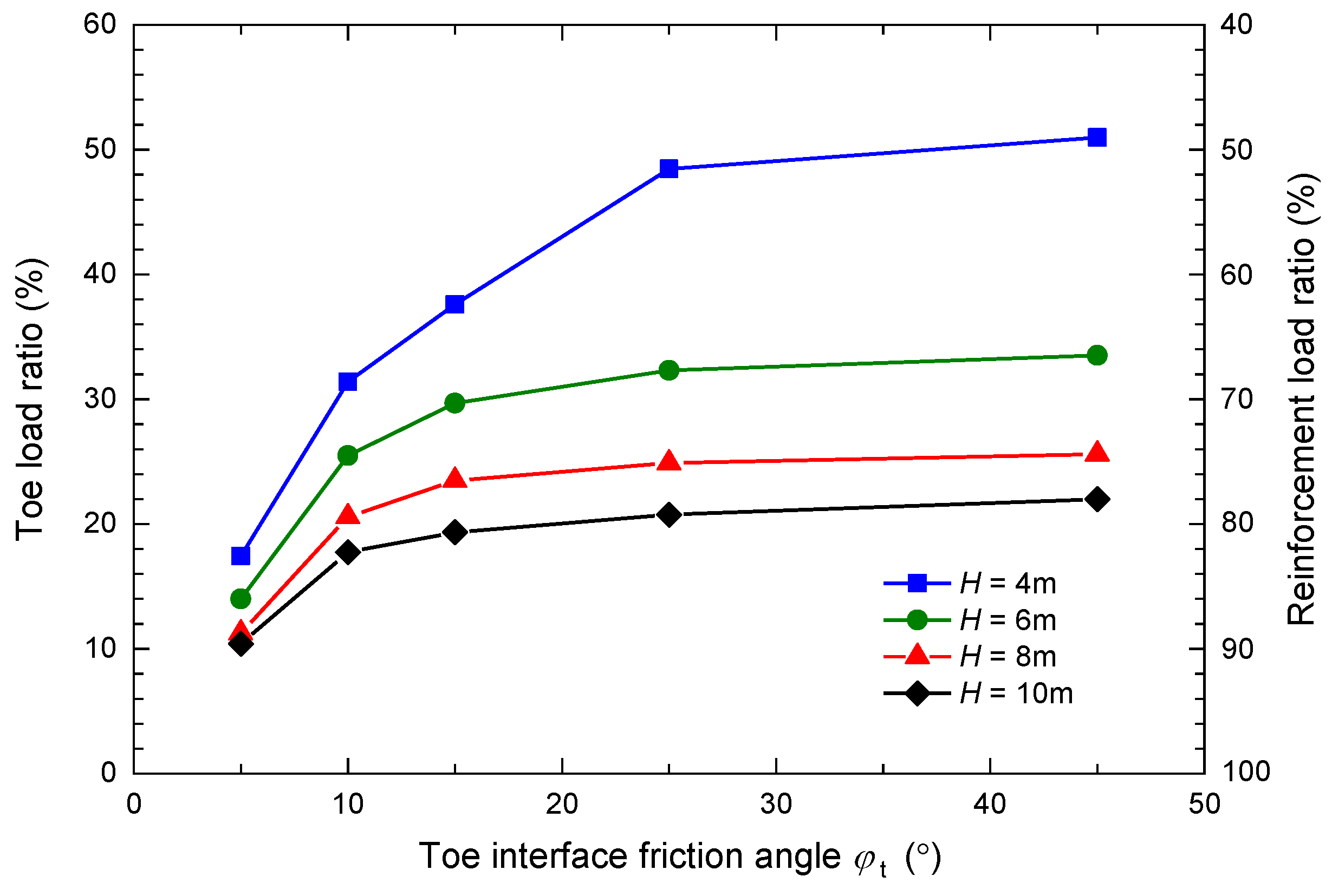
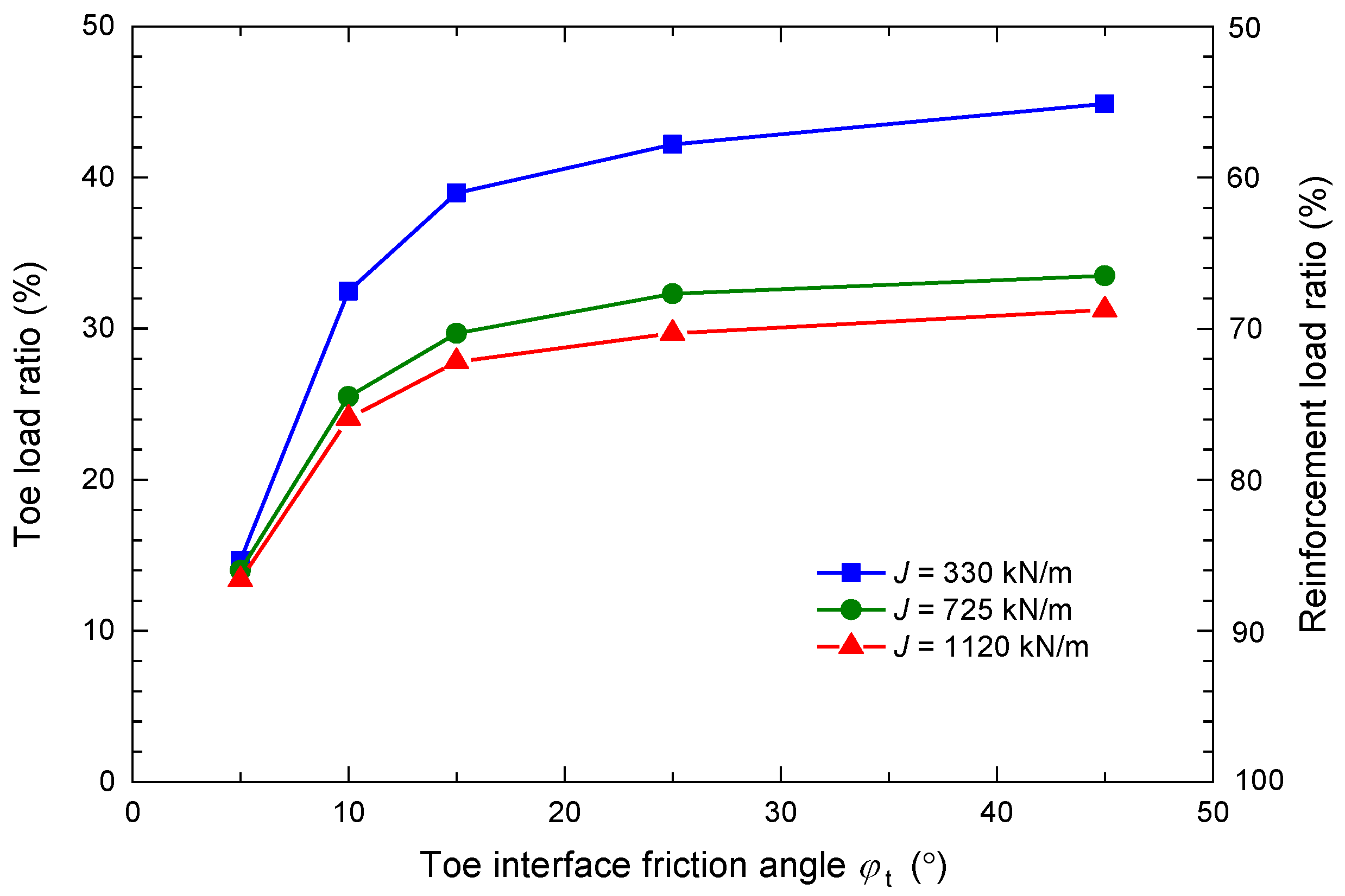
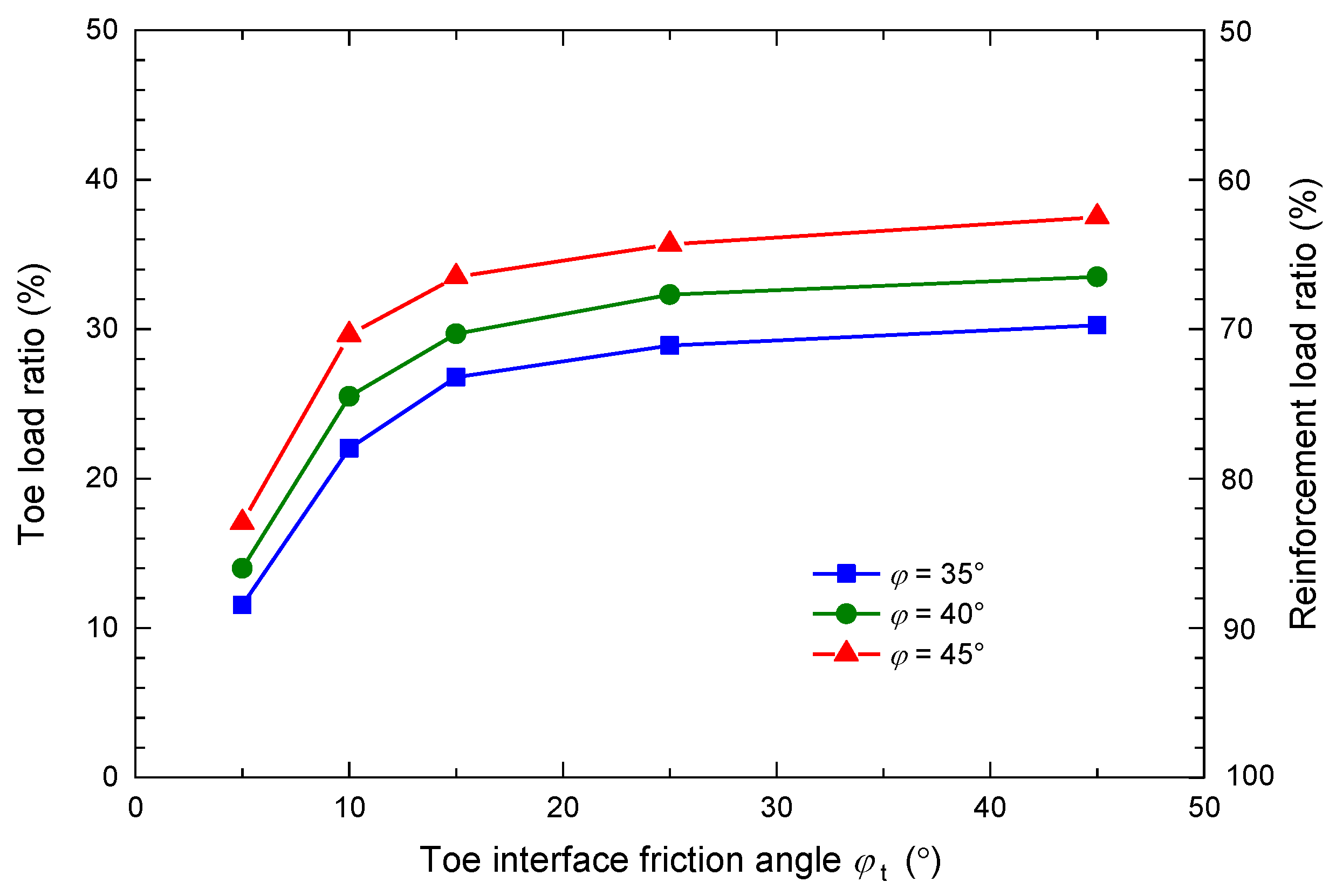
3.2. Influence Factors of the Toe Load Ratio
4. Prediction of Reinforcement Tensile Force
4.1. Calculation Method of Reinforcement Tensile Force
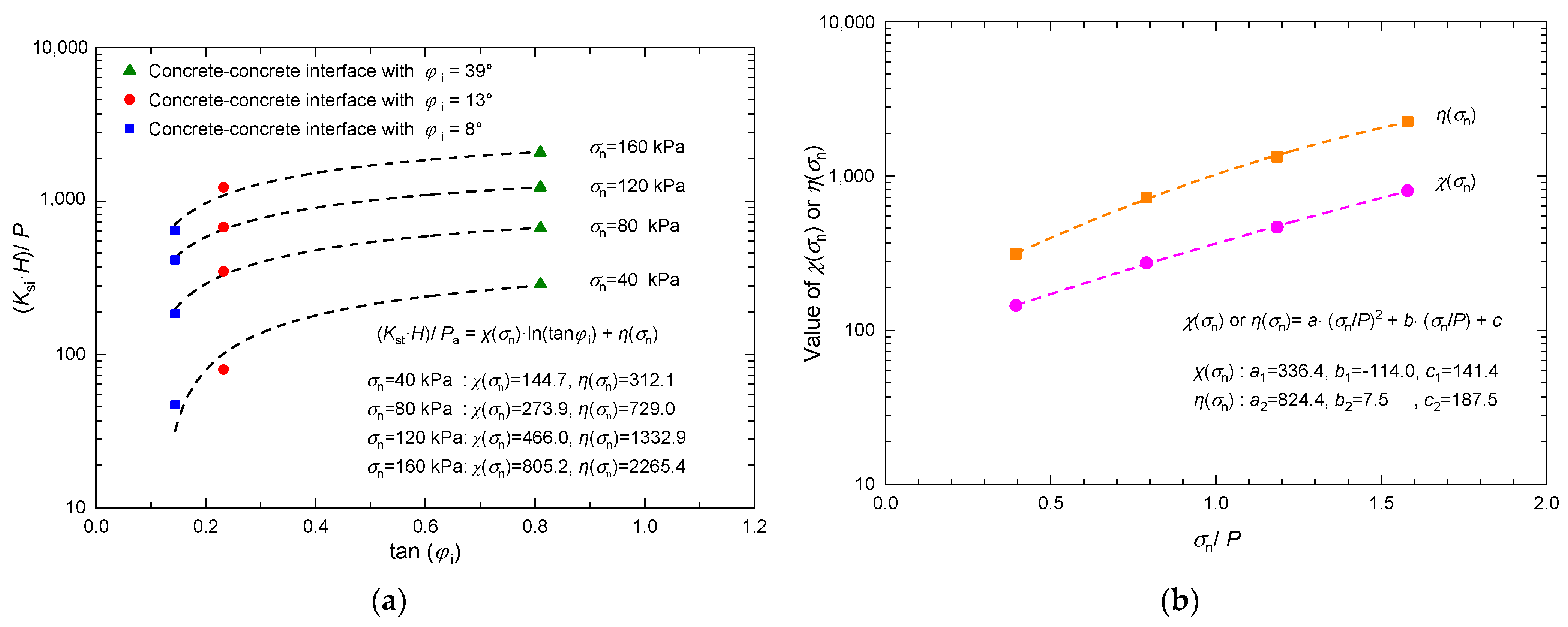
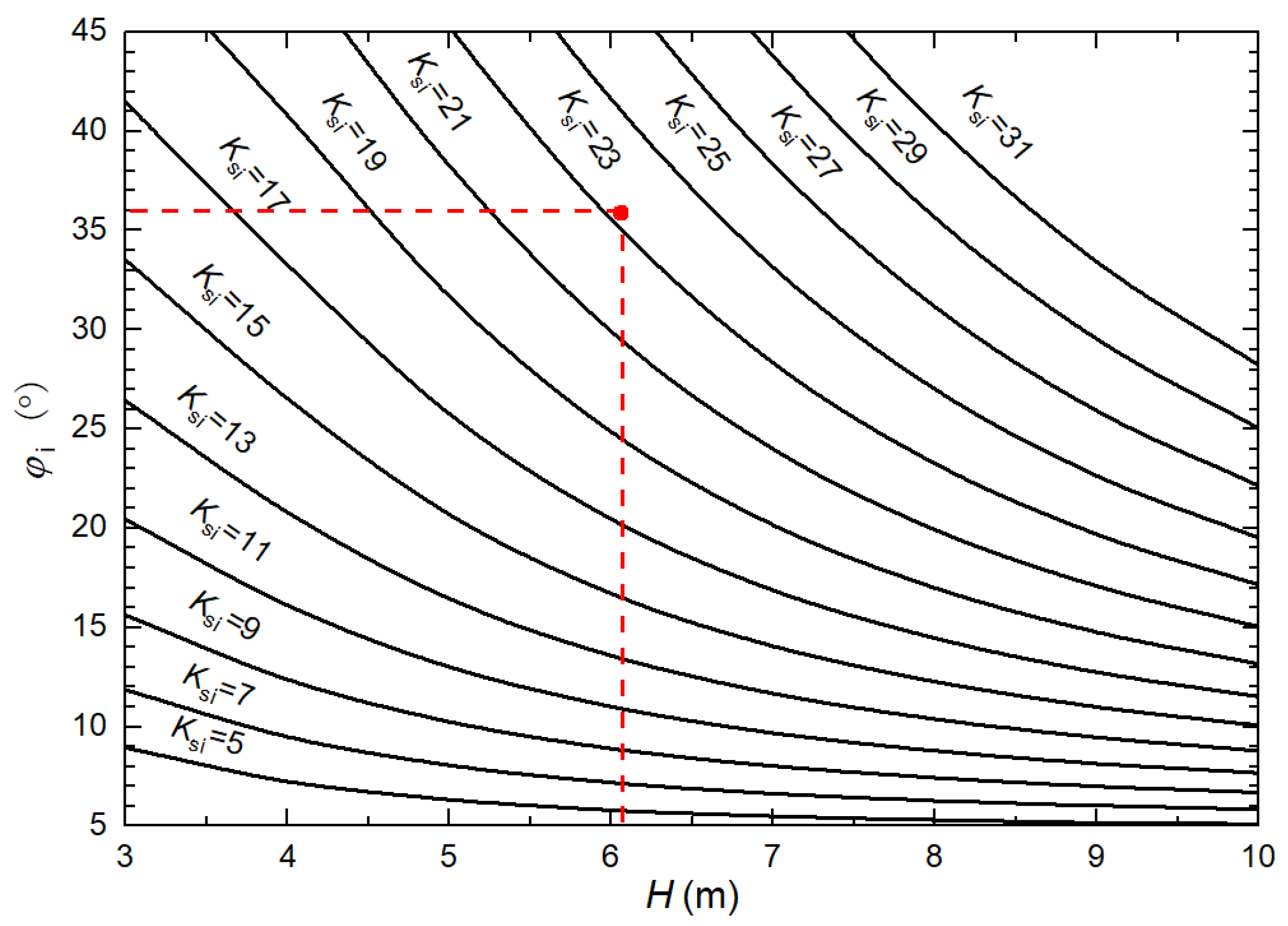
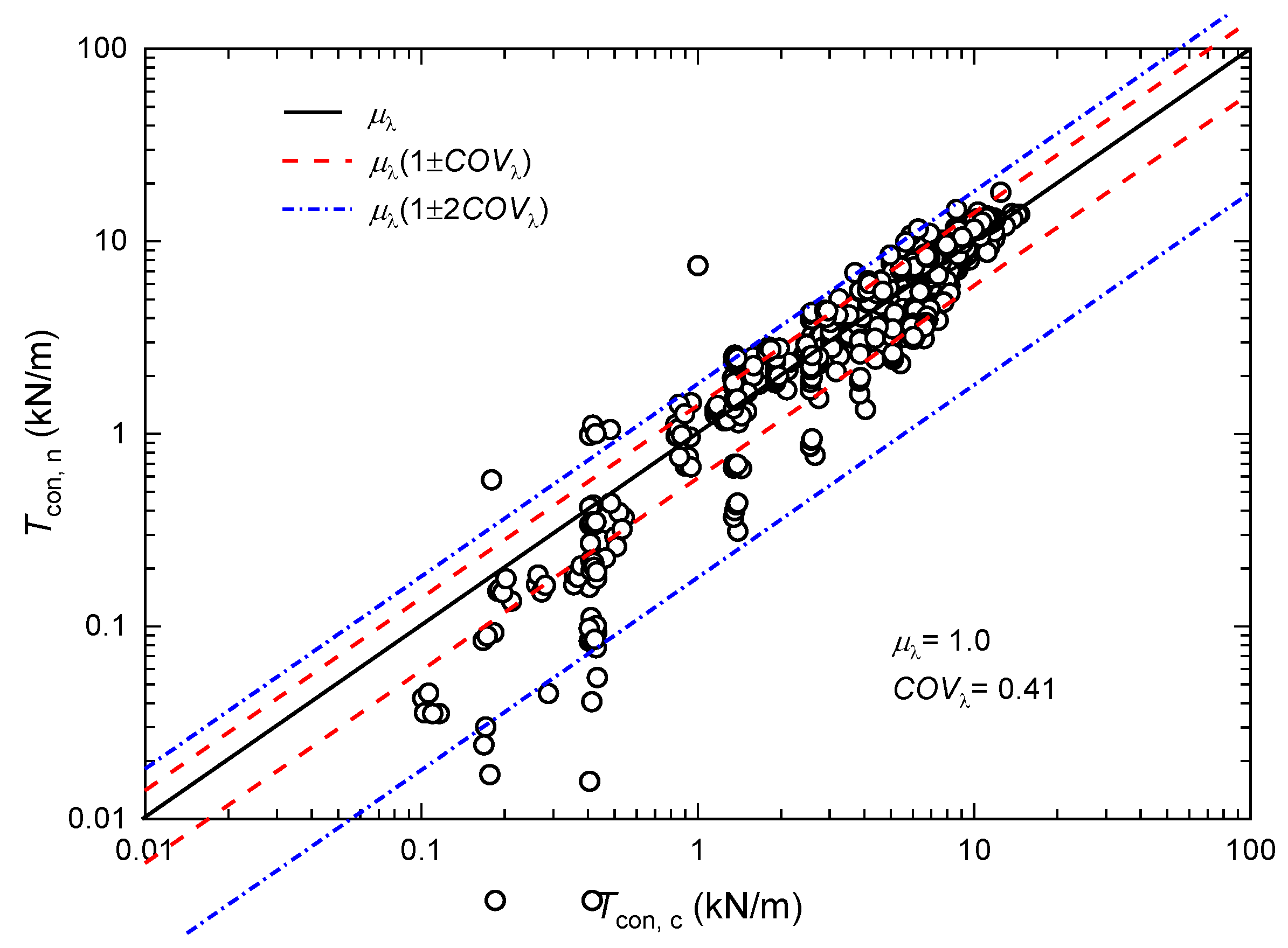
4.2. Response Surface Model of Kt
4.3. Calculation Result Analysis
5. Discussion
6. Conclusions
- (1)
- In GRS segmental walls with a typical toe restraint, the sum of the total connection load and toe resistance is close to the Coulomb active earth load acting on the facing column.
- (2)
- The ratio of the earth loads carried by the toe increases with the friction angle of the facing block–leveling pad interface but shows little change for interface friction angles greater than 25°.
- (3)
- Under the same toe restraint conditions, the toe load ratio increases with the facing batter, reinforcement spacing, and backfill friction angle, and decreases with wall height and reinforcement stiffness. In most cases in this paper, the toe load ratio was not higher than 50%.
- (4)
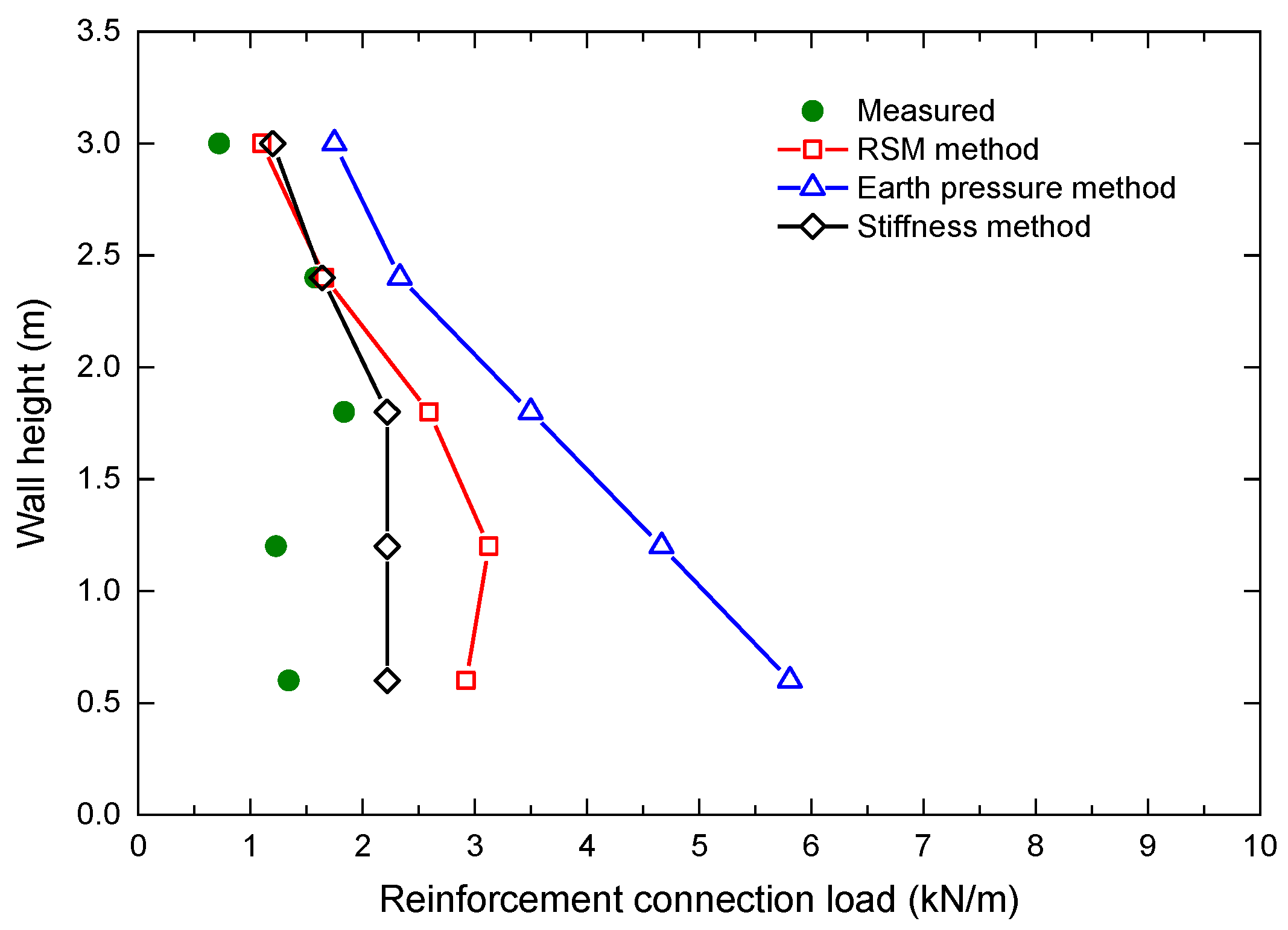
- No matter what toe restraint conditions, the predictions of the proposed RSM method are in better agreement with the measured connection loads than those of the stiffness method and the earth pressure method.
- (5)
- For GRS walls with proper toe restraint conditions, the reinforcement connection loads calculated using the proposed method show a bulge distribution shape, which is consistent with observations in GRS walls under working stress conditions.
- (6)
- For GRS walls with the loss of toe resistance, the proposed method yields a positive, approximately linear relationship between the connection loads and wall depth, which is close to the results of the earth pressure method.
- (7)
- The proposed method cannot consider the effects of the cohesion of backfill soil and the down-drag force induced by differential settlement of foundations on the connection loads and needs further optimization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xue, Y.; Liu, S.; Chai, J.; Liu, J.; Ranjith, P.G.; Cai, C.; Bai, X. Effect of water-cooling shock on fracture initiation and morphology of high-temperature granite: Application of hydraulic fracturing to enhanced geothermal systems. Appl. Energy 2023, 337, 120858. [Google Scholar] [CrossRef]
- Xue, Y.; Ranjith, P.G.; Gao, F.; Zhang, Z.; Wang, S. Experimental investigations on effects of gas pressure on mechanical behaviors and failure characteristic of coals. J. Rock Mech. Geotech. Eng. 2023, 15, 412–428. [Google Scholar] [CrossRef]
- Chen, Y.; Tan, L.; Xiao, N.; Liu, K.; Jia, P.; Zhang, W. The hydro-mechanical characteristics and micro-structure of loess enhanced by microbially induced carbonate precipitation. Geomech. Energy Environ. 2023, 34, 100469. [Google Scholar] [CrossRef]
- Wang, L.; Dong, Z.; Li, N.; Wang, W.; Tian, Y.; Xu, S. Experimental study on the mechanism of ice layer formation in fractured rock masses in cold regions. Sci. Rep. 2022, 12, 17954. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, W.; Jia, P.; Han, J.; Guan, Y. Dynamic behavior of an embedded foundation under horizontal vibration in a poroelastic half-space. Appl. Sci. 2019, 9, 740. [Google Scholar] [CrossRef] [Green Version]
- Tatsuoka, F. Recent practice and research of geosynthetic-reinforced earth structures in Japan. J. GeoEng. 2008, 3, 77–100. [Google Scholar]
- Allen, T.M.; Bathurst, R.J.; Holtz, R.D.; Walters, D.L.; Lee, W.F. A new working stress method for prediction of reinforcement loads in geosynthetic walls. Can. Geotech. J. 2003, 40, 976–994. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Miyata, Y.; Nernheim, A.; Allen, A.M. Refinement of K-stiffness method for geosynthetic reinforced soil walls. Geosynth. Int. 2008, 15, 269–295. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Vlachopoulos, N.; Walters, D.L.; Burgess, P.G.; Allen, T.M. The influence of facing stiffness on the performance of two geosynthetic reinforced soil retaining walls. Can. Geotech. J. 2006, 43, 1225–1237. [Google Scholar] [CrossRef]
- Allen, T.M.; Bathurst, R.J. Design and performance of 6.3-m-high, block-faced geogrid wall design using K-stiffness method. J. Geotech. Geoenviron. Eng. 2014, 140, 04013016. [Google Scholar] [CrossRef]
- Allen, T.M.; Bathurst, R.J. Performance of an 11 m high block-faced geogrid wall designed using the K-stiffness Method. Can. Geotech. J. 2014, 51, 16–29. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Bathurst, R.J.; Allen, T.M.; Nelson, N. Physical and numerical modelling of a geogrid-reinforced incremental concrete panel retaining wall. Can. Geotech. J. 2016, 53, 1883–1901. [Google Scholar] [CrossRef]
- Xiao, C.; Gao, S.; Liu, H.; Du, Y. Case history on failure of geosynthetics-reinforced soil bridge approach retaining walls. Geotext. Geomembr. 2021, 49, 1585–1599. [Google Scholar] [CrossRef]
- Gebremariam, F.; Tanyu, B.F.; Christopher, B.; Leshchinsky, D.; Zornberg, J.G.; Han, J. Evaluation of required connection load in GRS-IBS structures under service loads. Geosynth. Int. 2020, 27, 620–634. [Google Scholar] [CrossRef]
- FHWA. Design of Mechanically Stabilized Earth Walls and Reinforced Slopes; No. FHWA-NHI-10-024; Berg, R.R., Christopher, B.R., Samtani, N.C., Eds.; Federal Highway Administration: Washington, DC, USA, 2009; Volume I.
- Allen, T.M.; Bathurst, R.J. Improved simplified method for prediction of loads in reinforced soil walls. J. Geotech. Geoenviron. Eng. 2015, 141, 04015049. [Google Scholar] [CrossRef]
- Hatami, K.; Bathurst, R.J. Development and verification of a numerical model for the analysis of geosynthetic-reinforced soil segmental walls under working stress conditions. Can. Geotech. J. 2005, 42, 1066–1085. [Google Scholar] [CrossRef]
- Hatami, K.; Bathurst, R.J. A numerical model for reinforced soil segmental walls under surcharge loading. J. Geotech. Geoenviron. Eng. 2006, 132, 673–684. [Google Scholar] [CrossRef]
- Huang, B.; Bathurst, R.J.; Hatami, K. Influence of toe restraint on reinforced soil segmental walls. Can. Geotech. J. 2010, 47, 885–904. [Google Scholar] [CrossRef]
- Ehrlich, M.; Mirmoradi, S.H. Evaluation of the effects of facing stiffness and toe resistance on the behavior of GRS walls. Geotext. Geomembr. 2013, 40, 28–36. [Google Scholar] [CrossRef]
- Mirmoradi, S.H.; Ehrlich, M.; Dieguez, C. Evaluation of the combined effect of toe resistance and facing inclination on the behavior of GRS walls. Geotext. Geomembr. 2016, 44, 287–294. [Google Scholar] [CrossRef]
- Leshchinsky, D.; Ling, H.; Hanks, G. Unified design approach to geosynthetic reinforced slopes and segmental walls. Geosynth. Int. 1995, 2, 845–881. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Yang, G.; Hung, C. Analyzing reinforcement loads of vertical geosynthetic-reinforced soil walls considering toe restraint. Int. J. Geomech. 2017, 17, 04016140. [Google Scholar] [CrossRef]
- Leshchinsky, D.; Zhu, F.; Meehan, C.L. Required unfactored strength of geosynthetic in reinforced earth structures. J. Geotech. Geoenviron. Eng. 2010, 136, 281–289. [Google Scholar] [CrossRef]
- Allen, T.M.; Bathurst, R.J. Application of the Simplified Stiffness Method to design of reinforced soil walls. J. Geotech. Geoenviron. Eng. 2018, 144, 04018024. [Google Scholar] [CrossRef]
- Xie, Y.; Leshchinsky, B.; Yang, S. Evaluating reinforcement loading within surcharged segmental block reinforced soil walls using a limit state framework. Geotext. Geomembr. 2016, 44, 832–844. [Google Scholar] [CrossRef]
- Franco, Y.B.; Utili, S.; Da Silva, J.L. Design of reinforced cohesive soil walls accounting for wall facing contribution to stability. Géotechnique, 2022; in press. [Google Scholar] [CrossRef]
- AASHTO (American Association of State Highway and Transportation Officials). LRFD Bridge Design Specifications, 9th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2020; p. 1912. [Google Scholar]
- Leshchinsky, D.; Vahedifard, F. Impact of toe resistance in reinforced masonry block walls: Design dilemma. J. Geotech. Geoenviron. Eng. 2012, 138, 236–240. [Google Scholar] [CrossRef]
- Mirmoradi, S.H.; Ehrlich, M.; Magalhães, L.F.O. Numerical evaluation of the effect of foundation on the behaviour of reinforced soil walls. Geotext. Geomembr. 2021, 49, 619–628. [Google Scholar] [CrossRef]
- Mirmoradi, S.H.; Ehrlich, M. Effects of facing, reinforcement stiffness, toe resistance, and height on reinforced walls. Geotext. Geomembr. 2017, 45, 67–76. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J.F.; Yu, Y. Influence of toe restraint conditions on performance of geosynthetic-reinforced soil retaining walls using centrifuge model tests. Geotext. Geomembr. 2019, 47, 653–661. [Google Scholar] [CrossRef]
- Xu, P.; Hatami, K.; Yang, G.; Li, T.; Liang, X. Influence of facing toe condition on the bearing capacity of full-height panel MSE walls. Geosynth. Int. 2022, 29, 593–609. [Google Scholar] [CrossRef]
- Sayed, S.; Dodagoudar, G.R.; Rajagopal, K. Finite element reliability analysis of reinforced retaining walls. Geomech. Geoengin. Int. J. 2010, 5, 187–197. [Google Scholar] [CrossRef]
- Yu, Y.; Bathurst, R.J. Probabilistic assessment of reinforced soil wall performance using response surface method. Geosynth. Int. 2017, 24, 524–542. [Google Scholar] [CrossRef]
- Peng, M.; Sun, R.; Chen, J.F.; Rajesh, S.; Zhang, L.M.; Yu, S.B. System reliability analysis of geosynthetic reinforced soil slope considering local reinforcement failure. Comput. Geotech. 2020, 123, 103563. [Google Scholar] [CrossRef]
- Pramanik, R.; Mukherjee, S.; Babu, G.S. Deterministic and probabilistic prediction of maximum wall facing displacement of geosynthetic-reinforced soil segmental walls using multivariate adaptive regression splines. Transp. Geotech. 2022, 36, 100816. [Google Scholar] [CrossRef]
- Lee, K.Z.Z.; Chang, N.Y. Predictive modeling on seismic performances of geosynthetic-reinforced soil walls. Geotext. Geomembr. 2012, 35, 25–40. [Google Scholar] [CrossRef]
- Lin, B.H.; Yu, Y.; Bathurst, R.J.; Liu, C.N. Deterministic and probabilistic prediction of facing deformations of geosynthetic-reinforced MSE walls using a response surface approach. Geotext. Geomembr. 2016, 44, 813–823. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Yu, Y. Probabilistic prediction of reinforcement loads for steel MSE walls using a response surface method. Int. J. Geomech. 2018, 18, 04018027. [Google Scholar] [CrossRef]
- Yu, Y.; Bathurst, R.J.; Allen, T.M. Numerical modeling of the SR-18 geogrid reinforced modular block retaining walls. J. Geotech. Geoenviron. Eng. 2016, 142, 04016003. [Google Scholar] [CrossRef]
- Lade, P.V.; Lee, K.L. Engineering Properties of Soils; Report UCLA-ENG-7652; University of California: Los Angeles, CA, USA, 1976. [Google Scholar]
- Damians, I.P.; Bathurst, R.J.; Josa, A.; Lloret, A.; Albuquerque, P.J.R. Vertical-facing loads in steel-reinforced soil walls. J. Geotech. Geoenviron. Eng. 2013, 139, 1419–1432. [Google Scholar] [CrossRef]
- Mirmoradi, S.H.; Ehrlich, M. Numerical evaluation of the behavior of GRS walls with segmental block facing under working stress conditions. J. Geotech. Geoenviron. Eng. 2015, 141, 04014109. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Naftchali, F.M. Geosynthetic reinforcement stiffness for analytical and numerical modelling of reinforced soil structures. Geotext. Geomembr. 2021, 49, 921–940. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J.F. Numerical modeling of geosynthetic reinforced soil retaining walls with different toe restraint conditions. Geotext. Geomembr. 2023, 51, 16–29. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Tateyama, M.; Koseki, J.; Yonezawa, T. Geosynthetic-reinforced soil structures for railways in Japan. Transp. Infrastruct. Geotechnol. 2014, 1, 3–53. [Google Scholar] [CrossRef] [Green Version]
- Tarawneh, B.; Bodour, B.A.; Masada, T. Inspection and risk assessment of mechanically stabilized earth walls supporting bridge abutments. J. Perform. Constr. Facil. 2018, 32, 04017131. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C. Response Surface Methodology: Process and Product Optimization using Designed Experiments, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2002. [Google Scholar]
- Miyata, Y.; Bathurst, R.J.; Miyatake, H. Performance of three geogrid- reinforced soil walls before and after foundation failure. Geosynth. Int. 2015, 22, 311–326. [Google Scholar] [CrossRef]
- Xiao, C.; Han, J.; Zhang, Z. Experimental study on performance of geosynthetic-reinforced soil model walls on rigid foundations subjected to static footing loading. Geotext. Geomembr. 2016, 44, 81–94. [Google Scholar] [CrossRef]









| Parameters | Backfill and Foundation | Blocks |
|---|---|---|
| Density ρ (kg/m3) | 2200 | 2400 |
| Cohesion c (kPa) | 2 | - |
| Plane strain friction angle φ (°) | 54 | - |
| Dilation angle ψ (°) | 14 | - |
| Elastic modulus E (MPa) | 80 | 3.2 × 104 |
| Poisson’s ratio ν | 0.3 | 0.15 |
| Parameters | Value |
|---|---|
| Axial stiffness J (kN/m) | 310 |
| Ultimate tensile strength T (kN/m) | 62.5 |
| Cross-section area A (m2/m) | 2 × 10−3 |
| Soil-reinforcement interface cohesion csr (kN/m) | 2.5 |
| Soil-reinforcement interface friction angle φsr (°) | 43 |
| Soil-reinforcement interface shear stiffness Ksr (MN/m/m) | 1 |
| Parameters | Value |
|---|---|
| Facing block–leveling pad interface | |
| Interface cohesion cbp (kPa) | 1 |
| Interface friction angle φbp (°) | 36 |
| Interface normal stress Knbp (MPa/m) | 1000 |
| Interface shear stiffness Ksbp (MPa/m) | 23 |
| Leveling pad–foundation soil interface | |
| Interface cohesion cpf (kPa) | 1.3 |
| Interface friction angle φpf (°) | 43 |
| Interface normal stress Knbf (MPa/m) | 1000 |
| Interface shear stiffness Kspf (MPa/m) | 10 |
| Block–block interface | |
| Interface cohesion cbb (kPa) | 58 |
| Interface friction angle φbb (°) | 36 |
| Interface normal stress Knbb (MPa/m) | 1000 |
| Interface shear stiffness Ksbb (MPa/m) | 40 |
| Block–backfill interface | |
| Interface cohesion cbs (kPa) | 1.3 |
| Interface friction angle φbs (°) | 43 |
| Interface normal stress Knbs (MPa/m) | 100 |
| Interface shear stiffness Ksbs (MPa/m) | 1 |
| Parameters | Value |
|---|---|
| Facing block | |
| Density ρb (kg/m3) | 2200 |
| Backfill and foundation | |
| Density ρ (kg/m3) | 2000 |
| Friction angle φ (°) | 40 |
| Dilation angle ψ (°) | 10 |
| Elastic modulus E (MPa) | 40 |
| Reinforcement | |
| Axial stiffness (kN/m) | 725 |
| Ultimate tensile strength T (kN/m) | 115 |
| Soil-reinforcement interface friction angle φsr (°) | 30 |
| Facing block–leveling pad interface | |
| Interface friction angle φbp (°) | Variable |
| Interface shear stiffness Ksbp (MPa/m) | Variable |
| Leveling pad–foundation soil interface | |
| Interface cohesion cpf (kPa) | 1 |
| Interface friction angle φpf (°) | 40 |
| Block–block interface | |
| Interface cohesion cbb (kPa) | 46 |
| Interface friction angle φbb (°) | 57 |
| Block–backfill interface | |
| Interface normal stress Knbs (MPa/m) | 100 |
| Interface shear stiffness Ksbs (MPa/m) | 1 |
| Parameters | Value |
|---|---|
| Baseline model | |
| Toe interface friction angle (°) | 5, 10, 15, 25, 45 |
| Toe interface shear stiffness (MPa/m) | 3.6, 10.1, 14.0, 19.1, 26.1 |
| H = 4 m | |
| Toe interface friction angle (°) | 5, 10, 15, 25, 45 |
| Toe interface shear stiffness (MPa/m) | 2.3, 7.4, 10.5, 14.5, 20.1 |
| H = 8 m | |
| Toe interface friction angle (°) | 5, 10, 15, 25, 45 |
| Toe interface shear stiffness (MPa/m) | 4.4, 12.6, 17.5, 24, 33 |
| H = 10 m | |
| Toe interface friction angle (°) | 5, 10, 15, 25, 45 |
| Toe interface shear stiffness (MPa/m) | 4.8, 14.9, 20.9, 28.9, 39.9 |
| Factors | Value |
|---|---|
| Wall height H (m) | 4, 6, 8, 10 |
| Facing batter ω (°) | 0, 5, 10, 15 |
| Reinforcement stiffness J (kN/m) | 330, 725, 1120 |
| Reinforcement tensile strength T (kN/m) | J/6.3 |
| Reinforcement spacing (m) | 0.4, 0.6, 0.8 |
| Plane strain backfill friction angle φ (°) | 35, 40, 45 |
| Backfill dilation angle ψ (°) | φ-30 |
| Block–backfill interface friction angle φbs (°) | φ |
| Leveling pad–foundation soil interface friction angle φpf (°) | φ |
| Soil–reinforcement interface friction angle φsr (°) | tan−1 (2/3 × tanφ) |
| Coefficient | Value | Coefficient | Value |
|---|---|---|---|
| β0 | 0.0337 | β5 | 0.0064 |
| β1 | 0.3934 | β6 | −1.1232 |
| β2 | −0.0147 | β7 | 0.0222 |
| β3 | 0.5549 | β8 | −0.0129 |
| β4 | −0.3731 | β9 | −0.4998 |
| Parameter | Wall 1 | Wall 2 | Wall 3 | Wall 4 | Wall 5 |
|---|---|---|---|---|---|
| Wall height (m) | 3.6 | 3.6 | 4.1 | 10.7 | 6.1 |
| Facing batter (°) | 8 | 8 | 8 | 0 | 0 |
| Number of reinforcement layers | 5 | 5 | 5 | 17 | 10 |
| Reinforcement spacing (m) | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 |
| Reinforcement stiffness (kN/m) | 572 | 572 | 572 | 246 for the top 4 layers 393 for the middle 3 layers 598 for the bottom 10 layers | 232 |
| Backfill weight (kN/m3) | 15.7 | 15.7 | 15.7 | 21.7 | 21.7 |
| Backfill friction angle from triaxial or direct shear test (°) | 36 | 36 | 36 | 47 | 47 |
| Toe interface friction angle (°) | 39 | 13 | 8 | 36 | 36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Chen, J. Prediction of Reinforcement Connection Loads in Geosynthetic Reinforced Segmental Retaining Walls Using Response Surface Method. Appl. Sci. 2023, 13, 7239. https://doi.org/10.3390/app13127239
Zhang W, Chen J. Prediction of Reinforcement Connection Loads in Geosynthetic Reinforced Segmental Retaining Walls Using Response Surface Method. Applied Sciences. 2023; 13(12):7239. https://doi.org/10.3390/app13127239
Chicago/Turabian StyleZhang, Wan, and Jianfeng Chen. 2023. "Prediction of Reinforcement Connection Loads in Geosynthetic Reinforced Segmental Retaining Walls Using Response Surface Method" Applied Sciences 13, no. 12: 7239. https://doi.org/10.3390/app13127239
APA StyleZhang, W., & Chen, J. (2023). Prediction of Reinforcement Connection Loads in Geosynthetic Reinforced Segmental Retaining Walls Using Response Surface Method. Applied Sciences, 13(12), 7239. https://doi.org/10.3390/app13127239





