Axial Compression Performance and Bearing Capacity Calculation of Round-Ended Concrete-Filled Aluminum Tube Column
Abstract
:1. Introduction
2. Experimental Program
2.1. Design of Specimen
2.2. Raw Materials
2.3. Experimental Apparatus and Test Procedure
3. Test Results
3.1. Failure Process and Failure Mode
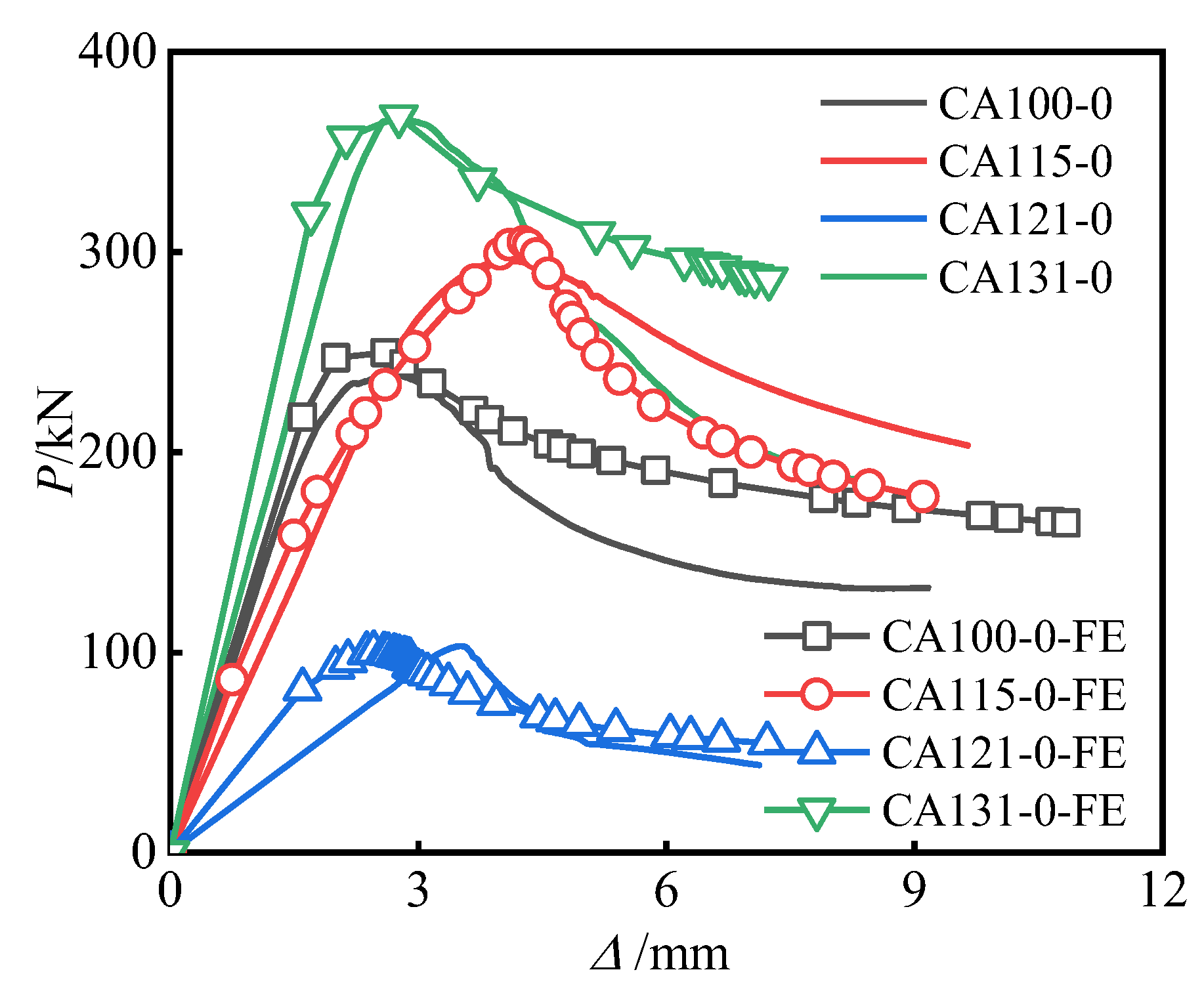
3.2. Axial Load–Displacement Curve
3.3. Bearing Capacity and Ductility
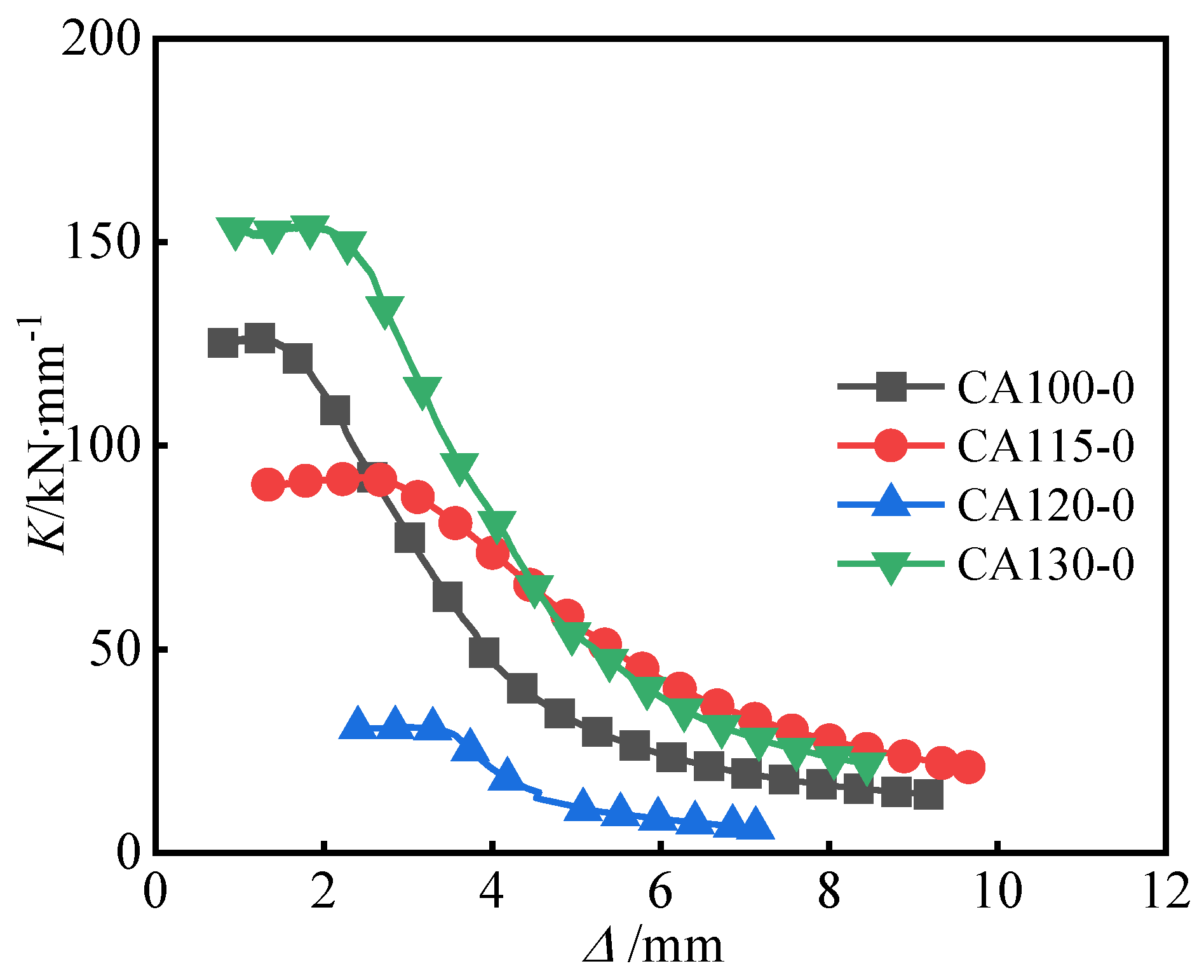
3.4. Stiffness Degradation
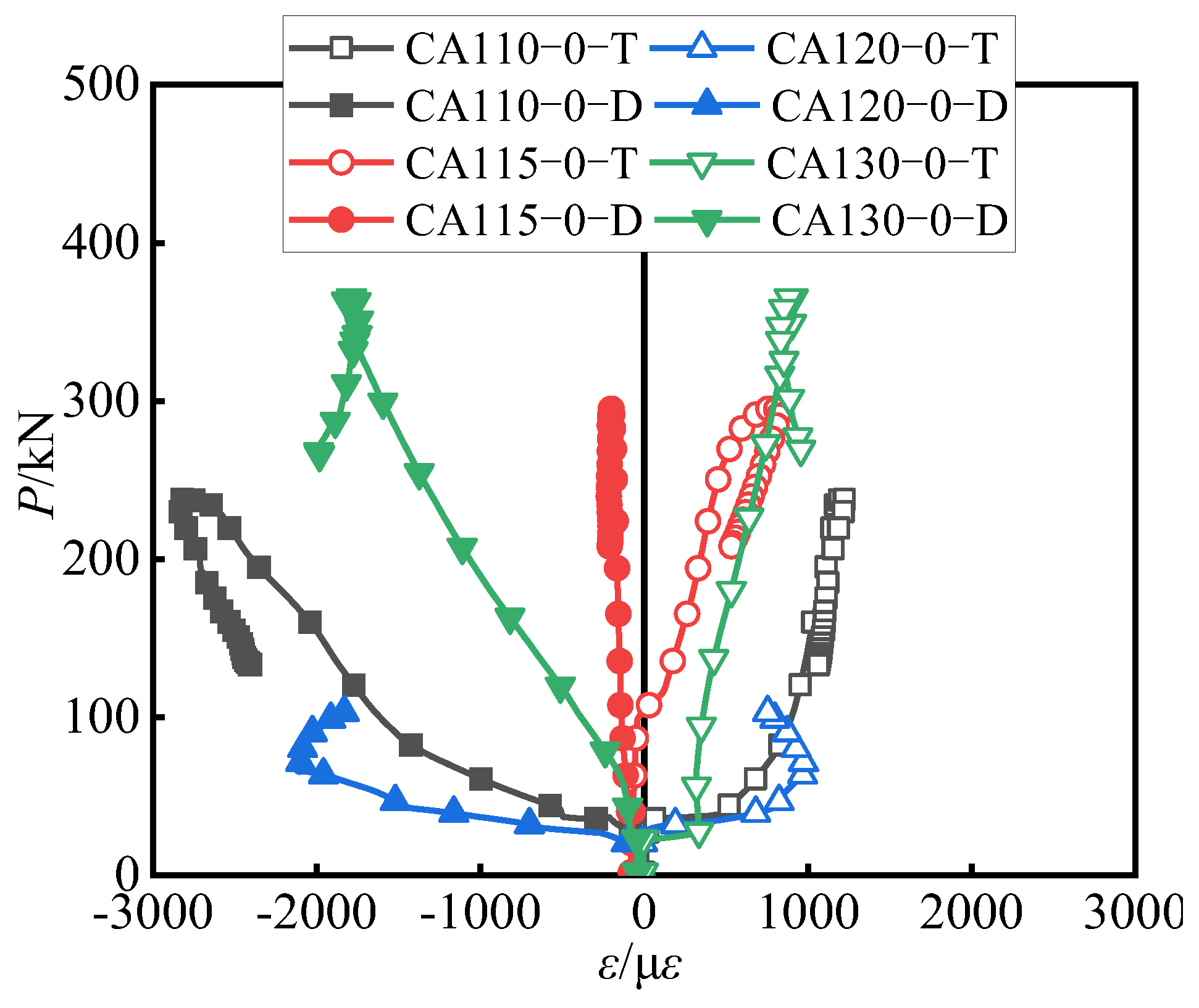
3.5. Strain Analysis
4. Finite Element Analysis
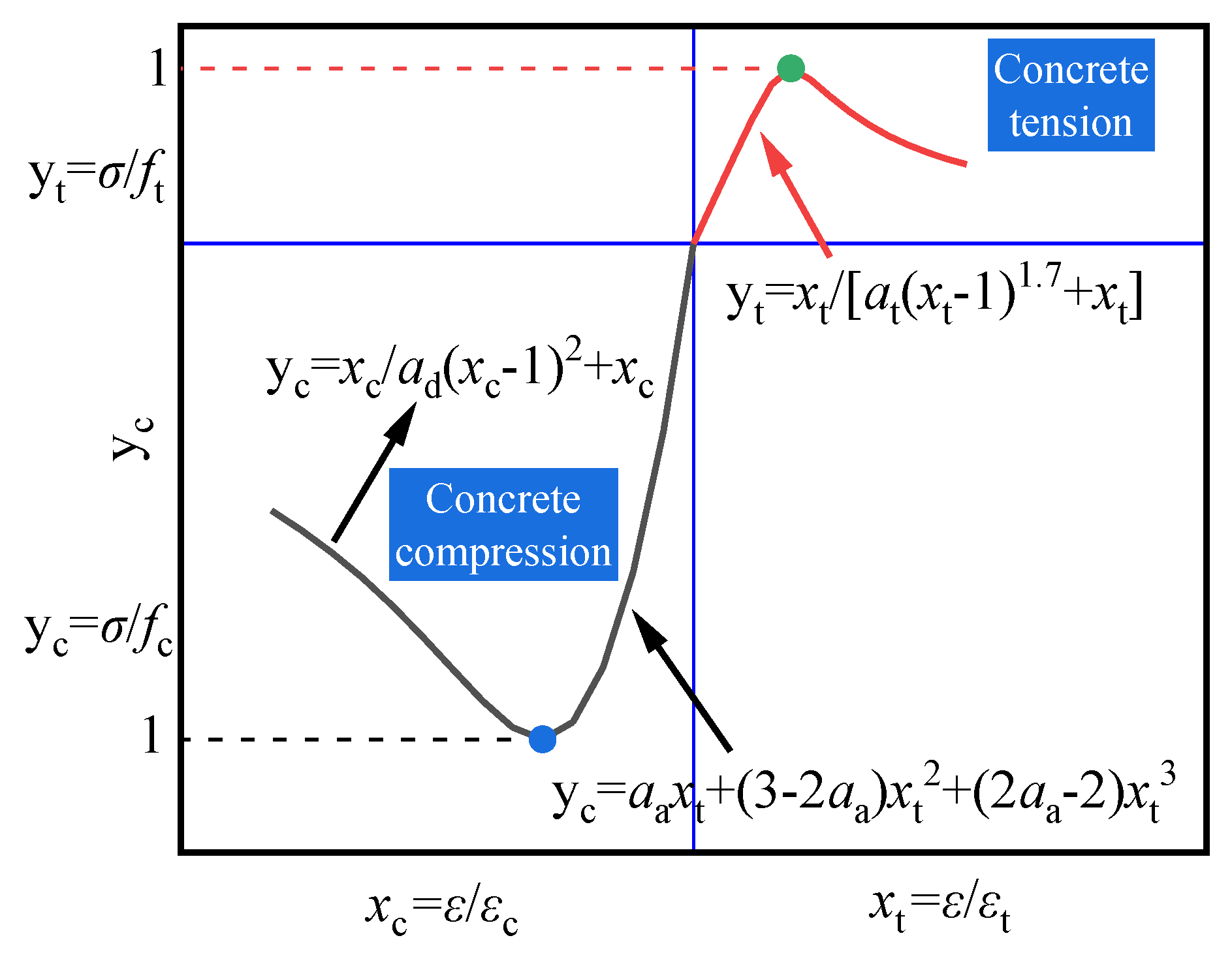
4.1. Constitutive Properties of Materials
4.1.1. Aluminum
4.1.2. Concrete
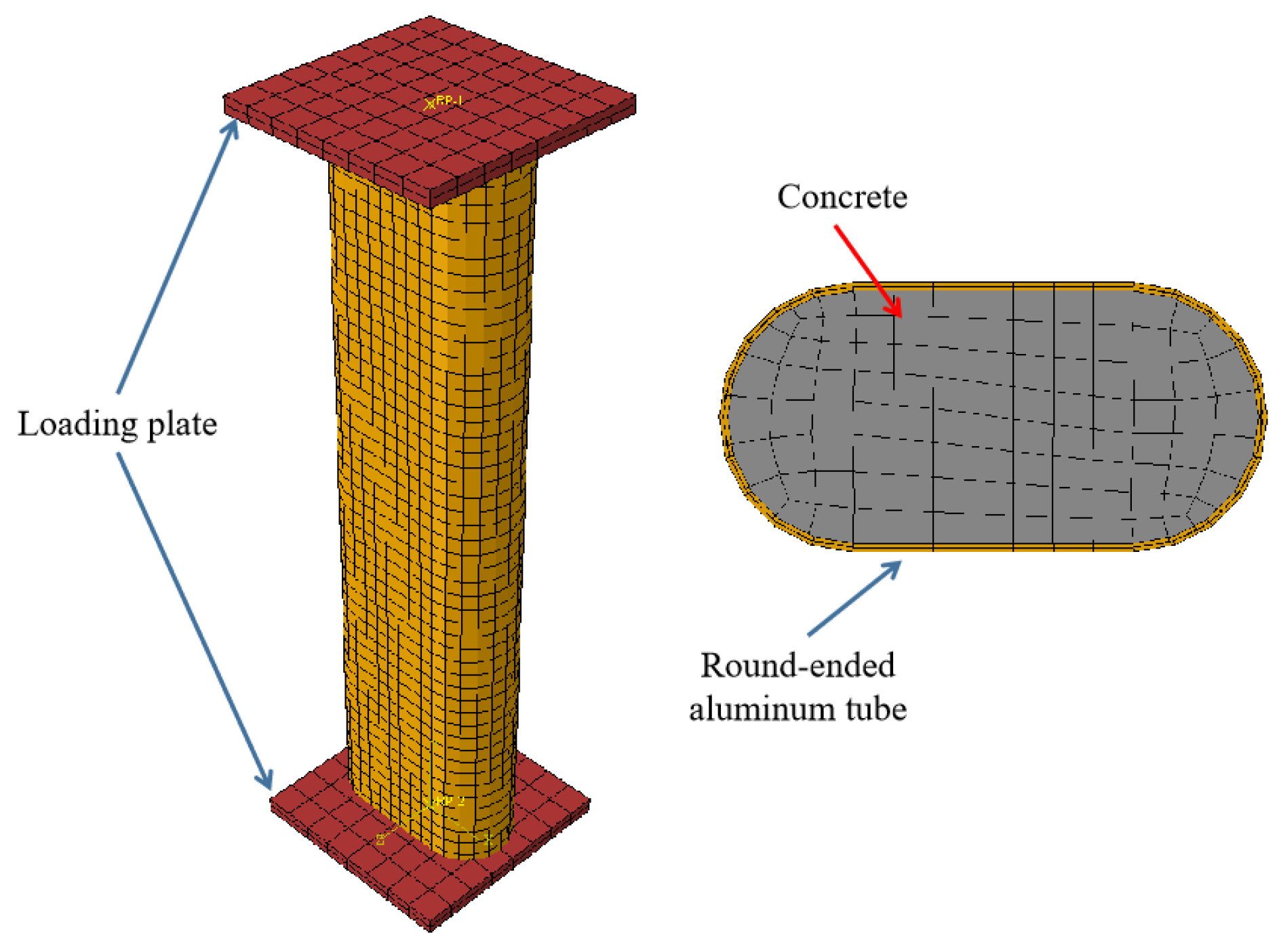
4.2. Mesh
4.3. Interaction and Boundary Conditions
4.4. Model Validation
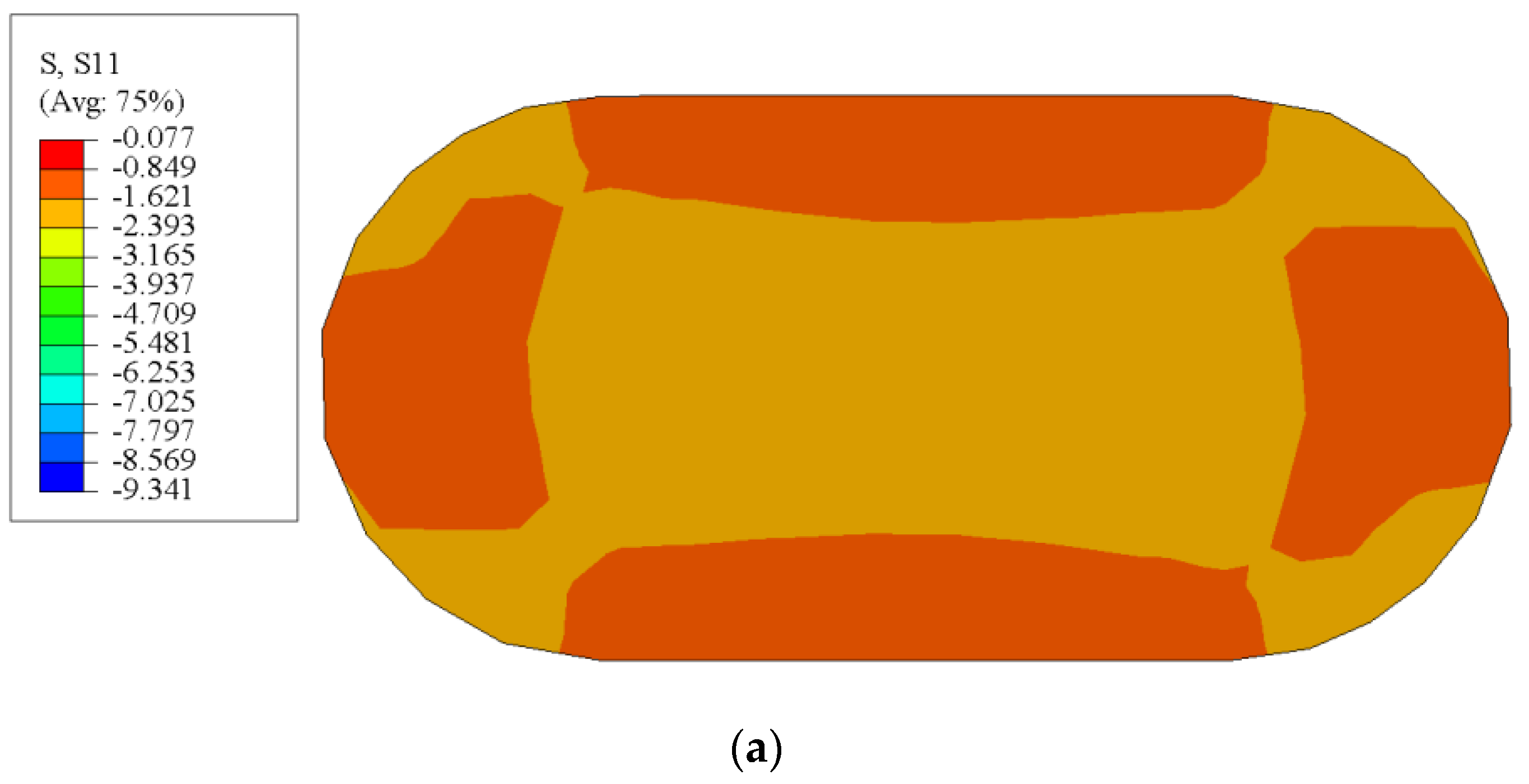
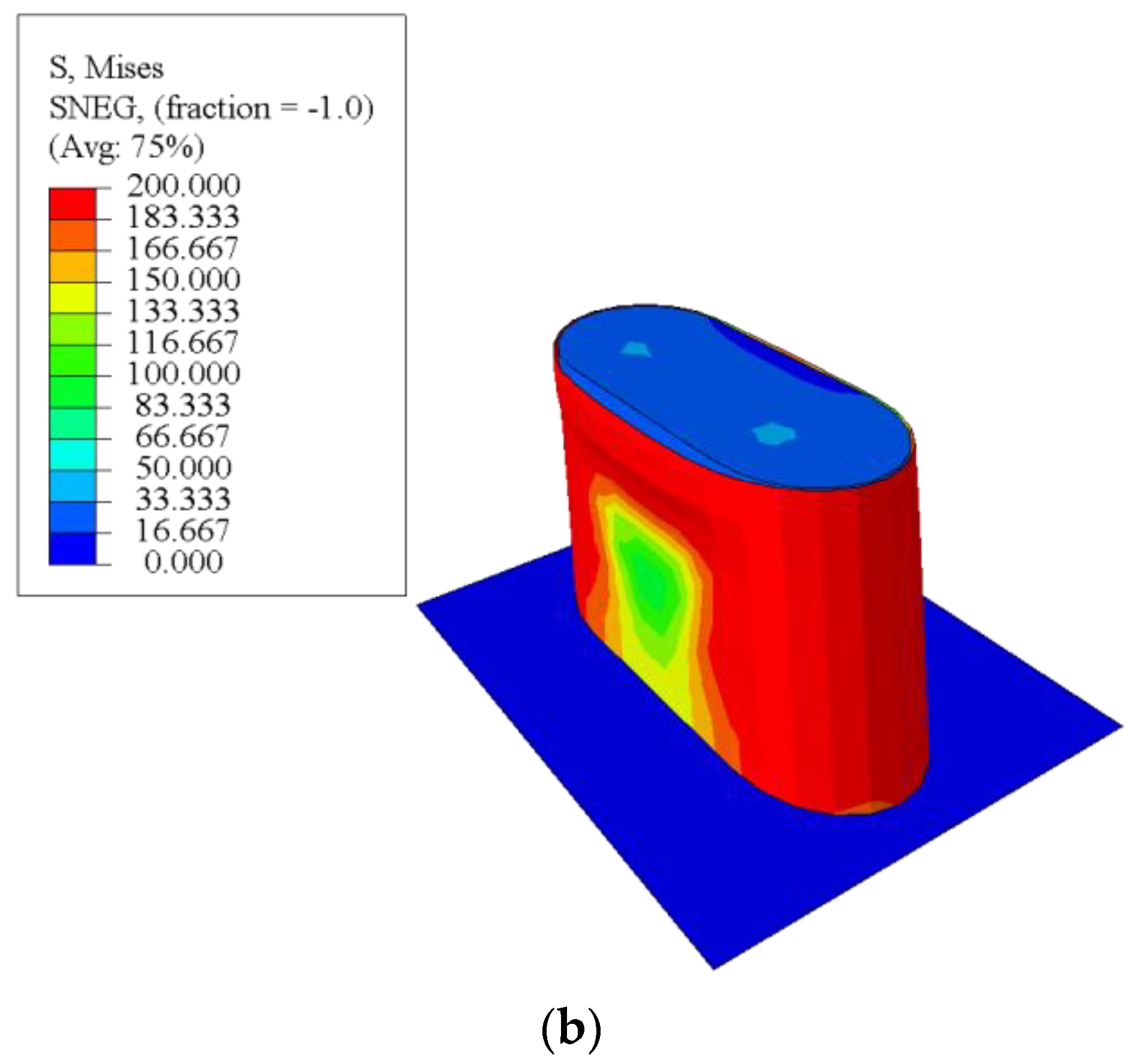
4.5. Stress Analysis
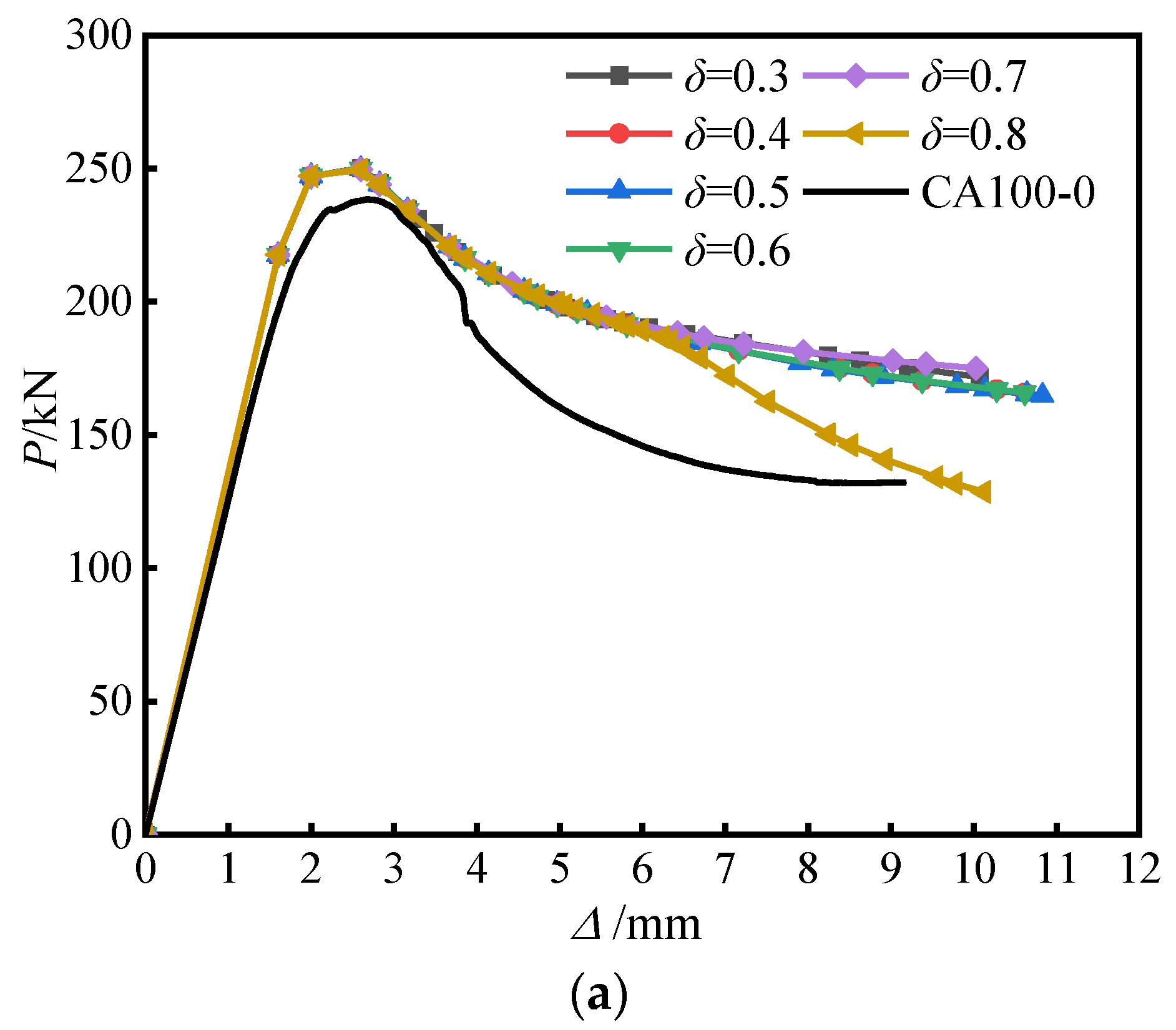
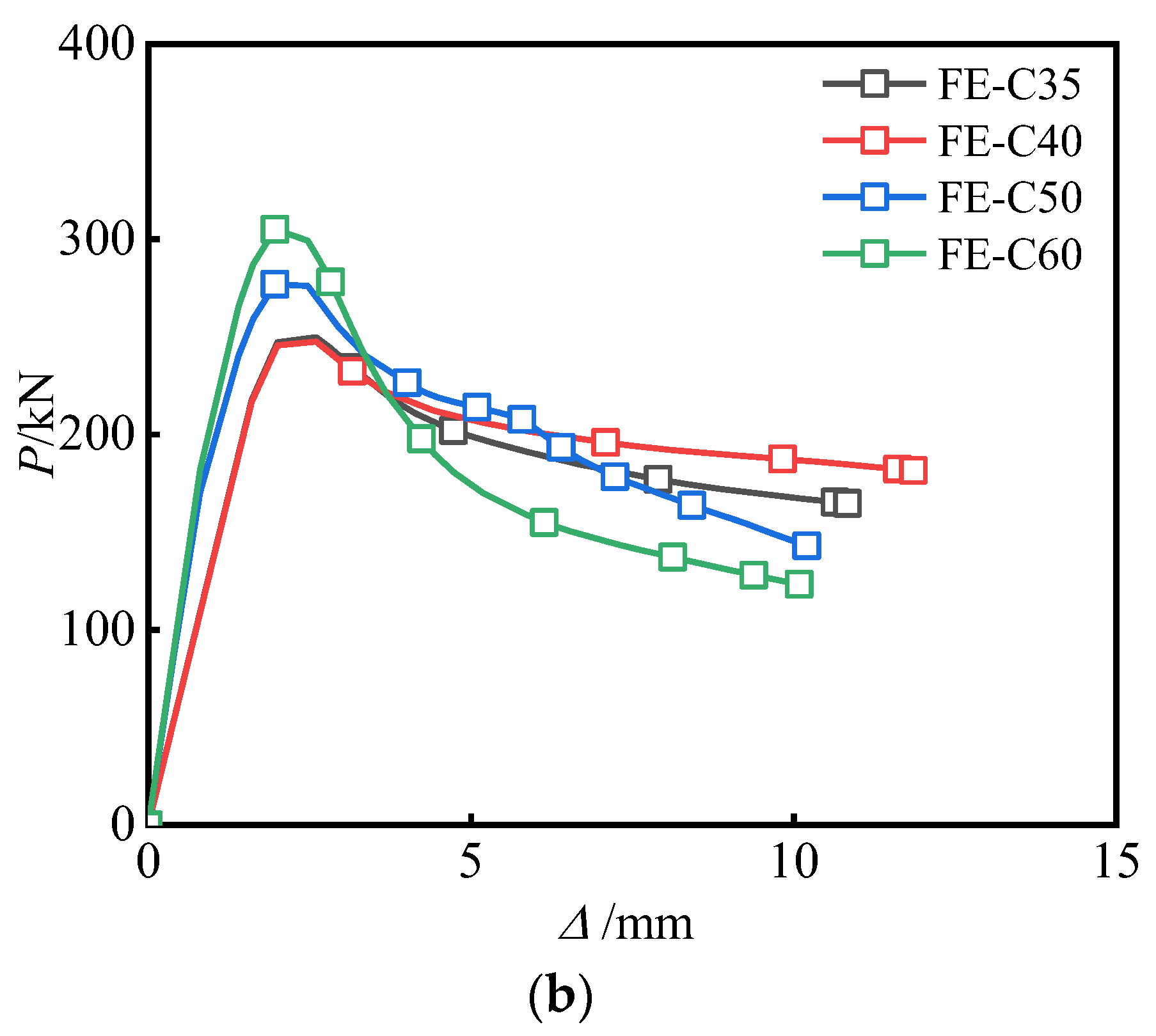
4.6. Parametric Study
5. Calculation Method for Bearing Capacity
6. Conclusions
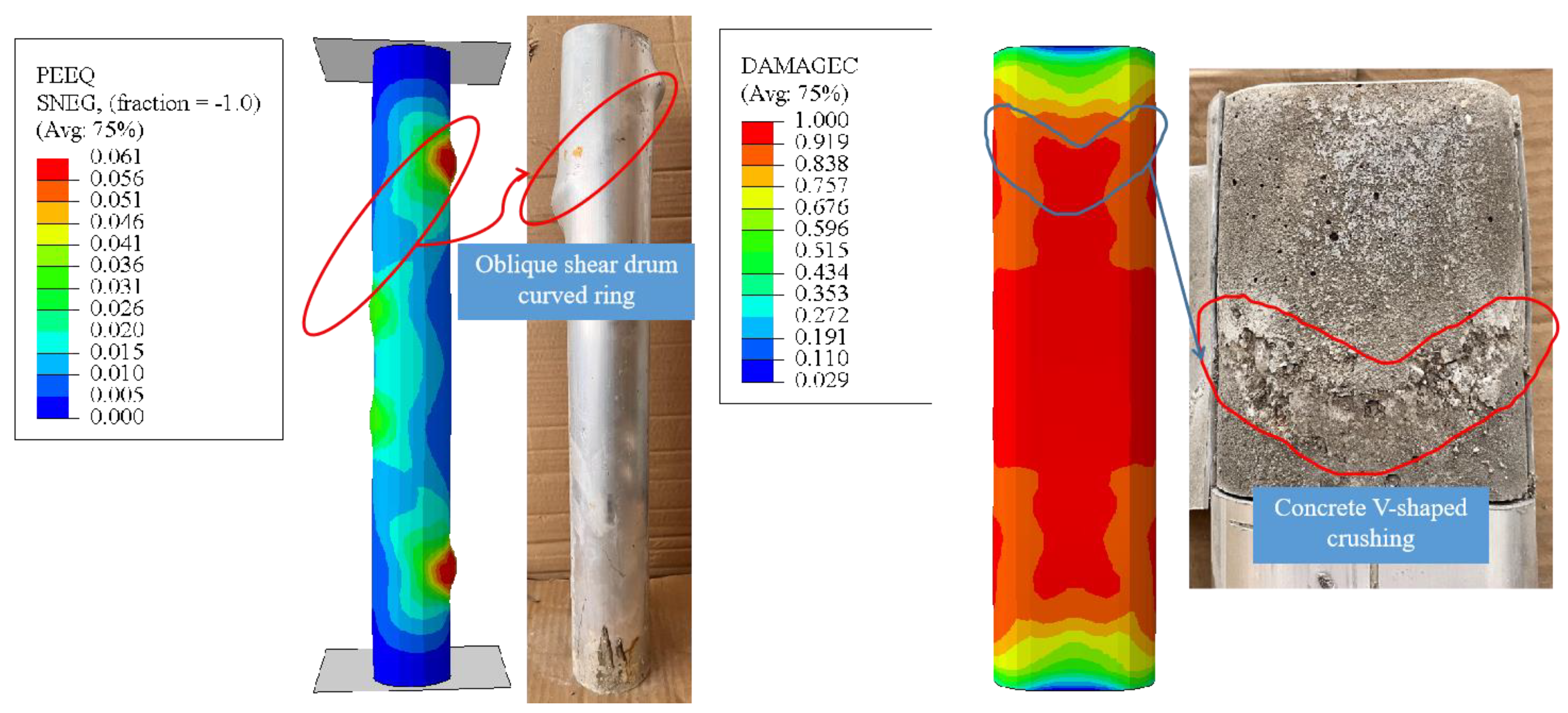
- The failure process of each specimen was generally consistent. After reaching the ultimate load, the two planes of the circular-end aluminum tube exhibited local bulging and formed oblique shear lines. Specimens with aspect ratios less than 4 exhibited localized bulging and oblique shear failure, while specimens with aspect ratios greater than 4 experienced overall instability failure.
- As the aspect ratio increased, the load enhancement coefficient and ductility coefficient of the specimens decreased. When the aspect ratio exceeded 2.5, the load enhancement coefficient was less than 1 and the critical aspect ratio was between 2.0 and 2.5. For specimens with the same aspect ratio, those with higher aluminum content had smaller enhancement coefficients but better ductility. The optimal aluminum content was recommended to be between 8.5% and 13.5%.
- Analysis of transverse and longitudinal strains in the plane of the circular-end aluminum alloy tube revealed that, due to the constraint effect of the aluminum tube, the transverse strain developed more rapidly after entering the plastic stage. The best constraint effect of the circular-end aluminum alloy tube was observed at an aspect ratio of around 2.0.
- The established refined finite element model matched well with the experimental results and captured the inclined shear bulging of the circular-end aluminum alloy tube and the “V”-shaped concrete compression failure during specimen failure.
- Finite element stress analysis and experimental strain measurements indicated the presence of an “arch effect” in the rectangular region of the circular-end aluminum alloy tube at the peak point. Due to the lower elastic modulus of the aluminum alloy, bulging occurred first when there was significant axial displacement, rather than concrete crushing and squeezing the aluminum alloy tube. Improving the strength of aluminum alloy would be more conducive to improving the axial compression bearing capacity of RECFST than increasing the strength of concrete.
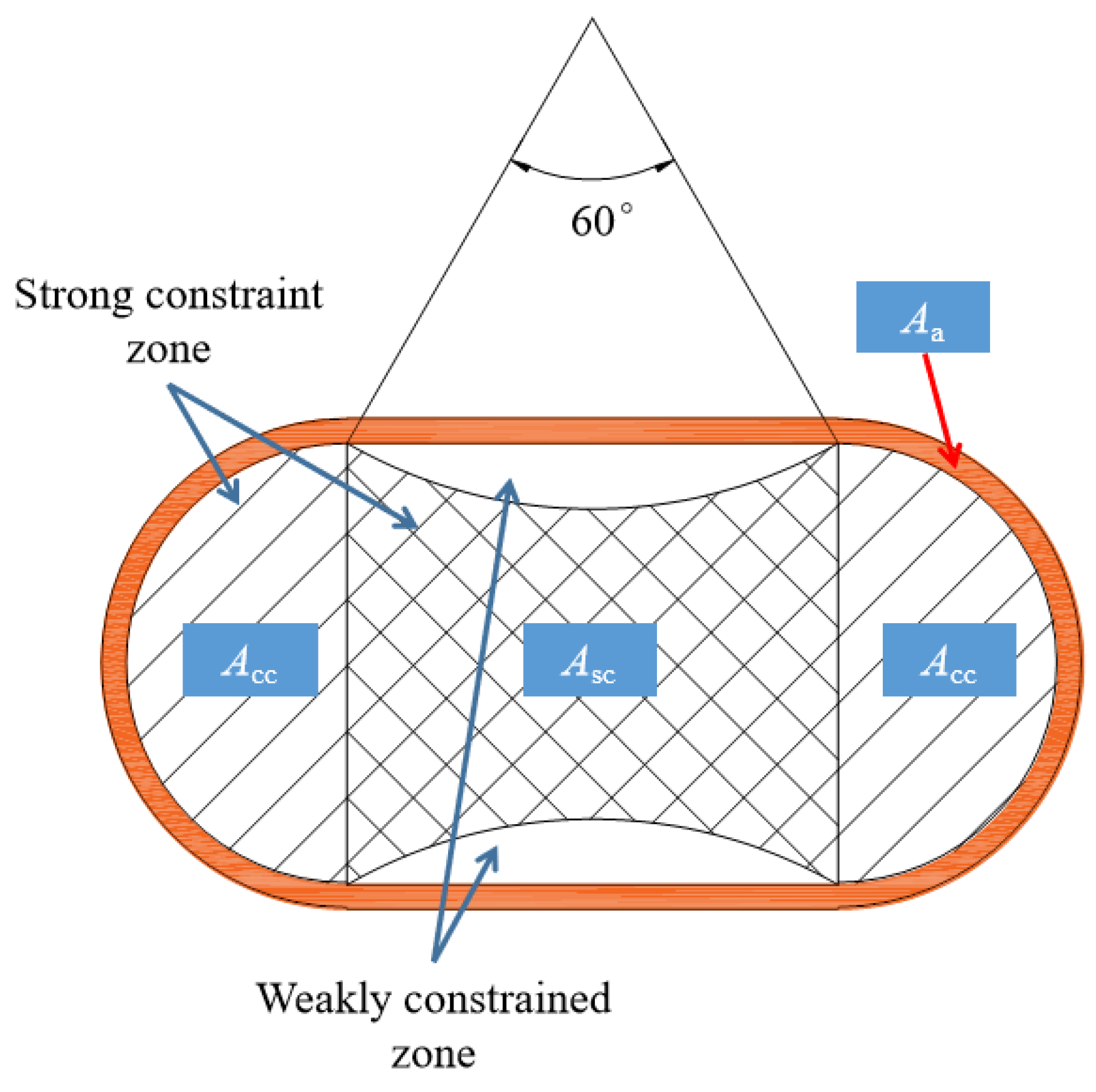
- Based on the experimental and finite element analysis results, a composite confinement model for circular-end aluminum alloy tubes was proposed, considering the efficiency of concrete strength enhancement in both the strong confinement and confinement regions. The calculated results had an error of 0.4%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, E.L. Research on Compressive Behavior and Reliability of Round-Ended Steel Tube-Filled Concrete Column. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2012. (In Chinese). [Google Scholar]
- Wang, J.F.; Wang, F.Q.; Shen, Q.H. Numerical modelling and design recommendation of axially-loaded thin-walled RCFST slender column. Thin-Walled Struct. 2019, 135, 210–226. [Google Scholar] [CrossRef]
- Shen, Q.; Wang, J.; Wang, W.; Wang, Z. Performance and design of eccentrically-loaded concrete-filled round-ended elliptical hollow section stub columns. J. Constr. Steel Res. 2018, 150, 99–114. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Patel, V.I. Round-ended rectangular concrete-filled steel tubular short columns: FE investigation under axial compression. J. Constr. Steel Res. 2018, 140, 222–236. [Google Scholar] [CrossRef]
- Ding, F.X.; Fu, L.W.; Yu, Z.; Li, G. Mechanical performances of concrete-filled steel tubular stub columns with round ends under axial loading. Thin-Walled Struct. 2015, 97, 22–34. [Google Scholar]
- Wang, Z.B.; Chen, J.; Xie, E.P.; Lin, S. Behavior of concrete-filled round-end steel tubular stub columns under axial compression. J. Build. Struct. 2014, 35, 123–130. [Google Scholar]
- Xie, E.P.; Wang, Z.B.; Lin, C.; Zhou, J.Z. Mechanism analysis on concrete-filled round-end steel tubular stub columns under axial load. J. Fuzhou Uni. 2015, 43, 1–6. [Google Scholar]
- Patel, V.I. Analysis of uniaxially loaded short round-ended concrete-filled steel tubular beam-columns. Eng. Struct. 2020, 205, 110098. [Google Scholar] [CrossRef]
- Piquer, A.; Ibañez, C.; Hernández-Figueirido, D. Structural response of concretefilled round-ended stub columns subjected to eccentric loads. Eng. Struct. 2019, 184, 318–328. [Google Scholar] [CrossRef]
- Wang, J.; Shen, Q. Numerical analysis and design of thin-walled RECFST stub columns under axial compression. Thin-Walled Struct. 2018, 129, 166–182. [Google Scholar] [CrossRef]
- Zhou, F.; Young, B. Tests of concrete-filled aluminum stub columns. Thin-Walled Struct. 2008, 46, 573–583. [Google Scholar] [CrossRef]
- Zhou, F.; Young, B. Concrete-filled aluminum circular hollow section column tests. Thin-Walled Struct. 2009, 47, 1272–1280. [Google Scholar] [CrossRef]
- Zhou, F.; Young, B. Concrete-filled double-skin aluminum circular hollow section stub columns. Thin-Walled Struct. 2018, 133, 141–152. [Google Scholar] [CrossRef]
- Wang, F.C.; Zhao, H.Y.; Han, L.H. Analytical behavior of concrete-filled aluminum tubular stub columns under axial compression. Thin-Walled Struct. 2019, 140, 21–30. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Zhang, J.; Lu, L.; Liang, H.; Ma, Z. The Strength in Axial Compression of Aluminum Alloy Tube Confined Concrete Columns with a Circular Hollow Section: Experimental Results. Buildings 2022, 12, 699. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, C.; Niu, K.; Zhao, J.; Huang, Y.; Li, X. Long-term corrosion behavior of the 7A85 aluminum alloy in an industrial-marine atmospheric environment. J. Mater Res. Technol. 2021, 12, 1350–1359. [Google Scholar] [CrossRef]
- Su, M.N.; Young, B.; Gardner, L. The continuous strength method for the design of aluminium alloy structural elements. Eng. Struct. 2016, 122, 338–348. [Google Scholar] [CrossRef]
- Chen, Z.P.; Xu, W.S.; Zhou, J. Mechanical performance of marine concrete filled CFRP-aluminum alloy tube columns under axial compression: Experiment and finite element analysis. Eng. Struct. 2022, 272, 114993. [Google Scholar] [CrossRef]
- GB 50010-2002; Code for Design of Reinforced Concrete Structures. China Planning Press: Beijing, China, 2002. (In Chinese)
- Foraboschi, P. Optimal Design of Seismic Resistant RC Columns. Materials 2020, 13, 1919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Foraboschi, P. Layered plate with discontinuous connection: Exact mathematical model. Compos. Part B 2013, 47, 365–378. [Google Scholar] [CrossRef]
- GB 50936-2014; Design Code for Steel Tube Concrete Structures. China Planning Press: Beijing, China, 2014. (In Chinese)
- Han, L.H. Concrete Filled Steel Tube Structures-Theory and Practice; Science Press: Beijing, China, 2004. (In Chinese) [Google Scholar]





| Specimen No. | a × b × t/mm | a/b | Weak Axis Slenderness Ratio λ | ρa/% |
|---|---|---|---|---|
| CA100-0 | 100 × 50 × 2.5 | 2.0 | 36.7 | 13.5 |
| CA115-0 | 115 × 45 × 5.0 | 2.5 | 40.2 | 26.8 |
| CA120-0 | 120 × 30 × 2.0 | 4.0 | 59.3 | 15.8 |
| CA130-0 | 130 × 65 × 2.0 | 2.0 | 28.2 | 8.5 |
| Types of Aluminum Tube | f0.2/MPa | fu/MPa | Elongation δ/% | Young’s Modulus E/GPa |
|---|---|---|---|---|
| 100 × 50 × 2.5 | 195.2 | 217.4 | 10.31 | 67.5 |
| 115 × 45 × 5.0 | 199.7 | 209.2 | 13.22 | 66.2 |
| 120 × 30 × 2.0 | 201.4 | 211.5 | 11.21 | 67.1 |
| 130 × 65 × 2.0 | 197.3 | 214.1 | 12.43 | 68.2 |
| Specimen No. | K/kN∙mm−1 | Py/kN | Pu/kN | Ps/kN | SI | μ | PFE/kN | Pu/PFE |
|---|---|---|---|---|---|---|---|---|
| CA100-0 | 125.2 | 223.7 | 238.4 | 228.0 | 1.05 | 1.95 | 249.7 | 0.95 |
| CA115-0 | 90.4 | 280.1 | 295.4 | 345.3 | 0.86 | 1.88 | 305.0 | 0.97 |
| CA120-0 | 30.7 | 101.6 | 103.2 | 183.0 | 0.56 | 1.15 | 100.3 | 1.03 |
| CA130-0 | 153.4 | 352.3 | 365.6 | 323.7 | 1.13 | 1.79 | 367.7 | 0.99 |
| Specimen No. | Pu/kN | Pc/kN | Pu/Pc |
|---|---|---|---|
| CA100-0 | 238.4 | 240.2 | 0.99 |
| CA115-0 | 295.4 | 348.9 | 0.85 |
| CA120-0 | 103.2 | 107.2 | 0.96 |
| CA130-0 | 365.6 | 361.7 | 1.01 |
| FE-f0.2 = 300 MPa | 297.4 | 288.6 | 1.03 |
| FE-f0.2 = 400 MPa | 342.5 | 337.1 | 1.02 |
| FE-f0.2 = 600 MPa | 402.2 | 394.2 | 1.02 |
| FE-C40 | 274.5 | 266.4 | 1.03 |
| FE-C50 | 276.9 | 269.1 | 1.03 |
| FE-C60 | 305.0 | 299.5 | 1.02 |
| Average | 0.996 | ||
| Standard deviation | 0.056 | ||
| Coefficient of variation | 0.056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, J.; Liu, Q.; Yu, Y.; Qiu, Q. Axial Compression Performance and Bearing Capacity Calculation of Round-Ended Concrete-Filled Aluminum Tube Column. Appl. Sci. 2023, 13, 7918. https://doi.org/10.3390/app13137918
Bu J, Liu Q, Yu Y, Qiu Q. Axial Compression Performance and Bearing Capacity Calculation of Round-Ended Concrete-Filled Aluminum Tube Column. Applied Sciences. 2023; 13(13):7918. https://doi.org/10.3390/app13137918
Chicago/Turabian StyleBu, Jianqing, Qin Liu, Yong Yu, and Qirong Qiu. 2023. "Axial Compression Performance and Bearing Capacity Calculation of Round-Ended Concrete-Filled Aluminum Tube Column" Applied Sciences 13, no. 13: 7918. https://doi.org/10.3390/app13137918
APA StyleBu, J., Liu, Q., Yu, Y., & Qiu, Q. (2023). Axial Compression Performance and Bearing Capacity Calculation of Round-Ended Concrete-Filled Aluminum Tube Column. Applied Sciences, 13(13), 7918. https://doi.org/10.3390/app13137918








