Field Test and Numerical Investigation of Tunnel Aerodynamic Effect Induced by High-Speed Trains Running at Higher Speeds
Abstract
:Featured Application
Abstract
1. Introduction
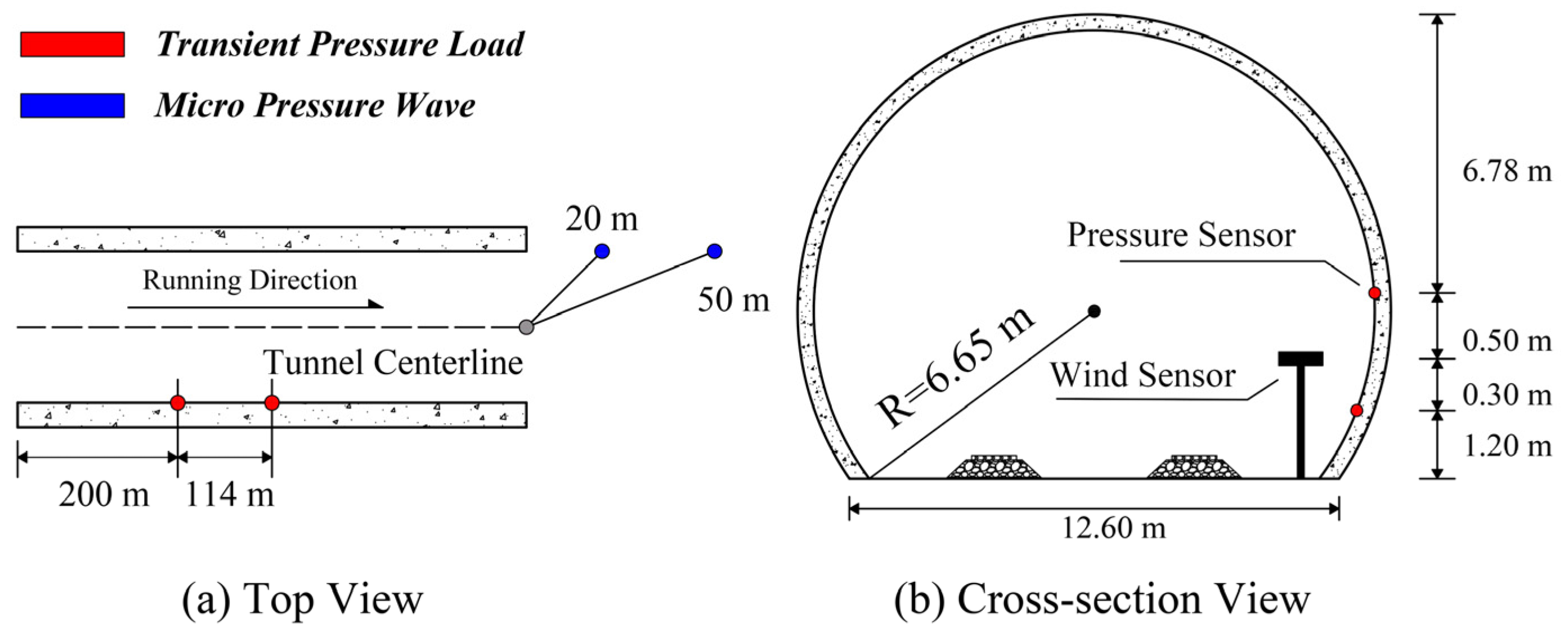
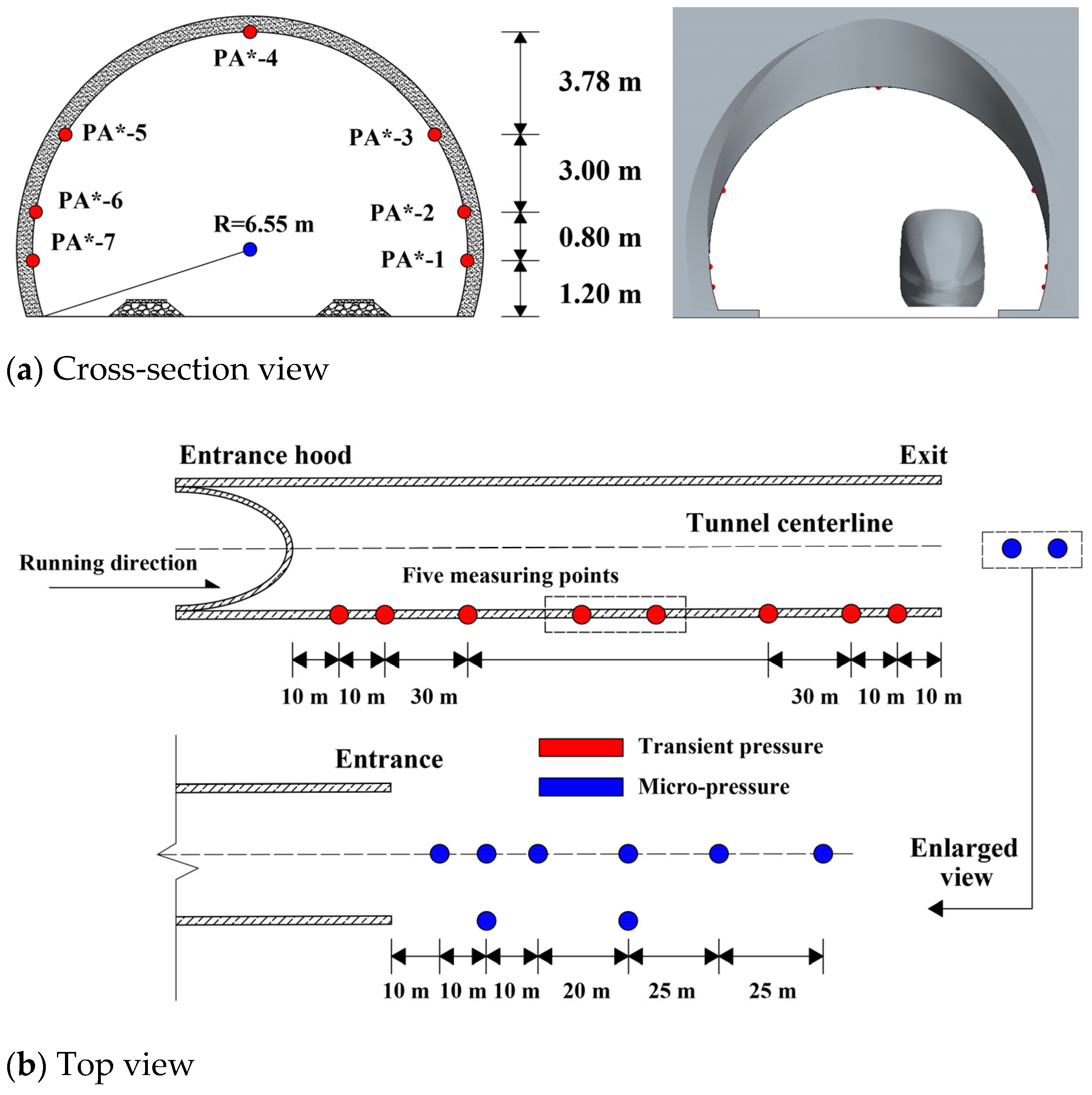
2. Full-Scale Tests
2.1. Test Condition
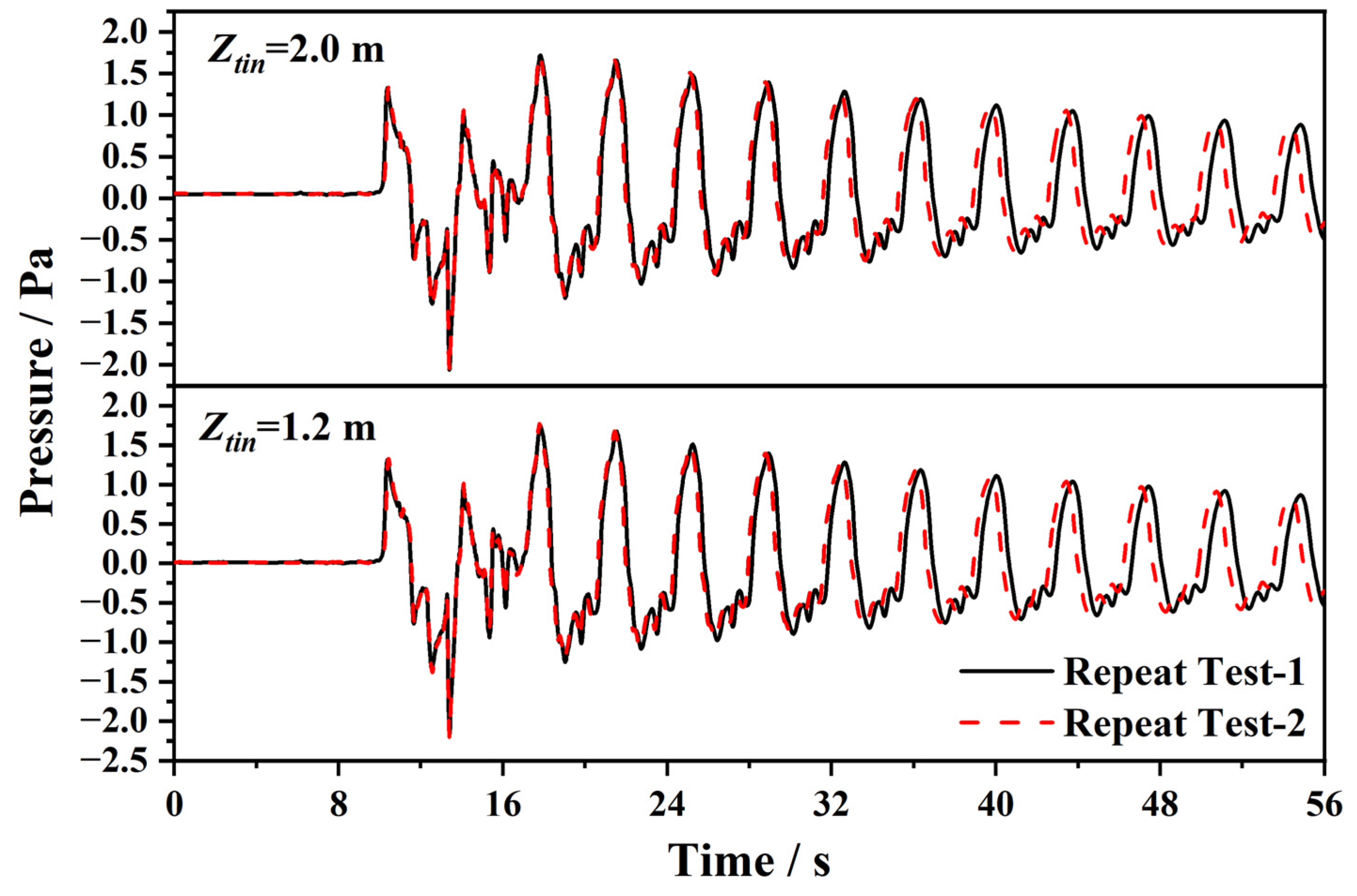
2.2. Measurements
3. Numerical Simulation
3.1. Methodology
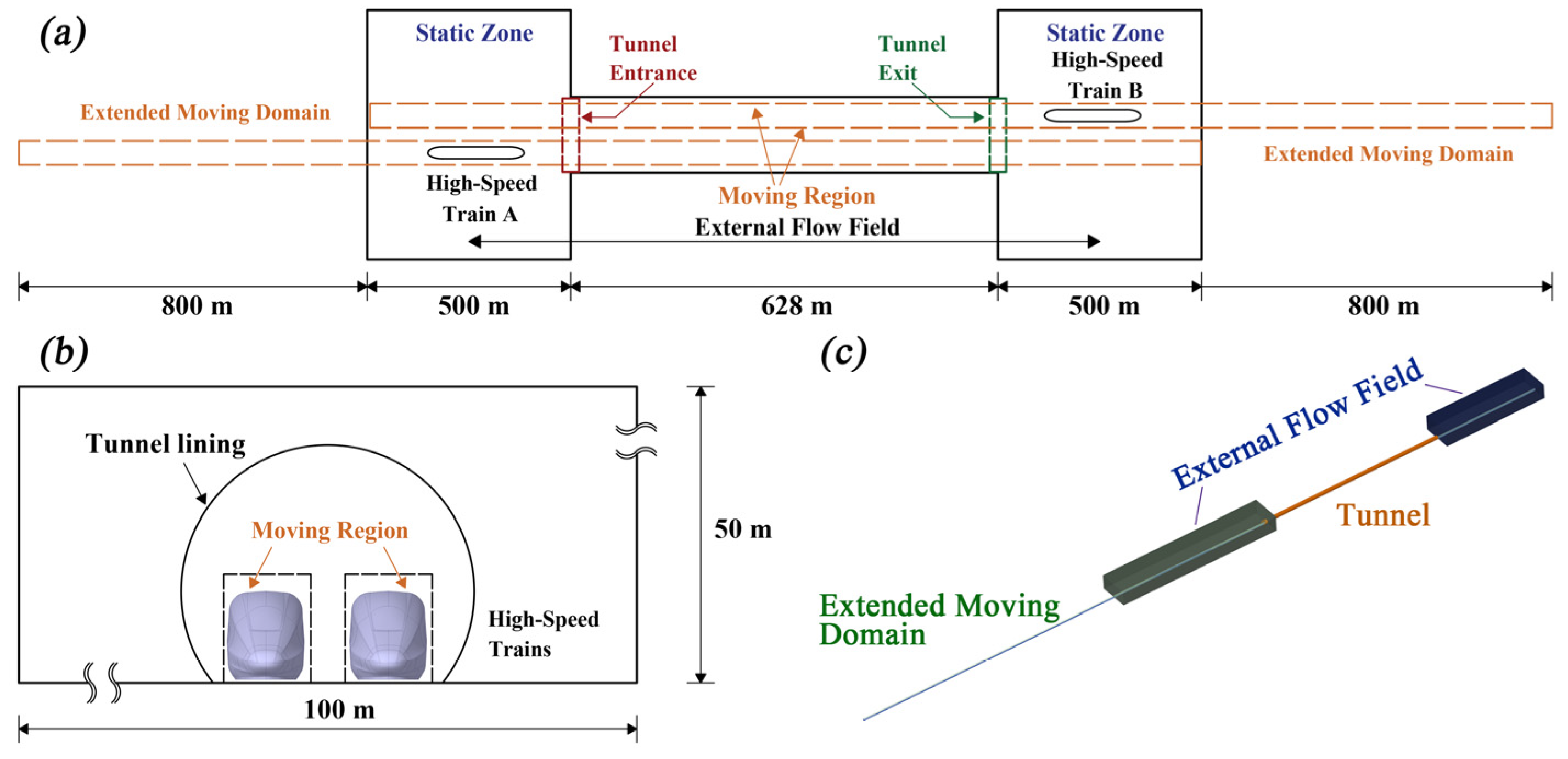
3.2. Computation Domain and Boundaries
3.2.1. Geometries
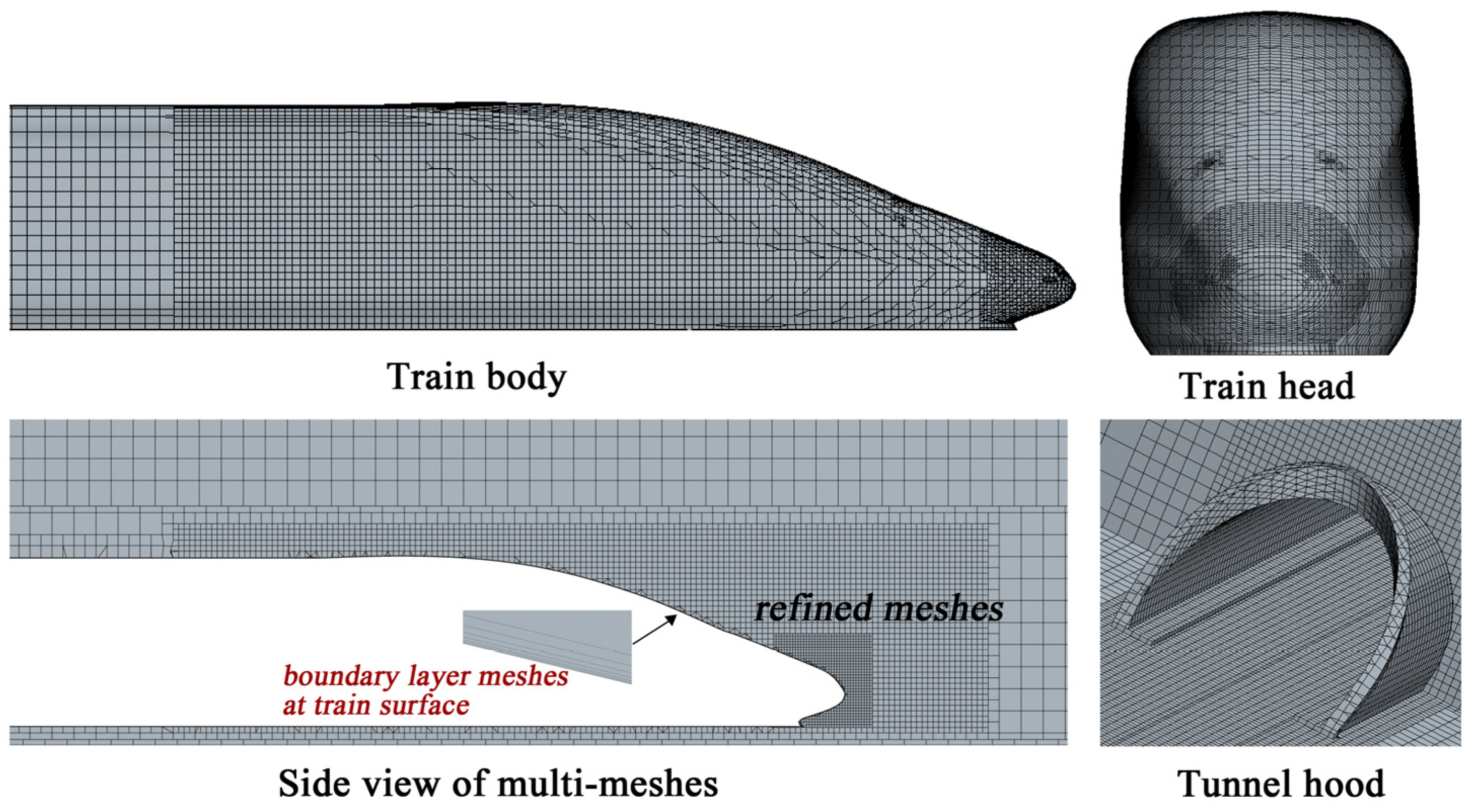
3.2.2. Meshes and Boundaries
3.2.3. Measurements and Scheme
4. Results and Discussion
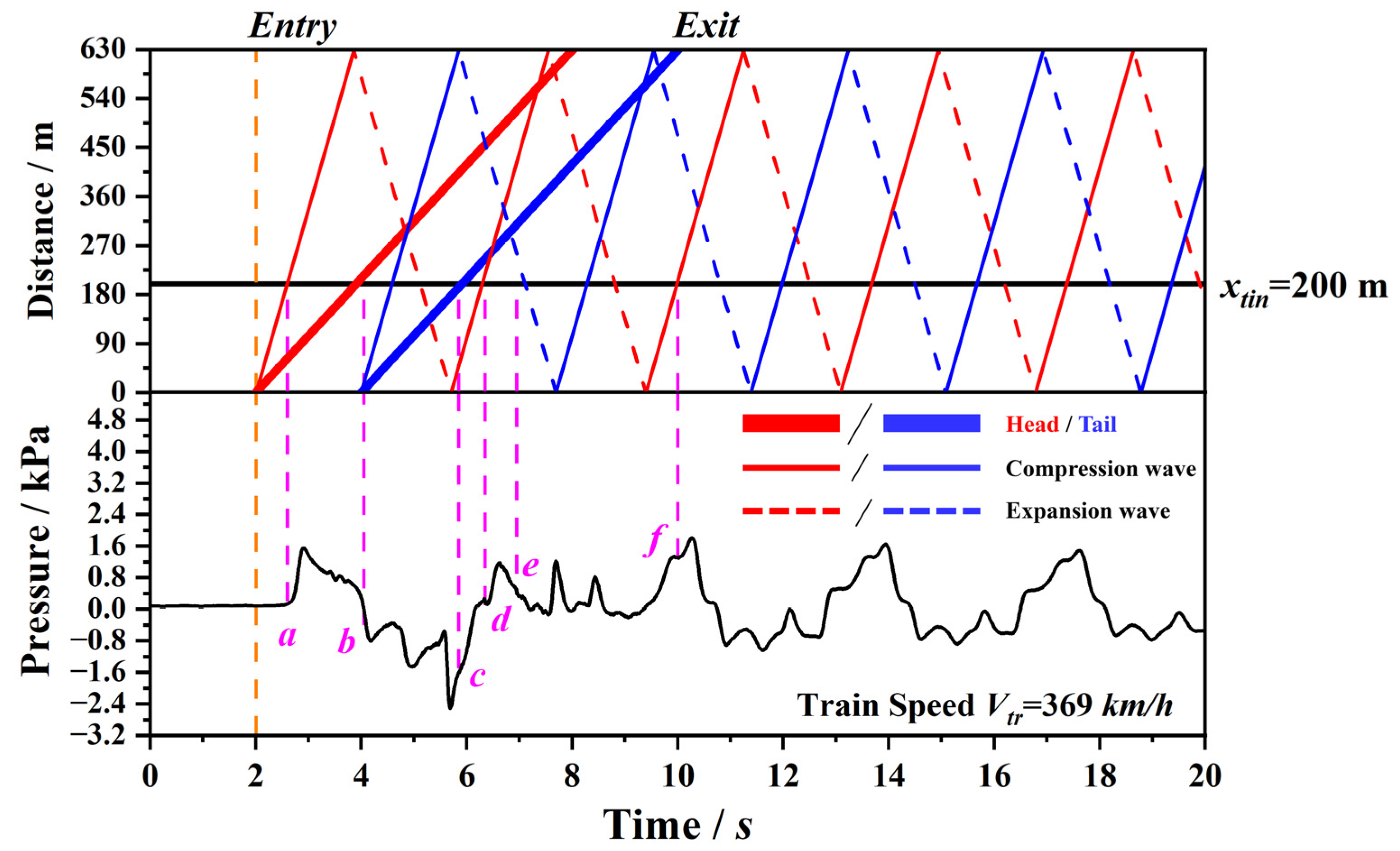
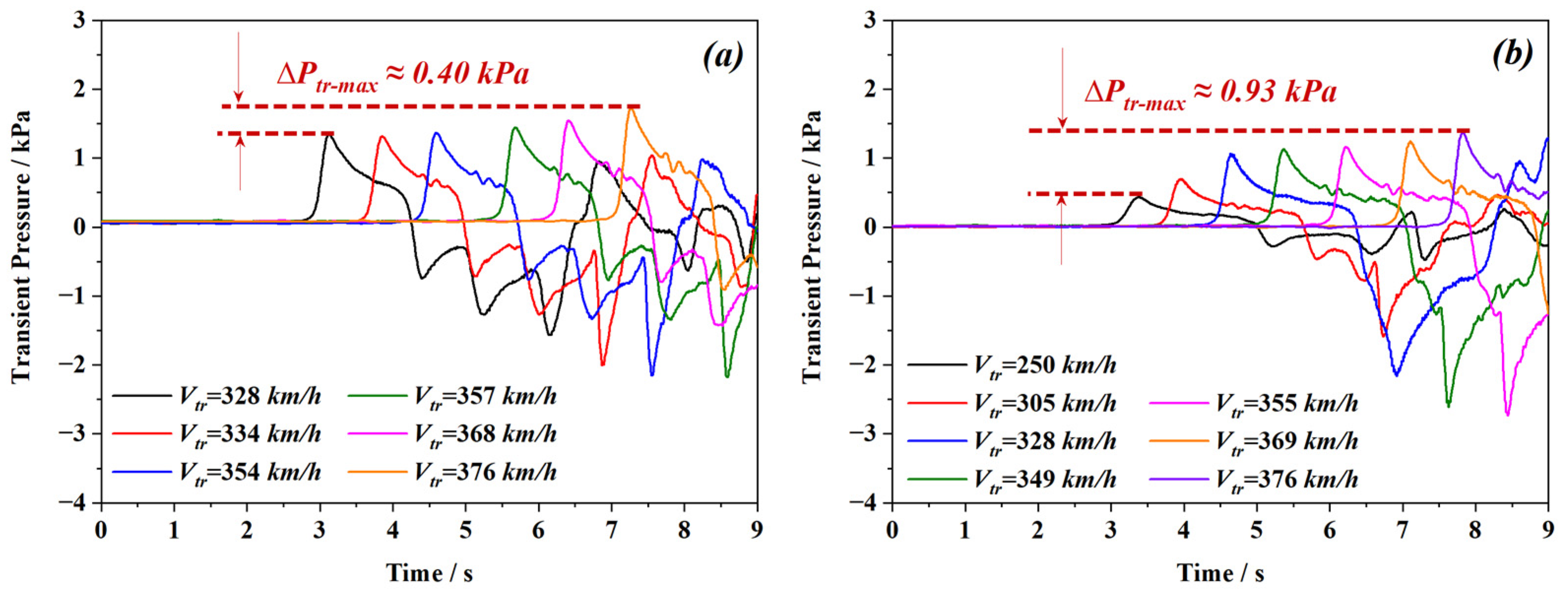
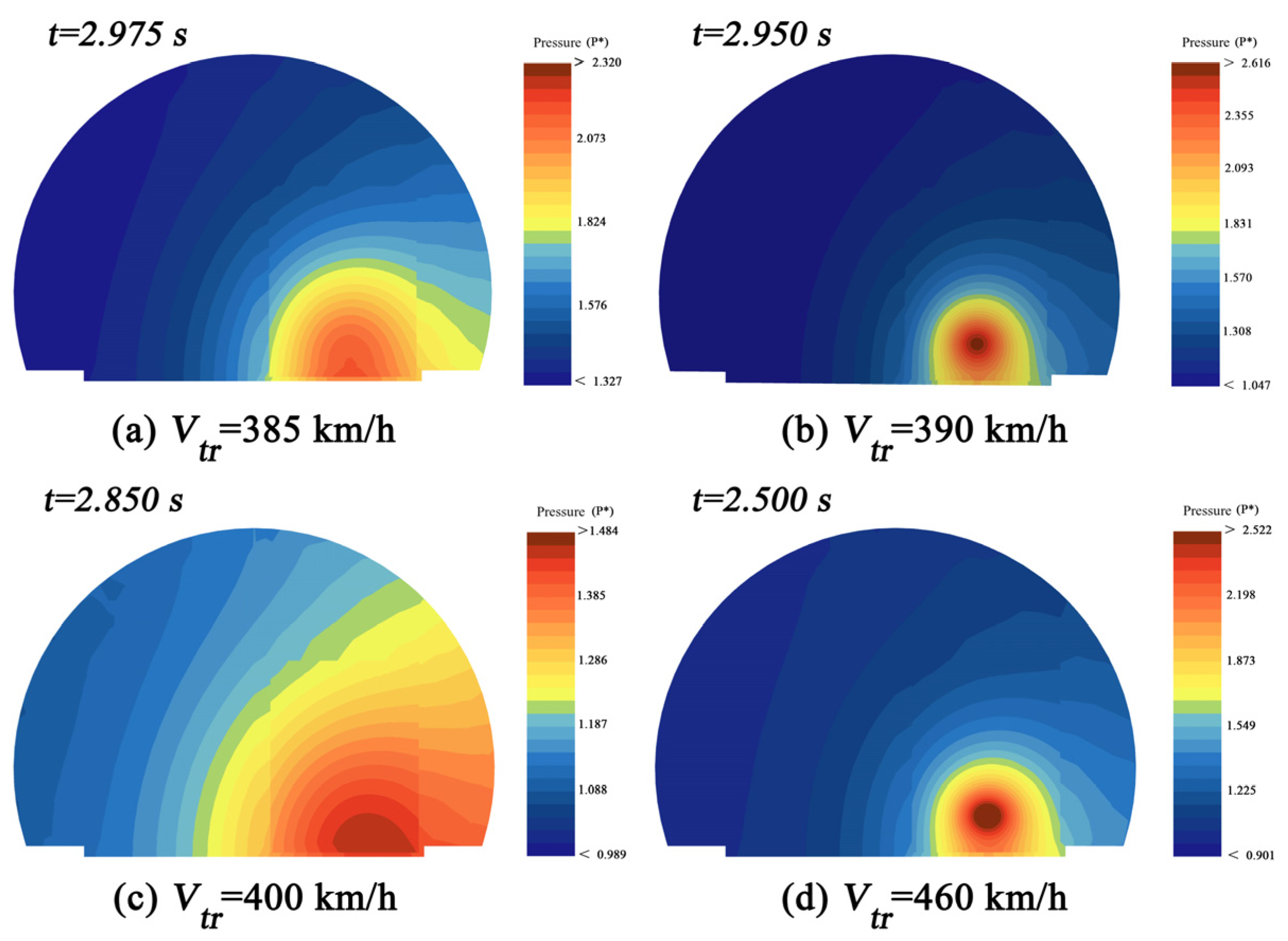
4.1. Aerodynamic Pressure Caused by the Single Train
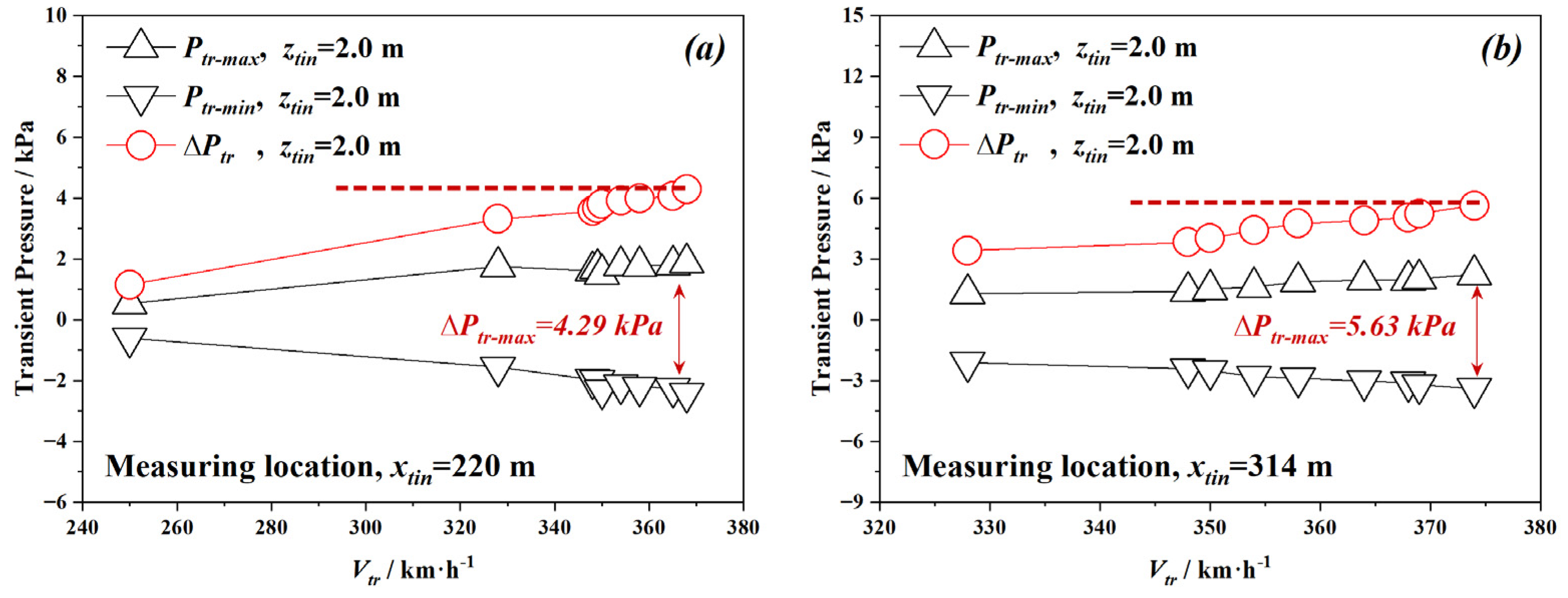
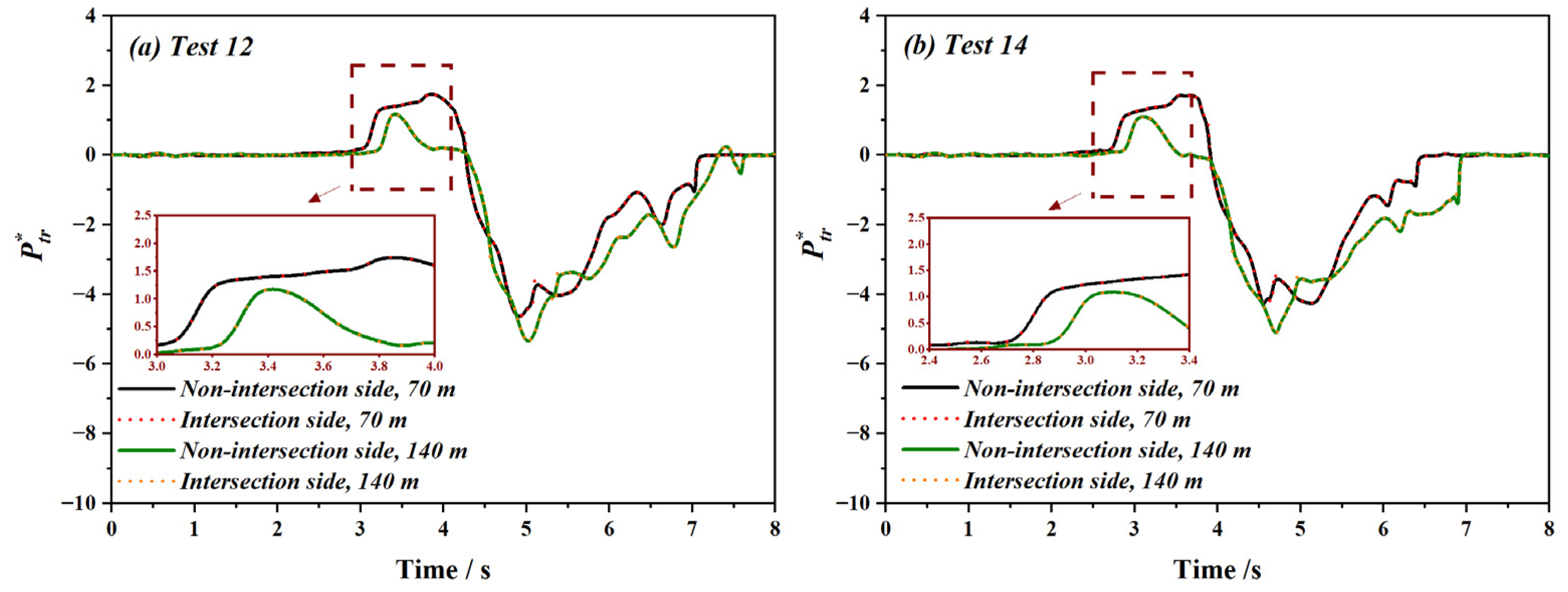
4.2. Aerodynamic Pressure Regrading Train-Intersection
5. Conclusions
- (1)
- TPL acting at tunnel surface and the train body presents unevenly distribution trend as the longitudinal distance to tunnel entrance increases. Pressures measured near tunnel center is generally higher than that those detected near tunnel portal. The pressure peak measured at tunnel surface first increases and then decreases with the maximum value appearing at the intersection position (tunnel center in the current research). Besides, for a given location, TPL nearby the train side increases with the measuring height and show slight difference on the other side.
- (2)
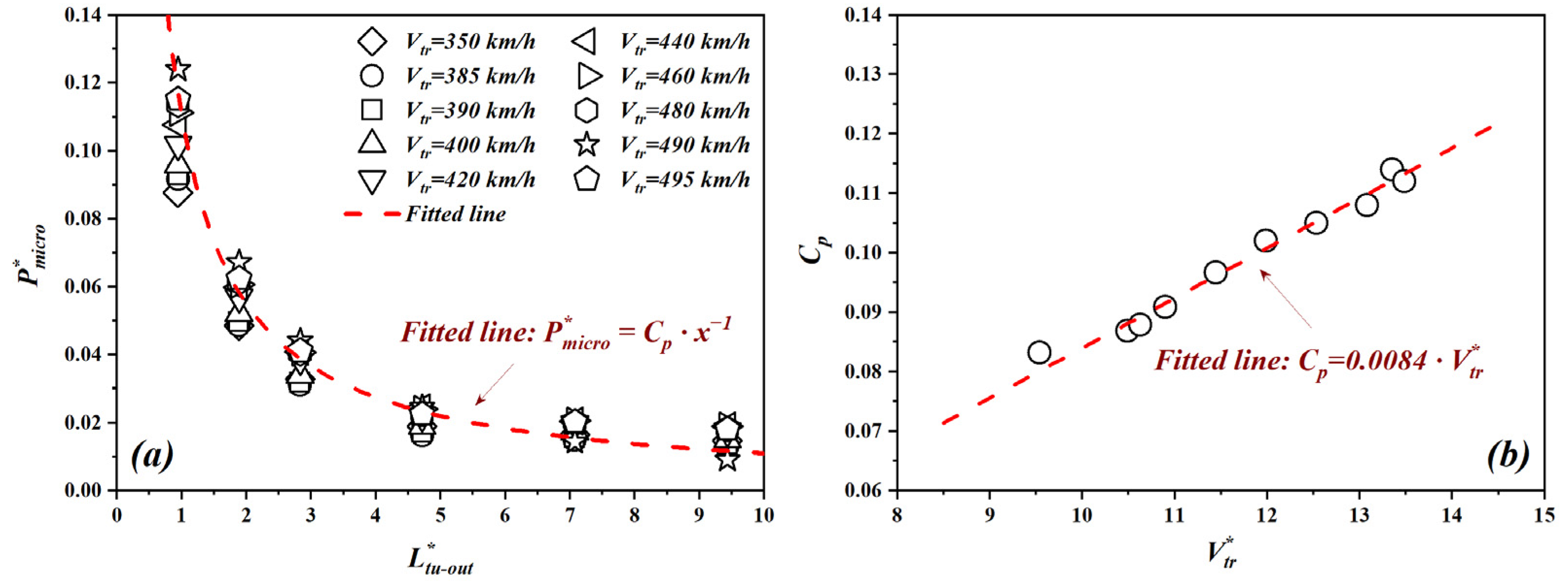
- Amplitude of micro-pressure wave increases with train’s velocity. The maximum value of MPW detected in the field test is approximately 37.63 Pa. Meanwhile, amplitude of MPW is inversely proportional to the attenuated distance, i.e., . Through data fitting, empirical model was established to predict the longitudinal attenuation of amplitude of MPW.
- (3)
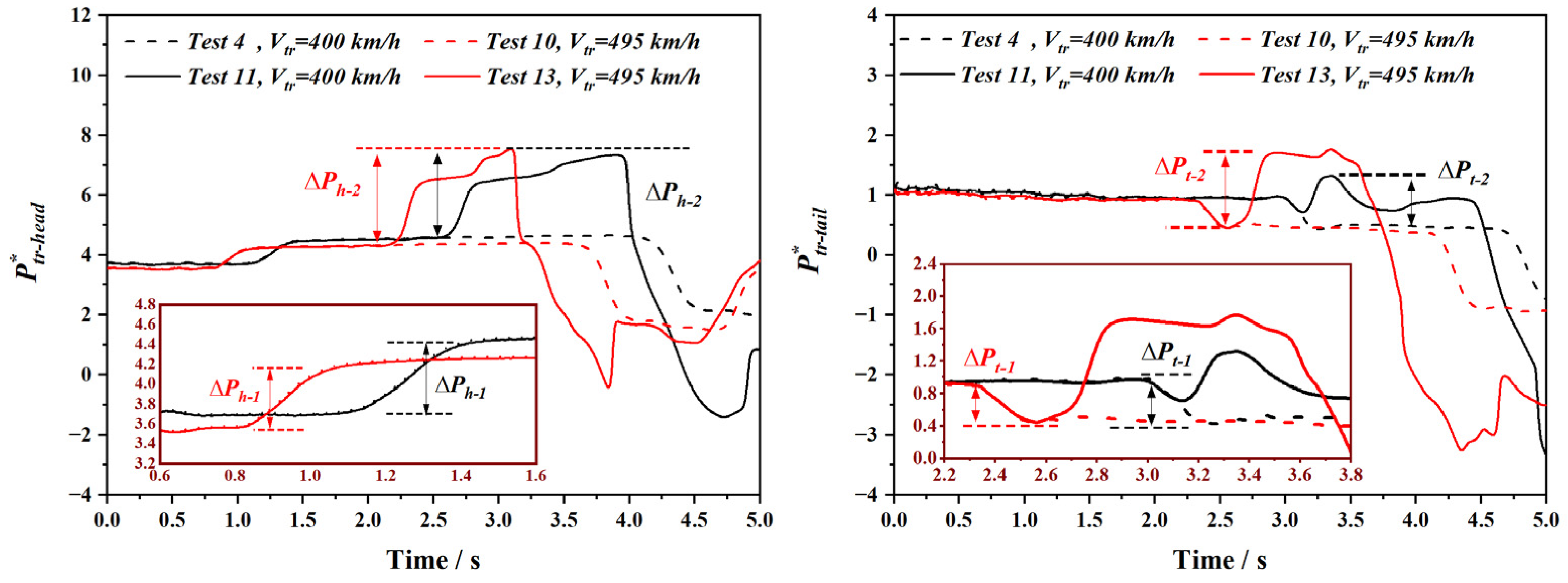
- Pressure rapidly increases before the heat-to-head intersection and then fast decreases due to the tail-to-tail intersection. In the situation of train’s intersection, variation of the pressure peak near the tunnel portals is insignificant though train’s velocity changes. On the contrary, pressure peaks measured at the intersection position are doubled. The peak pressure load appears at the train head while carriages of the train body will be within the negative region after the head-to-head intersection. For the given location, values of pressure peak obtained from both the intersection side and non-intersection side presents limited variation while values change when the longitudinal location varies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ozawa, S.; Uchida, T.; Maeda, T. Reduction of micro-pressure wave radiated from tunnel exit by hood at tunnel entrance. Railw. Tech. Res. Inst. Q. Rep. 1978, 19, 77–83. [Google Scholar]
- Ozawa, S.; Maeda, T. Tunnel entrance hoods for reduction of micro-pressure wave. Railw. Tech. Res. Inst. Q. Rep. 1988, 29, 134–139. [Google Scholar]
- Raghunathan, R.S.; Kim, H.D.; Setoguchi, T. Aerodynamics of high-speed railway train. Prog. Aerosp. Sci. 2002, 38, 469–514. [Google Scholar] [CrossRef]
- Howe, M.S. Design of a tunnel-entrance hood with multiple windows and variable cross-section. J. Fluids Struct. 2003, 17, 1111–1121. [Google Scholar] [CrossRef]
- Howe, M.S. On the design of a tunnel-entrance hood with multiple windows. J. Sound Vib. 2004, 273, 233–248. [Google Scholar] [CrossRef]
- Howe, M.S.; Iida, M.; Maeda, T.; Sakuma, Y. Rapid calculation of the compression wave generated by a train entering a tunnel with a vented hood. J. Sound Vib. 2006, 297, 267–292. [Google Scholar] [CrossRef]
- Howe, M.S.; Winslow, A.; Iida, M.; Fukuda, T. Rapid calculation of the compression wave generated by a train entering a tunnel with a vented hood: Short hoods. J. Sound Vib. 2008, 311, 254–268. [Google Scholar] [CrossRef]
- Baron, A.; Molteni, P.; Vigevano, L. High-speed trains: Prediction of micro-pressure wave radiation from tunnel portals. J. Sound Vib. 2006, 296, 59–72. [Google Scholar] [CrossRef]
- Liu, T.-h.; Tian, H.-q.; Liang, X.-f. Design and optimization of tunnel hoods. Tunn. Undergr. Space Technol. 2010, 25, 212–219. [Google Scholar] [CrossRef]
- Kim, D.H.; Cheol, S.Y.; Iyer, R.S.; Kim, H.D. A newly designed entrance hood to reduce the micro pressure wave emitted from the exit of high-speed railway tunnel. Tunn. Undergr. Space Technol. 2021, 108, 103728. [Google Scholar] [CrossRef]
- Kim, D.H.; Seo, Y.C.; Kim, T.H.; Kim, H.D. Effects of detailed shape of air-shaft entrance hood on tunnel pressure waves. J. Mech. Sci. Technol. 2021, 35, 615–624. [Google Scholar] [CrossRef]
- Miyachi, T.; Fukuda, T.; Saito, S. Model experiment and analysis of pressure waves emitted from portals of a tunnel with a branch. J. Sound Vib. 2014, 333, 6156–6169. [Google Scholar] [CrossRef]
- Okubo, H.; Miyachi, T.; Sugiyama, K. Pressure fluctuation and a micro-pressure wave in a high-speed railway tunnel with large branch shaft. J. Wind Eng. Ind. Aerodyn. 2021, 217, 104751. [Google Scholar] [CrossRef]
- Xiang, X.; Xue, L.; Wang, B.; Zou, W. Mechanism and capability of ventilation openings for alleviating micro-pressure waves emitted from high-speed railway tunnels. Build. Environ. 2018, 132, 245–254. [Google Scholar] [CrossRef]
- Wang, H.; Vardy, A.E.; Pokrajac, D. Perforated exit regions for the reduction of micro-pressure waves from tunnels. J. Wind Eng. Ind. Aerodyn. 2015, 146, 139–149. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Thurow, K.; Stoll, N.; Liu, H. Influence of the geometry of equal-transect oblique tunnel portal on compression wave and micro-pressure wave generated by high-speed trains entering tunnels. J. Wind Eng. Ind. Aerodyn. 2018, 178, 1–17. [Google Scholar] [CrossRef]
- Li, W.; Liu, T.; Huo, X.; Chen, Z.; Guo, Z.; Li, L. Influence of the enlarged portal length on pressure waves in railway tunnels with cross-section expansion. J. Wind Eng. Ind. Aerodyn. 2019, 190, 10–22. [Google Scholar] [CrossRef]
- Mashimo, S.; Nakatsu, E.; Aoki, T.; Matsuo, K. Attenuation and Distortion of a Compression Wave Propagating in a High-Speed Railway Tunnel. Nippon Kikai Gakkai Ronbunshu B Hen/Trans Jpn Soc. Mech. Eng. Part B 1996, 62, 1847–1854. [Google Scholar] [CrossRef] [Green Version]
- William-Louis, M.; Tournier, C. A wave signature based method for the prediction of pressure transients in railway tunnels. J. Wind Eng. Ind. Aerodyn. 2005, 93, 521–531. [Google Scholar] [CrossRef]
- Ricco, P.; Baron, A.; Molteni, P. Nature of pressure waves induced by a high-speed train travelling through a tunnel. J. Wind Eng. Ind. Aerodyn. 2007, 95, 781–808. [Google Scholar] [CrossRef]
- Chen, X.-D.; Liu, T.-H.; Zhou, X.-S.; Li, W.-h.; Xie, T.-Z.; Chen, Z.-W. Analysis of the aerodynamic effects of different nose lengths on two trains intersecting in a tunnel at 350 km/h. Tunn. Undergr. Space Technol. 2017, 66, 77–90. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, T.; Yang, M.; Qian, B. The influence of reduced cross-section on pressure transients from high-speed trains intersecting in a tunnel. J. Wind Eng. Ind. Aerodyn. 2020, 201, 104161. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, Y.; Shi, S.; Xu, F.; Zhao, W. Characteristics of transient pressure in lining cracks induced by high-speed trains. J. Wind Eng. Ind. Aerodyn. 2022, 228, 105120. [Google Scholar] [CrossRef]
- Du, J.; Fang, Q.; Wang, G.; Zhang, D.; Chen, T. Fatigue damage and residual life of secondary lining of high-speed railway tunnel under aerodynamic pressure wave. Tunn. Undergr. Space Technol. 2021, 111, 103851. [Google Scholar] [CrossRef]
- Reiterer, M.; Ehrendorfer, K.; Sockel, H. In Experimental Investigation of the Micro Pressure Wave. In TRANSAERO—A European Initiative on Transient Aerodynamics for Railway System Optimisation; Schulte-Werning, B., Grégoire, R., Malfatti, A., Matschke, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 290–301. [Google Scholar]
- Fukuda, T.; Iida, M.; Maeda, T.; Maeno, K.; Honma, H. Investigation of compression wave propagating in slab track tunnel of high-speed railway (field test and one-dimensional numerical analysis). Nihon Kikai Gakkai Ronbunshu B Hen/Trans. Jpn. Soc. Mech. Eng. Part B 1998, 64, 107–113. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Liu, T.; Xia, Y.; Liu, Z. Aerodynamic influence of the clearance under the cowcatcher of a high-speed train. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104844. [Google Scholar] [CrossRef]
- Deng, E.; Yang, W.; He, X.; Ye, Y.; Zhu, Z.; Wang, A. Transient aerodynamic performance of high-speed trains when passing through an infrastructure consisting of tunnel–bridge–tunnel under crosswind. Tunn. Undergr. Space Technol. 2020, 102, 103440. [Google Scholar] [CrossRef]
- Yang, W.; Liu, Y.; Deng, E.; He, X.; Lei, M.; Zou, Y. Comparative study on the wind characteristics of tunnel–bridge and tunnel–flat ground infrastructures on high-speed railway. J. Wind Eng. Ind. Aerodyn. 2022, 226, 105006. [Google Scholar] [CrossRef]
- Deng, E.; Yang, W.; He, X.; Zhu, Z.; Wang, H.; Wang, Y.; Wang, A.; Zhou, L. Aerodynamic response of high-speed trains under crosswind in a bridge-tunnel section with or without a wind barrier. J. Wind Eng. Ind. Aerodyn. 2021, 210, 104502. [Google Scholar] [CrossRef]
- Li, W.; Liu, T.; Chen, Z.; Guo, Z.; Huo, X. Comparative study on the unsteady slipstream induced by a single train and two trains passing each other in a tunnel. J. Wind Eng. Ind. Aerodyn. 2020, 198, 104095. [Google Scholar] [CrossRef]
- Liu, T.; Jiang, Z.; Chen, X.; Zhang, J.; Liang, X. Wave effects in a realistic tunnel induced by the passage of high-speed trains. Tunn. Undergr. Space Technol. 2019, 86, 224–235. [Google Scholar] [CrossRef]
- Howe, M.S.; Iida, M.; Fukuda, T.; Maeda, T. Theoretical and experimental investigation of the compression wave generated by a train entering a tunnel with a flared portal. J. Fluid Mech. 2000, 425, 111–132. [Google Scholar] [CrossRef]
- Bannister, F.K.; Mucklow, G.F. In Wave Action following Sudden Release of Compressed Gas from a Cylinder. Proc. Inst. Mech. Eng. 1948, 159, 269. [Google Scholar] [CrossRef]
- Mashimo, S.; Nakatsu, E.; Aoki, T.; Matsuo, K. Attenuation and Distortion of a Compression Wave Propagating in a High-Speed Railwav Tunnel. JSME Int. J. Ser. B Fluids Therm. Eng. 1997, 40, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Yao, S.; Zhang, J.; Wang, Y.-q. Field measurements of aerodynamic pressures in high-speed railway tunnels. Tunn. Undergr. Space Technol. 2018, 72, 97–106. [Google Scholar] [CrossRef]








| Test No. | Train A/km·h−1 | Train B/km·h−1 | Test Scenario |
|---|---|---|---|
| 1 | 350 | / | Single train |
| 2 | 385 | / | |
| 3 | 390 | / | |
| 4 | 400 | / | |
| 5 | 420 | / | |
| 6 | 440 | / | |
| 7 | 460 | / | |
| 8 | 480 | / | |
| 9 | 490 | / | |
| 10 | 495 | / | |
| 11 | 400 | 400 | Intersection |
| 12 | 450 | 450 | |
| 13 | 495 | 495 | |
| 14 | 495 | 450 | |
| 15 | 495 | 400 | |
| 16 | 450 | 400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ma, W.; Han, J.; Wang, C.; Cheng, A.; Yang, X.; Gao, H. Field Test and Numerical Investigation of Tunnel Aerodynamic Effect Induced by High-Speed Trains Running at Higher Speeds. Appl. Sci. 2023, 13, 8197. https://doi.org/10.3390/app13148197
Wang Y, Ma W, Han J, Wang C, Cheng A, Yang X, Gao H. Field Test and Numerical Investigation of Tunnel Aerodynamic Effect Induced by High-Speed Trains Running at Higher Speeds. Applied Sciences. 2023; 13(14):8197. https://doi.org/10.3390/app13148197
Chicago/Turabian StyleWang, Yong, Weibin Ma, Jiaqiang Han, Chen Wang, Aijun Cheng, Xu Yang, and Hongjie Gao. 2023. "Field Test and Numerical Investigation of Tunnel Aerodynamic Effect Induced by High-Speed Trains Running at Higher Speeds" Applied Sciences 13, no. 14: 8197. https://doi.org/10.3390/app13148197
APA StyleWang, Y., Ma, W., Han, J., Wang, C., Cheng, A., Yang, X., & Gao, H. (2023). Field Test and Numerical Investigation of Tunnel Aerodynamic Effect Induced by High-Speed Trains Running at Higher Speeds. Applied Sciences, 13(14), 8197. https://doi.org/10.3390/app13148197





