Aerodynamic Analysis of the Opening Hood Structures at Exits of High-Speed Railway Tunnels
Abstract
Featured Application
Abstract
1. Introduction
2. Theoretical Analysis of Key Parameters for Exit Hoods
- The air within the control volumes is treated as an ideal gas, and the total energy change of the system is attributed to thermodynamic energy.
- The tunnel walls act as adiabatic boundaries, and the system does not perform mechanical work on the external environment.
- The specific enthalpy entering and exiting through the opening interface is equal to the average specific enthalpy of the air within the control volume at that moment.
- The change in mass within the control volume during differential processes is entirely caused by variations in the mass of the air.
3. Methodology for Numerical Simulation
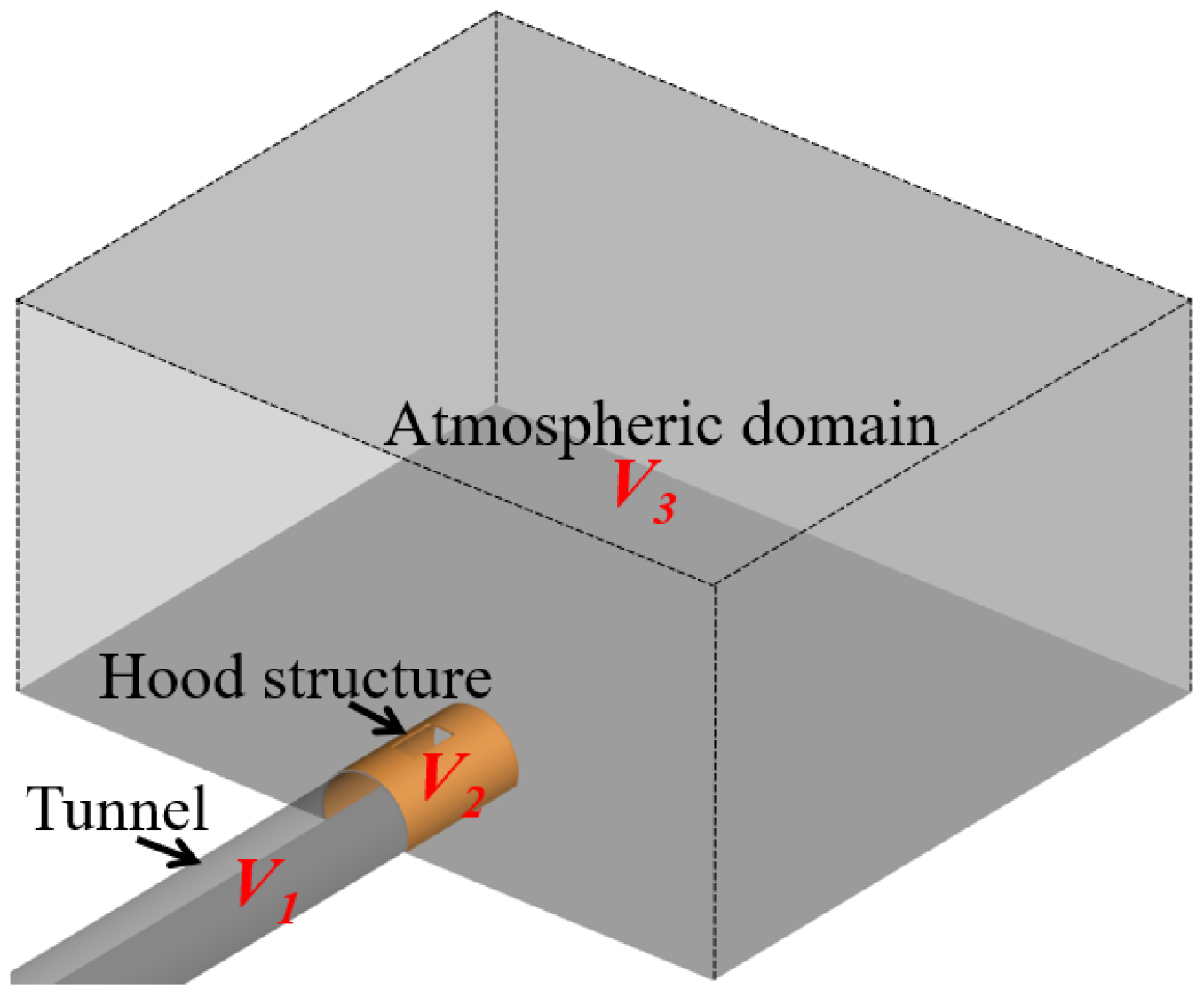
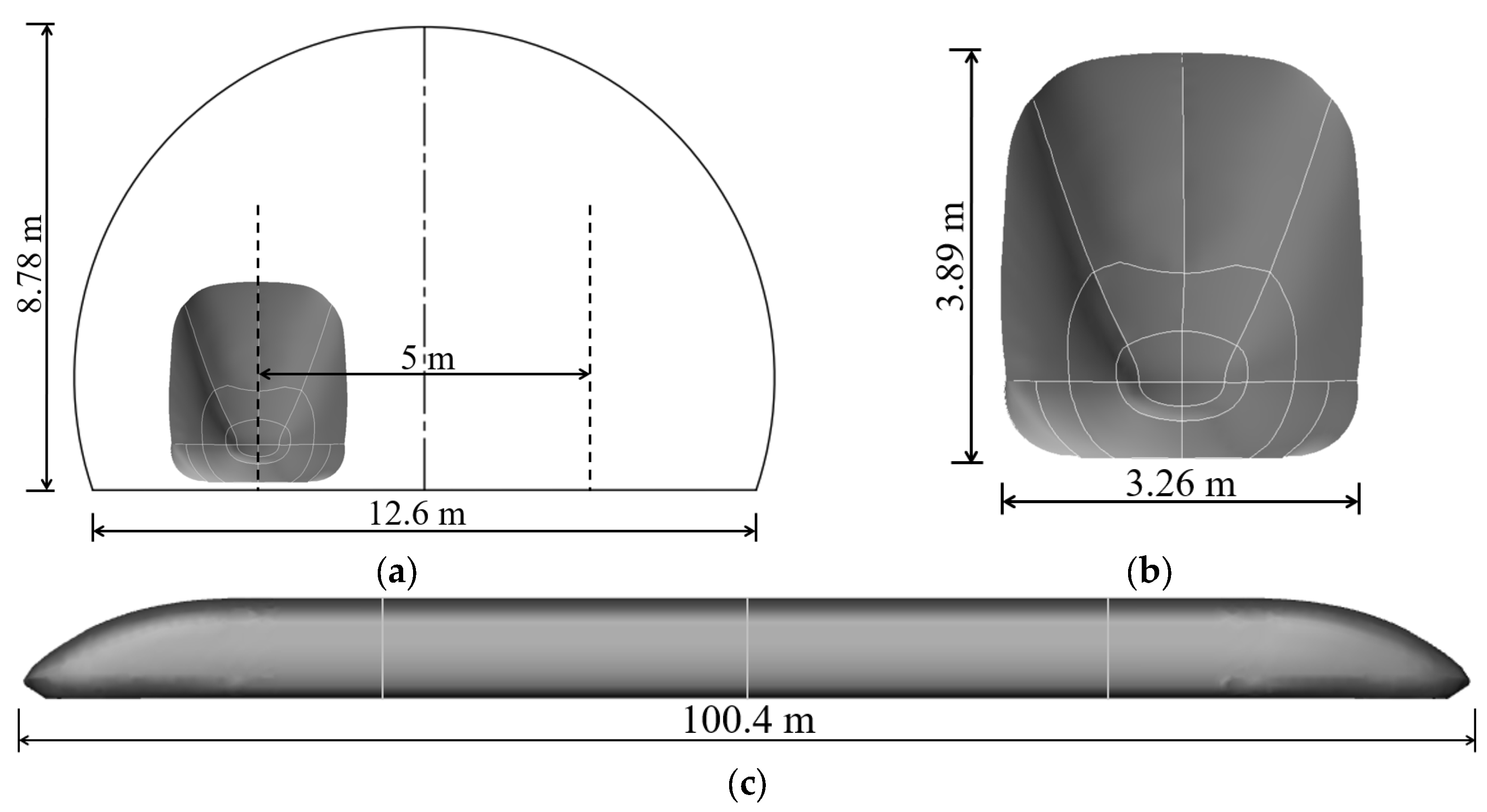
3.1. CFD Geometric Model
3.2. Numerical Setups
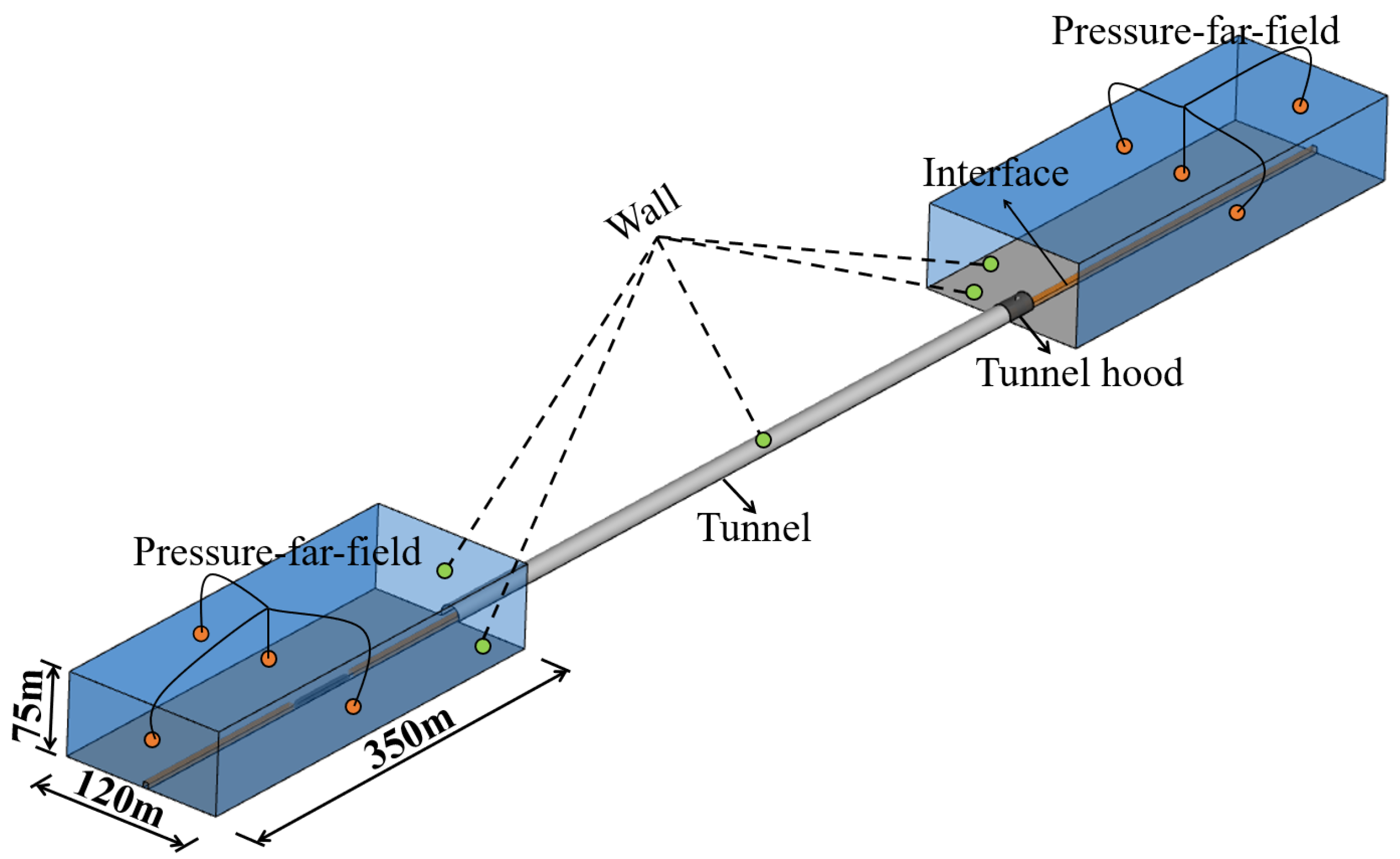
3.3. Layout of Monitoring Points
4. Numerical Validation
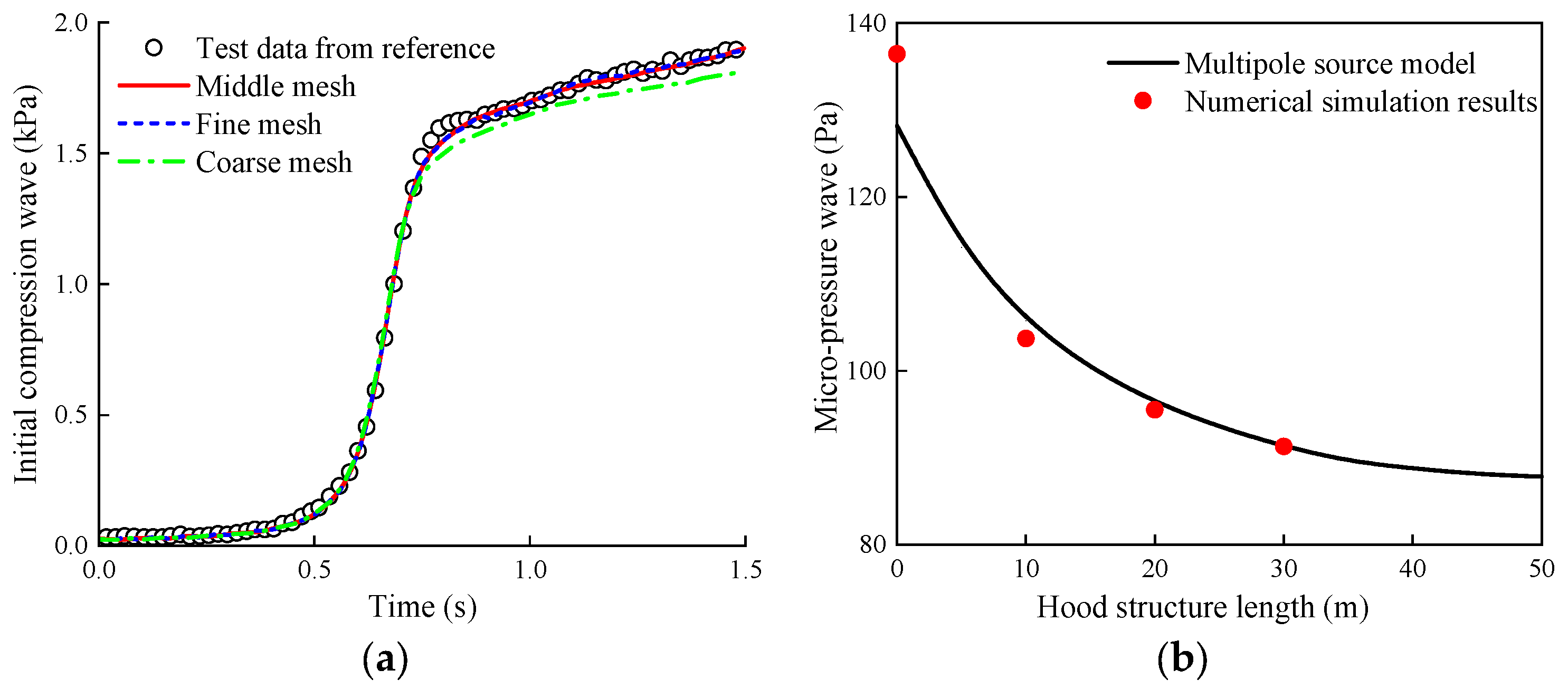
4.1. Grid-Independence Study
4.2. Validation of Numerical Method
5. Results and Discussion
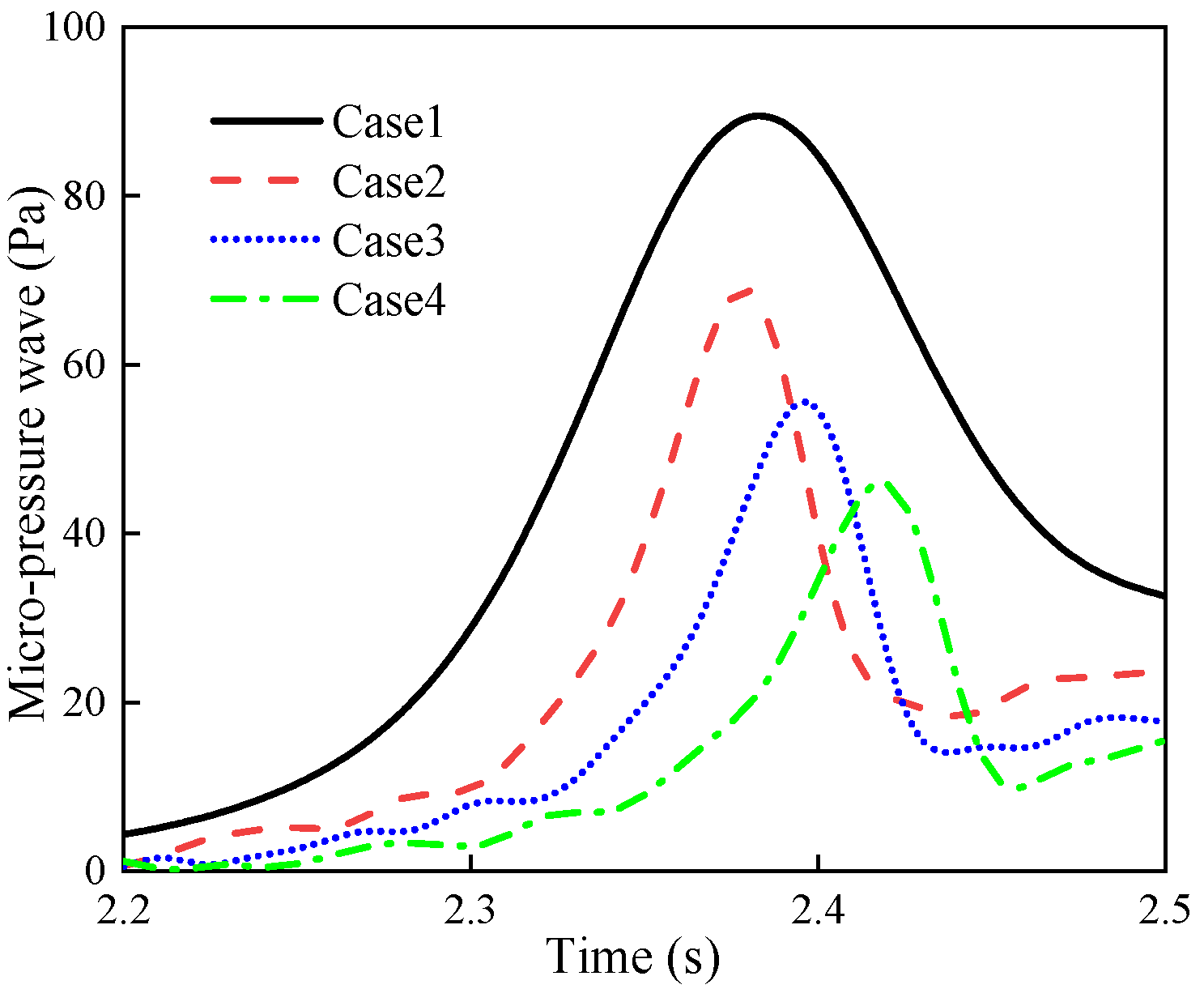
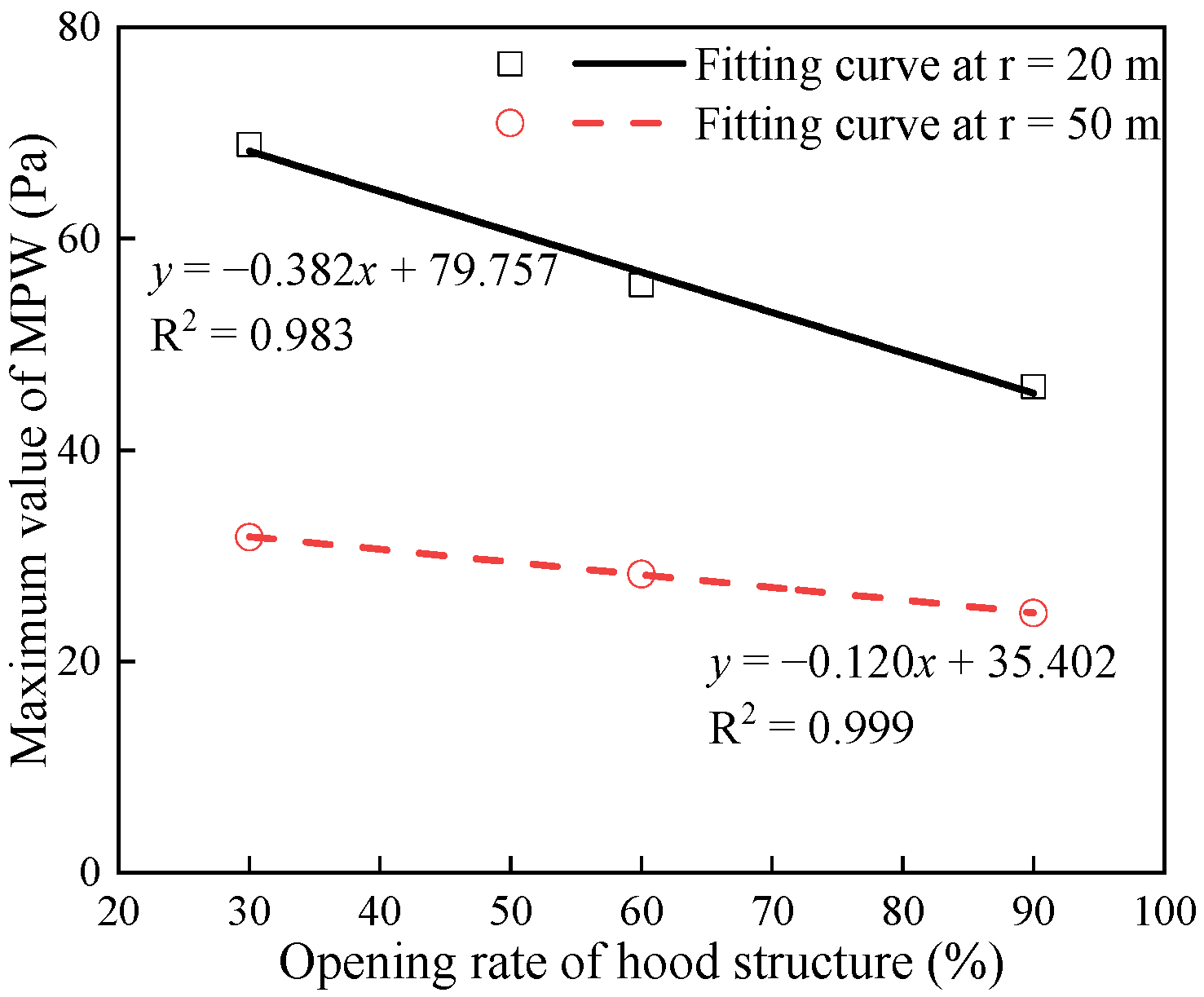
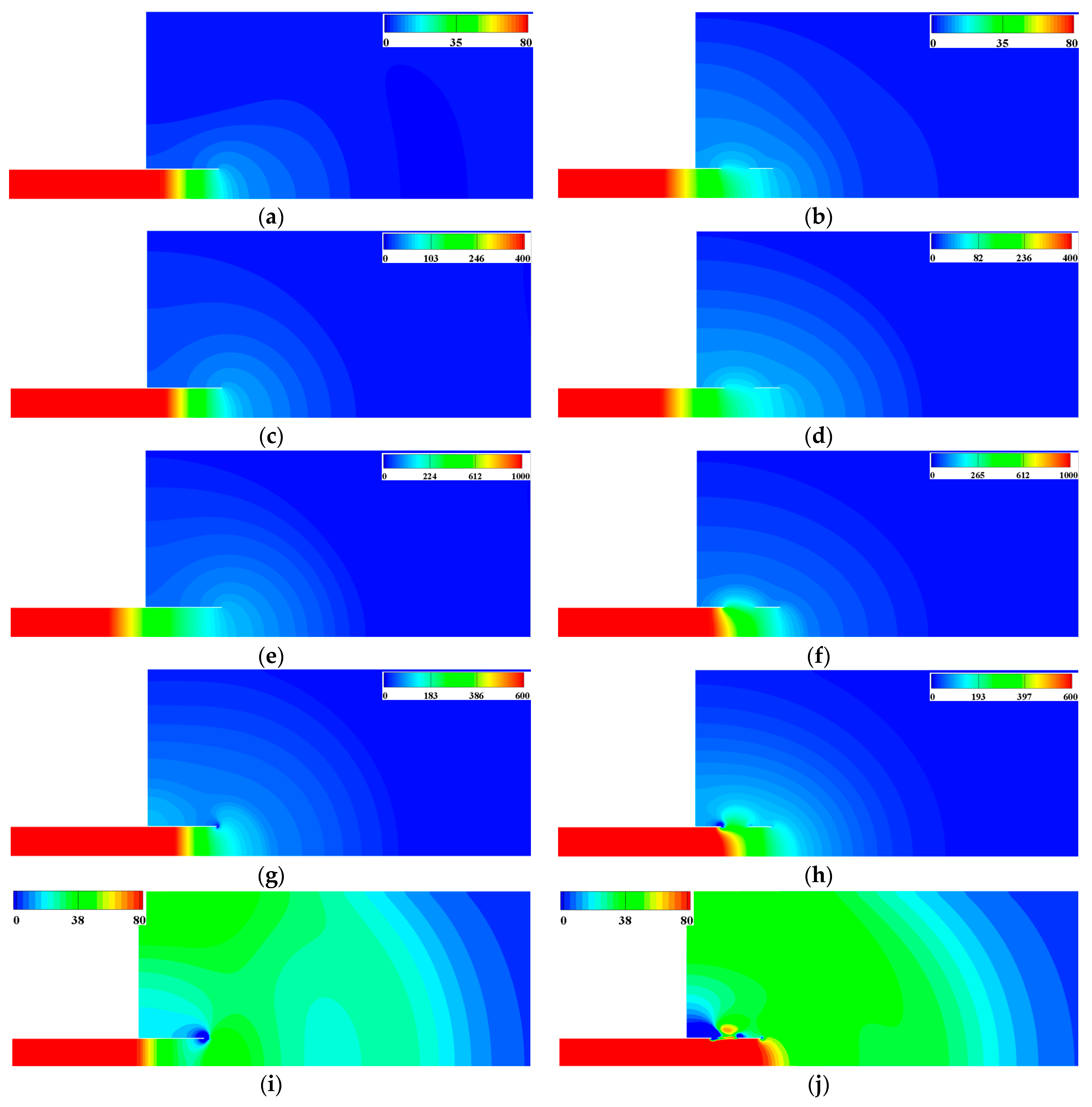
5.1. Analysis of the Impact of Exit Hood Opening Ratio
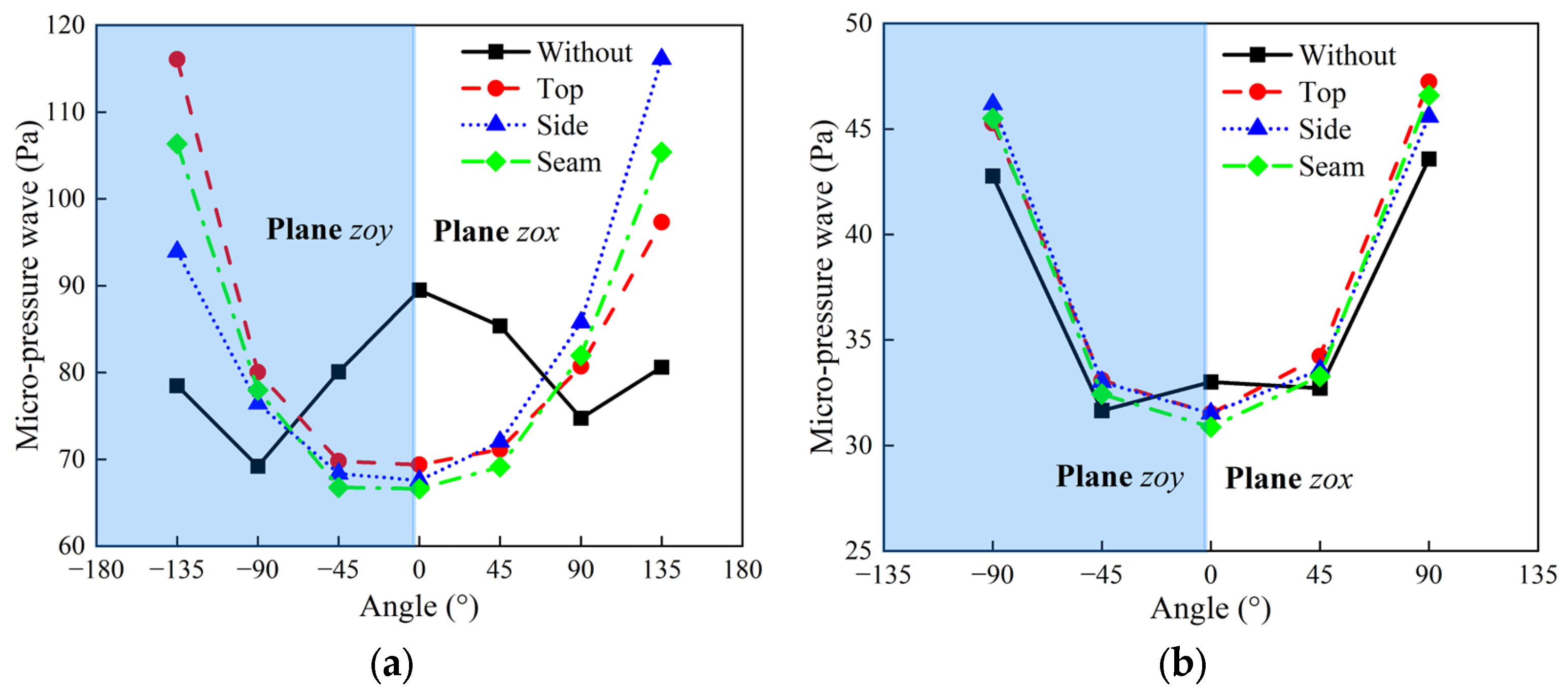
5.2. Analysis of the Effects of Different Exit Hood Opening Form
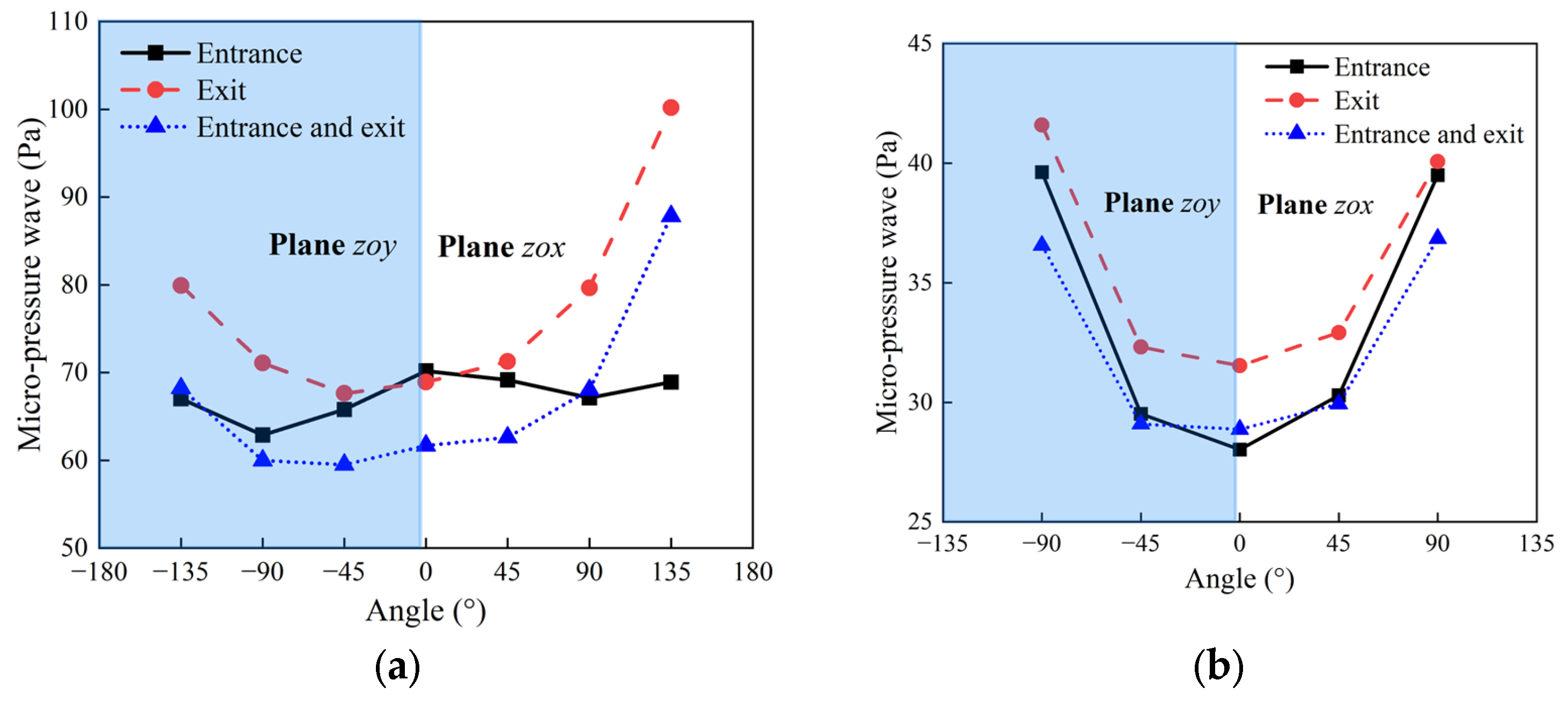
5.3. Analysis of the MPW Mitigation Effects by Entrance and Exit Hood
5.4. Design Methodology for Entrance and Exit Hood Structures
6. Conclusions
- (1)
- The influence parameters of the exit opening hood are theoretically analyzed using the control volume method, and the results are validated through three-dimensional numerical simulation. The research findings indicate that the opening ratio is a key parameter influencing the mitigation effectiveness of the exit hood on the MPWs. The amplitude of MPWs shows an inverse proportionality relationship with the opening ratio. Setting up a hood with openings at the tunnel exit can reduce the pressure amplitude at the exit of the hood, increasing the effective radiation solid angle of the MPWs and consequently enhancing the mitigation effectiveness of the exit hood on the MPWs.
- (2)
- Different opening forms have a relatively minor impact on the pressure amplitude of MPWs in front of the hood exit plane. However, they do affect the spatial distribution of MPWs and the effective solid angle in the vicinity of the openings. Hence, when determining the opening form and placement of hoods, reliance solely on past single-point evaluation methods should be avoided. It is crucial to comprehensively consider the relative significance of various positions outside the tunnel, ensuring that the design of hoods maximally mitigates the impact on residents and critical facilities.
- (3)
- The installation of hoods at the entrance and exit of a tunnel significantly influences the mitigation of MPWs, with distinct mechanisms governing the alleviation effects of entrance and exit hoods. Compared to entrance hoods, exit hoods exhibit a more significant efficiency in mitigating the amplitude of MPWs within a certain range in front of the hood exit plane. When both the tunnel entrance and exit are equipped with opening hoods, the amplitude of MPWs is minimized, resulting in the highest efficiency in mitigating MPWs.
- (4)
- When conducting hood design, it is essential to consider the impact of entrance and exit hoods on the MPWs. For single-track tunnels, opening hoods can be asymmetrically placed at the tunnel entrance and exit. The entrance hood should be designed using cases that ensure the proximity of pressure gradient peaks. For the exit hood, it is important to increase the total opening ratio to enhance its efficiency in mitigating MPWs.
- (5)
- For the design of opening hoods in double-track tunnels, a symmetrical arrangement should be adopted at both the entrance and exit while simultaneously increasing the overall opening area. Meanwhile, the hoods should adopt a design with small, numerous openings, and the positioning of these openings should be carefully planned. This strategy aims to prevent any adverse effects on the mitigation of MPWs when trains operate in both directions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gawthorpe, R.G. Aerodynamics of trains in tunnels. Railw. Eng. Int. 1978, 4, 41–47. [Google Scholar]
- Raghunathan, R.S.; Kim, H.D.; Setoguchi, T. Aerodynamics of high-speed railway train. Prog. Aerosp. Sci. 2002, 38, 469–514. [Google Scholar] [CrossRef]
- Duan, F.C.; Song, Y.; Gao, S.B.; Liu, Y.H.; Chu, W.P.; Lu, X.B.; Liu, Z.G. Study on aerodynamic instability and galloping response of rail overhead contact line based on wind tunnel tests. IEEE Trans. Veh. Technol. 2023, 72, 7211–7220. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Z.W.; Liu, Z.G.; Wang, R.C. A spatial coupling model to study dynamic performance of pantograph-catenary with vehicle-track excitation. Mech. Syst. Signal Process. 2021, 151, 107336. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.G.; Han, S.; Wang, F.; Gao, G.G. A novel arch lattice-shell of enlarged cross-section hoods for micro-pressure wave mitigation at exit of maglev tunnels. Tunn. Undergr. Space Technol. 2023, 132, 104859. [Google Scholar] [CrossRef]
- Zhang, L.; Kerstin, T.; Norbert, S.; Liu, H. Influence of the geometry of equal-transect oblique tunnel portal on compression wave and micro-pressure wave generated by high-speed trains entering tunnels. J. Wind. Eng. Ind. Aerodyn. 2018, 178, 1–17. [Google Scholar] [CrossRef]
- Howe, M.S.; Iida, M.; Fukuda, T. Influence of an unvented tunnel entrance hood on the compression wave generated by a high-speed train. J. Fluids Struct. 2003, 17, 833–853. [Google Scholar] [CrossRef]
- Howe, M.S. Design of a tunnel-entrance hood with multiple windows and variable cross-section. J. Fluids Struct. 2003, 17, 1111–1121. [Google Scholar] [CrossRef]
- Wang, Y.X.; Chang, Q.L.; Ren, W.Q.; Zhang, L.X. Seam opening tunnel large Eddy structure aerodynamic characteristics research. J. Railw. Eng. Soc. 2018, 15, 17–23. (In Chinese) [Google Scholar]
- Xiang, X.T.; Xue, L.P.; Wang, B.L.; Wang, Z. Mechanism and capability of ventilation openings for alleviating micro-pressure waves emitted from high-speed railway tunnels. Build Env. 2018, 132, 245–254. [Google Scholar] [CrossRef]
- Wang, H.L.; Alan, E.V.; Dubravka, P. Pressure radiation from a perforated duct exit region. J. Sound Vib. 2015, 351, 29–42. [Google Scholar] [CrossRef][Green Version]
- Wang, H.L.; Alan, E.V.; Dubravka, P. Perforated exit regions for the reduction of micro-pressure waves from tunnels. J. Wind. Eng. Ind. Aerodyn. 2015, 146, 139–149. [Google Scholar] [CrossRef][Green Version]
- Fukuda, T.; Saito, S.; Iida, M. Countermeasure Against the Micro-Pressure Wave by a Shelter link Neighboring Tunnel. In Proceedings of the 15th International Symposium on Aerodynamics, Ventilation and Fire in Tunnels, Barcelona, Spain, 18–20 September 2013. [Google Scholar]
- Satio, S.; Miyachi, T.; Iida, M. Countermeasure for reducing micro-pressure wave emitted from railway tunnel by installing hood at the exit of tunnel. Q. Rep. RTRI 2013, 54, 231–236. [Google Scholar] [CrossRef][Green Version]
- Miyachi, T. Acoustic model of micro-pressure wave emission from a high-speed train tunnel. J. Sound Vib. 2017, 391, 127–152. [Google Scholar] [CrossRef]
- Zhang, G.; Kim, D.H.; Kim, H.D. Numerical studies on the radiation of train-tunnel impulse waves. Tunn. Undergr. Space Technol. 2018, 80, 211–221. [Google Scholar] [CrossRef]
- Shen, W.D.; Tong, J.G. Engineering Thermodynamics, 5th ed.; Higher Education Press: Beijing, China, 2016; pp. 46–49. (In Chinese) [Google Scholar]
- Wang, H.L. Compression Wavefront Evolution During the Propagation of Compression Wave and Micro-Pressure Wave. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2016. (In Chinese). [Google Scholar]
- Li, F.L.; Lou, J.J.; Wang, L.; Wang, D.K.; Gao, L.P. Wave effects of high-speed trains passing through different tunnel lining types. J. Wind. Eng. Ind. Aerodyn. 2022, 224, 104971. [Google Scholar] [CrossRef]
- Li, W.H.; Liu, T.H.; Huo, X.S.; Chen, Z.W.; Guo, Z.J.; Li, L. Influence of the enlarged portal length on pressure waves in railway tunnels with cross-section expansion. J. Wind. Eng. Ind. Aerodyn. 2019, 190, 10–22. [Google Scholar] [CrossRef]
- Takanobu, O.; Kozo, F. Numerical investigation of three-dimensional compressible flows induced by a train moving into a tunnel. Comput. Fluids 1997, 26, 565–585. [Google Scholar] [CrossRef]
- Sahan, H.W.; Rupert, C.S.; Stuart, E.N.; John, E.C. Aeroacoustic noise prediction for wind turbines using large eddy simulation. J. Wind. Eng. Ind. Aerodyn. 2015, 145, 17–29. [Google Scholar] [CrossRef]
- Xiao, Y.G.; Qun, Y.; Sun, L.; Shi, Y. Longitudinal type-line optimization of high-speed train for low aerodynamic noise. J. Cent. South Univ. 2014, 21, 2494–2500. [Google Scholar] [CrossRef]
- Wang, Y.X.; Ren, W.Q.; Luo, Y. Analysis of Effect of Cross Adit on Train-Tunnel Aerodynamic Multiple Peak Characteristics. J. Southwest Jiaotong Univ. 2018, 53, 428–433. (In Chinese) [Google Scholar]
- Niu, J.Q.; Zhou, D.; Liang, X.F.; Liu, T.H.; Liu, S. Numerical study on the aerodynamic pressure of a metro train running between two adjacent platforms. Tunn. Undergr. Space Technol. 2017, 65, 187–199. [Google Scholar] [CrossRef]
- Li, F.L.; Luo, J.J.; Wang, L.; Guo, D.L.; Gao, L.P. Analysis of aerodynamic effects and load spectrum characteristics in high-speed railway tunnels. J. Wind. Eng. Ind. Aerodyn. 2021, 216, 104729. [Google Scholar] [CrossRef]
- Luo, J.J.; Wang, L.; Shang, S.Y.; Li, F.L.; Guo, D.L.; Gao, L.P.; Wang, D.K. Study of unsteady aerodynamic performance of a high-speed train entering a double-track tunnel under crosswind conditions. J Fluids Struct 2023, 118, 103836. [Google Scholar] [CrossRef]
- Wang, T.T.; Hu, C.; Gong, Y.F.; Yang, M.Z.; Xiong, X.H.; Zong, J.L.; Lu, Y.B. Mitigation of micro-pressure wave at 400 km/h railway tunnel exit by oblique enlarged tunnel-hood. Acta Aerodyn. 2021, 39, 151–161. (In Chinese) [Google Scholar]
- Fukuda, T.; Ozawa, S.; Iida, M.; Takasaki, T. Distortion of compression wave propagating through very long tunnel with slab tracks. JSME Int. J. 2006, 49, 1156–1164. [Google Scholar] [CrossRef]
- Miyachi, T. Theoretical model for micro-pressure wave emission considering the effect of topography around the tunnel portal. Q. Rep. RTRI 2011, 52, 117–122. [Google Scholar] [CrossRef]
- Miyachi, T.; Fukuda, T. Experimental Investigation of the effect of topography around the tunnel portal on Micro-pressure Waves. Q. Rep. RTRI 2014, 55, 235–240. [Google Scholar] [CrossRef]
- Miyachi, T.; Fukuda, T. Model experiments on area optimization of multiple openings of tunnel hoods to reduce micro-pressure waves. Tunn. Undergr. Space Technol. 2021, 115, 103996. [Google Scholar] [CrossRef]
- Yang, W.C.; Li, G.Z.; He, H.; Liu, Y.K.; Deng, E.; Luo, L.S. Optimization of ventilation window of combined buffer structure in 400 km/h high-speed railway tunnel. J. Railw. Eng. Soc. 2022. accepted (In Chinese) [Google Scholar] [CrossRef]
- Mei, Y.G.; Li, J.H.; Hu, X.; Du, J.T. Propagation characteristics of initial compression wave in cave and portal micro-pressure waves characteristics when 600 km·h−1 maglev train entering tunnels. J. Traffic Transp. Eng. 2021, 21, 150–162. (In Chinese) [Google Scholar]
- Wu, J.; Shi, X.M.; Wan, X.Y. Study on intensification and mitigation methods of micro pressure wave of double track tunnel in 300 to 350 km/h high speed railway. China Civ. Eng. J. 2017, 50, 209–214. (In Chinese) [Google Scholar]
- Zhang, Z.M.; Luca, G.D.; Archambault, B.; Chavez, J.M.; Rice, B. Traffic Dataset and Dynamic Routing Algorithm in Traffic Simulation. J. Artif. Intell. Technol. 2022, 2, 111–122. [Google Scholar] [CrossRef]
- Du, H.M.; Du, S.G.; Li, W. Probabilistic time series forecasting with deep non-linear state space models. CAAI TRIT 2023, 8, 3–13. [Google Scholar] [CrossRef]
- Chen, J.J.; Yu, S.H.; Wei, W.J.; Ma, Y. Matrix-based method for solving decision domains of neighbourhood multigranulation decision-theoretic rough sets. CAAI TRIT 2022, 7, 313–327. [Google Scholar] [CrossRef]
- Hsiao, I.H.; Chung, C.Y. AI-infused semantic model to enrich and expand programming question generation. J. Artif. Intell. Technol. 2022, 2, 47–54. [Google Scholar] [CrossRef]
- Zhao, H.M.; Ma, L.W. Several rough set models in quotient space. CAAI TRIT 2022, 7, 69–80. [Google Scholar] [CrossRef]
- Kutz, J.N. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef]
- Kjetil, O.L.; Siddhartha, M.; Deep, R. Deep learning observables in computational fluid dynamics. J. Comput. Phys. 2020, 410, 109339. [Google Scholar] [CrossRef]






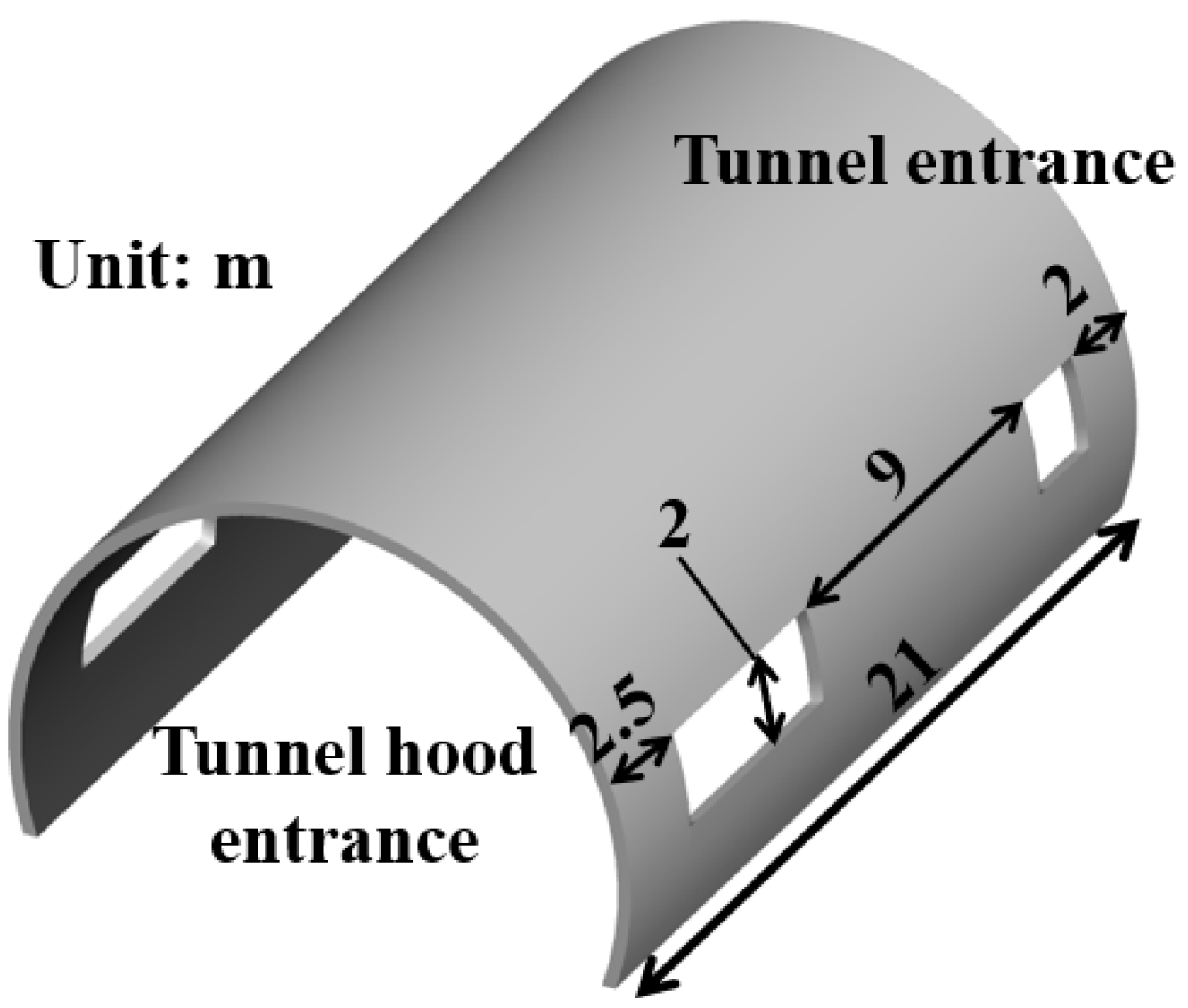
| Hood Parameters | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| X (m) | — | 7.5 | 15 | 22.5 |
| Total length of the hood (m) | 21 | 21 | 28.5 | 36 |
| Opening ratio of the hood (%) | — | 30 | 60 | 90 |
| Simulation Case | Pmpw (Pa) | Reduction Ratio (%) | ||
|---|---|---|---|---|
| r = 20 | r = 50 | r = 20 | r = 50 | |
| Case 1 | 89.5 | 33.0 | — | — |
| Case 2 | 68.9 | 31.8 | 23.0 | 3.6 |
| Case 3 | 55.6 | 28.3 | 37.8 | 14.2 |
| Case 4 | 45.9 | 24.6 | 48.7 | 25.5 |
| Azimuth Angle (°) | The Opening Ratio of Hood (%) | Observation Plane | |||
|---|---|---|---|---|---|
| 0 | 30 | 60 | 90 | ||
| 135 | 1.0 | 0.6 | 0.6 | 0.7 | Top (Plane zoy) |
| 90 | 1.3 | 1.1 | 1.3 | 1.4 | |
| 45 | 1.1 | 1.5 | 1.8 | 2.1 | |
| 0 | 1.0 | 1.6 | 2.0 | 2.5 | |
| 45 | 1.1 | 1.5 | 1.8 | 2.1 | Side (Plane zox) |
| 90 | 1.2 | 1.1 | 1.2 | 1.4 | |
| 135 | 0.9 | 0.8 | 0.8 | 0.9 | |
| Azimuth Angle (°) | The Opening Ratio of Hood (%) | Observation Plane | |||
|---|---|---|---|---|---|
| 0 | 30 | 60 | 90 | ||
| 90 | 0.8 | 0.8 | 0.8 | 0.9 | Top (Plane zoy) |
| 45 | 1.2 | 1.2 | 1.3 | 1.4 | |
| 0 | 1.2 | 1.3 | 1.4 | 1.6 | |
| 45 | 1.2 | 1.1 | 1.2 | 1.4 | Side (Plane zox) |
| 90 | 0.8 | 0.8 | 0.8 | 0.9 | |
| Azimuth Angle (°) | The Opening Form of the Tunnel Hood | Observation Plane | |||
|---|---|---|---|---|---|
| without | Top | Side | Seam | ||
| 135 | 1.0 | 0.6 | 0.8 | 0.7 | Top (Plane zoy) |
| 90 | 1.3 | 1.1 | 1.2 | 1.2 | |
| 45 | 1.1 | 1.5 | 1.6 | 1.6 | |
| 0 | 1.0 | 1.6 | 1.7 | 1.7 | |
| 45 | 1.1 | 1.5 | 1.5 | 1.5 | Side (Plane zox) |
| 90 | 1.2 | 1.1 | 1.1 | 1.1 | |
| 135 | 0.9 | 0.8 | 0.6 | 0.7 | |
| Azimuth Angle (°) | The Opening Form of the Tunnel Hood | Observation Plane | |||
|---|---|---|---|---|---|
| without | Top | Side | Seam | ||
| 90 | 0.8 | 0.8 | 0.8 | 0.8 | Top (Plane zoy) |
| 45 | 1.2 | 1.2 | 1.2 | 1.2 | |
| 0 | 1.2 | 1.3 | 1.3 | 1.3 | |
| 45 | 1.2 | 1.1 | 1.2 | 1.2 | Side (Plane zox) |
| 90 | 0.8 | 0.8 | 0.8 | 0.8 | |
| Hood Parameters | Entrance | Exit | Entrance and Exit |
|---|---|---|---|
| Opening ratio of entrance hood (%) | 30 | — | 30 |
| Opening ratio of exit hood (%) | — | 30 | 30 |
| Length of the hoods (m) | 21 | 21 | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Wang, Y.; Jin, X.; Liu, H.; Luo, Y. Aerodynamic Analysis of the Opening Hood Structures at Exits of High-Speed Railway Tunnels. Appl. Sci. 2023, 13, 11365. https://doi.org/10.3390/app132011365
Sun H, Wang Y, Jin X, Liu H, Luo Y. Aerodynamic Analysis of the Opening Hood Structures at Exits of High-Speed Railway Tunnels. Applied Sciences. 2023; 13(20):11365. https://doi.org/10.3390/app132011365
Chicago/Turabian StyleSun, Haocheng, Yingxue Wang, Xianghai Jin, Hengyuan Liu, and Yang Luo. 2023. "Aerodynamic Analysis of the Opening Hood Structures at Exits of High-Speed Railway Tunnels" Applied Sciences 13, no. 20: 11365. https://doi.org/10.3390/app132011365
APA StyleSun, H., Wang, Y., Jin, X., Liu, H., & Luo, Y. (2023). Aerodynamic Analysis of the Opening Hood Structures at Exits of High-Speed Railway Tunnels. Applied Sciences, 13(20), 11365. https://doi.org/10.3390/app132011365





