Information Gap Decision Theory-Based Stochastic Optimization for Smart Microgrids with Multiple Transformers

Featured Application

Optimal operation for renewable energy integrated smart microgrid under uncertainty.

Abstract

Multi-microgrid collaborative scheduling can promote the local consumption of renewable energy in the smart grid and reduce the operating costs of the power grid park. At the same time, the access of the distributed energy storage (ES) system provides an opportunity to further enhance the park’s peak shaving and valley filling capacity, thereby reducing costs. However, the uncertainty of photovoltaic (PV) power generation and load demand seriously affects the profit maximization of the microgrid in the park. To address this challenge, this paper proposes a stochastic optimal scheduling strategy for industrial park smart microgrids with multiple transformers based on the information gap decision theory (IGDT). We first introduce a revenue maximization model for industrial parks, incorporating a two-part tariff system and distributed ES. Subsequently, we employ an envelope constraint model to accurately represent the uncertainty associated with PV generation and load demand. By integrating these components, we establish the IGDT stochastic optimization scheduling model for industrial parks with multiple transformers. Finally, we simulate and analyze the performance of the proposed IGDT model under various cost deviation factors during typical spring and summer days. The simulation results demonstrate the effectiveness of the proposed control strategy in mitigating the impact of PV generation and load uncertainty on industrial parks. The IGDT-based scheduling approach provides an efficient solution for maximizing revenue and enhancing the operational stability of industrial park microgrids.

1. Introduction

With the proposal of global low-carbon goals and the extensive application of user-side energy storage (ES), multi-microgrid collaborative scheduling in industrial parks has developed rapidly [1]. However, the uncertainty and volatility of renewable energy and loads pose substantial challenges to the safety and stability of multi-microgrid operation in industrial parks [2,3]. ES can alleviate the impact of photovoltaic (PV) and load uncertainty on the park to a certain extent but the high cost of ES is still a limiting factor for its widespread implementation [4]. Consequently, it becomes crucial to investigate the integration of PV generation and load management within industrial park smart microgrids [5,6], especially for the optimization control of smart microgrids [7].

In fact, an industrial park comprises various types of topological structures, each equipped with a transformer for connection to the main grid [8]. To address challenges such as low renewable energy penetration and increasing peak-to-valley load differentials, an interconnected multi-microgrid approach is adopted to mitigate uncertainty and balance the peak-to-valley differentials of the net load [9]. By establishing decentralized and coordinated dispatch among the microgrids, it has been demonstrated that multi-microgrid systems can reduce the risks associated with renewable energy integration and operating costs [10]. Research on the energy management framework of multi-microgrids confirms that collaborative scheduling among these microgrids yields greater economic benefits compared to individual microgrid operations [11]. Furthermore, a hierarchical power outage scheme for multi-microgrids is proposed to enhance system resilience against disasters and improve overall system security [12]. To flexibly coordinate distributed energy resources and improve the system’s economic performance, a resource-sharing multi-microgrid model predictive control framework is proposed [13]. However, it is worth noting that the accuracy of PV and load forecasts is prone to errors which can significantly impact the collaborative dispatch of multi-microgrids [14,15].

The presence of PV and load forecast errors introduces uncertainties into the system’s operation; robust optimization and stochastic optimization are two commonly used methods to address such uncertainties [16,17]. For instance, a scenario-based approach using the Monte Carlo method is employed to generate scenarios and corresponding probabilities considering multiple uncertainties such as PV, wind turbine output, and load power. The resulting stochastic optimization model is then solved using mixed-integer linear programming techniques [18]. Another approach proposes a two-stage adaptive robust trading model for interconnecting multi-microgrids. This model minimizes the operating costs under worst-case scenarios of uncertain PV outputs [19]. However, both robust and stochastic optimizations have their limitations [20]. On the one hand, robust optimization entails considering the worst case of the system to obtain the optimality of the system whereby the uncertainty parameters always belong to the uncertainty set. Although this optimization method can ensure the robustness of the system, it loses some economy. Without considering the preferences of decision makers, in the actual operation process it will be subject to cost constraints and cannot obtain the optimal solution. On the other hand, stochastic optimization needs to know or assume the probability distribution function of uncertainty so as to establish the expected value function of the system. This not only requires a large amount of original data to fit the probability distribution function or rely on the uncertainty probability distribution but also increases the difficulty of solving according to the number of selected probabilities.

To overcome these limitations, this paper presents a stochastic optimal scheduling model for industrial parks based on the information gap decision theory (IGDT). Initially, a revenue maximization model for the industrial park is proposed considering a two-part tariff and distributed ES. Subsequently, the IGDT stochastic optimal scheduling model is developed, incorporating an envelope constraint model to effectively handle uncertainty. Finally, simulations and analyses are conducted under various cost deviation factors to evaluate the performance of the proposed model. The main work and innovations of this paper are as follows:

(1)

A stochastic optimization framework based on IGDT is proposed to study the optimal scheduling of smart grid industrial parks considering transformer loss, two-part tariff, distributed ES, and other factors;

(2)

It is proposed to use IGDT to deal with the uncertainty of net load. Compared with traditional robust optimization, the IGDT optimization model proposed in this paper has both economy and robustness;

(3)

Starting from the practical application, considering the transformer loss and multi-microgrid collaborative scheduling in the smart grid industrial park it is verified that distributed ES and multi-microgrid interconnection have great advantages in reducing the cost of the park.

By utilizing the IGDT-based approach, this research aims to address the aforementioned challenges and provide a more robust and efficient solution for the scheduling of industrial park microgrids. The simulation results and analysis will shed light on the effectiveness of the proposed model and its capability to handle uncertainties, contributing to the advancement of optimal scheduling strategies for industrial parks. In the following sections of this paper, we present the methodology, models, and simulation results followed by a discussion of the findings and their implications for industrial park planning and operation.

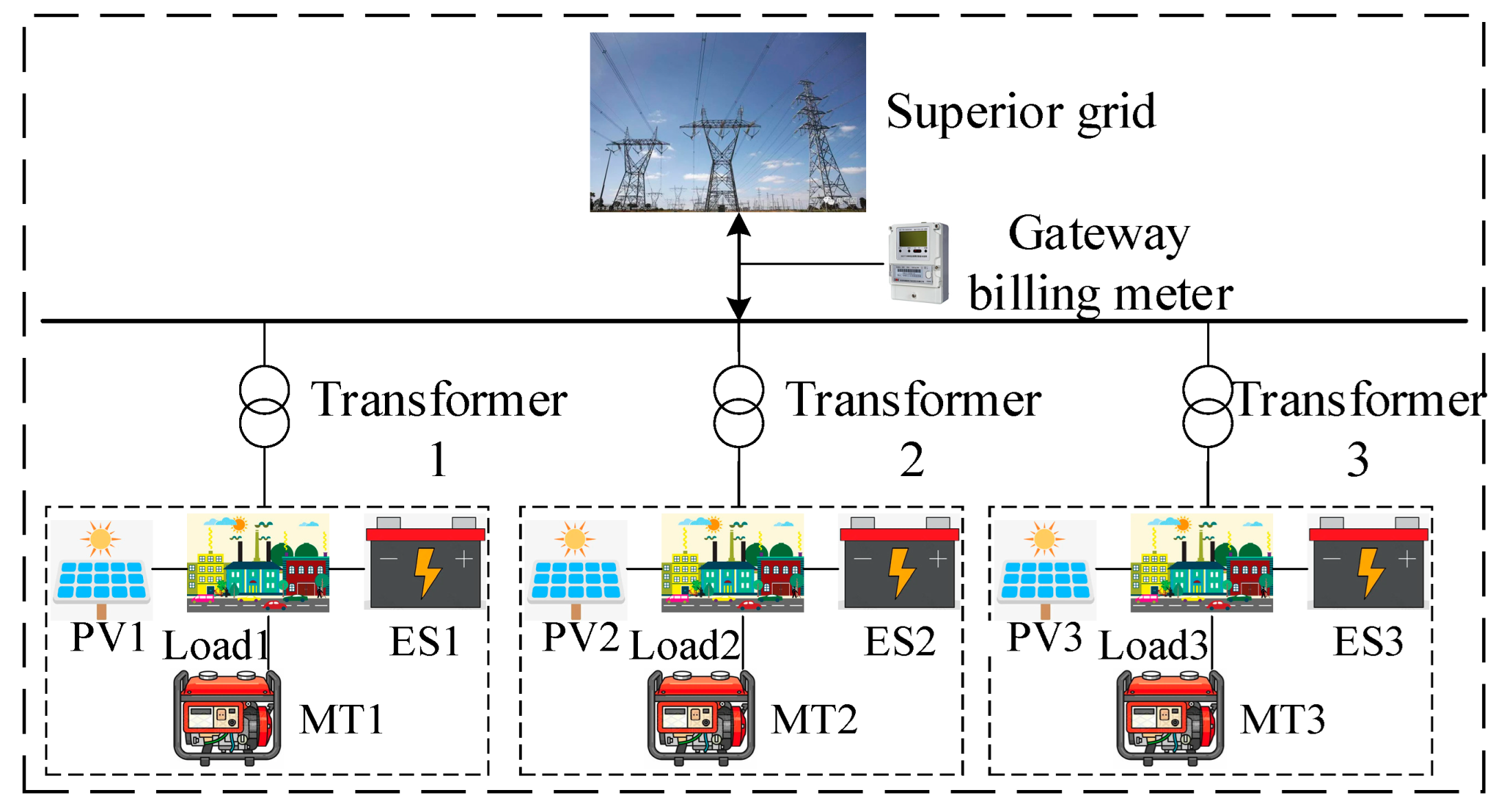
2. IGDT-Based Optimization Model for Industrial Parks

2.1. Economic Model of Industrial Parks

An industrial park comprises multiple interconnected microgrids under a multi-transformer topological structure which facilitates the efficient consumption of renewable energy and enhances the overall stability and security of the system. Moreover, the integration of distributed ES systems offers additional benefits by increasing the penetration of renewable energy and reducing transformer losses.

In line with real-world operational scenarios, this paper establishes an economic optimization model for the industrial park. The model incorporates various components, including a two-part tariff structure [21] consisting of a time-of-use tariff, on-grid tariff, and demand tariff. Additionally, it considers the operational and maintenance costs associated with the ES and micro-turbine (MT). The economic optimization model for the industrial park is formulated as follows:

$$\min f=f_1+f_2+f_3$$

(1)

where $f$ is the cost of microgrids. $f_1$, $f_2$, and $f_3$ are the cost of MT, the cost of electricity consumption, and the cost of using ES, respectively.

For users, MT can help cope with emergencies and alleviate the peak of ES or power grid. Moreover, the high efficiency and reliability of the MT are suitable for application to the smart grid with multiple transformers. Therefore, this paper considers the use of the square equation to describe the cost of MT [22]:

$$f_1={\displaystyle \sum _{t=1}^T\left\{{\displaystyle \sum _{i=1}^N{\alpha }_i{\left(P_{i,\mathrm{g}}\left(t\right)\Delta t\right)}^2+{\beta }_i{P}_{i,\mathrm{g}}\left(t\right)\Delta t+c_i}\right\}}$$

(2)

where ${\alpha }_i$, ${\beta }_i$, and $c_i$ are cost coefficients of MT and $P_{i,\mathrm{g}}\left(t\right)$ is the MT power. $T$, $N$, and $\Delta t$ are the optimization time, the number of microgrids, and time interval, respectively.

For users, they need to pay electricity according to the maximum monthly demand and actual electricity consumption. Therefore, this paper uses a two-part tariff to charge users.

$$f_2={\displaystyle \sum _{t=1}^T\left\{c_{\mathrm{b}}\left(t\right)P_{\mathrm{b}}\left(t\right)\Delta t+c_{\mathrm{dec}}{P}_{\mathrm{dec}}\left(t\right)-c_{\mathrm{s}}\left(t\right)P_{\mathrm{s}}\left(t\right)\Delta t\right\}}$$

(3)

where $c_{\mathrm{b}}\left(t\right)$, $c_{\mathrm{dec}}$, and $c_{\mathrm{s}}$ are the time-of-use tariff, demand tariff, and on-grid tariff, respectively. $P_{\mathrm{b}}\left(t\right)$, $P_{\mathrm{dec}}(t)$, and $P_{\mathrm{s}}\left(t\right)$ are the buying power, demand power, and on-grid power, respectively.

ES can transfer the user demand in time and space, charging in the flat and valley period of time-of-use tariff, and discharging in the peak period, thus reducing user costs. Therefore, the operation and maintenance cost of ES needs to be considered.

$$f_3={\displaystyle \sum _{t=1}^T\left\{c_{\mathrm{v}}\left(P_{i,\mathrm{c}}\left(t\right)+P_{i,\mathrm{d}}\left(t\right)\right)\Delta t\right\}}$$

(4)

where $c_{\mathrm{v}}$ denotes operation and maintenance cost of ES and $P_{i,\mathrm{c}}\left(t\right)$ and $P_{i,\mathrm{d}}\left(t\right)$ are, respectively, the charging and discharging power of ES.

To enhance the solution efficiency and effectiveness of the proposed economic optimization model for the industrial park, this paper introduces two categories of constraints: distributed generator constraints and power balance constraints.

(1)

Operation constraints of distributed generators [6,23]

$$\left\{\begin{array}{ll}{P}_{i,\mathrm{g}}^{\min }\le P_{i,\mathrm{g}}\left(t\right)\le P_{i,\mathrm{g}}^{\max }\hfill & \hfill \\ {\mu }_1{P}_{i,\mathrm{c}}^{\min }\le P_{i,\mathrm{c}}\left(t\right)\le {\mu }_1{P}_{i,\mathrm{c}}^{\max }\left(t\right)\hfill & \hfill \\ \left(1-{\mu }_1\right)P_{i,\mathrm{d}}^{\min }\left(t\right)\le P_{i,\mathrm{d}}\left(t\right)\le \left(1-{\mu }_1\right)P_{i,\mathrm{d}}^{\max }\left(t\right)\hfill & \hfill \\ SOC\left(t\right)=SOC\left(t-\Delta t\right)+({\eta }_{\mathrm{c}}\Delta t{P}_{i,\mathrm{c}}\left(t\right)-P_{i,\mathrm{d}}\left(t\right)\Delta t/{\eta }_{\mathrm{d}})/E\hfill & \hfill \\ SOC\left(0\right)=SOC\left(T\right)\hfill & \hfill \\ 0.2\le SOC\left(t\right)\le 1\hfill & \hfill \end{array}\right.$$

(5)

where $P_{i,\mathrm{g}}^{\max }$ and $P_{i,\mathrm{g}}^{\min }$ are the upper and lower generation limits of MT, respectively. $P_{i,\mathrm{c}}^{\max }$ and $P_{i,\mathrm{c}}^{\min }$ are the upper and lower limits of the charging power, respectively. $P_{i,\mathrm{d}}^{\max }$ and $P_{i,\mathrm{d}}^{\min }$ are the lower and upper limits of the discharging power, respectively. $\mathrm{E}$ and $SOC$ represent the ES capacity and state of capacity, respectively. ${\mu }_1$ represents the 0–1 variable, indicating that ES cannot charge and discharge at the same time. The fifth formula of Equation (5) indicates that the first and last states of ES are equal. The last formula of Equation (5) indicates that that the ES capacity state cannot be less than 0.2 and greater than 1.

(2)

Power balance constraints

$$\left\{\begin{array}{ll}{P}_{\mathrm{b}}\left(t\right)+{\displaystyle \sum _{i=1}^N{P}_{i,\mathrm{ex}}\left(t\right)}=P_{\mathrm{s}}\left(t\right)\hfill & \hfill \\ P_{i,\mathrm{out}}\left(t\right)+P_{i,\mathrm{ex}}\left(t\right)+P_{i,\mathrm{c}}\left(t\right)+P_{i,\mathrm{load}}\left(t\right)=P_{i,\mathrm{g}}\left(t\right)+P_{i,\mathrm{pv}}\left(t\right)+P_{i,\mathrm{d}}\left(t\right)+P_{i,\mathrm{in}}\left(t\right)\hfill & \hfill \\ P_{i,\mathrm{ex}}\left(t\right)={\eta }_{\mathrm{tr}}{P}_{i,\mathrm{out}}\left(t\right)-P_{i,\mathrm{in}}\left(t\right)/{\eta }_{\mathrm{tr}}\hfill & \hfill \end{array}\right.$$

(6)

where the first two formulas of (6) denote the power balance of the industrial park and microgrid, respectively. $P_{i,\mathrm{ex}}\left(t\right)$ denotes the exchange power of the microgrid. $P_{i,\mathrm{in}}\left(t\right)$ and $P_{i,\mathrm{out}}\left(t\right)$ are the input and output power of the microgrid, respectively. ${\eta }_{\mathrm{tr}}$ is the transformer loss factor. $P_{i,\mathrm{load}}\left(t\right)$ and $P_{i,\mathrm{pv}}\left(t\right)$ are the load demand and PV output, respectively.

The economic optimization model proposed for the industrial park focuses solely on the economic aspects without considering the uncertainties associated with PV generation and load demand. This oversight can compromise the security and reliability of the industrial park’s operation. Hence, it is crucial to develop a method that effectively addresses PV and load uncertainties while ensuring the economic efficiency and robustness of the optimization model. In order to address this challenge, this paper emphasizes the integration of a method that accounts for PV and load uncertainties within the industrial park optimization model. By incorporating uncertainty handling techniques, the model aims to strike a balance between economic considerations and the robustness of the operation.

In the subsequent sections of this paper, the specific methodology to handle PV and load uncertainties, based on IGDT, will be presented. The proposed stochastic optimal scheduling model, which integrates IGDT and envelope constraint modeling, will be simulated and analyzed under various scenarios. The findings of the simulation analysis will demonstrate the effectiveness of the proposed method in coping with PV and load uncertainties within the industrial park setting.

2.2. IGDT Stochastic Scheduling for Industrial Parks with Multiple Transformers

When addressing uncertainty in the industrial park optimization model, two common approaches are robust optimization and stochastic optimization. However, robust optimization tends to be overly conservative in handling uncertain variables, while stochastic optimization requires a significant number of samples for effective optimization. In contrast, IGDT offers a more favorable solution by imposing less information requirements on uncertain variables and not relying heavily on their probability distribution [24]. In view of the above discussions, this paper adopts IGDT as the chosen method to handle the uncertainties associated with PV and load. IGDT provides a robust and practical framework for dealing with uncertainty in the optimization model, allowing for more reliable and efficient decision making in the industrial park setting.

The general optimization problem can be described as:

$$\begin{array}{c}\min F(x,l)\\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{l}{H}_i(x,l)\le 0,i\in {\mathsf{\rho }}_{\mathrm{ineq}}\\ G_j(x,l)=0,j\in {\mathsf{\rho }}_{\mathrm{eq}}\end{array}\right.\end{array}$$

(7)

where $F$ is the objective function. $x$ and $l$ are the decision variable and uncertainty variable, respectively. $H_i(x,l)$ and $G_j(x,l)$ are the inequality constraints and equality constraints, respectively. ${\mathsf{\rho }}_{\mathrm{ineq}}$ and ${\mathsf{\rho }}_{\mathrm{eq}}$ are the sets of inequality constraints and equality constraints, respectively.

Based on the risk aversion strategy, a general IGDT robust optimization model can be constructed as follows [25]:

$$\begin{array}{c}\max \phi \\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{l}\max F(x,l)\le F_{\mathrm{c}}\\ F_{\mathrm{c}}=(1+\beta )F_0\\ H(x,l)\le 0\\ G(x,l)=0\\ U(\phi ,\tilde{x})\end{array}\right.\end{array}$$

(8)

where $\phi$ is the uncertainty. $F_0$ is the optimal solution in the deterministic environment. $\beta$ is the cost deviation factor for the IGDT model. $U(\phi ,\tilde{x})$ is the fluctuation range of uncertain variables.

Equation (8) shows that the IGDT robust optimization model solves for the maximum value of the uncertainty in the upper layer and the maximum value of the objective function in the lower layer.

Nevertheless, as the number of uncertain variables increases, the IGDT model transitions from a single-objective problem to a multi-objective problem, significantly intensifying the complexity of solving the model. To address this challenge, this paper employs the concept of net load shown by Equation (9) to describe the uncertainty within the optimization model, thereby reducing the complexity of the problem. Net load, in this context, refers to the difference between the forecasted load and the forecasted PV generation. By utilizing the net load, the uncertainty associated with PV and load can be effectively characterized within the optimization model. This simplification facilitates the resolution of the model and enables more efficient decision making in real-world scenarios.

$$\Delta P_{i,\mathrm{L}}=P_{i,\mathrm{load}}-P_{i,\mathrm{pv}}$$

(9)

To provide a more accurate representation of the uncertainty variables, this paper employs the envelope model as a means to describe the variability and uncertainty associated with these variables [26]. The envelope model is chosen due to its effectiveness in capturing the range of potential values for uncertain variables. It provides a concise and flexible representation allowing for a comprehensive analysis of the uncertainty within the optimization model. The specific form of the envelope model adopted in this paper is as follows:

$$U\left(a_i,\Delta {\tilde{P}}_{i,\mathrm{L}}\right)=\left\{a_i:\left|\frac{\Delta P_{i,\mathrm{L}}-\Delta {\tilde{P}}_{i,\mathrm{L}}}{\Delta {\tilde{P}}_{i,\mathrm{L}}}\right|\le a_i\right\}$$

(10)

where $\Delta {\tilde{P}}_{i,\mathrm{L}}$ is the predicted value of net load and $a_i$ is the radius of uncertainty.

The proposed IGDT stochastic optimization model for industrial parks, based on the industrial park economic model and the envelope constraint model, can be expressed as follows:

$$\begin{array}{l}\max \left[a_1,a_2,\dots ,a_i\right]\hfill \\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{l}\max C\le \left(1+\beta \right)C_0\hfill \\ \Delta P_{i,\mathrm{L}}\in U\left(a_i,\Delta {\tilde{P}}_{i,\mathrm{L}}\right)\hfill \\ \mathrm{s}.\mathrm{t}.\left(1\right)\sim \left(3\right)\hfill \end{array}\right.\hfill \end{array}$$

(11)

where $C_0$ and $C$ are the costs of the industrial park in deterministic and uncertain environments, respectively.

The IGDT stochastic optimization model of industrial parks is a bi-level optimization model which is difficult to solve directly. Therefore, this paper uses the idea of robust optimization to transform $\max \left[a_1,a_2,\dots ,a_i\right]$ into $\max \min \left[a_1,a_2,\dots ,a_i\right]$.

In addition, when the fluctuation of net load reaches the maximum fluctuation, it can be written as Equation (12). The second formula of Equation (6) can be written as Equation (13).

$$\mathsf{\Delta }{P}_{i,\mathrm{L}}=(1+a_i)\mathsf{\Delta }{\tilde{P}}_{i,\mathrm{L}}$$

(12)

$$P_{i,\mathrm{out}}(t)+P_{i,\mathrm{ex}}(t)+P_{i,\mathrm{c}}(t)+(1+a_i)\mathsf{\Delta }{\tilde{P}}_{i,\mathrm{L}}=P_{i,\mathrm{g}}(t)+P_{i,\mathrm{d}}(t)+P_{i,\mathrm{in}}$$

(13)

At this time, the cost of the proposed IGDT model is the highest. The $\max C\le \left(1+\beta \right)C_0$ of the lower model can be written as:

$$C\le \left(1+\beta \right)C_0$$

(14)

The development of such a method is of the utmost importance to address the practical challenges associated with PV and load uncertainties. By incorporating it into the industrial park optimization model, the proposed approach seeks to provide a comprehensive solution that encompasses both economic efficiency and operational robustness.

In summary, the IGDT stochastic optimization model of industrial parks can be expressed as:

$$\begin{array}{l}\max \min \left[a_1,a_2,\dots ,a_i\right]\hfill \\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{l}C\le \left(1+\beta \right)C_0\hfill \\ \Delta P_{i,\mathrm{L}}=\left(1+a_i\right)\Delta {\tilde{P}}_{i,\mathrm{L}}\hfill \\ \mathrm{s}.\mathrm{t}.\left(1\right)\sim \left(3\right)\hfill \end{array}\right.\hfill \end{array}$$

(15)

We calculate $\max \min \left[a_1,a_2,\dots ,a_i\right]$ according to the enumeration method mentioned in [27]. The enumeration method is essentially based on a property [28]: if D is a closed convex set and F is a convex function, if F has a maximum value on D then the maximum value will be obtained at a certain pole of D.

By formulating this economic optimization model, the paper aims to provide a comprehensive framework that maximizes the economic benefits of the industrial park while considering various tariff structures, operational costs, and renewable energy integration. The optimization model serves as a valuable tool for decision makers in the industrial park to make informed choices regarding tariff selection, ES utilization, and MT operation, thus contributing to the sustainable and cost-effective operation of the industrial park.

In summary, the flow of IGDT-based stochastic optimization for smart microgrids with multiple transformers in this paper is shown in Figure 1.

When we solve the MILP problem according to Figure 1, we divide the problem into a deterministic environment and an uncertain environment. Firstly, we solve the model in a deterministic environment and obtain the cost in a deterministic environment. Then, the cost in the deterministic environment is brought into the IGDT model to solve the IGDT stochastic optimization model.

3. Case Study

In order to verify the effectiveness and reliability of the proposed method, an industrial park composed of three transformers is selected as the case study, as depicted in Figure 2. The loss of each transformer is set to 0.02. The industrial park consists of three microgrids with transformers. Each micro-grid includes an MT, an ES, a PV power generation device, and a load. The selected cases are general which can not only avoid the contingency of the results of a single system but also verify the advantages between inter-connected microgrids. At the same time, the uncertainty planning method selected in this paper requires multiple systems to verify the effectiveness of the proposed method. The equipment parameters within the industrial park are presented in

Table 1. Industrial park parameters.

Microgrid	MT Rated Power (kW)	ES Rated Power (kW)	ES Rated Capacity (kWh)
1	800	350	800
2	800	450	1000
3	850	500	1200

and the PV and load profiles for typical days are illustrated in Figure 3 [29]. As the industrial park is located in the same area and shares common environmental conditions, the PV outputs of the internal microgrids are identical. According to the time-of-use electricity price description of China’s Jiangsu Province, the electricity price varies based on different time intervals: from 0:00 to 8:00, the price is 0.37 CNY/kW; from 8:00 to 12:00 and 17:00 to 21:00, the price is 1.3612 CNY/kW; and from 12:00 to 17:00 and 21:00 to 24:00, the price is 0.82 CNY/kW. The time interval considered for analysis is 15 min.

3.1. Analysis of the Cost Deviation Factor Results

In order to investigate the influence of deviation factors on the optimization cost and uncertainty, the economy, robustness, and generality of the system studied in this paper are considered. For a typical spring day, different $\beta$($\beta$ = 0.01, 0.02, 0.03, 0.04, 0.05) values were used for simulation analysis. From the results presented in

Table 2. Simulation results of different deviation factors of a typical spring day.

$\mathit{\beta }$		0.01	0.02	0.03	0.04	0.05
Cost(CNY)	MT	12,797.6756	12,926.5608	13,075.4533	13,200.2291	13,071.3108
	ES	1480.3489	1480.3492	1480.3495	14,918.847	1462.4225
	Grid	24,842.6745	25,101.1227	25,339.5636	25,590.5863	26,136.3004
	Total	39,120.6990	39,508.0327	39,895.3664	40,282.7001	40,670.0337
$a$		0.00884	0.01729	0.02487	0.03272	0.04283

, it can be observed that as $\beta$ increases both the optimization cost and the uncertainty radius also increase. This can be attributed to the more pessimistic approach taken by decision makers towards the uncertainty associated with PV and load. As $\beta$ increases, the economic performance gradually decreases while the conservatism and the ability to manage risks increase. And in the range of maximum uncertainty radius, the planning cost is not greater than $\left(1+\beta \right)C_0$. The development trend is consistent with the image change trend which proves the effectiveness of the IGDT robust model.

In order to verify the universality of the model proposed in this paper, this paper chooses to simulate the influence of deviation factors on the cost and uncertainty on a typical summer day. The simulation results are shown in

Table 3. Simulation results of different deviation factors of a typical summer day.

$\mathit{\beta }$		0.01	0.02	0.03	0.04	0.05
Cost(CNY)	MT	13,172.5418	13,253.6666	13,122.6272	13,297.1882	13,436.1970
	ES	1171.7510	1185.7495	1188.6066	1184.6710	1194.382
	Grid	41,518.1605	41,976.2072	42,657.4839	43,039.9528	43,444.3274
	Total	55,862.4533	56,415.6233	56,968.7177	57,521.8120	58,074.9064
$a$		0.00560	0.01516	0.02455	0.03323	0.04244

. As shown in Table 3, as with a typical spring day, costs and uncertainty increase with the increase in the bias factor. Furthermore, the validity and versatility of the model in this paper are verified.

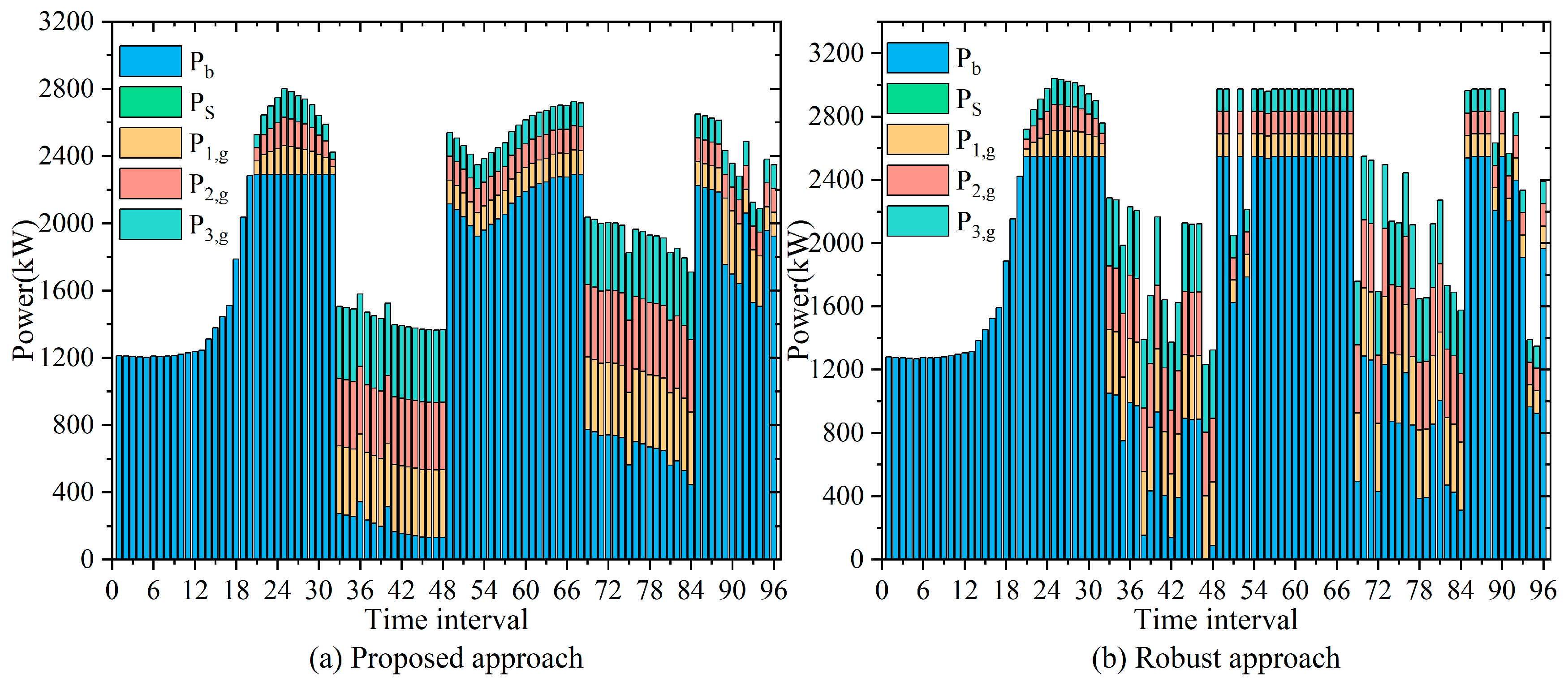
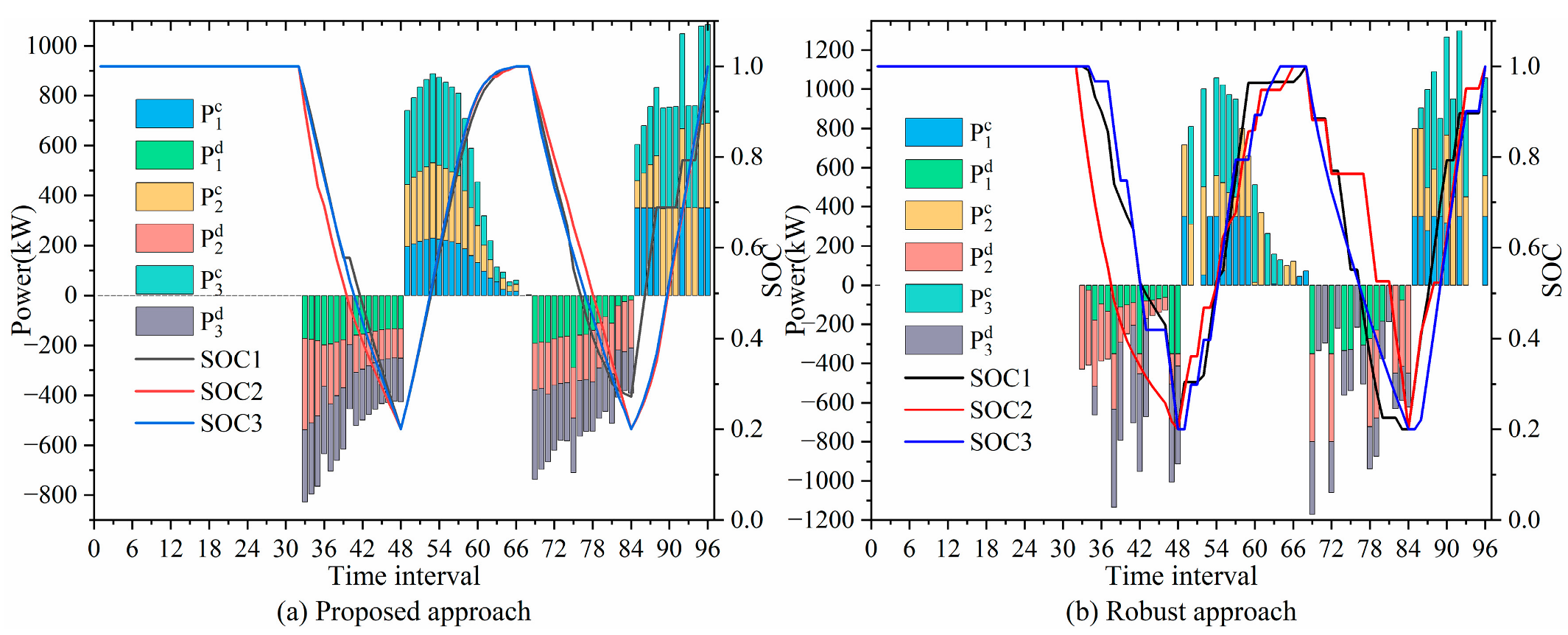
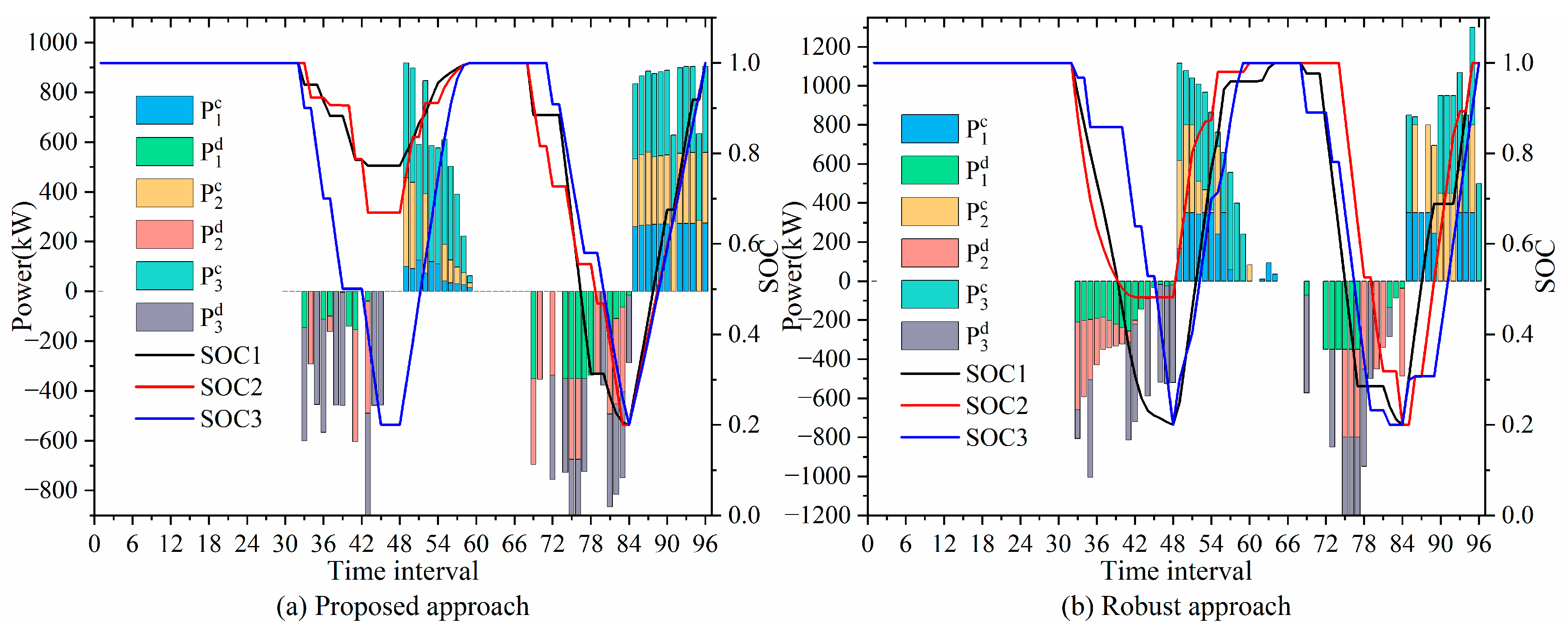
3.2. Optimization Results of Distributed ES

Distributed ES plays a crucial role in promoting the local consumption of renewable energy, smoothing load peaks and filling valleys, and enhancing system stability. However, ES is divided into centralized ES and distributed ES, each with its own advantages. In order to verify the superiority of distributed ES in improving the economy, a comparison of system costs is conducted for a typical spring day under different deviation factors, as presented in

Table 4. Different types of ES simulation on a typical spring day (CNY).

$\mathit{\beta }$	0.01	0.02	0.03	0.04	0.05
Distributed ES	39,120.6995	39,508.0332	39,895.3668	40,282.7005	40,670.0341
Centralized ES	39,519.2745	39,910.5545	40,301.8344	40,693.1144	41,084.3943

.

The results shown in Table 4 demonstrate that, for varying deviation factors, the cost of utilizing distributed ES in the industrial park is lower compared to using centralized ES. This cost advantage can be attributed to the ability of distributed ES to reduce transformer losses, thereby resulting in an overall cost reduction. Furthermore, as the deviation factor increases, the cost difference between distributed ES and centralized ES becomes more pronounced. Additionally, the centralized ES solution experiences higher transformer losses as the deviation factor increases.

In order to further reflect the superiority of distributed ES, this paper chooses to compare the cost of centralized ES and distributed ES on typical days in summer. The simulation results are shown in

Table 5. Different types of ES simulation on a typical summer day (CNY).

$\mathit{\beta }$	0.01	0.02	0.03	0.04	0.05
Distributed ES	55,862.4533	56,415.6233	56,968.7177	57,521.8120	58,074.9064
Centralized ES	56,247.3610	56,803.1515	57,361.1702	57,918.0747	58,474.9794

. As shown in Table 5, the cost of distributed ES under five deviation factors is lower than that of centralized ES. This is because the distributed ES does not need to go through the loss of the transformer which is more conducive to the application of the microgrid.

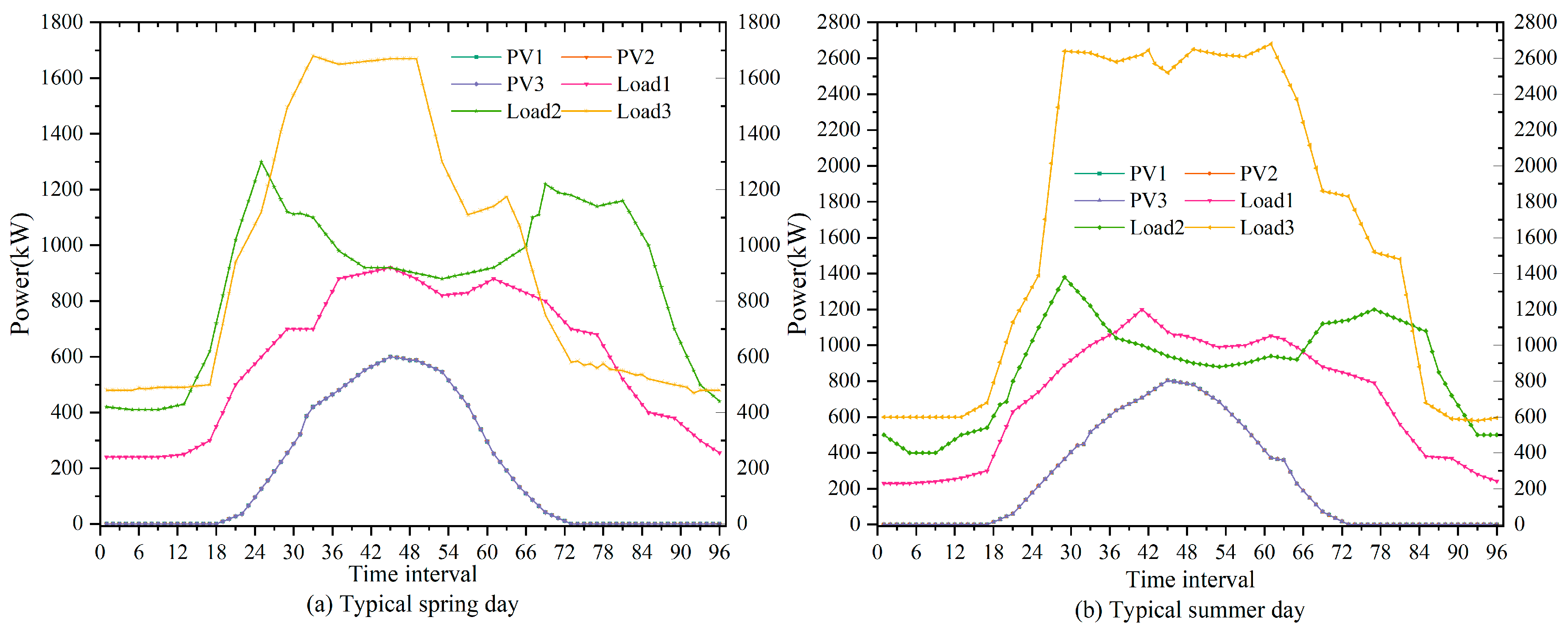
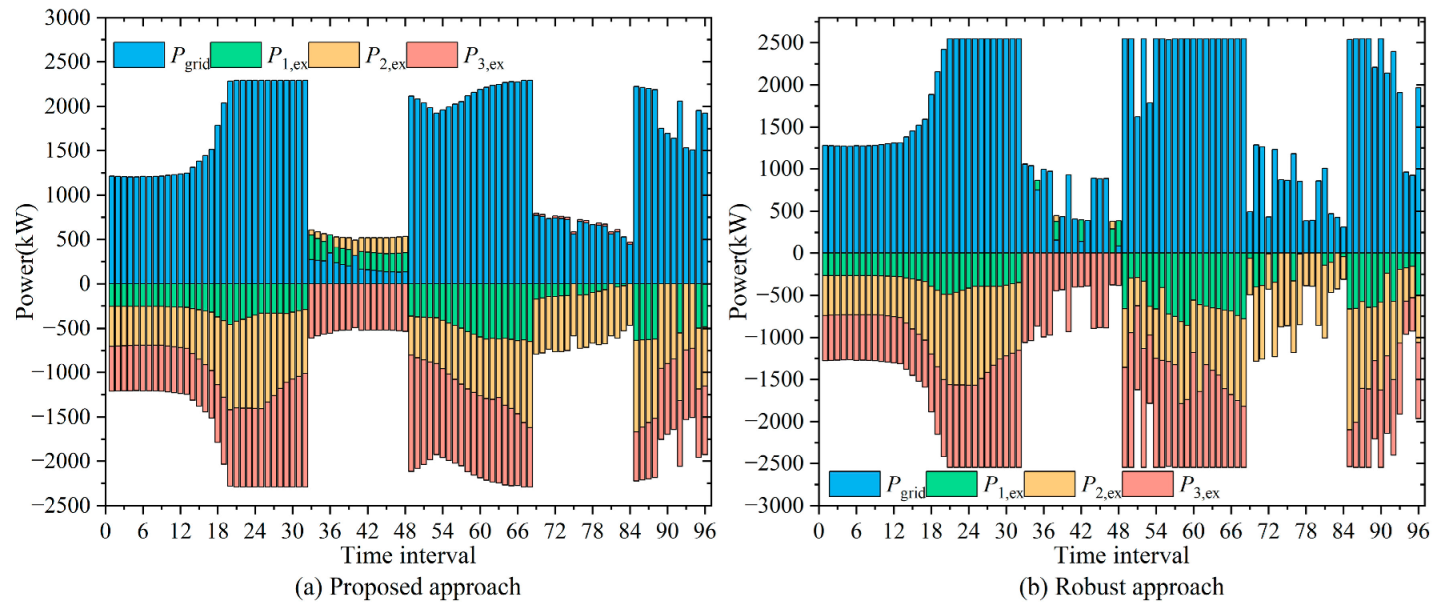
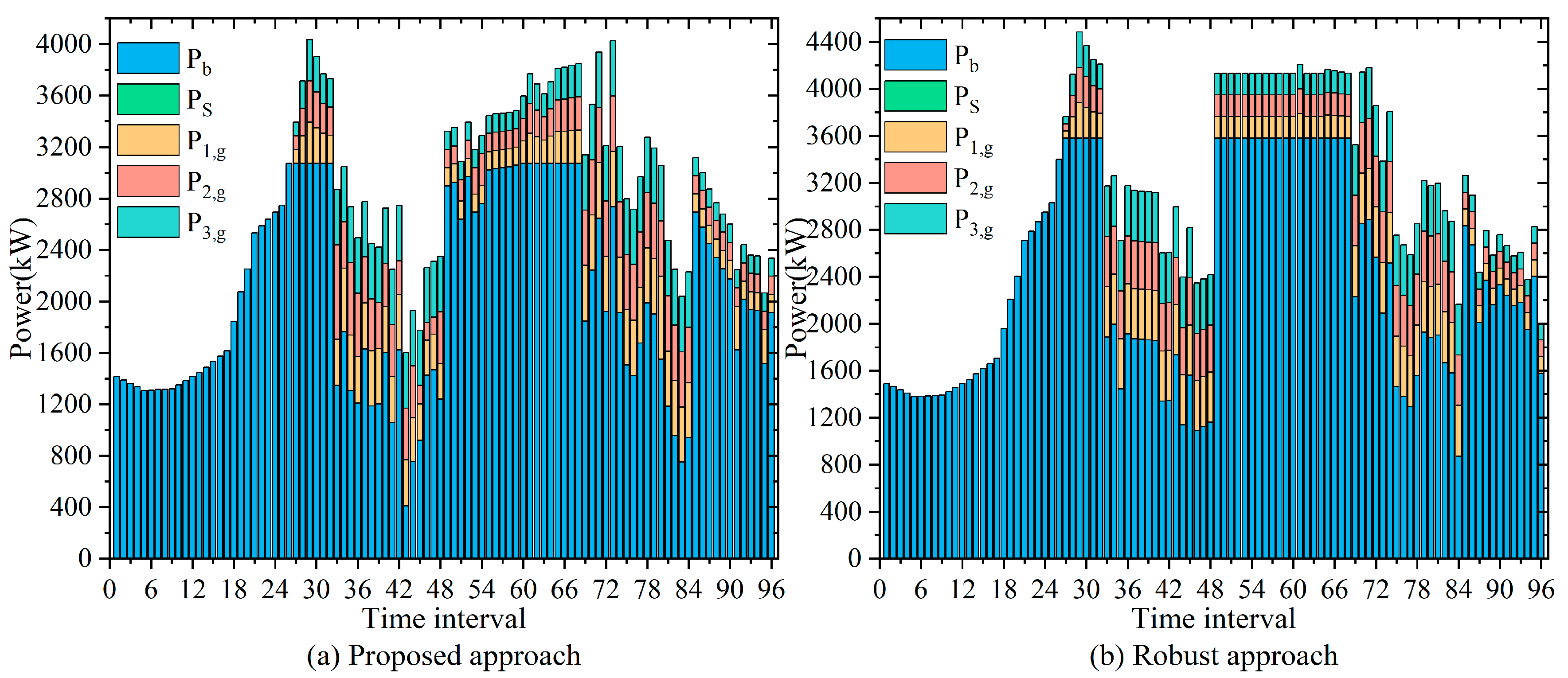
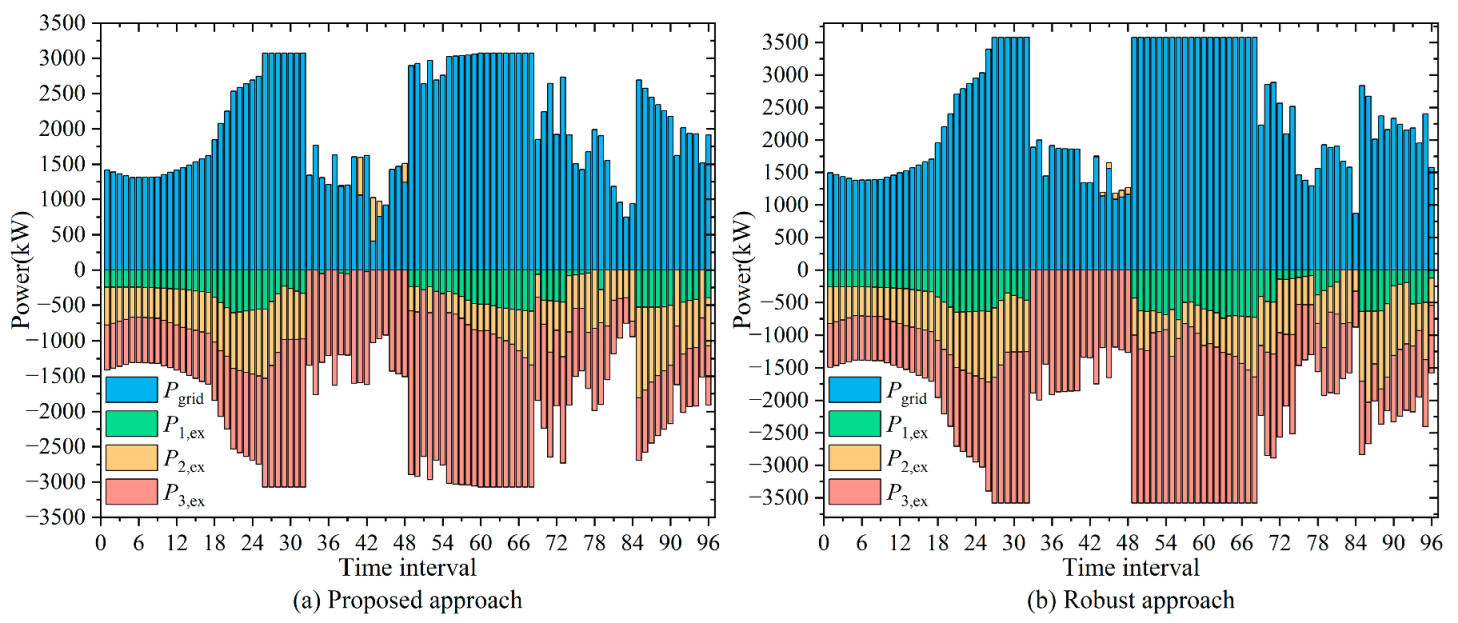
3.3. Optimization Results of a Typical Spring Day

To validate the effectiveness of the proposed control strategy, a simulation analysis is conducted with a deviation factor of $\beta =0.05$. Furthermore, a traditional robust optimization method is selected for comparison with the approach proposed in this paper and the simulation results are presented in Figure 4, Figure 5 and Figure 6.

Based on the observations from Figure 4 and Figure 5, it is evident that during the initial 33 time intervals the industrial park primarily relies on purchasing electricity from the upper grid to meet its power deficit. This is because the time-of-use tariff during this period corresponds to the valley tariff, which is significantly lower than the costs associated with ES and MT operation. As the time-of-use tariff transitions to the peak tariff, the power deficit of the industrial park is primarily met through the utilization of ES and MT, resulting in a sharp drop in the state of charge (SOC) of the ES. During the flat time-of-use tariff period, the industrial park utilizes purchased electricity to charge the ES, enabling peak tariff reductions and cost reductions for the park.

Comparing the optimization results of Figure 5a,b, it can be observed that the output of the unit utilizing the robust method is higher than that of the proposed approach but it is less economically efficient.

From Figure 6, it can be concluded that in addition to purchasing electricity from the upper grid to meet their own power shortage, the three microgrids will also exchange power, thereby reducing operating costs. The power shortage of the third microgrid is large. When the time-of-use tariff is the peak-time tariff, the power shortage is shared by the grid and the other two interconnected microgrids which reflects the complementary characteristics of the interconnected microgrid energy.

In summary, the method proposed in this paper demonstrates both economic and robust characteristics. The optimized ES operation strategy exhibits a smoother performance and better adaptability to the operational control of the industrial park. These findings validate the effectiveness of the proposed control strategy in achieving economic and reliable operation of the industrial park.

3.4. Optimization Results of a Typical Summer Day

The optimization results for a typical summer day are depicted in Figure 7, Figure 8 and Figure 9. By considering the optimization outcomes from both the typical spring day and typical summer day, it can be inferred that the proposed model is not limited by seasonality and maintains both economic efficiency and robustness throughout different seasons.

From Figure 7 and Figure 8, it can be seen that on a typical summer day both the approach proposed in this paper and the robust optimization are to purchase electricity from the power grid during the valley and flat periods for its power shortage and ES charging. The electricity purchased by robust optimization is significantly higher than that of the approach in this paper and the economy is reduced. From Figure 8, it can be seen that during the peak period the ES will be discharged for the use of the microgrid which is in line with the change rule of the time-of-use tariff. ES will transfer electricity in time and space, thereby reducing operating costs. It can be seen from Figure 9 that, consistent with a typical day in spring, the interconnected microgrid can exchange power and reduce costs which proves the superiority of the system proposed in this paper.

The combined analysis of the spring and summer simulations demonstrates that the proposed model can effectively address the uncertainty of PV and load, ensuring the economic optimization of the industrial park while maintaining robustness in the face of uncertainties. This indicates that the model’s performance is not restricted to specific seasons and can be reliably applied throughout the year, providing a comprehensive solution for industrial park operations. At same time, interconnected microgrids can exchange power with each other and reduce dependence on the grid, thereby reducing the cost of microgrids and improving the economy.

By considering the optimization results from both typical spring and summer days, it is evident that the proposed model is capable of ensuring both economic efficiency and robustness, thereby demonstrating its effectiveness and applicability across different seasons.

4. Conclusions

This study introduces an IGDT-based stochastic optimal scheduling control strategy for industrial parks, aiming to enhance the operational reliability of industrial parks with multiple transformers. Through comprehensive simulation analysis and comparative evaluations, the following conclusions can be drawn:

(1)

In practical operations, the utilization of distributed ES exhibits superior economic advantages compared to centralized ES. This finding suggests that implementing distributed ES can effectively reduce transformer losses and subsequently lower overall costs within the industrial park;

(2)

The proposed IGDT model demonstrates both economic efficiency and robustness. In comparison to the traditional robust optimization approach, the IGDT model proves to be more suitable for real-world industrial park operations. It strikes a balance between economic optimization and robust decision making, making it a viable choice for operational control in industrial parks;

(3)

The collaboration and interaction among multiple microgrids within the industrial park contribute to load peak reduction and the promotion of renewable energy consumption. This result showcases the positive impacts of multi-microgrid systems in improving the overall efficiency and sustainability of industrial park operations.