Calculation Method of Earth Pressure Considering Wall Displacement and Axial Stress Variations

Abstract

Current earth pressure calculation methods suffer from certain limitations because they do not consider the effect of retaining wall displacement. In this study, the soil behind the wall is assumed to be in a plane strain state, and drawing upon nonlinear elastic constitutive theory, an earth pressure calculation method is proposed, capable of considering both axial stress and wall displacement. To account for changes in soil modulus with confining pressure, the tangent modulus from the Duncan-Chang nonlinear model is introduced. Depending on the direction of the principal stress behind the retaining wall, the static earth pressure point, the major principal stress inflection point, and the minor principal stress second inflection point are determined. The conditions for the existence of the second inflection point are also given. These specific points, together with the limit earth pressure point, divide the earth pressures acting on the wall into six regions. The study provides earth pressure calculation formulas for T (translation) mode, RBT (rotation about a point below the base) mode, and RTT (rotation about a point above the top) mode based on the characteristics of wall displacement distribution in each mode. The proposed method exhibits good agreement with the test results, offering an effective approach for accurately calculating earth pressures related to displacement.

1. Introduction

Accurate earth pressure calculations are of paramount importance in engineering. Deviations from reality can make the design of retaining walls unreasonable. In practice, the earth pressure theory of Rankine [1] and Coulomb [2] is commonly used, which gives the earth pressure at the limit state. However, experiments by Terzaghi [3] and Fang [4] showed a robust correlation between the earth pressure behind the retaining wall and the wall displacement. Subsequent experiments have shown that the soil arching effect [5,6] and the displacement pattern [7,8,9] also affect the earth pressure distribution.

Advances in computational science have brought the finite element method [10] and the discrete element method [11] into focus. The finite element method can account for the constitutive relation of the soil [12,13,14], forecast localized deformations along the slip surface [15,16], and predict the variation of earth pressure under seismic conditions [17]. Nevertheless, appropriate parameter selection [18] largely determines the accuracy of the finite element method, and mesh division has an impact as well [19]. In contrast, the use of the discrete element method requires more complex process for selecting contact models [20,21] and their microscale parameters [22]. These considerations make its application in engineering contexts more challenging [23]. Additionally, due to the limitations of previous contact models, the method is mainly used to investigate non-cohesive soils [24,25,26,27].

Furthermore, there are researchers who explore the laws of variation in retaining wall displacement and earth pressure using analytical methods [28,29]. The experiments of Ishihara [30] demonstrated the variation of the friction angle with the displacement of the retaining wall. Bang [31] proposed a method to determine the non-limit active earth pressure in the cohesionless soil. The findings of Fang [32] and Chang [13] further support this view and indicate that the external friction angle between the wall and the soil reaches its peak prior to the internal friction angle of the soil. Rao [33] presented a semi-empirical approach for estimating the non-limit passive earth pressure. Xu [34] assumed that the mobilized friction angle is non-linear, based on the work of Chang [13]. Hu [35] not only considered the effective internal friction angle of the soil, but also considered the impact of seepage on the active earth pressure. However, establishing the correlation between soil strength parameters and wall displacement remains a challenge.

Meanwhile, the limit equilibrium theory and the horizontal thin layer method are common approaches to investigate the non-limit earth pressures [36,37]. Li [38] developed a predictive approach for the active earth pressure in the translational mode by incorporating the soil arching effect. Patki [39] applied the limit equilibrium method and the Kötter equation to determine the slip surface for solving the passive earth pressure on an inclined retaining wall. Chen [40] developed a calculation method for active earth pressure by considering the moment equilibrium of the soil wedge. Regarding the rotation mode around the wall base, Wang [41] proposed that the soil slip surface behind the wall is a log-spiral surface [36]. Then, both the horizontal slice method and the graphical procedure were used to estimate the displacement-dependent earth pressure. By using the curvilinear thin layer element method, Wang [42] included the effect of soil arching on active earth pressure.

In addition, some researchers have investigated the non-limit state earth pressure using the curve-fitting method. Mei [43,44] used exponential and hyperbolic models for prediction, but did not consider the effect of the retaining wall displacement mode. On this basis, Tang [45] investigated the influence of the displacement mode and the center of rotation on the earth pressure distribution pattern. Peng [46] and Fan [47] postulated a linear relationship between passive earth pressure and retaining wall displacement, which led to the development of predictive models for earth pressure under different displacement modes. Xie [48] assumed a planar damage surface with constant shear strain along the slip plane, but this assumption does not adequately represent the actual behavior during the displacement process. Zhang [49] assumed that the stress in the soil behind the wall along the axial direction of the wall is the static earth pressure, which is different from the actual situation. A review of the relevant literature indicates that most of these studies have certain limitations. Those studies that can consider different displacement modes and are applicable to both clay and cohesionless soils are comparatively rare.

In this study, a finite displacement earth pressure calculation method is developed by applying the non-linear elasticity theory under the assumption that the soil behind the wall is in a plane strain state, while also considering the axial stress changes during the wall displacement. Based on the different directions of principal stress behind the wall, three special earth pressure points are derived. The conditions for the existence of the minor principal stress second inflection point were investigated. Subsequently, the earth pressure behind the wall was categorized into different regions by incorporating the limit earth pressure points. According to the distribution characteristics of the wall displacement, formulas for calculating the earth pressure under different displacement modes are presented. The soundness of the proposed method is validated by numerical simulations and existing model tests.

2. Theoretical Analysis

The schematic diagram for the x, y, and z directions in this paper is presented in Figure 1, where the x and y directions represent the horizontal plane. The x direction is perpendicular to the retaining wall, while the y direction represents the axial direction of the retaining wall. The z direction is vertical.

In order to simplify the earth pressure analysis, the following assumptions are made in this paper: (1) The soil behind the wall is treated as a semi-infinite space. (2) From the force characteristics inherent in the retaining wall, it is assumed that the soil behind the wall is in a plane strain state under finite displacement conditions. (3) Considering the modulus difference between the retaining wall and the soil, the retaining wall is treated as a rigid body. (4) The back of the retaining wall is vertical and there is no friction between the wall back and the soil.

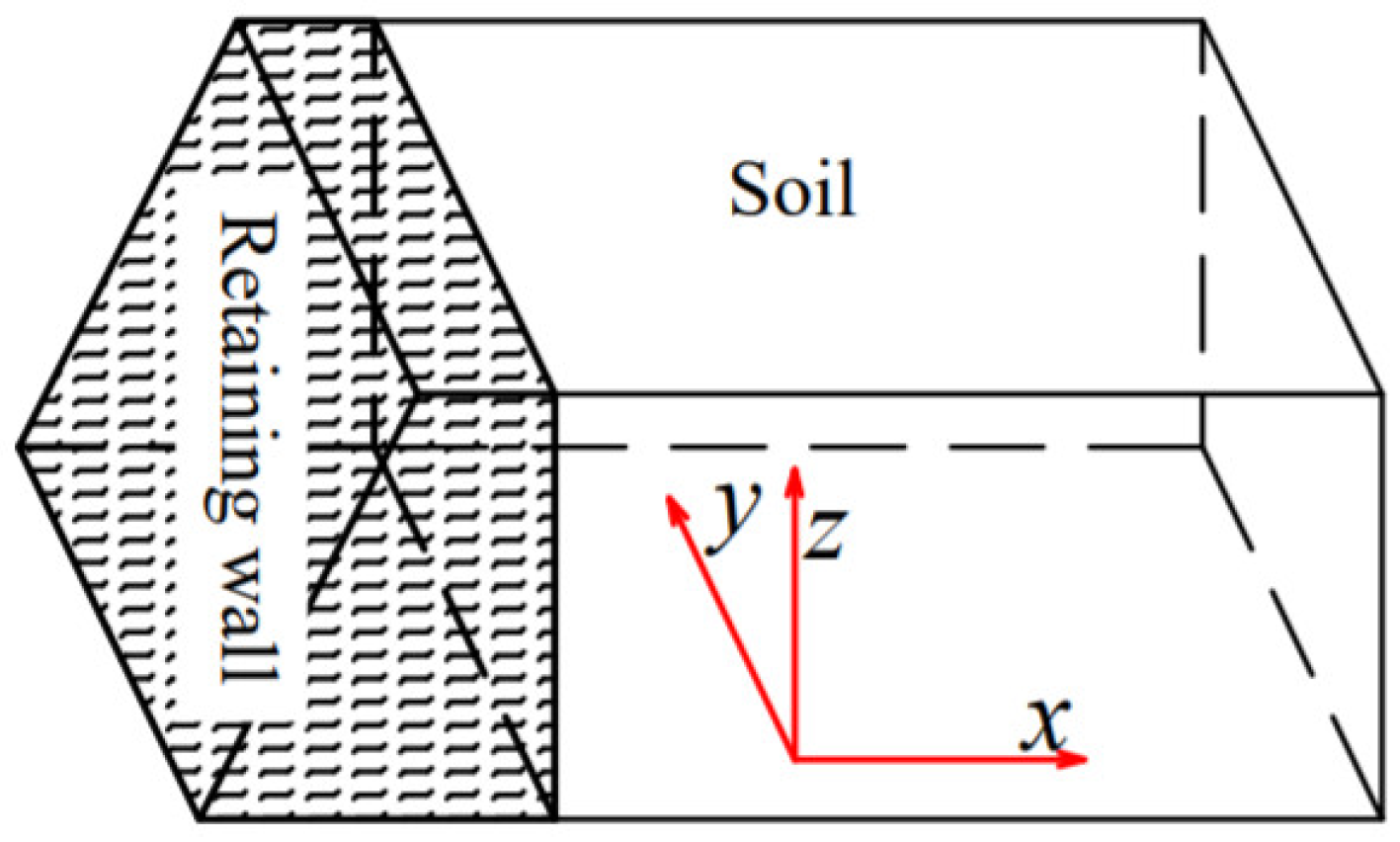
2.1. Calculation Method for Earth Pressure Considering Axial Stress

According to the elastic theory, the relationship between the strain in the x direction and the stresses in the x, y, and z directions is shown in Equation (1):

$${\epsilon }_x=\frac{{\sigma }_x}{E}-\frac{\mu ({\sigma }_y+{\sigma }_z)}{E}$$

(1)

In the above equation, the stress in the z direction ${\sigma }_z$, represents the self-weight stress of the soil, where ${\sigma }_z$ = $\gamma z$, with $z$ is the depth of the soil.

According to the plane strain assumption, the y direction strain ${\epsilon }_y$ = 0. Since the y direction stress ${\mathsf{\sigma }}_y$ satisfies the following formula.

$${\epsilon }_y=\frac{{\sigma }_y}{E}-\frac{\mu ({\sigma }_x+{\sigma }_z)}{E}$$

(2)

Therefore, the relationship between ${\sigma }_y$ and the stresses in other directions can be expressed as follows:

$${\sigma }_y=\mu ({\sigma }_x+{\sigma }_z)$$

(3)

By substituting Equation (3) into Equation (1), the relationship between ${\sigma }_x$ and ${\epsilon }_x$ can be obtained as expressed in Equation (4).

$${\sigma }_x=\frac{\mu }{1-\mu }{\sigma }_z+\frac{E{\epsilon }_x}{1-{\mu }^2}=K_0{\sigma }_z+\frac{E{\epsilon }_x}{1-{\mu }^2}$$

(4)

The ${\sigma }_x$ is the earth pressure on the retaining wall. It is a unified calculation formula of active and passive earth pressure expressed by strain, taking into account the change of axial stress of the soil along the retaining wall. Where K₀ is the static earth pressure coefficient. The above equation indicates that the earth pressure behind the wall consists of two components: the static earth pressure when the retaining wall has no displacement, and the incremental earth pressure which varies with the direction and magnitude of the wall displacement.

Substituting Equation (4) into Equation (3), the relationship between ${\sigma }_y$ and ${\epsilon }_x$ strain is obtained as shown in Equation (5).

$${\sigma }_y=K_0{\sigma }_z+\frac{E\mu }{1-{\mu }^2}{\epsilon }_x$$

(5)

It can be seen that the ${\sigma }_y$ is also a function of the ${\epsilon }_x$, that is, it varies with the direction and amount of displacement of the retaining wall, and it can be seen that Zhang [49] assumed that the ${\sigma }_y$ in the soil behind the wall is the static earth pressure is not appropriate.

The total earth pressure $F_{\Sigma x}$ of earth pressure behind the wall is as follows:

$$F_{\Sigma x}={\displaystyle {\int }_0^h{\sigma }_x\mathrm{d}z}=\frac{1}{2}{K}_0\gamma h^2+\frac{E}{1-{\mu }^2}{\displaystyle {\int }_0^h{\epsilon }_x\mathrm{d}z}$$

(6)

where h is the depth of the soil behind the wall. The above formula is derived from elastic theory and seems theoretically reasonable. However, comparison with the test results shows that while the results of this paper and the test results are in good agreement at the bottom of the retaining wall, the results of this paper are generally much greater than the test results at the top of the retaining wall, with a significant difference between the two. The problem lies in the modulus of the soil, which varies with changes in stress state. However, the above formula treats the modulus of the soil as a constant and ignores the difference between soil and other elastic materials. This leads to a deviation of the earth pressure from the actual value calculated by the method in this paper.

2.2. Calculation Method for Earth Pressure Considering Material Non-Linear

The modulus of the soil in practical engineering tends to increase with increasing confining pressure, and the tangent modulus $E_t$ in the Duncan-Chang non-linear elastic constitutive model has exactly this property.

$$\begin{array}{cc}\hfill E_t& ={\left[1-\frac{R_f(1-\sin \phi )({\sigma }_1-{\sigma }_3)}{2c\cos \phi +2{\sigma }_3\sin \phi }\right]}^{2}K{P}_a{(\frac{{\sigma }_3}{P_a})}^n\hfill \\ & ={\left(1-R_{f}S\right)}^2{E}_i\hfill \end{array}$$

(7)

In the formula, $S$ is the stress level; $E_i$ is the Janbu empirical formula; $R_f$ is the failure ratio, the value range is 0.75~1.0; $K$ is the modulus parameter, the range of soft clay is 50~200, the range of hard clay is 200~500, the range of sand is 200~3000; n is a dimensionless index, which is about 0.3~0.8; $P_a$ is the atmospheric pressure, the value is 101.325 kPa.

The $E_t$ is used to replace the modulus E in the previous section, and the improved calculation equations for ${\sigma }_x$ and $F_{\Sigma x}$ are shown below:

$${\sigma }_x=K_0{\sigma }_z+\frac{{\left(1-R_{f}S\right)}^2}{1-{\mu }^2}{E}_i{\epsilon }_x$$

(8)

$$F_{\Sigma x}=\frac{1}{2}{K}_0\gamma h^2+{\displaystyle {\int }_0^h\frac{{\left(1-R_{f}S\right)}^2{E}_i}{1-{\mu }^2}{\epsilon }_x\mathrm{d}z}$$

(9)

The relationship between ${\sigma }_y$ and strain ${\epsilon }_x$ is as follows:

$${\sigma }_y=K_0{\sigma }_z+\frac{{\left(1-R_{f}S\right)}^2{E}_i\mu }{1-{\mu }^2}{\epsilon }_x$$

(10)

2.3. Special Earth Pressure Points

In this paper, it is assumed that the soil behind the retaining wall is in a plane strain state, namely the y direction being the principal stress direction. The retaining wall is assumed to be vertical, and the friction angle between the wall and the soil is assumed to be zero. This means that both the x and z directions are also principal stress directions. Based on Mohr-Coulomb strength theory, the soil behind the retaining wall is considered to be in limit equilibrium state when the Mohr circle formed by the major and minor principal stresses is tangent to the Coulomb line. This is illustrated in Figure 2.

In the figure, ${\sigma }_o$ represents the static earth pressure. As the retaining wall is moved away from the soil, the soil behind the wall produces active strain, causing the earth pressure behind the wall to decrease. The minimum value of the earth pressure is the active limit earth pressure ${\sigma }_{xa}$, and this interval is known as the active earth pressure zone. If the retaining wall has no displacement, it experiences static earth pressure and at this point ${\sigma }_x$ = ${\sigma }_y$. The direction of the minor principal stress changes after this point, making it a special earth pressure point. As the retaining wall is displaced toward the soil, the soil behind the wall produces passive strain, resulting in an increase in earth pressure behind the wall. As ${\sigma }_x$ increases and becomes equal to ${\sigma }_z$, the major principal stress inflection point ${\sigma }_{x1r}$ occurs. Similarly, when ${\sigma }_y$ increases and becomes equal to ${\sigma }_z$, the minor principal stress inflection point ${\sigma }_{x3r}$ occurs. The maximum value of the earth pressure is the passive limit earth pressure ${\sigma }_{xp}$, and this interval is known as the passive earth pressure zone. The stress-strain calculation formulas for these earth pressure points are described below.

(1) Limit earth pressure point

Based on the above assumptions, the soil behind the retaining wall satisfies the Rankine earth pressure condition in the limit state. In the active limit state, the x direction earth pressure is minor principal stress. The limit equilibrium condition gives the active limit earth pressure ${\sigma }_{xa}$ shown in Equation (11).

$$\begin{array}{ll}{\sigma }_{xa}& ={\sigma }_z{\tan }^2({45}^{\circ }-\frac{\phi }{2})-2c\tan ({45}^{\circ }-\frac{\phi }{2})\\ & ={\sigma }_z{K}_a-2c\sqrt{K_a}\end{array}$$

(11)

By assigning ${\sigma }_x$ = ${\sigma }_{xa}$, the active limit strain ${\epsilon }_{xa}$ can be determined using Equation (8), as shown in Equation (12).

$${\epsilon }_{xa}=\left[\left(K_a-K_0\right){\sigma }_z-2c\sqrt{K_a}\right]\frac{(1-{\mu }^2)}{E_{ta}}$$

(12)

$E_{ta}$ is the tangent modulus in the active limit state, where ${\sigma }_z$ is the major principal stress and ${\sigma }_x$ is the minor principal stress. Substituting Equation (12) into Equation (9) gives the $F_{\Sigma x}$ acting on the back of the retaining wall as shown in Equation (13).

$$\begin{array}{ll}{F}_{\Sigma xa}& =\frac{1}{2}{K}_0\gamma h^2+{\displaystyle {\int }_0^h\left[\left({\sigma }_z{K}_a-2c\sqrt{K_a}\right)-K_0{\sigma }_z\right]dz}\\ & =\frac{1}{2}{K}_a\gamma h^2-2ch\sqrt{K_a}\end{array}$$

(13)

In the passive limit state, the ${\sigma }_x$ corresponds to the major principal stress. The passive limit earth pressure ${\sigma }_{xp}$ is given by Equation (14).

$$\begin{array}{ll}{\sigma }_{xp}& ={\sigma }_z{\tan }^2({45}^{\circ }+\frac{\phi }{2})+2c\tan ({45}^{\circ }+\frac{\phi }{2})\\ & ={\sigma }_z{K}_p+2c\sqrt{K_p}\end{array}$$

(14)

Similarly, let ${\sigma }_x$ = ${\sigma }_{xp}$, the passive limit strain ${\epsilon }_{xp}$ can be obtained using Equation (8), as depicted in Equation (15).

$${\epsilon }_{xp}=\left[\left(K_p-K_0\right){\sigma }_z+2c\sqrt{K_p}\right]\frac{(1-{\mu }^2)}{E_{tp}}$$

(15)

$E_{tp}$ is the tangent modulus in the passive limit state, where ${\sigma }_x$ is the major principal stress. The direction of the minor principal stress is determined from the presence of the minor principal stress second inflection point. If the point exists, the minor principal stress is ${\sigma }_z$, otherwise the minor principal stress is ${\sigma }_y$. The specific conditions for the determination are described in Section 2.5.

Substituting Equation (15) into Equation (9) gives the $F_{\Sigma x}$ acting on the back of the retaining wall as shown in Equation (16).

$$F_{\Sigma xa}=\frac{1}{2}{K}_p\gamma h^2+2ch\sqrt{K_p}$$

(16)

(2) Static earth pressure point

At the static earth pressure, both horizontal strains in the soil are zero, noted as ${\epsilon }_0$ = 0. The two horizontal stresses are equal and equal to the static earth pressure, as shown in the following equation.

$${\sigma }_y={\sigma }_x=K_0{\sigma }_z$$

(17)

It is clear from Equations (8) and (10) that ${\sigma }_x$ < ${\sigma }_y$ in the active earth pressure zone and ${\sigma }_x$ > ${\sigma }_y$ in the passive earth pressure zone. Therefore, the static earth pressure point is the minor principal stress inflection point.

(3) Major principal stress inflection point

When ${\epsilon }_x$ = 0, the retaining wall is subjected to static earth pressure, where ${\sigma }_x$ < ${\sigma }_z$. As the strain ${\epsilon }_x$ increases, there exists a point within the interval (0, ${\epsilon }_{xp}$) where ${\sigma }_x={\sigma }_z$. Before this point, ${\sigma }_x>{\sigma }_z$, and after this point, ${\sigma }_x$ < ${\sigma }_z$. Based on Equation (3) and the range of values of $\mu$, it is known that ${\sigma }_x({\sigma }_z$) > ${\sigma }_y$ at this point. Therefore, this point is called the major principal stress inflection point.

Let ${\sigma }_x={\sigma }_z$, and the strain ${\epsilon }_{x1r}$ at this point can be obtained from Equation (8) as indicated in Equation (18).

$${\epsilon }_{x1r}=\frac{(1+\mu )(1-2\mu ){\sigma }_z}{{\left(1-R_{f}S\right)}^2{E}_i}$$

(18)

(4) Minor principal stress second inflection point

Within the interval $({\epsilon }_{x1r}$, ${\epsilon }_{xp})$, ${\sigma }_x$ is the major principal stress. When ${\epsilon }_x={\epsilon }_{x1r}$, ${\sigma }_y$ is the minor principal stress. As the soil strain ${\epsilon }_x$ gradually approaches ${\epsilon }_{xp}$, according to Equation (10), ${\sigma }_y$ continuously increases. There may be a point where ${\sigma }_y={\sigma }_z$, before which ${\sigma }_y>{\sigma }_z$, and after which ${\sigma }_y$ < ${\sigma }_z$. This point is called the minor principal stress second inflection point. Substituting ${\sigma }_y={\sigma }_z$ into Equation (10) gives the strain at this point (${\epsilon }_{x3r}$) as shown in Equation (19).

$${\epsilon }_{x3r}=\frac{(1+\mu )(1-2\mu ){\sigma }_z}{{\left(1-R_{f}S\right)}^2{E}_i\mu }$$

(19)

By substituting Equation (19) into Equation (8), we obtain the stress ${\sigma }_{x3r}$ at this point, as depicted in Equation (20).

$${\sigma }_{x3r}=K_0{\sigma }_z+\frac{\left(1-2\mu \right)}{\mu (1-\mu )}{\sigma }_z=\frac{1}{K_0}{\sigma }_z$$

(20)

(5) Discussion of the order of the special points

The special points mentioned above consist of the active limit earth pressure point, the static earth pressure point, the major principal stress inflection point, the minor principal stress second inflection point, and the passive limit earth pressure point. The corresponding sequence of soil strain and earth pressure acting on the retaining wall at these points, arranged from small to large, is presented in Equations (21) and (22).

$${\epsilon }_{xa}<{\epsilon }_0=0<{\epsilon }_{x1r}<{\epsilon }_{x3r}<{\epsilon }_{xp}$$

(21)

$${\sigma }_z{K}_a-2c\sqrt{K_a}<K_0{\sigma }_z<{\sigma }_z<\frac{1}{K_0}{\sigma }_z<{\sigma }_z{K}_p+2c\sqrt{K_p}$$

(22)

If the minor principal stress second inflection point occurs after the passive limit earth pressure point, it does not exist. Equations (21) and (22) describe the scenario where the minor principal stress second inflection point occurs before the passive limit earth pressure point.

2.4. Earth Pressure Zoning

According to the five special points in the soil behind the wall proposed above, the earth pressure on the retaining wall can be divided into six partitions, as shown in Figure 3.

(1)

Active failure zone: ${\epsilon }_x$ < ${\epsilon }_{xa}$. The stresses in the x, y, and z directions in the soil are the minor, intermediate and major principal stresses, respectively. A failure plane has developed in the soil behind the wall and active failure has occurred.

(2)

Active earth pressure zone: ${\epsilon }_x$∈$({\epsilon }_{xa}$, ${\epsilon }_0)$. The stresses in the x, y, and z directions in the soil are the minor, intermediate and major principal stresses, respectively. The major principal stress is the self-weight stress ${\sigma }_z$, while the earth pressure on the retaining wall in the x direction represents the minor principal stress.

(3)

Passive earth pressure zone before the major principal stress reversal: ${\epsilon }_x$∈$\left({\epsilon }_0,{\epsilon }_{x1r}\right)$. The stresses in the x, y, and z directions in the soil are the intermediate, minor and major principal stresses, respectively. Compared to the active earth pressure zone, the direction of the minor principal stress has changed.

(4)

Passive earth pressure zone between the major and minor principal stress inflection points: ${\epsilon }_x$∈$({\epsilon }_{x1r}$, ${\epsilon }_{x3r})$. The stresses in the x, y, and z directions in the soil are the major, minor and intermediate principal stresses, respectively. In this zone, the self-weight stress ${\sigma }_z$ is the intermediate principal stress, and the earth pressure on the retaining wall is the major principal stress.

(5)

Passive earth pressure zone after the second reversal of the minor principal stress: ${\epsilon }_x$∈$({\epsilon }_{x3r}$, ${\epsilon }_{xp})$. The stresses in the x, y, and z directions in the soil are the major, intermediate and minor principal stresses, respectively. The major principal stress is the earth pressure ${\sigma }_x$ on the retaining wall, while the self-weight stress ${\sigma }_z$ in the soil is the minor principal stress.

(6)

Passive failure zone: ${\epsilon }_x>{\epsilon }_{xp}$. The direction of the principal stresses in this zone is consistent with the previous zone. The soil behind the wall undergoes passive failure along the failure plane.

However, it is not always possible to divide the earth pressure zones into six regions. In some cases, the earth pressure on the retaining wall when the minor principal stress second reversal occurs is greater than the passive limit earth pressure, which means that the minor principal stress second inflection point does not exist. This indicates that the earth pressure behind the wall is divided into five zones as shown in Figure 4.

2.5. Discussion on the Existence of Inflection Point

As mentioned above, the condition for the existence of the minor principal stress second inflection point is ${\sigma }_{xp}$ ≥ ${\sigma }_{x3r}$. For cohesionless soil, the equation derived on the basis of this condition is given by Equation (23).

$${\sigma }_{xp}-{\sigma }_{x3r}=(K_p-\frac{1}{K_0}){\sigma }_z\ge 0$$

(23)

After simplification, the following formula can be obtained.

$${\tan }^2({45}^{\circ }+\frac{\phi }{2})\ge \frac{1-\mu }{\mu }$$

(24)

$$\phi \ge \frac{360}{\pi }\arctan \sqrt{\frac{1-\mu }{\mu }}-90$$

(25)

From Figure 5 it can be concluded that for cohesionless soils, the existence of the inflection point can be determined by the location of the point with a given Poisson’s ratio $\mu$ and friction angle $\phi$ relative to the φ-μ curve. If the point is above the curve, the inflection point exists. If the point is exactly on the curve, the inflection point also exists, and ${\sigma }_{x3r}={\sigma }_{xp}$. If the point is below the curve, the inflection point does not exist.

For cohesive soils, the situation is somewhat more complex. The conditions for the existence of the minor principal stress second inflection point are given in Equation (26).

$${\sigma }_x{}_p-{\sigma }_{x3r}=\left[{\tan }^2({45}^{\circ }+\frac{\phi }{2})-\frac{1-\mu }{\mu }\right]{\sigma }_z+2c\tan ({45}^{\circ }+\frac{\phi }{2})\ge 0$$

(26)

Based on Equation (26), the condition to be satisfied by the self-weight stress ${\sigma }_z$ is expressed in Equation (27).

$${\sigma }_z\le \frac{2\mu c\tan ({45}^{\circ }+\frac{\phi }{2})}{1-\mu {\sec }^2({45}^{\circ }+\frac{\phi }{2})}$$

(27)

Alternatively, the depth $z_{x3r}$ of the soil behind the wall should satisfy the following condition.

$$z_{x3r}\le \frac{2\mu c\tan ({45}^{\circ }+\frac{\phi }{2})}{\gamma -\mu \gamma {\sec }^2({45}^{\circ }+\frac{\phi }{2})}$$

(28)

This indicates that even if the φ and μ distribution of the clay is below the $\phi -\mu$ curve, an inflection point still exists if the self-weight stress ${\sigma }_z$ or depth $z_{x3r}$ of the soil satisfies the aforementioned conditions.

2.6. Earth Pressure under Different Displacement Modes

In previous studies, Fang [4] classified the displacement modes of retaining walls into three categories: translational mode (T), rotation about a point above the top (RTT), and rotation about a point below the wall base (RBT), as illustrated in Figure 6. The parameter $\lambda$ is used to determine the location of the rotation center.

Based on the distribution characteristics of the wall displacement under different displacement modes, the formulas for the earth pressure behind the wall in each mode are given below.

In the T mode, the soil displacement and strain are uniform at different depths, which means that the strain distribution function along the depth z can be represented as ${\epsilon }_x\left(z\right)={\epsilon }_x$. Based on this, ${\sigma }_x$ and $F_{\mathsf{\Sigma }x}$ are determined by Equations (29) and (30)$.$

$${\sigma }_x=K_0{\sigma }_z+\frac{{\left(1-R_{f}S\right)}^2{E}_i{\epsilon }_x}{1-{\mu }^2}$$

(29)

$$F_{\Sigma x}=\frac{1}{2}{K}_0\gamma h^2+{\displaystyle {\int }_0^h\frac{{\left(1-R_{f}S\right)}^2{E}_i{\epsilon }_x}{1-{\mu }^2}\mathrm{d}z}$$

(30)

In the RBT mode, the displacement and strain of the soil are largest at the top of the wall, while they are zero at the center of rotation. Based on this, ${\epsilon }_x\left(z\right)={\epsilon }_x(\lambda H$ + $H$ − $z)/(\lambda H$ + $H)$, ${\sigma }_x$ and $F_{\mathsf{\Sigma }x}$ are determined by Equations (31) and (32)$.$

$${\sigma }_x=K_0{\sigma }_z+\frac{{\left(1-R_{f}S\right)}^2{E}_i(\lambda H+H-z){\epsilon }_x}{(1-{\mu }^2)(\lambda H+H)}$$

(31)

$$F_{\Sigma x}=\frac{1}{2}{K}_0\gamma h^2+{\displaystyle {\int }_0^h\frac{{\left(1-R_{f}S\right)}^2{E}_i(\lambda H+H-z){\epsilon }_x}{(1-{\mu }^2)(\lambda H+H)}\mathrm{d}z}$$

(32)

In the RTT mode, the soil experiences its maximum displacement and strain at the bottom of the wall, while the displacement and strain at the center of rotation is zero. Based on this, ${\epsilon }_x\left(z\right)={\epsilon }_x(\lambda H$ + $Z)/(\lambda H$ + $H)$, ${\sigma }_x$ and $F_{\mathsf{\Sigma }x}$ are determined by Equations (33) and (34)$.$

$${\sigma }_x=K_0{\sigma }_z+\frac{{\left(1-R_{f}S\right)}^2{E}_i(\lambda H+z){\epsilon }_x}{(1-{\mu }^2)(\lambda H+H)}$$

(33)

$$F_{\Sigma x}=\frac{1}{2}{K}_0\gamma h^2+{\displaystyle {\int }_0^h\frac{{\left(1-R_{f}S\right)}^2{E}_i(\lambda H+z){\epsilon }_x}{(1-{\mu }^2)(\lambda H+H)}\mathrm{d}z}$$

(34)

3. Example Verification

In this study, the proposed method was validated through discrete element experiments and existing model tests. Discrete element experiments were used to simulate the variation of earth pressure at a point behind the retaining wall, and the earth pressure distribution curve behind the wall was obtained by connecting the earth pressure points at different depths. The proposed method was further validated using existing model tests.

3.1. Discrete Element Experiment

The discrete element software PFC2d was used in this study, with the Adhesive Rolling Resistance Linear Model (ARRL) as the contact model. The contact model was fitted to the clay of the Doumen Reservoir, and its macroscopic mechanical parameters were determined using the GDS stress-path triaxial instrument. These parameters are listed in

Table 1. Macroscopic mechanical parameters of clay.

Specific Gravity of Soil Particle/Gs	Density/g·cm−3	Void Ratio/e	c/kPa	φ/°
2.7	1.78	0.808	14	24.6

.

The contact model parameters were calibrated using numerical biaxial tests, as shown in Figure 7. The stress-strain curve resulting from the calibrated parameters is illustrated in Figure 8, which exhibits good agreement with the results of the indoor experiments.

The calibrated parameters are given in

Table 2. Discrete element model parameters.

Particle Density kg/m3	Particle Radius Rmax/mm	Particle Radius Rmin/mm	Effective Modulus E*/MPa	Stiffness Ratio k*	Friction Coefficient μ	Rotational Friction Coefficient	Maximum Attraction N	Domain of Attraction
2650	0.714	0.1785	33	3.6	0.21	0.8	10	0.5 $R_{max}$

. The cohesion and friction angle were obtained as 13.8 kPa and 24.32°, respectively, using the stress circles formed by the numerical experiments under three different confining pressures (Figure 9), which are in good agreement with the results from the indoor tests.

The model shown in Figure 7 was also used to simulate the change in earth pressure behind the retaining wall at a given point during wall displacement. Prior to loading, the model was subjected to $K_0$ consolidation with a consolidation factor of $\mu /(1$ − $\mu )$ to simulate soils with different burial depths by adjusting the confining pressure.

(1) Active earth pressure

In the active pressure zone, the soil can be considered to undergo a process from the static state to the active limit state, where the vertical stress ${\sigma }_z$ remains constant and the lateral stress ${\sigma }_x$ decreases continuously until failure. In this process, ${\sigma }_z$ is set to 100 kPa, 150 kPa, and 200 kPa and held constant, while ${\sigma }_x$ decreases continuously until failure. The Duncan model is used with a failure ratio $R_f$ of 0.75, a modulus parameter $K$ of 145, a dimensionless index $n$ of 0.75, and a Poisson’s ratio $\mu$ of 0.35.

The numerical results were compared with the results of this study, Zhang [49] and Rankine theory, as shown in Figure 10.

As depicted in Figure 10, it is evident that ${\sigma }_x$ exhibits a decreasing trend with increasing strain. Once the strain exceeds 1.5%, ${\sigma }_x$ shows fluctuations within a specific range. This fluctuation is attributed to the unevenness of the failure surface, which causes the soil on both sides of the surface to interact under vertical pressure, leading to ${\sigma }_x$ fluctuations. The upper limit of this fluctuation corresponds to the result of Zhang [49], while the lower limit corresponds to the method in this paper, which exhibits good consistency with the numerical results.

Within this range, the principal stress direction remains constant, and ${\sigma }_y$ is the intermediate principal stress. Therefore, the difference between the method in this paper and Zhang [49] in the active earth pressure region is not significant, differing by ${\mu }^2{E}_t{\epsilon }_x/(1$ − ${\mu }^2)$.

(2) Passive earth pressure

In the passive earth pressure zone, from the static state to the passive limit state, the major principal stress inflection point ${\epsilon }_{x1r}$ appears first. The soil chosen for this paper is calculated to show that $K_p>1/K_0$. According to Equation (26), it can be inferred that the minor principal stress second inflection point ${\epsilon }_{x3r}$ also exists.

To avoid changing the direction of the principal stress in the numerical model, the passive zone was divided into two sections. In the first section, ${\sigma }_x$ was continuously increased until it equaled ${\sigma }_z$. This section corresponds to the passive earth pressure zone before the major principal stress reversal. In the second section, ${\sigma }_x$ was held constant while ${\sigma }_z$ was increased until soil failure. This section includes the minor principal stress second inflection point ${\epsilon }_{x3r}$.

The numerical results were compared with the results of this study, Zhang [49] and Rankine theory, as shown in Figure 11.

Figure 11 shows that as the strain increases, ${\sigma }_x$ gradually increases but the rate of increase slows down. When the strain exceeds 3%, the soil fails and ${\sigma }_x$ oscillates within a certain range. The results obtained in this study are slightly smaller than the experimental results, and the strains obtained by the proposed method are on the high side at special earth pressure points.

The results of Zhang [49] exhibit a similar trend to the numerical test results, but there is a noticeable discrepancy in the numerical values. The reason for this is that in the passive earth pressure zone, the direction of the minor principal stress is changed, resulting in ${\sigma }_y$ becoming the minor principal stress. This has a significant effect on the tangent modulus. Zhang [49] assumed that the minor principal stress is the static earth pressure, which is inconsistent with the situation where ${\sigma }_y$ increases with ${\sigma }_x$. The tangent modulus obtained from this stress state is much smaller than the actual situation. Therefore, the method proposed in this paper is closer to the numerical test results.

3.2. Model Experiment

To explore the effect of wall displacement on earth pressure, Xia [7] conducted model experiments using clay under different displacement modes, as shown in Figure 6, with $\lambda$ = 0. The model was constructed with a length of 1.9 m and a width of 1 m, while the soil inside had a height of 0.95 m. The clay used had a friction angle of 34°, a cohesion of 5 kPa, and a unit weight of 15.73 kN/m³. In the Duncan model, the failure ratio $R_f$ was set to 0.95, the modulus parameter $K$ was set to 145, the dimensionless index $n$ was set to 0.75 and the Poisson’s ratio was set to 0.3.

According to Equation (24), it can be concluded that the minor principal stress second inflection point exists. The earth pressure acting behind the wall can be divided into six regions by using five special points. Specifically, the active failure zone is (−$\infty$, −0.57z − 0.75), the active earth pressure zone is (−0.57z − 0.75, 0), the passive earth pressure zone before the major principal stress reversal is (0, 1.01z), the passive earth pressure zone between the major and minor principal stress inflection points is (1.01z, 3.14z), the passive earth pressure zone after the minor principal stress reversal is (3.14z, 3.49z + 2.52) and the passive failure zone is (3.49z + 2.52, +$\infty$).

The results extracted from Figure 12 clearly show that, in the T mode, the wall displacement is not affected by the soil depth. The earth pressure exhibits a parabolic distribution, and the magnitude of the earth pressure increment is positively correlated with the soil depth. In the RTT mode, there exists a positive correlation between wall displacement and the soil depth. The magnitude of the earth pressure increment is also positively correlated with the soil depth. In the RBT mode, there is a negative correlation between the wall displacement and the soil depth. In addition, the earth pressure initially has a positive correlation and then changes to a negative correlation with the soil depth. At the bottom of the wall, where the retaining wall displacement is zero, the soil strain is also zero, so the earth pressure has not changed.

For a given soil, it is established by Equation (8) that the variation in earth pressure due to the wall displacement is governed by two factors: the tangent modulus $E_t$ and the soil strain ${\epsilon }_x$. The wall displacement affects the ${\epsilon }_x$, while the soil depth affects the soil confining pressure and hence the tangent modulus $E_t$. The absence of changes in surface earth pressure during the wall displacement process can be attributed to the fact that the confining pressure of the surface soil is zero, indicating that the tangent modulus is zero. In the T mode, the strain ${\epsilon }_x$ remains constant, and only the tangent modulus $E_t$ increases with soil depth. In the RTT mode, both ${\epsilon }_x$ and $E_t$ increase with soil depth. In the RBT mode, ${\epsilon }_x$ decreases with soil depth, while $E_t$ increases with soil depth. The interaction of these two factors results in an increase followed by a decrease in earth pressure. Overall, the results of this paper are in close agreement with the findings of Xia [7]. The Pearson correlation coefficients for each displacement mode surpass 0.75, affirming the rationality of the proposed approach.

Fang [4] carried out a study of the earth pressure distribution using a cohesionless soil under different displacement modes. The model is 2 m long, 1 m wide and 0.5 m high. The cohesionless soil has a unit weight of 15.5 kN/m³ and a friction angle of 30.9°. The Duncan model was used with a failure ratio of 0.65, a modulus parameter of 550, a dimensionless index of 0.45 and a Poisson’s ratio of 0.26.

According to Equation (24), it can be concluded that the minor principal stress second inflection point exists. The earth pressure acting behind the wall can be divided into six regions by using five special points. Specifically, the active failure zone is (−$\infty$, −0.045z), the active earth pressure zone is (−0.045z, 0), the passive earth pressure zone before the major principal stress reversal is (0, 0.451z), the passive earth pressure zone between the major and minor principal stress inflection points is (0.451z, 1.894z), the passive earth pressure zone after the minor principal stress reversal is (1.894z, 2.14z) and the passive failure zone is (2.14z, +$\infty$).

Under the T mode, the comparison between the method proposed in this study and the experimental results is shown in Figure 13. In the absence of wall displacement, the earth pressure has an almost linear distribution. However, once the wall is displaced, the earth pressure follows a parabolic distribution. As the displacement increases, the rate of increase in earth pressure gradually decreases until it reaches the passive limit.

The comparison between the RBT modes ($\lambda$ = 0, 0.21, 0.5 and 13.78) and the proposed method is shown in Figure 14. When $\lambda$ = 0, the wall rotates around the base and the displacement at the bottom of the wall is zero. Consequently, there is no change in the earth pressure, and the variation of the earth pressure measured in the model test is also small. Although the displacement is the greatest at the top of the wall, the tangent modulus is zero, resulting in no change in earth pressure. In this mode, the earth pressure bulges in the direction away from the retaining wall. As $\lambda$ increases, the center of rotation gradually moves away from the bottom of the wall and the displacement at the bottom of the wall gradually increases. The position of the maximum stress gradually moves downward, and the bulge gradually disappears. When $\lambda$ = 13.78, the earth pressure distribution behind the wall is basically the same as in the T mode.

The comparison between the RTT modes ($\lambda$ = 0, 0.5, 1.81 and 7.43) and the proposed method is shown in Figure 15. In the case of $\lambda$ = 0, the wall rotates around the top, which transforms the RTT mode into the RT mode. In this mode, the distribution of wall displacement along the soil depth gradually increases, so that the increase of earth pressure behind the wall to also gradually increases with depth. The earth pressure distribution in this mode shows a certain concavity toward the wall, and although the proposed method also captures this phenomenon, there are some numerical differences from the experiment conducted by Fang [4]. As $\lambda$ gradually increases, the center of rotation moves away from the top of the wall and the difference in displacement at different heights of the wall gradually decreases. The earth pressure distribution behind the wall gradually takes on a parabolic shape. When $\lambda$ = 7.43, the influence of the difference in wall displacement at different heights on the earth pressure can be almost neglected, and the earth pressure distribution behind the wall in this mode is similar to that in the T mode.

In the RBT and RTT modes, when $\lambda$ is small, there is a discrepancy between the results obtained in this study and the experimental findings. This discrepancy can be primarily attributed to the omission of the soil arching effect caused by wall-soil friction in this study [50,51]. As the value of $\lambda$ gradually increases, the earth pressure distribution behind the wall tends toward the T mode, and the difference between the results of this study and the model test results gradually decreases. Analysis of Figure 13, Figure 14 and Figure 15 reveals a remarkable similarity between the change patterns for the two under each displacement mode, with Pearson’s correlation coefficient exceeding 0.75. Therefore, the method proposed in this paper effectively responds to displacement-related earth pressure.

4. Conclusions

Based on the non-linear elastic constitutive theory and assuming that the soil behind the wall is in a plane strain state, this study presents a predictive model for earth pressure under finite displacement conditions that takes into account the variation of axial stress. The axial stress considerations have a clear advantage over the static earth pressure assumption of Zhang [49]. The model incorporates the tangent modulus from the Duncan model to accurately capture the influence of confining pressure on the soil modulus. Notably, when the retaining wall has no displacement, the model automatically reduces to the static earth pressure. Moreover, leveraging the specific characteristics of the displacement distribution for each displacement mode, the study provides earth pressure calculation formulas for each respective mode.

The movement of the retaining wall causes a change in the direction of principal stresses in the soil behind it, as the earth pressure increases. Considering the effect of axial stress changes at specific points, the formula for calculating the static earth pressure point (${\sigma }_x={\sigma }_y$) and the major principal stress inflection point (${\sigma }_x={\sigma }_z$) has been improved. In addition, the minor principal stress second inflection point (${\sigma }_y={\sigma }_z$) is introduced for the first time. However, the earth pressure at this point should be less than or equal to the passive limit earth pressure, otherwise this point does not exist. Based on this, the paper proposes conditions for judging the existence of this point for different soils. These points are then combined with the active and passive limit earth pressure points to divide the earth pressure behind the retaining wall into different zones.

The discrete element tests have demonstrated that the method proposed in this study exhibits good agreement with experimental results in the limit state and at specific earth pressure points, particularly in the passive earth pressure zone. Furthermore, the earth pressure prediction models developed for different displacement modes can also effectively predict the results of the cohesionless soil and clay model tests. However, due to the omission of arching effects, there exists a deviation between the predicted results and the actual observations when the rotation center approaches the top or bottom of the wall. Addressing and refining this aspect will be a focus of the upcoming research phase.