Dynamic Bending Model Describing the Generation of Negative Stiffness by Buckled Beams: Qualitative Analysis and Experimental Verification

Abstract

This work addresses the dynamic modeling of a negative stiffness absorber consisting of an assembly of curved beams. Design rules are derived from the orders of magnitude of stiffness and elastic energy stored by the negative stiffness elements. Although static and dynamic performances are widely documented using equivalent spring–mass system equations of motion, this paper presents a modeling approach based on beam dynamics to predict the behavior by incorporating the generation of negative stiffness with prestressed Euler beams. The static behavior is first recalled to feed the dynamic beam model with realistic orders of magnitude. The latter is derived from the beam balance instead of the spring–mass system and aims at solving the beam problem, which encompasses more realistic phenomena compared to introducing the equivalent stiffness in the spring–mass equation of motion. The consistency of the beam modeling is confirmed by comparison with available models in the literature and finite element simulations. A mock-up is built in which beam-type components are 3D-printed. Axial loading is introduced on the curved beams to evaluate its influence on the response of the isolator, and the observed softening trend complies with the theoretical predictions.

1. Introduction

A tuned mass damper (TMD) is a mechanical device designed to reduce the effects of vibrations on a structure. It consists of a mass, a spring, and a damper, which are tuned to a specific frequency close to the frequency of the primary system. It operates on the concept of anti-resonance in such a way that, when the primary system vibrates at its resonance frequency, the damper oscillates in the opposite direction, thereby countering the oscillations and decreasing its amplitude. When properly calibrated, these devices are effective even with a small additional mass (10% of the primary system). This concept was formalized in terms of a two degree of freedom system, together with associated design rules and optimized tuning parameters by [1]. For a more recent state of the art, one may refer to [2], which compiles chronological progress on the design and modeling and challenges in the field of passive vibration control. However, one limitation of the TMD is that stiffness should be reduced, or mass should be increased, as a lower frequency range of performance is expected. This would result in a large static displacement that would be unsuitable for some applications. To overcome this limitation, negative stiffness can be introduced to reach low-frequency ranges of efficiency.

The negative stiffness system itself does not provide a stable operating regime and should be supplemented by a positive spring, which is expected to compensate for the negative stiffness and become stable. The overall stiffness will then be quasi-zero but still positive. The combination of these two stiffnesses of opposite signs gives the resonator great flexibility over the frequency range to be isolated, especially the low frequencies.

The concept of negative stiffness was first proposed by [3], who used three springs to achieve the negative stiffness. The negative stiffness assembly is usually presented as two horizontal springs in series, whose connecting point is also attached to a vertical spring. In this way, the two horizontal springs provide the negative stiffness, while the vertical spring provides the positive stiffness. This assembly is already documented to identify its high static and low dynamic features, as well as the conditions under which the negative stiffness compensates for or overcome the positive one. A summary of various prototypes with quasi-zero stiffness characteristics is provided in [4] and numerous ways to produce quasi-zero stiffness are documented in [5].

Negative stiffness springs take the form of elastic rubber rods, slender beams, or bar systems, or even magnets repulsing each other. It is specifically introduced in the form of curved beams by [6] and it was shown that such nonlinear springs provide low-frequency performance while they support the static load of the equipment. Prestressed negative stiffness springs were investigated in [7], as an industrial vibration isolator for sensitive equipment such as microscopes. The substitution of the linear spring by a buckled beam to form Euler springs was described by [8] to achieve a vibration isolator with high-static low-dynamic stiffness properties.

The buckled beam setup takes advantage of the snap-through behavior of beams to generate the negative stiffness mechanism. The aspect of symmetric buckling of Euler beams is reported in [9], which also constrains the connecting point to realize negative stiffness in the tangential direction. Very interesting is the derivation of static criteria describing the performance of compressed beams from a fine analysis of displacement and stresses. This mechanism was recently addressed by [10] from an analytical point of view. The specific nonlinear behaviors relying on the buckling instability motivated numerous fundamentals studies, as [11] followed by [12,13]. Most of these studies focus on the mathematical way to obtain low dynamic stiffness [14,15], and some show experimental results on prototypes for various industrial applications as [16] or as [17,18] to improve the comfort seat suspension of the vehicle. The performance of more recent systems is demonstrated experimentally under harmonic and random conditions [19]. Shock excitation is also investigated [20] and specifically using a buckled beams setup [21]. As examples of other configurations, negative stiffness can be used to bring damping to composites [22,23] or can be inserted as magnets, as in [24,25].

As part of vibration control solutions, different types of negative stiffness systems are reviewed by [19,26]. As for more recent developments, these devices are used in periodic arrangement of beams to produce negative-stiffness honeycombs [27,28,29,30] and negative-stiffness metamaterials providing band gaps [31,32].

From this literature review, a widely used approach is to formulate the dynamic behavior through the equation of motion of the equivalent spring–mass system, in which the stiffness parameters are considered as the equivalent stiffness of the structural elements. This approach is well suited to assess the nonlinear behavior since the stiffness is supplemented by higher-order terms, either derived analytically or numerically using Taylor expansions. The obtained equation is generally reduced to a Duffing oscillator, whose nonlinear resonance and unstable nature are extensively documented.

Deriving a dynamic beam model would be of interest because solving the beam problem would encompass more realistic phenomena. In fact, the negative stiffness components are rarely ideal springs but rather structural elements such as elastic rubber rods, slender beams or bar systems, or repulsing magnets. For some operating regimes, even a linear one assuming small displacements, the ability to obtain an analytical description of such a system based on a bending model would be beneficial.

The objective of this work is to present some design rules and equations associated with the description of a negative stiffness resonator prototype. The design under study is largely inspired from [6,33]. The analysis is complemented by finite element comparisons performed on the different components. Experimental measurements are finally conducted on a mock-up and demonstrate the tunable aspect of the resonator with respect to different axial loads.

This paper is organized into three sections. A primary description of the structure under study is introduced in Section 2, together with the underlying physics and associated mechanisms. Along with the analytical model comes the numerical investigation in Section 3. Particularly, force–displacement relations and eigenfrequency computations are presented in order to confirm the validity of theoretical predictions. Finally, Section 4 describes experiments conducted on a mock-up of the resonator. Measured frequency responses show the softening effect as axial load increases and exhibit similar trends to the theoretical model, justifying its consistency.

2. Theoretical Insight

This section gives an overview of the preliminary theoretical calculations that can be made to assess the static behavior and dynamic performance of the resonator depicted in Figure 1.

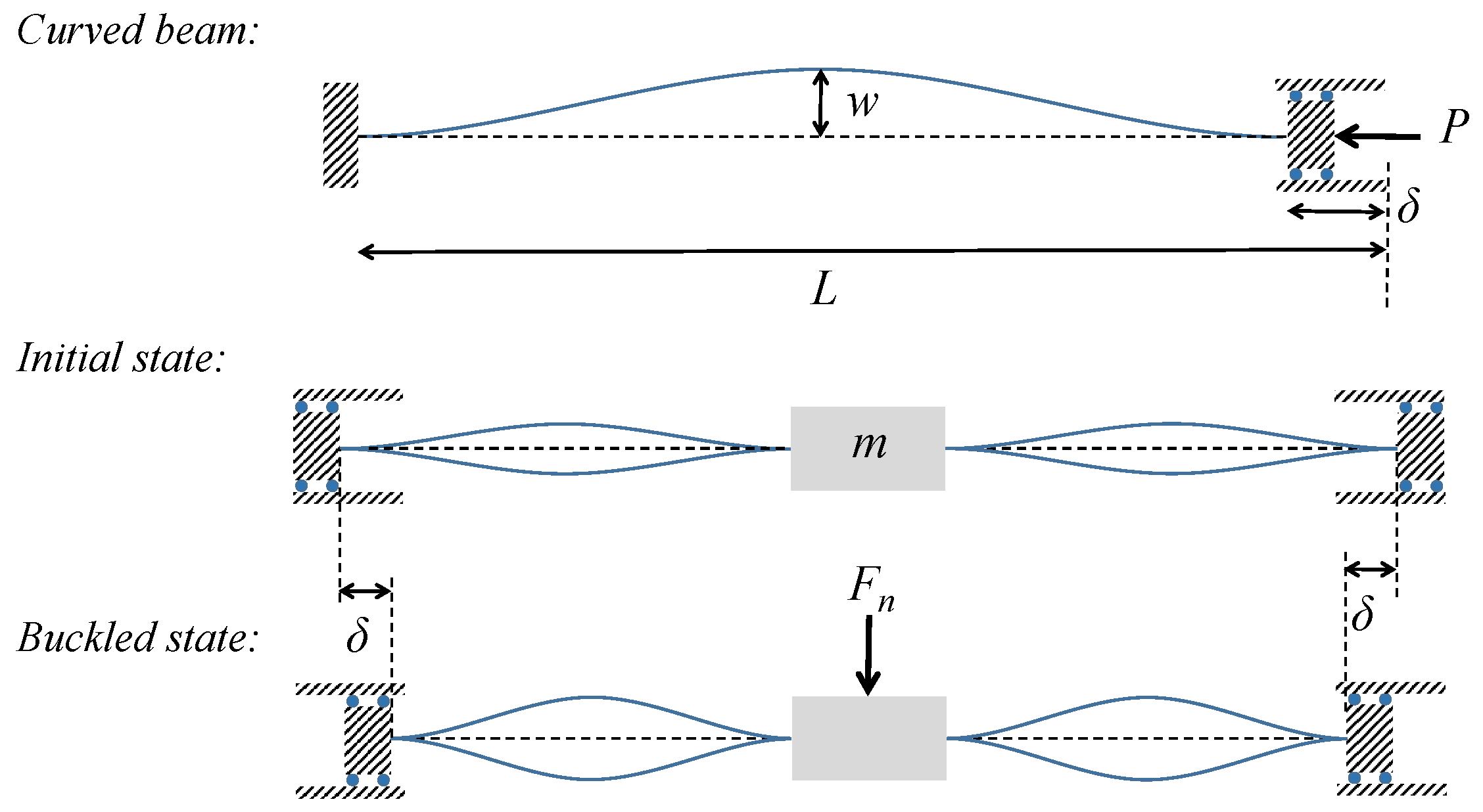
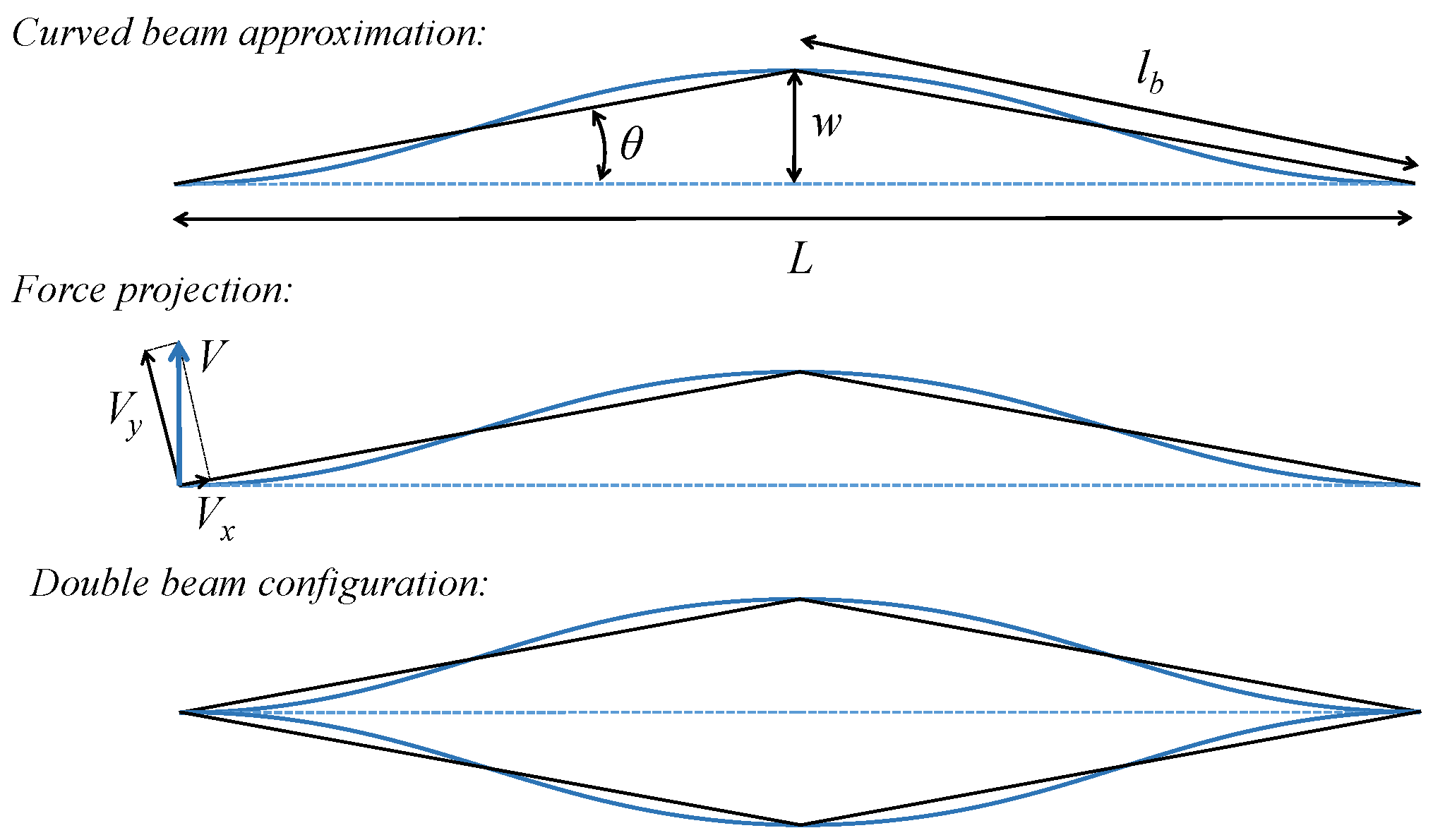
2.1. Negative Stiffness from Buckled Euler Beams

The different components are drawn in Figure 1. The first element considered is the beam with initial imperfection $w=Q_0$, length L, depth b, and thickness h. As for the case of a straight beam, the beam will not deform until the applied load reaches the critical buckling load $P_e$, but in case of initial imperfection, a corrected expression can be found between the end shortening $\delta$ and the axial force P, as derived in [34]. Assuming $w<0.2L$, the force displacement relation is given by (1)

$$P=P_e\left(1-\frac{\pi Q_0}{L}{\left({\left(\frac{\pi Q_0}{L}\right)}^2+4\left(\frac{\delta }{L}\right)\right)}^{-1/2}\right)\left(1+\frac{1}{8}{\left(\frac{\pi Q_0}{L}\right)}^2+\frac{1}{2}\left(\frac{\delta }{L}\right)\right)$$

(1)

with $P_e=nEI{(\pi /L)}^2$ the Euler critical load of the beam with $n=4$ in case it has both ends clamped, $EI$ is the bending stiffness, L is initial the length of the beam.

The axial force P is plotted in Figure 2 as a function of the axial displacement $\delta$. Both quantities are normalized. It is also plotted for different values of initial imperfection, ranging from $Q_0=0$ (straight beam) to $Q_0=0.2L$ (initially curved beam). For the straight beam, the applied displacement results in a linearly growing force while specifying an initial imperfection leads to (i) a sudden decrease in force for very low values of displacement and (ii) a quasi-linear increase in force for large displacement values, which is gradually decreasing when increasing the imperfection. This observation confirms the softening of the system as it experiences an axial force.

Geometric parameters and mechanical properties of curved beam are indicated in

Table 1. Geometrical parameters and mechanical properties of curved beams.

Dimensions (m)	Young’s Modulus (GPa)	Density (kg/m${}^3$)
$L=0.14$, $Q_0$ = 0.004	2.5	1008
$b=0.06$, h = 0.004

.

Two pairs of curved beams are then connected on both sides of the center mass, as illustrated in Figure 1, and an initial axial displacement $\delta$ is applied in the opposite direction. Increasing the initial displacement causes the beams to buckle and provides a vertical restoring force F. Assuming $\delta <0.1L$ as recommended by [34], and assuming the two pairs of curved beams and mass are aligned, the vertical reaction force F is formulated as

$$F\left(x\right)=-4P_e\left(1-s{a}_1^{-1/2}\right)a_2\frac{x}{\gamma }$$

(2)

with $s=\pi Q_0/L$, $\gamma =\sqrt{{(L-\delta )}^2+x^2}$, $a_1=s^2+4-4\gamma /L$, and $a_2=3/2+s^2/8-\gamma /2L$.

Differentiating (2) versus the displacement gives the effective stiffness provided by the element as

$$k\left(x\right)=-2s{a}_3{a}_2{a}_1^{-3/2}-\frac{a_3}{2}\left(1-s{a}_1^{-1/2}\right)+a_2\left(1-s{a}_1^{-1/2}\right)\left(\frac{{\gamma }^2-x^2}{{\gamma }^3}\right)$$

(3)

with $a_3=x^2/\left(L{\gamma }^2\right)$. The resulting expression of effective stiffness (3) exhibits the unconventional nature of the resulting force with respect to initial axial displacement $\delta$. This aspect is closely reported in [6,12].

The behavior of (2) is illustrated in Figure 3. It shows the vertical force F as a function of the vertical displacement x. A maximum value $x_m=0.3L$ is chosen for the following analysis. Both quantities are normalized and plotted in two ways. First is a fixed value of horizontal displacement $\delta =0.1L$ with different values of initial imperfection, ranging from $Q_0=[0:0.2]L$. The second a is fixed value of imperfection $Q_0=0.2L$ with increasing values of horizontal displacement $\delta$. For the curved beam with initial displacement $\delta$, increasing the initial imperfection tends to slowly reduce the negative stiffness to a quasi-zero stiffness, although this is not fully reached due to the limit of the analytical description. However, setting the imperfection to its maximum value (admissible by the model) and increasing the horizontal displacement produces a sudden change in the resulting force. This observation confirms the softening of the system as it experiences an axial force.

2.2. Qualitative Analysis

From these observations, a negative stiffness system does not offer a stable operating regime. This is why a positive stiffness is introduced, which will have the role of sufficiently compensating this negative stiffness to ensure the stable operation of the system. The overall stiffness will then be quasi-zero but positive. The combination of these two stiffnesses of opposite signs gives the resonator great flexibility over the frequency range to be isolated, especially the low frequencies.

As a preliminary qualitative analysis, a static perception may lead to the two following considerations. First, the mass is suspended by four identical folded beams providing the positive stiffness that is considered as four springs having individual stiffness $k_s$. The equivalent positive stiffness $k_p$ is evaluated from the dynamic balance as $k_p=4k_s$. The bending stiffness of the folded beam is approximated by the equivalent stiffness of the cantilever beam as $k_s=3E_s{I}_s/L_s^3$. This is later validated in Section 3.1. Second, since the supported–supported (S–S) and clamped–clamped (C–C) beam with load at midspan has an equivalent bending stiffness of $k_b=48EI/L^3$, respectively, $k_b=129EI/L^3$, the S–S or C–C beam with spring $k_p$ at midspan has an equivalent stiffness of $k_{eq}=k_b+k_p$. This qualitative analysis is used in the next sections to weight parameters and evaluate dynamic features.

2.3. Spring–Mass System Modeling

This section introduces a simple and efficient spring–mass model available in the literature [35]. It describes the structure using an analytical model derived from the dynamic balance of a spring–mass system. The full developments are not rewritten for the sake of brevity; only the key parameters are presented using notations consistent with those of the present paper. The positive stiffness component has a stiffness $k_p$, and the two pairs of beams generating the negative stiffness have a stiffness $k_n$ defined as

$$k_n=\frac{2{\pi }^{4}EI}{L^3}\left(1-\frac{\delta }{{\delta }_{cr1}}\right)$$

(4)

where $\delta$ is the horizontal displacement, and ${\delta }_{cr1}=4{\pi }^{2}I/SL$ is the critical horizontal displacement leading to the first mode buckling. The overall stiffness of the assembly is defined as $k=k_p+k_n$. The transmissibility $T\left(\omega \right)$ is obtained by deriving the displacement–force equations and calculating the ratio of input velocity to output velocity of the center mass.

$$T\left(\omega \right)=\frac{K/m}{-{\omega }^2+K/m}$$

(5)

Transmissibility is then a frequency-dependent quantity that will account for the performance of the vibration mitigation. It will be compared to experimental results together with results of the dynamic bending model derived in Section 2.4.

2.4. Bending Behavior of Beam with Mass and Spring at Midspan

The model proposed in this section is based on the bending behavior of a beam of total length $l=2L$, with added mass and spring foundation located at L. Due to the curved nature of the beams, a preliminary investigation is proposed to identify the model to be used.

Let us consider the curved beam as an assembly of two noncollinear beams connected with an angle $\theta =\arctan (2Q_0/L)$, as illustrated in Figure 4, each beam experiencing coupled flexural and longitudinal motions. The longitudinal motion is associated with an axial displacement $v_i$, and axial effort $F_i$, and the bending motion is associated with a transverse displacement $u_i$, section rotation $u_i^{\prime }$, bending moment $M_i$, and shear effort $V_i$, where $i=1,2$ corresponds to the two segments. The continuity conditions at the connecting point are

$$\begin{array}{cc}\hfill v_1& =v_2\cos \left(\theta \right)-u_2\sin \left(\theta \right)\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill F_1& =F_2\cos \left(\theta \right)-V_2\sin \left(\theta \right)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill u_1& =u_2\cos \left(\theta \right)+v_2\sin \left(\theta \right)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill u_1^{\prime }& =u_2^{\prime }\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill M_1& =M_2\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill V_1& =F_2\sin \left(\theta \right)+V_2\cos \left(\theta \right)\hfill \end{array}$$

(11)

The solution for the bending motion of the i-th segment is

$$u_i(x,\omega )=C_{1,i}\sin \left(kx\right)+C_{2,i}\cos \left(kx\right)+C_{3,i}\sinh \left(kx\right)+C_{4,i}\cosh \left(kx\right)$$

(12)

with k is the bending wavenumber $k^4={\omega }^2\rho S/EI$, and the one for the longitudinal motion is

$$v_i(x,\omega )=C_{5,i}\sin \left(\lambda x\right)+C_{6,i}\cos \left(\lambda x\right)$$

(13)

with $\lambda$ is the compression wavenumber ${\lambda }^2={\omega }^2\rho /E$.

In order to verify the consistency of this modeling, we consider a straight beam two-times thicker than the curved beam, a pair of curved beams, and a pair of noncollinear beams, together with clamped-free boundary conditions. Stating $v=u=u^{\prime }=0,$ at $x=0$ and $v^{\prime }=u^{″}=u^{‴}=0$ at $x=L$ provides an analytical benchmark case. In such conditions, the first cantilever mode of the straight beam is 455 Hz, the one associated with the pair of curved beams is calculated using a finite element model and yields 450 Hz. The first mode of the pair of noncollinear straight beams is calculated by solving the transcendental equation that is obtained by equating to zero the determinant of the $6\times 6$ matrix system formed by the six continuity equations. This leads to 453 Hz and is confirmed by the finite element model. This modeling is correct for small values of $\theta$; otherwise, the length of each noncollinear beam is $l_b=L(2-cos\left(\theta \right))/2$.

From this macroscopic analysis, the equivalent beam associated to a pair of curved beam is two-times thicker than a single curved beam and can be described by the Euler–Bernoulli beam equation:

$$EI\frac{{\partial }^{4}u}{\partial x^4}=\rho S{\omega }^{2}u$$

(14)

from which the solution for the transverse displacement is

$$u(x,\omega )=C_1\sin \left(kx\right)+C_2\cos \left(kx\right)+C_3\sinh \left(kx\right)+C_4\cosh \left(kx\right)$$

(15)

with k as the bending wavenumber $k^4={\omega }^2\rho S/EI$. In the following, the added mass is denoted m, and the stiffness of the vertical spring associated with positive stiffness is denoted $k_p$. Thanks to the symmetry, one half of the beam is considered through a set of four boundary conditions, two at the extremity (supported or clamped), and two at the mid-length, accounting for mass and spring. Specifically, it is assumed that the mass can only move vertically and that the motion of curved beams is symmetric on both sides of it. This point does not experience rotation and is subjected to (i) the difference in shear forces on both sides of the mass, which is related to the mass and its acceleration as $2EI{u}^{‴}=-m{\omega }^{2}u$, and (ii) the restoring force from the spring as $2EI{u}^{‴}=-k_{p}u$. A dimensionless parameter $\gamma =k_p/m{\omega }^2$ is introduced to describe the relative importance of the elastic effect compared to inertia.

In case the beam is simply supported at both ends, the solution form simplifies as ${\varphi }_{\omega }\left(x\right)=C_1\sin \left(kx\right)+C_3\sinh \left(kx\right)$, and the equation of motion together with the zero-slope condition give the following system:

$$\left\{\begin{array}{c}2EI{k}^3[-C_1\cos \left(k^{*}\right)+C_3\cosh \left(k^{*}\right)]\hfill \\ =-(m{\omega }^2+k_p)[C_1\sin \left(k^{*}\right)+C_3\sinh \left(k^{*}\right)],\hfill \\ k[C_1\cos \left(k^{*}\right)+C_3\cosh \left(k^{*}\right)]=0\hfill \end{array}\right.$$

(16)

Solving these equations gives the frequency equation, and rearranging with respect to mass ratio $m_b/m$, it follows that

$$\frac{m_b}{m}=\frac{k^{*}}{2}(\tan k^{*}-\tanh k^{*})(1+\gamma )$$

(17)

with $m_b$ as the weight of the beam, $k^{*}$ as the dimensionless wavenumber defined as $kl/2$.

The first solutions are illustrated in Figure 5. Expression (17) contains the frequency equation of a beam with support-slide boundary conditions, as well as a corrective term related to the added mass and supporting spring. It shows the rapid decrease in the first root as the added mass increases. As expected, it also shows the shifting of the first root to higher values as the elastic contribution prevails over the mass effects.

In case the beam is clamped at one end, the solution form simplifies as $u(x,\omega )=C_1(\sin \left(kx\right)-\sinh \left(kx\right))+C_2(\cos \left(kx\right)-\cosh \left(kx\right))$, and the equation of motion together with the zero-slope condition give the following system:

$$\left\{\begin{array}{c}2EI{k}^3[C_1(-\cos \left(k^{*}\right)-\cosh \left(k^{*}\right))+C_2(\sin \left(k^{*}\right)-\sinh \left(k^{*}\right))]\hfill \\ =-(m{\omega }^2+k_p)[C_1(\sin \left(k^{*}\right)-\sinh \left(k^{*}\right))+C_2(\cos \left(k^{*}\right)-\cos \left(k^{*}\right))],\hfill \\ k[C_1(\cos \left(k^{*}\right)+\cosh \left(k^{*}\right))+C_2(-\sin \left(k^{*}\right)-\sinh \left(k^{*}\right))]=0\hfill \end{array}\right.$$

(18)

Solving these equations gives the frequency equation, and rearranging with respect to the mass ratio $m_b/m$, it follows that

$$\frac{m_b}{m}=k^{*}\left(\frac{1-\cosh k^{*}\cos k^{*}}{\sin k^{*}\cosh k^{*}+\sinh k^{*}\cos k^{*}}\right)(1+\gamma )$$

(19)

The first solutions are illustrated in Figure 6. Expression (19) contains the frequency equation of a fixed beam $1-\cosh k^{*}\cos k^{*}=0$, as well as a term related to the added mass and supporting spring.

A comparison of the roots calculated analytically and by a two-dimensional finite element model (by making the frequencies dimensionless with respect to the characteristics of the beam) is presented in

Table 2. First root $kl/2$ of Equation (17) calculated analytically and by finite elements as a function of the ratio $m_b/m$.

	${\mathit{m}}_{\mathit{b}}/\mathit{m}$
	2	1	0.5	0.1
Analytical	1.92	1.72	1.50	1.04
Finite element	1.92	1.72	1.49	1.03

to show the relevance of the formulation. The finite element model, as used in Section 3.3, is a beam element clamped or supported at both ends. Spring foundation and added mass are specified at mid-length. An eigenfrequency study is performed that leads to the characteristic frequencies of the system. Considering the mechanical properties and geometrical parameters, the roots of the characteristic transcendental equation can be obtained.

Let us define $\mu =m/m_b$ as the mass ratio between the middle mass and the mass of the beam, and $\kappa =k_p/k_b$ the stiffness ratio between the linear spring and the equivalent bending stiffness of the beam.

A preliminary parametric study is presented in the following. It allows $\kappa$ and $\mu$ to vary respectively within the range [0; 10]. The resonance frequency of the obtained spring–mass system is represented versus these two parameters in Figure 7. Additionally, the fundamental frequency of the clamped beam with mass and spring foundation at mid-length is evaluated from the analytical expression presented above. This gives a representation to better visualize the design space and the frequency behavior of the full resonator versus the simple case of a spring–mass damper. Figure 7 is shown for $P=0$, that is, no axial loading of the beam. It appears that the isofrequency limit grows with respect to $\mu$ and $\kappa$, as predicted by the theory. Next section extends the study by introducing the axial loading in beams.

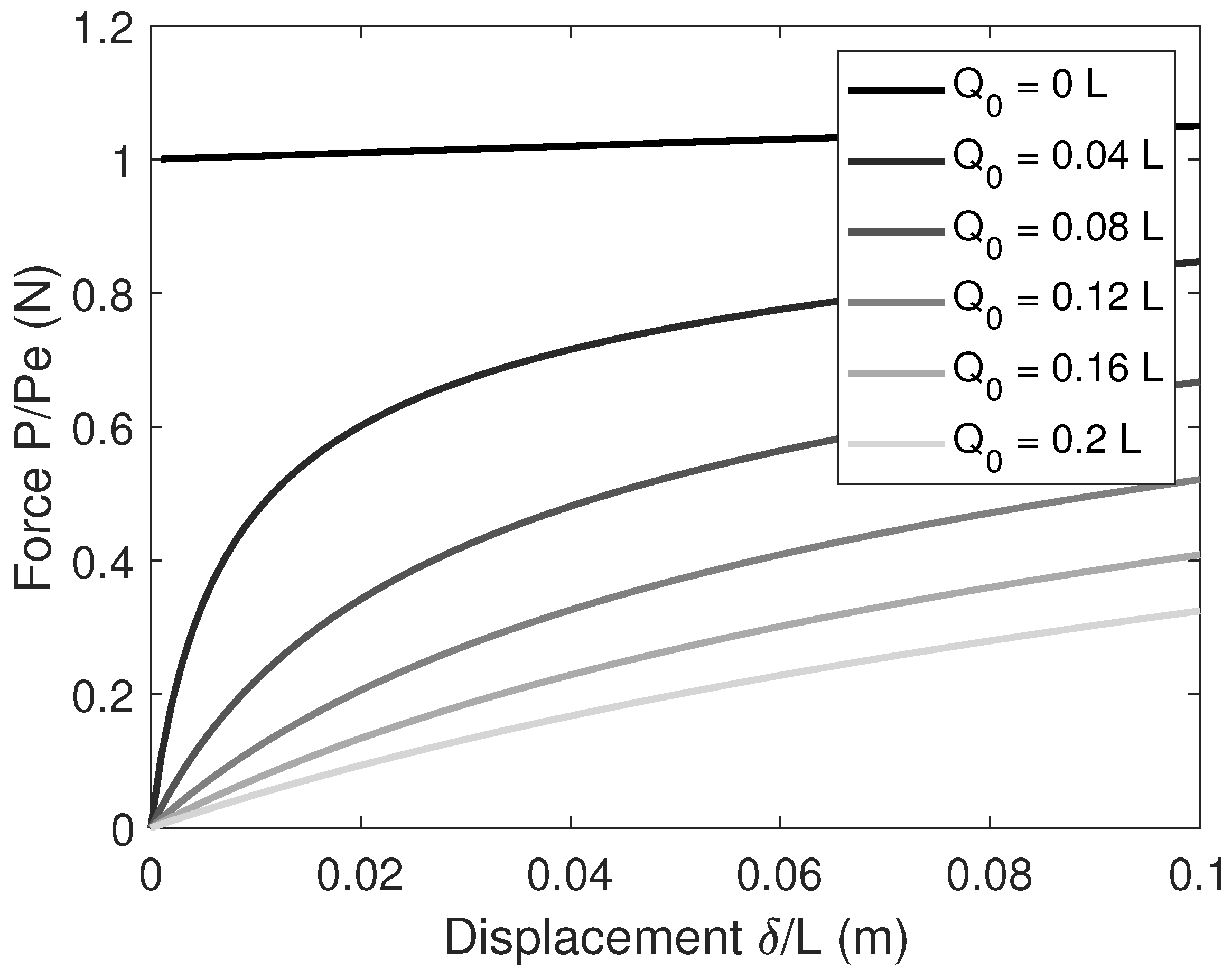
2.5. Introduction of Axial Force in Beams

Initial axial effort is now introduced in the previous model. If it is tensile, it increases the bending stiffness, whereas if it is compressive, it lowers it, leading to buckling instability. Only compression is considered. In the case of axial compression, the force term contributes to the balance of moments, and the Euler beam equation is supplemented by the second order spatial derivative term associated with the force P as

$$EI\frac{{\partial }^{4}u}{\partial x^4}-P\frac{{\partial }^{2}u}{\partial x^2}=\rho S{\omega }^{2}u$$

(20)

for which the solution for the transverse displacement is now

$$u(x,\omega )=C_1\sin \left(k_{1}x\right)+C_2\cos \left(k_{1}x\right)+C_3\sinh \left(k_{2}x\right)+C_4\cosh \left(k_{2}x\right)$$

(21)

with $k_{1,2}$ as the bending wavenumbers

$$k_{1,2}=\pm \frac{1}{\sqrt{2EI}}{\left(-P\pm \sqrt{P^2+4EI\rho S{\omega }^2}\right)}^{1/2}$$

(22)

From this solution form and considering the same boundary conditions as in Section 2.4, the analytical description of the structure is achieved, although equations become lengthy and are not presented here. In addition to the previous case, Figure 7 shows the isofrequency line as the axial load increases, resulting in the lowering of eigenfrequencies. Augmenting the axial load in the beam from 0 to 0.14 $P_{crit}$ shows the frequency shift in the fundamental frequency to the low frequencies. For a given mass ratio, decreasing the stiffness ratio makes it possible to lower the fundamental frequency of the resonator. In this context, this effect is obtained by the axial compression of the beam rather than by decreasing the positive stiffness.

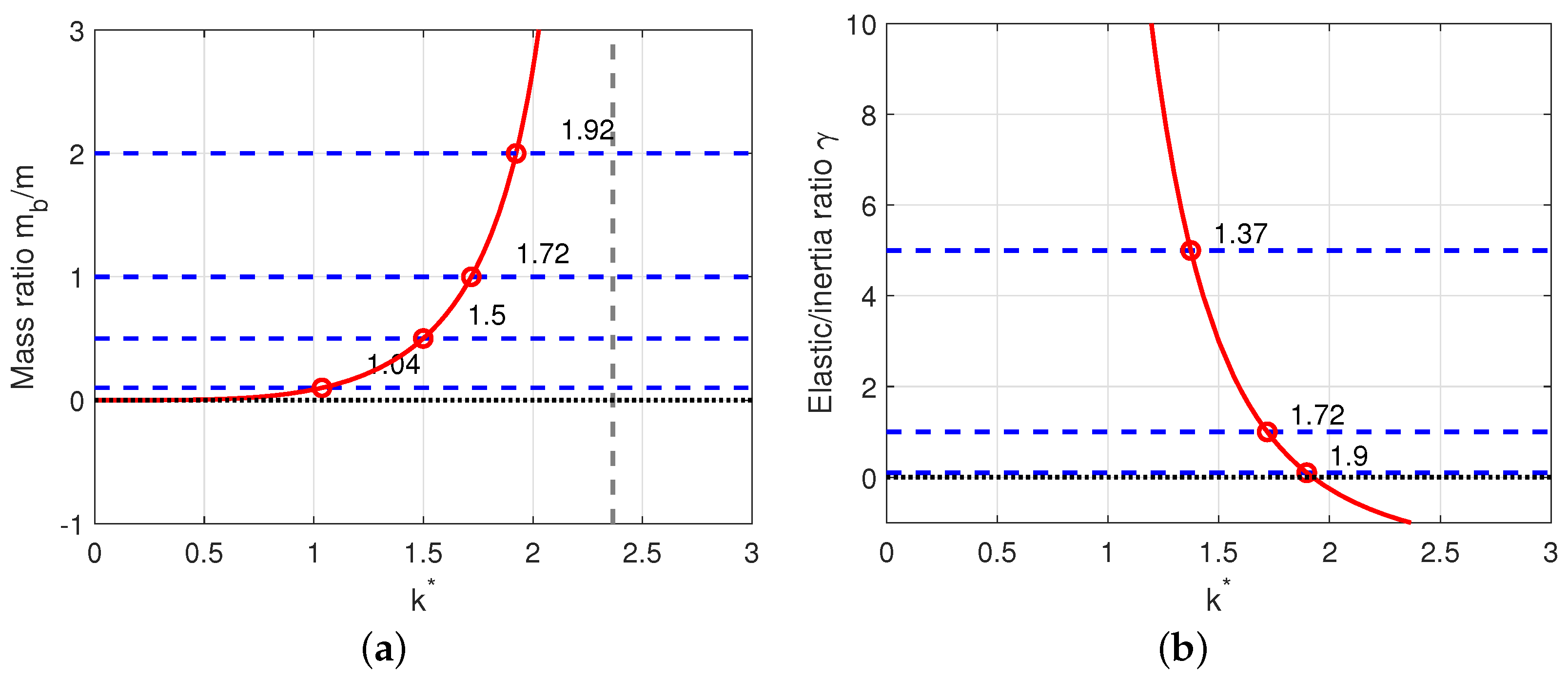
3. Finite Element Modeling of the Positive and Negative Stiffness Components

Numerical simulations were conducted at different scales to emphasize the relevancy of the theoretical approach introduced above. These address the computation of the restoring force with respect to initial deflection in Section 3.2, bending response of the mass supported by springs, in Section 3.3, and eigenfrequency study of the mock-up in Section 3.4.

3.1. Estimation of Positive Stiffness

A preliminary computation is performed to estimate the accuracy of the assumption stated in Section 2.2. First, the mass is suspended by four identical folded beams providing positive stiffness which are considered as four springs having individual stiffness $k_s$. The equivalent stiffness $k_p$ is evaluated from the dynamic balance as $k_p=4k_s$. The bending stiffness of the folded beam is approximated by the equivalent stiffness of the cantilever beam as $k_s=3E_s{I}_s/L_s^3$. Considering $L_s=0.094$, $b_s=0.06$, $h_s=0.004$ mm, the obtained analytical value is $3.17\times {10}^3$ N/m. From the finite element side, representing our full geometry with clamped-free boundary conditions, running a stationary analysis and dividing the input force by resulting transverse displacement leads to an apparent stiffness of $3.17\times {10}^3$ N/m, which is a relative error of less than 2%. Even if the kinematics expected on the structure restrict the side to moving only vertically due to the attachment to the mass, the cantilever assumption is considered satisfactory.

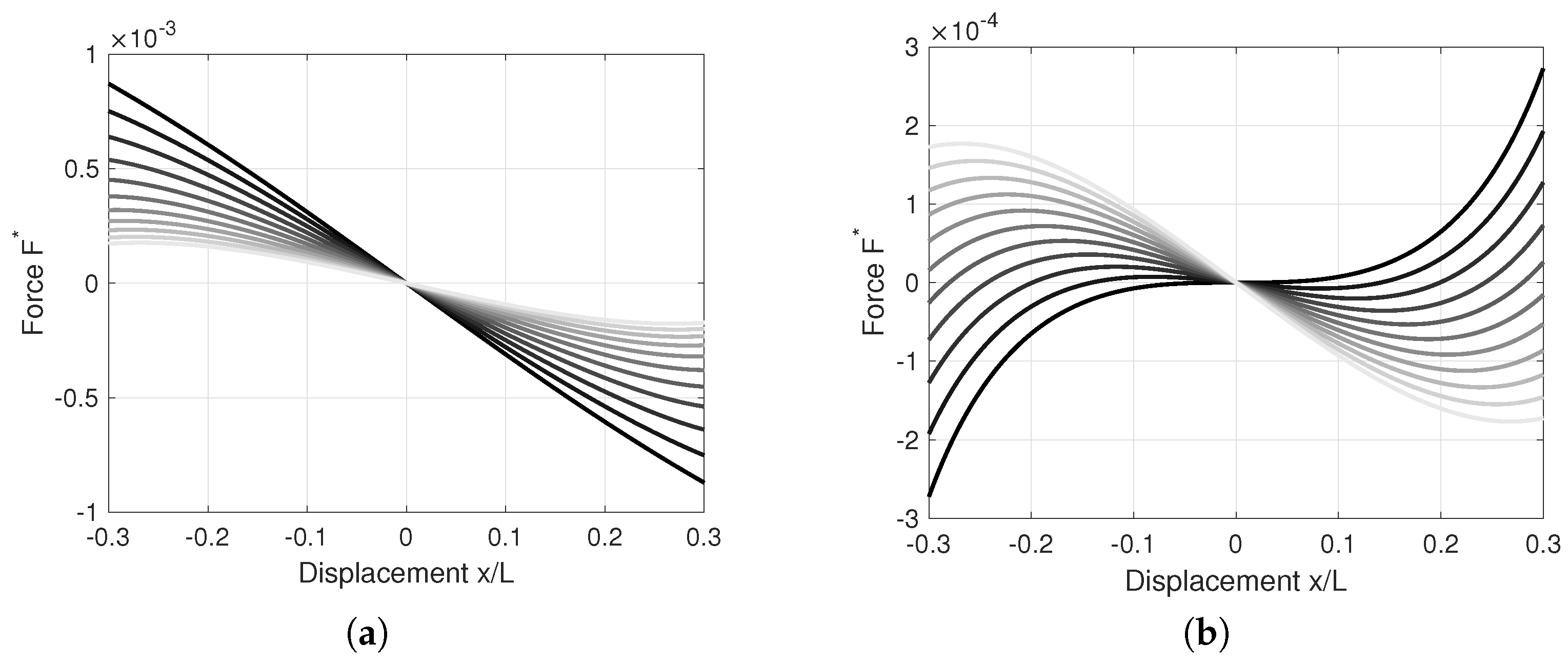
3.2. Force–Displacement Relation

The two pairs of curved beams are modeled to numerically compute the force–displacement relation. The reaction force is plotted in Figure 8 as a function of the imposed vertical displacement. A parametric study is performed to verify the influence of initial axial displacement $\delta$ on the response. Two comments can be formulated. First, for the same values of vertical displacements, the tension restored diminishes as $\delta$ increases, which is consistent with the softening of the assembly. Second is the flattening of the curve and especially the widening of the area where the stiffness is negative and/or quasi zero, which appears as a fundamental feature for the design of the resonator. Since negative stiffness is achieved even for low values of axial displacement, the introduction of the linear vertical spring would be efficient even for small deflection values. The deflection associated with several positions is depicted for illustrative purposes.

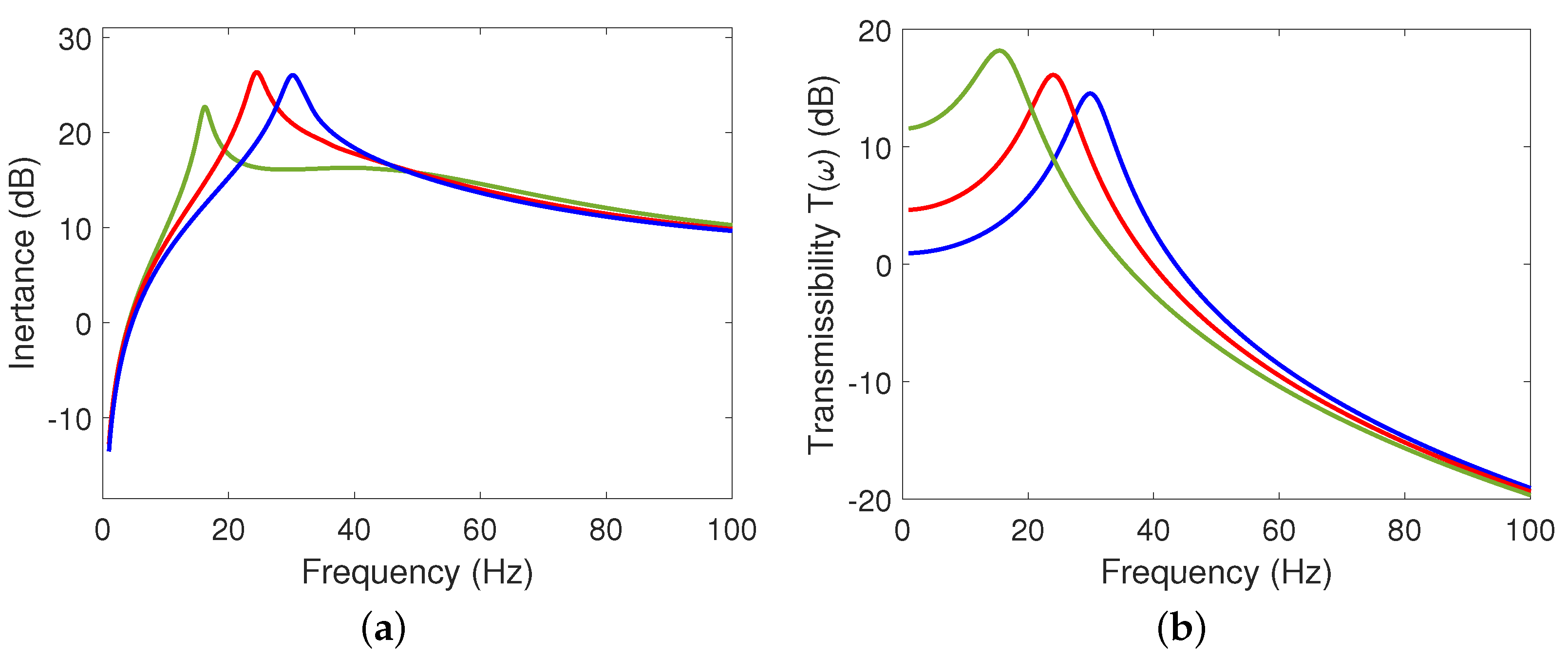
3.3. Frequency Domain Computations

The system in Figure 1 is modeled as a beam element clamped at both ends. Prescribed vertical displacement is applied at clamped ends to account for the excitation. The middle point is supplemented by two boundary conditions: first is the point mass $m=8m_b$, second is the linear spring foundation accounting for positive stiffness $k_p=4k_s$.

The comparison of the structural response of the beam in Figure 9 shows that the analytical model built in Section 2.4 and enriched with axial loading as in Section 2.5 is totally consistent. It is able to handle the introduction of a point mass significantly larger than the mass of the support beam, the effect of the positive spring, as well as the axial loading of the beams. In the following, only the frequency range 0–100 Hz will be of interest.

3.4. Eigenfrequency Study

From the geometrical parameters and mechanical properties indicated above, a preliminary eigenfrequency computation is performed on a three-dimensional finite element model of the assembly. Fixed boundary conditions are specified on the left, right, top, and bottom boundaries of the assembly to mimic clamped conditions with the frame. This results in the modal shapes illustrated in Figure 10. The modes of interest are the ones having in-plane kinematics, and particularly the first one associated with the symmetrical bending of curved beams on each side of the mass, resulting in its vertical motion. For this specific kinematic to occur, it is outlined that the negative stiffness introduced by the curved beam should overcome the positive stiffness produced by the four supports. The second mode presenting the rotation of the mass is not of interest in this contribution, although it is in some applications related to structure stabilization and damping in joints of reticulated structures.

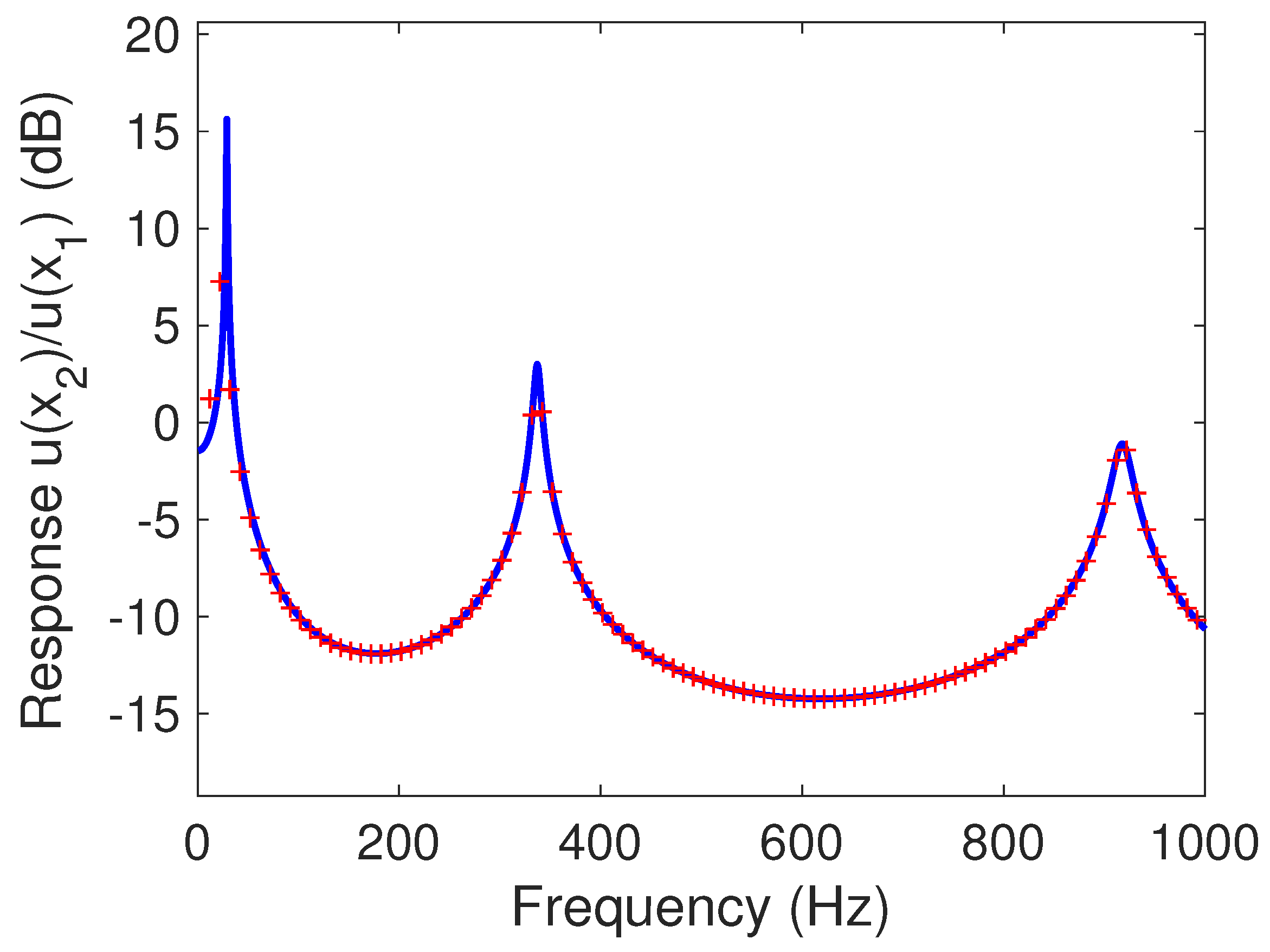
4. Experimental Validation

The objective of this section is to verify the influence of initial force on the response from experimental measurements. A mock-up was designed in accordance with the structure described above. The structural response was obtained by exciting the structure using an impact hammer, and measuring the resulting transverse acceleration. The experimental results are compared with an existing spring–mass model available in the literature presented in Section 2.3 and the dynamic bending model of interest in this paper, derived in Section 2.4 and Section 2.5.

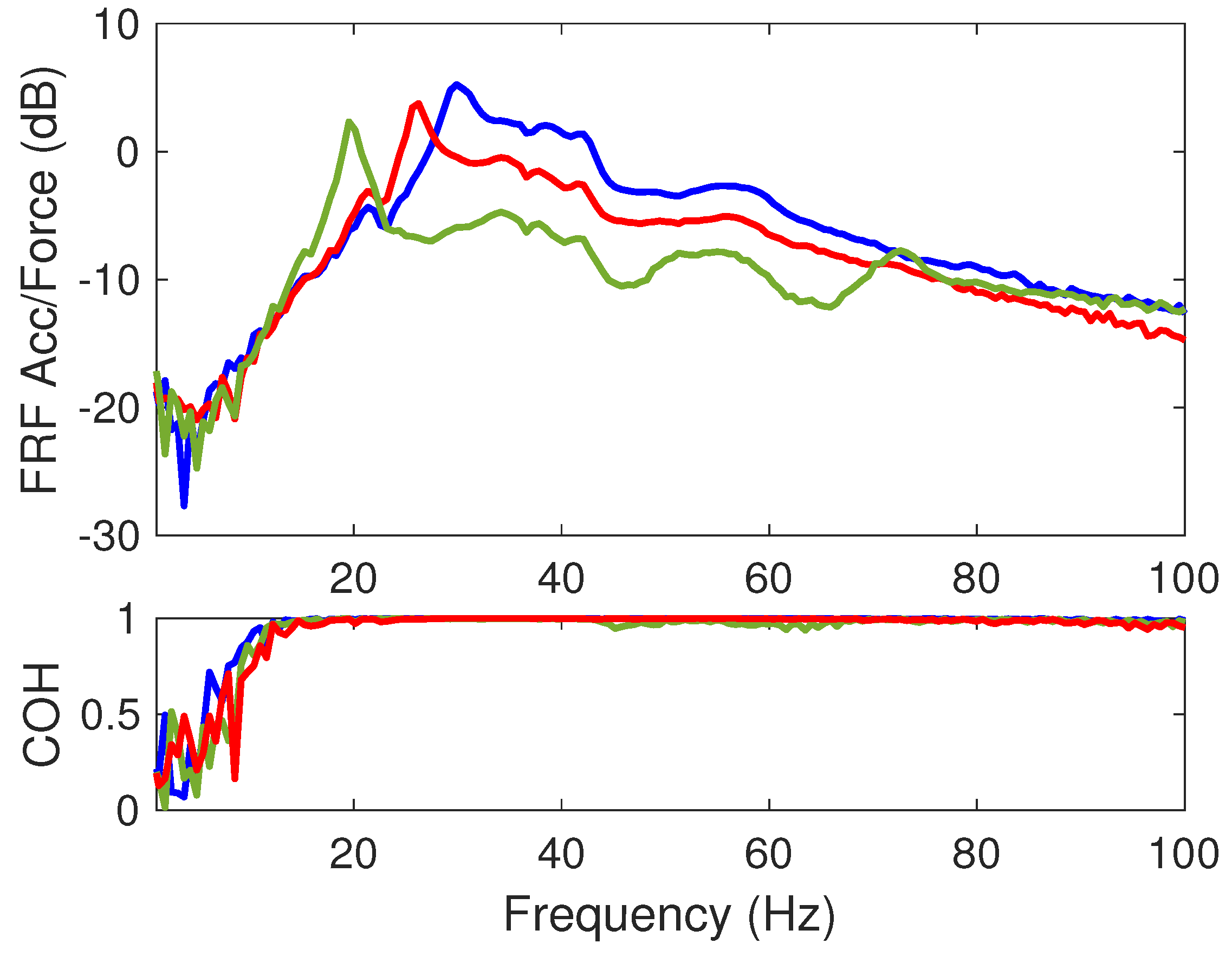
4.1. Measurement Setup

The mock-up of the system is depicted in Figure 11. It consists of an aluminum frame assumed to be rigid, inside which there are three moving parts. The components governing the behavior are (i) the four folded beams that provide positive stiffness in the vertical direction ($k_p=4k_s$ in the analytical model), (ii) two pairs of curved beams that provide negative stiffness, (iii) the center mass attached to these six components. As for the soft components, the four folded beams and the two pairs of curved beams are 3D-printed. Two aluminum sliders are designed to move horizontally to induce axial force in the curved beams. The position of the sliders is adjusted using two screws and determines the initial force experienced by the curved beams. The same displacement is applied to the sliders so as to not introduce any asymmetry into the system. As for the excitation, the impact is applied to the mass, and the calculated transfer function is the mass acceleration versus the input force.

The frame with sliders and center mass are made of structural aluminium, with mass density $\rho =2700$ kg/m${}^3$ and Young’s modulus $E=69$ GPa. After weighing the 3D-printed spring components and modal testing, the mass density of the ABS parts and the Young’s modulus are estimated from the first cantilever mode. Values are reported in Table 1.

4.2. Response of the Resonator

The ratio of acceleration and input force, namely the structural inertance, is shown in Figure 12 for values of initial horizontal displacement $\delta$ increasing from 1.5 to 5 mm. These values are within the validity range of (1) since the maximum value of $\delta$ as 5 mm corresponds to 0.035L. The values of axial forces required by the analytical model were calculated using the theoretical curved beam model (1), supplied with the real values of measured axial displacements.

Experimental responses in Figure 12 are plotted together with the corresponding coherence function to attest to the quality of the measurement. The trend associated with a decrease in frequency as increasing force is applied is confirmed experimentally for values of initial displacement $\delta$ from 1.5 to 5 mm. The analytical results from the dynamic bending model and spring–mass model are also shown in Figure 13 and they predict the same operating frequencies. Good qualitative agreement is obtained between experimental and theoretical responses, mostly in terms of frequency prediction. The structural response shows the frequency shift due to the softening effect as a consequence of increasing initial load, from 30 Hz down to 20 Hz, as well as the marked gradual decrease in amplitudes.

For large values of force, the structural integrity of the 3D-printed curved beams is uncertain and questionable, as they become inelastic and brittle. Other discrepancies may be caused by fabrication tolerances and slight misalignment in the manufacturing of the experimental setup.

5. Conclusions

This paper discusses how a dynamic vibration absorber can achieve lower frequencies by incorporating a negative stiffness component. This paper presents a theoretical analysis, FEM simulations, and experimental measurements. Axial loading is introduced on the springs to evaluate its influence on the negative stiffness effect. The efficiency of the negative stiffness resonator on vibration isolation is evaluated for different conditions of axial force. The novelty of this work is the derivation of a moderately complex beam bending analytical model instead of a spring–mass system. This is relevant because solving the beam problem encompasses more realistic phenomena compared to introducing the equivalent stiffness in the spring–mass equation of motion. The investigation is performed in three steps.

This paper first recalls theoretical formulations describing the relation between restoring force and initial deflection, and shows how the standard linear force–displacement is altered with respect to the geometrical parameters of the spring-like components. This is supplemented by qualitative analysis and design rules based on static bending considerations.

Along with the static aspect, the dynamic aspect is also explored. A theoretical model describing the flexural behavior of a beam supplemented by point mass, positive stiffness, and axial force associated with negative stiffness components is explained. In this way, the key parameters are correlated to the negative stiffness mechanism as well as the overall bending kinematics governing the motion of the resonator. Finite element simulations confirmed static assumptions, and dynamic analysis confirmed the relevancy of the proposed model.

Finally, according to the qualitative analysis suggested and the design procedure presented, a variable passive negative stiffness resonator is manufactured and tested. Although setting the overall stiffness to zero and overcoming the positive stiffness at equilibrium point is challenging due to the uncertainties when manufacturing the frame and junctions between the components, the decrease in frequency as axial force increases is evidenced experimentally. Comparisons with the analytical model demonstrate that the proposed bending model captures the behavior in terms of frequency and amplitude.

Further improvements could focus on a more accurate bending behavior of the two pairs of curved beams, which is the key component responsible for the bending kinematic of the resonator. Qualitative analysis may be pushed forward to determine whether the axial or bending stiffness governs the performance of the structure. This would be related to the nonlinear response of the structure and would require the evaluation of a force–displacement relation in the scope of large displacements.