Fragility Analysis Based on Damaged Bridges during the 2021 Flood in Germany
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
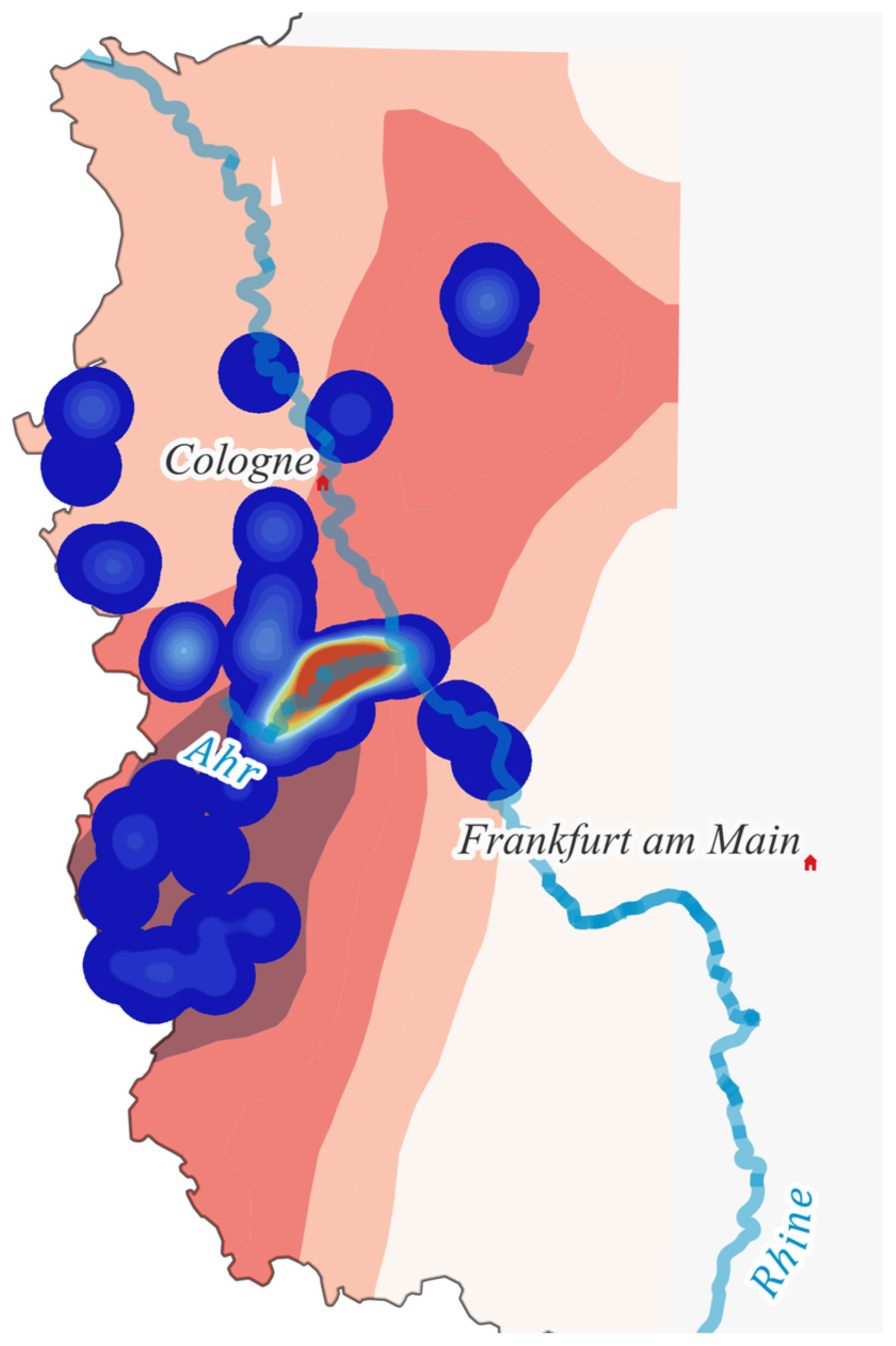
2.1. Bridge Database
2.2. Damage Categories and Bridge Condition Rating
- undamaged—D1;
- slightly damaged—D2;
- moderately damaged—D3;
- extensively damaged—D4.
2.3. Statistics of Population
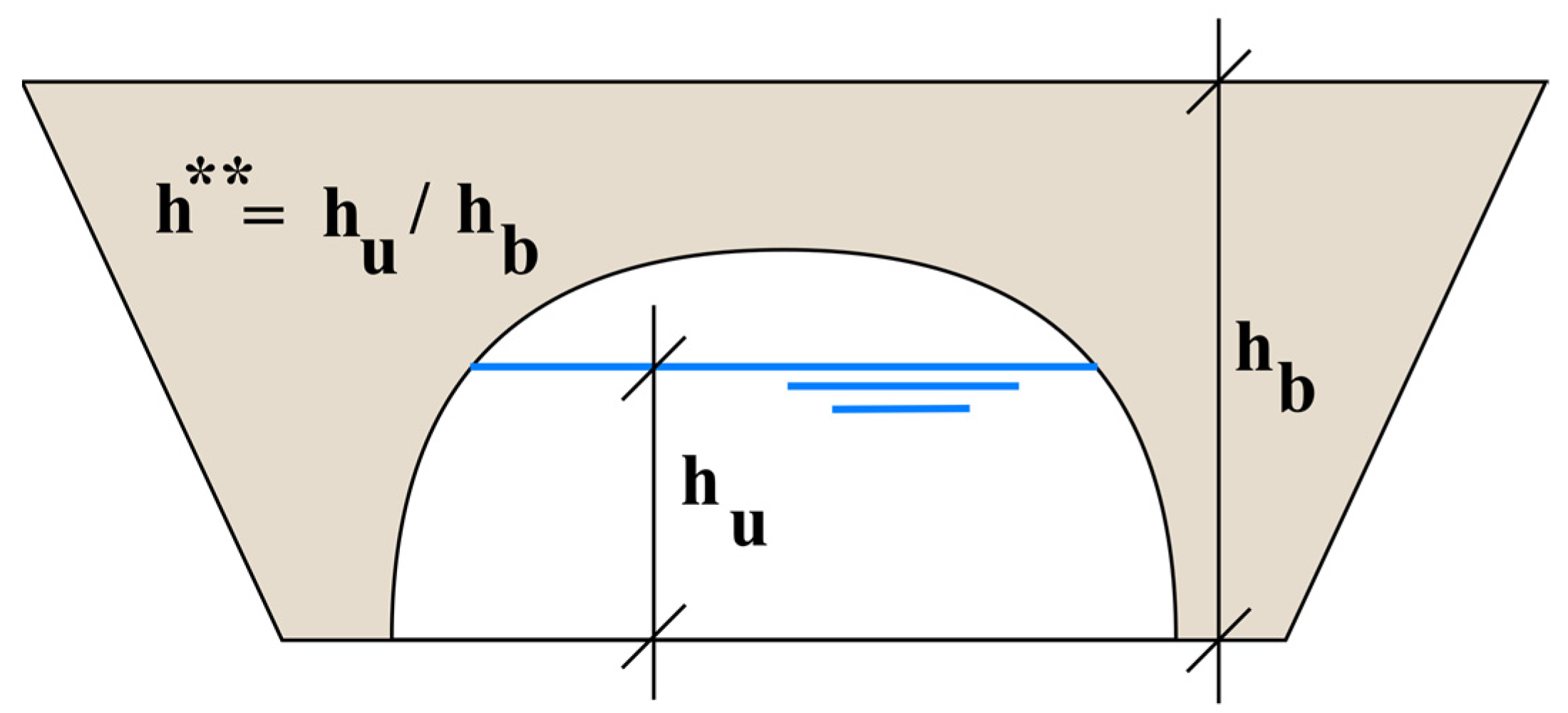
2.4. Fragility Curves Generation
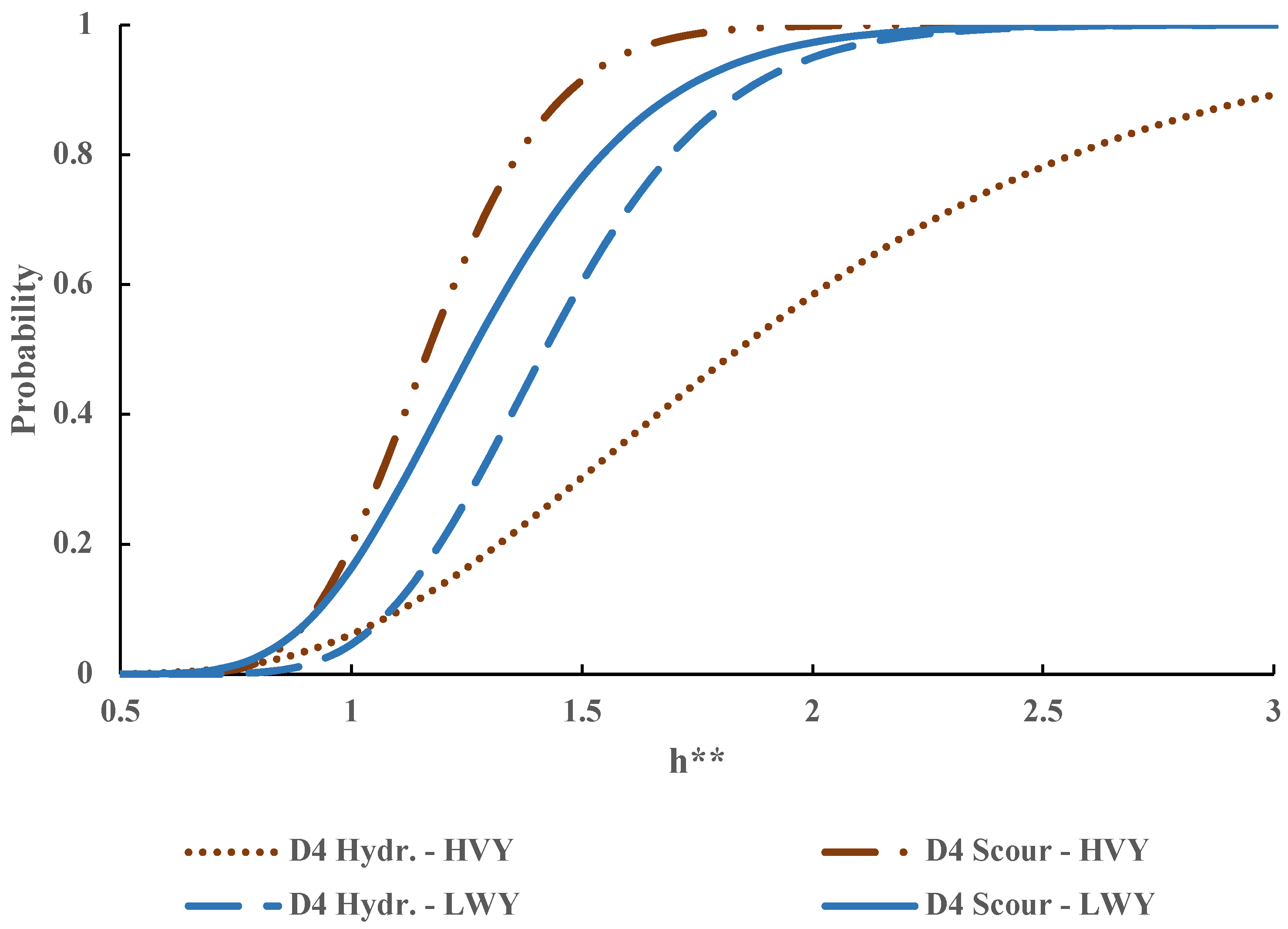
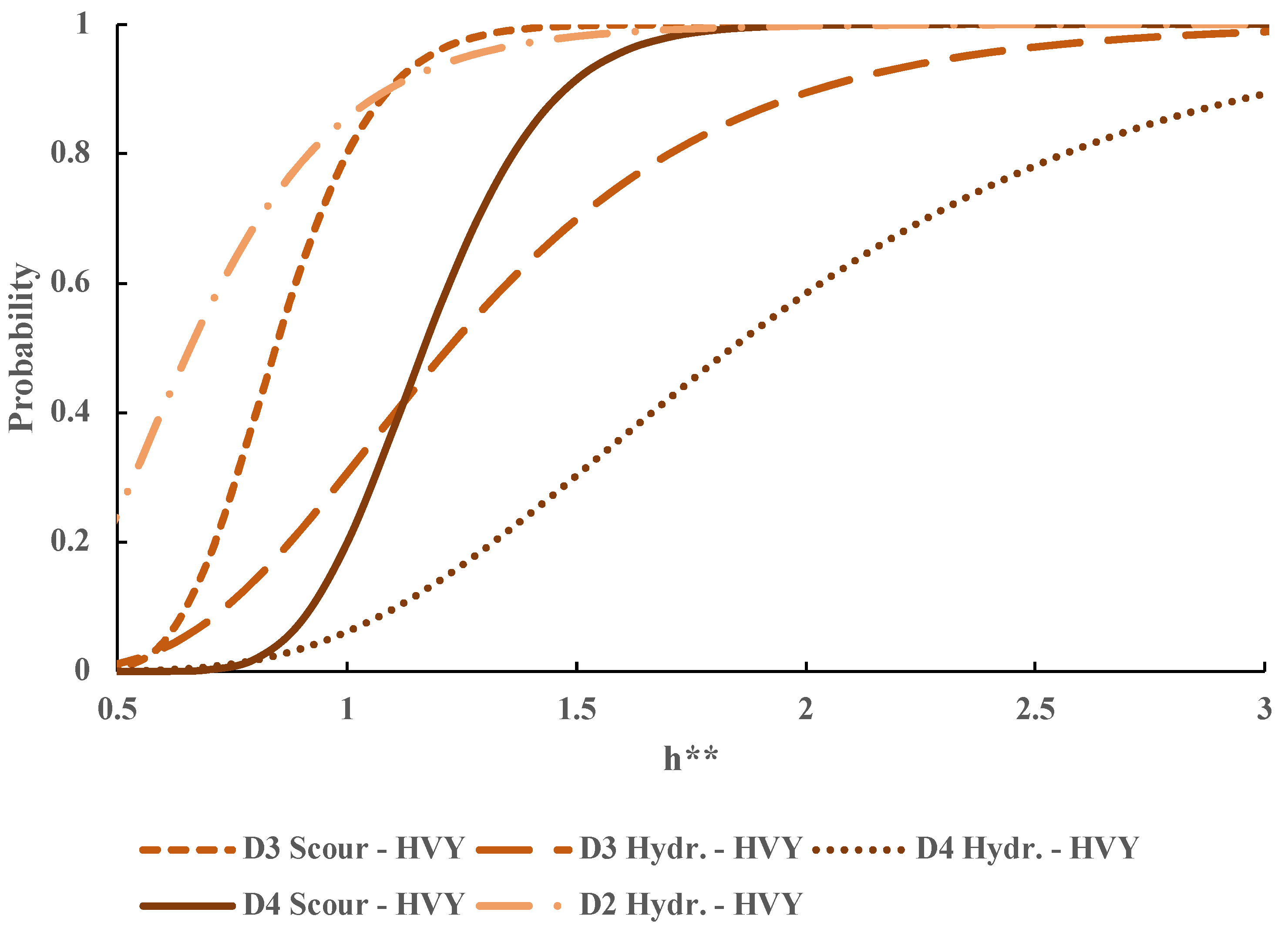
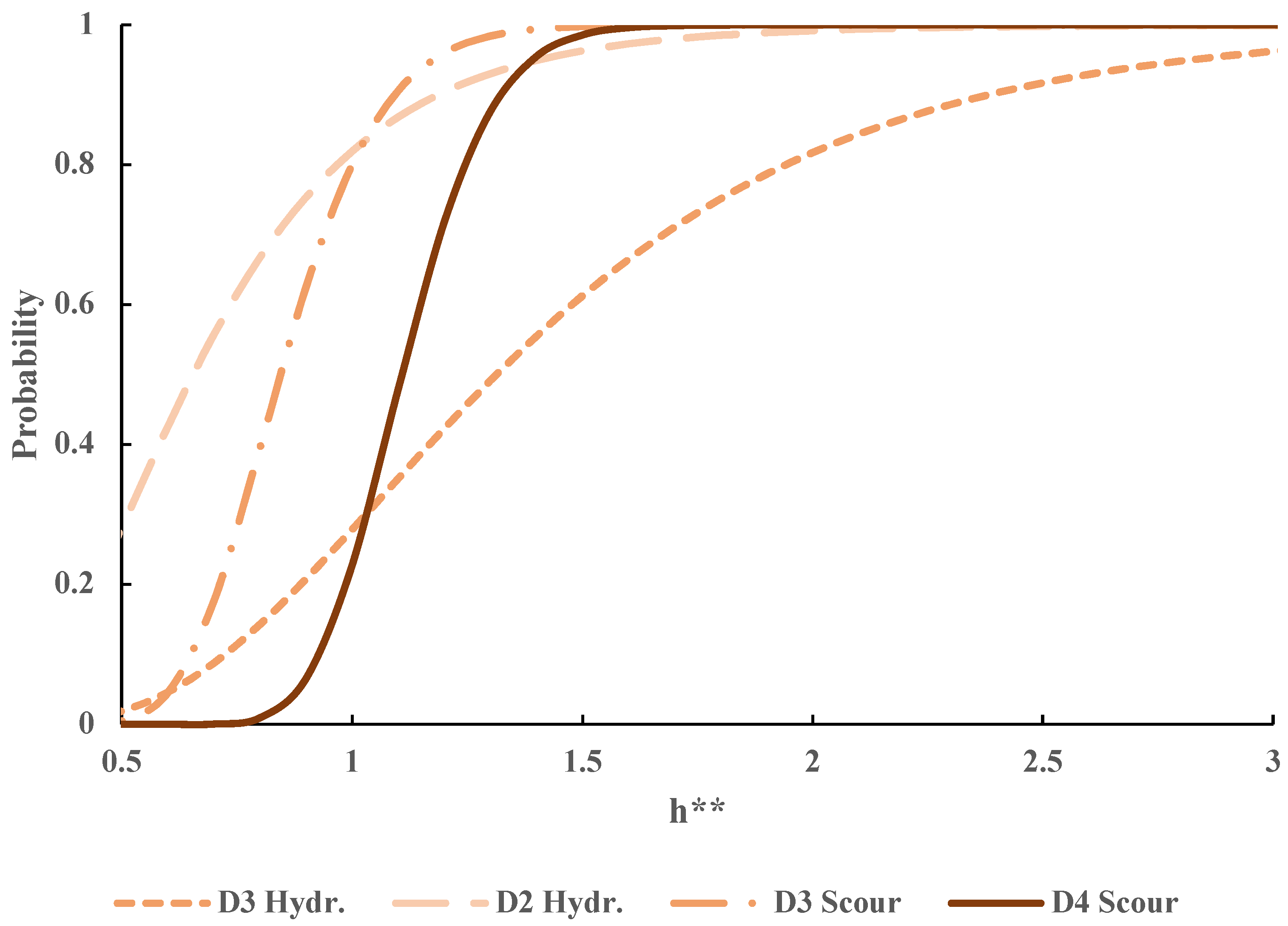
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wardhana, K.; Hadipriono, F.C. Analysis of Recent Bridge Failures in the United States. J. Perform. Constr. Facil. 2003, 17, 144–150. [Google Scholar] [CrossRef]
- Proske, D. Bridge Collapse Frequencies versus Failure Probabilities; Risk Engineering; Springer: Cham, Switzerland, 2018; Volume 8, ISBN 978-3-319-73833-8. [Google Scholar]
- Zhang, G.; Liu, Y.; Liu, J.; Lan, S.; Yang, J. Causes and Statistical Characteristics of Bridge Failures: A Review. J. Traffic Transp. Eng. 2022, 9, 388–406. [Google Scholar] [CrossRef]
- Hodgkins, G.A.; Whitfield, P.H.; Burn, D.H.; Hannaford, J.; Renard, B.; Stahl, K.; Fleig, A.K.; Madsen, H.; Mediero, L.; Korhonen, J.; et al. Climate-Driven Variability in the Occurrence of Major Floods across North America and Europe. J. Hydrol. 2017, 552, 704–717. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing Climate Both Increases and Decreases European River Floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef]
- Merz, B.; Basso, S.; Fischer, S.; Lun, D.; Blöschl, G.; Merz, R.; Guse, B.; Viglione, A.; Vorogushyn, S.; Macdonald, E.; et al. Understanding Heavy Tails of Flood Peak Distributions. Water Resour. Res. 2022, 58, e2021WR030506. [Google Scholar] [CrossRef]
- Miao, Q. Are We Adapting to Floods? Evidence from Global Flooding Fatalities. Risk Anal. 2019, 39, 1298–1313. [Google Scholar] [CrossRef]
- Merz, B.; Blöschl, G.; Vorogushyn, S.; Dottori, F.; Aerts, J.C.J.H.; Bates, P.; Bertola, M.; Kemter, M.; Kreibich, H.; Lall, U.; et al. Causes, Impacts and Patterns of Disastrous River Floods. Nat. Rev. Earth Environ. 2021, 2, 592–609. [Google Scholar] [CrossRef]
- Douben, K.-J. Characteristics of River Floods and Flooding: A Global Overview, 1985–2003. Irrig. Drain. 2006, 55, S9–S21. [Google Scholar] [CrossRef]
- Duan, Y.; Xiong, J.; Cheng, W.; Wang, N.; He, W.; He, Y.; Liu, J.; Yang, G.; Wang, J.; Yang, J. Assessment and Spatiotemporal Analysis of Global Flood Vulnerability in 2005–2020. Int. J. Disaster Risk Reduct. 2022, 80, 103201. [Google Scholar] [CrossRef]
- EC; EEA. Economic Losses from Climate-Related Extremes in Europe. Available online: https://www.eea.europa.eu/ims/economic-losses-from-climate-related (accessed on 10 February 2023).
- Wing, O.E.J.; Pinter, N.; Bates, P.D.; Kousky, C. New Insights into US Flood Vulnerability Revealed from Flood Insurance Big Data. Nat. Commun. 2020, 11, 1444. [Google Scholar] [CrossRef]
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Review Article “Assessment of Economic Flood Damage”. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Mitoulis, S.A.; Winter, M.G.; Kaynia, A.M. Fragility of Transport Assets Exposed to Multiple Hazards: State-of-the-Art Review toward Infrastructural Resilience. Reliab. Eng. Syst. Saf. 2019, 191, 106567. [Google Scholar] [CrossRef]
- Sassu, M.; Giresini, L.; Puppio, M.L. Failure Scenarios of Small Bridges in Case of Extreme Rainstorms. Sustain. Resil. Infrastruct. 2017, 2, 108–116. [Google Scholar] [CrossRef]
- Benedict, S.T.; Knight, T.P. Benefits of Compiling and Analyzing Hydraulic-Design Data for Bridges. Transp. Res. Rec. 2021, 2675, 1073–1081. [Google Scholar] [CrossRef]
- Cao, X.-Y. An Iterative PSD-Based Procedure for the Gaussian Stochastic Earthquake Model with Combined Intensity and Frequency Nonstationarities: Its Application into Precast Concrete Structures. Mathematics 2023, 11, 1294. [Google Scholar] [CrossRef]
- Elmer, F.; Seifert, I.; Kreibich, H.; Thieken, A.H. A Delphi Method Expert Survey to Derive Standards for Flood Damage Data Collection. Risk Anal. 2010, 30, 107–124. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.-Y.; Feng, D.-C.; Wu, G.; Xu, J.-G. Probabilistic Seismic Performance Assessment of RC Frames Retrofitted with External SC-PBSPC BRBF Sub-Structures. J. Earthq. Eng. 2022, 26, 5775–5798. [Google Scholar] [CrossRef]
- Xu, J.-G.; Cao, X.-Y.; Wu, G. Seismic Collapse and Reparability Performance of Reinforced Concrete Frames Retrofitted with External PBSPC BRBF Sub-Frame in near-Fault Regions. J. Build. Eng. 2023, 64, 105716. [Google Scholar] [CrossRef]
- Li, S.-Q.; Chen, Y.-S. Vulnerability and Economic Loss Evaluation Model of a Typical Group Structure Considering Empirical Field Inspection Data. Int. J. Disaster Risk Reduct. 2023, 88, 103617. [Google Scholar] [CrossRef]
- Sfahani, M.G.; Guan, H.; Loo, Y.-C. Seismic Reliability and Risk Assessment of Structures Based on Fragility Analysis—A Review. Adv. Struct. Eng. 2015, 18, 1653–1669. [Google Scholar] [CrossRef]
- Guo, X.; Badroddin, M.; Chen, Z. Scour-Dependent Empirical Fragility Modelling of Bridge Structures under Earthquakes. Adv. Struct. Eng. 2019, 22, 1384–1398. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Mitoulis, S.A. Vulnerability of Bridges to Individual and Multiple Hazards- Floods and Earthquakes. Reliab. Eng. Syst. Saf. 2021, 210, 107564. [Google Scholar] [CrossRef]
- Leal, M.; Boavida-Portugal, I.; Fragoso, M.; Ramos, C. How Much Does an Extreme Rainfall Event Cost? Material Damage and Relationships between Insurance, Rainfall, Land Cover and Urban Flooding. Hydrol. Sci. J. 2019, 64, 673–689. [Google Scholar] [CrossRef]
- Webb, B.M.; Cleary, J.C. Drag-Induced Displacement of a Simply Supported Bridge Span during Hurricane Katrina. J. Perform. Constr. Facil. 2019, 33, 04019040. [Google Scholar] [CrossRef]
- Padgett, J.E.; Spiller, A.; Arnold, C. Statistical Analysis of Coastal Bridge Vulnerability Based on Empirical Evidence from Hurricane Katrina. Struct. Infrastruct. Eng. 2012, 8, 595–605. [Google Scholar] [CrossRef]
- Anderson, I.; Rizzo, D.M.; Huston, D.R.; Dewoolkar, M.M. Analysis of Bridge and Stream Conditions of over 300 Vermont Bridges Damaged in Tropical Storm Irene. Struct. Infrastruct. Eng. 2017, 13, 1437–1450. [Google Scholar] [CrossRef]
- Balomenos, G.P.; Kameshwar, S.; Padgett, J.E. Parameterized Fragility Models for Multi-Bridge Classes Subjected to Hurricane Loads. Eng. Struct. 2020, 208, 110213. [Google Scholar] [CrossRef]
- Forouzan, B.; Baragamage, D.S.A.; Shaloudegi, K.; Nakata, N.; Wu, W. Hybrid Simulation of a Structure to Tsunami Loading. Adv. Struct. Eng. 2020, 23, 3–21. [Google Scholar] [CrossRef]
- de Bruijn, J.A.; Daniell, J.E.; Pomonis, A.; Gunasekera, R.; Macabuag, J.; de Ruiter, M.C.; Koopman, S.J.; Bloemendaal, N.; de Moel, H.; Aerts, J.C.J.H. Using Rapid Damage Observations for Bayesian Updating of Hurricane Vulnerability Functions: A Case Study of Hurricane Dorian Using Social Media. Int. J. Disaster Risk Reduct. 2022, 72, 102839. [Google Scholar] [CrossRef]
- Montalvo, C.; Cook, W.; Keeney, T. Retrospective Analysis of Hydraulic Bridge Collapse. J. Perform. Constr. Facil. 2020, 34, 04019111. [Google Scholar] [CrossRef]
- Choudhury, J.R.; Hasnat, A. Bridge Collapses around the World: Causes and Mechanisms. In Proceedings of the IABSE-JSCE Joint Conference on Advances in Bridge Engineering-III, Dhaka, Bangladesh, 21–22 August 2015; Okui, A., Ueda, B., Eds.; University of Asia Pacific: Dhaka, Bangladesh, 2015; pp. 26–34. [Google Scholar]
- Cook, W.; Barr, P.J. Observations and Trends among Collapsed Bridges in New York State. J. Perform. Constr. Facil. 2017, 31, 04017011. [Google Scholar] [CrossRef]
- Tubaldi, E.; White, C.J.; Patelli, E.; Mitoulis, S.A.; de Almeida, G.; Brown, J.; Cranston, M.; Hardman, M.; Koursari, E.; Lamb, R.; et al. Invited Perspectives: Challenges and Future Directions in Improving Bridge Flood Resilience. Nat. Hazards Earth Syst. Sci. 2022, 22, 795–812. [Google Scholar] [CrossRef]
- ATC. Seismic Performance Assessment of Buildings, Volume 1—Methodology, 2nd ed.; P-58; FEMA: Washington, DC, USA, 2018; p. 340.
- George, J.; Menon, A. A Mechanism-Based Assessment Framework for Masonry Arch Bridges under Scour-Induced Support Rotation. Adv. Struct. Eng. 2021, 24, 2637–2651. [Google Scholar] [CrossRef]
- Mondoro, A.; Frangopol, D.M. Risk-Based Cost-Benefit Analysis for the Retrofit of Bridges Exposed to Extreme Hydrologic Events Considering Multiple Failure Modes. Eng. Struct. 2018, 159, 310–319. [Google Scholar] [CrossRef]
- Tanasić, N.; Hajdin, R. Management of Bridges with Shallow Foundations Exposed to Local Scour. Struct. Infrastruct. Eng. 2018, 14, 468–476. [Google Scholar] [CrossRef]
- Yilmaz, T.; Banerjee, S.; Johnson, P.A. Uncertainty in Risk of Highway Bridges Assessed for Integrated Seismic and Flood Hazards. Struct. Infrastruct. Eng. 2018, 14, 1182–1196. [Google Scholar] [CrossRef]
- Maiwald, H.; Schwarz, J.; Abrahamczyk, L.; Kaufmann, C. Das Hochwasser 2021: Ingenieuranalyse Der Bauwerksschäden. Bautechnik 2022, 99, 878–890. [Google Scholar] [CrossRef]
- Apel, H.; Vorogushyn, S.; Merz, B. Brief Communication—Impact Forecasting Could Substantially Improve the Emergency Management of Deadly Floods: Case Study July 2021 Floods in Germany. NHESS 2022, 22, 3005–3014. [Google Scholar] [CrossRef]
- Kreienkamp, F.; Philip, S.Y.; Tradowsky, J.S.; Kew, S.F.; Lorenz, P.; Arrighi, J.; Belleflamme, A.; Bettmann, T.; Caluwaerts, S.; Chan, S.C.; et al. Rapid Attribution of Heavy Rainfall Events Leading to the Severe Flooding in Western Europe during July 2021; World Weather Attribution: Oxford, UK, 2021; p. 54. [Google Scholar]
- Mohr, S.; Ehret, U.; Kunz, M.; Ludwig, P.; Caldas-Alvarez, A.; Daniell, J.E.; Ehmele, F.; Feldmann, H.; Franca, M.J.; Gattke, C.; et al. A Multi-Disciplinary Analysis of the Exceptional Flood Event of July 2021 in Central Europe. Part 1: Event Description and Analysis. Hydrol. Hazards 2022, 23, 525–551. [Google Scholar] [CrossRef]
- Schüttrumpf, H.; Birkmann, J.; Brüll, C.; Burghardt, L.; Johann, G.; Klopries, E.; Lehmkuhl, F.; Schüttrumpf, A.; Wolf, S. Herausforderungen an den Wiederaufbau nach dem Katastrophenhochwasser 2021 in der Eifel; Technische Universität Dresden, Institut für Wasserbau und technische Hydromechanik: Dresden, Germany, 2022; pp. 5–16. [Google Scholar]
- Szymczak, S.; Backendorf, F.; Bott, F.; Fricke, K.; Junghänel, T.; Walawender, E. Impacts of Heavy and Persistent Precipitation on Railroad Infrastructure in July 2021: A Case Study from the Ahr Valley, Rhineland-Palatinate, Germany. Atmosphere 2022, 13, 1118. [Google Scholar] [CrossRef]
- Truedinger, A.J.; Jamshed, A.; Sauter, H.; Birkmann, J. Adaptation after Extreme Flooding Events: Moving or Staying? The Case of the Ahr Valley in Germany. Sustainability 2023, 15, 1407. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Jackson, T. GPM IMERG Final Precipitation L3 1 Day 0.1 Degree × 0.1 Degree V06; NASA: Washington, DC, USA, 2019.
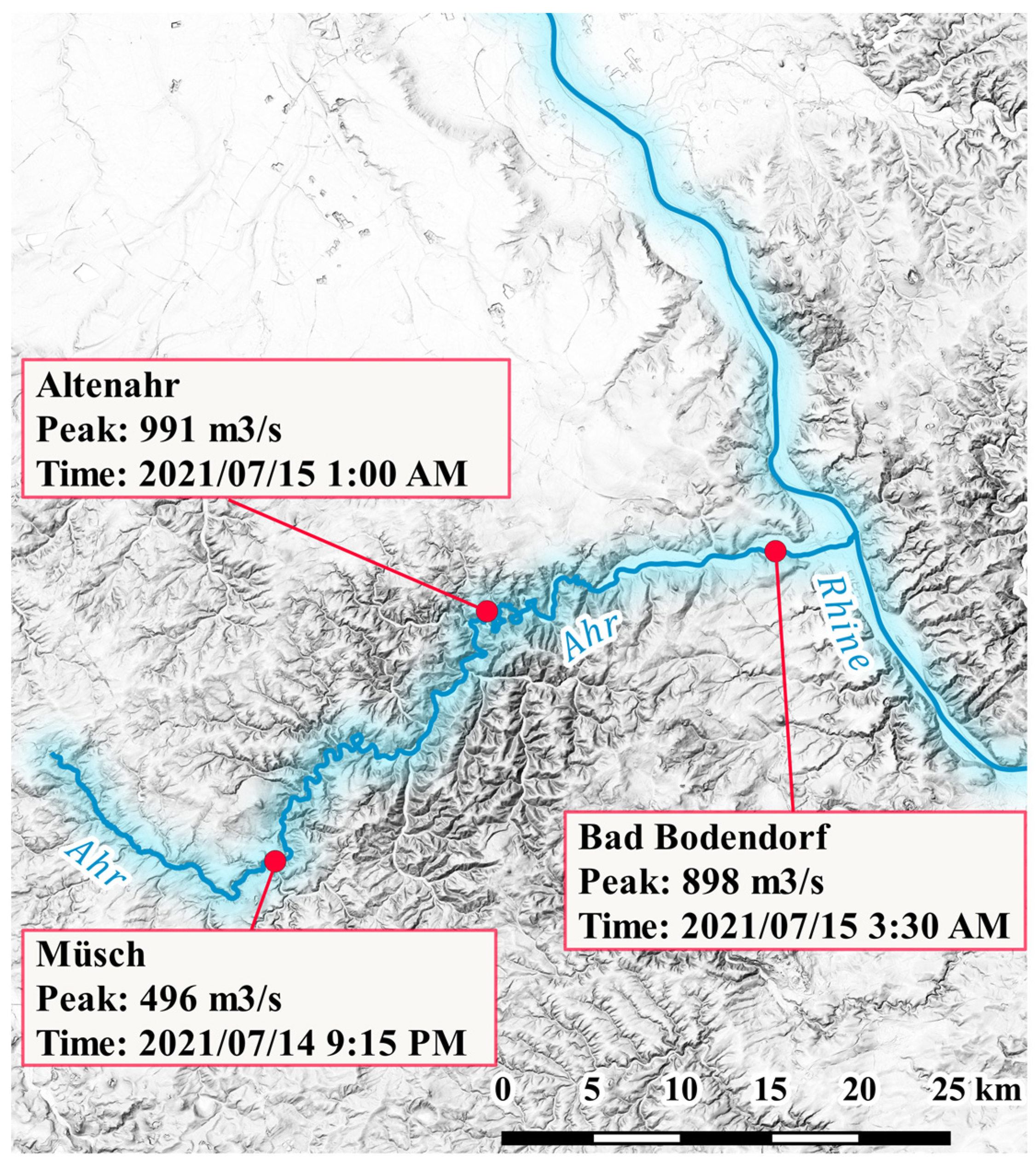
- Roggenkamp, T.; Herget, J. Hochwasser der Ahr im Juli 2021–Abflussabschätzung und Einordnung. Hydrol. Not. 2022, 66, 40–49. [Google Scholar]
- BKG NUTS250. Available online: https://daten.gdz.bkg.bund.de/produkte/vg/nuts250_1231/aktuell/nuts250_12-31.utm32s.shape.zip (accessed on 3 November 2022).
- BfG Waterbody-DE. Available online: https://geoportal.bafg.de/inspire/download/HY/servicefeed.xml (accessed on 3 November 2022).
- Landesamt für Umwelt Rheinland-Pfalz. Hochwassermeldedienst; LfU: Mainz, Germany, 2022.
- Roggenkamp, T.; Herget, J. Reconstructing Peak Discharges of Historic Floods of the River Ahr, Germany. Erdkunde 2014, 68, 49–59. [Google Scholar] [CrossRef]
- Ludwig, P.; Ehmele, F.; Franca, M.J.; Mohr, S.; Caldas-Alvarez, A.; Daniell, J.E.; Ehret, U.; Feldmann, H.; Hundhausen, M.; Knippertz, P.; et al. A Multi-Disciplinary Analysis of the Exceptional Flood Event of July 2021 in Central Europe. Part 2: Historical Context and Relation to Climate Change. Nat. Hazards Earth Syst. Sci. Discuss. 2022, 23, 1287–1311. [Google Scholar] [CrossRef]
- Vorogushyn, S.; Apel, H.; Kemter, M.; Thieken, A. Statistical and Hydraulic Analysis of Flood Hazard in the Ahr Valley, Germany Considering Historical Floods. In Proceedings of the IAHS-AISH Scientific Assembly 2022, Montpellier, France, 29 May–3 June 2022; p. IAHS2022-660. [Google Scholar]
- Seeger, M. Agricultural Soil Degradation in Germany; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–17. [Google Scholar]
- Oudenbroek, K.; Naderi, N.; Bricker, J.D.; Yang, Y.; van der Veen, C.; Uijttewaal, W.; Moriguchi, S.; Jonkman, S.N. Hydrodynamic and Debris-Damming Failure of Bridge Decks and Piers in Steady Flow. Geosciences 2018, 8, 409. [Google Scholar] [CrossRef]
- BKG Digitales Geländemodell Gitterweite 5 M (DGM5). Available online: https://gdz.bkg.bund.de/index.php/default/digitales-gelandemodell-gitterweite-5-m-dgm5.html (accessed on 15 August 2022).
- LVermGeo Digitales Geländemodell Gitterweite 1 M (DGM1). Available online: https://lvermgeo.rlp.de/fileadmin/lvermgeo/pdf/produktblaetter/ProduktbeschreibungRP_DGM.pdf (accessed on 15 August 2022).
- Civera, M.; Calamai, G.; Zanotti Fragonara, L. System Identification via Fast Relaxed Vector Fitting for the Structural Health Monitoring of Masonry Bridges. Structures 2021, 30, 277–293. [Google Scholar] [CrossRef]
- Civera, M.; Mugnaini, V.; Zanotti Fragonara, L. Machine Learning-based Automatic Operational Modal Analysis: A Structural Health Monitoring Application to Masonry Arch Bridges. Struct. Control Health 2022, 29, e3028. [Google Scholar] [CrossRef]
- Giordano, P.F.; Prendergast, L.J.; Limongelli, M.P. Quantifying the Value of SHM Information for Bridges under Flood-Induced Scour. Struct. Infrastruct. Eng. 2023, 19, 1616–1632. [Google Scholar] [CrossRef]
- Arneson, L.A.; Zevenbergen, L.W.; Lagasse, P.F.; Clopper, P.E. Evaluating Scour at Bridges, 5th ed.; HEC-18; Federal Highway Administration: Springfield, VA, USA, 2012; p. 340.
- Schmocker, L.; Hager, W.H. Probability of Drift Blockage at Bridge Decks. J. Hydraul. Eng. 2011, 137, 470–479. [Google Scholar] [CrossRef]
- Gschnitzer, T.; Gems, B.; Mazzorana, B.; Aufleger, M. Towards a Robust Assessment of Bridge Clogging Processes in Flood Risk Management. Geomorphology 2017, 279, 128–140. [Google Scholar] [CrossRef]
- Majtan, E.; Cunningham, L.S.; Rogers, B.D. Experimental and Numerical Investigation of Floating Large Woody Debris Impact on a Masonry Arch Bridge. JMSE 2022, 10, 911. [Google Scholar] [CrossRef]
- Naumann, J.; Holst, R. Bauwerkspruefung Nach DIN 1076-Eine Verantwortungsvolle Aufgabe Fuer Die Sicherheit/Bridge Inspection According to DIN 1076-A Responsible Task for Safety. Straße Autob. 2005, 56, 319–326. [Google Scholar]
- Haardt, P. Algorithmen zur Zustandsbewertung von Ingenieurbauwerken; Bundesanstalt für Straßenwesen: Bergisch Gladbach, Germany, 1999; p. 41.
- Brown, M.B.; Forsythe, A.B. Robust Tests for the Equality of Variances. J. Am. Statist. Assoc. 1974, 69, 364–367. [Google Scholar] [CrossRef]
- Bonferroni, C. Teoria Statistica Delle Classi e Calcolo Delle Probabilità. Pubbl. R Ist. Super. Sci. Econ. Commericiali Firenze 1936, 8, 3–62. [Google Scholar]
- Merz, B.; Apel, H.; Kreibich, H.; Vorogushyn, S. Disastrous Flooding in July 2021 in Germany—Event Analysis and Consequences for Risk Assessment Approaches. In Proceedings of the IAHS-AISH Scientific Assembly 2022, Montpellier, France, 29 May–3 June 2022; p. IAHS2022-183. [Google Scholar]
- Lilliefors, H.W. On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. J. Am. Statist. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Ross, S.M. Peirce’s Criterion for the Elimination of Suspect Experimental Data. J. Eng. Technol. 2003, 20, 38–41. [Google Scholar]
- Falconer, R.; Boughton, B.; Lane, R.; Paterson, F.; Way, W. Strenghtening of Masonry Bridges against Traffic and Flooding. In Proceedings of the Structural Faults and Repair 2010 13th International Congress and Exhibition, Edinburgh, UK, 15–17 June 2010; pp. 1–10. [Google Scholar]
- Majtan, E.; Cunningham, L.S.; Rogers, B.D. Numerical Study on the Structural Response of a Masonry Arch Bridge Subject to Flood Flow and Debris Impact. Structures 2023, 48, 782–797. [Google Scholar] [CrossRef]
- Jempson, M. Flood and Debris Loads on Bridges. Ph.D. Thesis, University of Queensland, St. Lucia, Australia, 2000. [Google Scholar]
- Kerenyi, K.; Sofu, T.; Guo, J. Hydrodynamic Forces on Inundated Bridge Decks; U.S. DOT: McLean, VA, USA, 2009; pp. 1–48.
- Dean, M.T. Laboratory Study of Hydrodynamics of Submerged Bridges. Master’s Thesis, University of Texas at Arlington, Arlington, TX, USA, 2020. [Google Scholar]
- Grates, H. Domhof-Brücke Schuld. Available online: https://www.aw-wiki.de/w/images/1/16/Schuld_-_Heinz_Grates_%28337%29.jpg (accessed on 20 February 2023).
- Pucci, A.; Sousa, H.S.; Giresini, L.; Matos, J.C.; Castelli, F. Fragility of Bridge Decks Exposed to Hydraulic and Driftwood Actions. Struct. Infrastruct. Eng. 2023; accepted for publication. [Google Scholar]
- CEN EN 1991-1-6:2005; Eurocodes. Euopean Committee for Standardization: Brussels, Belgium, 2005; p. 31.
- Committee BD-090 AS 5100.2:2017; Bridge Design Design Loads. Standards Australia: Sydney, Australia, 2017; p. 137.









| Rating | Structural Safety | Traffic Safety | Durability |
|---|---|---|---|
| 1.0–1.4 | Not compromised | Not compromised | Not compromised |
| 1.5–1.9 | Not compromised | Not compromised | Can be compromised in the long-term |
| 2.0–2.4 | Not compromised | Not compromised | Can be compromised in the medium-term |
| 2.5–2.9 | Not compromised | Can be compromised | Can be compromised |
| 3.0–3.4 | Is compromised | Is compromised | Extensively compromised |
| 3.5–4.0 | Extensively compromised | Extensively compromised | Extensively compromised |
| D1 | D2 | D3 | D4 |
|---|---|---|---|
| 1.0–1.9 | 2.0–2.9 | 3.0–3.4 | 3.5–4.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pucci, A.; Eickmeier, D.; Sousa, H.S.; Giresini, L.; Matos, J.C.; Holst, R. Fragility Analysis Based on Damaged Bridges during the 2021 Flood in Germany. Appl. Sci. 2023, 13, 10454. https://doi.org/10.3390/app131810454
Pucci A, Eickmeier D, Sousa HS, Giresini L, Matos JC, Holst R. Fragility Analysis Based on Damaged Bridges during the 2021 Flood in Germany. Applied Sciences. 2023; 13(18):10454. https://doi.org/10.3390/app131810454
Chicago/Turabian StylePucci, Alessandro, Daniel Eickmeier, Hélder S. Sousa, Linda Giresini, José C. Matos, and Ralph Holst. 2023. "Fragility Analysis Based on Damaged Bridges during the 2021 Flood in Germany" Applied Sciences 13, no. 18: 10454. https://doi.org/10.3390/app131810454
APA StylePucci, A., Eickmeier, D., Sousa, H. S., Giresini, L., Matos, J. C., & Holst, R. (2023). Fragility Analysis Based on Damaged Bridges during the 2021 Flood in Germany. Applied Sciences, 13(18), 10454. https://doi.org/10.3390/app131810454










