Probability Distributions of Asphalt Pavement Responses and Performance under Random Moving Loads and Pavement Temperature
Abstract
:1. Introduction
2. Analytical Solutions of Pavement Response under Random Moving Loads and Pavement Temperatures
2.1. Analytical Solutions of Viscoelastic Multilayered System
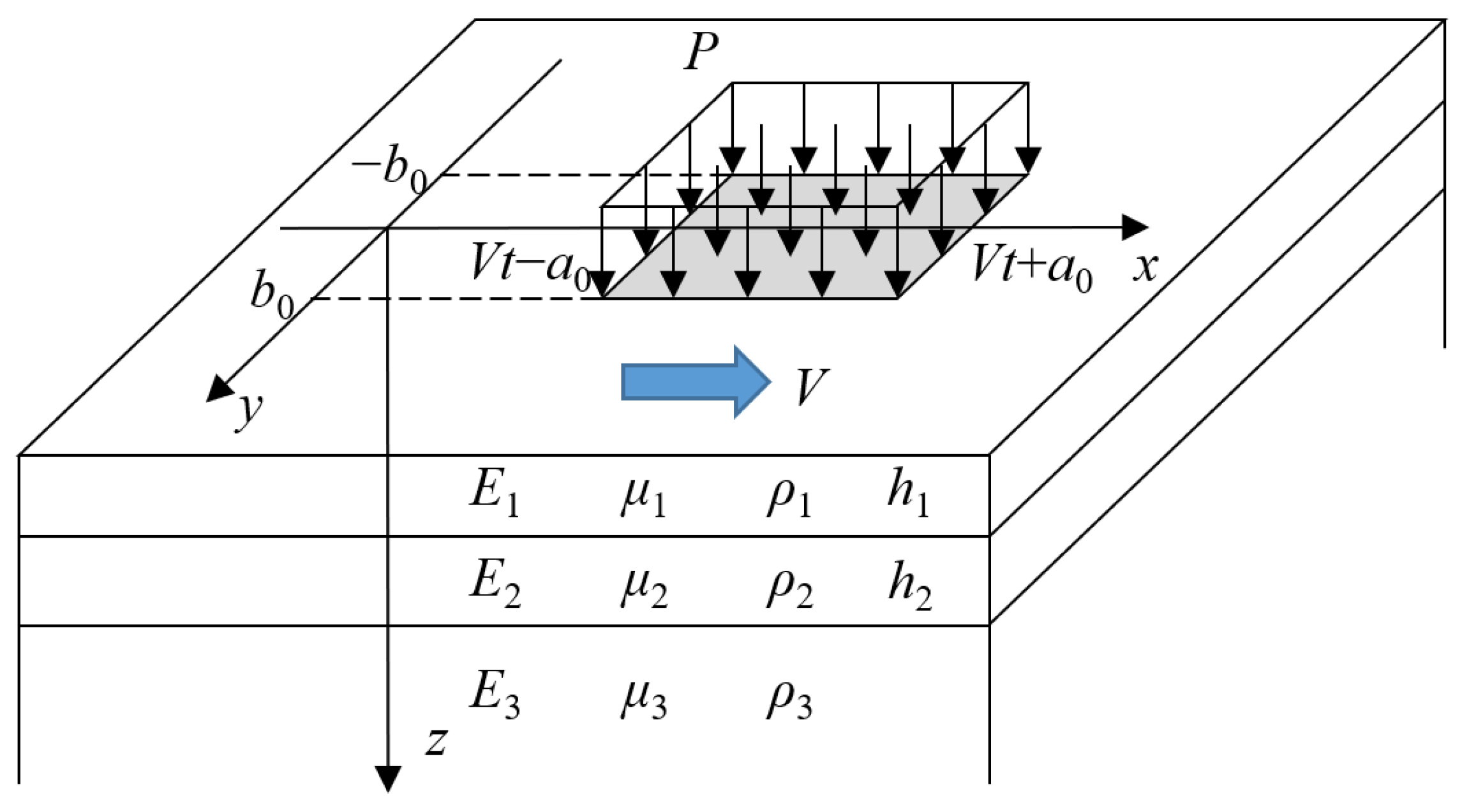
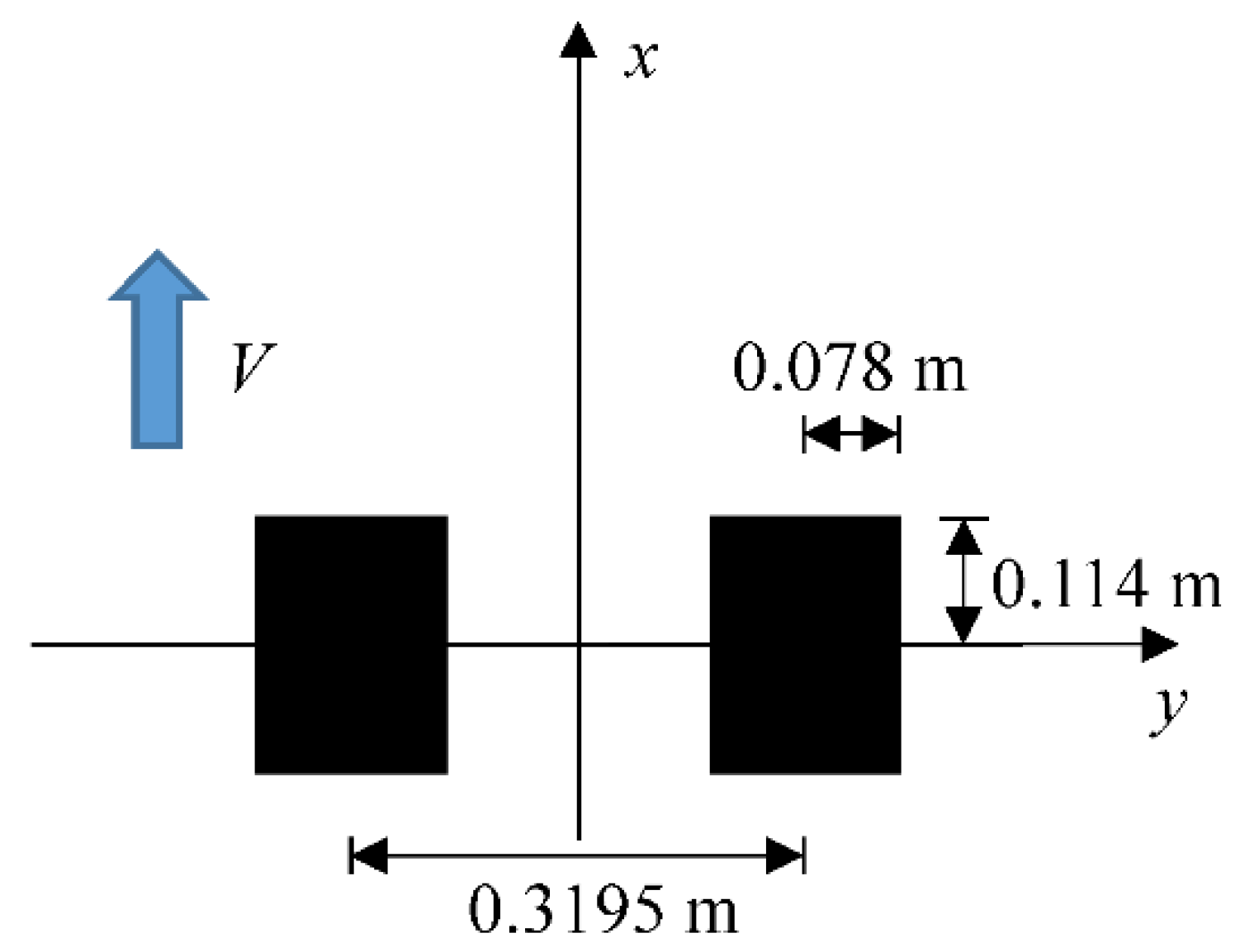
2.2. Definition of Random Moving Loads and Pavement Temperature
3. Probability Modeling of Asphalt Pavement Responses
3.1. Response Surface Methodology
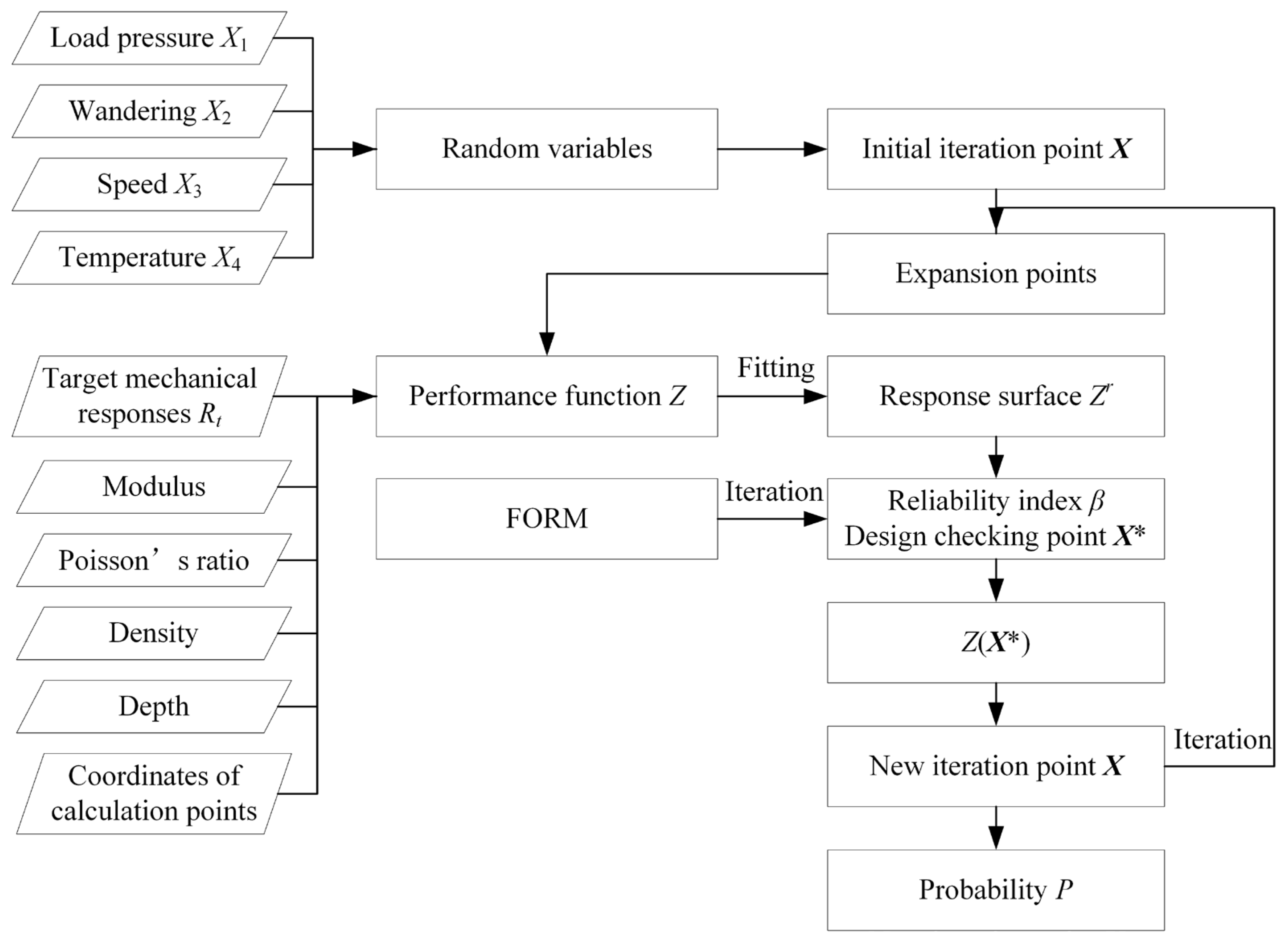
3.2. Probability Calculation Procedure
3.3. Monte-Carlo Simulation
4. Results and Discussions
4.1. Pavement Parameters and Random Variable Parameters
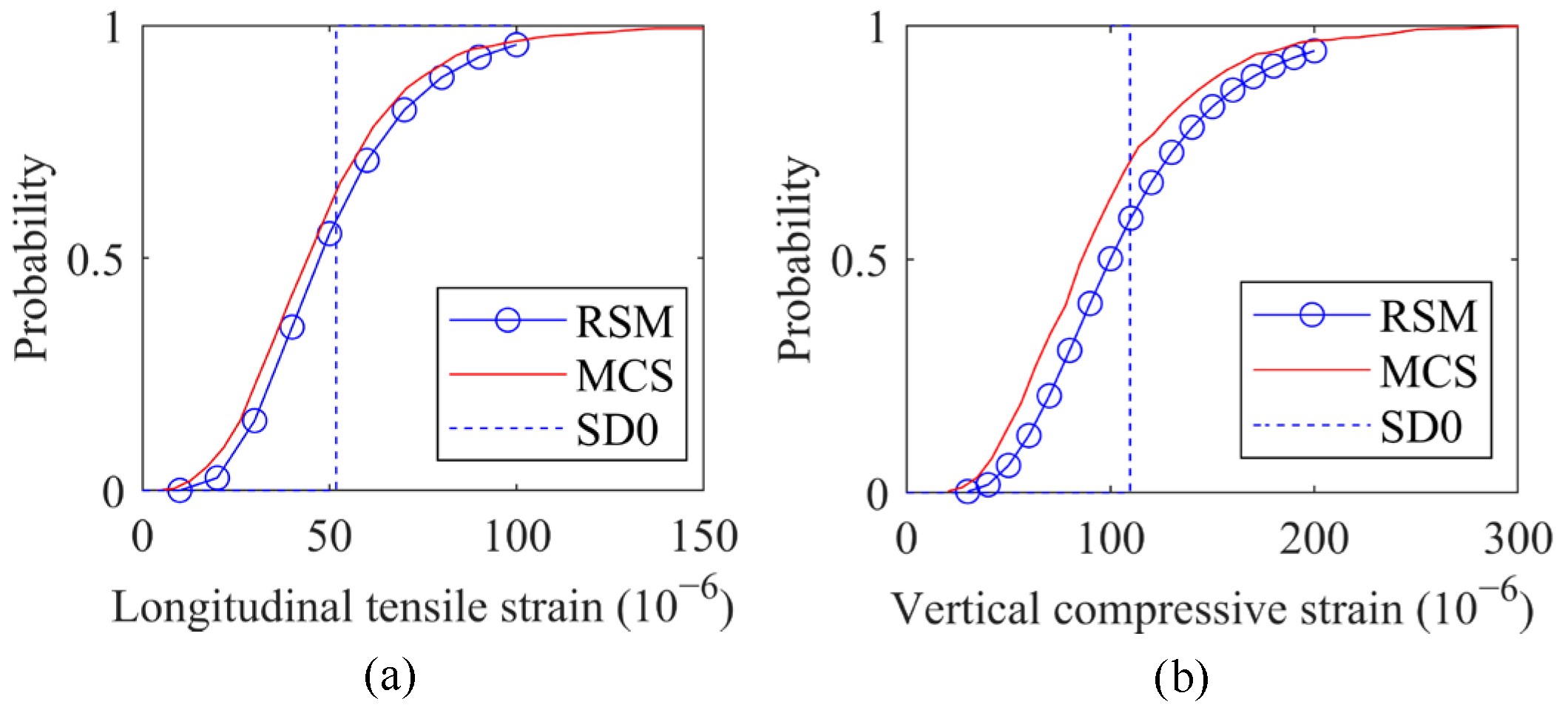
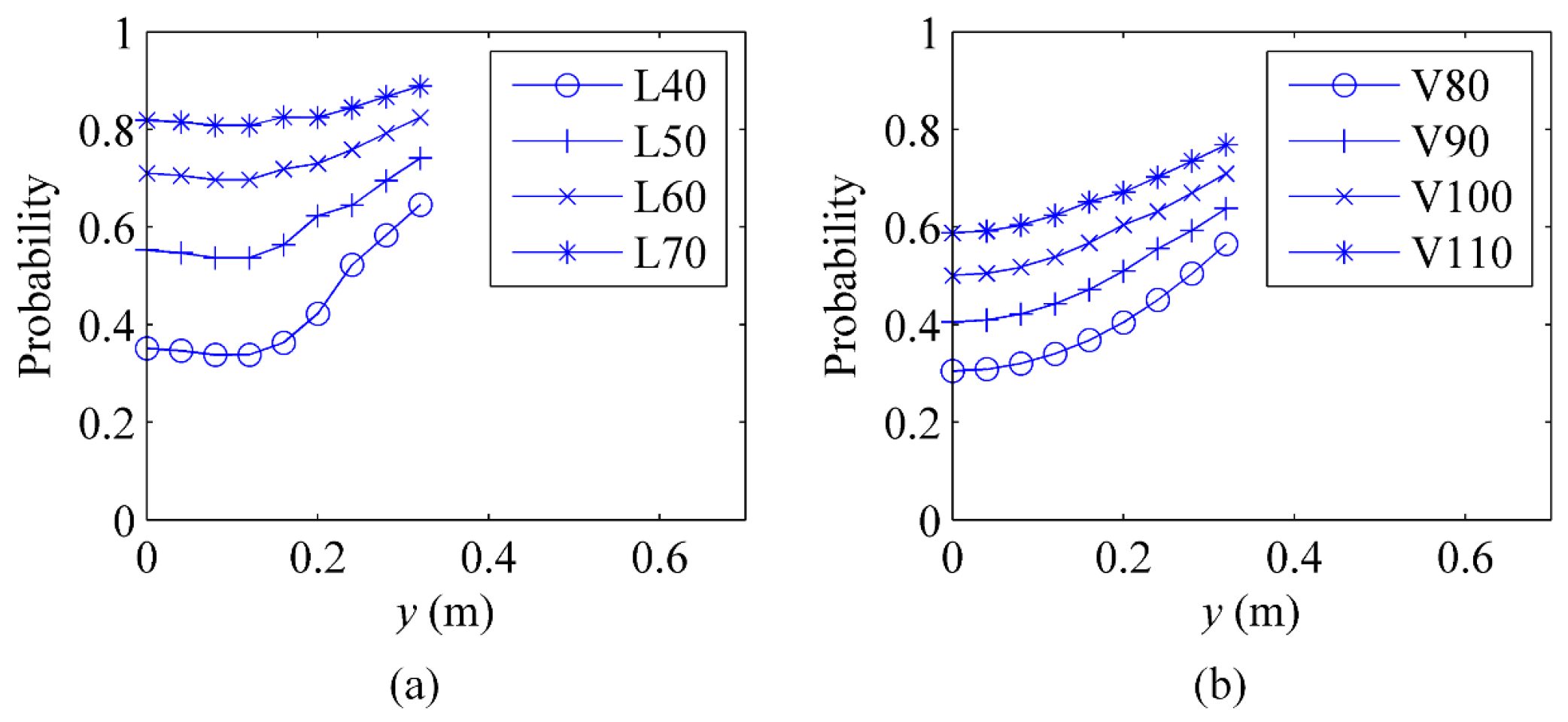
4.2. Probability Distributions of Mechanical Responses
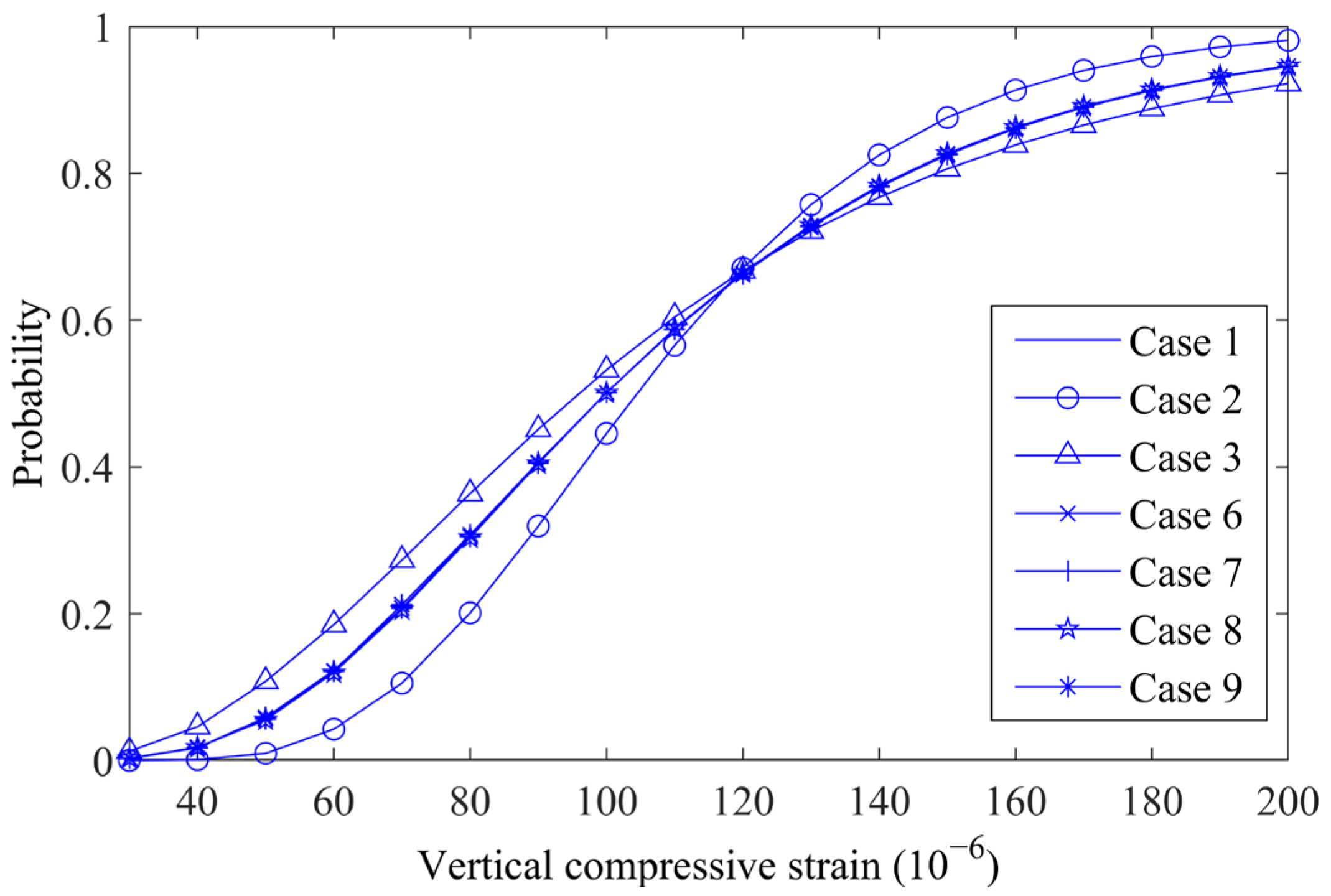
4.3. Effects of Random Variable Parameters
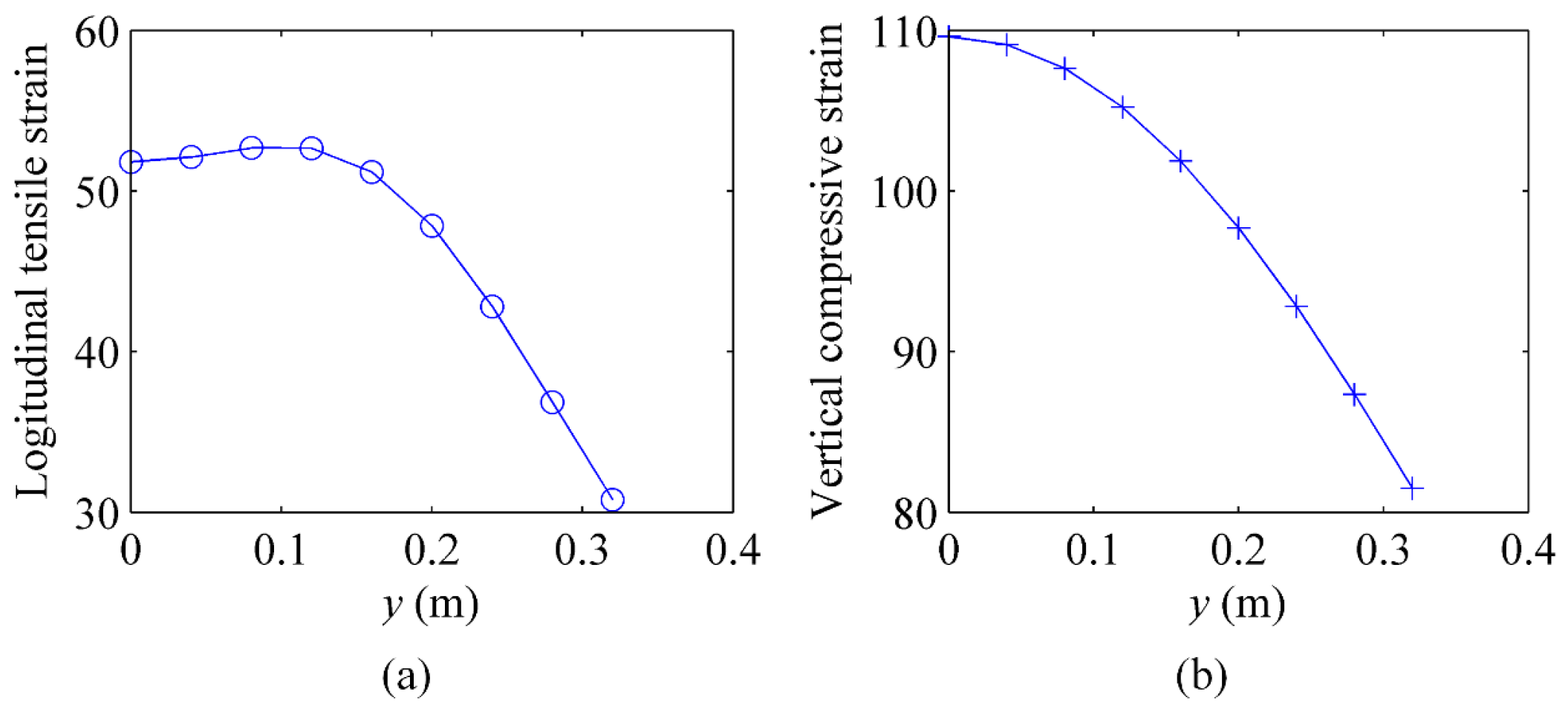
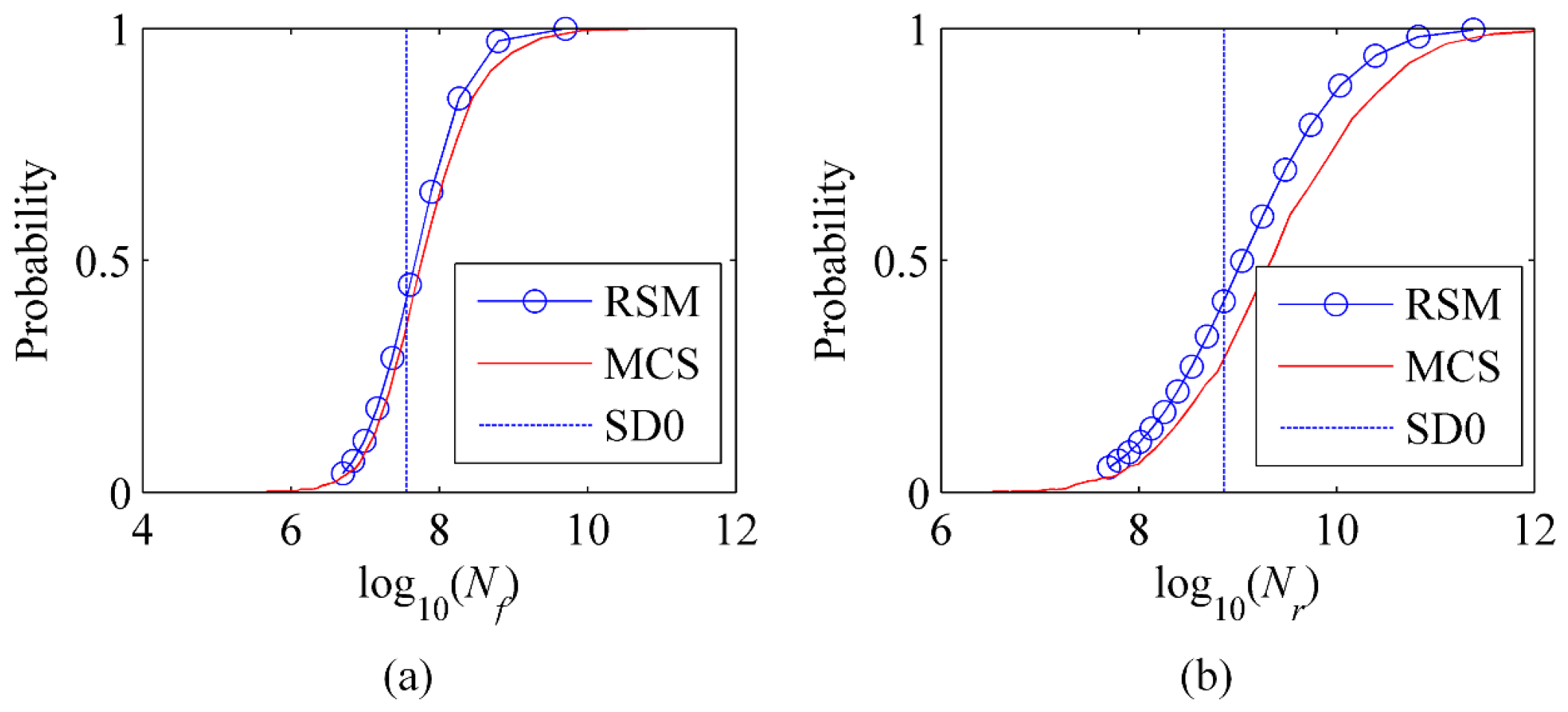
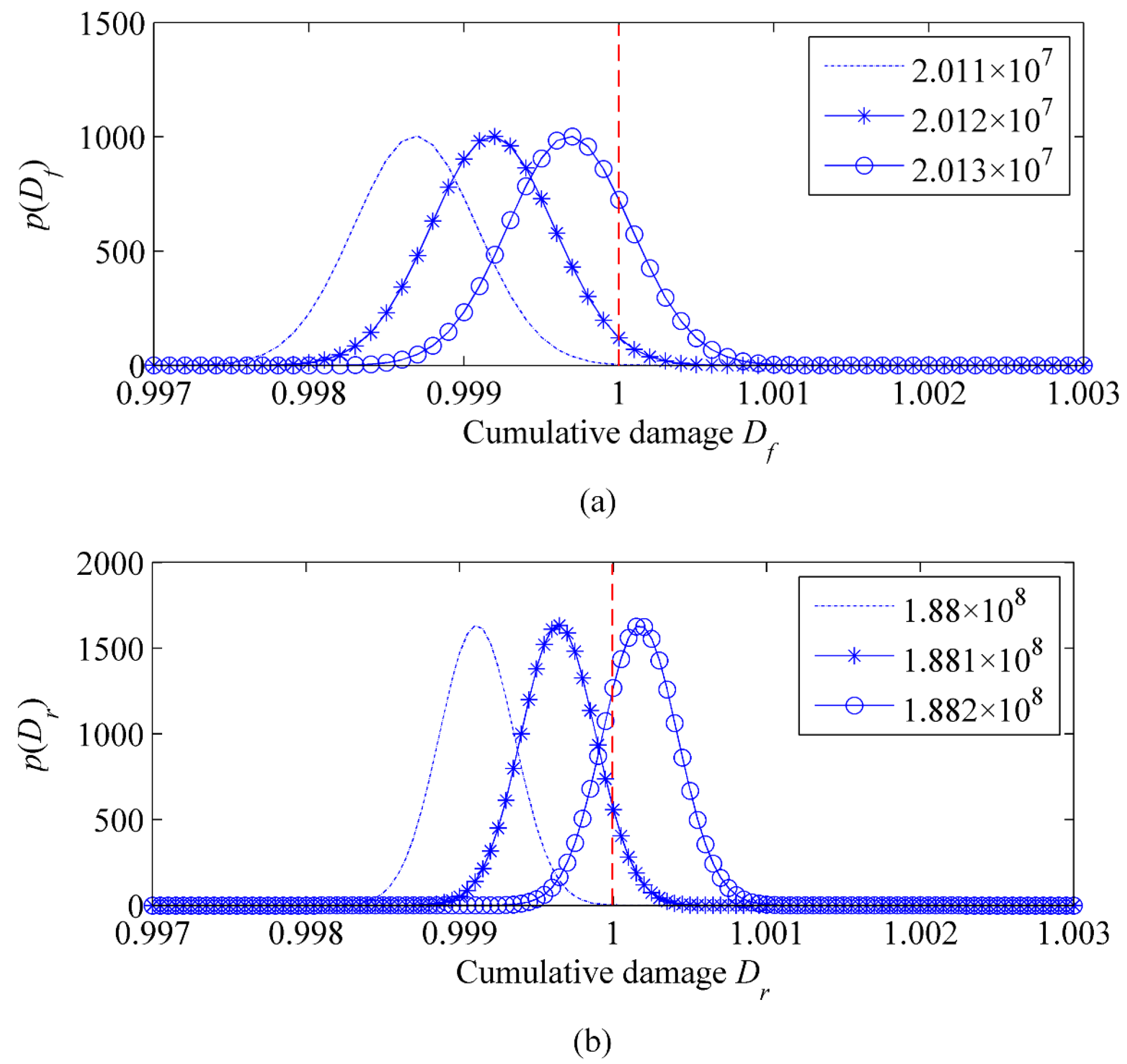
4.4. Probability Distributions of Pavement Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Al-Qadi, I.L. Near-Surface Pavement Failure under Multiaxial Stress State in Thick Asphalt Pavement. Transp. Res. Rec. 2010, 2154, 91–99. [Google Scholar] [CrossRef]
- Wang, H.; Al-Qadi, I.L. Evaluation of Surface-Related Pavement Damage due to Tire Braking. Road Mater. Pavement Des. 2010, 11, 101–122. [Google Scholar] [CrossRef]
- Wang, H.; Al-Qadi, I.L.; Stanciulescu, I. Effect of Surface Friction on Tire-Pavement Contact Stresses during Vehicle Maneuvering. J. Eng. Mech. 2014, 140, 04014001. [Google Scholar] [CrossRef] [Green Version]
- ARA (Applied Research Associates). Guide for Mechanistic-Empirical Design of New and Rehabilitated Pavement Structures; Final Rep. 1-37A; National Cooperative Highway Research Program: Albuquerque, NM, USA, 2004. [Google Scholar]
- Huang, Y. Pavement Analysis and Design, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Retherford, J.; McDonald, M. Reliability methods applicable to mechanistic-empirical pavement design method. Transp. Res. Rec. 2010, 2154, 130–137. [Google Scholar] [CrossRef]
- Tarefder, R.A.; Saha, N.; Stormont, J.C. Evaluation of subgrade strength and pavement designs for reliability. J. Transp. Eng. 2010, 136, 379–391. [Google Scholar] [CrossRef]
- Luo, Z.; Xiao, F.; Sharma, R. Efficient reliability-based approach for mechanistic-empirical asphalt pavement design. Constr. Build. Mater. 2014, 64, 157–165. [Google Scholar] [CrossRef]
- Timm, D.; Newcomb, D.; Galambos, T. Incorporation of reliability into mechanistic-empirical pavement design. Transp. Res. Rec. 2000, 1730, 73–80. [Google Scholar] [CrossRef]
- Maji, A.; Das, A. Reliability considerations of bituminous pavement design by mechanistic–empirical approach. Int. J. Pavement Eng. 2008, 9, 19–31. [Google Scholar] [CrossRef]
- Thyagarajan, S.; Muhunthan, B.; Sivaneswaran, N.; Petros, K. Efficient simulation techniques for reliability analysis of flexible pavements using the mechanistic-empirical pavement design guide. J. Transp. Eng. 2011, 137, 796–804. [Google Scholar] [CrossRef]
- Hu, S.; Zhou, F.; Scullion, T.; Leidy, J. Reliability-based mechanistic-empirical flexible pavement design. Transp. Res. Rec. 2014, 2456, 85–95. [Google Scholar] [CrossRef]
- Hall, K.; Xiao, D.; Pohl, E.; Wang, K. Reliability-based mechanistic-empirical pavement design with statistical methods. Transp. Res. Rec. 2012, 2305, 121–130. [Google Scholar] [CrossRef]
- Dinegdae, Y.H.; Birgisson, B. Reliability-based calibration for a mechanics-based fatigue cracking design procedure. Road Mater. Pavement Des. 2016, 17, 529–546. [Google Scholar] [CrossRef]
- Dong, Z.; Ma, X. Analytical solutions of asphalt pavement responses under moving loads with arbitrary non-uniform tire contact pressure and irregular tire imprint. Road Mater. Pavement Des. 2017, 19, 1887–1903. [Google Scholar] [CrossRef]
- Thompson, M.R. ILLI-PAVE Based Full-Depth Asphalt Concrete Pavement Design Procedure. In Proceedings of the 6th International Conference on Structural Design of Asphalt Pavements, Ann Arbor, MI, USA, 13–17 July 1987. [Google Scholar]
- AI (Asphalt Institute). Thickness Design-Asphalt Pavements for Highways and Streets, 9th ed.; Asphalt Institute: Lexington, KY, USA, 1999. [Google Scholar]




| Modulus (MPa) | Poisson’s Ratio | Density (kg/m3) | Depth (m) | |
|---|---|---|---|---|
| Asphalt layer | - | 0.35 | 2400 | 0.2 |
| Base layer | 1000 | 0.3 | 2000 | 0.4 |
| Subgrade | 200 | 0.4 | 1500 | - |
| τj | gj |
|---|---|
| 1000 | 0.017837 |
| 100 | 0.022262 |
| 10 | 0.044653 |
| 1 | 0.066893 |
| 0.1 | 0.104727 |
| 0.01 | 0.105207 |
| 0.001 | 0.164525 |
| 0.0001 | 0.002653 |
| 0.00001 | 0.451526 |
| Tref (°C) | C1 | C2 |
|---|---|---|
| 20 | 21.6 | 170.1 |
| X1 (MPa) | X2 (m) | X3 (m/s) | X4 (°C) | |
|---|---|---|---|---|
| Mean value | 0.7 | 0 | 25 | 20 |
| Standard deviation | 0.1 | 0.2 | 3 | 5 |
| X1 (MPa) | X2 (m) | X3 (m/s) | X4 (°C) | ||
|---|---|---|---|---|---|
| Mean value | Case A | 0.7 | 0 | 25 | 20 |
| Case B | 0.5 | 0 | 25 | 20 | |
| Case C | 0.9 | 0 | 25 | 20 | |
| Case D | 0.7 | 0 | 15 | 20 | |
| Case E | 0.7 | 0 | 35 | 20 | |
| Case F | 0.7 | 0 | 25 | 10 | |
| Case G | 0.7 | 0 | 25 | 30 | |
| Standard deviation | 0.1 | 0.2 | 3 | 5 | |
| X1 (MPa) | X2 (m) | X3 (m/s) | X4 (°C) | ||
|---|---|---|---|---|---|
| Mean value | 0.7 | 0 | 25 | 20 | |
| Standard deviation | Case 1 | 0.1 | 0.2 | 3 | 5 |
| Case 2 | 0.05 | 0.2 | 3 | 5 | |
| Case 3 | 0.15 | 0.2 | 3 | 5 | |
| Case 4 | 0.1 | 0.1 | 3 | 5 | |
| Case 5 | 0.1 | 0.3 | 3 | 5 | |
| Case 6 | 0.1 | 0.2 | 1.5 | 5 | |
| Case 7 | 0.1 | 0.2 | 4.5 | 5 | |
| Case 8 | 0.1 | 0.2 | 3 | 2.5 | |
| Case 9 | 0.1 | 0.2 | 3 | 7.5 | |
| Fatigue Failure | Rutting | ||
|---|---|---|---|
| Load Repetitions | Failure Probability | Load Repetitions | Failure Probability |
| 2.011 × 107 | 0.0005 | 1.88 × 108 | 0.0001 |
| 2.012 × 107 | 0.0199 | 1.881 × 108 | 0.0714 |
| 2.013 × 107 | 0.2101 | 1.882 × 108 | 0.7613 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Shangguan, L.; Si, C. Probability Distributions of Asphalt Pavement Responses and Performance under Random Moving Loads and Pavement Temperature. Appl. Sci. 2023, 13, 715. https://doi.org/10.3390/app13020715
Ma X, Shangguan L, Si C. Probability Distributions of Asphalt Pavement Responses and Performance under Random Moving Loads and Pavement Temperature. Applied Sciences. 2023; 13(2):715. https://doi.org/10.3390/app13020715
Chicago/Turabian StyleMa, Xianyong, Lingxiao Shangguan, and Chundi Si. 2023. "Probability Distributions of Asphalt Pavement Responses and Performance under Random Moving Loads and Pavement Temperature" Applied Sciences 13, no. 2: 715. https://doi.org/10.3390/app13020715




