Seismic Behavior and Modeling of Ductile Composite Steel-Trussed Concrete Beam to Column Joints
Abstract
:1. Introduction
2. Experimental Tests
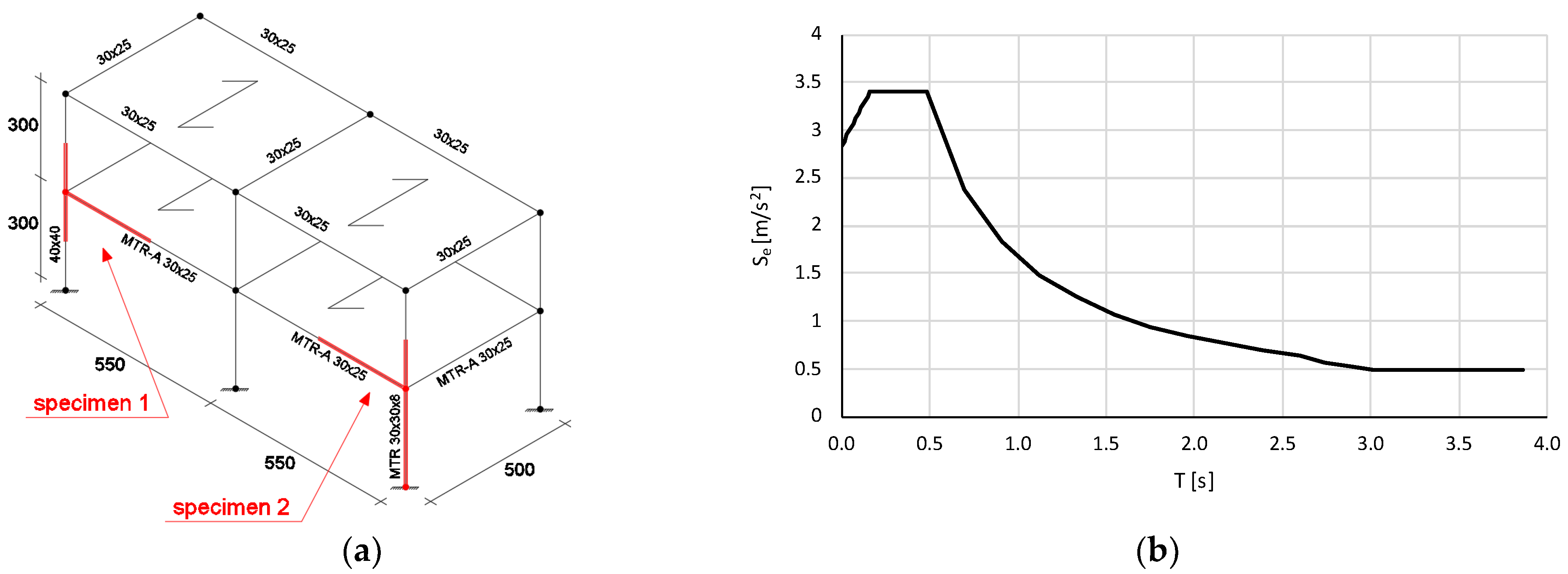
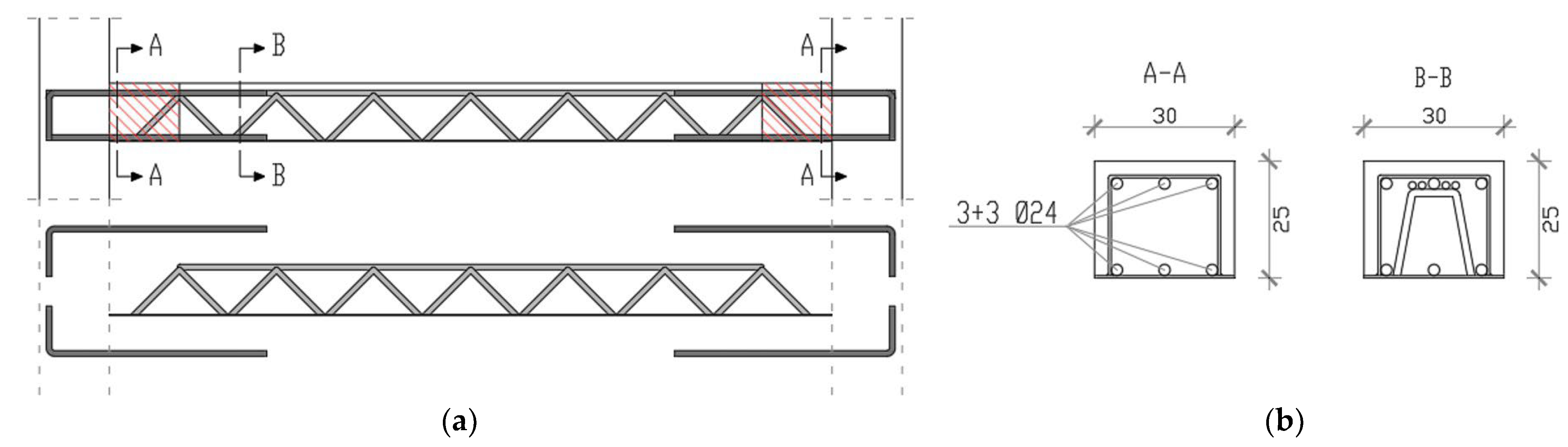
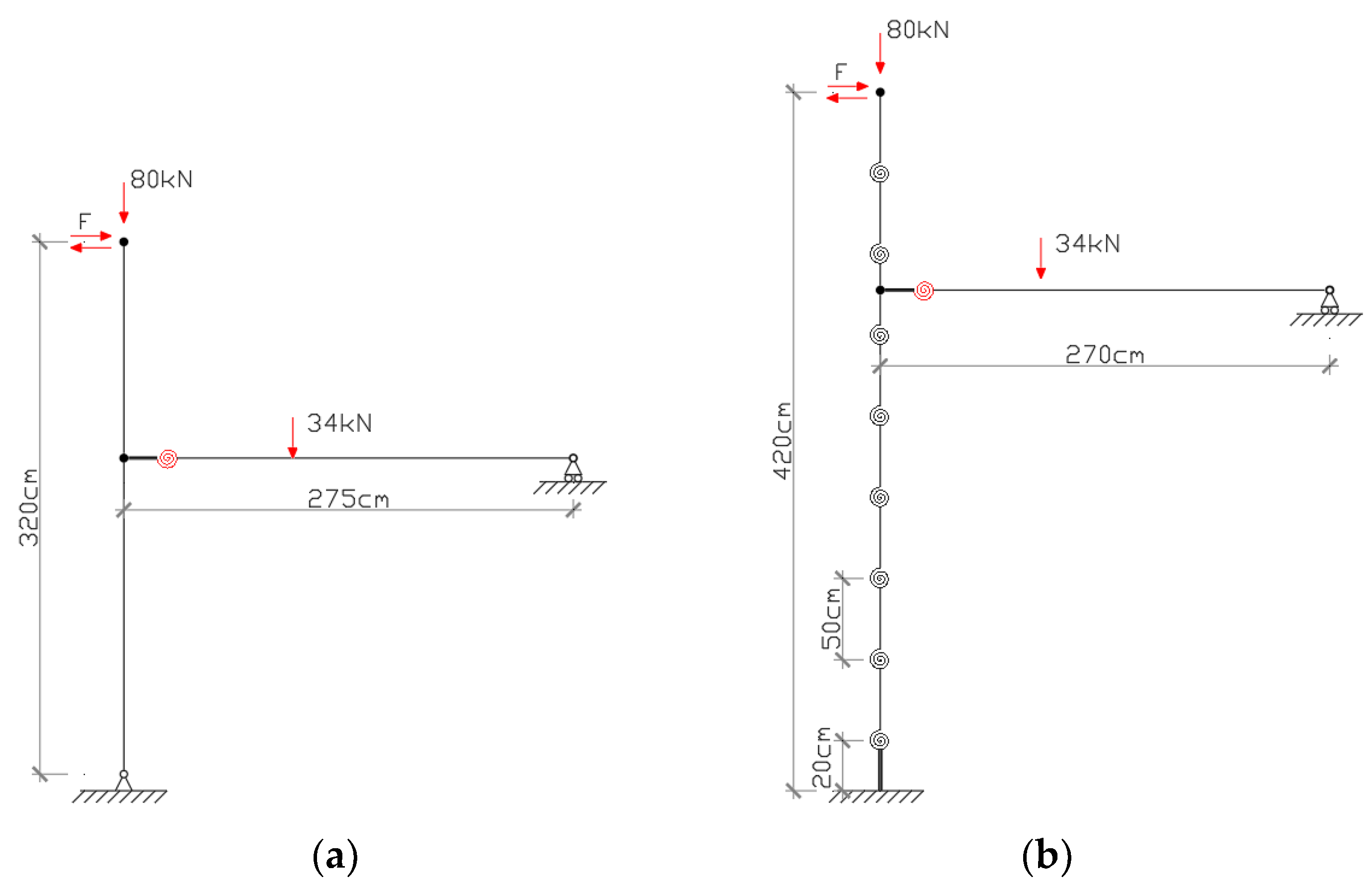
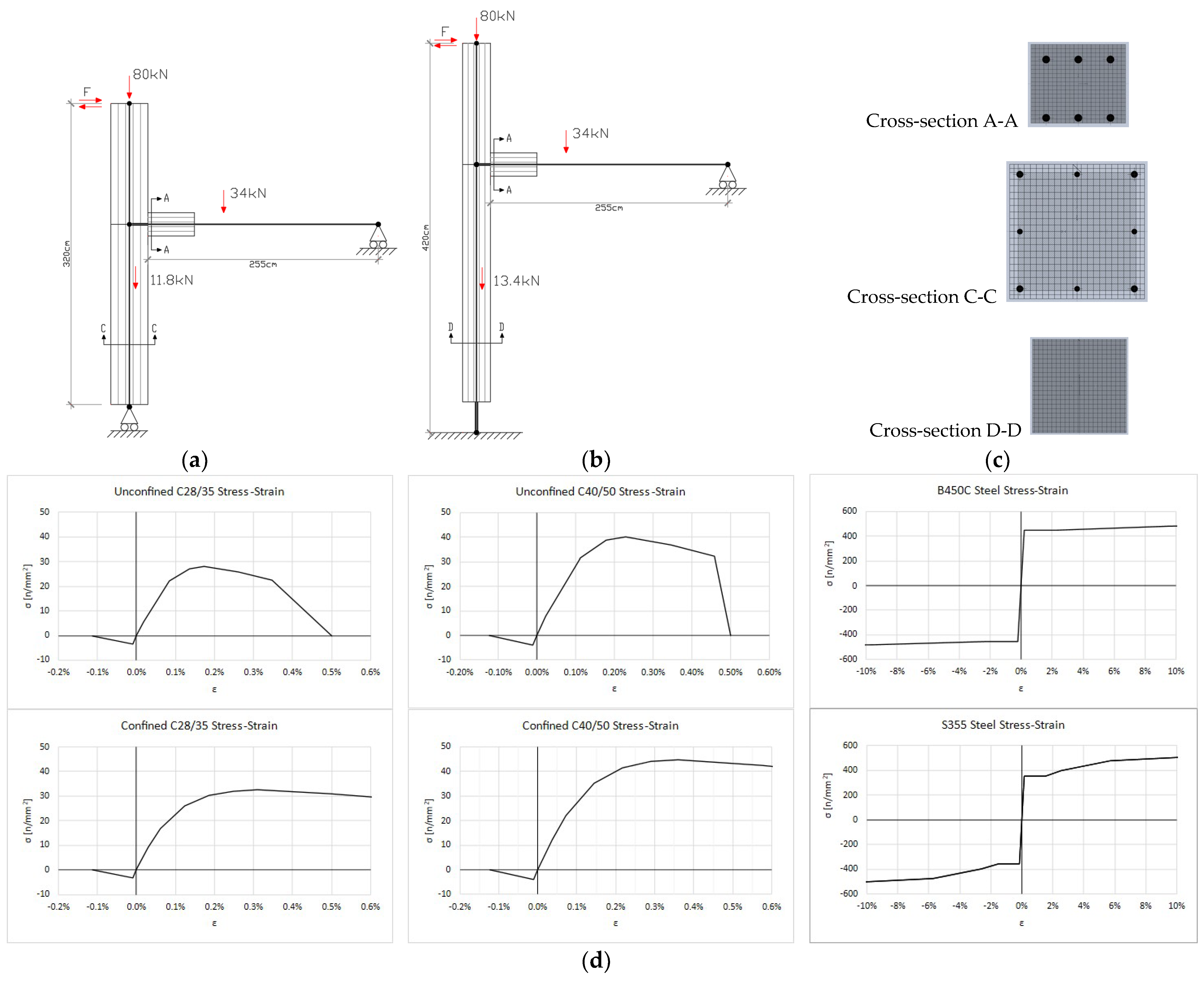
2.1. Experimental Specimens
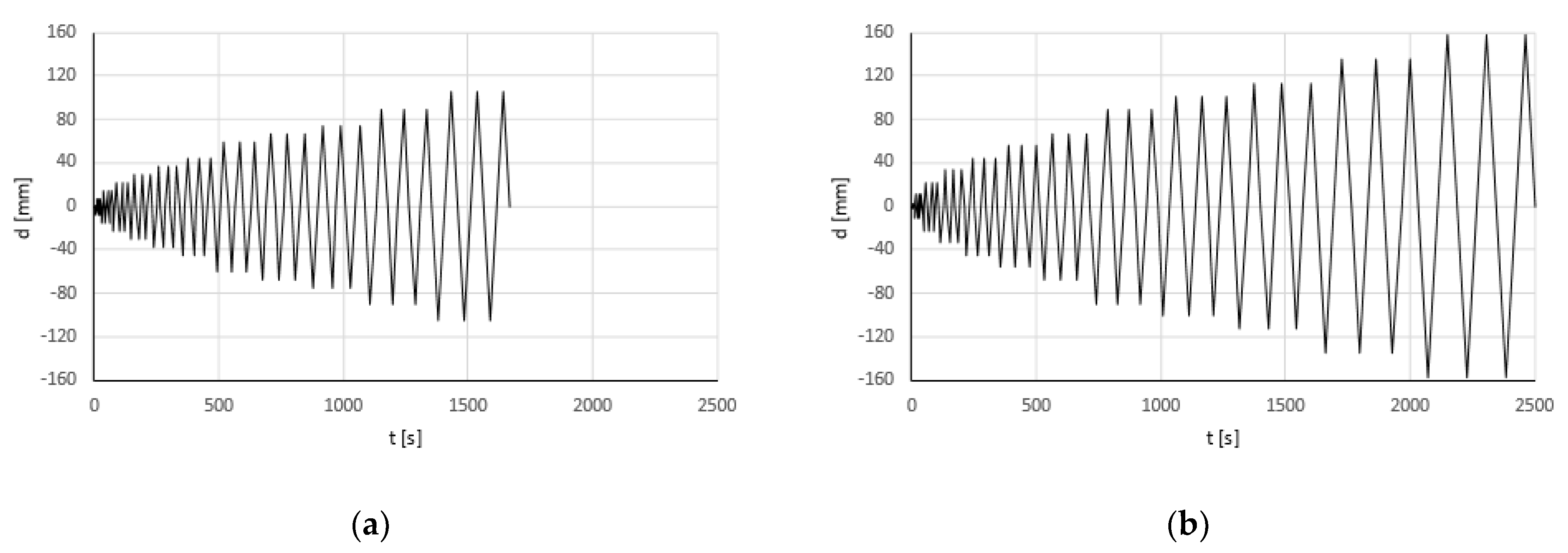
2.2. Test Apparatus and Load Pattern
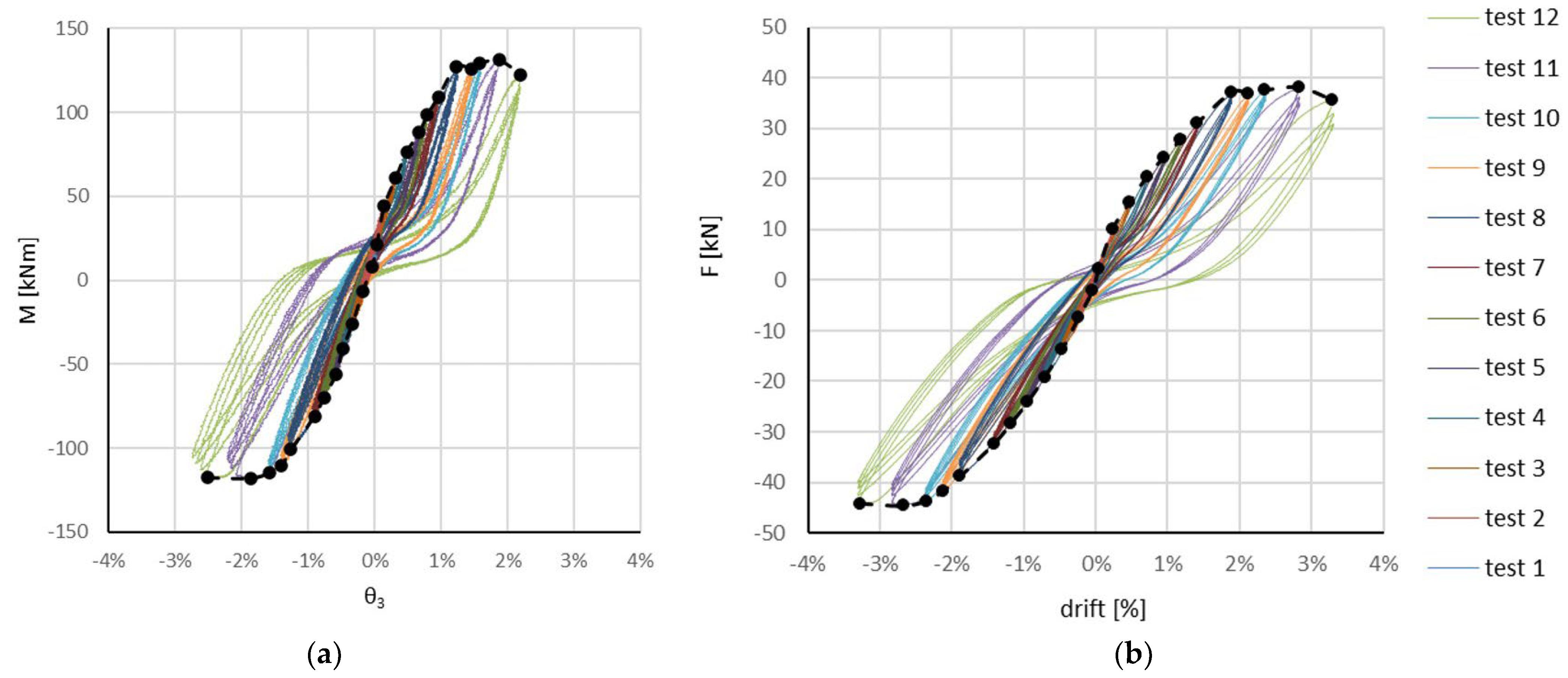
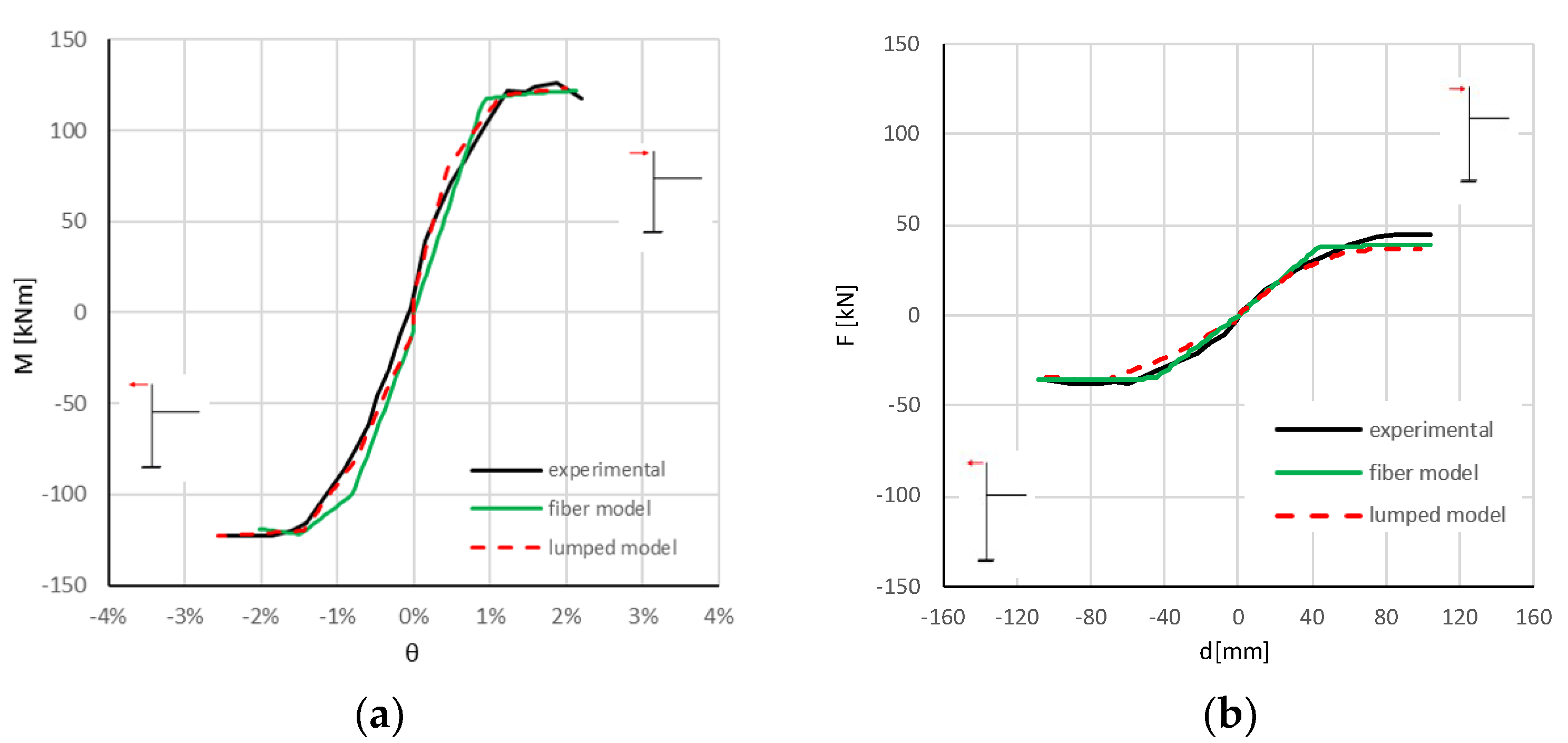
2.3. Experimental Results
3. Numerical Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ministero delle Infrastrutture e dei Trasporti (MIT). Aggiornamento delle Norme Tecniche per le Costruzioni NTC 2018; D.M. del 17/01/2018; MIT: Rome, Italy, 2018. (In Italian)
- CEN. Eurocode 3: Design of Steel Structures Part 1-1: General Rules and Rules for Buildings; Comité Européen de Normalisation: Bruxelles, Belgium, 2003. [Google Scholar]
- CEN. Eurocode 4: Design of Composite Steel and Concrete Structures Part 1-1: General Rules and Rules for Buildings; Comité Européen de Normalisation: Bruxelles, Belgium, 2004. [Google Scholar]
- Huang, Y.; Mazzarolo, E.; Briseghella, B.; Zordan, T.; Chen, A. Experimental and numerical investigation of the cyclic behaviour of an innovative prefabricated beam-to-column joint. Eng. Struct. 2017, 150, 373–389. [Google Scholar] [CrossRef]
- Colajanni, P.; La Mendola, L.; Monaco, A.; Spinella, N. Cyclic behavior of composite truss beam-to-rc column joints in MRFS. Key Eng. Mater. 2016, 711, 681–689. [Google Scholar] [CrossRef]
- Scotta, R.; Tesser, L. Comportamento di nodi trave-pilastro sismo-resistenti in struttura mista di tipo tralicciato soggetti ad azioni cicliche. Progett. Sismica 2011, 3, 47–62. (In Italian) [Google Scholar]
- Amadio, C.; Sorgon, S.; Macorini, L.; Suraci, G. Analisi di un sistema ibrido sismo-resistente costituito da elementi tralicciati in acciaio inglobati nel calcestruzzo. In Proceedings of the 17° Italian Concrete Conference C.T.E., Roma, Italy, 5–8 November 2008; Available online: https://d1wqtxts1xzle7.cloudfront.net/39298659/00b7d52d4e0550c585000000-libre.pdf (accessed on 8 October 2023).
- Pampanin, S.; Priestley, M.N.; Sritharan, S. Analytical modeling of the seismic behavior of precast concrete frames designed with ductile connections. J. Earthq. Eng. 2001, 5, 329–367. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, X.; Rong, X.; Li, Y. Experimental study of high-strength steel fiber concrete exterior beam-column joints with high-strength steel reinforcements. Bull. Earthq. Eng. 2023, 21, 2785–2815. [Google Scholar] [CrossRef]
- Palermo, A.; Pampanin, S.; Fragiacomo, M.; Buchanan, A.H.; Deam, B.L.; Pasticier, L. Quasi-static cyclic tests on seismic-resistant beam-to-column and column-to-foundation subassemblies using Laminated Veneer Lumber (LVL). In Proceedings of the 19th Australasian Conference on Mechanics of Structures and Materials (ACMSM19), Christchurch, New Zealand, 29 November–1 December 2006; Available online: http://hdl.handle.net/10092/178 (accessed on 8 October 2023).
- Masi, A.; Santarsiero, G.; Nigro, D. Cyclic Tests on External RC Beam-Column Joints: Role of Seismic Design Level and Axial Load Value on the Ultimate Capacity. J. Earthq. Eng. 2013, 17, 110–136. [Google Scholar] [CrossRef]
- Laterza, M.; D’Amato, M.; Gigliotti, R. Modeling of gravity-designed RC sub-assemblages subjected to lateral loads. Eng. Struct. 2017, 130, 242–260. [Google Scholar] [CrossRef]
- Smith, T.; Ponzo, F.C.; Di Cesare, A.; Auletta, G.; Pampanin, S.; Carradine, D.; Palermo, A.; Nigro, D. Seismic performance of a post-tensioned glue laminated beam to column joint: Experimental and numerical results. In Proceedings of the World Conference on Timber Engineering WCTE 2012, Auckland, New Zealand, 16–19 July 2012; pp. 385–393. [Google Scholar]
- Smith, T.; Ponzo, F.C.; Di Cesare, A.; Pampanin, S.; Carradine, D.; Buchanan, A.H.; Nigro, D. Post-Tensioned Glulam Beam-Column Joints with Advanced Damping Systems: Testing and Numerical Analysis. J. Earthq. Eng. 2014, 18, 147–167. [Google Scholar] [CrossRef]
- Colajanni, P.; La Mendola, L.; Monaco, A.; Pagnotta, S. Low-damage friction connections in hybrid joints of frames of reinforced-concrete buildings. Appl. Sci. 2023, 13, 7876. [Google Scholar] [CrossRef]
- Colajanni, P.; La Mendola, L.; Monaco, A.; Pagnotta, S. Design of RC joints equipped with hybrid trussed beams and friction dampers. Eng. Struct. 2021, 227, 111442. [Google Scholar] [CrossRef]
- Colajanni, P.; La Mendola, L.; Monaco, A.; Pagnotta, S. Seismic performance of earthquake-resilient RC frames made with HSTC beams and friction damper devices. J. Earthq. Eng. 2022, 26, 7787–7813. [Google Scholar] [CrossRef]
- Chisari, C.; Amadio, C. An experimental, numerical and analytical study of hybrid RC-encased steel joist beams subjected to shear. Eng. Struct. 2014, 61, 84–98. [Google Scholar] [CrossRef]
- Colajanni, P.; La Mendola, L.; Monaco, A.; Pagnotta, S. Dissipative connections of rc frames with prefabricated steel-trussed-concrete beams. Ing. Sismica Int. J. Earthq. Eng. 2020, 37, 51–63. [Google Scholar]
- Tavakol, M.; HajiKazemi, H.; Rajabzadeh-Safaei, N.; Masoodi, A.R. Influence of shape memory alloy on seismic behaviour of hollow-section concrete columns. In Proceedings of the Institution of Civil Engineers—Structures and Buildings; ICE Publishing: London, UK, 2021; pp. 1–18. [Google Scholar]
- SAP2000 Structural Analysis and Design. Available online: https://www.csiamerica.com/products/sap2000 (accessed on 8 October 2023).
- Bruschi, E.; Calvi, P.M.; Quaglini, V. Concentrated plasticity modelling of RC frames in time-history analyses. Eng. Struct. 2021, 243, 112716. [Google Scholar] [CrossRef]
- Colajanni, P.; La Mendola, L.; Monaco, A. Stiffness and strength of composite truss beam to RC column connection in MRFS. J. Constr. Steel Res. 2015, 113, 86–100. [Google Scholar] [CrossRef]







| N° Test | Drift [%] | Hinged Column Displ. [mm] | Fixed Column Displ. [mm] |
|---|---|---|---|
| Test 1 | 0.05% | ±1.50 | ±2.25 |
| Test 2 | 0.25% | ±7.50 | ±11.25 |
| Test 3 | 0.50% | ±15.00 | ±22.50 |
| Test 4 | 0.75% | ±22.50 | ±33.75 |
| Test 5 | 1.00% | ±30.00 | ±45.00 |
| Test 6 | 1.25% | ±37.50 | ±56.25 |
| Test 7 | 1.50% | ±45.00 | ±67.50 |
| Test 8 | 2.00% | ±60.00 | ±90.00 |
| Test 9 | 2.25% | ±67.50 | ±101.25 |
| Test 10 | 2.50% | ±75.00 | ±112.50 |
| Test 11 | 3.00% | ±90.00 | ±135.00 |
| Test 12 | 3.50% | ±105.00 | ±157.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Cesare, A.; Belviso, P.; Ponzo, F.C.; Vitone, G. Seismic Behavior and Modeling of Ductile Composite Steel-Trussed Concrete Beam to Column Joints. Appl. Sci. 2023, 13, 11139. https://doi.org/10.3390/app132011139
Di Cesare A, Belviso P, Ponzo FC, Vitone G. Seismic Behavior and Modeling of Ductile Composite Steel-Trussed Concrete Beam to Column Joints. Applied Sciences. 2023; 13(20):11139. https://doi.org/10.3390/app132011139
Chicago/Turabian StyleDi Cesare, Antonio, Prospero Belviso, Felice Carlo Ponzo, and Giovanni Vitone. 2023. "Seismic Behavior and Modeling of Ductile Composite Steel-Trussed Concrete Beam to Column Joints" Applied Sciences 13, no. 20: 11139. https://doi.org/10.3390/app132011139
APA StyleDi Cesare, A., Belviso, P., Ponzo, F. C., & Vitone, G. (2023). Seismic Behavior and Modeling of Ductile Composite Steel-Trussed Concrete Beam to Column Joints. Applied Sciences, 13(20), 11139. https://doi.org/10.3390/app132011139








