Structural Strength Analysis of a Rotary Drum Mower in Transportation Position
Abstract
:1. Introduction
2. Materials and Methods
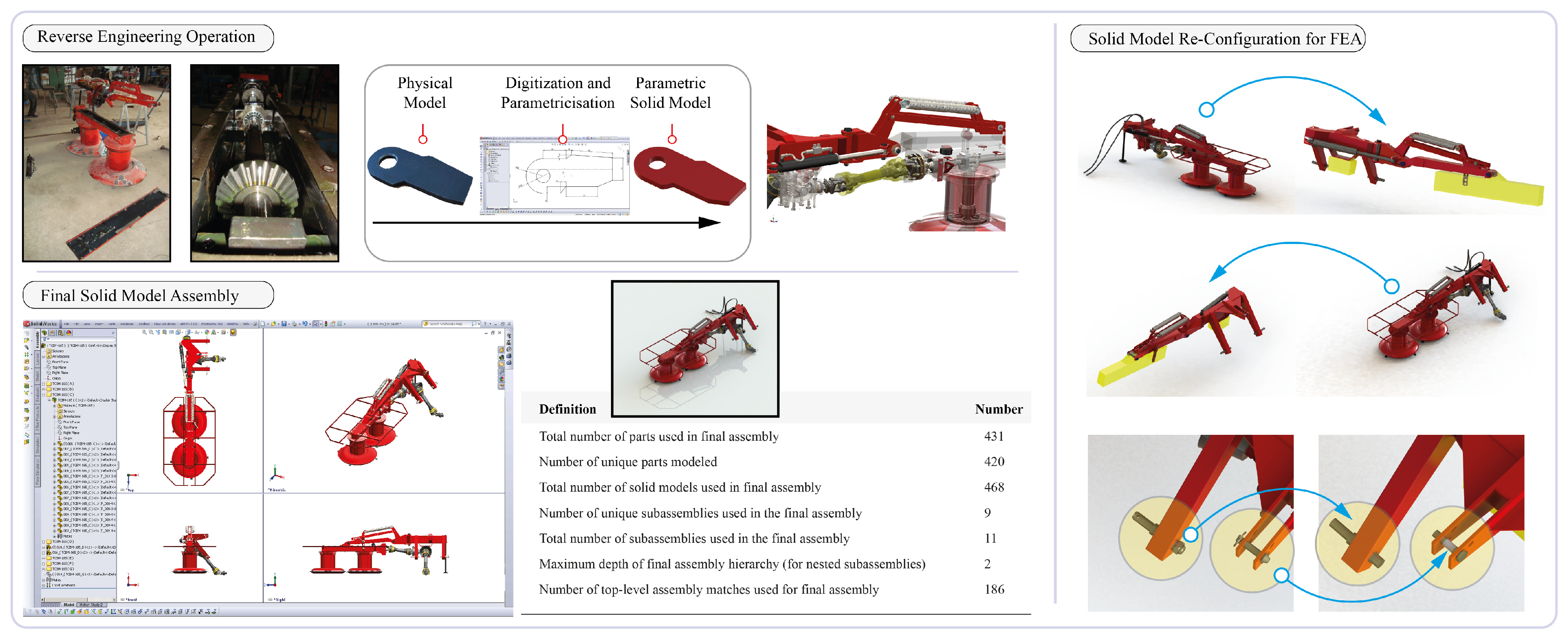
2.1. Rotary Drum Mower
2.2. Loading Scenario
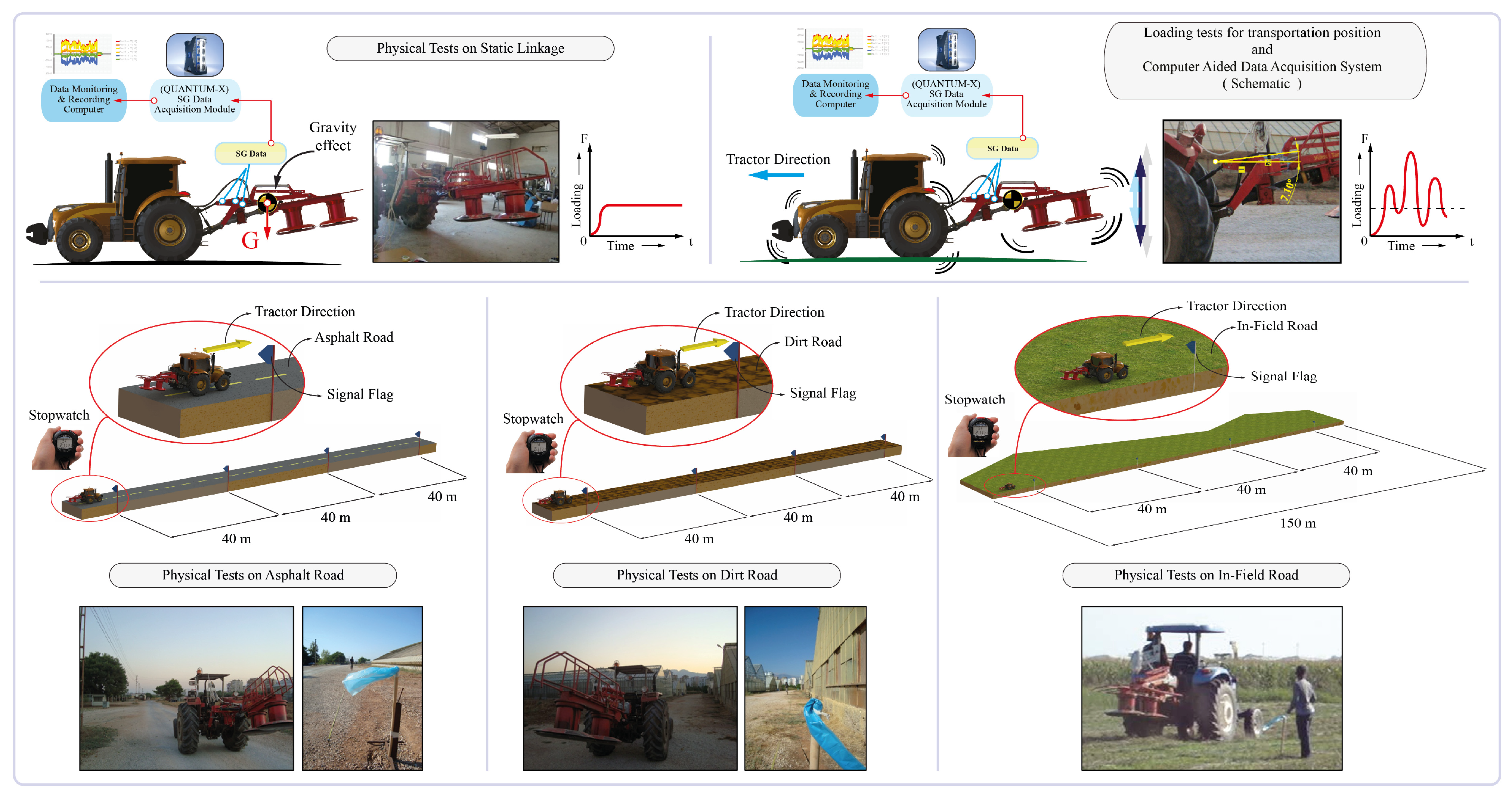
2.3. Experimental Set Up
2.3.1. Weight Measurement
2.3.2. Material Confirmation Tensile Tests
2.3.3. Strain Gauge-Based Strain Measurement
2.3.4. Physical Static Linkage Test
2.3.5. Physical Transportation (Road) Tests
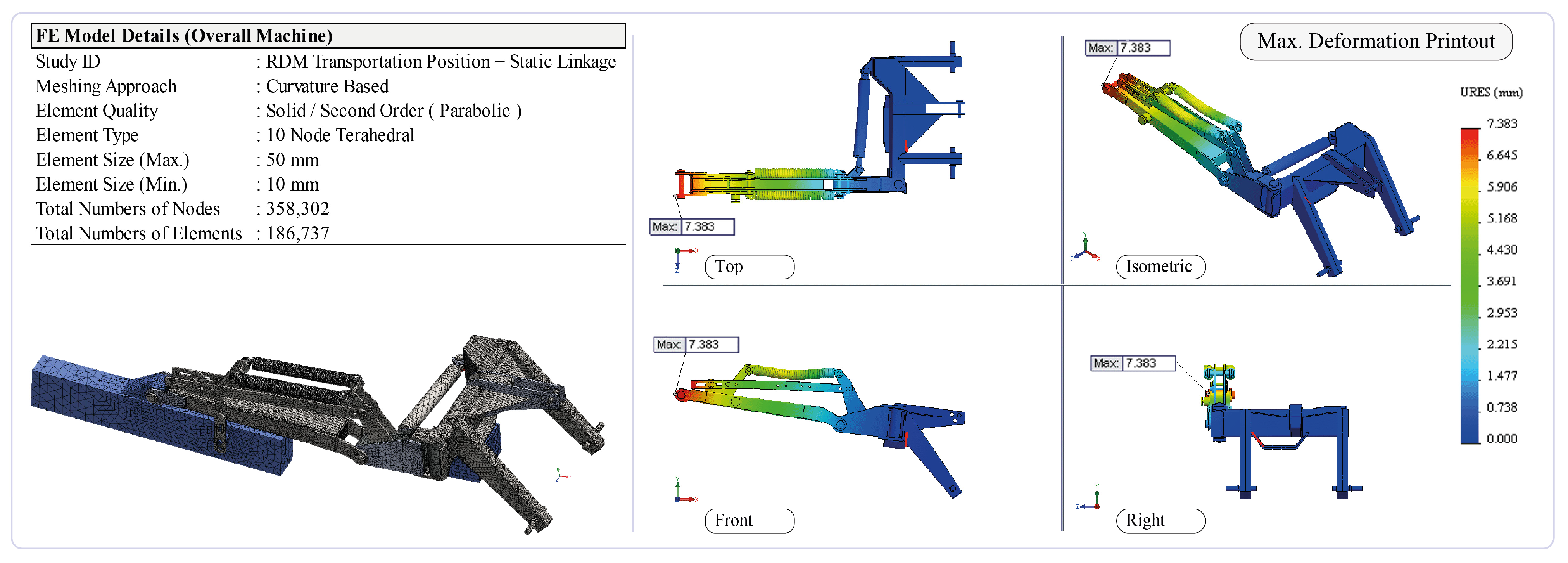
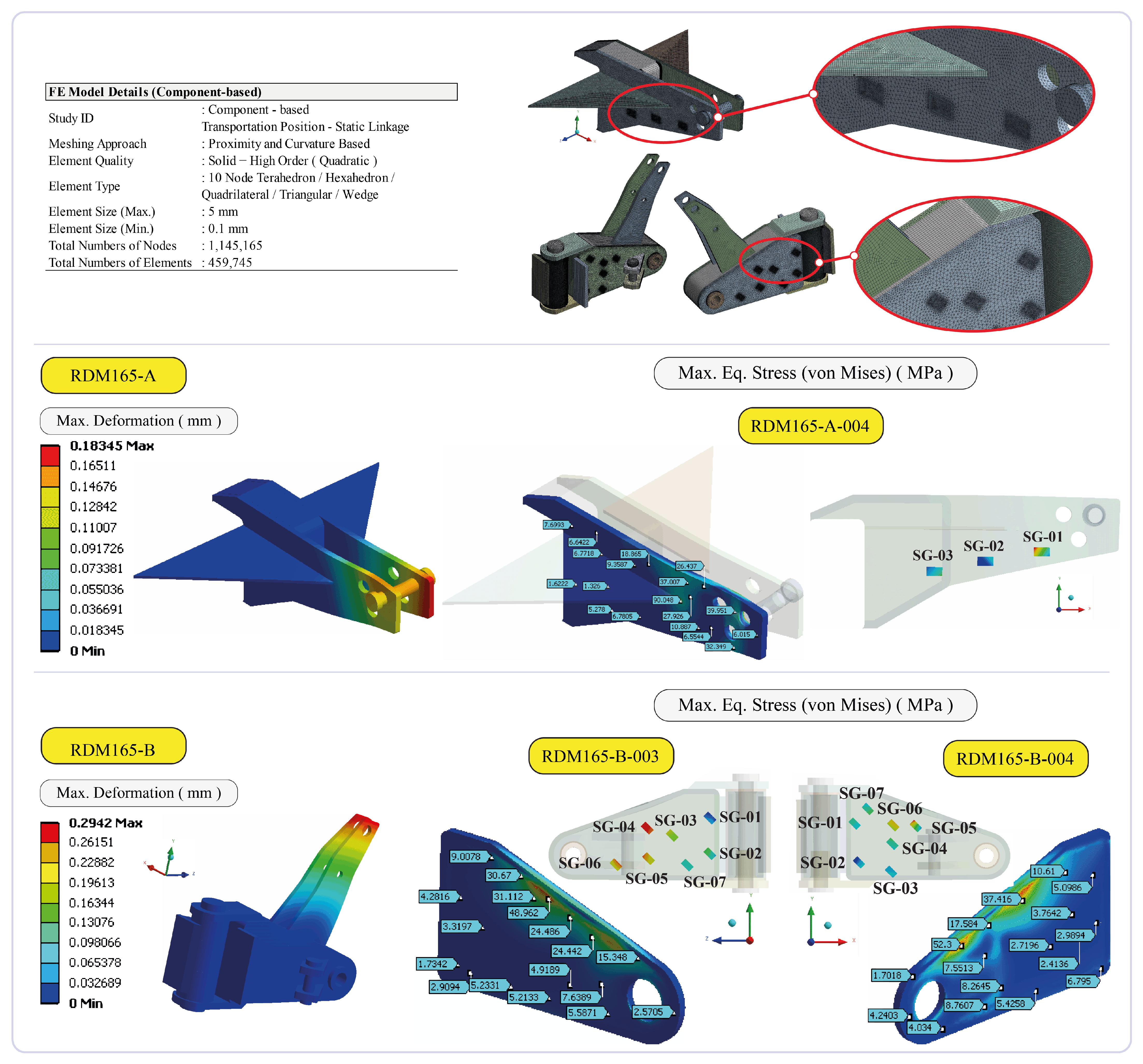
2.4. Finite Element Analysis
3. Results and Discussion
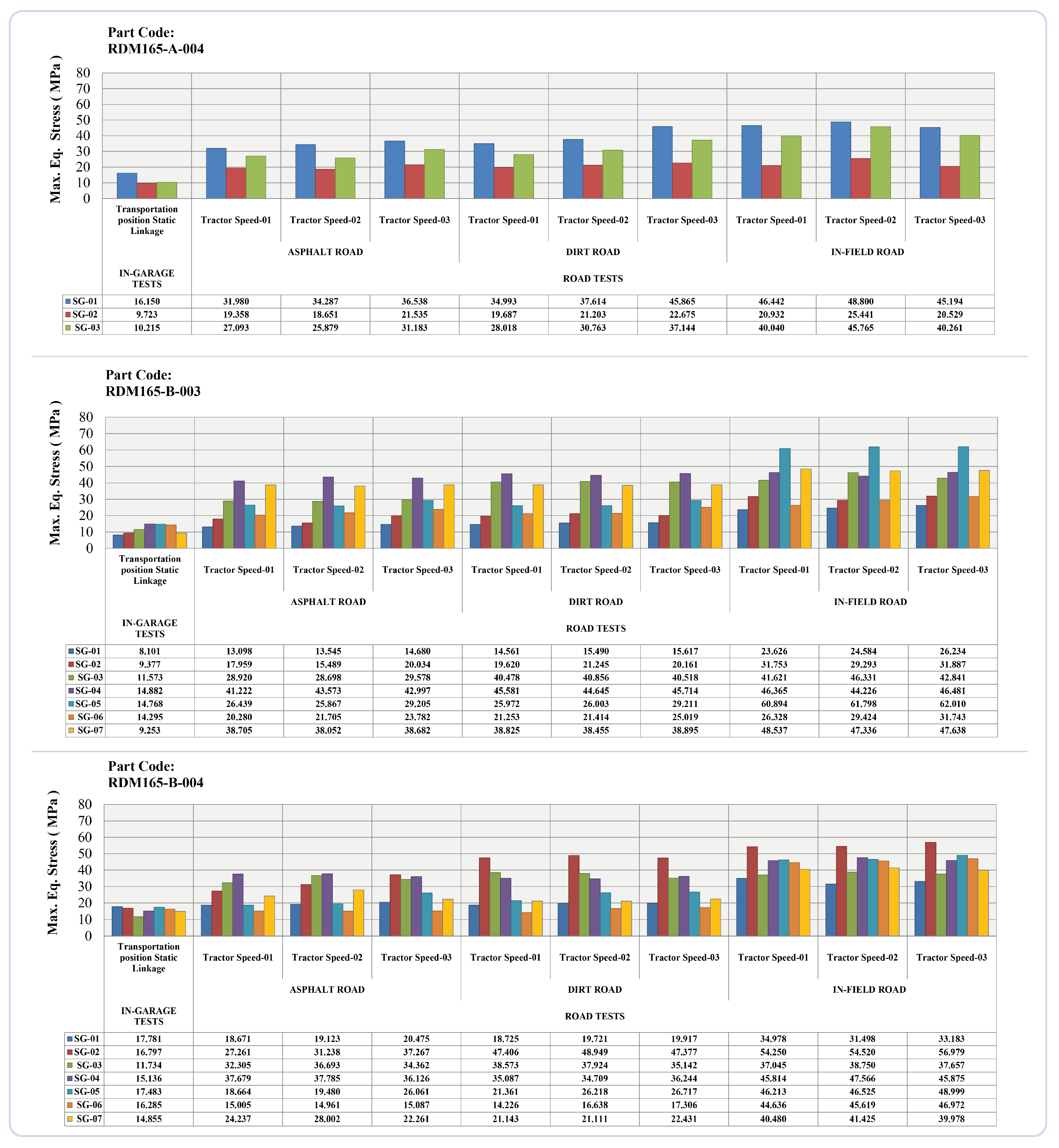
3.1. Evaluation of the Physical Test Results
3.2. Evaluation of the FEA Results
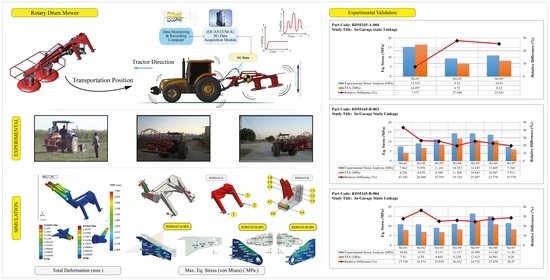
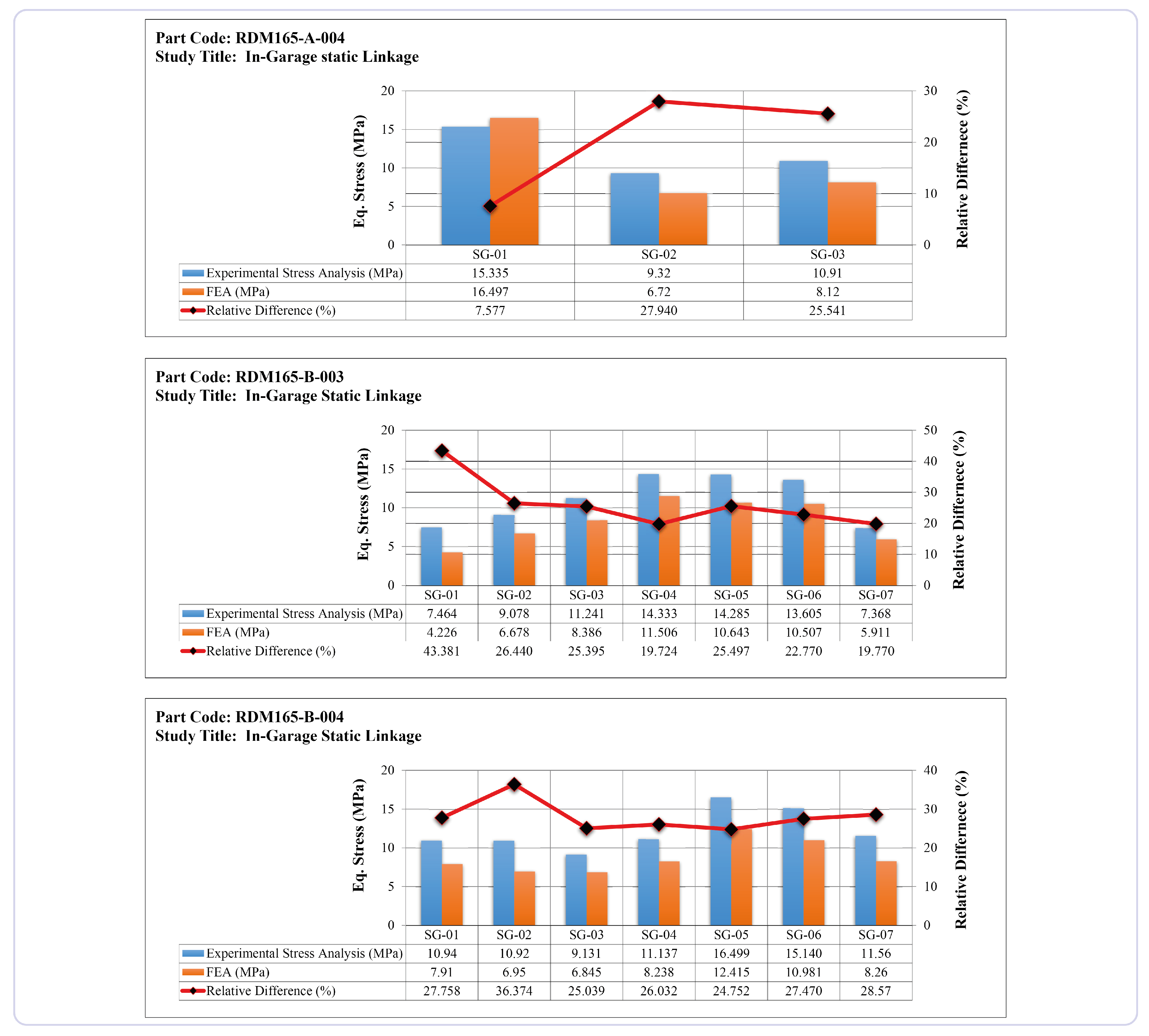
3.3. FEA Verification and Validation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sha, L. An Application of Industrial Design in Large-Scale Agricultural Machinery. In Proceedings of the 2008 9th International Conference on Computer-Aided Industrial Design and Conceptual Design, Beijing, China, 22–25 November 2008; pp. 823–828. [Google Scholar] [CrossRef]
- Sun, H.; Guo, W.; Wang, L.; Rong, B. An Analysis Method of Dynamic Requirement Change in Product Design. Comput. Ind. Eng. 2022, 171, 108477. [Google Scholar] [CrossRef]
- Akhtar Khan, A.; Sultan, U.; Rudra, R.P.; Ehsan, F.; Kashif, M.; Mohsin Khan, M.; Hashim, S.; Zohaib, M.; Imran Ahmad, S. Structural Analysis of Cotton Stalk Puller and Shredder Machine. Alex. Eng. J. 2022, 64, 335–347. [Google Scholar] [CrossRef]
- Guzel, E. Harvest Threshing Principles and Machines-Lecture Notes No:116 (Hasat-Harman İlkeleri ve Makinaları Ders Kitabı), 1st ed.; Publication of Faculty of Agriculture, Cukurova University: Adana, Turkey, 1993. [Google Scholar]
- Srivastava, A.K.; Goering, C.E.; Rohrbach, R.P. Engineering Principles of Agricultural Machines; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1993; ISBN 09-293-55334. [Google Scholar]
- El-Baily, M.M. A Study of Rotary Drum Mower Blade Wear and Its Effects on Forage Productivity. Poljopr. Teh. 2022, 47, 87–100. [Google Scholar] [CrossRef]
- TRMoNE. Green Forage Harvesters (Agricultural Technologies Lecture Notes); TRMoNE, Turkish Republic Ministry of National Education: Ankara, Turkey, 2009. (In Turkish) [Google Scholar]
- Wu, B.; Zuo, T.; Li, Z.; Qian, H.; Huang, T.; Xiang, Y. Numerical Simulation and Optimization of the Airflow Field of a Forage Drum Mower. Appl. Sci. 2023, 13, 5910. [Google Scholar] [CrossRef]
- Bartoň, S. The Dynamics of the Drum Mower Blade. In Proceedings of the Programs and Algorithms of Numerical Mathematics 19, Institute of Mathematics, Czech Academy of Sciences, Prague, Czech Republic, 20 April 2019; pp. 7–14. [Google Scholar]
- Celik, H.K.; Akinci, I. Analytical and Finite Element Method Based Stress Analysis of the Motion Transmission Axels of A Rotary Drum Mower. J. Agric. Mach. Sci. 2015, 11, 247–255. (In Turkish) [Google Scholar]
- Celik, H.K.; Akinci, I. Analytical and Finite Element Method Based Stress Analysis of Rotary Elements: Case Study for the Motion Transmission Gears of a Rotary Drum Mower. J. Fail. Anal. Prev. 2016, 16, 293–301. [Google Scholar] [CrossRef]
- Persson, S. Development of a Rotary Countershear Mower. Trans. ASAE 1993, 36, 1517–1523. [Google Scholar] [CrossRef]
- Yuksel Tarim Inc. YUKSEL TARIM—Agricultural Machinery Inc. Available online: http://www.yukseltarim.com/ (accessed on 4 September 2013).
- TS EN ISO 6892-1; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature (ISO 6892-1:2019). ISO: Geneva, Switzerland, 2020.
- HBM Datasheet: QuantumX MX840A. Doc. No: B2924-2.0 En 2011, 16.
- HBM Strain Gages and Accessories. Doc. No: S 1265-1.0 En 2011, 100.
- HBM Inc. DAQ Software|Data Acquisition Software|Catman|HBM. Available online: https://www.hbm.com/en/2290/catman-data-acquisition-software/?product_type_no=DAQ Software (accessed on 5 November 2022).
- Hoffmann, K. An Introduction to Measurements Using Strain Gages; Hottinger Baldwin Messtechnik GmbH: Darmstadt, Germany, 1989. [Google Scholar]
- Vishay. M-Bond 200 Adhesive—Material Safety Datasheet (MSDS#MGM007T /.14027); Vishay: Malvern, PA, USA, 2007. [Google Scholar]
- MKE. MKE Norm Special Steel Types Catalog, 1st ed.; MKE, Ed.; Machinery and Chemical Industry Corporation (MKE): Ankara, Turkey, 1978. [Google Scholar]
- Davis, J.R. Metals Handbook; CRC Press: Boca Raton, FL, USA, 1998; p. 2571. [Google Scholar]
- Kutay, G. The Machinist’s Guide, 1st ed.; Birsen Publication: Ankara, Turkey, 2003; ISBN 9799755113424. [Google Scholar]
- Rice, R.C.; Jackson, J.L.; Bakuckas, J.; Thompson, S. Metallic Materials Properties Development and Standardization (MMPDS); U.S. Department of Transportation Federal Aviation Administration: Roanoke, VA, USA, 2003; ISBN 6094854004. [Google Scholar]
- Kulaksiz, O. Tables in Metal Profession (Metal Mesleğinde Tablolar); Turkish Republic Ministry of National Education: Istanbul, Turkey, 1995; ISBN 9751124123. [Google Scholar]
- Bringas, J.E. Handbook of Comparative World Steel Standards, 5th ed.; Bringas, J.E., Ed.; ASTM International: West Conshohocken, PA, USA, 2016; ISBN 978-0-8031-7077-3. [Google Scholar]
- Cardarelli, F. Materials Handbook: A Concise Desktop Reference, 2nd ed.; Springer London: London, UK, 2008; ISBN 9781846286681. [Google Scholar]
- Wakabayashi, N.; Ona, M.; Suzuki, T.; Igarashi, Y. Nonlinear Finite Element Analyses: Advances and Challenges in Dental Applications. J. Dent. 2008, 36, 463–471. [Google Scholar] [CrossRef] [PubMed]
- SolidWorks Doc. SolidWorks Simulation Premium: Nonlinearity Training Manual Document No: 22658021044-ENG0001; 22658021044-ENG0001; SolidWorks Corporation: Waltham, MA, USA, 2010. [Google Scholar]
- Schwer, L.E. An Overview of the PTC 60/V&V 10: Guide for Verification and Validation in Computational Solid Mechanics. Eng. Comput. 2007, 23, 245–252. [Google Scholar] [CrossRef]
- ANSYS. Product Doc. ANSYS Meshing User’s Guide: Skewness (Release 2019 R2); ANSYS Inc.: San Diego, CA, USA, 2019. [Google Scholar]
- Brys, G.; Hubert, M.; Struyf, A. A Robust Measure of Skewness. J. Comput. Graph. Stat. 2004, 13, 996–1017. [Google Scholar] [CrossRef]
- Kurowski, P. and Szabo, B. How to Find Errors in Finite-Element Models. Mach. Des. 1997, 1, 93–98. [Google Scholar]
- Celik, H.K.; Caglayan, N.; Topakci, M.; Rennie, A.E.W.; Akinci, I. Strength-Based Design Analysis of a Para-Plow Tillage Tool. Comput. Electron. Agric. 2020, 169, 105168. [Google Scholar] [CrossRef]
- Celik, H.K.; Rennie, A.E.W.; Akinci, I. Design and Structural Optimisation of a Tractor Mounted Telescopic Boom Crane. J. Brazilian Soc. Mech. Sci. Eng. 2017, 39, 909–924. [Google Scholar] [CrossRef]
- Celik, H.K.; Caglayan, N.; Çinar, R.; Ucar, M.; Ersoy, H.; Rennie, A.E.W. Stress Analysis of a Sample Marine Crane’s Boom under Static Loading Condition. In Proceedings of the 5th International Mechanical Engineering Forum 2012, Prague, Czech Republic, 20–22 June 2012; pp. 246–255. [Google Scholar]
- Caliskan, K. The Optimisation of Cab Protective Structure with Finite Element Method Simulation Verified with Laboratory Tests. Ph.D. Thesis, Ege University, İzmir, Turkey, 2011. [Google Scholar]
- Yurdem, H.; Degirmencioglu, A.; Cakir, E.; Gulsoylu, E. Measurement of Strains Induced on a Three-Bottom Moldboard Plough under Load and Comparisons with Finite Element Simulations. Meas. J. Int. Meas. Confed. 2019, 136, 594–602. [Google Scholar] [CrossRef]
- Degirmencioglu, A. Determination of Stress Under Load on a Three-Bottom Moulboard Plough (Research Project: 98 ZRF046); Scientific Research Projects Coordination Unit: Izmir, Turkey, 2003. [Google Scholar]
- Ruiz de Galarreta, S.; Jeffers, J.R.T.; Ghouse, S. A Validated Finite Element Analysis Procedure for Porous Structures. Mater. Des. 2020, 189, 108546. [Google Scholar] [CrossRef]
- Torre, R.; Brischetto, S. Experimental Characterization and Finite Element Validation of Orthotropic 3D-Printed Polymeric Parts. Int. J. Mech. Sci. 2022, 219, 107095. [Google Scholar] [CrossRef]
- Ariza, O.; Gilchrist, S.; Widmer, R.P.; Guy, P.; Ferguson, S.J.; Cripton, P.A.; Helgason, B. Comparison of Explicit Finite Element and Mechanical Simulation of the Proximal Femur during Dynamic Drop-Tower Testing. J. Biomech. 2015, 48, 224–232. [Google Scholar] [CrossRef]
- Krutz, G.; Thompson, L.; Claar, P. Design of Agricultural Machinery; John Wiley and Sons: New York, NY, USA, 1984; ISBN 047108672X. [Google Scholar]
- Kuna, M. Finite Elements in Fracture Mechanics; Solid Mechanics and Its Applications; Springer Netherlands: Dordrecht, The Netherlands, 2013; Volume 201, ISBN 978-94-007-6679-2. [Google Scholar]



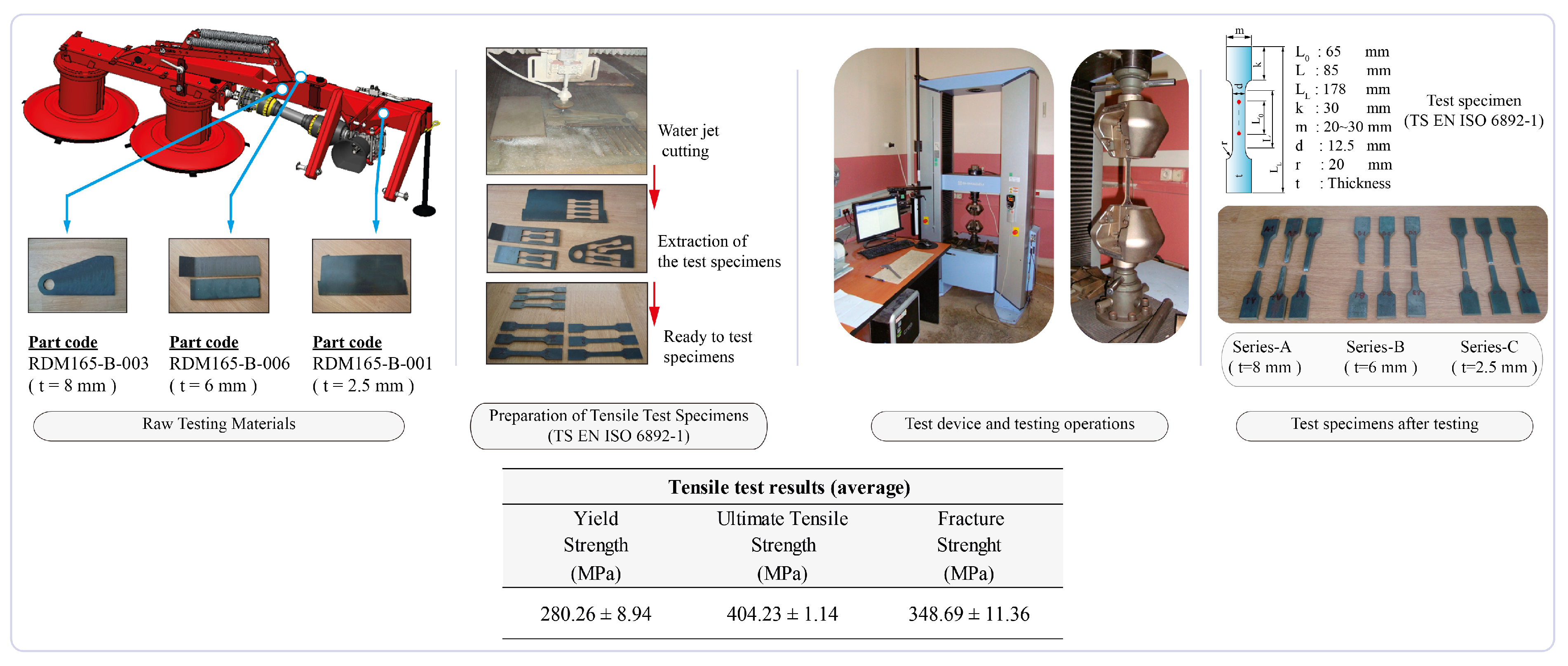


| Properties * | Unit | Components | |||
|---|---|---|---|---|---|
| Structural Steel | Spring (DIN EN 10270-1) | Key/Pin/Shaft (DIN 1.5755/31NiCr14/ AISI 3330) | Bolt-Nut Standard: 8.8 | ||
| Modulus of Elasticity | (GPa) | 210 | 210 | 210 | 210 |
| Poisson’s Ratio | (-) | 0.30 | 0.28 | 0.30 | 0.30 |
| Yield Strength (Max.) | (MPa) | 280 ** | 700 | 550 | 640 |
| Ultimate Tensile Strength (Max.) | (MPa) | 404 ** | 1000 | 750 | 800 |
| Density | (kg m−3) | 7850 | 7850 | 7850 | 7850 |
| Tractor Speed | |||
|---|---|---|---|
| (km h−1) | |||
| Test Order | Asphalt Road | Dirt Road | In-Field Road |
| Tractor Speed-01 | 8.50 ± 0.48 | 8.81 ± 0.03 | 8.55 ± 0.60 |
| Tractor Speed-02 | 13.44 ± 1.20 | 14.01 ± 0.37 | 12.67 ± 0.53 |
| Tractor Speed-03 | 23.40 ± 2.53 | 24.96 ± 0.10 | 17.55 ± 2.18 |
| Strain-Gauge No | Part Code | ||
|---|---|---|---|
| RDM165-A-004 | RDM165-B-003 | RDM165-B-004 | |
| SG-01 | 3.02 | 3.51 | 3.20 |
| SG-02 | 2.43 | 3.51 | 5.22 |
| SG-03 | 4.12 | 4.12 | 4.24 |
| SG-04 | - | 3.24 | 4.27 |
| SG-05 | - | 4.34 | 2.97 |
| SG-06 | - | 2.33 | 3.10 |
| SG-07 | - | 6.59 | 3.58 |
| Average | 3.19 ± 0.86 | 3.95 ± 1.33 | 3.80 ± 0.82 |
| Overall Average | 3.65 ± 0.40 | ||
| Strain-Gauge No | FEA Equivalent Stress (von Mises) (MPa) | ||
|---|---|---|---|
| Part Code | |||
| RDM165-A-004 | RDM165-B-003 | RDM165-B-004 | |
| SG-01 | 16.497 | 4.226 | 8.110 |
| SG-02 | 6.716 | 6.678 | 6.892 |
| SG-03 | 8.122 | 8.386 | 5.379 |
| SG-04 | - | 11.506 | 10.329 |
| SG-05 | - | 10.643 | 13.247 |
| SG-06 | - | 10.507 | 13.354 |
| SG-07 | - | 5.911 | 8.112 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Celik, H.K.; Akinci, I.; Caglayan, N.; Rennie, A.E.W. Structural Strength Analysis of a Rotary Drum Mower in Transportation Position. Appl. Sci. 2023, 13, 11338. https://doi.org/10.3390/app132011338
Celik HK, Akinci I, Caglayan N, Rennie AEW. Structural Strength Analysis of a Rotary Drum Mower in Transportation Position. Applied Sciences. 2023; 13(20):11338. https://doi.org/10.3390/app132011338
Chicago/Turabian StyleCelik, H. Kursat, Ibrahim Akinci, Nuri Caglayan, and Allan E. W. Rennie. 2023. "Structural Strength Analysis of a Rotary Drum Mower in Transportation Position" Applied Sciences 13, no. 20: 11338. https://doi.org/10.3390/app132011338
APA StyleCelik, H. K., Akinci, I., Caglayan, N., & Rennie, A. E. W. (2023). Structural Strength Analysis of a Rotary Drum Mower in Transportation Position. Applied Sciences, 13(20), 11338. https://doi.org/10.3390/app132011338