The Design of a System for the Induction Hardening of Steels Using Simulation Parameters
Abstract
:1. Introduction
- Heating the steel to a temperature slightly above the critical temperature;
- Holding the steel at this temperature until complete normalization and the completion of structural transformations;
- Cooling the steel at a rate necessary to obtain the martensitic structure that gives the steel excellent hardness.
- Lower energy consumption;
- Higher productivity;
- The greater possibility of automating the process;
- Higher-quality tempered steel;
- Less material deformation.
2. Materials and Methods
2.1. Realization of the Prototype System for Induction Hardening
- Power supply: 3 × 400 V, 50 Hz;
- Nominal power: 15 kW;
- The inductance of the inductor coil: 32–50 μH;
- Maximum energy efficiency: 95%;
- Output frequency: 10–25 kHz.

2.2. Inductor and Batch Modeling
- Batch: carbon steel;
- Inductor diameter: Dind = 100 mm;
- Inductor length: hind = 800 mm;
- Number of inductor turns: 60;
- Batch diameter: Dch = 35 mm;
- Power supply frequency: 10–25 kHz;
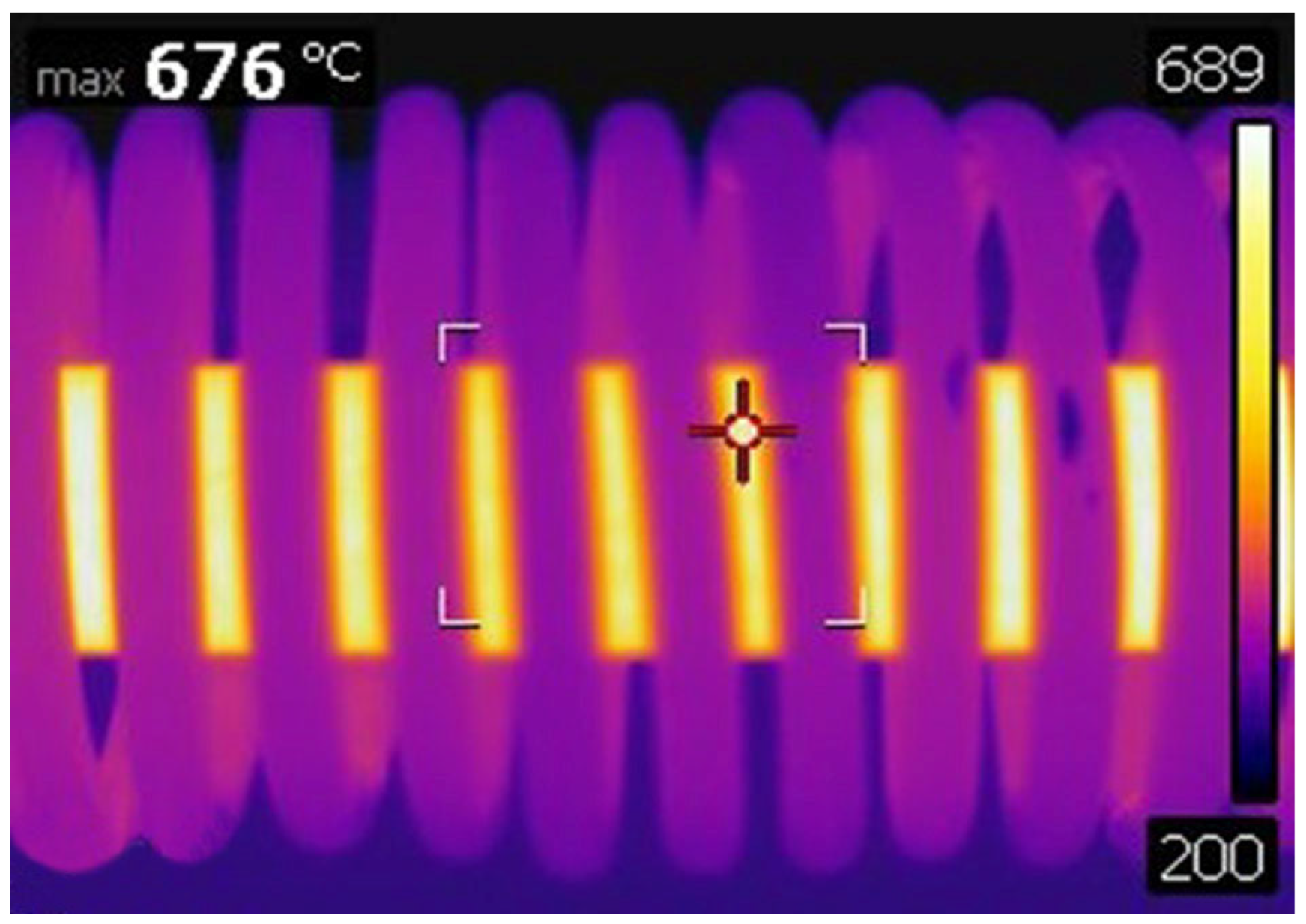
- Maximum batch temperature: 800 °C.
2.3. Energy Efficiency
- -
- Network power consumption: Pnet = 12.87 kW;
- -
- DC link voltage: VDC = 250 V;
- -
- DC link current: IDC = 50.92 A;
- -
- Inductor effective current: Iind eff = 120 A;
- -
- Equivalent serial resistance: Rind,ch = 0.85 Ω;
- -
- Power of induction heating: Pheat = 0.85 × 1202 = 12.24 kW.
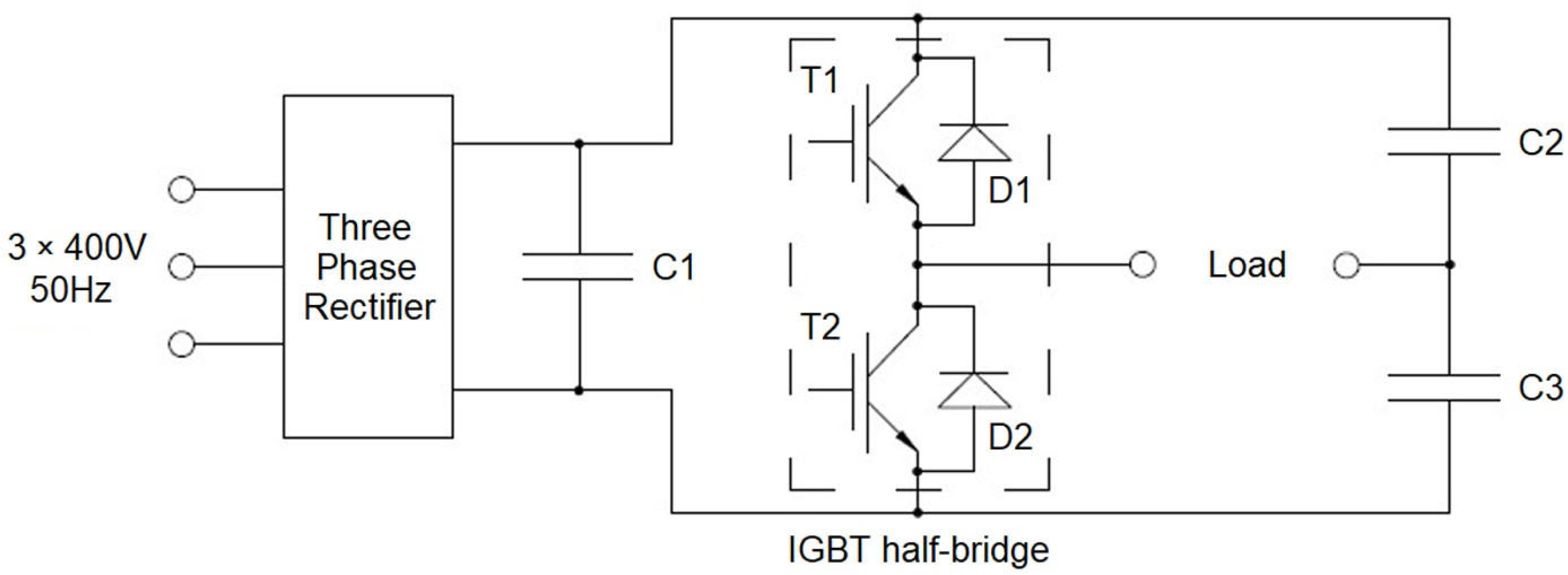
2.4. Simulation of a Half-Bridge Resonant Inverter
2.5. Simulation Scheme and Parameters
3. Results and Discussion
4. Conclusions
- -
- The use of simulation was successfully performed for the system optimization. The parameters from the simulation had differences ranging from 1.3% to 4.8% compared to the measurements in the application of the equipment;
- -
- The optimized system achieves impressive utilization rates between 75.3% and 95.1%;
- -
- The designed system achieved the goals of flexibility since it was used for various steel grades, and was inexpensive and economical in use as well as being portable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gandhewar, V.R.; Bansod, S.V.; Borade, A.B. Induction Furnace: A Review. Int. J. Eng. Technol. 2011, 3, 277–284. [Google Scholar]
- Mühlbauer, A. History of Induction Heating and Melting; Vulkan-Verlag GmbH: Essen, Germany, 2008. [Google Scholar]
- Schmitz, W.; Trauzeddel, D. Latest Developments in Recycling Production Residues Employing Coreless Induction Furnaces. In Proceedings of the European Metallurgical Conference - EMC 2013, Weimar, Germany, 23–26 June 2013. [Google Scholar]
- ECM-FURNACES. Available online: https://www.ecm-furnaces.com/induction-melting-furnaces/laboratory-induction-furnace (accessed on 1 July 2023).
- Brogden, S.D. Applications for Induction Furnaces in Manufacturing Technology Courses. Ph.D. Thesis, California State University, Fresno, CA, USA, 2015. [Google Scholar]
- Hang, N.T.T.; Lüdtke, U. Numerical Simulation of Induction Channel Furnace to Investigate Efficiency for low Frequencies. Proc. IOP Conf. Ser. Mater. Sci. Eng. 2018, 355, 012012. [Google Scholar] [CrossRef]
- Hou, Y.J.; Tian, H.M.; Qu, X.D.; Teng, J.Z.; Liu, G.X.; Li, Y. Development of digital control system for medium frequency induction furnaces. Proc. IOP Conf. Ser. Earth Environ. Sci. 2018, 188, 012005. [Google Scholar] [CrossRef]
- Solanki, V.; Joshi, S.R.; Chavda, J.; Mokariya, K. Simulation of Induction Furnace and Comparison with Actual Induction Furnace. Int. J. Recent Technol. Eng. 2013, 2, 105–109. [Google Scholar]
- Gbadamosi, S.L.; Melodi, A.O. Harmonic distortion from induction furnace loads in a steel production plant. Netw. Complex Syst. 2013, 3, 8–16. [Google Scholar]
- Yılmaz, İ.; Durna, E.; Ermiş, M. Design and Implementation of a Hybrid System for the Mitigation of PQ Problems of Medium-Frequency Induction Steel-Melting Furnaces. IEEE Trans. Ind. Appl. 2016, 52, 2700–2713. [Google Scholar] [CrossRef]
- Tan, A. Modeling and Analysis of Power Quality Compensation Systems for Current Source Inverter Based Induction Furnace. Master’s Thesis, Institute of Natural and Applied Sciences, Çukurova University, Adana, Turkey, 2011. [Google Scholar]
- Asai, S. Birth and Recent Activities of Electromagnetic Processing of Materials. ISIJ Int. 1989, 29, 981–992. [Google Scholar] [CrossRef]
- Biesuz, M.; Saunders, T.; Ke, D.; Reece, M.J.; Hu, C.; Grasso, S. A review of electromagnetic processing of materials (EPM): Heating, sintering, joining and forming. J. Mater. Sci. Technol. 2021, 69, 239–272. [Google Scholar] [CrossRef]
- Moghanizadeh, A.; Ashrafizadeh, F.; Bazmara, M. Development the Flexible Magnetic Abrasive Finishing Process by Transmitting the Magnetic Fields. Int. J. Adv. Manuf. Technol. 2022, 119, 2115–2125. [Google Scholar] [CrossRef]
- Marczak, M.; Zawora, J. Finite Element Analysis of the Magnetic Field Distribution in a Magnetic Abrasive Finishing Station and its Impact on the Effects of Finishing Stainless Steel AISI 304L. Metals 2021, 11, 194. [Google Scholar] [CrossRef]
- Michalowska, J.; Józwik, J. Prediction of the Parameters of Magnetic Field of CNC Machine Tools. Prz. Elektrotech. 2019, 95, 134–136. [Google Scholar] [CrossRef]
- Rudnev, V.I.; Loveless, D. 12.15—Induction Hardening: Technology, Process Design, and Computer Modeling. In Comprehensive Materials Processing; Hashmi, S., Batalha, G.F., Van Tyne, C.J., Yilbas, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 12, pp. 489–580. [Google Scholar]
- Wu, B. High-Power Converters and AC Drives; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Remya, M.N.; Barai, M. Study of Induction Heating using Half Bridge Series Resonant Inverter. Int. J. Sci. Eng. Res. 2018, 9, 1520–1526. [Google Scholar]
- Babu, P.D.; Balasubramanian, K.R.; Buvanashekaran, G. Laser Surface Hardening: A review. Int. J. Surf. Sci. Eng. 2011, 5, 131–151. [Google Scholar] [CrossRef]
- Choo, S.-H.; Lee, S.; Golkovski, M.G. Effects of Accelerated Electron Beam Irradiation on Surface Hardening and Fatigue Properties in an AISI 4140 Steel used for Automotive Crankshaft. Mater. Sci. Eng. 2000, 293, 56–70. [Google Scholar] [CrossRef]
- Ahmed, O.M.H.; Song, Y. A Review of Common Beam Hardening Correction Methods for Industrial X-ray Computed Tomography. Sains Malays. 2018, 47, 1883–1890. [Google Scholar] [CrossRef]
- Skeeba, V.Y.; Ivancivsky, V.V.; Martyushev, N.V. Peculiarities of High-Energy Induction Heating during Surface Hardening in Hybrid Processing Conditions. Metals 2021, 11, 1354. [Google Scholar] [CrossRef]
- Eastwood, M.D.; Haapala, K.R. An Induction Hardening Process Model to Assist Sustainability Assessment of a Steel Bevel Gear. Int. J. Adv. Manuf. Technol. 2015, 80, 1113–1125. [Google Scholar] [CrossRef]
- Brøtan, V.; Berg, O.Å.; Sørby, K. Additive Manufacturing for Enhanced Performance of Molds. Procedia CIRP 2016, 54, 186–190. [Google Scholar] [CrossRef]
- Choi, J.; Lee, S. High-Frequency Heat Treatment of AISI 1045 Specimens and Current Calculations of the Induction Heating Coil Using Metal Phase Transformation Simulations. Metals 2020, 10, 1484. [Google Scholar] [CrossRef]
- Derouiche, K.; Garois, S.; Champaney, V.; Daoud, M.; Traidi, K.; Chinesta, F. Data-Driven Modeling for Multiphysics Parametrized Problems-Application to Induction Hardening Process. Metals 2021, 11, 738. [Google Scholar] [CrossRef]
- Cajner, F.; Smoljan, B.; Landek, D. Computer simulation of induction hardening. J. Mater. Process. Technol. 2004, 157–158, 55–60. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, D.; Liu, Y.; Li, G. Influence of Induction Hardening Process on Camshafts’ Residual Stresses. Arab. J. Sci. Eng. 2020, 45, 9651–9659. [Google Scholar] [CrossRef]
- Tong, D.; Gu, J.; Yang, F. Numerical simulation on induction heat treatment process of a shaft part: Involving induction hardening and tempering. J. Mater. Process. Technol. 2018, 262, 277–289. [Google Scholar] [CrossRef]
- Garois, S.; Daoud, M.; Chinesta, F. Data-Driven Inverse Problem for Optimizing the Induction Hardening Process of C45 Spur-Gear. Metals 2023, 13, 997. [Google Scholar] [CrossRef]
- Asadzadeh, M.Z.; Roppert, K.; Raninger, P. Material Data Identification in an Induction Hardening Test Rig with Physics-Informed Neural Networks. Materials 2023, 16, 5013. [Google Scholar] [CrossRef] [PubMed]
- Denk, F.; Haehre, K.; Simon, C.; Eizaguirre, S.; Heidinger, M.; Kling, R.; Heering, W. 25 kW High Power Resonant Inverter Operating at 2.5 MHz based on SiC SMD phase-leg modules. In Proceedings of the PCIM Europe 2018: International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 5–7 June 2018. [Google Scholar]
- Haema, J.; Phudungthin, R. Full bridge resonant inverter for blade induction heating application. Energy Procedia 2019, 156, 391–395. [Google Scholar] [CrossRef]
- Hammouma, C.; Zeroug, H. Enhanced frequency adaptation approaches for series resonant inverter control under workpiece permeability effect for induction hardening applications. Eng. Sci. Technol. Int. J. 2022, 27, 101006. [Google Scholar] [CrossRef]
- Kierepka, K.; Legutko, P.; Zimoch, P.; Kasprzak, M. Dual-frequency induction heating for gear hardening: Converter, resonant circuit, and FEM modelling. IET Power Electron. 2018, 11, 2396–2402. [Google Scholar] [CrossRef]
- Kilic, V.T.; Unal, E.; Demir, H.V. High-efficiency flow-through induction heating. IET Power Electron. 2020, 13, 2119–2126. [Google Scholar] [CrossRef]
- ALLDATASHEET. Available online: https://www.alldatasheet.com/datasheet-pdf/pdf/27318/TI/SG3524.html (accessed on 11 July 2023).
- ALLDATASHEET. Available online: https://www.alldatasheet.com/datasheet-pdf/pdf/609004/IRF/IR2213.html (accessed on 11 July 2023).
- Kokuhennadige, Y.; Billah, M.M.; Hietanen, J.-M.; Lind, J. Induction Heater for Melting Aluminum; School of Electrical Engineering, Automation and Electrical Engineering (AEE) Master’s Programme; Aalto University: Helsinki, Finland, 2019. [Google Scholar]
- Radetić, R. Small Induction Heating Devices—Theory and Practice; Infoelektronika: Niš, Serbia, 2019. [Google Scholar]









| Measurement | Equipment |
|---|---|
| V, I, R, L | 0.1% class instruments |
| Waveform, frequency | Oscilloscope ROHDE & SCHWARZ RTB2004 (Munich, Germany) |
| Power (active, reactive) | Digital Energy meter Saving Electronics DTSU 1218 (Jiangsu, China) |
| Temperature | Thermography camera FLIR T420, FLIR Systems, Inc., (Santa Barbara, CA, USA) |
| Parameter | Measurement | Simulation |
|---|---|---|
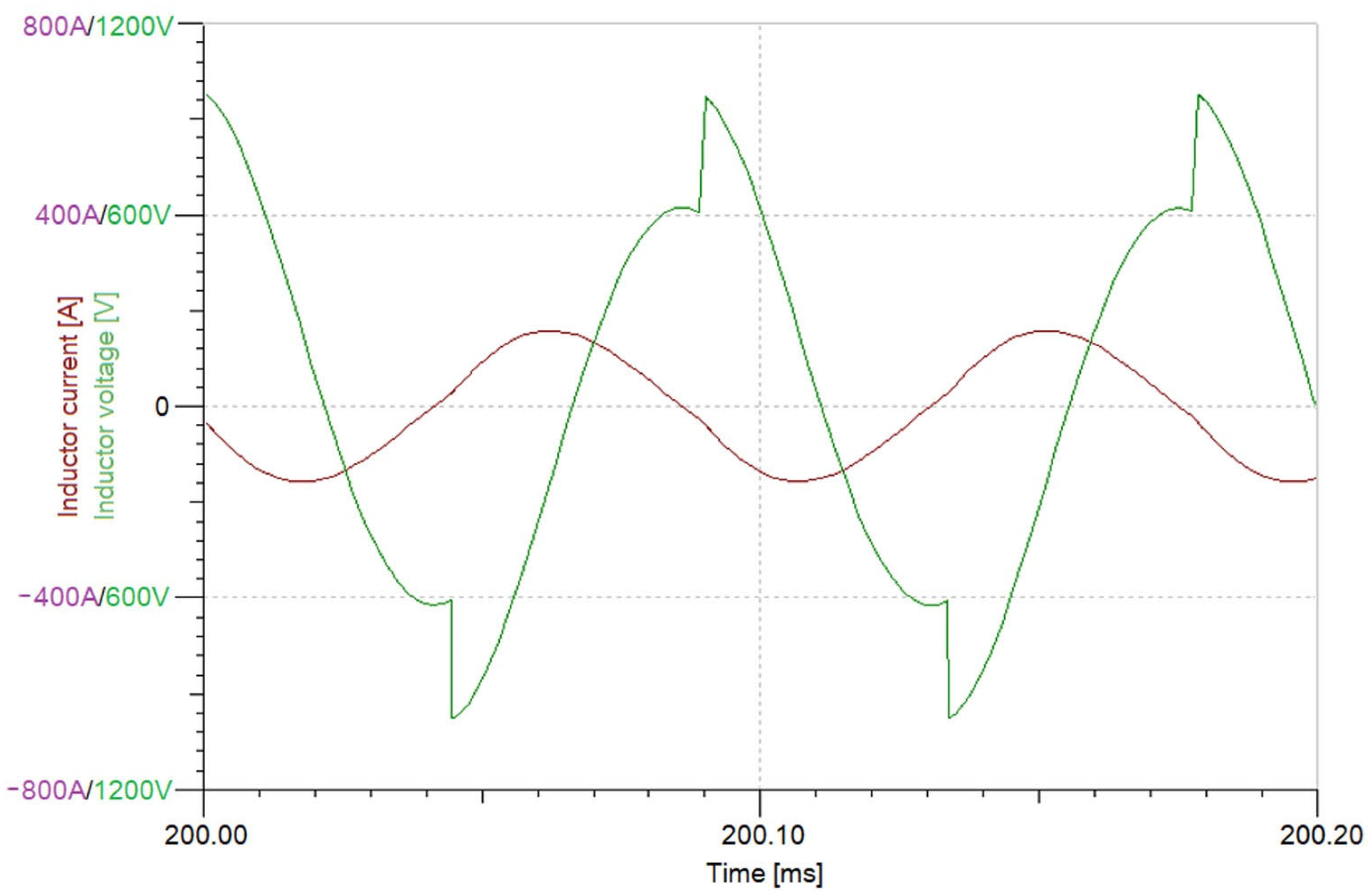
| Maximum inductor current [A] | 154.7 | 158.5 |
| Maximum inductor voltage [V] | 610.4 | 618.2 |
| Voltage spike [V] | 415.3 | 396.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stević, Z.; Dimitrijević, S.P.; Stević, M.; Stolić, P.; Petrović, S.J.; Radivojević, M.; Radovanović, I. The Design of a System for the Induction Hardening of Steels Using Simulation Parameters. Appl. Sci. 2023, 13, 11432. https://doi.org/10.3390/app132011432
Stević Z, Dimitrijević SP, Stević M, Stolić P, Petrović SJ, Radivojević M, Radovanović I. The Design of a System for the Induction Hardening of Steels Using Simulation Parameters. Applied Sciences. 2023; 13(20):11432. https://doi.org/10.3390/app132011432
Chicago/Turabian StyleStević, Zoran, Stevan P. Dimitrijević, Miša Stević, Predrag Stolić, Sanja J. Petrović, Milan Radivojević, and Ilija Radovanović. 2023. "The Design of a System for the Induction Hardening of Steels Using Simulation Parameters" Applied Sciences 13, no. 20: 11432. https://doi.org/10.3390/app132011432
APA StyleStević, Z., Dimitrijević, S. P., Stević, M., Stolić, P., Petrović, S. J., Radivojević, M., & Radovanović, I. (2023). The Design of a System for the Induction Hardening of Steels Using Simulation Parameters. Applied Sciences, 13(20), 11432. https://doi.org/10.3390/app132011432






