Elastoplastic Analysis of Frame Structures Using Radial Point Interpolation Meshless Methods
Abstract
1. Introduction
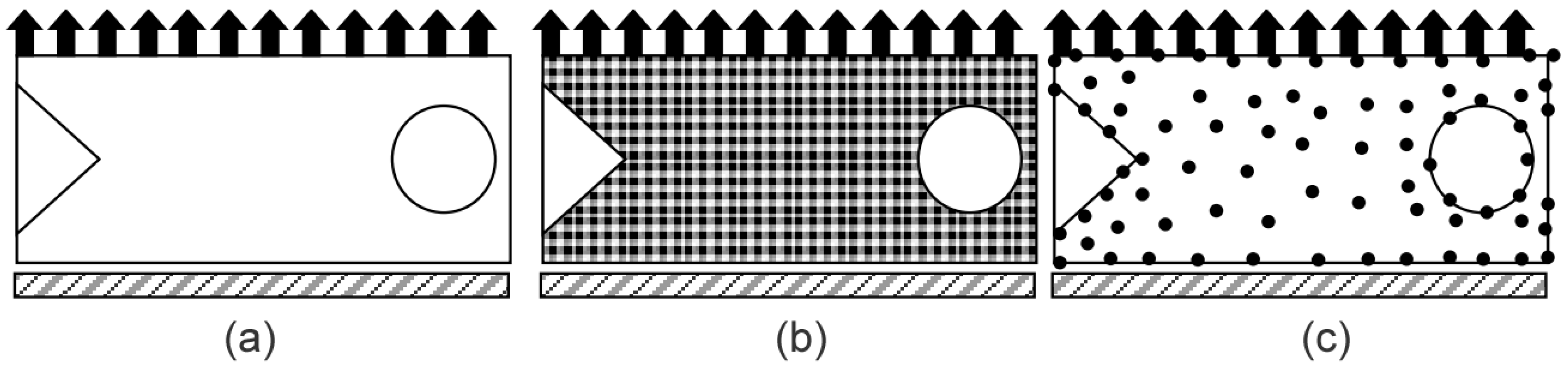
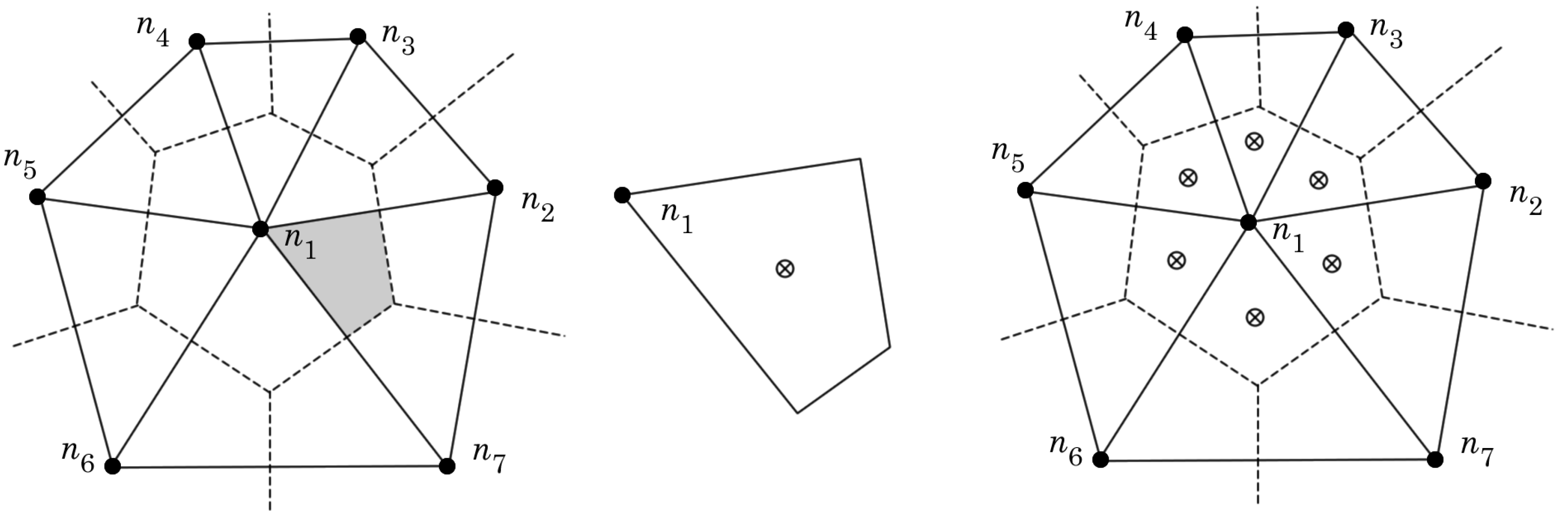
2. Radial Point Interpolation Meshless Methods
3. Elastoplastic Model
3.1. Elastoplastic Constitutive Matrix
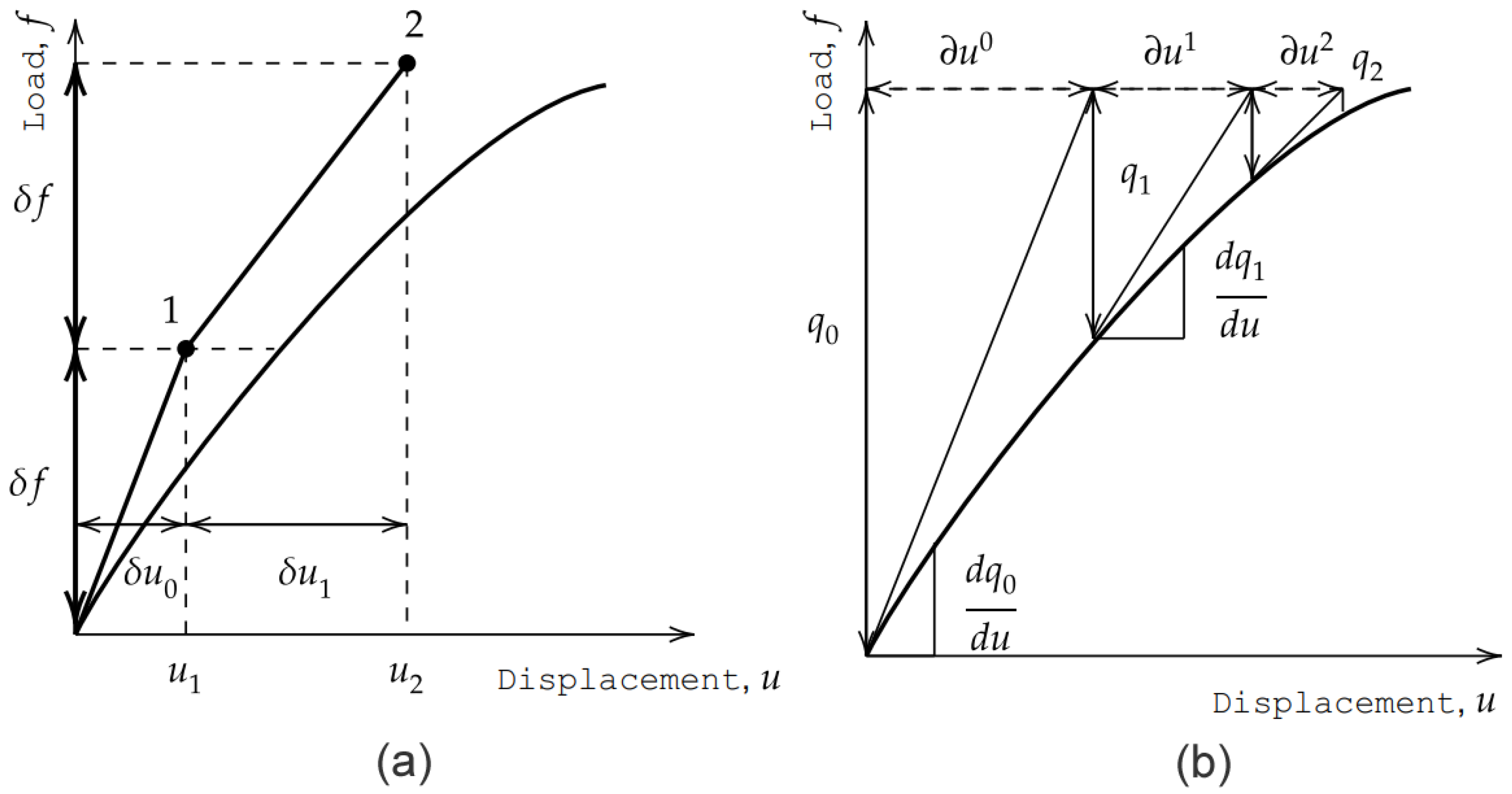
3.2. Non-Linear Solution Algorithm
4. Numerical Results
4.1. Elastoplastic Analysis of 2D Frames
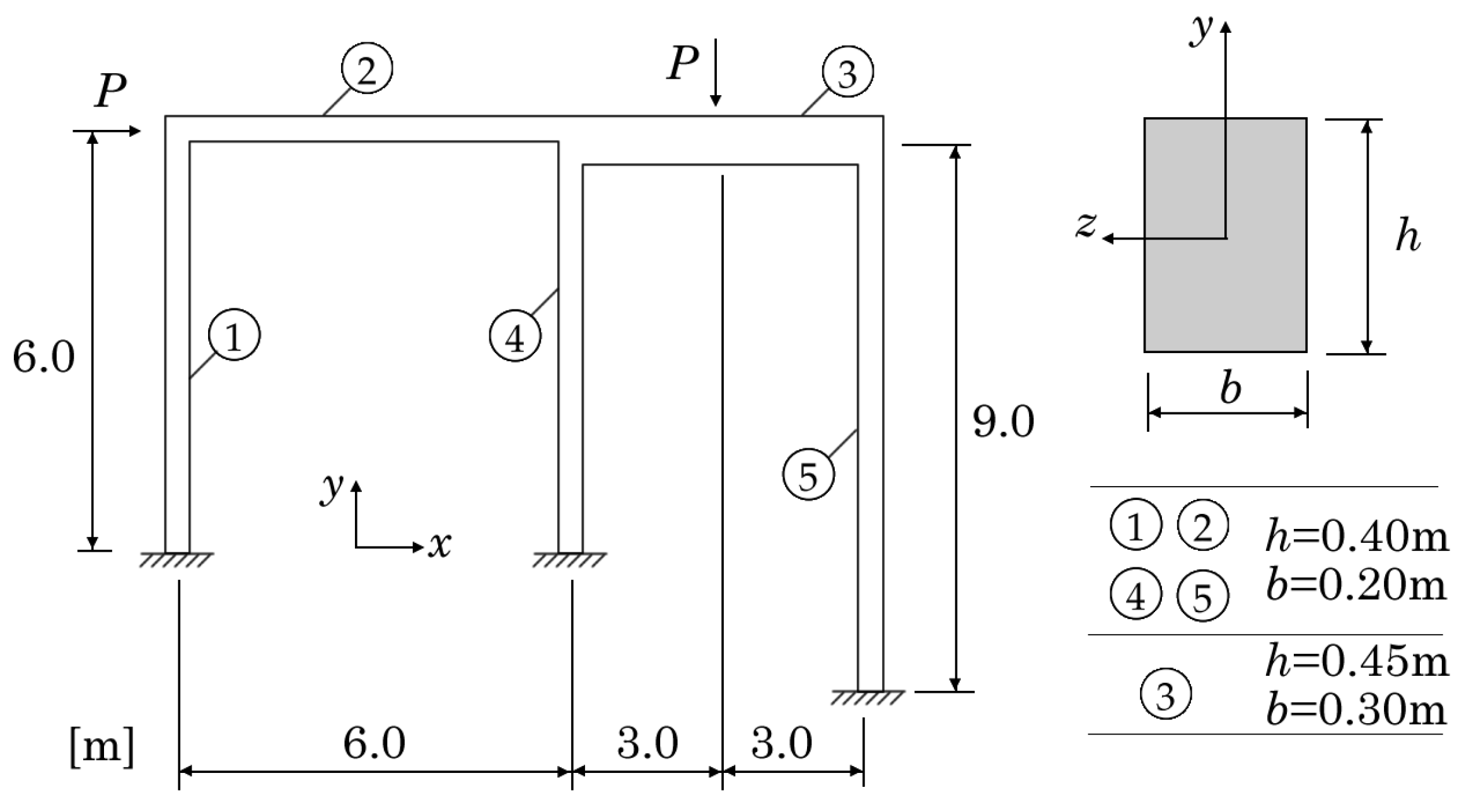
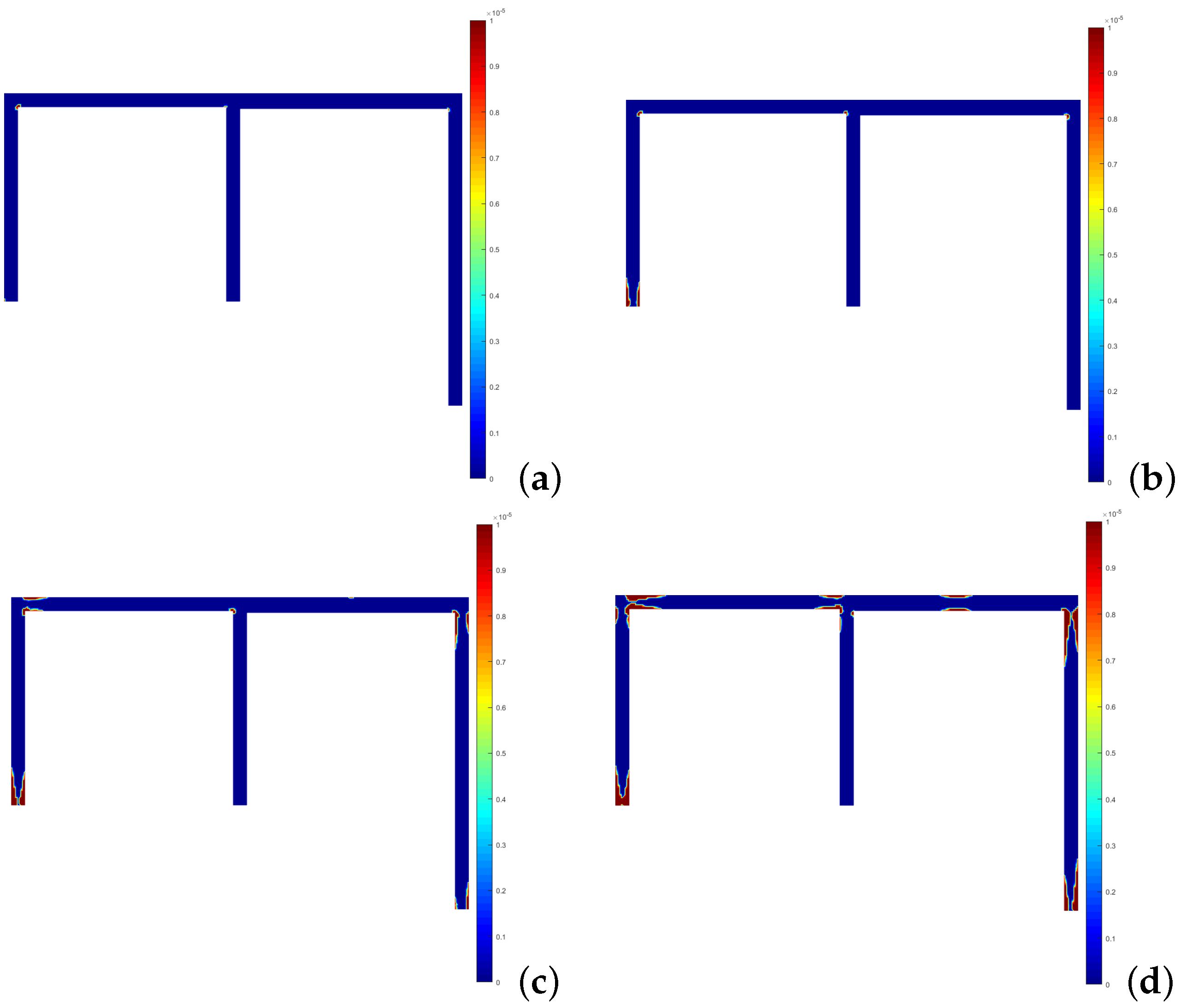
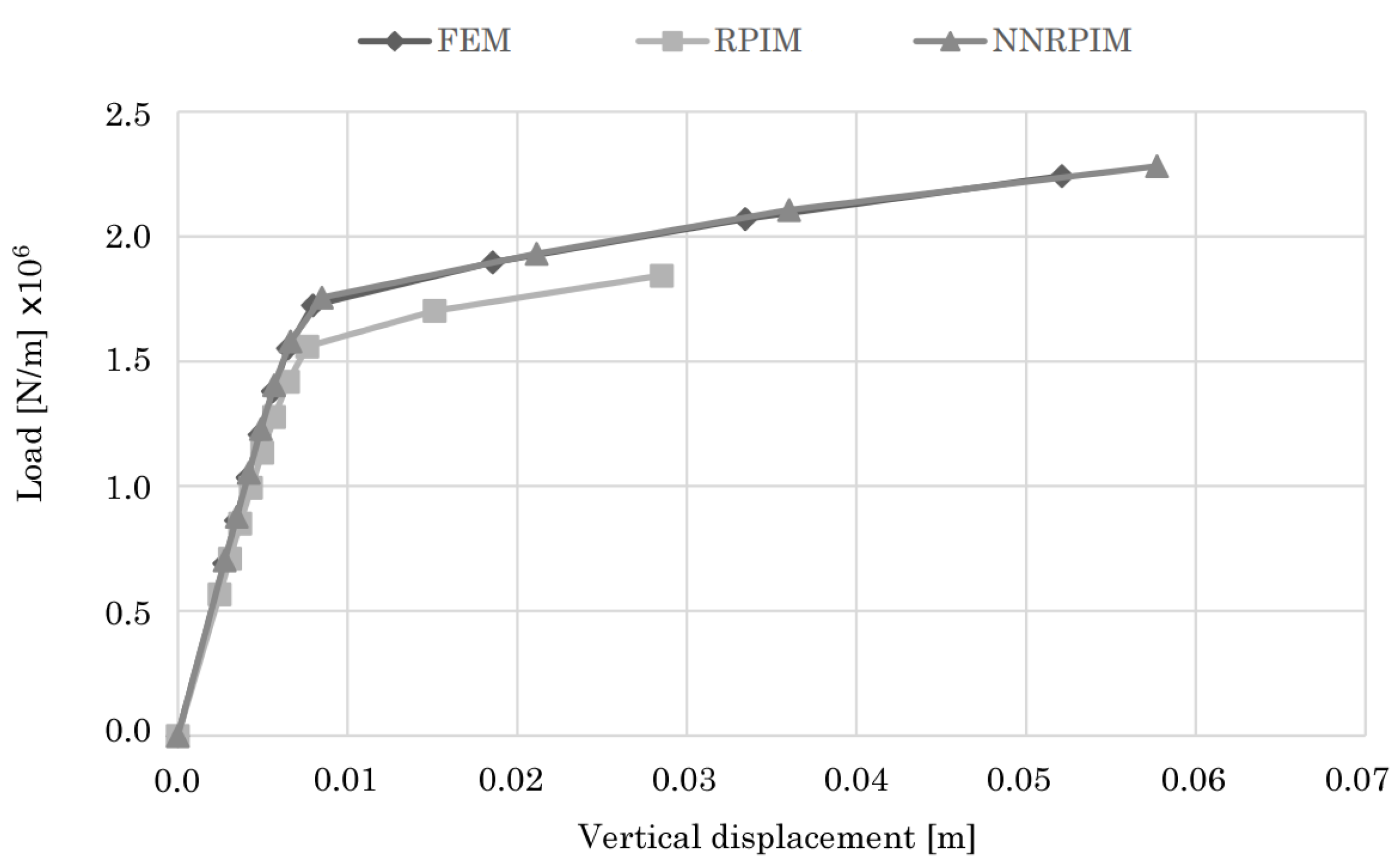
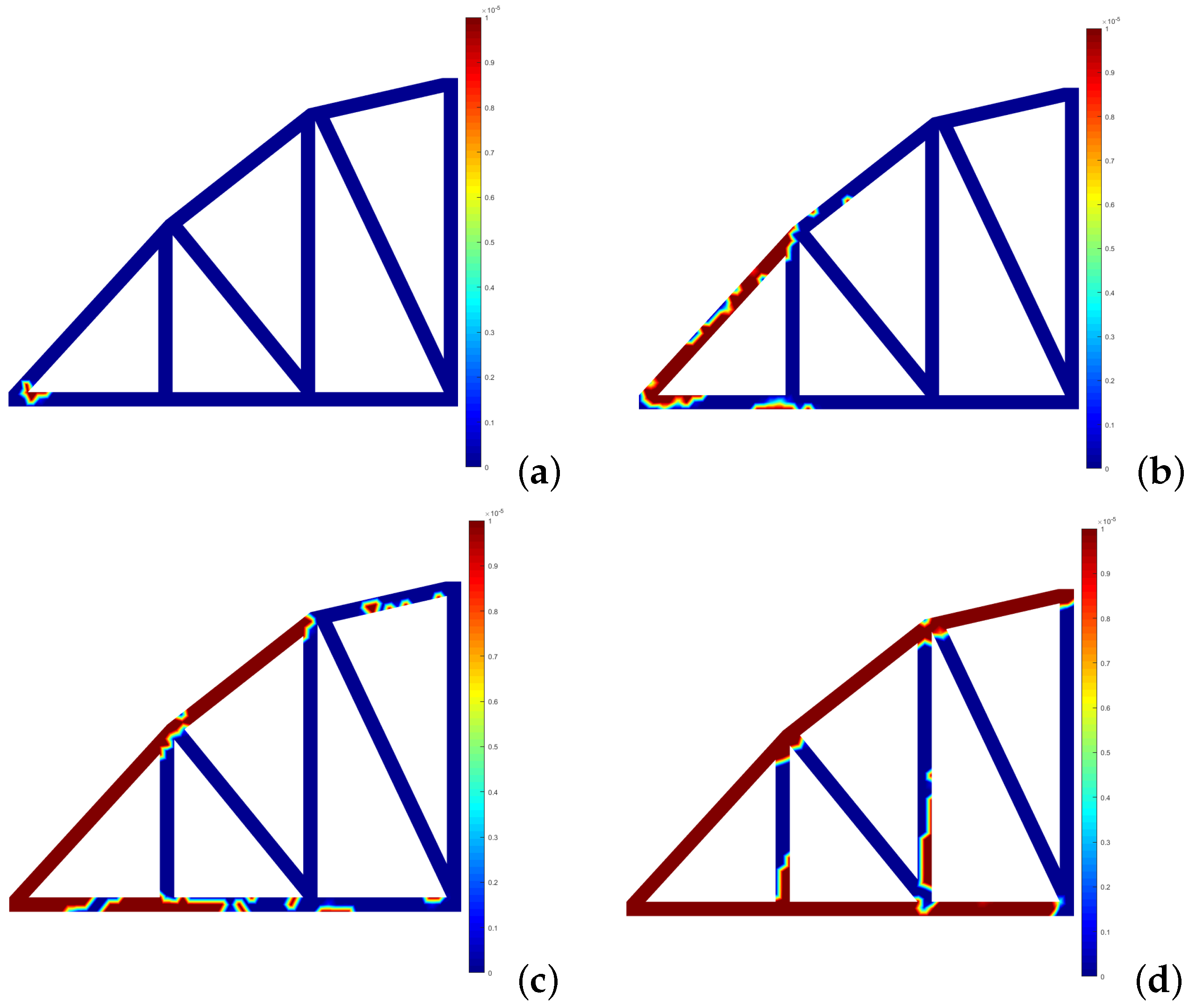
4.1.1. Two-Bay Asymmetric Frame
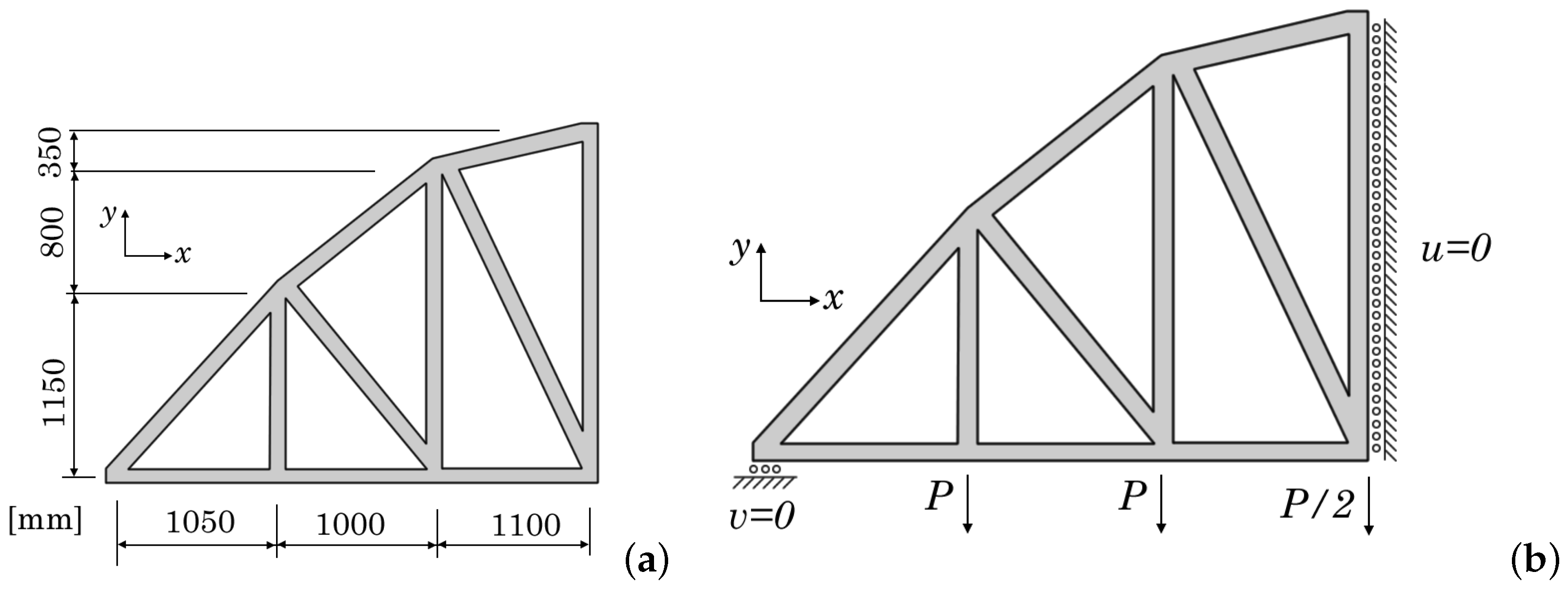
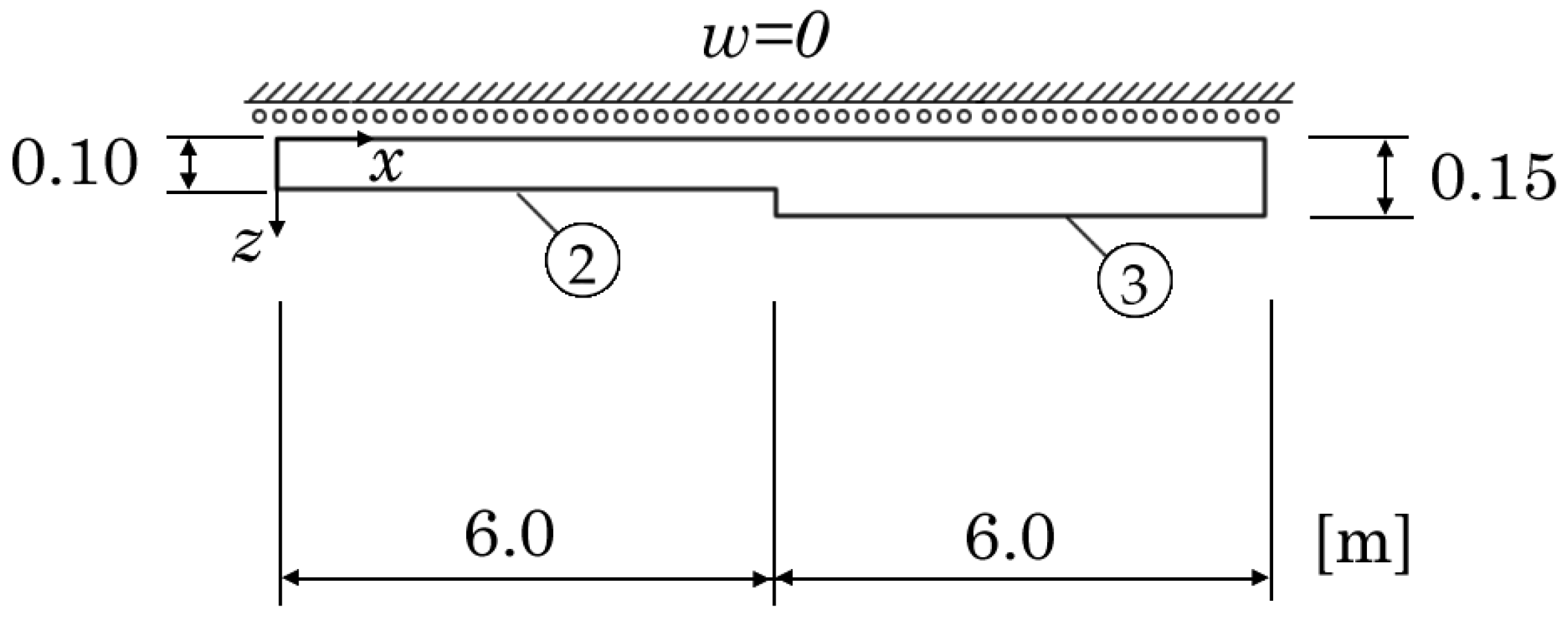
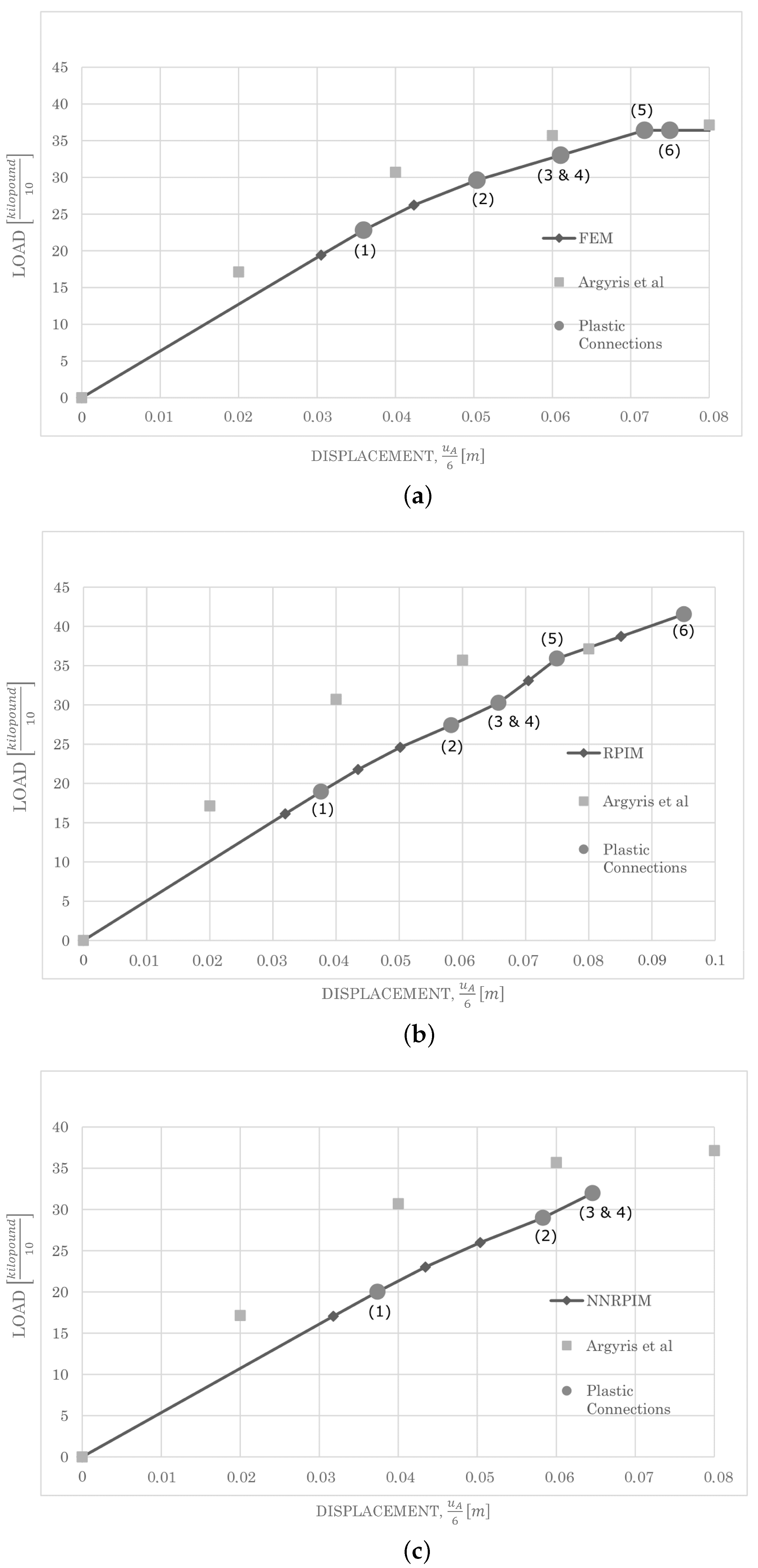
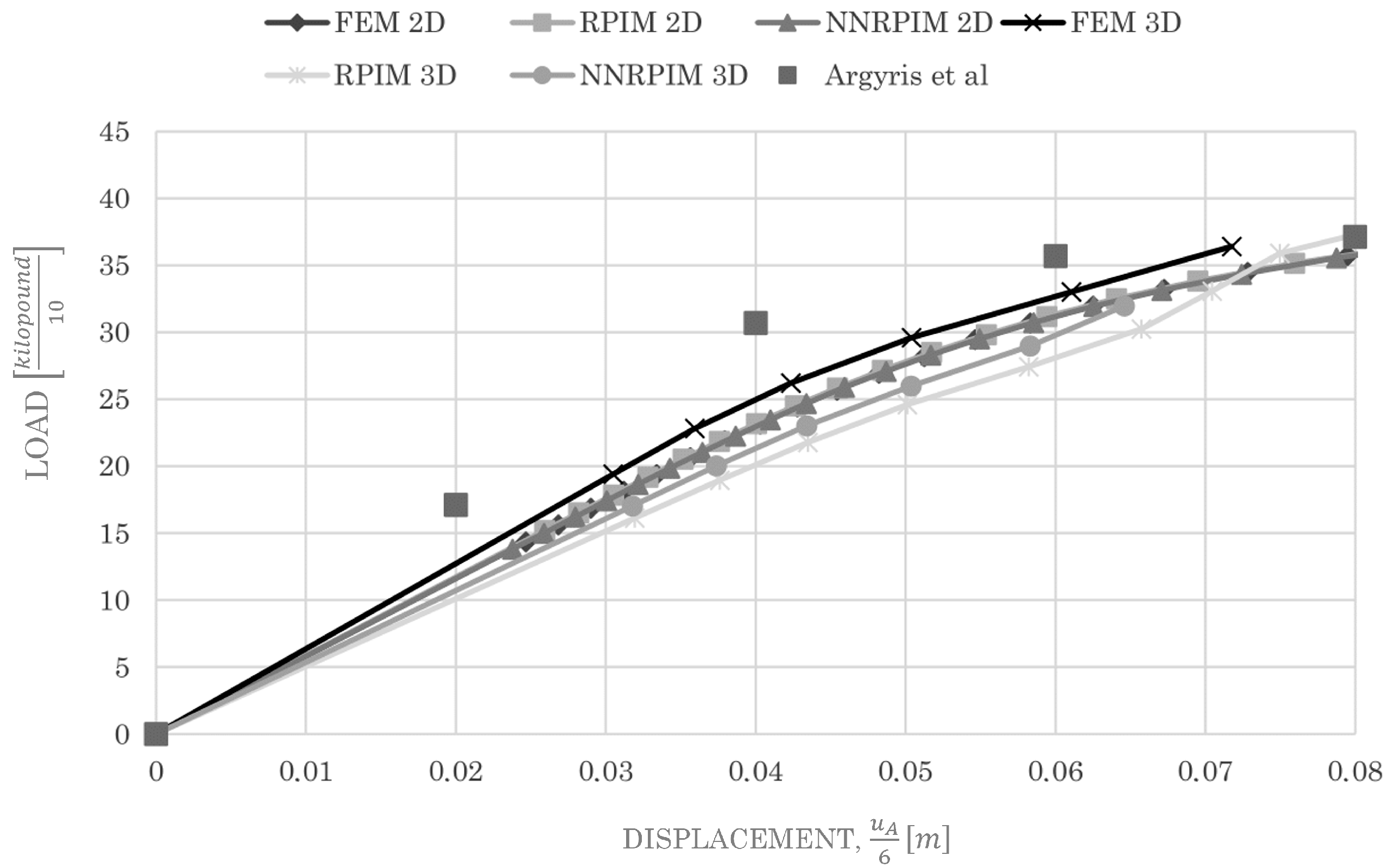
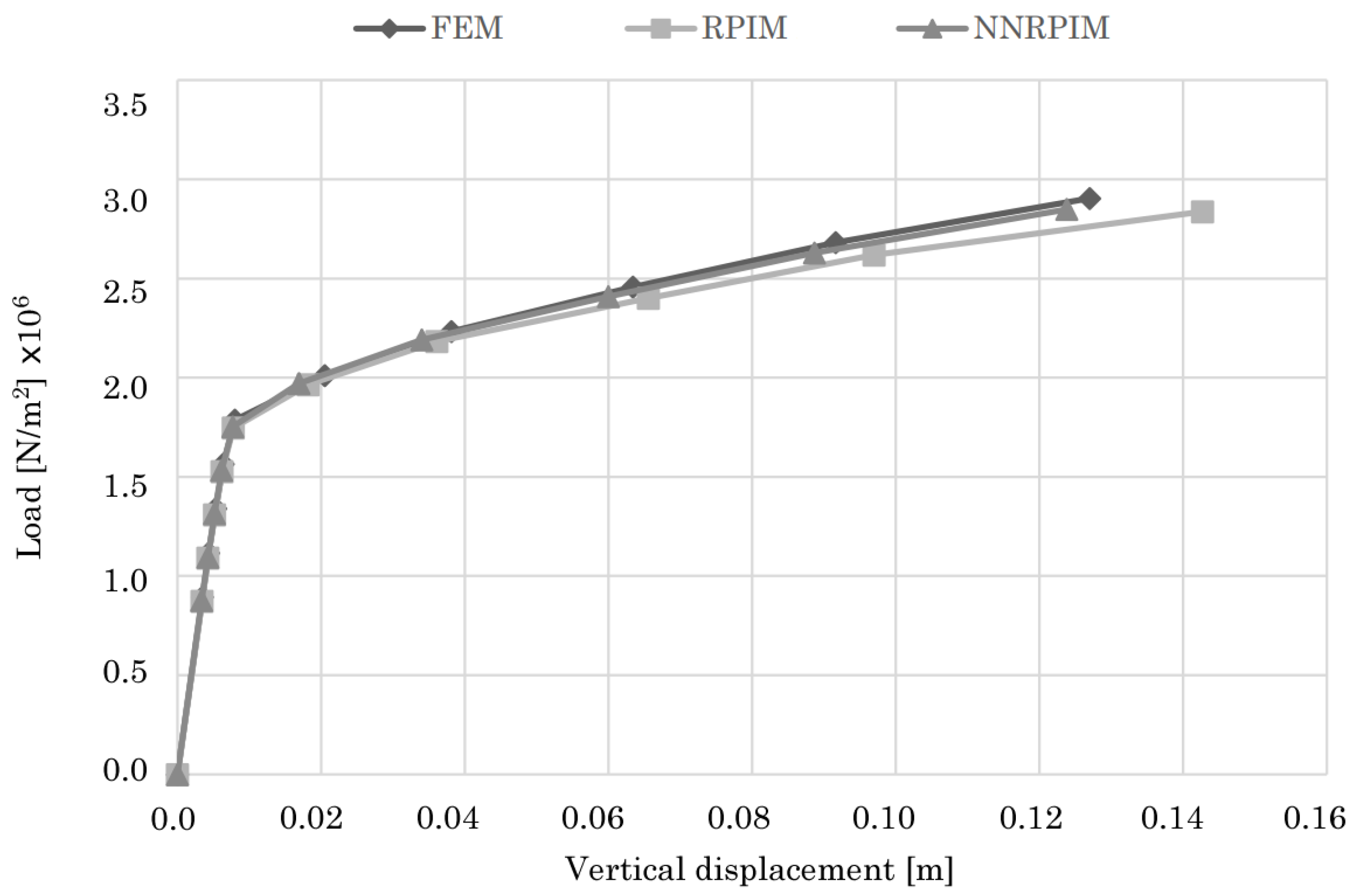
4.1.2. Bowstring Bridge
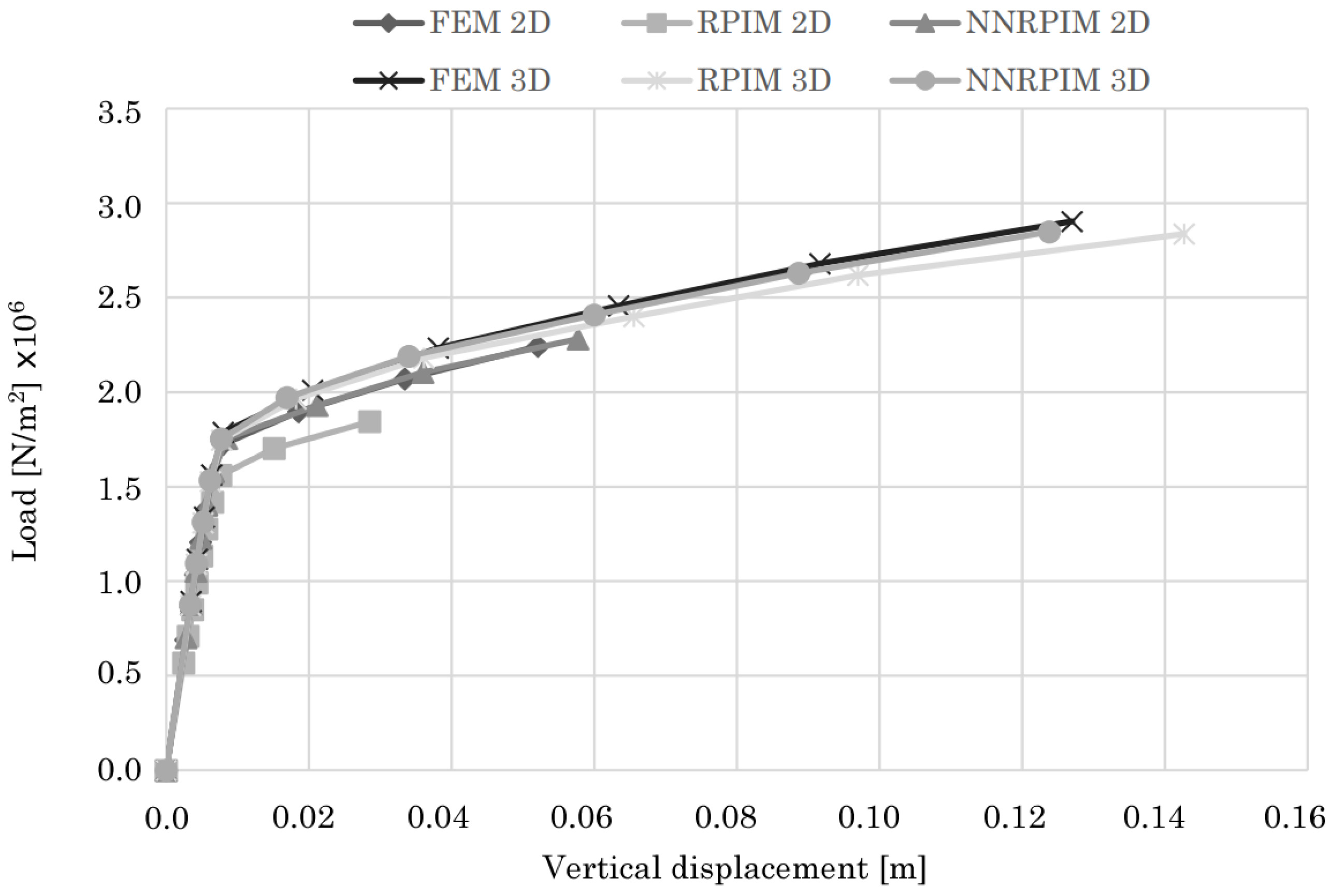
4.2. Elastoplastic Analysis of 3D Structures
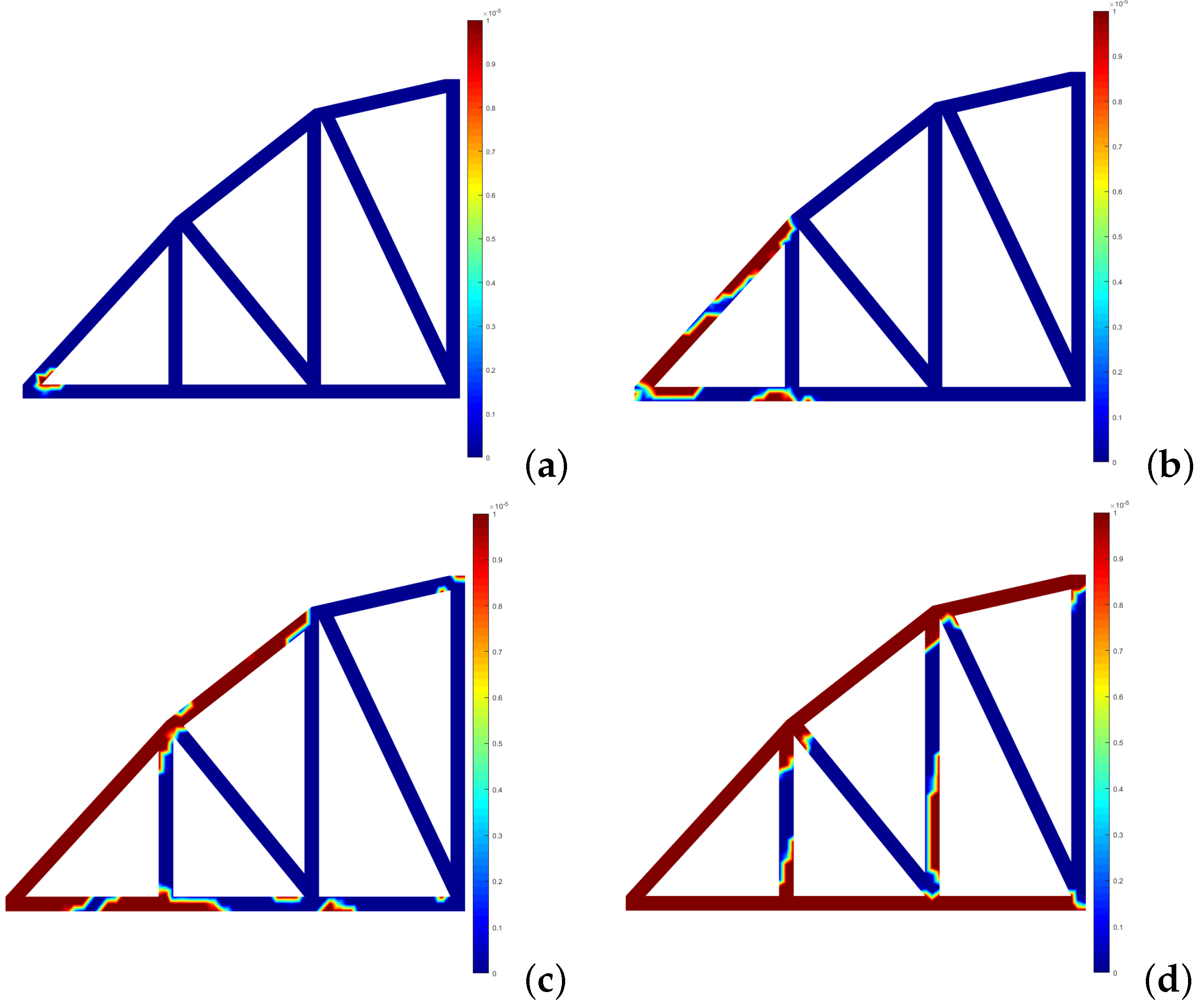
4.2.1. Two-Bay Asymmetric Frame
4.2.2. Bowstring Bridge
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Belytschko, T.; Krongauz, Y.; Organ, D.; Fleming, M.; Krysl, P. Meshless methods: An overview and recent developments. Comput. Methods Appl. Mech. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef]
- Gu, Y. Meshfree methods and their comparisons. Int. J. Comput. Methods 2005, 2, 477–515. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Rabczuk, T.; Bordas, S.; Duflot, M. Meshless methods: A review and computer implementation aspects. Math. Comput. Simul. 2008, 79, 763–813. [Google Scholar] [CrossRef]
- Wang, C.A.; Sadat, H.; Ledez, V.; Lemonnier, D. Meshless method for solving radiative transfer problems in complex two-dimensional and three-dimensional geometries. Int. J. Therm. Sci. 2010, 49, 2282–2288. [Google Scholar] [CrossRef][Green Version]
- Belinha, J. Meshless Methods in Biomechanics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Libersky, L.D.; Petschek, A.G. Smooth particle hydrodynamics with strength of materials. In Advances in the Free-Lagrange Method Including Contributions on Adaptive Gridding and the Smooth Particle Hydrodynamics Method; Springer: Berlin/Heidelberg, Germany, 1991; pp. 248–257. [Google Scholar]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Atluri, S.N.; Zhu, T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics. Comput. Mech. 1998, 22, 117–127. [Google Scholar] [CrossRef]
- Sukumar, N.; Moran, B.; Belytschko, T. The natural element method in solid mechanics. Int. J. Numer. Methods Eng. 1998, 43, 839–887. [Google Scholar] [CrossRef]
- De, S.; Bathe, K.J. The method of finite spheres. Comput. Mech. 2000, 25, 329–345. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. A point interpolation method for two-dimensional solids. Int. J. Numer. Methods Eng. 2001, 50, 937–951. [Google Scholar] [CrossRef]
- Liu, G.R. A point assembly method for stress analysis for two-dimensional solids. Int. J. Solids Struct. 2002, 39, 261–276. [Google Scholar] [CrossRef]
- Idelsohn, S.R.; Onate, E.; Calvo, N.; Del Pin, F. The meshless finite element method. Int. J. Numer. Methods Eng. 2003, 58, 893–912. [Google Scholar] [CrossRef]
- Dinis, L.; Jorge, R.N.; Belinha, J. Analysis of 3D solids using the natural neighbour radial point interpolation method. Comput. Methods Appl. Mech. Eng. 2007, 196, 2009–2028. [Google Scholar] [CrossRef]
- Wang, J.; Liu, G. A point interpolation meshless method based on radial basis functions. Int. J. Numer. Methods Eng. 2002, 54, 1623–1648. [Google Scholar] [CrossRef]
- Zhou, X.W.; Jin, Y.F.; Yin, Z.Y.; Liu, F.T. A centroid-enriched strain-smoothed radial point interpolation method for nearly incompressible elastoplastic problems in solid mechanics. Eng. Anal. Bound. Elem. 2023, 155, 888–906. [Google Scholar] [CrossRef]
- Vaghefi, R.; Hematiyan, M.; Nayebi, A. Three-dimensional thermo-elastoplastic analysis of thick functionally graded plates using the meshless local Petrov–Galerkin method. Eng. Anal. Bound. Elem. 2016, 71, 34–49. [Google Scholar] [CrossRef]
- Vaghefi, R. Thermo-elastoplastic analysis of functionally graded sandwich plates using a three-dimensional meshless model. Compos. Struct. 2020, 242, 112144. [Google Scholar] [CrossRef]
- Liu, Z.; Wei, G.; Qin, S.; Wang, Z. The elastoplastic analysis of functionally graded materials using a meshfree RRKPM. Appl. Math. Comput. 2022, 413, 126651. [Google Scholar] [CrossRef]
- Gao, H.; Wei, G. A meshless solution of nonlinear elastoplastic problems based on the RRKPM. Results Phys. 2021, 31, 104986. [Google Scholar] [CrossRef]
- Li, D.; Liew, K.; Cheng, Y. An improved complex variable element-free Galerkin method for two-dimensional large deformation elastoplasticity problems. Comput. Methods Appl. Mech. Eng. 2014, 269, 72–86. [Google Scholar] [CrossRef]
- Ullah, Z.; Augarde, C. Finite deformation elasto-plastic modelling using an adaptive meshless method. Comput. Struct. 2013, 118, 39–52. [Google Scholar] [CrossRef][Green Version]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. J. Die Reine Angew. Math. 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Hardy, R.L. Theory and applications of the multiquadric-biharmonic method 20 years of discovery 1968–1988. Comput. Math. Appl. 1990, 19, 163–208. [Google Scholar] [CrossRef]
- Wang, J.; Liu, G. On the optimal shape parameters of radial basis functions used for 2-D meshless methods. Comput. Methods Appl. Mech. Eng. 2002, 191, 2611–2630. [Google Scholar] [CrossRef]
- Rodrigues, D.; Belinha, J.; Jorge, R. The elasto-plastic analysis of 3D-printed thermoplastics using the NNRPIM and a modified hill yield criterion. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1368–1381. [Google Scholar] [CrossRef]
- Rodrigues, D.; Belinha, J.; Jorge, R.N.; Dinis, L. Numerical simulation of compression and tensile tests on thermoplastics: A meshless approach. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 286–306. [Google Scholar] [CrossRef]
- Ochsner, A. Elasto-Plasticity of Frame Structure Elements; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Hinton, E.; Owen, D.R.J. Finite Elements in Plasticity: Theory and Practice; Pineridge Press Limited: Swansea, UK, 2017. [Google Scholar]
- De Borst, R.; Crisfield, M.A.; Remmers, J.J.; Verhoosel, C.V. Nonlinear Finite Element Analysis of Solids and Structures; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Belinha, J.A.O.P. The Natural Neighbour Radial Point Interpolation Method: Solid Mechanics and Mechanobiology Applications. Ph.D. Thesis, Faculty of Engineering of the University of Porto, Porto, Portugal, 2010. [Google Scholar]
- Argyris, J.; Boni, B.; Hindenlang, U.; Kleiber, M. Finite element analysis of two-and three-dimensional elasto-plastic frames—The natural approach. Comput. Methods Appl. Mech. Eng. 1982, 35, 221–248. [Google Scholar] [CrossRef]

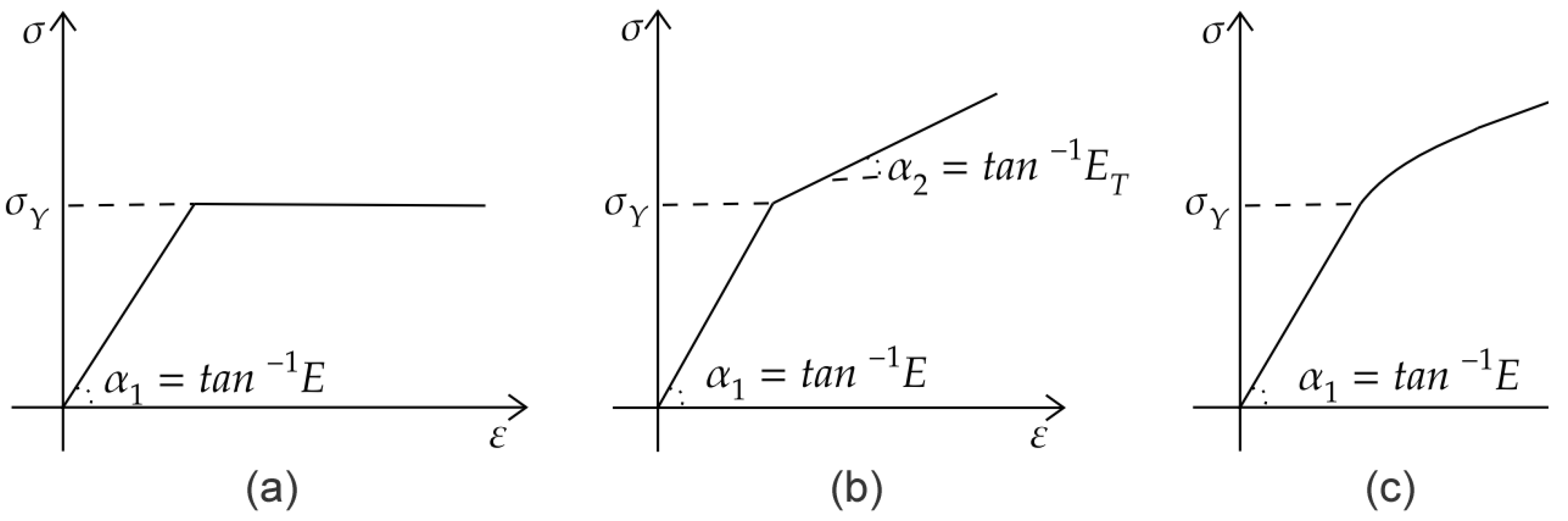




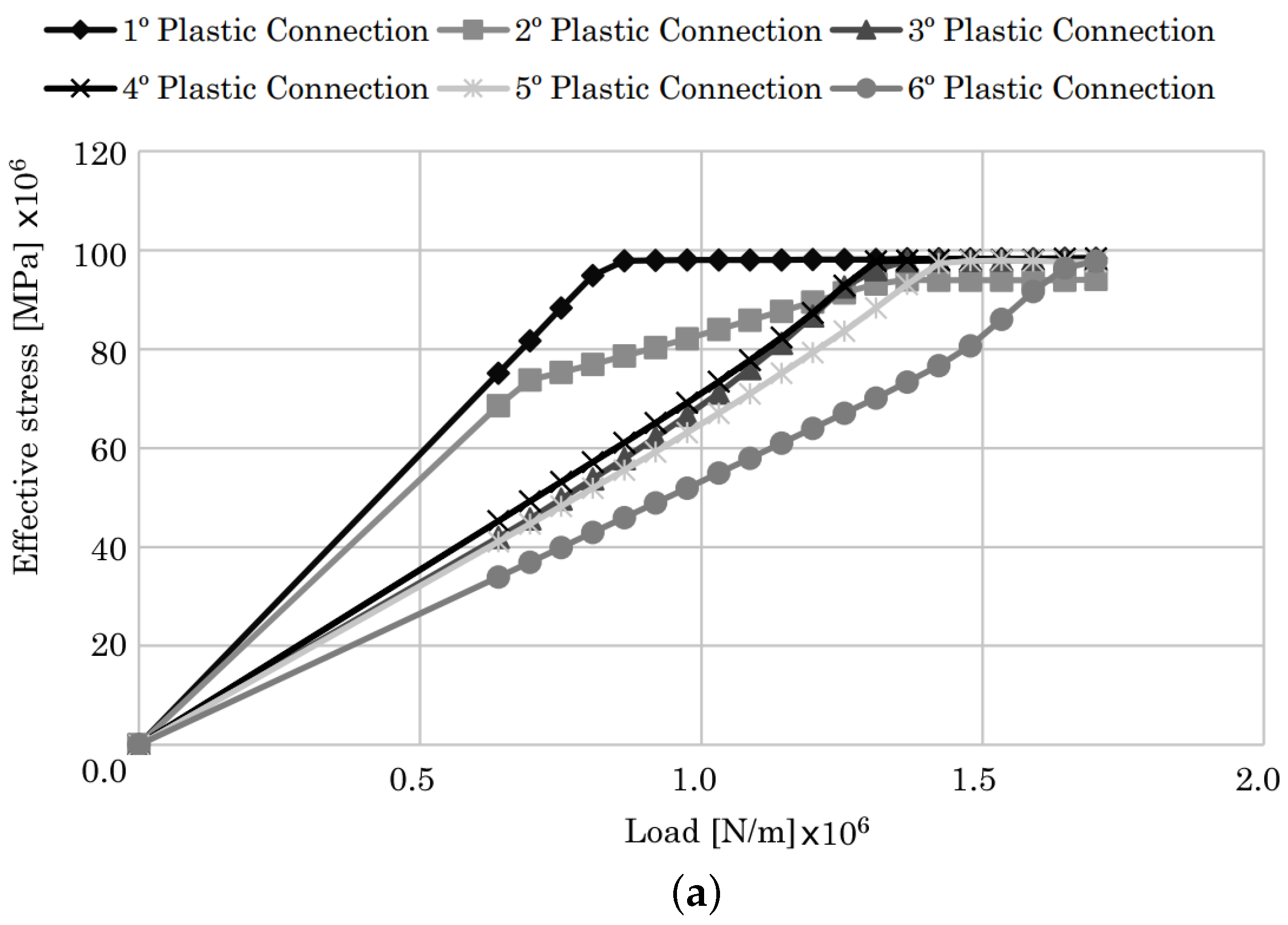




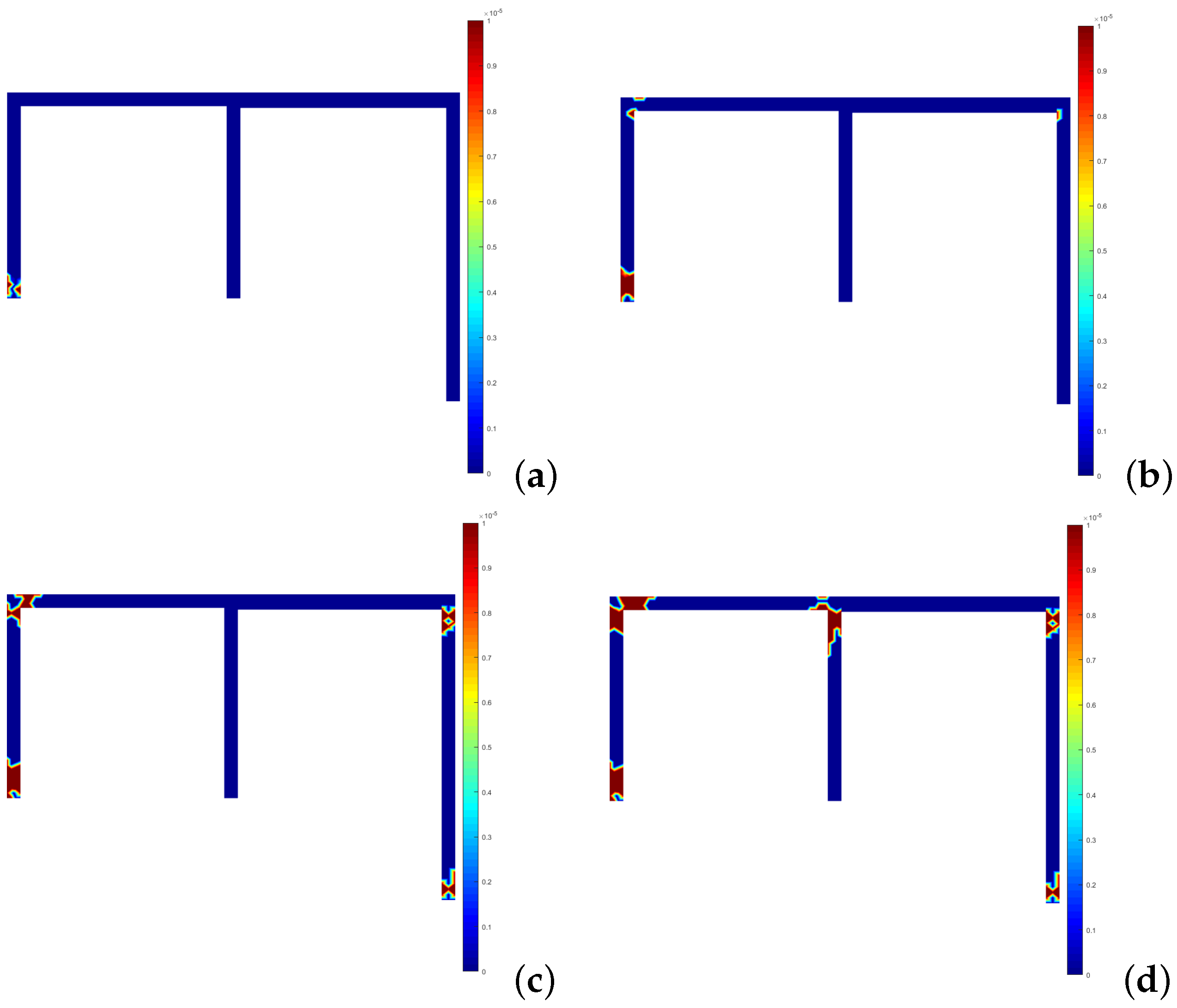
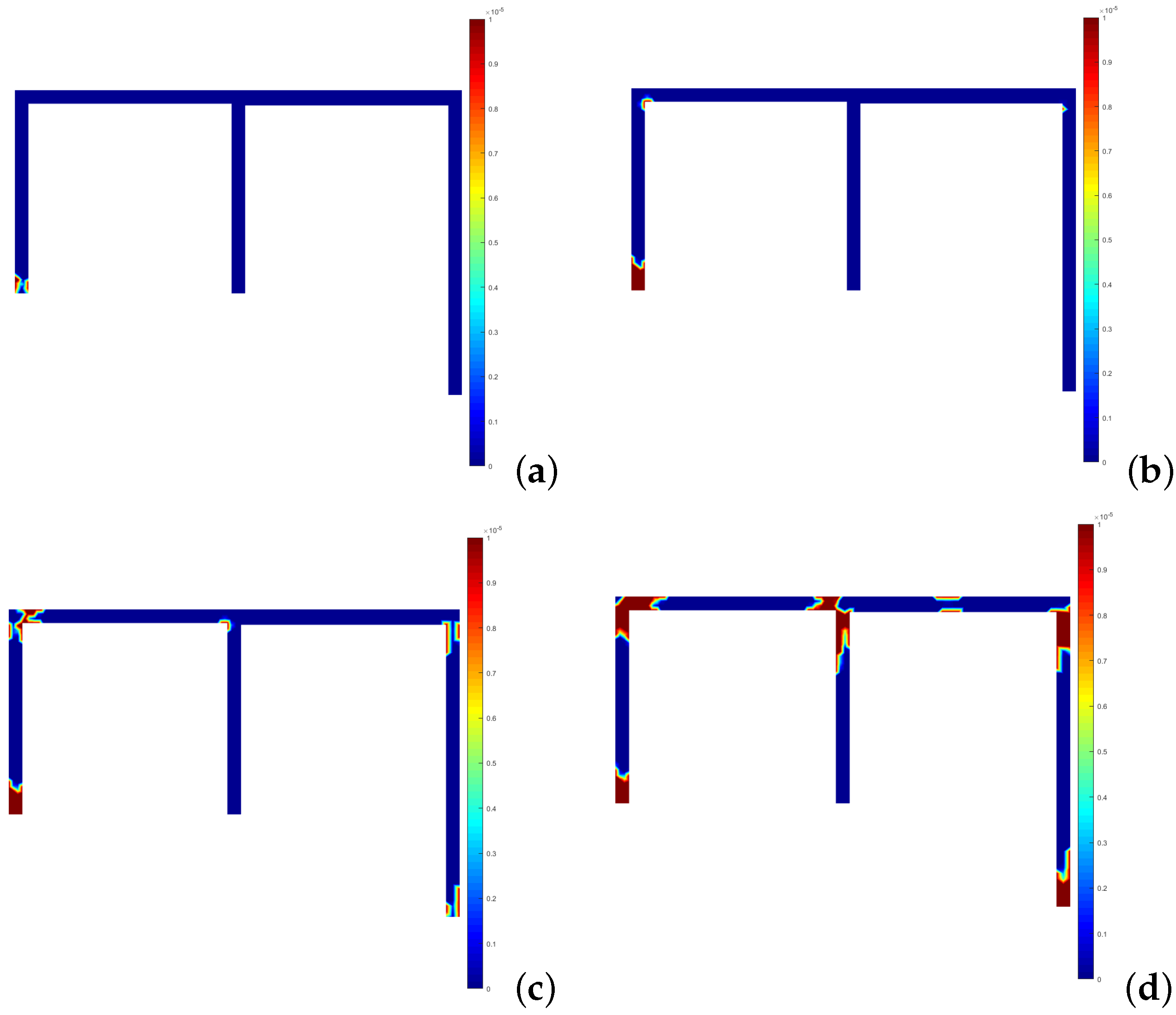

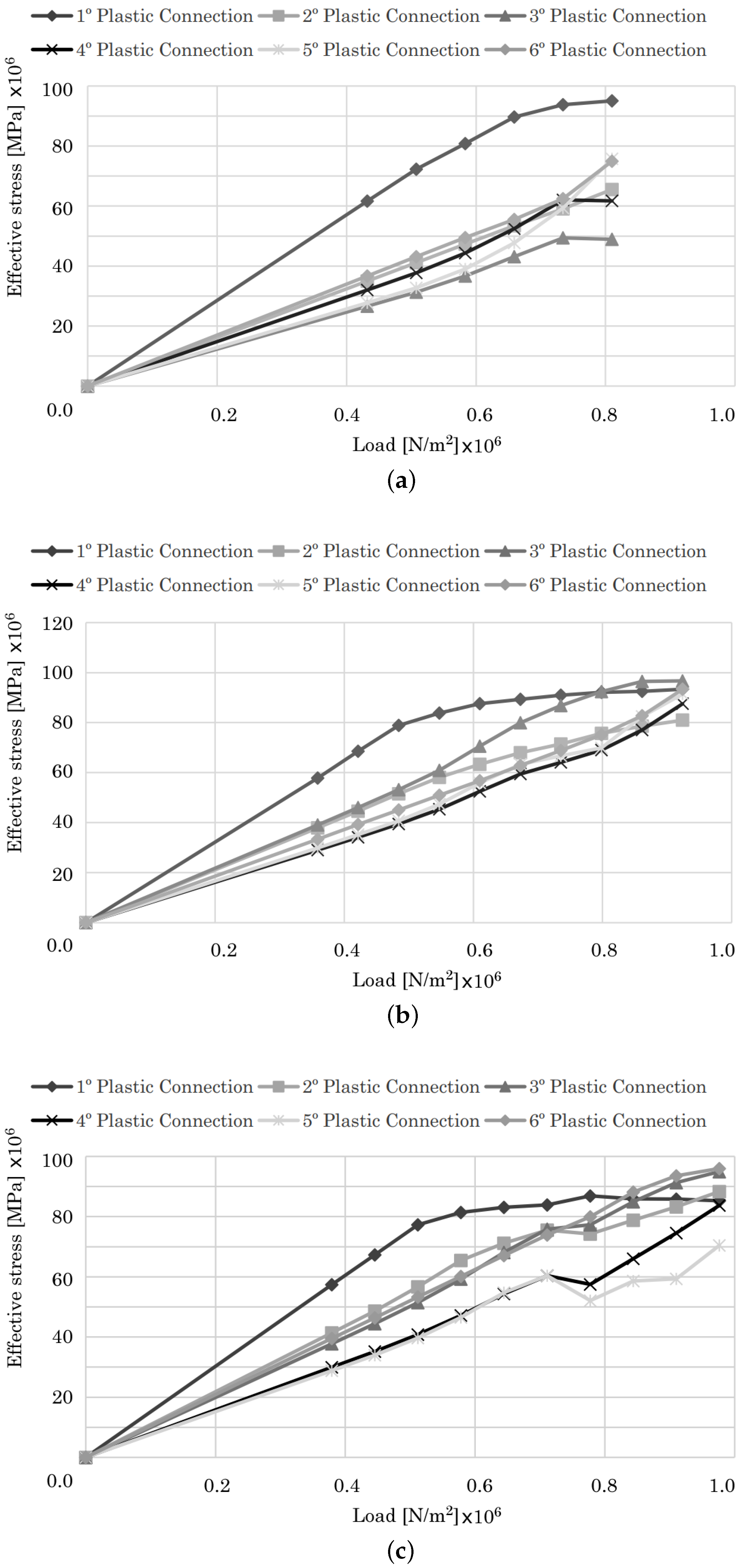

| Elastic unloading occurs (elastic behavior) and the stress point returns inside the yield surface. Hook’s law is still valid. | |
| Stress point is on the yield surface. Neutral loading (plastic behavior for an elastic–perfectly plastic material). If the material has hardening, this situation corresponds to the beginning of the plasticity. | |
| Plastic loading. The stress point is on a constantly expanding yield surface (plastic behavior for a strain-hardening material). |
| Mechanical Properties | Value |
|---|---|
| E [Pa] | 19,613.3 × |
| [Pa] | 19,613.3 × |
| 0.3 | |
| [Pa] | 98.0665 × |
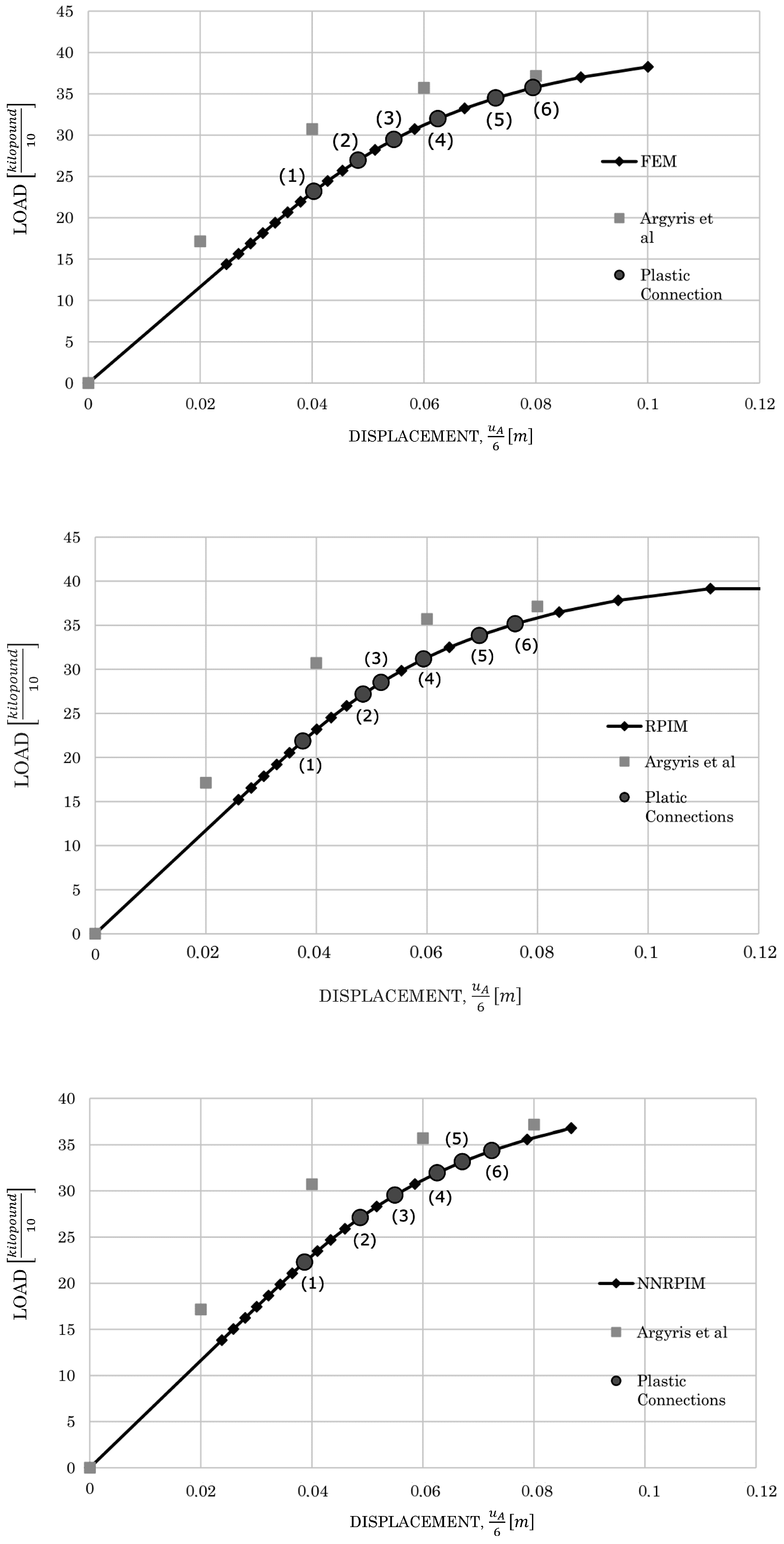
| Plastic Connection | Load in | % Difference Regarding FEM | |||
|---|---|---|---|---|---|
| FEM | RPIM | NNRPIM | RPIM | NNRPIM | |
| 1 | 23.227 | 21.763 | 22.283 | 6.73 | −4.06 |
| 2 | 26.883 | 27.151 | 27.201 | −0.98 | 1.18 |
| 3 | 29.352 | 28.349 | 29.659 | 3.54 | 1.04 |
| 4 | 32.017 | 31.141 | 32.027 | 2.81 | 0.03 |
| 5 | 34.482 | 33.831 | 33.167 | 1.92 | −3.81 |
| 6 | 35.763 | 35.124 | 34.306 | 1.81 | −4.07 |
| Mechanical Properties | Value |
|---|---|
| E [MPa] | 205,000 |
| [MPa] | 6700 |
| 0.3 | |
| [MPa] | 230 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belinha, J.; Aires, M.; Rodrigues, D.E.S. Elastoplastic Analysis of Frame Structures Using Radial Point Interpolation Meshless Methods. Appl. Sci. 2023, 13, 12591. https://doi.org/10.3390/app132312591
Belinha J, Aires M, Rodrigues DES. Elastoplastic Analysis of Frame Structures Using Radial Point Interpolation Meshless Methods. Applied Sciences. 2023; 13(23):12591. https://doi.org/10.3390/app132312591
Chicago/Turabian StyleBelinha, Jorge, Miguel Aires, and Daniel E.S. Rodrigues. 2023. "Elastoplastic Analysis of Frame Structures Using Radial Point Interpolation Meshless Methods" Applied Sciences 13, no. 23: 12591. https://doi.org/10.3390/app132312591
APA StyleBelinha, J., Aires, M., & Rodrigues, D. E. S. (2023). Elastoplastic Analysis of Frame Structures Using Radial Point Interpolation Meshless Methods. Applied Sciences, 13(23), 12591. https://doi.org/10.3390/app132312591






