Coupled Thermo-Mechanical Phase-Field Modeling to Simulate the Crack Evolution of Defective Ceramic Materials under Flame Thermal Shock
Abstract
:1. Introduction
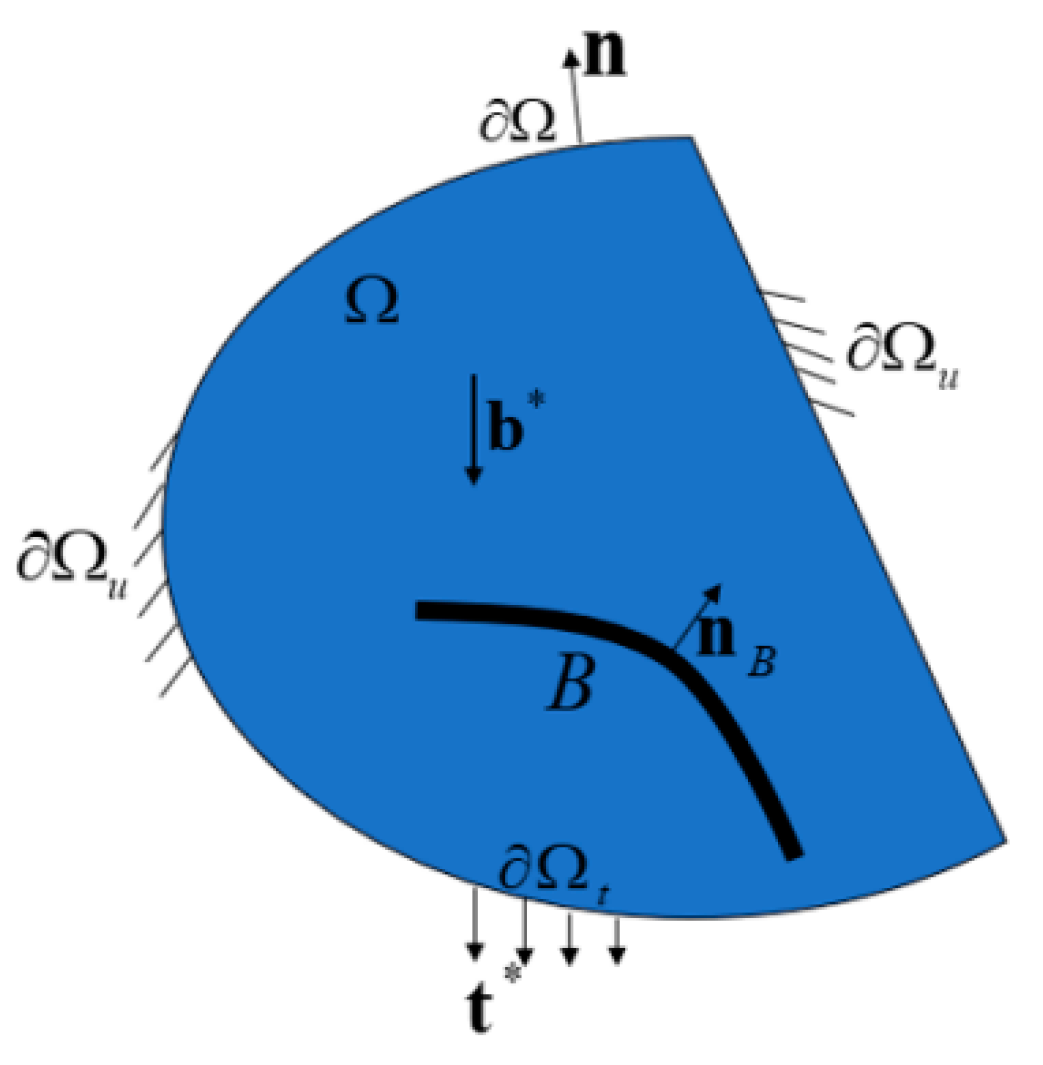
2. Coupled Thermo-Mechanical Phase-Field Modeling
2.1. Energy Imbalance
2.2. Damage
2.3. Considering the Temperature-Dependent Phase-Field Fracture Model
2.4. Heat Conduction
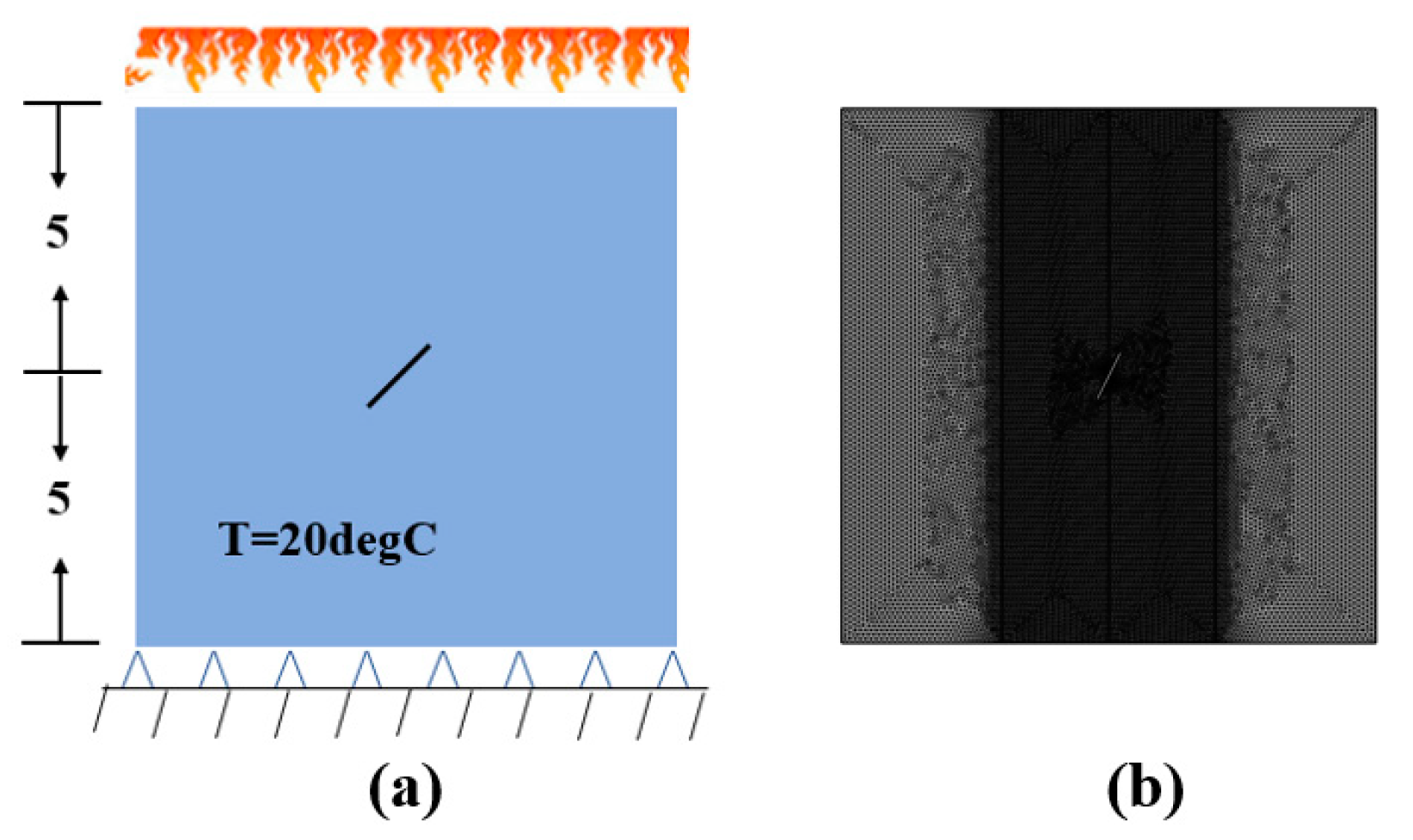
3. Finite Element Modeling
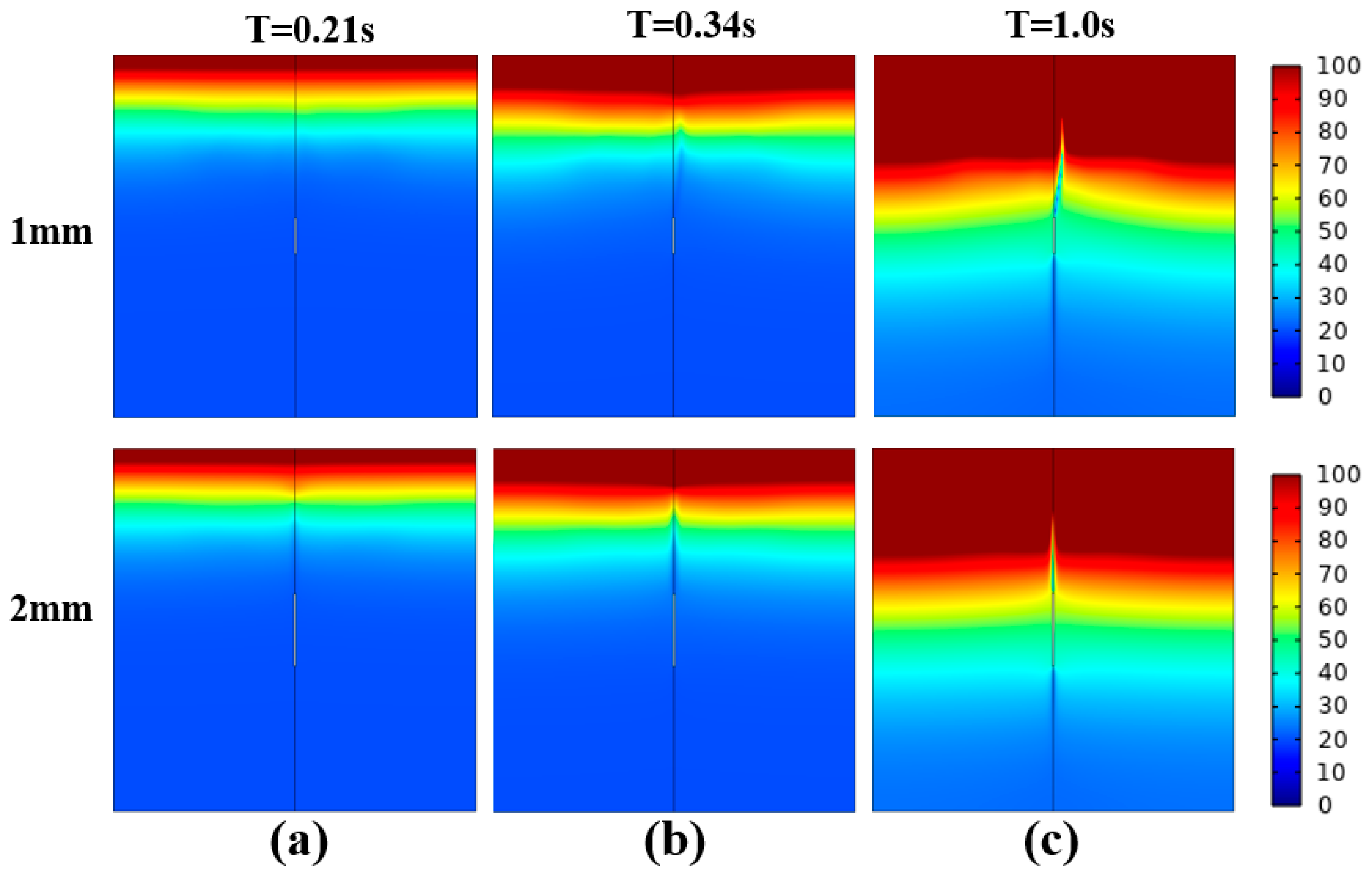
4. Results and Discussion
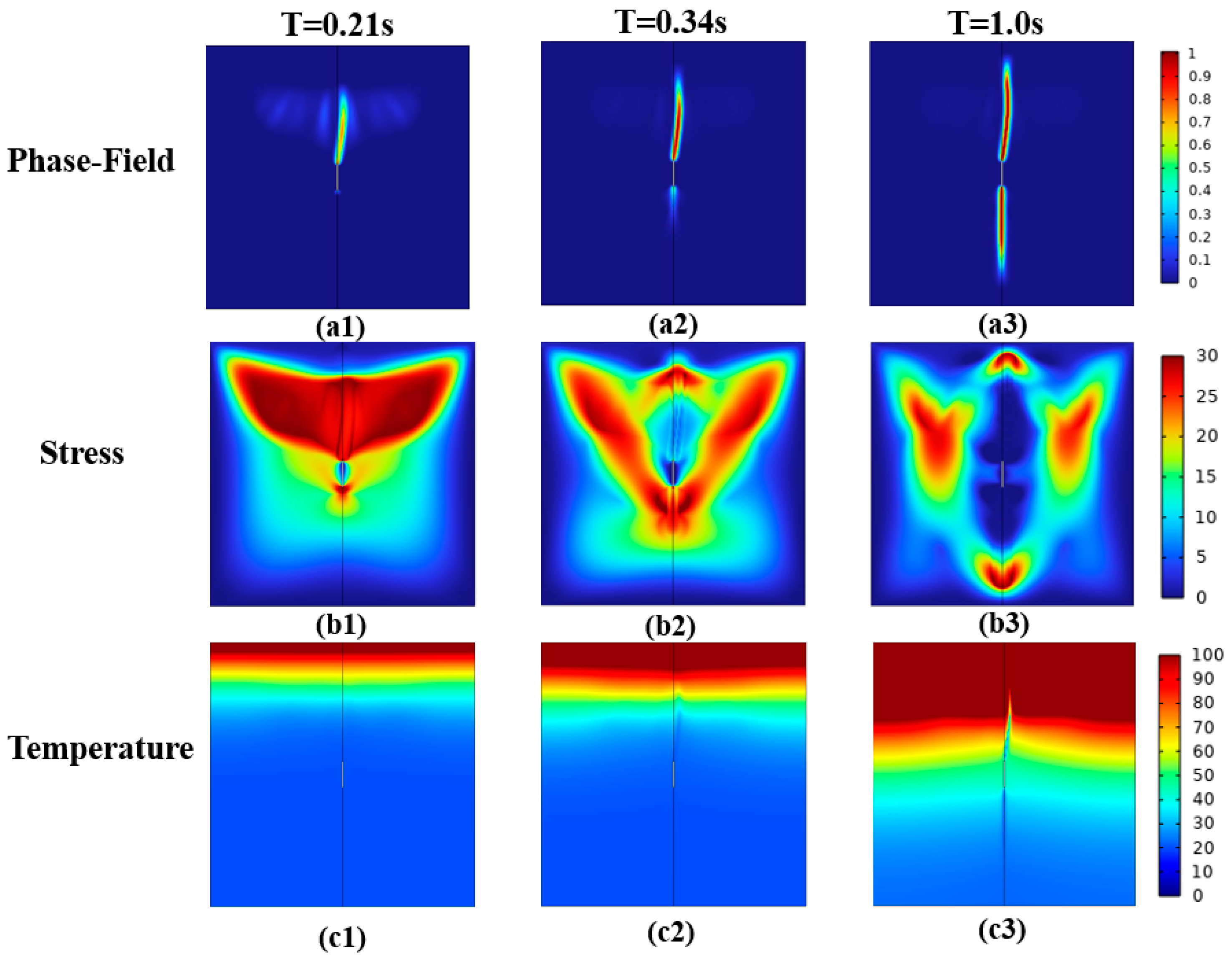
4.1. The Influence of Initial Crack Angle on Crack Propagation
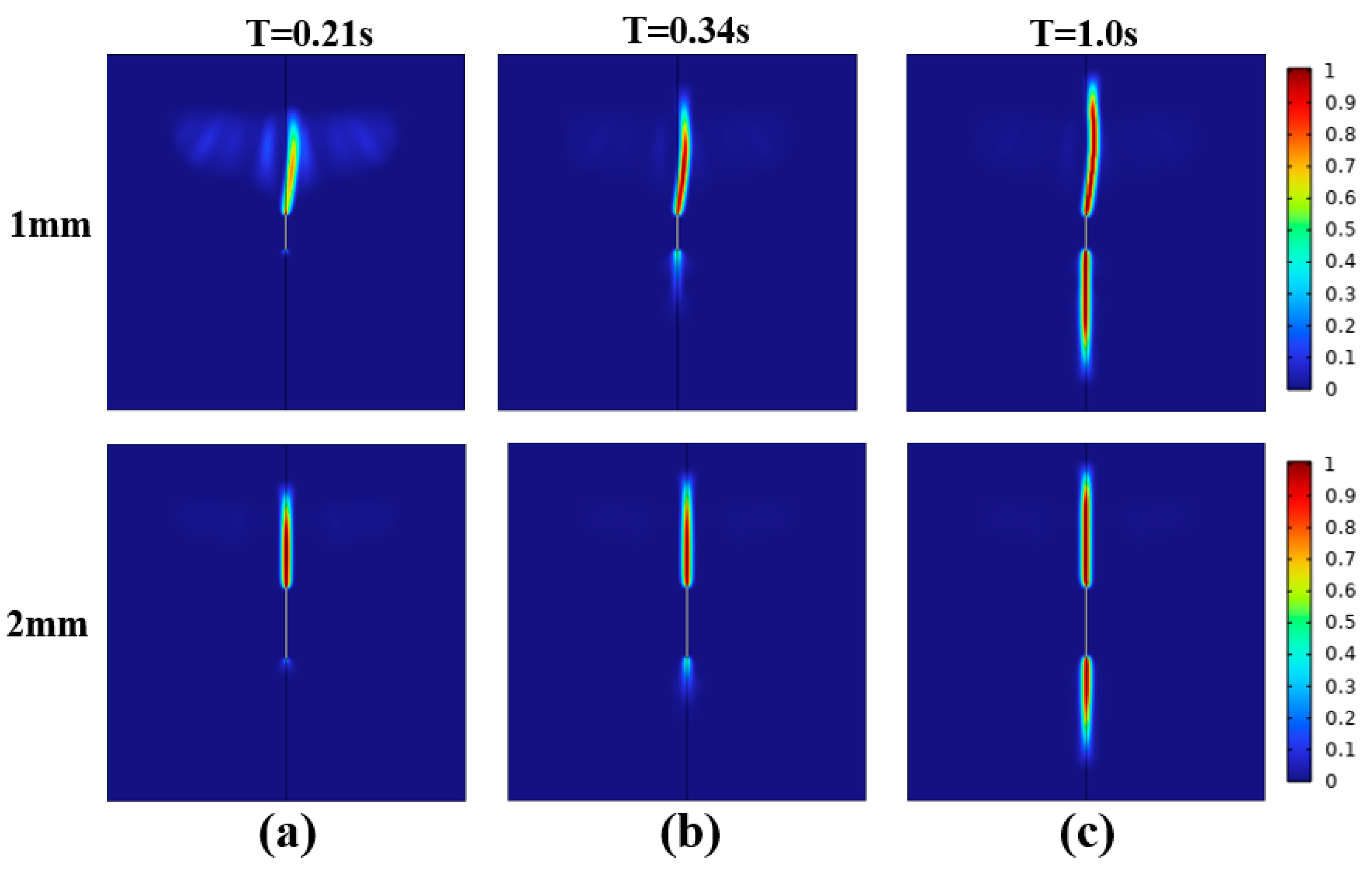
4.2. The Influence of Initial Crack Length on Crack Propagation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Zhou, X.; Zhang, T. Size effect of thermal shock crack patterns in ceramics: Insights from a nonlocal numerical approach. Mech. Mater. 2019, 137, 103133. [Google Scholar] [CrossRef]
- Fahrenholtz, W.G.; Hilmas, G.E. Ultra-high temperature ceramics: Materials for extreme environments. Scr. Mater. 2017, 129, 94–99. [Google Scholar] [CrossRef]
- Monteverde, F.; Savino, R. ZrB2-SiC Sharp Leading Edges in High Enthalpy Supersonic Flows. J. Am. Ceram. Soc. 2012, 95, 2282–2289. [Google Scholar] [CrossRef]
- Savino, R.; Mungiguerra, S.; Di Martino, G.D. Testing ultra-high-temperature ceramics for thermal protection and rocket applications. Adv. Appl. Ceram. 2018, 117 (Suppl. S1), s9–s18. [Google Scholar] [CrossRef]
- Wei, K.; Liang, D.; Mei, M.; Yang, X.; Chen, L. A viscoelastic model of compression and relaxation behaviors in preforming process for carbon fiber fabrics with binder. Compos. Part. B Eng. 2019, 158, 1–9. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Q.; Ning, X.; Liu, Y. Evaluation of the phase stability, and mechanical and thermal properties of Ba(Sr1/3Ta2/3)O3 as a potential ceramic material for thermal barrier coatings. Ceram. Int. 2019, 45, 12989–12993. [Google Scholar] [CrossRef]
- Han, J.-C.; Wang, B.-L. Thermal shock resistance of ceramics with temperature-dependent material properties at elevated temperature. Acta Mater. 2011, 59, 1373–1382. [Google Scholar] [CrossRef]
- Wang, A.; Hu, P.; Du, B.; Fang, C.; Zhang, D.; Zhang, X. Cracking behavior of ZrB2-SiC-Graphite sharp leading edges during thermal shock. Ceram. Int. 2018, 44, 7694–7699. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, B.; Su, H.; Chen, H.; Feng, X. Improving the thermal shock resistance of ceramics by crack arrest blocks. Sci. China Technol. Sci. 2016, 59, 913–919. [Google Scholar] [CrossRef]
- Li, Y.; Li, Q.; Wu, X.; Shao, Y.; Li, L.; Song, F. Cracking in the translucent alumina ceramic during flame thermal shock. Ceram. Int. 2021, 47, 30974–30979. [Google Scholar] [CrossRef]
- Su, X.; Liu, G.; Dai, B.; Hu, B.; Fu, S.; Wan, D.; Bao, Y.; Feng, Q.; Grasso, S.; Hu, C. Ablation mechanisms of Ti3SiC2 ceramic at 1600 °C in nitrogen plasma flame. Ceram. Int. 2022, 48, 14004–14013. [Google Scholar] [CrossRef]
- Liu, C.; Cai, C.; Xie, J.; Guo, W.; Qin, H.; Gao, P.; Xiao, H. Effect of surface brittle-to-ductile transition on high-temperature thermal shock resistance of Al2O3 ceramics. Ceram. Int. 2022, 48, 20627–20638. [Google Scholar] [CrossRef]
- Tang, S.B.; Zhang, H.; Tang, C.A.; Liu, H.Y. Numerical model for the cracking behavior of heterogeneous brittle solids subjected to thermal shock. Int. J. Solids Struct. 2016, 80, 520–531. [Google Scholar] [CrossRef]
- Bourdin, B.; Marigo, J.-J.; Maurini, C.; Sicsic, P. Morphogenesis and Propagation of Complex Cracks Induced by Thermal Shocks. Phys. Rev. Lett. 2014, 112, 014301. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhou, X.; Kou, M. An improved coupled thermo-mechanic bond-based peridynamic model for cracking behaviors in brittle solids subjected to thermal shocks. Eur. J. Mech.-A/Solids 2019, 73, 282–305. [Google Scholar] [CrossRef]
- Chu, D.; Li, X.; Liu, Z. Study the dynamic crack path in brittle material under thermal shock loading by phase field modeling. Int. J. Fract. 2017, 208, 115–130. [Google Scholar] [CrossRef]
- Li, J.; Song, F.; Jiang, C. Direct numerical simulations on crack formation in ceramic materials under thermal shock by using a non-local fracture model. J. Eur. Ceram. Soc. 2013, 33, 2677–2687. [Google Scholar] [CrossRef]
- Jiang, W.; Spencer, B.W.; Dolbow, J.E. Ceramic nuclear fuel fracture modeling with the extended finite element method. Eng. Fract. Mech. 2020, 223, 106713. [Google Scholar] [CrossRef]
- Menouillard, T.; Belytschko, T. Analysis and computations of oscillating crack propagation in a heated strip. Int. J. Fract. 2011, 167, 57–70. [Google Scholar] [CrossRef]
- Meng, J.; Cao, P.; Huang, J.; Lin, H.; Chen, Y.; Cao, R. Second-order cone programming formulation of discontinuous deformation analysis. Int. J. Numer. Methods Eng. 2019, 118, 243–257. [Google Scholar] [CrossRef]
- Giannakeas, I.N.; Papathanasiou, T.K.; Bahai, H. Simulation of thermal shock cracking in ceramics using bond-based peridynamics and FEM. J. Eur. Ceram. Soc. 2018, 38, 3037–3048. [Google Scholar] [CrossRef]
- Cao, C.; Zhao, Y.; Dai, D.; Zhang, X.; Song, Z.; Liu, Q.; Liu, G.; Gao, Y.; Zhang, H.; Zheng, Z. Simulation analysis and optimization of laser preheating SiC ceramics based on RSM. Int. J. Therm. Sci. 2023, 185, 108070. [Google Scholar] [CrossRef]
- Dong, X.; Shin, Y.C. Crack formation within ceramics via coupled multiscale genome and XFEM predictions under various loading conditions. Eng. Fract. Mech. 2018, 204, 517–530. [Google Scholar] [CrossRef]
- Francfort, G.A.; Marigo, J.-J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.-J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. A phase field model of electromechanical fracture. J. Mech. Phys. Solids 2010, 58, 1716–1740. [Google Scholar] [CrossRef]
- Wu, J.-Y.; Nguyen, V.P. A length scale insensitive phase-field damage model for brittle fracture. J. Mech. Phys. Solids 2018, 119, 20–42. [Google Scholar] [CrossRef]
- Wu, J.-Y. A geometrically regularized gradient-damage model with energetic equivalence. Comput. Methods Appl. Mech. Eng. 2018, 328, 612–637. [Google Scholar] [CrossRef]
- Yu, Y.; Hou, C.; Zhao, M. Phase field model for brittle fracture using threshold strategy. Theor. Appl. Fract. Mech. 2023, 125, 103831. [Google Scholar] [CrossRef]
- Xing, C.; Yu, T.; Sun, Y.; Wang, Y. An adaptive phase-field model with variable-node elements for fracture of hyperelastic materials at large deformations. Eng. Fract. Mech. 2023, 281, 109115. [Google Scholar] [CrossRef]
- Zheng, S.; Huang, R.; Lin, R.; Liu, Z. A phase field solution for modelling hyperelastic material and hydrogel fracture in ABAQUS. Eng. Fract. Mech. 2022, 276, 108894. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, X.; Rabczuk, T. A phase-field modeling approach of fracture propagation in poroelastic media. Eng. Geol. 2018, 240, 189–203. [Google Scholar] [CrossRef]
- Ruan, H.; Rezaei, S.; Yang, Y.; Gross, D.; Xu, B.-X. A thermo-mechanical phase-field fracture model: Application to hot cracking simulations in additive manufacturing. J. Mech. Phys. Solids 2023, 172, 105169. [Google Scholar] [CrossRef]
- Miehe, C.; Sch¨anzel, L.-M.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 449–485. [Google Scholar] [CrossRef]
- Li, D.; Li, P.; Li, W.; Li, W.; Zhou, K. Three-dimensional phase-field modeling of temperature-dependent thermal shock-induced fracture in ceramic materials. Eng. Fract. Mech. 2022, 268, 108444. [Google Scholar] [CrossRef]
- Mandal, T.K.; Nguyen, V.P.; Wu, J.-Y.; Nguyen-Thanh, C.; de Vaucorbeil, A. Fracture of thermo-elastic solids: Phase-field modeling and new results with an efficient monolithic solver. Comput. Methods Appl. Mech. Eng. 2021, 376, 113648. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Schrefler, B.A.; Gawin, D. The Effective Stress Principle: Incremental or Finite Form? Int. J. Numer. Anal. Methods Geomech. 1996, 20, 785–814. [Google Scholar] [CrossRef]
- Coleman, B.D.; Noll, W. The thermodynamics of elastic materials with heat conduction and viscosity. In The Foundations of Mechanics and Thermodynamics; Springer: Berlin/Heidelberg, Germany, 1974; pp. 145–156. [Google Scholar]
- Wu, J.-Y.; Mandal, T.K.; Nguyen, V.P. A phase-field regularized cohesive zone model for hydrogen assisted cracking. Comput. Methods Appl. Mech. Eng. 2020, 358, 112614. [Google Scholar] [CrossRef]
- Kitamura, K. Crack Surface Energy: Temperature and Force Dependence. Mater. Trans. 2008, 49, 643–649. [Google Scholar] [CrossRef]
- Bayoumi, M.R.; Bassim, M.N. Temperature dependence of fracture toughness J IC and ductility for BCC materials in the transition region. Int. J. Fract. 1983, 23, 259–269. [Google Scholar] [CrossRef]
- Wu, J.-Y.; Chen, W.-X. On the phase-field modeling of fully coupled chemo-mechanical deterioration and fracture in calcium leached cementitious solids. Int. J. Solids Struct. 2022, 238, 111380. [Google Scholar] [CrossRef]
- Stumpf, H.; Hackl, K. Micromechanical concept for the analysis of damage evolution in thermo-viscoelastic and quasi-brittle materials. Int. J. Solids Struct. 2003, 40, 1567–1584. [Google Scholar] [CrossRef]
- Chen, W.-X.; Wu, J.-Y. Phase-field cohesive zone modeling of multi-physical fracture in solids and the open-source implementation in Comsol Multiphysics. Theor. Appl. Fract. Mech. 2022, 117, 103153. [Google Scholar] [CrossRef]
- Zhuang, X.; Zhou, S.; Huynh, G.; Areias, P.; Rabczuk, T. Phase field modeling and computer implementation: A review. Eng. Fract. Mech. 2022, 262, 108234. [Google Scholar] [CrossRef]
- Li, Q.; Li, Y.; Li, J.; Li, L.; Wu, X.; Shao, Y.; Charles, Y.; Barboura, S.; Song, F. Prefabricated crack propagation in translucent alumina ceramic sheets during flame thermal shock. Eng. Fract. Mech. 2022, 263, 108285. [Google Scholar] [CrossRef]



| E | |||||
|---|---|---|---|---|---|
| 0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhang, S.Y.; Shen, Q. Coupled Thermo-Mechanical Phase-Field Modeling to Simulate the Crack Evolution of Defective Ceramic Materials under Flame Thermal Shock. Appl. Sci. 2023, 13, 12633. https://doi.org/10.3390/app132312633
Wang Z, Zhang SY, Shen Q. Coupled Thermo-Mechanical Phase-Field Modeling to Simulate the Crack Evolution of Defective Ceramic Materials under Flame Thermal Shock. Applied Sciences. 2023; 13(23):12633. https://doi.org/10.3390/app132312633
Chicago/Turabian StyleWang, Zai, Shi Yi Zhang, and Qiang Shen. 2023. "Coupled Thermo-Mechanical Phase-Field Modeling to Simulate the Crack Evolution of Defective Ceramic Materials under Flame Thermal Shock" Applied Sciences 13, no. 23: 12633. https://doi.org/10.3390/app132312633
APA StyleWang, Z., Zhang, S. Y., & Shen, Q. (2023). Coupled Thermo-Mechanical Phase-Field Modeling to Simulate the Crack Evolution of Defective Ceramic Materials under Flame Thermal Shock. Applied Sciences, 13(23), 12633. https://doi.org/10.3390/app132312633





