Experimental Study of the Multiple Fractalisation of Coal and Rock Failure Subjected to the Coupled Effects of Water, Temperature and Dynamic Loads
Abstract
:1. Introduction
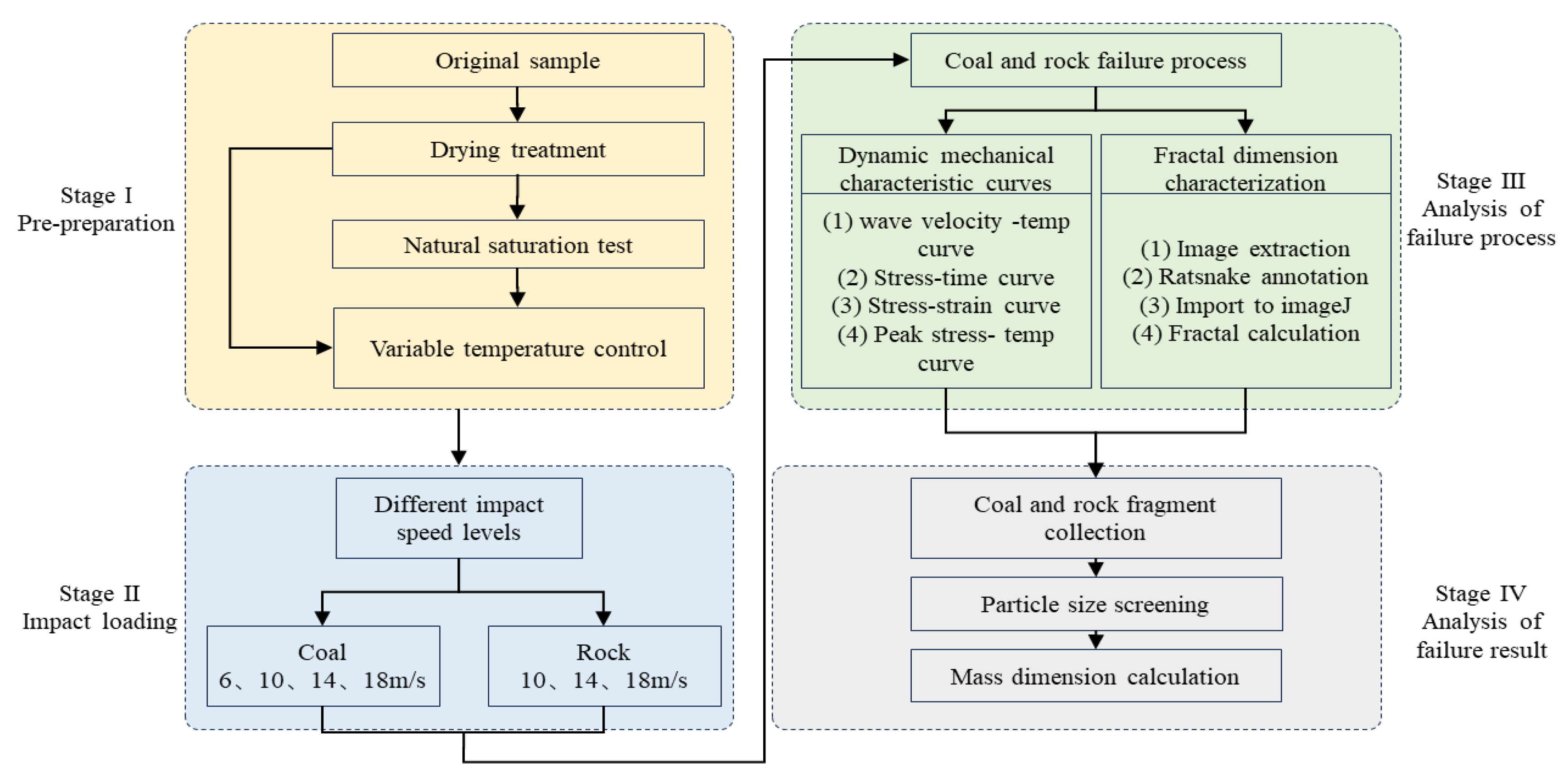
2. Materials and Methods
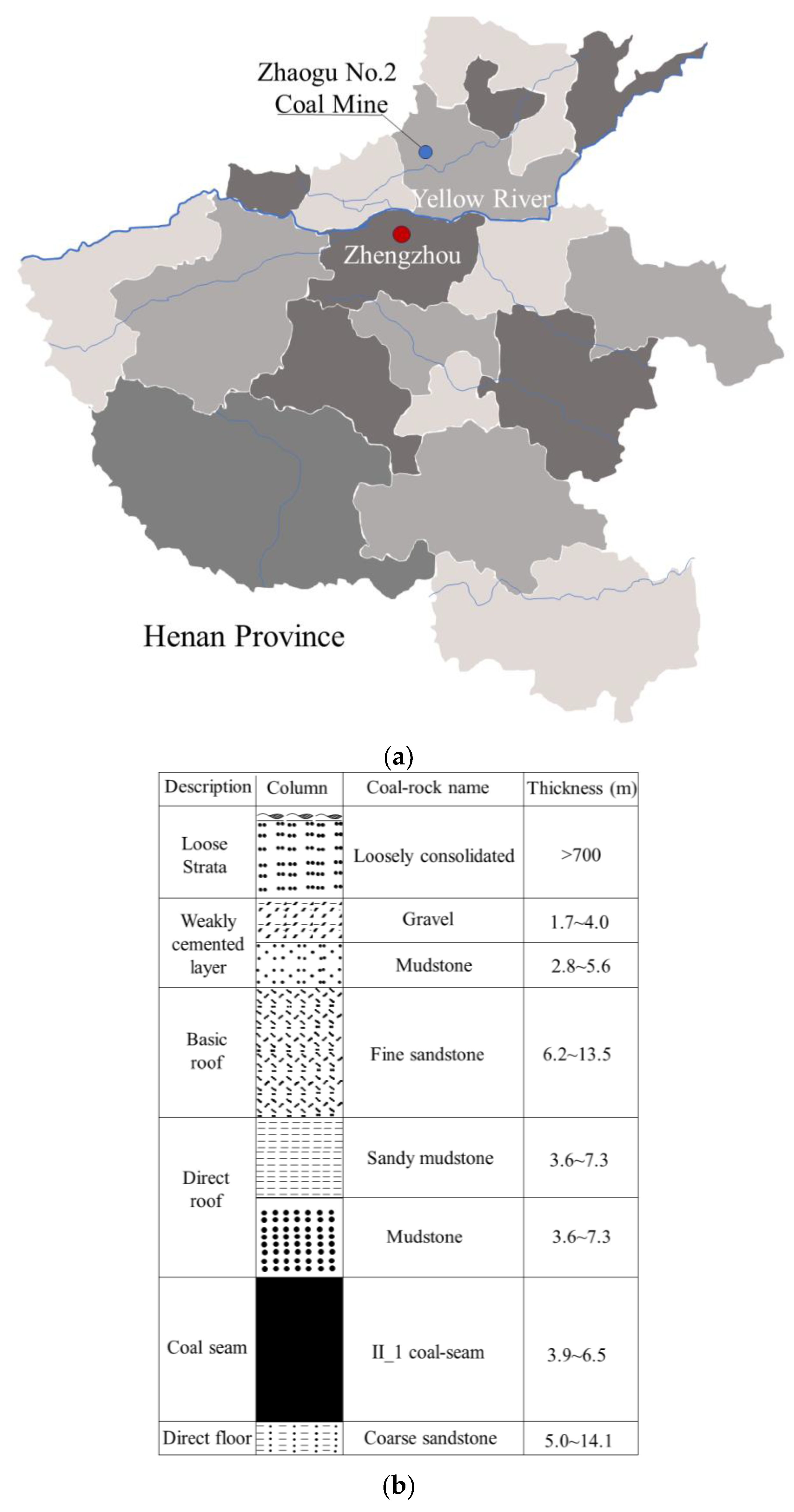
2.1. Specimen Preparation
2.2. Testing Equipment
2.3. Test Condition and Procedure
2.4. Introduction to the Theory
2.4.1. Principles of the SHPB Test
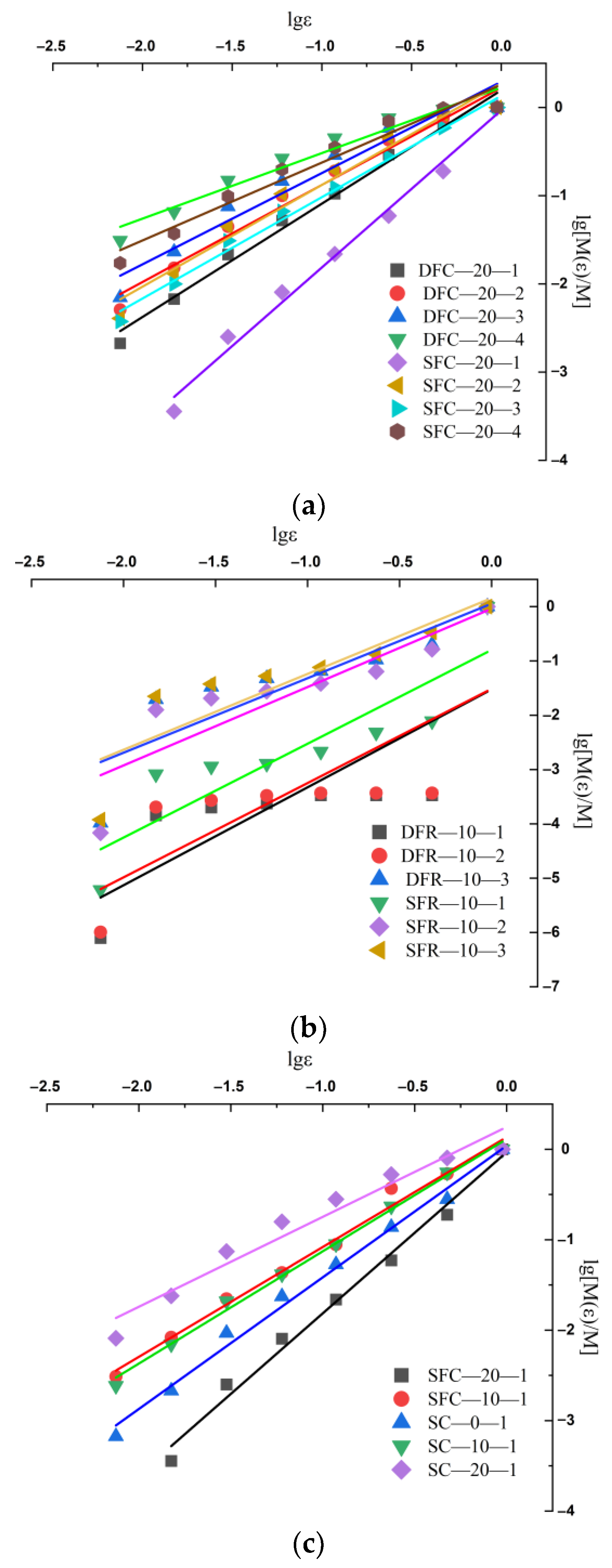
2.4.2. Box Dimension Calculation Model
2.4.3. Mass–Frequency Relationship Model
3. Analysis of Test Results
3.1. Basic Physical Parameters and Wave Velocity Determination of Coal Stone Samples
3.1.1. Basic Physical Parameters
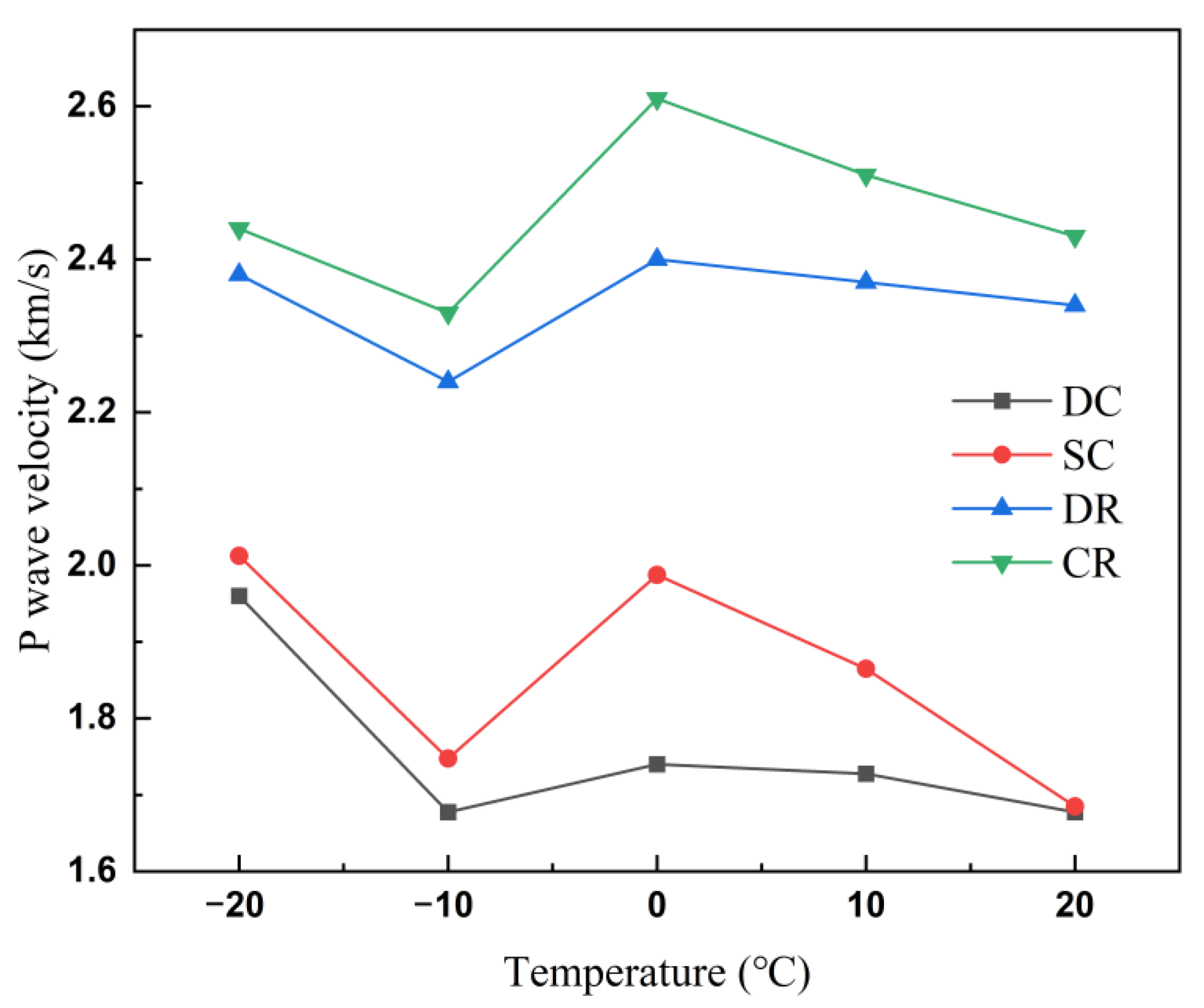
3.1.2. Characteristics of the Wave Velocity Measurements at Different Temperatures and Saturation Levels
3.2. Dynamic Mechanical Characteristics
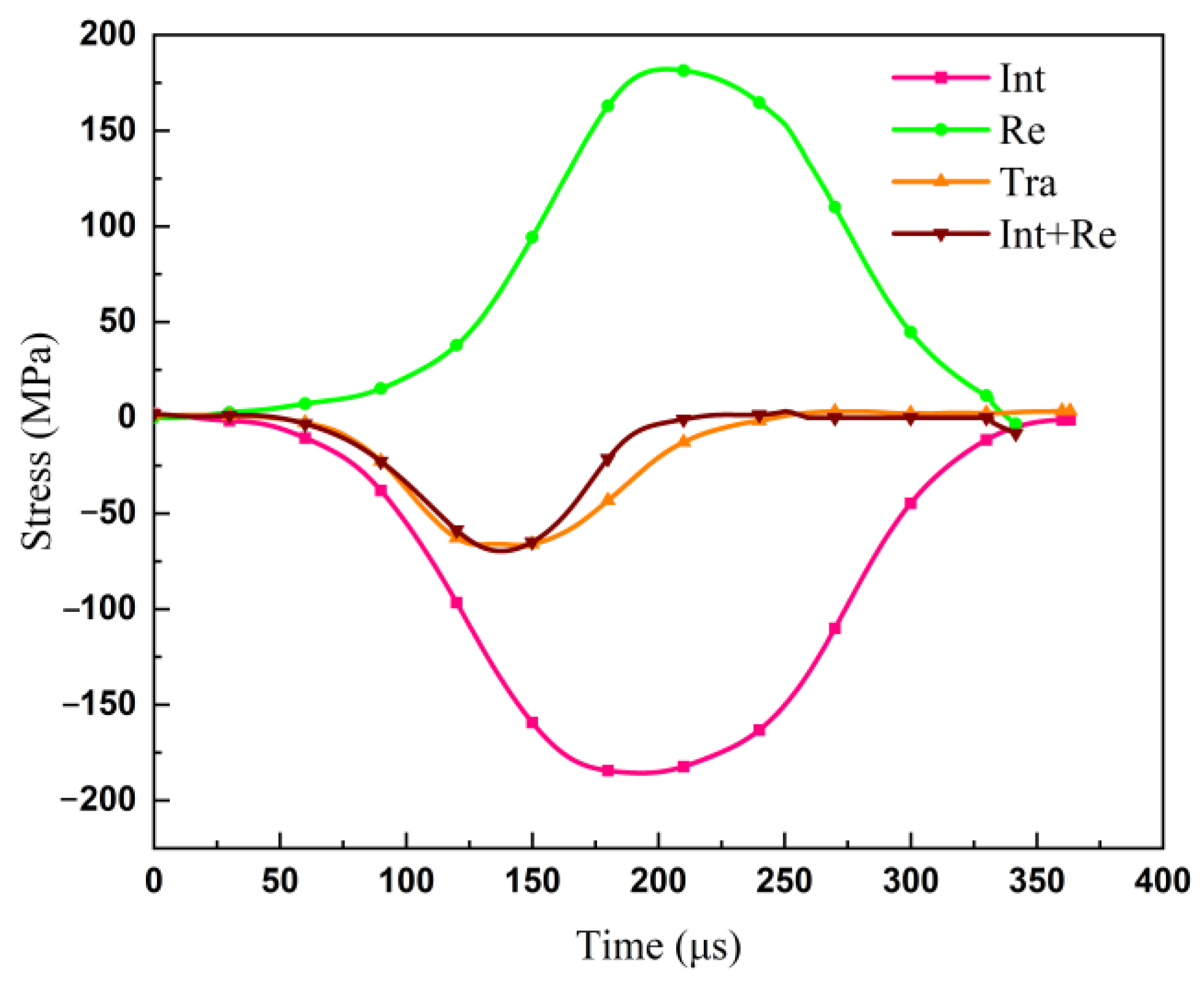
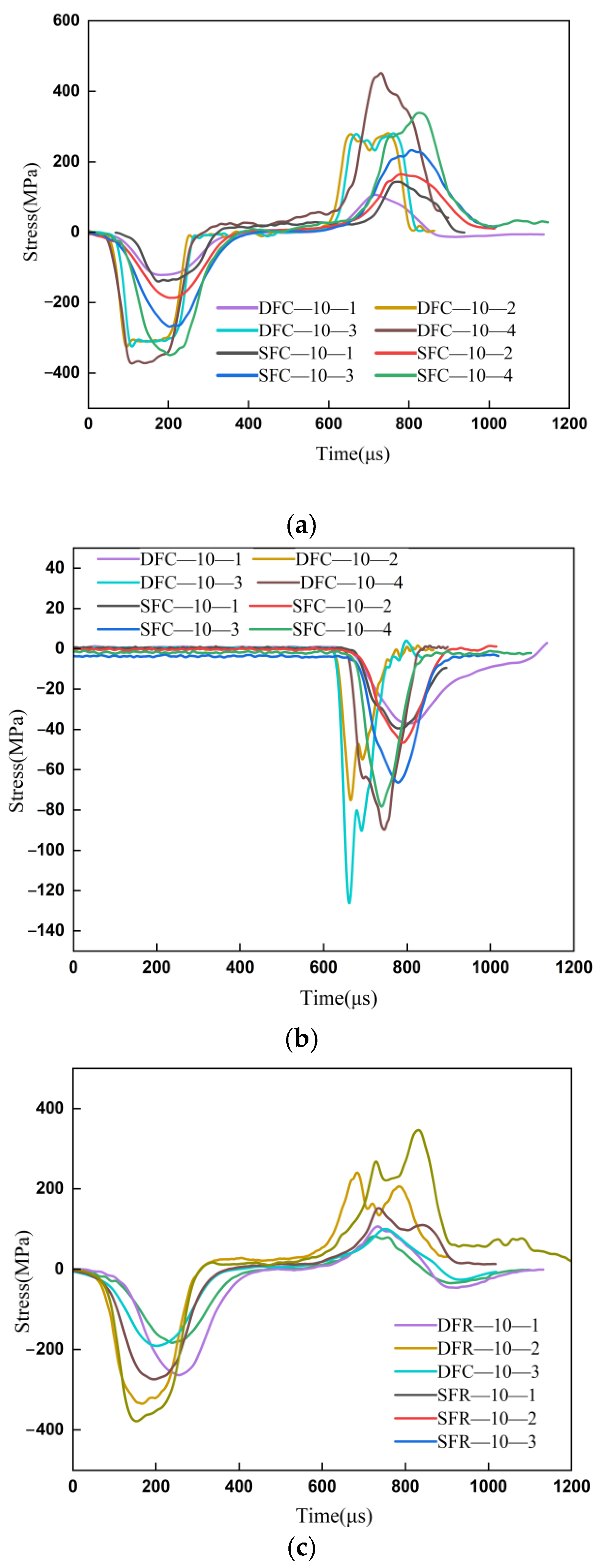
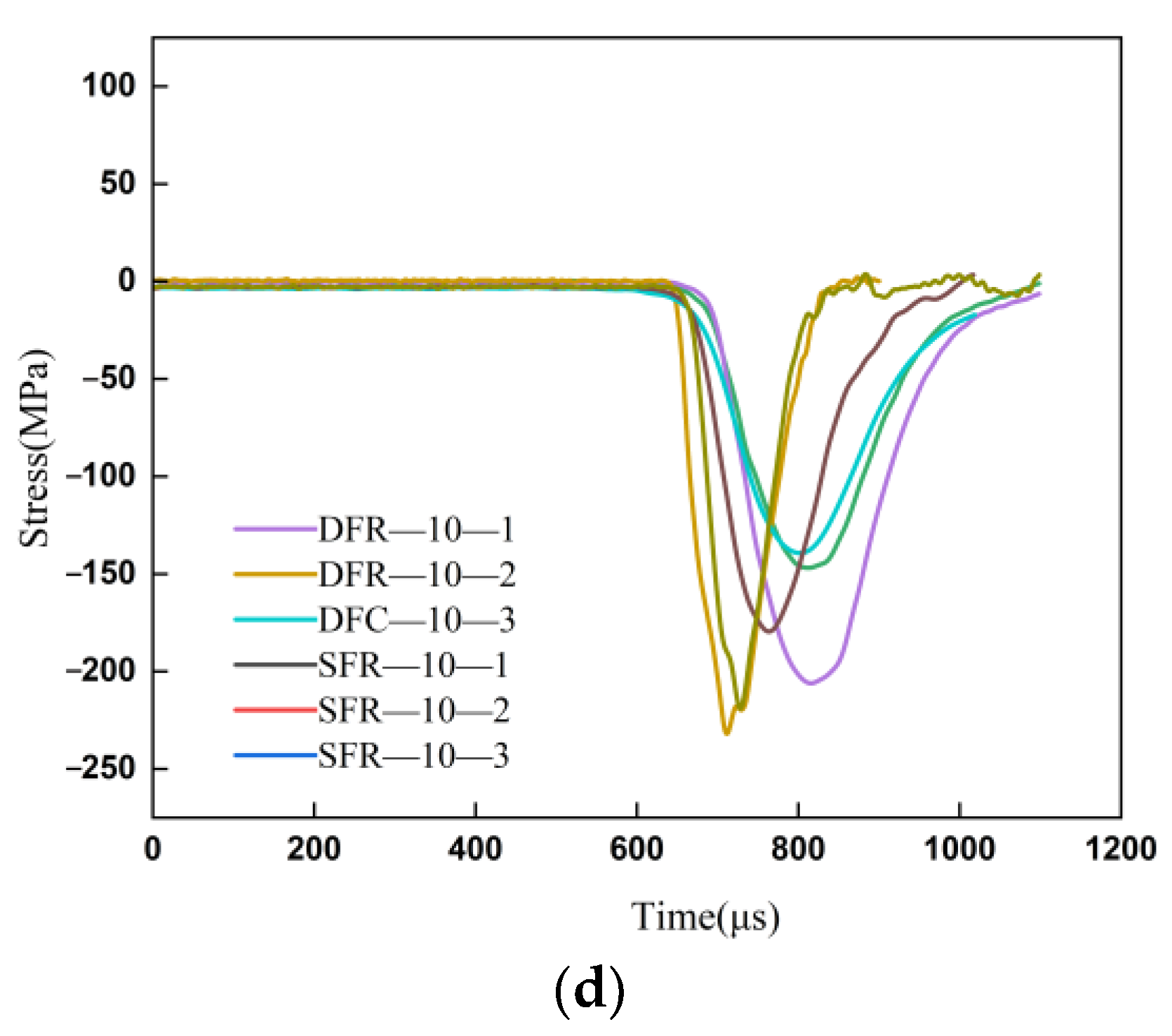
3.2.1. Time History Curve of Stress Wave
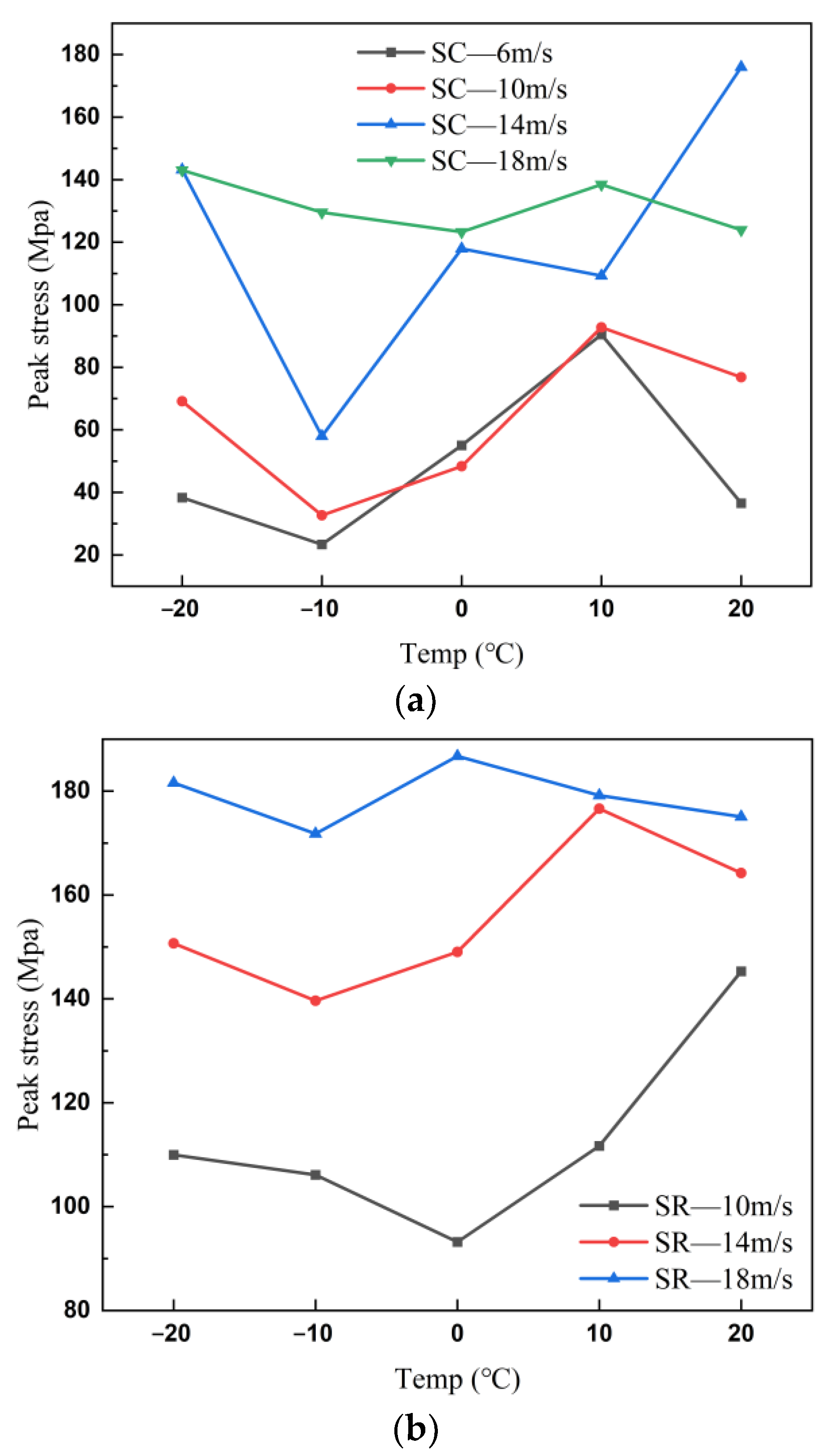
3.2.2. Dynamic Mechanical Characteristics of Coal and Rock during Impact
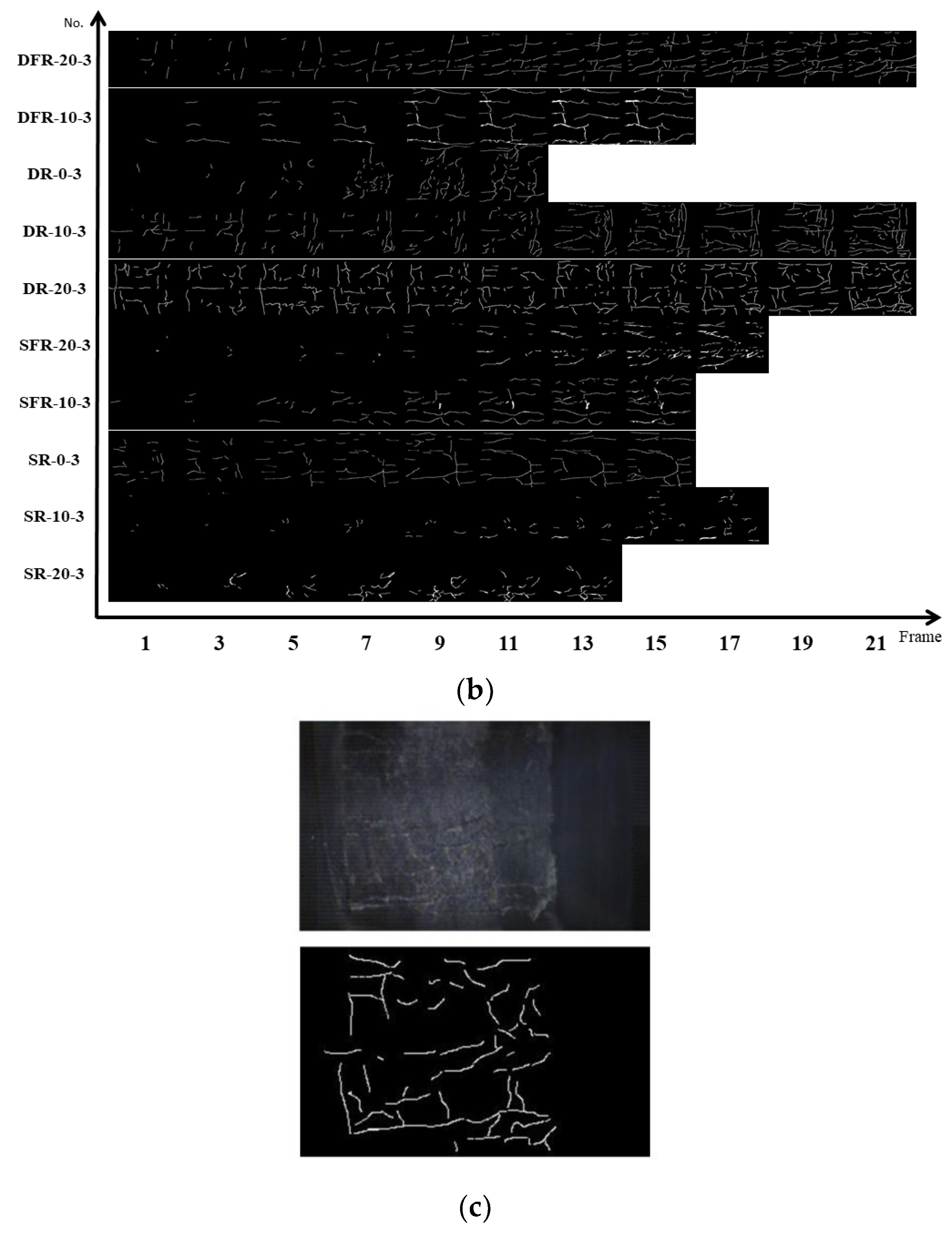
3.3. Process of Crack Propagation and Specimen Failure
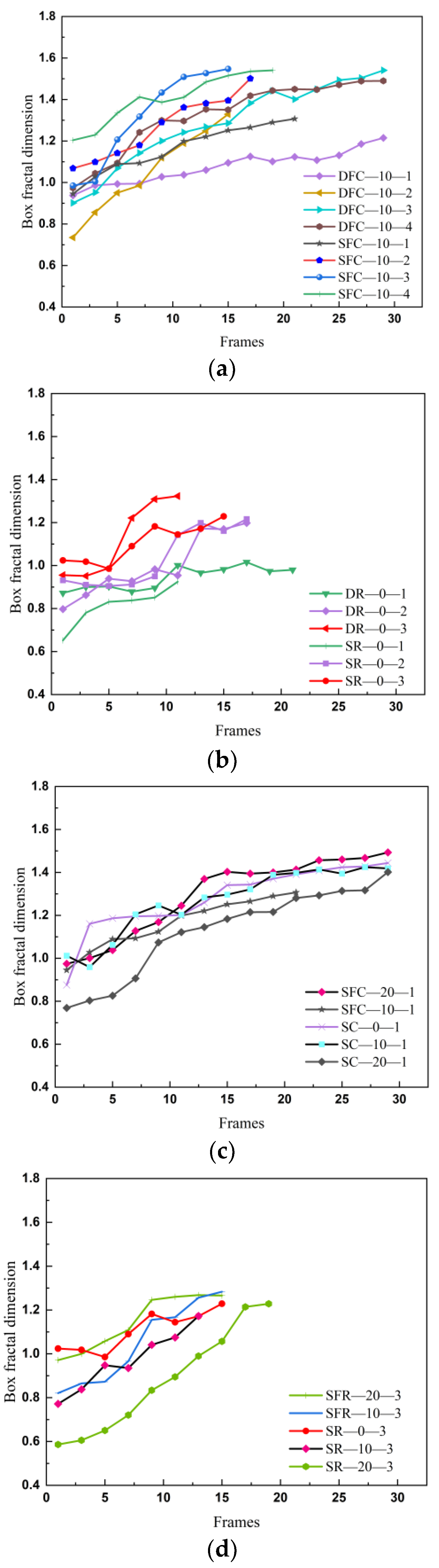
3.3.1. Recognition and Feature Extraction of Surface Cracks
3.3.2. Crack Quantification and Box Dimension Calculation
3.4. Fractal Characteristics of Crushing Products
4. Discussion
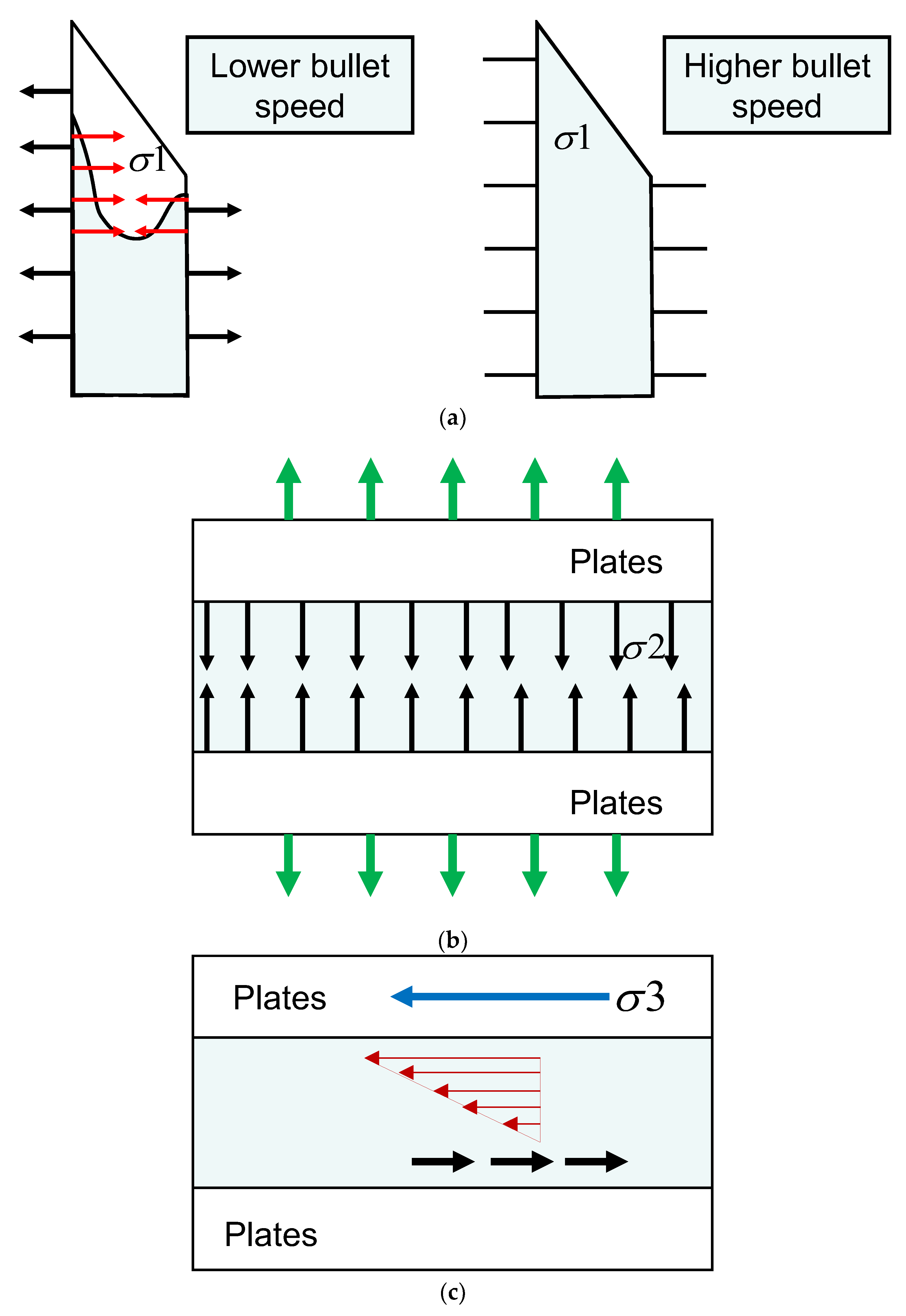
4.1. Mechanism of Water Action on Cracking Microcosm
4.2. Mechanism of Temperature Effect on the Crack Microcosm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Liu, Q.; Lin, H.; Wang, Y.; Tang, W.; Liao, J.; Wang, X. A review of hydromechanical coupling tests, theoretical and numerical analyses in rock materials. Water 2023, 15, 2309. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Zhang, Y.; Wang, J. Dynamic mechanical properties of coals subject to the low temperature-impact load coupling effect. Sci. Rep. 2019, 9, 20218. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Yu, Y.; Li, W.; Lu, Q. Study on temperature field evolution and frozen wall closure judgment criteria of inclined shaft under inclined holes freezing condition. Geofluids 2022, 2022, 8002667. [Google Scholar] [CrossRef]
- Paul, J.; Sengupta, M. Computer aided blasting-round design in an arctic coal mine. Int. J. Min. Sci. Technol. 1987, 5, 299–308. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, W.; Zhao, G.; Dong, F.; Geng, X. Aging Stability Analysis of Slope Considering Cumulative Effect of Freeze–Thaw Damage—A Case Study. Minerals 2022, 12, 598. [Google Scholar] [CrossRef]
- Li, H. Study on construction technology for tunnelling in the Plateau permafrost region. In Cold Regions Engineering. Cold Regions Impacts on Research, Design, and Construction; American Society Civil Engineers: Reston, VA, USA, 2009; pp. 16–21. [Google Scholar]
- Fan, L.; Fan, Y.; Xi, Y.; Gao, J. Spatial failure mode analysis of frozen sandstone under uniaxial compression based on CT technology. Rock Mech. Rock Eng. 2022, 55, 4123–4138. [Google Scholar] [CrossRef]
- Kodama, J.; Goto, T.; Fujii, Y.; Hagan, P. The effects of water content, temperature and loading rate on strength and failure process of frozen rocks. Int. J. Rock Mech. Min. 2013, 62, 1–13. [Google Scholar] [CrossRef]
- Sun, X.; Liu, B.; Dong, Q.; Shi, F. Experimental investigation on damage characteristics and early warning of frozen coal under uniaxial compression. Adv. Mater. Sci. Eng. 2023, 2023, 1607529. [Google Scholar] [CrossRef]
- Wang, T.; Sun, Q.; Jia, H.; Ren, J.; Luo, T. Linking the mechanical properties of frozen sandstone to phase composition of pore water measured by LF-NMR at subzero temperatures. Bull. Eng. Geol. Environ. 2021, 80, 4501–4513. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Z.; Liu, Q. Dynamic mechanical properties of dry and water-saturated siltstones under sub-zero temperatures. Rock Mech. Rock Eng. 2020, 53, 4381–4401. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, N.; Wang, J. Fracture morphology analysis of frozen red sandstone under impact. Shock Vib. 2021, 2021, 4388132. [Google Scholar] [CrossRef]
- Xu, J.; Pu, H.; Sha, Z. Dynamic mechanical behavior of the frozen red sandstone under coupling of saturation and impact loading. Appl. Sci. 2022, 12, 7767. [Google Scholar] [CrossRef]
- Yang, R.; Fang, S.; Li, W.; Yang, Y.; Yue, Z. Experimental study on the dynamic properties of three types of rock at negative temperature. Geotech. Geol. Eng. 2019, 37, 455–464. [Google Scholar] [CrossRef]
- Shan, R.; Song, Y.; Song, L.; Bai, Y. Dynamic property tests of frozen red sandstone using a split hopkinson pressure bar. Earthq. Eng. Eng. Vib. 2019, 18, 511–519. [Google Scholar]
- Zhao, Y.; Liu, Q.; Zhang, C.; Liao, J.; Lin, H.; Wang, Y. Coupled seepage-damage effect in fractured rock masses: Model development and a case study. Int. J. Rock Mech. Min. 2021, 144, 104822. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Wang, W.; Tang, L.; Liu, Q.; Cheng, G. Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mech. 2019, 101, 59–66. [Google Scholar] [CrossRef]
- Yu, G.; Vozoff, K.; Durney, D. Effects of confining pressure and water saturation on ultrasonic compressional wave velocities in coals. Int. J. Rock Mech. Min. 1991, 28, 28–36. [Google Scholar] [CrossRef]
- Liu, J.; Liu, D.; Cai, Y.; Gan, Q.; Yao, Y. Effects of water saturation on P-wave propagation in fractured coals: An experimental perspective. J. Appl. Geophys. 2017, 144, 94–103. [Google Scholar] [CrossRef]
- Zhao, E. Dynamic Characteristics and Damage Mechanism of Coal and Rock under Dynamic-Static Load and Temperature Coupling Effects; China University of Mining and Technology: Beijing, China, 2023. [Google Scholar]
- Wang, J.; Yang, Y.; Guo, Y. Low temperature effect of saturated granite on dynamic characteristics at high strain rates. Rock Soil Mech. 2017, 38 (Suppl. S2), 163–169. [Google Scholar]
- Wang, Z.; Tang, Y.; Li, M. Development and application of overburden structure composed of caving arch and towering roof beam in deep lonawall panel with thin bedrock. Chin. Coal J. 2023, 48, 563–575. [Google Scholar]
- Yang, S.; Wu, S.; Wang, Z. Surface subsidence and its prediction method of mining deep-buried seam with thick alluvial layer and thin bedrock. Chin. Coal J. 2023, 48, 523–537. [Google Scholar]
- Chen, Y.; Kang, T.; Wu, C. Study on mechanical behavior and mechanism of sandstone under the coupling effect of water content and dynamic load. Processes 2023, 11, 2318. [Google Scholar] [CrossRef]
- Kuruppu, M.D.; Obara, Y.; Ayatollahi, M.R. ISRM-suggested method for determining the mode I static fracture toughness using semi-circular bend specimen. Rock Mech. Rock Eng. 2014, 47, 267–274. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, K.; Li, X.; Li, H.; Ma, G.; Zhao, J. Suggested methods for determining the dynamic strength parameters and mode-i fracture toughness of rock materials. Int. J. Rock Mech. Min. Sci. 2012, 49, 105–112. [Google Scholar] [CrossRef]
- GB/T 23561.5-2009; National Standard Compilation Groups of People′s Republic of China. Methods for Determining the Physical and Mechanical Properties of Coal and Rock. Standards Press of China: Beijing, China, 2009.
- Sun, X.; Chen, G.; Li, J.; Xu, X.; Fu, S.; Xie, J.; Liang, L. Propagation characteristics of ultrasonic P-wave velocity in artificial jointed coal briquettes. J. Geophys. Eng. 2020, 5, 827–837. [Google Scholar] [CrossRef]
- Xie, B.; Chen, M.; Chen, S.; Luan, Z.; Li, X.; Liang, T. Experimental study on dynamic impact failure mechanical properties of ice samples. Chin. J. Disaster Prev. Mitig. Eng. 2023, 1–8. [Google Scholar] [CrossRef]
- Deshpande, V.; Chakraborty, P.; Chakraborty, T.; Tiwari, V. Application of copper as a pulse shaper in SHPB tests on brittle materials-experimental study, constitutive parameters identification, and numerical simulations. Mech. Mater. 2022, 171, 104336. [Google Scholar] [CrossRef]
- Feng, D.; Peng, Y.; Liu, Y. Study on SHPB technique. Chin. Prog. Geophys. 2006, 273–278. [Google Scholar]
- Sun, X.; Jin, T.; Li, J.; Xie, J.; Li, C.; Li, X. Dynamic characteristics and crack evolution laws of coal and rock under split Hopkinson pressure bar impact loading. Meas. Sci. Technol. E. 2023, 34, 075601. [Google Scholar] [CrossRef]
- Chen, W.; Bo, S. Split Hopkinson (Kolsky) Bar: Design, Testing and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- ASTM D 2845; ASTM Committee D-18 on Soil and Rock. Standard Test Method for Laboratory Determination of Pulse Velocities and Ultrasonic Elastic Constants of Rock. ASTM International: West Conshohocken, PA, USA, 2008.
- Zhao, Y.; Zhang, C.; Wang, Y.; Lin, H. Shear-related roughness classification and strength model of natural rock joint based on fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. Sci. 2021, 137, 104550. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.; Zhang, C.; Zhang, H.; Liao, J.; Zhu, S.; Zhang, L. Mechanical behavior of sandstone during post-peak cyclic loading and unloading under hydromechanical coupling. Int. J. Rock Mech. Min. Sci. 2023, 33, 927–947. [Google Scholar] [CrossRef]
- Li, Y.; Chang, X.; Dou, K. Research of ice mechanical properties parameters based on ultrasonic wave. China Meas. Test 2019, 45, 36–40. [Google Scholar]
- Sun, X.; He, Y.; Jin, T.; Xie, J.; Li, C.; Pang, J. Microseismic signal characteristics of the coal failure process under weak-energy and low-frequency disturbance. Sustainability 2023, 15, 14387. [Google Scholar] [CrossRef]
- Iakovidis, D.K. Ratsnake: A versatile image annotation tool with application to computer-aided diagnosis. Sci. World J. 2014, 2014, 286856. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.; Jiang, Y.; Zhang, B.; Song, H.; Liu, B. Characteristics of pore and fracture of coal with bursting proneness based on DIC and fractal theory. Energies 2020, 13, 5404. [Google Scholar] [CrossRef]
- Yang, R.; Li, Y.; Zeng, D.; Guo, P. Deep DIC: Deep learning-based digital image correlation for end-to-end displacement and strain measurement. J. Mater. Process Tech. 2022, 302, 117474. [Google Scholar] [CrossRef]
- Gerdes, L.; Berger, S.; Saelzer, J.; Franck, P.; Helwing, R.; Zabel, A.; Walther, F. Application-Oriented Digital Image Correlation for the High-Speed Deformation and Fracture Analysis of AISI 1045 and Ti6Al4V Materials. Appl. Mech. 2022, 3, 1190–1205. [Google Scholar] [CrossRef]
- Ai, D.; Zhao, Y.; Wang, Q.; Li, C. Experimental and numerical investigation of crack propagation and dynamic properties of rock in shpb indirect tension test. Int. Impact Eng. 2019, 126, 135–146. [Google Scholar] [CrossRef]
- Wu, N.; Fu, J.; Xiong, C. Studying the characteristics of chaos and fractals of construction rocks under different loading velocities. Materials 2022, 15, 7890. [Google Scholar] [CrossRef]






| Temperature /°C | Sample ID | Size (Diameter × Height)/mm | Density ρ(g/cm3) | Initial Wave Speed | Drying Wave Velocity | Saturation Wave Speed | P Wave Velocity v(km/s) | Average Wave Velocity v(km/s) | Uniaxial Compressive Strength (MPa) | Elastic Modulus Etan (GPa) | Poisson’s Ratio μ | Impact Speed v(m/s) | Experimental Result |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −20 | DFC-20-1 | 50 × 50 | 1.53 | 1.85 | 1.74 | — | 2.12 | 1.96 | — | — | — | 6.16 | impact smash |
| DFC-20-2 | 50 × 50 | 1.54 | 1.79 | 1.64 | — | 2.12 | — | — | — | 9.31 | impact smash | ||
| DFC-20-3 | 50 × 50 | 1.57 | 1.74 | 1.46 | — | 2.04 | — | — | — | 15.29 | impact smash | ||
| DFC-20-4 | 50 × 50 | 1.48 | 1.41 | 1.36 | — | 1.56 | — | — | — | 18.00 | impact smash | ||
| DFC-20-5 | 50 × 100 | — | — | — | — | — | 14.40 | 2.51 | 0.35 | ||||
| SFC-20-1 | 50 × 50 | 1.45 | 1.55 | 1.52 | 1.56 | 1.64 | 2.01 | — | — | — | 6.17 | impact smash | |
| SFC-20-2 | 50 × 50 | 1.45 | 1.52 | 1.60 | 1.88 | 2.33 | — | — | — | 9.54 | impact smash | ||
| SFC-20-3 | 50 × 50 | 1.82 | 1.51 | 1.40 | 1.5 | 1.81 | — | — | — | 14.68 | impact smash | ||
| SFC-20-4 | 50 × 50 | 1.64 | 2.03 | 1.64 | 1.93 | 2.27 | — | — | — | 18.07 | impact smash | ||
| SFC-20-5 | 50 × 100 | — | — | — | — | — | 18.24 | 2.74 | 0.33 | ||||
| −10 | DFC-10-1 | 50 × 50 | 1.54 | 1.70 | 1.56 | — | 1.8 | 1.68 | — | — | — | 6.15 | impact smash |
| DFC-10-2 | 50 × 50 | 1.58 | 1.67 | 1.33 | — | 1.72 | — | — | — | 9.43 | impact smash | ||
| DFC-10-3 | 50 × 50 | 1.45 | 1.64 | 1.56 | — | 1.67 | — | — | — | 14.48 | impact smash | ||
| DFC-10-4 | 50 × 50 | 1.48 | 1.37 | 1.36 | — | 1.52 | — | — | — | 17.96 | impact smash | ||
| SFC-10-1 | 50 × 50 | 1.60 | 1.51 | 1.20 | 1.48 | 1.9 | 1.75 | — | — | — | 6.35 | impact smash | |
| SFC-10-2 | 50 × 50 | 1.45 | 1.49 | 1.45 | 1.64 | 1.67 | — | — | — | 10.26 | impact smash | ||
| SFC-10-3 | 50 × 50 | 1.62 | 1.46 | 1.42 | 1.51 | 1.72 | — | — | — | 14.08 | impact smash | ||
| SFC-10-4 | 50 × 50 | 1.59 | 1.48 | 1.32 | 1.46 | 1.7 | — | — | — | 18.07 | impact smash | ||
| 0 | DC-0-1 | 50 × 50 | 1.62 | 1.63 | 1.38 | — | 1.69 | 1.74 | — | — | — | 6.38 | impact smash |
| DC-0-2 | 50 × 50 | 1.64 | 1.62 | 1.42 | — | 1.68 | — | — | — | 9.74 | impact smash | ||
| DC-0-3 | 50 × 50 | 1.61 | 1.59 | 1.49 | — | 1.79 | — | — | — | 14.55 | impact smash | ||
| DC-0-4 | 50 × 50 | 1.45 | 1.77 | 1.68 | — | 1.80 | — | — | — | 18.24 | impact smash | ||
| DC-0-5 | 50 × 100 | — | — | — | — | — | 24.78 | 3.75 | 0.3 | ||||
| SC-0-1 | 50 × 50 | 1.46 | 1.44 | 1.28 | 1.44 | 1.90 | 1.99 | — | — | — | 6.03 | impact smash | |
| SC-0-2 | 50 × 50 | 1.61 | 1.90 | 1.62 | 1.86 | 2.19 | — | — | — | 9.30 | impact smash | ||
| SC-0-3 | 50 × 50 | 1.45 | 1.38 | 1.54 | 1.86 | 1.98 | — | — | — | 14.26 | impact smash | ||
| SC-0-4 | 50 × 50 | 1.54 | 1.7 | 1.28 | 1.6 | 1.88 | — | — | — | 17.92 | impact smash | ||
| SC-0-5 | 50 × 100 | — | — | — | — | — | 28.20 | 3.98 | 0.29 | impact smash | |||
| 10 | DC-10-1 | 50 × 50 | 1.67 | 1.59 | 1.54 | — | 1.78 | 1.73 | — | — | — | 5.55 | impact smash |
| DC-10-2 | 50 × 50 | 1.48 | 1.58 | 1.39 | — | 1.67 | — | — | — | 9.54 | impact smash | ||
| DC-10-3 | 50 × 50 | 1.49 | 1.58 | 1.44 | — | 1.77 | — | — | — | 15.51 | impact smash | ||
| DC-10-4 | 50 × 50 | 1.43 | 1.81 | 1.60 | — | 1.69 | — | — | — | 17.96 | impact smash | ||
| SC-10-1 | 50 × 50 | 1.59 | 1.38 | 1.32 | 1.69 | 1.71 | 1.87 | — | — | — | 5.99 | impact smash | |
| SC-10-2 | 50 × 50 | 1.66 | 1.33 | 1.49 | 1.70 | 1.95 | — | — | — | 9.47 | impact smash | ||
| SC-10-3 | 50 × 50 | 1.62 | 1.33 | 1.64 | 1.79 | 1.88 | — | — | — | 15.18 | impact smash | ||
| SC-10-4 | 50 × 50 | 1.42 | 1.02 | 1.14 | 1.51 | 1.92 | — | — | — | 17.92 | impact smash | ||
| 20 | DC-20-1 | 50 × 50 | 1.55 | 1.56 | 1.48 | — | 1.59 | 1.68 | — | — | — | 6.07 | impact smash |
| DC-20-2 | 50 × 50 | 1.60 | 1.56 | 1.54 | — | 1.71 | — | — | — | 9.80 | impact smash | ||
| DC-20-3 | 50 × 50 | 1.46 | 1.55 | 1.44 | — | 1.62 | — | — | — | 12.79 | impact smash | ||
| DC-20-4 | 50 × 50 | 1.52 | 1.81 | 1.61 | — | 1.79 | — | — | — | 17.86 | impact smash | ||
| DC-20-5 | 50 × 100 | — | — | — | — | — | 16.37 | 3.21 | 0.33 | ||||
| SC-20-1 | 50 × 50 | 1.36 | 1.33 | 1.27 | 1.30 | 1.42 | 1.69 | — | — | — | 6.15 | impact smash | |
| SC-20-2 | 50 × 50 | 1.50 | 1.33 | 1.35 | 1.86 | 1.97 | — | — | — | 9.12 | impact smash | ||
| SC-20-3 | 50 × 50 | 1.47 | 1.31 | 1.47 | 1.54 | 1.68 | — | — | — | 14.40 | impact smash | ||
| SC-20-4 | 50 × 50 | 1.87 | 1.55 | 1.89 | 1.67 | — | — | — | 17.37 | impact smash | |||
| SC-20-5 | 50 × 100 | — | — | — | — | — | 20.02 | 3.97 | 0.31 |
| Temperature /°C | Sample ID | Size (Diameter × Height)/mm | Density ρ(g/cm3) | Initial Wave Speed | Drying Wave Velocity | Saturation Wave Speed | P Wave Velocity v(km/s) | Average Wave Velocity v(km/s) | Uniaxial Compressive Strength (MPa) | Elastic Modulus Etan (GPa) | Poisson’s Ratio μ | Impact Speed v(m/s) | Experimental Result |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −20 | DFR-20-1 | 50 × 50 | 2.76 | 2.36 | 2.11 | — | 2.37 | 2.38 | — | — | — | 9.70 | impact fracture |
| DFR-20-2 | 50 × 50 | 2.74 | 2.36 | 2.12 | — | 2.35 | — | — | — | 14.74 | impact smash | ||
| DFR-20-3 | 50 × 50 | 2.73 | 2.24 | 2.14 | — | 2.41 | — | — | — | 18.95 | impact smash | ||
| DFR-20-4 | 50 × 100 | — | — | — | — | — | 31.68 | 8.37 | 0.26 | impact smash | |||
| SFR-20-1 | 50 × 50 | 2.75 | 2.16 | 2.12 | 2.26 | 2.48 | 2.44 | — | — | — | 10.71 | impact fracture | |
| SFR-20-2 | 50 × 50 | 2.77 | 2.14 | 2.06 | 2.29 | 2.46 | — | — | — | 14.80 | impact smash | ||
| SFR-20-3 | 50 × 50 | 2.71 | 2.14 | 2.09 | 2.21 | 2.38 | — | — | — | 18.13 | impact smash | ||
| SFR-20-4 | 50 × 100 | — | — | — | — | — | — | 20.55 | 8.59 | 0.24 | impact smash | ||
| −10 | DFR-10-1 | 50 × 50 | 2.73 | 2.22 | 2.05 | — | 2.21 | 2.24 | — | — | — | 10.21 | impact fracture |
| DFR-10-2 | 50 × 50 | 2.75 | 2.22 | 2.11 | — | 2.25 | — | — | — | 14.07 | impact fracture | ||
| DFR-10-3 | 50 × 50 | 2.70 | 2.22 | 2.14 | — | 2.27 | — | — | — | 17.21 | impact smash | ||
| SFR-10-1 | 50 × 50 | 2.71 | 2.12 | 2.10 | 2.32 | 2.3 | 2.33 | — | — | — | 10.20 | impact smash | |
| SFR-10-2 | 50 × 50 | 2.73 | 2.12 | 1.90 | 2.24 | 2.35 | — | — | — | 14.20 | impact smash | ||
| SFR-10-3 | 50 × 50 | 2.67 | 2.12 | 1.82 | 2.29 | 2.34 | — | — | — | 17.80 | impact smash | ||
| 0 | DR-0-1 | 50 × 50 | 2.67 | 2.21 | 2.11 | — | 2.42 | 2.40 | — | — | — | 9.38 | impact fracture |
| DR-0-2 | 50 × 50 | 2.71 | 2.21 | 2.03 | — | 2.40 | — | — | — | 14.02 | impact smash | ||
| DR-0-3 | 50 × 50 | 2.71 | 2.19 | 2.13 | — | 2.38 | — | — | — | 17.30 | impact smash | ||
| DR-0-4 | 50 × 100 | — | — | — | — | — | 39.36 | 8.64 | 0.23 | impact smash | |||
| SR-0-1 | 50 × 50 | 2.70 | 2.10 | 1.98 | 2.30 | 2.60 | 2.61 | — | — | — | 9.12 | impact smash | |
| SR-0-2 | 50 × 50 | 2.67 | 2.10 | 2.08 | 2.24 | 2.64 | — | — | — | 14.02 | impact smash | ||
| SR-0-3 | 50 × 50 | 2.67 | 2.10 | 1.95 | 2.17 | 2.60 | — | — | — | 17.81 | impact smash | ||
| SR-0-4 | 50 × 100 | — | — | — | — | — | 20.83 | 8.82 | 0.21 | impact smash | |||
| 10 | DR-10-1 | 50 × 50 | 2.74 | 2.19 | 2.04 | — | 2.50 | 2.37 | — | — | — | 10.61 | impact fracture |
| DR-10-2 | 50 × 50 | 2.66 | 2.19 | 2.10 | — | 2.28 | — | — | — | 13.80 | impact smash | ||
| DR-10-3 | 50 × 50 | 2.73 | 2.19 | 1.90 | — | 2.32 | — | — | — | 17.87 | impact smash | ||
| SR-10-1 | 50 × 50 | 2.70 | 2.08 | 1.85 | 2.19 | 2.40 | 2.51 | — | — | — | 9.69 | impact smash | |
| SR-10-2 | 50 × 50 | 2.73 | 2.08 | 1.77 | 2.20 | 2.60 | — | — | — | 13.91 | impact smash | ||
| SR-10-3 | 50 × 50 | 2.75 | 2.08 | 1.91 | 2.31 | 2.52 | — | — | — | 10.30 | impact smash | ||
| 20 | DR-20-1 | 50 × 50 | 2.70 | 2.19 | 1.96 | — | 2.29 | 2.34 | — | — | — | 10.39 | impact fracture |
| DR-20-2 | 50 × 50 | 2.75 | 2.18 | 2.02 | — | 2.34 | — | — | — | 15.80 | impact smash | ||
| DR-20-3 | 50 × 50 | 2.72 | 2.17 | 1.98 | — | 2.38 | — | — | — | 17.96 | impact smash | ||
| DR-20-4 | 50 × 100 | — | — | — | — | — | — | 38.50 | 8.72 | 0.25 | impact smash | ||
| SR-20-1 | 50 × 50 | 2.72 | 2.08 | 2.07 | 2.38 | 2.43 | 2.43 | — | — | — | 9.92 | impact fracture | |
| SR-20-2 | 50 × 50 | 2.71 | 2.07 | 2.02 | 2.41 | 2.44 | — | — | — | 14.76 | impact smash | ||
| SR-20-3 | 50 × 50 | 2.69 | 2.07 | 1.95 | 2.34 | 2.41 | — | — | — | 18.32 | impact smash | ||
| SR-20-4 | 50 × 100 | — | — | — | — | — | — | 23.19 | 8.75 | 0.23 | impact smash |
| Sample No. | Impact Speed (m/s) | Cumulative Mass Percent of Each Particle Size Under the Sieve/% | Fitting Results | Fractal Dimension | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.075 | 0.15 | 0.3 | 0.6 | 1.18 | 2.36 | 4.75 | 9.5 | Fitting Slope | Intercept Distance | Decision Factor (R2 Value) | |||
| DFC-20-1 | 6.16 | 0.21 | 0.67 | 2.15 | 5.23 | 10.49 | 29.17 | 65.95 | 100.00 | 1.28 | 0.19 | 0.99 | 1.72 |
| DFC-20-2 | 9.31 | 0.51 | 1.52 | 4.44 | 9.97 | 19.03 | 42.49 | 75.10 | 100.00 | 1.10 | 0.22 | 0.99 | 1.90 |
| DFC-20-3 | 15.29 | 0.70 | 2.31 | 7.49 | 14.54 | 28.62 | 58.06 | 92.60 | 100.00 | 1.03 | 0.29 | 0.95 | 1.97 |
| DFC-20-4 | 18.00 | 3.10 | 6.54 | 14.89 | 26.42 | 45.02 | 75.91 | 95.11 | 100.00 | 0.74 | 0.22 | 0.95 | 2.26 |
| SFC-20-1 | 6.17 | 0.00 | 0.04 | 0.25 | 0.80 | 2.18 | 5.91 | 18.88 | 100.00 | 1.78 | −0.01 | 0.99 | 1.22 |
| SFC-20-2 | 9.54 | 0.41 | 1.32 | 4.50 | 10.48 | 19.60 | 46.08 | 84.13 | 100.00 | 1.15 | 0.08 | 0.97 | 1.85 |
| SFC-20-3 | 14.68 | 0.37 | 1.00 | 3.08 | 6.65 | 12.41 | 27.17 | 58.75 | 100.00 | 1.15 | 0.07 | 0.99 | 1.85 |
| SFC-20-4 | 18.07 | 1.72 | 3.71 | 9.83 | 19.84 | 35.06 | 69.46 | 97.71 | 100.00 | 0.88 | 0.21 | 0.96 | 2.12 |
| DFC-10-1 | 6.15 | 0.05 | 0.23 | 0.82 | 1.94 | 3.96 | 9.63 | 28.76 | 100.00 | 1.47 | 0.18 | 0.99 | 1.53 |
| DFC-10-2 | 9.43 | 0.28 | 0.73 | 2.05 | 4.47 | 8.48 | 20.71 | 52.05 | 100.00 | 1.21 | 0.20 | 1.00 | 1.79 |
| DFC-10-3 | 14.48 | 0.84 | 1.81 | 4.49 | 8.97 | 15.93 | 29.82 | 50.91 | 100.00 | 0.97 | 0.11 | 0.99 | 2.03 |
| DFC-10-4 | 17.96 | 3.04 | 6.46 | 14.82 | 25.14 | 43.04 | 71.13 | 91.55 | 100.00 | 0.74 | 0.26 | 0.95 | 2.26 |
| SFC-10-1 | 6.35 | 0.42 | 0.94 | 2.33 | 4.43 | 8.93 | 37.02 | 53.82 | 100.00 | 1.17 | −0.01 | 0.99 | 1.83 |
| SFC-10-2 | 10.26 | 0.39 | 0.93 | 2.34 | 4.71 | 9.29 | 23.54 | 60.56 | 100.00 | 1.16 | 0.17 | 1.00 | 1.84 |
| SFC-10-3 | 14.08 | 0.90 | 2.41 | 6.38 | 11.72 | 22.28 | 50.18 | 84.28 | 100.00 | 0.99 | 0.17 | 0.98 | 2.01 |
| SFC-10-4 | 17.69 | 1.88 | 4.30 | 11.05 | 19.55 | 33.77 | 55.64 | 82.94 | 100.00 | 0.83 | 0.23 | 0.96 | 2.17 |
| DC-0-1 | 6.38 | 0.48 | 1.08 | 3.02 | 6.55 | 13.33 | 36.50 | 74.99 | 100.00 | 1.15 | −0.05 | 0.99 | 1.85 |
| DC-0-2 | 9.74 | 0.55 | 1.35 | 4.11 | 9.22 | 17.81 | 38.89 | 73.21 | 100.00 | 1.10 | 0.12 | 0.98 | 1.90 |
| DC-0-3 | 14.55 | 0.81 | 1.84 | 4.56 | 8.75 | 15.33 | 33.39 | 64.75 | 100.00 | 1.00 | 0.14 | 0.99 | 2.00 |
| DC-0-4 | 18.24 | 2.28 | 4.93 | 12.65 | 25.34 | 42.90 | 75.82 | 96.59 | 100.00 | 0.81 | 0.17 | 0.94 | 2.19 |
| SC-0-1 | 6.03 | 0.07 | 0.21 | 0.93 | 2.35 | 5.32 | 13.77 | 27.94 | 100.00 | 1.46 | −0.03 | 0.99 | 1.54 |
| SC-0-2 | 9.30 | 0.53 | 1.31 | 3.56 | 6.84 | 13.79 | 29.97 | 64.21 | 100.00 | 1.09 | 0.27 | 0.99 | 1.91 |
| SC-0-3 | 14.26 | 1.98 | 4.16 | 10.28 | 20.03 | 33.90 | 64.08 | 95.43 | 100.00 | 0.85 | 0.13 | 0.96 | 2.15 |
| SC-0-4 | 17.92 | 1.48 | 3.15 | 7.79 | 15.37 | 27.23 | 54.01 | 89.19 | 100.00 | 0.91 | 0.26 | 0.98 | 2.09 |
| DC-10-1 | 5.55 | 0.18 | 0.47 | 1.38 | 2.77 | 5.69 | 15.02 | 38.49 | 100.00 | 1.28 | 0.11 | 1.00 | 1.72 |
| DC-10-2 | 9.54 | 0.69 | 1.63 | 4.54 | 8.95 | 18.16 | 39.68 | 70.26 | 100.00 | 1.05 | 0.09 | 0.99 | 1.95 |
| DC-10-3 | 15.51 | 1.12 | 2.72 | 6.50 | 11.61 | 22.10 | 45.45 | 80.37 | 100.00 | 0.94 | 0.21 | 0.98 | 2.06 |
| DC-10-4 | 18.32 | 1.71 | 3.81 | 9.77 | 18.75 | 37.00 | 65.68 | 84.80 | 100.00 | 0.87 | 0.19 | 0.96 | 2.13 |
| SC-10-1 | 5.99 | 0.32 | 0.78 | 2.17 | 4.23 | 9.05 | 23.44 | 55.65 | 100.00 | 1.20 | 0.04 | 1.00 | 1.80 |
| SC-10-2 | 9.47 | 0.81 | 1.95 | 5.35 | 11.53 | 20.77 | 43.81 | 75.21 | 100.00 | 1.01 | 0.13 | 0.98 | 1.99 |
| SC-10-3 | 15.18 | 1.22 | 2.77 | 6.83 | 11.64 | 20.86 | 40.67 | 76.00 | 100.00 | 0.92 | 0.23 | 0.99 | 2.08 |
| SC-10-4 | 17.93 | 1.33 | 2.83 | 6.53 | 12.17 | 20.45 | 42.24 | 70.68 | 100.00 | 0.99 | 0.21 | 0.90 | 2.01 |
| DC-20-1 | 6.15 | 0.99 | 2.57 | 7.59 | 15.95 | 28.22 | 52.72 | 80.24 | 100.00 | 1.25 | 0.09 | 0.98 | 1.75 |
| DC-20-2 | 9.80 | 1.50 | 3.67 | 8.79 | 15.71 | 23.85 | 40.37 | 68.05 | 100.00 | 0.84 | 0.19 | 0.98 | 2.16 |
| DC-20-3 | 12.79 | 0.88 | 2.08 | 5.26 | 9.96 | 17.87 | 37.37 | 70.80 | 100.00 | 0.99 | 0.14 | 0.99 | 2.01 |
| DC-20-4 | 17.86 | 2.24 | 4.49 | 10.34 | 17.84 | 31.53 | 56.07 | 83.96 | 100.00 | 0.81 | 0.13 | 0.98 | 2.19 |
| SC-20-1 | 6.15 | 0.99 | 2.57 | 7.59 | 15.95 | 28.22 | 52.72 | 80.24 | 100.00 | 0.96 | 0.23 | 0.96 | 2.04 |
| SC-20-2 | 9.12 | 0.83 | 1.94 | 5.27 | 10.97 | 20.42 | 45.56 | 79.36 | 100.00 | 1.02 | 0.20 | 0.98 | 1.98 |
| SC-20-3 | 14.40 | 0.75 | 2.15 | 5.25 | 9.29 | 17.33 | 37.46 | 70.73 | 100.00 | 1.00 | 0.15 | 0.99 | 2.00 |
| SC-20-4 | 17.37 | 1.25 | 2.61 | 6.32 | 11.78 | 19.37 | 38.71 | 74.77 | 100.00 | 0.99 | 0.13 | 0.92 | 2.01 |
| Sample No. | Impact Speed (m/s) | Cumulative Mass Percent of Each Particle Size Under the Sieve/% | Fitting Results | Fractal Dimension | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.075 | 0.15 | 0.3 | 0.6 | 1.18 | 2.36 | 4.75 | 9.5 | Fitting Slope | Intercept Distance | Decision Factor (R2 Value) | |||
| DFR-20-1 | 9.70 | 0.00 | 0.03 | 0.07 | 0.14 | 0.23 | 0.41 | 0.61 | 100.00 | 1.52 | −0.98 | 0.75 | 1.48 |
| DFR-20-2 | 14.74 | 0.01 | 1.35 | 2.33 | 3.36 | 5.02 | 8.31 | 22.73 | 100.00 | 1.47 | 0.06 | 0.79 | 1.53 |
| DFR-20-3 | 18.95 | 0.01 | 2.38 | 4.22 | 6.28 | 8.78 | 14.68 | 37.59 | 100.00 | 1.39 | 0.19 | 0.76 | 1.61 |
| SFR-20-1 | 10.71 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | |
| SFR-20-2 | 14.80 | 0.01 | 1.59 | 2.71 | 3.72 | 5.23 | 9.68 | 24.77 | 100.00 | 1.44 | −1.53 | 0.78 | 1.56 |
| SFR-20-3 | 18.13 | 0.01 | 2.61 | 4.69 | 6.76 | 9.97 | 16.18 | 36.63 | 100.00 | 1.38 | −1.51 | 0.75 | 1.62 |
| DFR-10-1 | 10.21 | 0.00 | 0.01 | 0.02 | 0.02 | 0.03 | 0.03 | 0.03 | 100.00 | 1.80 | 0.05 | 0.64 | 1.20 |
| DFR-10-2 | 14.07 | 0.00 | 0.02 | 0.03 | 0.03 | 0.04 | 0.04 | 0.04 | 100.00 | 1.74 | −0.49 | 0.62 | 1.26 |
| DFR-10-3 | 17.21 | 0.01 | 1.95 | 3.30 | 4.75 | 6.47 | 10.46 | 19.87 | 100.00 | 1.37 | −0.17 | 0.75 | 1.63 |
| SFR-10-1 | 10.20 | 0.00 | 0.08 | 0.11 | 0.13 | 0.22 | 0.48 | 0.78 | 100.00 | 1.73 | 0.15 | 0.79 | 1.27 |
| SFR-10-2 | 14.20 | 0.01 | 1.25 | 2.05 | 2.76 | 3.85 | 6.37 | 16.33 | 100.00 | 1.64 | −0.41 | 0.79 | 1.36 |
| SFR-10-3 | 17.80 | 0.01 | 2.23 | 3.76 | 5.24 | 7.58 | 13.31 | 33.56 | 100.00 | 1.40 | 0.17 | 0.77 | 1.60 |
| DR-0-1 | 9.38 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | |
| DR-0-2 | 14.02 | 0.01 | 1.36 | 2.16 | 2.97 | 4.07 | 6.31 | 19.06 | 100.00 | 1.71 | −0.03 | 0.83 | 1.29 |
| DR-0-3 | 17.30 | 0.01 | 2.38 | 4.06 | 5.92 | 8.38 | 15.24 | 30.00 | 100.00 | 1.46 | 0.15 | 0.78 | 1.54 |
| SR-0-1 | 9.12 | 0.00 | 0.04 | 0.08 | 0.14 | 0.22 | 0.32 | 0.88 | 100.00 | 1.95 | 0.08 | 0.80 | 1.05 |
| SR-0-2 | 14.02 | 0.01 | 1.20 | 1.99 | 2.78 | 3.63 | 6.21 | 18.15 | 100.00 | 1.46 | 0.20 | 0.78 | 1.54 |
| SR-0-3 | 17.81 | 0.01 | 1.52 | 2.47 | 3.57 | 5.14 | 8.83 | 21.52 | 100.00 | 1.43 | −0.80 | 0.78 | 1.57 |
| DR-10-1 | 10.61 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | |
| DR-10-2 | 13.80 | 0.00 | 0.23 | 0.39 | 0.58 | 0.82 | 1.33 | 3.41 | 100.00 | 1.68 | 0.16 | 0.80 | 1.32 |
| DR-10-3 | 17.87 | 0.01 | 2.55 | 4.36 | 6.26 | 8.49 | 14.20 | 35.17 | 100.00 | 1.37 | −0.70 | 0.76 | 1.63 |
| SR-10-1 | 9.69 | 0.00 | 0.04 | 0.09 | 0.13 | 0.20 | 0.28 | 0.43 | 100.00 | 1.88 | −0.02 | 0.76 | 1.12 |
| SR-10-2 | 13.91 | 0.00 | 0.57 | 0.99 | 1.45 | 2.01 | 3.43 | 8.99 | 100.00 | 1.56 | 0.05 | 0.80 | 1.44 |
| SR-10-3 | 10.30 | 0.01 | 1.87 | 3.24 | 4.72 | 6.65 | 11.43 | 26.42 | 100.00 | 1.41 | 0.77 | 1.59 | |
| DR-20-1 | 10.39 | -- | -- | -- | -- | -- | -- | -- | -- | -- | −0.83 | -- | -- |
| DR-20-2 | 15.80 | 0.00 | 0.32 | 0.59 | 0.88 | 1.38 | 2.50 | 9.73 | 100.00 | 1.42 | −0.18 | 0.78 | 1.58 |
| DR-20-3 | 17.96 | 0.01 | 1.65 | 3.07 | 4.68 | 6.97 | 12.68 | 28.54 | 100.00 | 1.37 | 0.11 | 0.76 | 1.63 |
| SR-20-1 | 9.92 | 0.00 | 0.04 | 0.07 | 0.11 | 0.15 | 0.35 | 1.18 | 100.00 | 2.00 | −0.67 | 0.83 | 1.00 |
| SR-20-2 | 14.76 | 0.01 | 1.60 | 2.73 | 3.96 | 5.77 | 9.91 | 25.98 | 100.00 | 1.45 | 0.10 | 0.78 | 1.55 |
| SR-20-3 | 18.32 | 0.01 | 2.59 | 4.60 | 6.89 | 9.81 | 17.59 | 41.69 | 100.00 | 1.38 | 0.23 | 0.76 | 1.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, T.; Sun, X.; Liu, K.; Lin, S.; Yang, S.; Xie, J. Experimental Study of the Multiple Fractalisation of Coal and Rock Failure Subjected to the Coupled Effects of Water, Temperature and Dynamic Loads. Appl. Sci. 2023, 13, 13004. https://doi.org/10.3390/app132413004
Jin T, Sun X, Liu K, Lin S, Yang S, Xie J. Experimental Study of the Multiple Fractalisation of Coal and Rock Failure Subjected to the Coupled Effects of Water, Temperature and Dynamic Loads. Applied Sciences. 2023; 13(24):13004. https://doi.org/10.3390/app132413004
Chicago/Turabian StyleJin, Tingxu, Xiaoyuan Sun, Kai Liu, Shurong Lin, Shaoqiang Yang, and Jianlin Xie. 2023. "Experimental Study of the Multiple Fractalisation of Coal and Rock Failure Subjected to the Coupled Effects of Water, Temperature and Dynamic Loads" Applied Sciences 13, no. 24: 13004. https://doi.org/10.3390/app132413004
APA StyleJin, T., Sun, X., Liu, K., Lin, S., Yang, S., & Xie, J. (2023). Experimental Study of the Multiple Fractalisation of Coal and Rock Failure Subjected to the Coupled Effects of Water, Temperature and Dynamic Loads. Applied Sciences, 13(24), 13004. https://doi.org/10.3390/app132413004






