Technical Reviews of Power Loss Optimization in High-Frequency PSiPs—In Relation to Power Switches and Power Inductors
Abstract
:1. Introduction
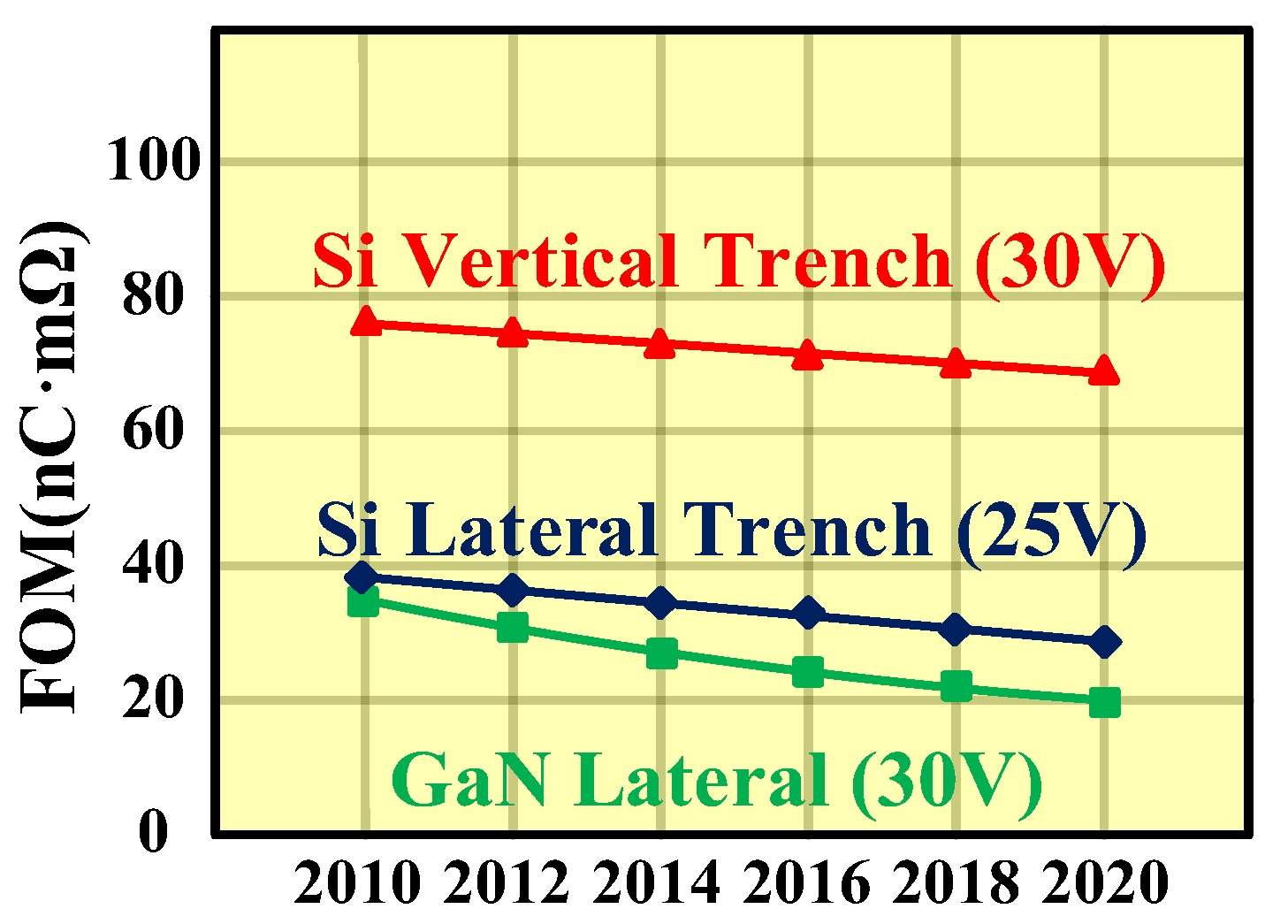
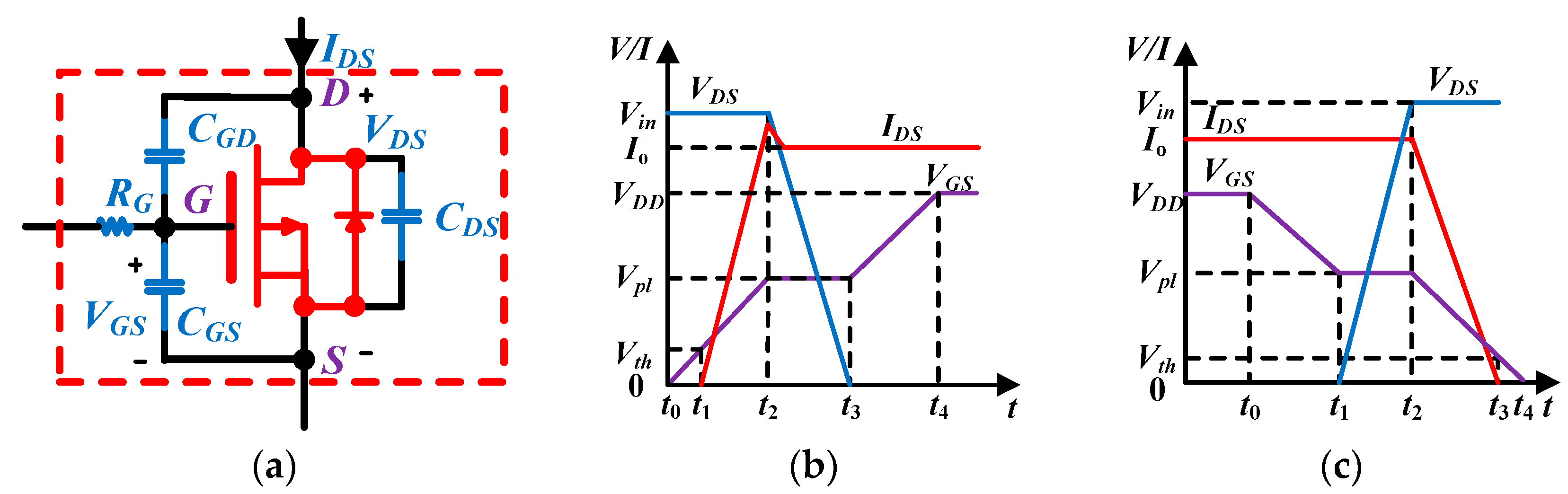
2. Power Loss Analysis of Integrated Si LDMOSFET
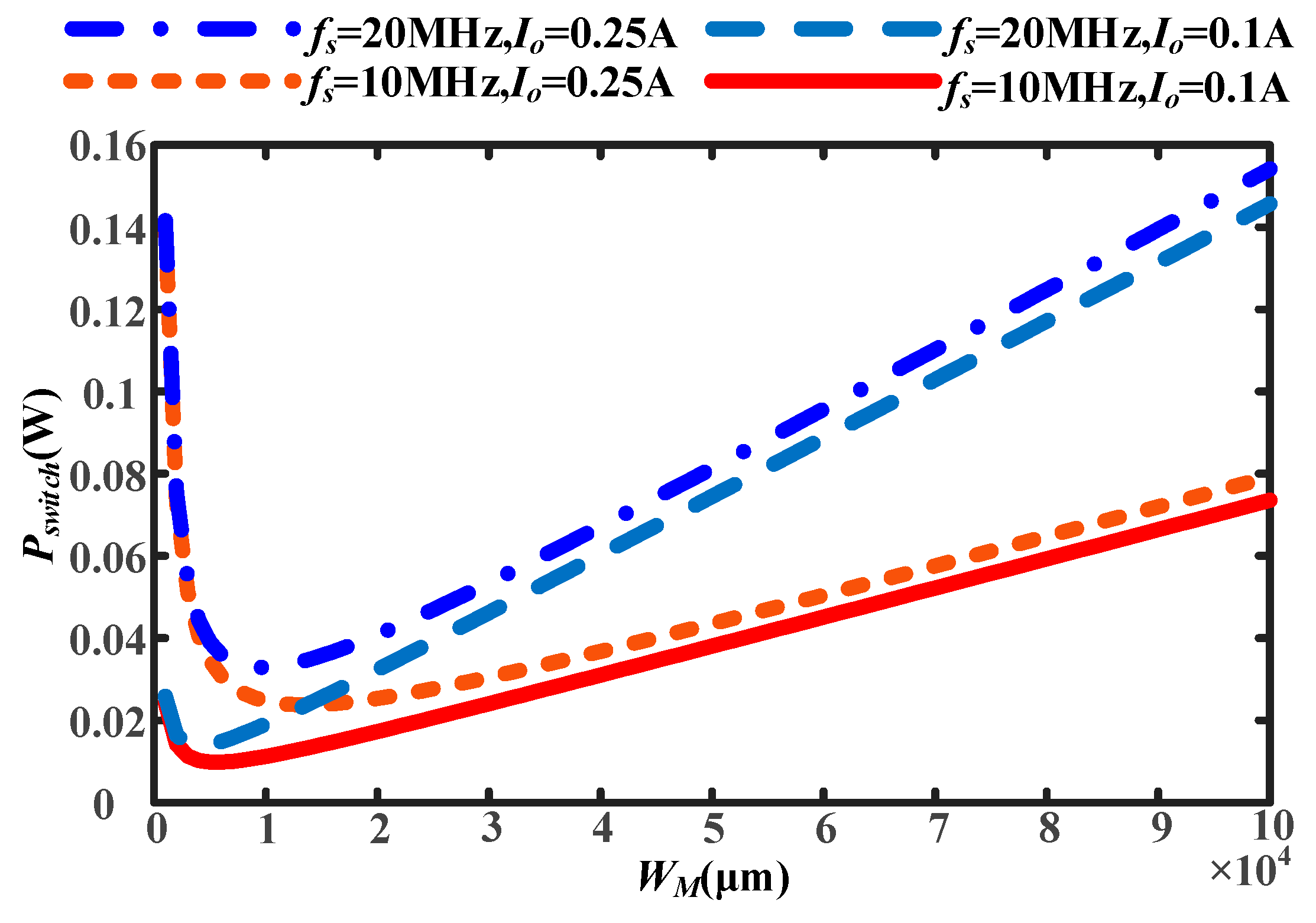
- M = 1: According to (10), taking Vin = 5 V and the 350 nm process as an example, the power loss is plotted with the integrated Si LDMOSFET size in Figure 5. It is obvious that there are different optimal sizes to minimize power loss at different switching frequencies and output currents [38]. This optimal size can be obtained by the simulation scan.
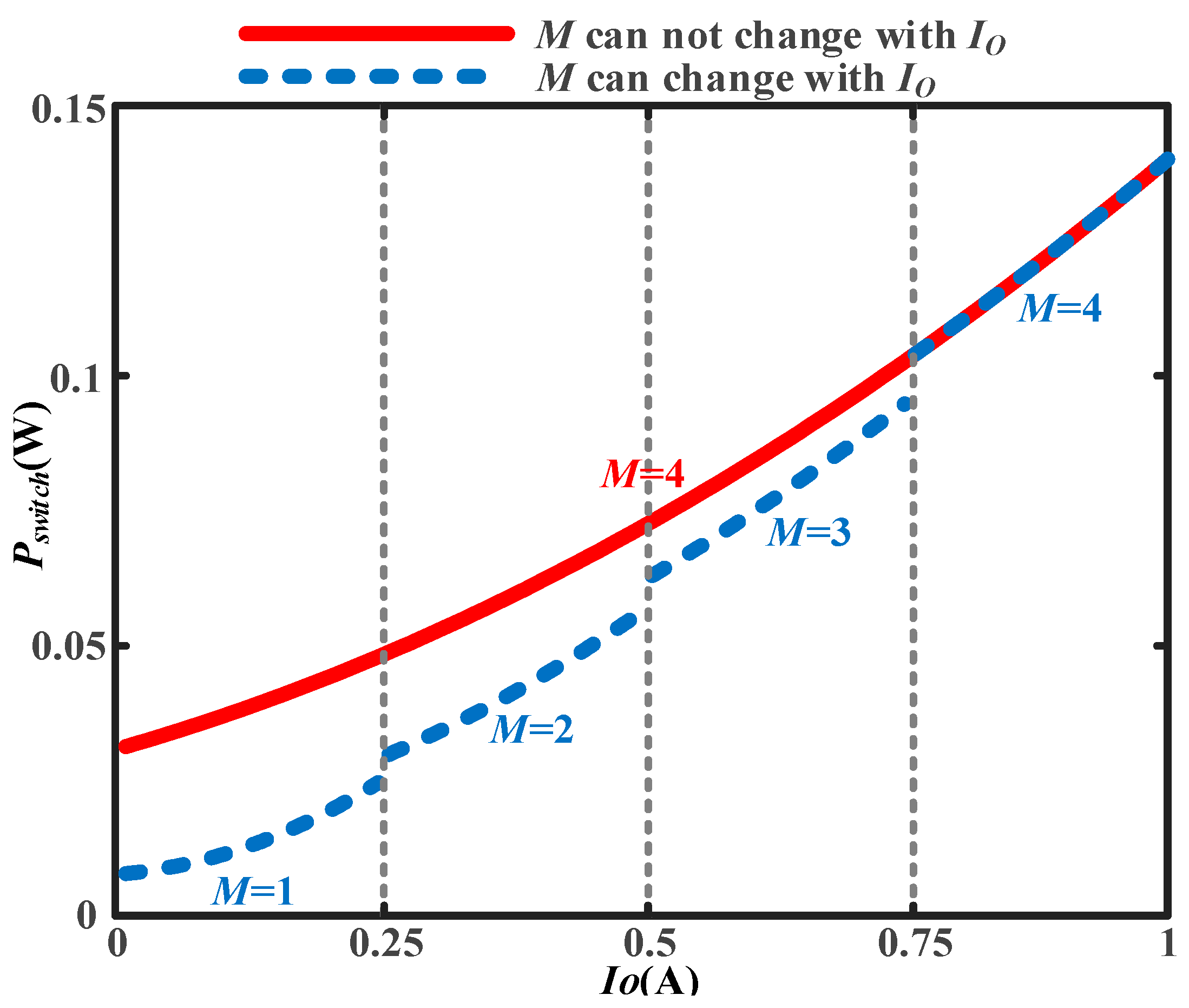
- M ≠ 1: In fact, switch size is limited by the process. Therefore, the power switch is composed of multiple units in parallel. According to (10), the power loss is plotted with the output current in Figure 6. The size of a single unit is optimized at fs = 10 MHz and Io = 0.25 A, according to Figure 5. In Figure 6, comparing M = 4 to all load current ranges, the parallel quantity of power switch changing with drain-source current is more beneficial to improving overall efficiency [39].
3. Quality Factor Analysis of Air-Core Inductors
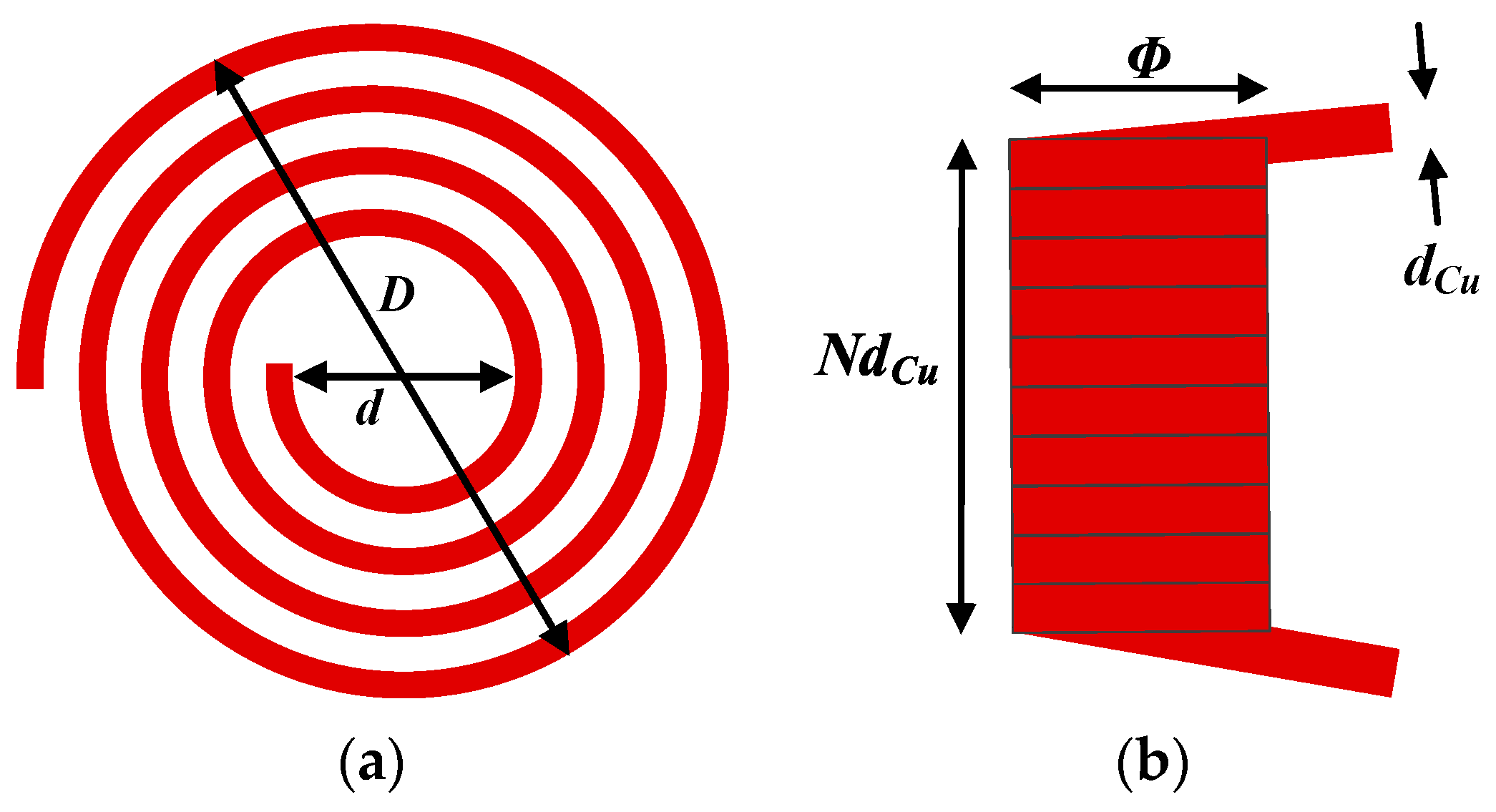
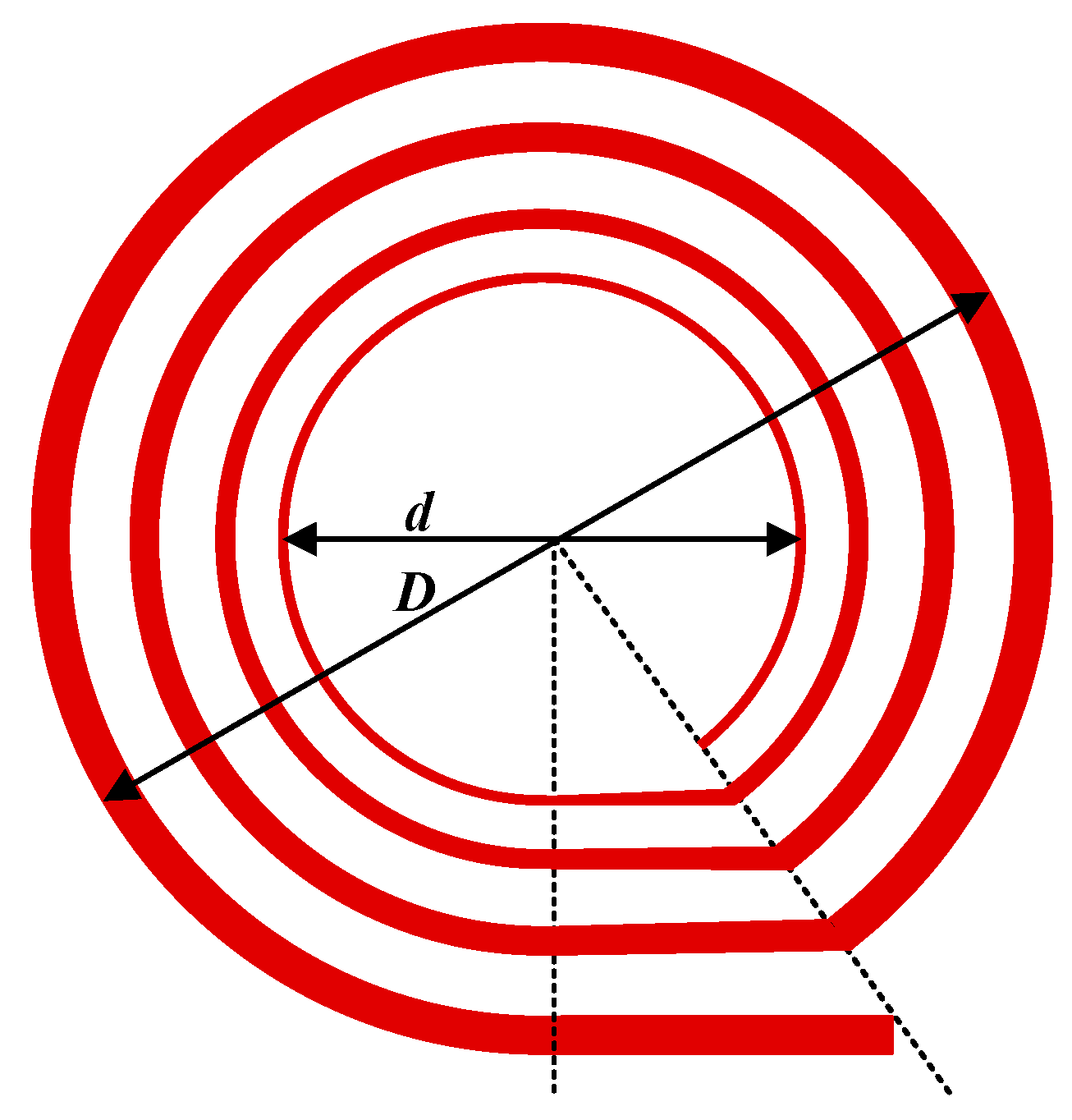
3.1. Winding Structure Optimization of Planar Spiral Inductors
3.2. Winding Structure Optimization of Solenoid Inductors
4. Efficiency Boundary Prediction of PSiP
- For the tightly winding solenoid inductor, its wire width and coil turn are set as 1 mm and 10.
- For the planar spiral inductor, its thickness and coil turn are set as 100 μm and 10. Since it has a wide outside winding and narrow inside winding structure, its width is set as 1~2 mm.
5. Conclusions
- For power switches, a parallel quantity of integrated Si LDMOSFET is designed based on power level. The size of each power switch is optimized based on switching frequency and power level.
- For power inductors, the planar spiral inductor provides a low profile for monolithic integration. An optimal winding structure with narrow inner and wider outer windings dramatically reduces power losses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| fs | Switching frequency |
| Vin | Input voltage of PoL power supply |
| Vout | Output voltage of PoL power supply |
| IL0, ILn | DC value and nth harmonic amplitude of inductance current |
| ΔiL | Ripple of inductance current |
| Io | Load current of PoL power supply |
| CGD | Capacitance between gate and drain of integrated Si LDMOSFT |
| CGS | Capacitance between gate and source of integrated Si LDMOSFT |
| CDS | Capacitance between drain and source of integrated Si LDMOSFT |
| CISS | Input capacitance of integrated Si LDMOSFET |
| COSS | Output capacitance of integrated Si LDMOSFET |
| CRSS | Reverse transfer capacitance of integrated Si LDMOSFET |
| RG | Gate resistance of integrated Si LDMOSFET |
| Ron | Drain-source on-resistance of integrated Si LDMOSFET |
| VDS | Drain and source voltage of integrated Si LDMOSFT |
| VGS | Gate and source voltage of integrated Si LDMOSFT |
| IDS | Drain and source current of integrated Si LDMOSFT |
| VPL | Miller voltage of integrated Si LDMOSFT |
| Vth | Gate threshold voltage of integrated Si LDMOSFT |
| VDD | Power supply voltage of driver |
| mn | Electron mobility |
| WM | Channel width of integrated Si LDMOSFET |
| LM | Channel length of integrated Si LDMOSFET |
| EM | Drain/source width of integrated Si LDMOSFET |
| Cox | Gate oxide capacitance per unit area of integrated Si LDMOSFET |
| Cov | Gate-to-source/drain overlap capacitance per unit width of integrated Si LDMOSFET |
| Cj | Source/drain junction capacitance per unit area of integrated Si LDMOSFET |
| Cjsw | Source/drain sidewall junction capacitance per unit length of integrated Si LDMOSFET |
| L | Inductance value |
| l | Coil-wire length of inductor |
| A, φ | Cross-section area and perimeter of inductance coil-wire |
| μ0 | Space permeability |
| ρ | Resistivity of inductance coil-wire material |
| δn | Skin depth of nth harmonic inductance current |
| RDC, RAC,n | DC and nth harmonic AC equivalent resistances of inductor |
References
- Lin, H.; Van der Plas, G.; Sun, X.; Velenis, D.; Beyne, E.; Lauwereins, R. System Optimization: High-Frequency Buck Converter with 3D In-Package Air-Core Inductor. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 12, 401–409. [Google Scholar] [CrossRef]
- Sun, Q.; Ma, Y.; Ye, Z.; Wang, X.; Zhang, H. A Pseudo-Constant Frequency Constant On-Time Buck Converter with Internal Current Ripple Injection and Output DC Offset Cancellation. IEEE Access 2019, 7, 175443–175453. [Google Scholar] [CrossRef]
- Seo, G.; Das, R.; Le, H. Dual Inductor Hybrid Converter for Point-of-Load Voltage Regulator Modules. IEEE Trans. Ind. Appl. 2020, 56, 367–377. [Google Scholar] [CrossRef]
- Hernandez, J.C.; Mira, M.C.; Petersen, L.P.; Andersen, M.A.E.; Petersen, N.H. Zero Voltage Switching Control Method for MHz Boundary Conduction Mode Converters. IEEE Trans. Ind. Electron. 2020, 67, 1544–1554. [Google Scholar] [CrossRef]
- Wang, K.; Qi, Z.; Li, F.; Wang, L.; Yang, X. Review of state-of-the-art integration technologies in power electronic systems. CPSS Trans. Power Electron. Appl. 2017, 2, 292–305. [Google Scholar] [CrossRef]
- Feeney, C.; Wang, N. A new Electronic Design Automation tool for the optimization of PwrSoC/PwrSiP DC-DC converters. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 2905–2909. [Google Scholar]
- Doyle, J.T.; Stiff, J.C.; Kulkarni, S.; Yildiz, A. A Low Cost 100 MHz 2-Stage PSiP and Evolution to a Co-Packaged/Fully-Integrated Voltage Regulator for SoC Power Delivery. In Proceedings of the 2019 IEEE Custom Integrated Circuits Conference (CICC), Austin, TX, USA, 14–17 April 2019; pp. 1–8. [Google Scholar]
- You, X.; Sun, X.; Fei, J.; Zhang, M.; Zhang, B.; Chen, T.; Qin, Y.; Rong, N.; Wan, C. A Gallium-Nitride Point-of-load DC-DC Converter for Space Applications. In Proceedings of the 2019 European Space Power Conference (ESPC), Juan-les-Pins, France, 30 September–4 October 2019; pp. 1–6. [Google Scholar]
- Qi, Z.; Zhao, C.; Wang, L.; Yang, F.; Pei, Y.; Zheng, Z. Three-Dimensional Integrated GaN-based DC-DC Converter with an Inductor Substrate. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 832–838. [Google Scholar]
- Yu, L.; Mu, W.; Li, H.; Yang, C.; Wang, C.; Wang, L. An Integrated GaN-Based Converter Based on Cooling-System-Inductor Structure for point-of-load converters. In Proceedings of the 2021 IEEE Workshop on Wide Bandgap Power Devices and Applications in Asia (WiPDA Asia), Wuhan, China, 25–27 August 2021; pp. 236–240. [Google Scholar]
- Waldron, F.; Foley, R.; Slowey, J.; Alderman, A.N.; Narveson, B.C.; Mathúna, S.C.Ó. Technology Roadmapping for Power Supply in Package (PSiP) and Power Supply on Chip (PwrSoC). IEEE Trans. Power Electron. 2013, 28, 4137–4145. [Google Scholar] [CrossRef]
- Tang, N.; Nguyen, B.; Tang, Y.; Hong, W.; Zhou, Z.; Heo, D. Fully Integrated Buck Converter with 78% Efficiency at 365mW Output Power Enabled by Switched-Inductor Capacitor Topology and Inductor Current Reduction Technique. In Proceedings of the 2019 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 17–21 February 2019; pp. 152–154. [Google Scholar]
- Amin, S.S.; Mercier, P.P. A Fully Integrated Li-Ion-Compatible Hybrid Four-Level DC–DC Converter in 28-nm FDSOI. IEEE J. Solid-State Circuits 2019, 54, 720–732. [Google Scholar] [CrossRef]
- Renz, P.; Kaufmann, M.; Lueders, M.; Wicht, B. A Fully Integrated 85%-Peak-Efficiency Hybrid Multi Ratio Resonant DC-DC Converter with 3.0-to-4.5V Input and 500μA-to-120mA Load Range. In Proceedings of the 2019 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 17–21 February 2019; pp. 156–158. [Google Scholar]
- Schrom, G.; Vunnam, R.S.; Makala, S.; Lyakhov, A. High-Speed ZVS-ZCS Soft-Switching CMOS Bridge Drivers for a DC-DC Fully Integrated Voltage Regulator (FIVR) operating at 100–320 MHz on 22 nm process node. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 2263–2267. [Google Scholar]
- Udabe, A.; Baraia-Etxaburu, I.; Diez, D.G. Gallium Nitride Power Devices: A State of the Art Review. IEEE Access 2023, 11, 48628–48650. [Google Scholar] [CrossRef]
- Reusch, D.; Strydom, J. Understanding the Effect of PCB Layout on Circuit Performance in a High-Frequency Gallium-Nitride-Based Point of Load Converter. IEEE Trans. Power Electron. 2014, 29, 2008–2015. [Google Scholar] [CrossRef]
- Reusch, D.; Gilham, D.; Su, Y.; Lee, F.C. Gallium Nitride based 3D integrated non-isolated point of load module. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 38–45. [Google Scholar]
- Ujita, S.; Kinoshita, Y.; Umeda, H.; Morita, T.; Kaibara, K.; Tamura, S.; Ishida, M.; Ueda, T. A fully integrated GaN-based power IC including gate drivers for high-efficiency DC-DC Converters. In Proceedings of the 2016 IEEE Symposium on VLSI Circuits (VLSI-Circuits), Honolulu, HI, USA, 15–17 June 2016; pp. 1–2. [Google Scholar]
- Yu, L.; Mu, W.; Yang, C.; Zhu, L.; Qi, Z.; Wang, L.; Yao, Y.; Su, Y.; Zhang, C. Symmetric Four-Phase Inverse Coupled Inductors for GaN-Based Interleaving Four-Phase Point-of-load Converters. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 5453–5458. [Google Scholar]
- Cook, T.; Phillips, A.; Siak, C.; George, A.D.; Grainger, B.M. Evaluation of Point of Load Converters for Space Computational Loads. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–12. [Google Scholar]
- AlMukhtar, B.; Harriman, P.; Burke, K. The analysis of multi-phase current feedforward type-III constant on-time control with ultrafast load transient response for voltage regulator modules. In Proceedings of the 2016 IEEE International Conference on Electronics, Circuits and Systems (ICECS), Monte Carlo, Monaco, 11–14 December 2016; pp. 201–204. [Google Scholar]
- Available online: https://product.tdk.com/en/products/ferrite/index.html (accessed on 9 December 2023).
- Available online: https://www.mag-inc.com/Products/Powder-Cores/Magnetics-Powder-Core-Material-Property-Curves/Permeability-versus-Frequency-Curves-for-Powder-Co (accessed on 9 December 2023).
- Available online: https://www.mag-inc.com/Products/Tape-Wound-Cores/Nanocrystalline/Nanocrystalline-Material-Property-Curves (accessed on 9 December 2023).
- Le, H.T.; Nour, Y.; Pavlovic, Z.; Mathúna, C.O.; Knott, A.; Jensen, F.; Han, A.; Kulkarni, S.; Ouyang, Z. High-Q Three-Dimensional Microfabricated Magnetic-Core Toroidal Inductors for Power Supplies in Package. IEEE Trans. Power Electron. 2019, 34, 74–85. [Google Scholar] [CrossRef]
- Liu, J.; Mei, Y.; Lu, S.; Li, X.; Lu, G. Continuously Variable Multi-Permeability Inductor for Improving the Efficiency of High-Frequency DC–DC Converter. IEEE Trans. Power Electron. 2020, 35, 826–834. [Google Scholar] [CrossRef]
- Schaef, C.; Desai, N.; Krishnamurthy, H.K.; Liu, X.; Ahmed, K.Z.; Kim, S.; Weng, S.; Do, H.; Lambert, W.J.; Radhakrishnan, K.; et al. A Light-Load Efficient Fully Integrated Voltage Regulator in 14-nm CMOS with 2.5-nH Package-Embedded Air-Core Inductors. IEEE J. Solid-State Circuits 2019, 54, 3316–3325. [Google Scholar] [CrossRef]
- Available online: https://www.coilcraft.com/en-us/products/rf/air-core-inductors/#/ (accessed on 9 December 2023).
- Krishnamurthy, H.K.; Vaidya, V.; Weng, S.; Ravichandran, K.; Kumar, P.; Kim, S.; Jain, R.; Matthew, G.; Tschanz, J.; De, V. A digitally controlled fully integrated voltage regulator with on-die solenoid inductor with planar magnetic core in 14 nm tri-gate CMOS. In Proceedings of the 2017 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 5–9 February 2017; pp. 336–337. [Google Scholar]
- Krishnamurthy, H.K.; Weng, S.; Mathew, G.E.; Desai, N.; Saraswat, R.; Ravichandran, K.; Tschanz, J.W.; De, V. A Digitally Controlled Fully Integrated Voltage Regulator with 3-D-TSV-Based On-Die Solenoid Inductor with a Planar Magnetic Core for 3-D-Stacked Die Applications in 14-nm Tri-Gate CMOS. IEEE J. Solid-State Circuits 2018, 53, 1038–1048. [Google Scholar] [CrossRef]
- Abdulslam, A.; Mohammad, B.; Ismail, M.; Mercier, P.P.; Ismail, Y. A 93% Peak Efficiency Fully-Integrated Multilevel Multistate Hybrid DC–DC Converter. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 2617–2630. [Google Scholar] [CrossRef]
- Nour, Y.; Ouyang, Z.; Knott, A.; Jørgensen, I.H.H. Design and implementation of high frequency buck converter using multi-layer PCB inductor. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 1313–1317. [Google Scholar]
- Lee, M.; Choi, Y.; Kim, J. A 500-MHz, 0.76-W/mm Power Density and 76.2% Power Efficiency, Fully Integrated Digital Buck Converter in 65-nm CMOS. IEEE Trans. Ind. Appl. 2016, 52, 3315–3323. [Google Scholar] [CrossRef]
- Musunuri, S.; Chapman, P.L. Optimization of CMOS Transistors for Low Power DC-DC Converters. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 16 June 2005; pp. 2151–2157. [Google Scholar]
- Qahouq, J.A.A.; Abdel-Rahman, O.; Huang, L.; Batarseh, I. On Load Adaptive Control of Voltage Regulators for Power Managed Loads: Control Schemes to Improve Converter Efficiency and Performance. IEEE Trans. Power Electron. 2007, 22, 1806–1819. [Google Scholar] [CrossRef]
- Razavi, B. Design of Analog CMOS Integrated Circuits; McGraw-Hill Education: New York, NY, USA, 2001. [Google Scholar]
- Jia, T.; Gu, J. A Fully Integrated Buck Regulator with 2-GHz Resonant Switching for Low-Power Applications. IEEE J. Solid-State Circuits 2018, 53, 2663–2674. [Google Scholar] [CrossRef]
- Kudva, S.S.; Harjani, R. Fully integrated on-chip DC-DC converter with a 450x output range. In Proceedings of the IEEE Custom Integrated Circuits Conference 2010, San Jose, CA, USA, 19–22 September 2010; pp. 1–4. [Google Scholar]
- Kazimierczuk, M.K. High-Frequency Magnetic Components; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Guan, Y.; Wang, Y.; Wang, W.; Xu, D. A 20 MHz Low-Profile DC–DC Converter with Magnetic-Free Characteristics. IEEE Trans. Ind. Electron. 2020, 67, 1555–1567. [Google Scholar] [CrossRef]
- Park, J.; Lee, H.M.; Shin, S.U.; Choi, W.; Hong, S.W. A 0.46 mm2 On-Chip Compensated Type-III Buck Converter Using an Inner Feedback Loop with a Seamless CCM/DCM Transition Technique. IEEE Trans. Power Electron. 2020, 35, 4477–4482. [Google Scholar] [CrossRef]
- Huang, Q.; Zhan, C.; Burm, J. A 4-MHz Digitally Controlled Voltage-Mode Buck Converter with Embedded Transient Improvement Using Delay Line Control Techniques. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4029–4040. [Google Scholar] [CrossRef]
- Hong, W.; Lee, M. A 7.4-MHz Tri-Mode DC-DC Buck Converter with Load Current Prediction Scheme and Seamless Mode Transition for IoT Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4544–4555. [Google Scholar] [CrossRef]
- Huang, W.; Liu, L.; Liao, X.; Xu, C.; Li, Y. A 240-nA Quiescent Current, 95.8% Efficiency AOT-Controlled Buck Converter with A2-Comparator and Sleep-Time Detector for IoT Application. IEEE Trans. Power Electron. 2021, 36, 12898–12909. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Fayed, A.A. A Current-Mode Delay-Based Hysteretic Buck Regulator with Enhanced Efficiency at Ultra-Light Loads for Low-Power Microcontrollers. IEEE Trans. Power Electron. 2020, 35, 471–483. [Google Scholar] [CrossRef]
- Chen, J.J.; Hwang, Y.S.; Ku, Y.; Li, Y.H.; Chen, J.A. A Current-Mode-Hysteretic Buck Converter with Constant-Frequency-Controlled and New Active-Current-Sensing Techniques. IEEE Trans. Power Electron. 2021, 36, 3126–3134. [Google Scholar] [CrossRef]
- Yuan, B.; Liu, M.X.; Ng, W.T.; Lai, X.Q. A Fast-Response RBAOT-Controlled Buck Converter with Pseudofixed Switching Frequency and Enhanced Output Accuracy. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 79–88. [Google Scholar] [CrossRef]
- Qu, Y.; Shu, W.; Chang, J.S. A Fully Soft Switched Point-of-Load Converter for Resource Constraint Drone Applications. IEEE Trans. Power Electron. 2020, 35, 2705–2713. [Google Scholar] [CrossRef]
- Chen, J.J.; Hwang, Y.S.; Wu, J.H.; Lai, C.H.; Ku, Y.T. A New Improved V-Square-Controlled Buck Converter with Rail-to-Rail OTA-Based Current-Sensing Circuits. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, 29, 1428–1436. [Google Scholar] [CrossRef]
- Ting, C.Y.; Lin, J.Y.; Chen, C.C.P. A Quasi-V2 Hysteretic Buck Converter with Adaptive COT Control for Fast DVS and Load-Transient Response in RF Applications. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 531–535. [Google Scholar] [CrossRef]
- Qu, Y.; Shu, W.; Chang, J. An Air-Core Coupled-Inductor Based Dual-Phase Output Stage for Point-of-Load Converters. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–4. [Google Scholar]
- Ting, C.Y.; Ko, C.C.; Lin, J.Y.; Chen, C.C.P. An Inductor Current Balancing Technique for FLDLL Based Four-phase Buck Converter with Transient-modulated Constant On-time Control for Load Transient Response. In Proceedings of the 2019 4th International Conference on Intelligent Green Building and Smart Grid (IGBSG), Yichang, China, 6–9 September 2019; pp. 1–4. [Google Scholar]
- Chen, J.J.; Hwang, Y.S.; Tzeng, T.S.; Lai, C.H.; Ku, J. A Low-Noise Fast-Transient-Response Delta-Sigma-Modulation Buck Converter with Hysteresis-Voltage-Controlled Techniques. IEEE Access 2022, 10, 63063–63072. [Google Scholar] [CrossRef]
- Wang, C.; Lu, Y.; Huang, M.; Martins, R.P. A Two-Phase Three-Level Buck Converter with Cross-Connected Flying Capacitors for Inductor Current Balancing. IEEE Trans. Power Electron. 2021, 36, 13855–13866. [Google Scholar] [CrossRef]
- Lee, C.H.; Park, H.J.; Cho, J.M.; Choi, H.J.; Park, S.M.; Baik, E.; Oh, Y.J.; Ahn, H.C.; Lee, C.K.; Shin, J.; et al. An Input-Independent Loop Type-III Buck Converter with PSRR Improvement and EMI Suppression for Enhancing the Security of Edge Devices. IEEE Trans. Power Electron. 2022, 37, 10070–10074. [Google Scholar] [CrossRef]
- Huang, Y.W.; Kuo, T.H. Fixed-Switching-Frequency Background Capacitor-Current-Sensor Calibration for DC–DC Converters. IEEE Journal of Solid-State Circuits 2022, 57, 1504–1516. [Google Scholar] [CrossRef]
- Seo, J.I.; Lim, B.M.; Choi, W.J.; Noh, Y.S.; Lee, S.G. A 95.1% Efficiency Hybrid Hysteretic Reconfigurable 3-Level Buck Converter with Improved Load Transient Response. IEEE Trans. Power Electron. 2022, 37, 14916–14925. [Google Scholar] [CrossRef]
- Wang, C.; Lu, Y.; Martins, R.P. A Highly Integrated Tri-Path Hybrid Buck Converter with Reduced Inductor Current and Self-Balanced Flying Capacitor Voltage. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 3841–3850. [Google Scholar] [CrossRef]
- Kim, S.; Krishnamurthy, H.K.; Amin, S.S.; Weng, S.; Feng, J.; Do, H.; Radhakrishnan, K.; Ravichandran, K.; Tschanz, J.W.; De, V. A 1S Direct-Battery-Attach Buck Voltage Regulator with 5-Stack Thin-Gate 22-nm FinFET CMOS Featuring Active Voltage Balancing and Cascaded Self-Turn-ON Drivers. IEEE Solid-State Circuits Lett. 2021, 4, 234–237. [Google Scholar] [CrossRef]
- Huang, Y.W.; Yu, T.Y.; Kuo, T.H. Transient Output-Current Regulator with Background Calibration Applied to a Buck Converter for Fast Load-Transient Response. IEEE Solid-State Circuits Lett. 2020, 3, 462–465. [Google Scholar] [CrossRef]
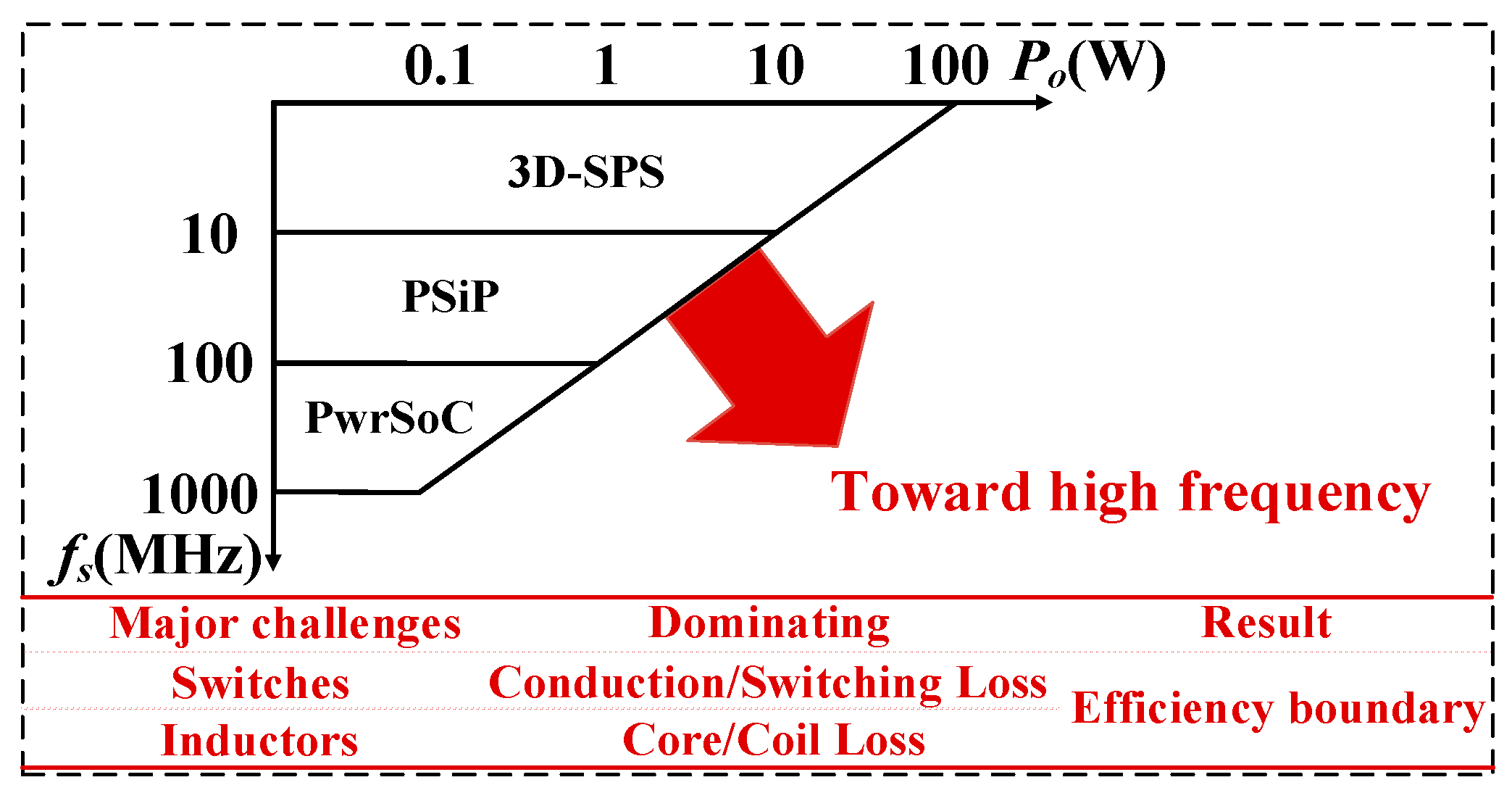




| Integration Level | 3D-SPS | PSiP | PwrSoC |
|---|---|---|---|
| Switching Frequency | <10 MHz | <100 MHz | >100 MHz |
| Power Level | <100 W | <10 W | <2 W |
| Application | Primary PoL power supply | Compact primary PoL power supply | Secondary PoL power supply (on chip) |
| Inductor Type | Literature | Operating Frequency | Inductance |
|---|---|---|---|
| Solenoid Inductor | 0806SQ, 0807SQ, 0908SQ [29] | 1~1000 MHz | 5.5 nH~27.3 nH |
| 1111SQ [29] | 1~500 MHz | 27 nH~47 nH | |
| 1515SQ, 2222SQ, 2929SQ [29] | 1~100 MHz | 47 nH~500 nH | |
| Planar Spiral Inductor | [30] | 150 MHz | 1.5 nH |
| [31] | 10 MHz | 2.7 nH | |
| [32] | 100 MHz | 5.8 nH | |
| [33] | 10 MHz | 220 nH | |
| [34] | 550 MHz | 1.54 nH | |
| [12] | 450 MHz | 0.85 nH |
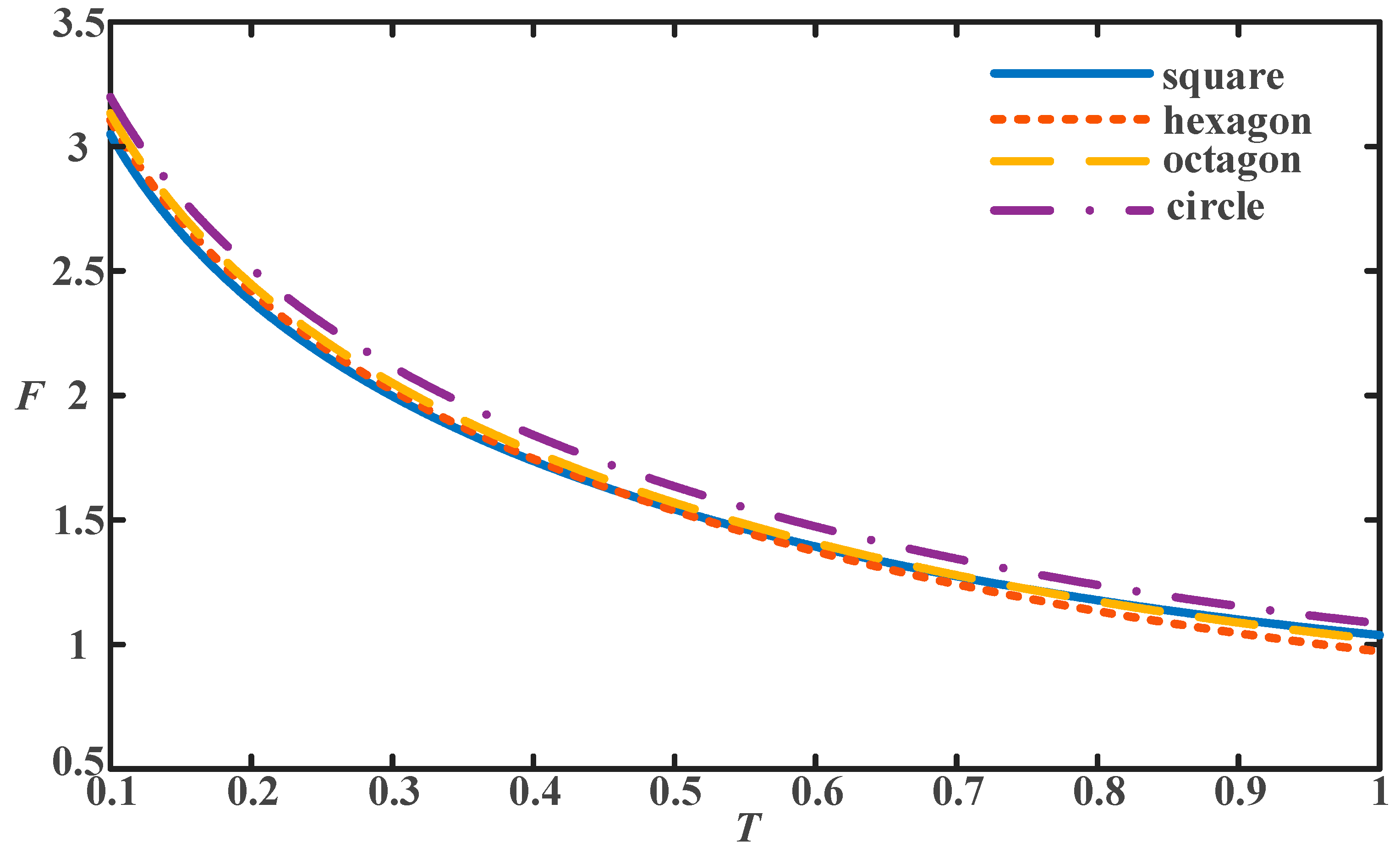
| Winding Structure | Square | Hexagon | Octagon | Circle |
|---|---|---|---|---|
| p | 2 | 1.732 | 1.657 | 1.571 |
| q1 | 0.3175 | 0.2725 | 0.2675 | 0.25 |
| q2 | 2.07 | 2.23 | 2.29 | 2.46 |
| q3 | 0.18 | 0 | 0 | 0 |
| q4 | 0.13 | 0.17 | 0.19 | 0.19 |
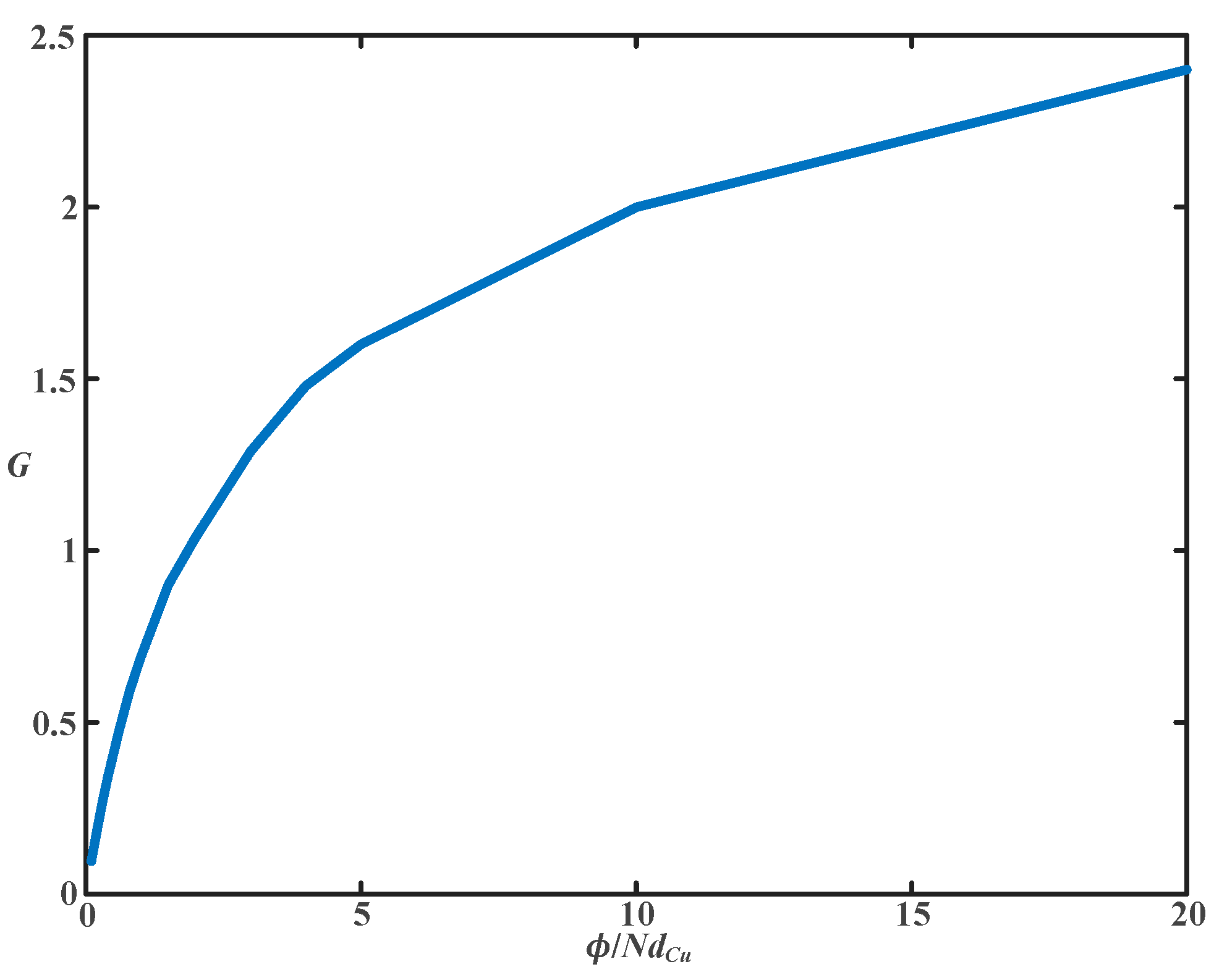
| ϕ/(NdCu) | 0.1 | 0.2 | 0.3 | 0.4 | 0.6 | 0.8 | 1 |
| k | 0.96 | 0.92 | 0.88 | 0.85 | 0.79 | 0.74 | 0.69 |
| ϕ/(NdCu) | 1.5 | 2 | 3 | 4 | 5 | 10 | 20 |
| k | 0.6 | 0.52 | 0.43 | 0.37 | 0.32 | 0.2 | 0.12 |
| Process | fs (MHz) | Ron (mΩ) | CISS (pF) | CRSS (pF) | COSS (pF) |
|---|---|---|---|---|---|
| 350 nm | 1 | 35 | 295 | 147 | 355 |
| 10 | 112 | 93 | 47 | 112 | |
| 100 | 354 | 29 | 15 | 35 | |
| 180 nm | 1 | 22 | 208 | 104 | 253 |
| 10 | 69 | 66 | 33 | 80 | |
| 100 | 217 | 21 | 10 | 25 | |
| 90 nm | 1 | 18 | 176 | 88 | 179 |
| 10 | 57 | 57 | 28 | 57 | |
| 100 | 179 | 17 | 9 | 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, D.; Lu, L.; Huang, B.; Xu, H.; Min, R.; Zou, X. Technical Reviews of Power Loss Optimization in High-Frequency PSiPs—In Relation to Power Switches and Power Inductors. Appl. Sci. 2023, 13, 13166. https://doi.org/10.3390/app132413166
Wang Y, Zhang D, Lu L, Huang B, Xu H, Min R, Zou X. Technical Reviews of Power Loss Optimization in High-Frequency PSiPs—In Relation to Power Switches and Power Inductors. Applied Sciences. 2023; 13(24):13166. https://doi.org/10.3390/app132413166
Chicago/Turabian StyleWang, Yinyu, Desheng Zhang, Liangliang Lu, Baoqiang Huang, Haoran Xu, Run Min, and Xuecheng Zou. 2023. "Technical Reviews of Power Loss Optimization in High-Frequency PSiPs—In Relation to Power Switches and Power Inductors" Applied Sciences 13, no. 24: 13166. https://doi.org/10.3390/app132413166
APA StyleWang, Y., Zhang, D., Lu, L., Huang, B., Xu, H., Min, R., & Zou, X. (2023). Technical Reviews of Power Loss Optimization in High-Frequency PSiPs—In Relation to Power Switches and Power Inductors. Applied Sciences, 13(24), 13166. https://doi.org/10.3390/app132413166







