Enhancing Autonomous Vehicle Stability through Pre-Emptive Braking Control for Emergency Collision Avoidance
Abstract
:1. Introduction
1.1. Motivations
1.2. State of the Art
1.3. Contributions
1.4. Structure Overview
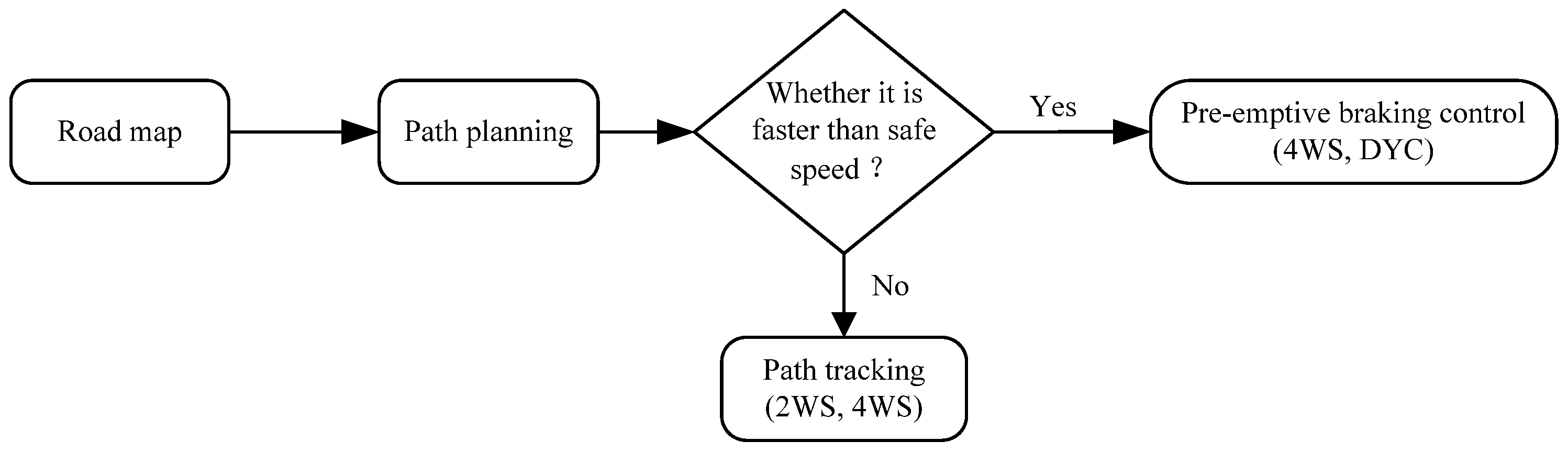
2. Control Strategies
2.1. Control Objectives
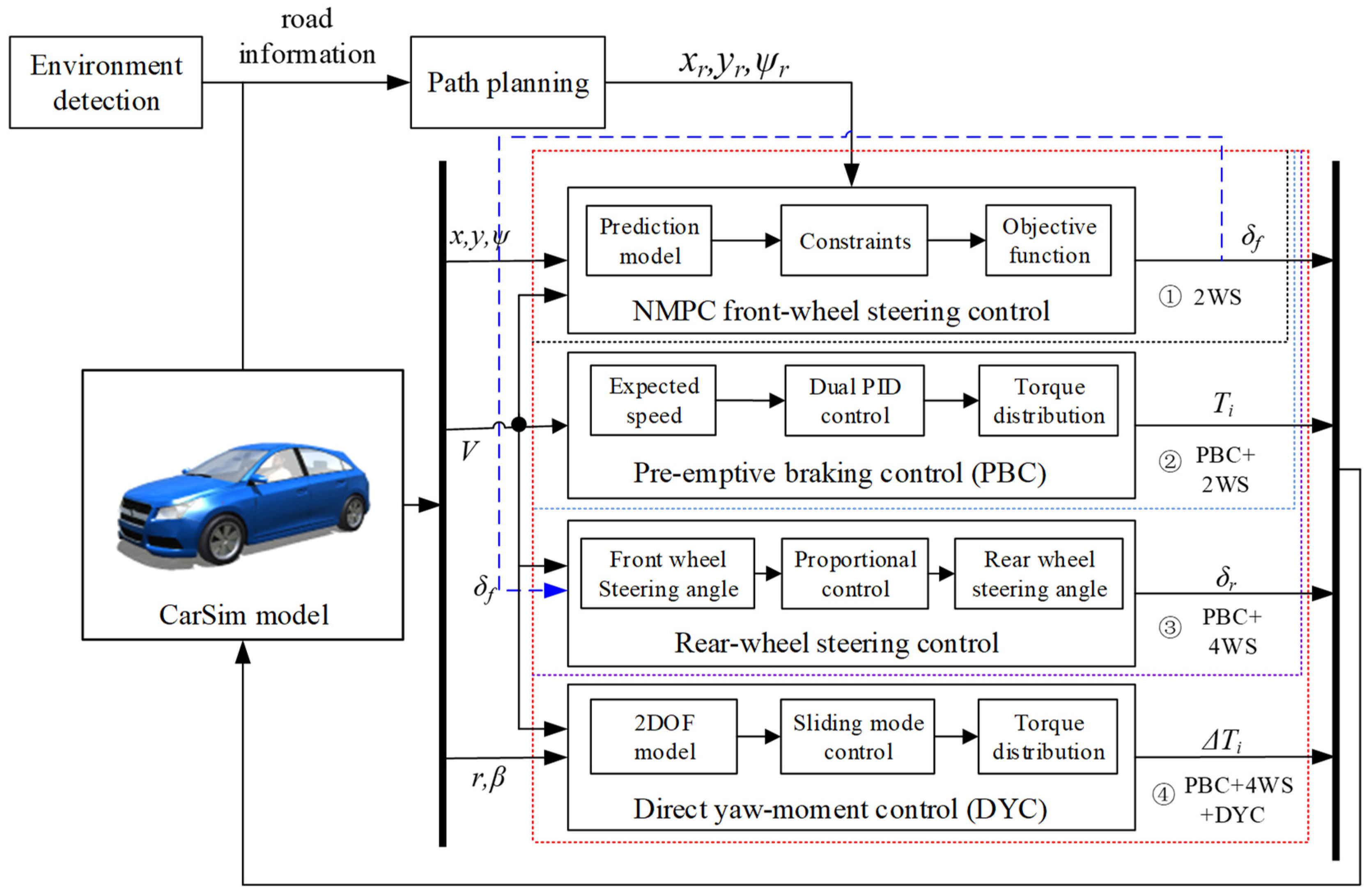
2.2. Overall Control Framework
3. Control System Design
3.1. Path Planning
3.2. Vehicle Dynamics Modeling
3.3. Pre-Emptive Braking Controller
3.3.1. Safe Speed
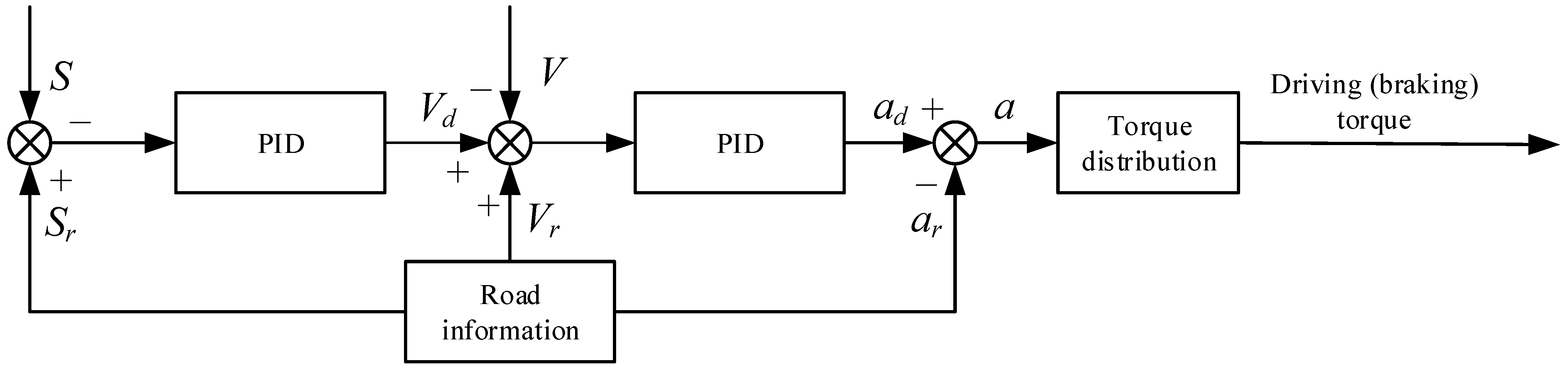
3.3.2. Dual PID Longitudinal Motion Control
3.3.3. Torque Distribution
3.4. 2WS Controller
3.5. Four-Wheel Steering Control
3.6. Direct Yaw-Moment Control
3.6.1. Expected Reference Value
3.6.2. Sliding Mode Controller
3.6.3. Torque Distribution
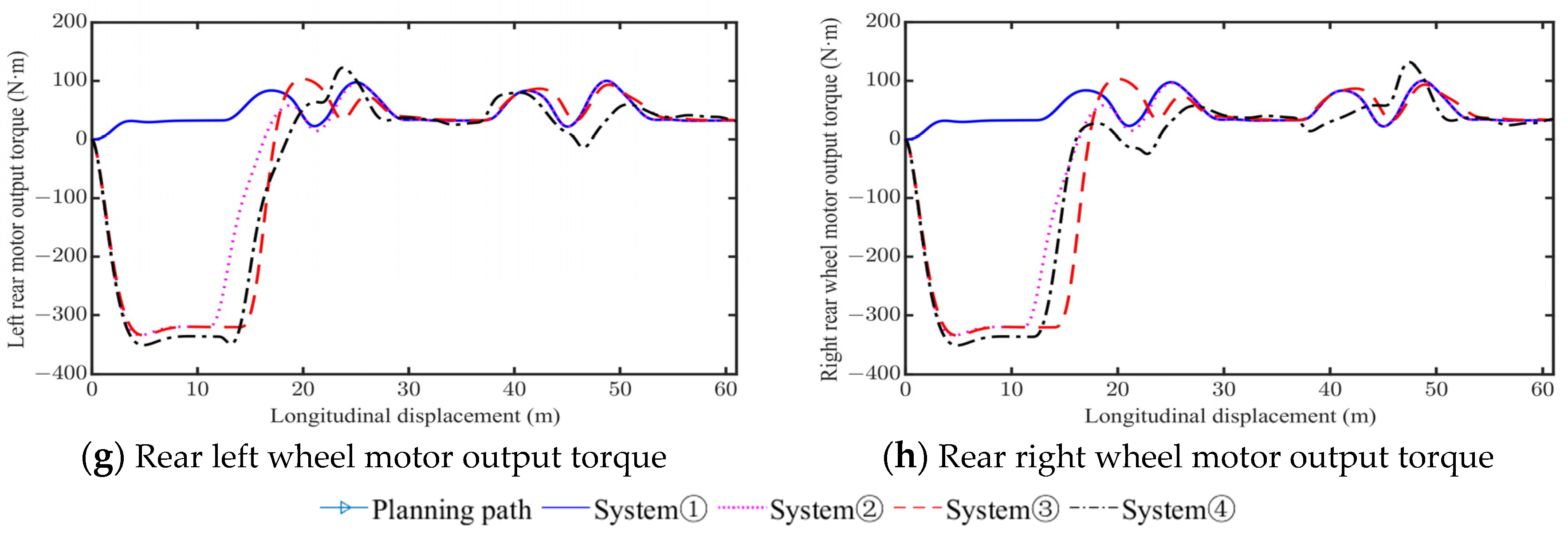
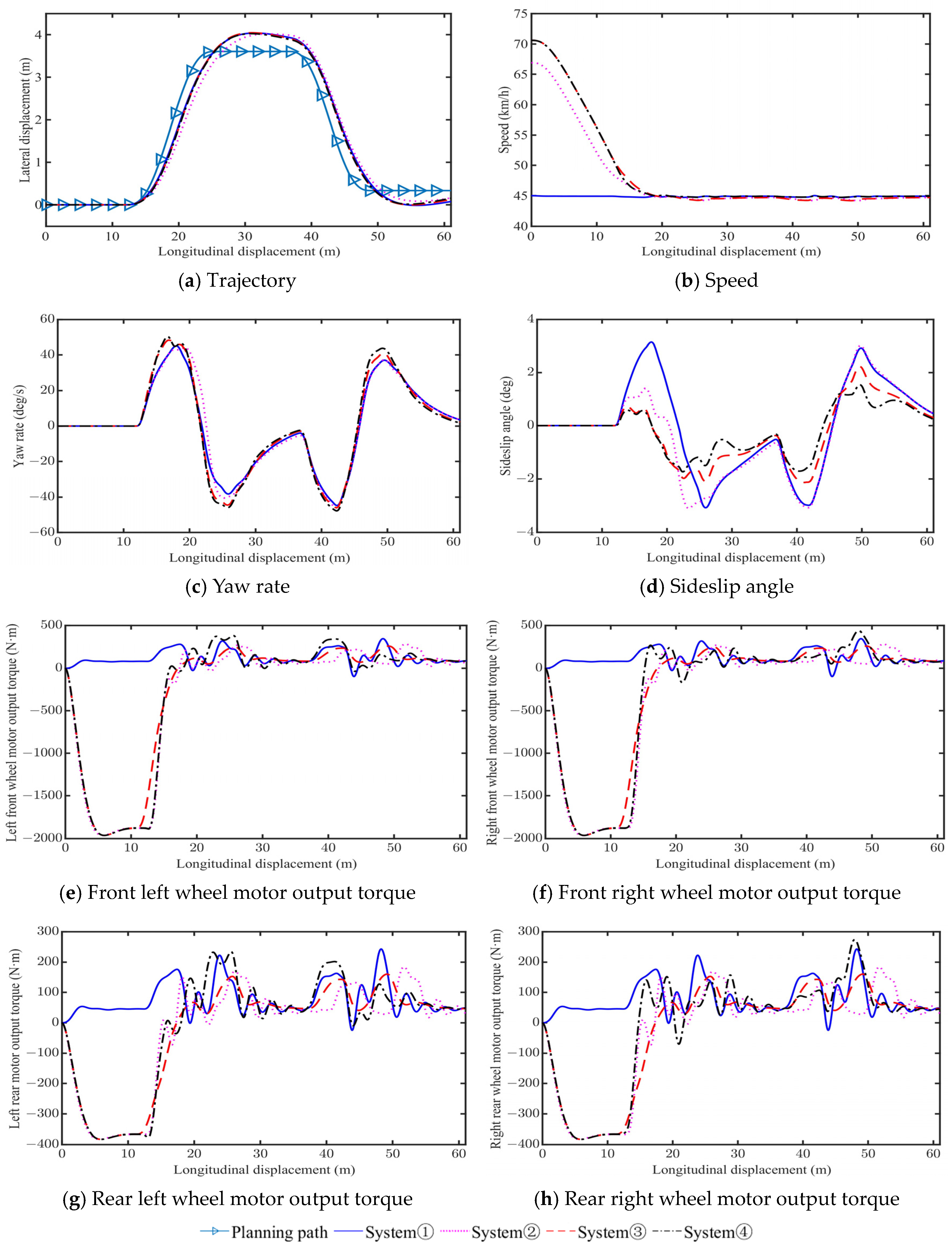
4. Simulation and Analysis
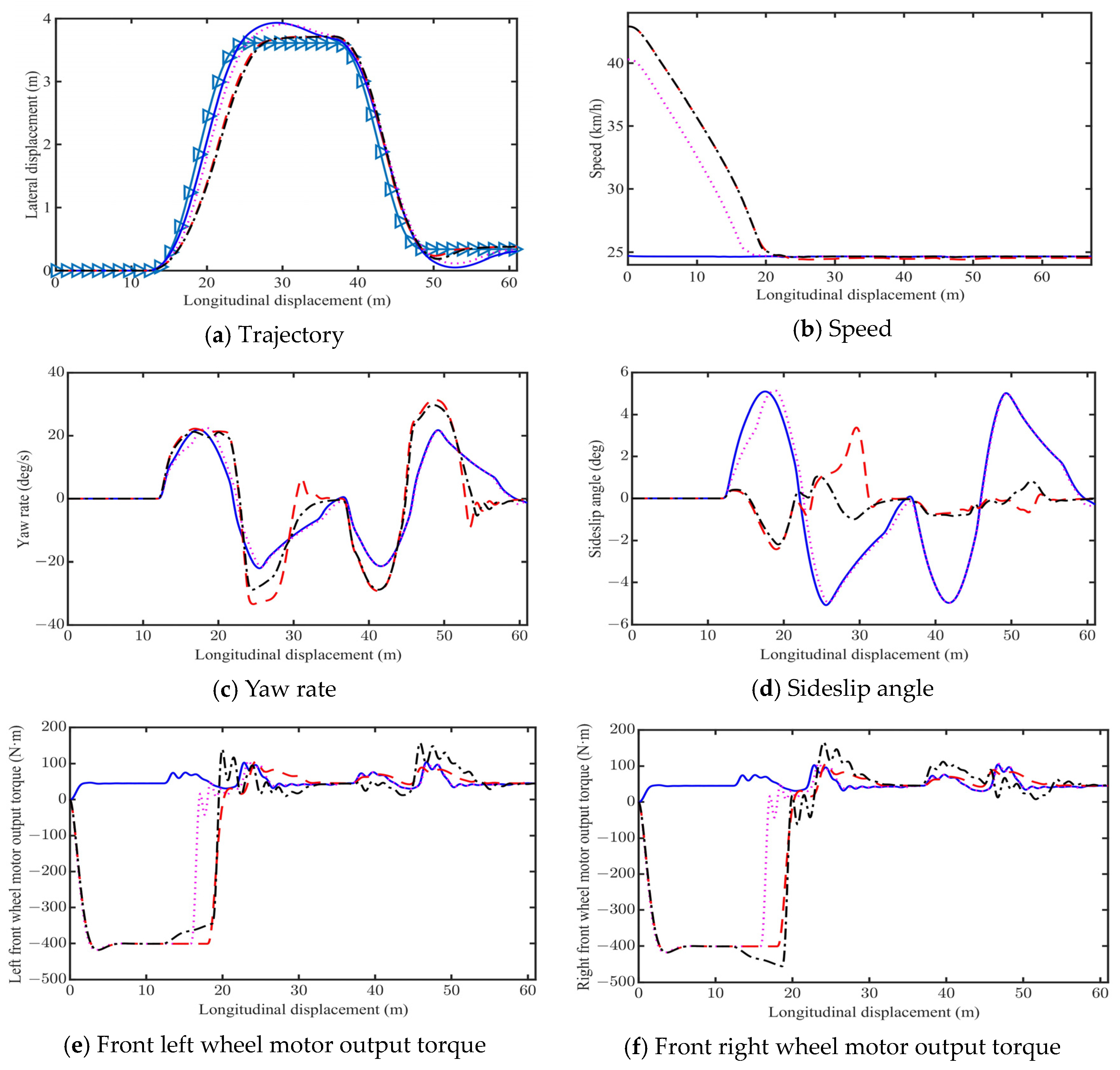
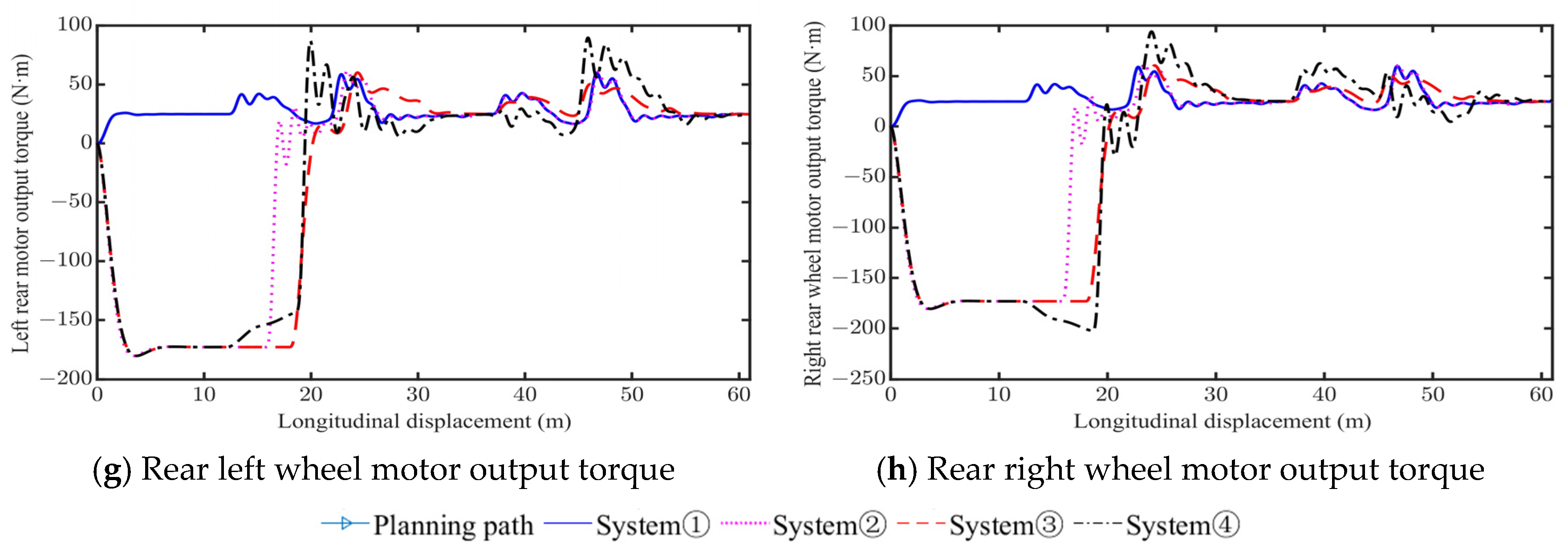
4.1. Low Friction (µ = 0.3)
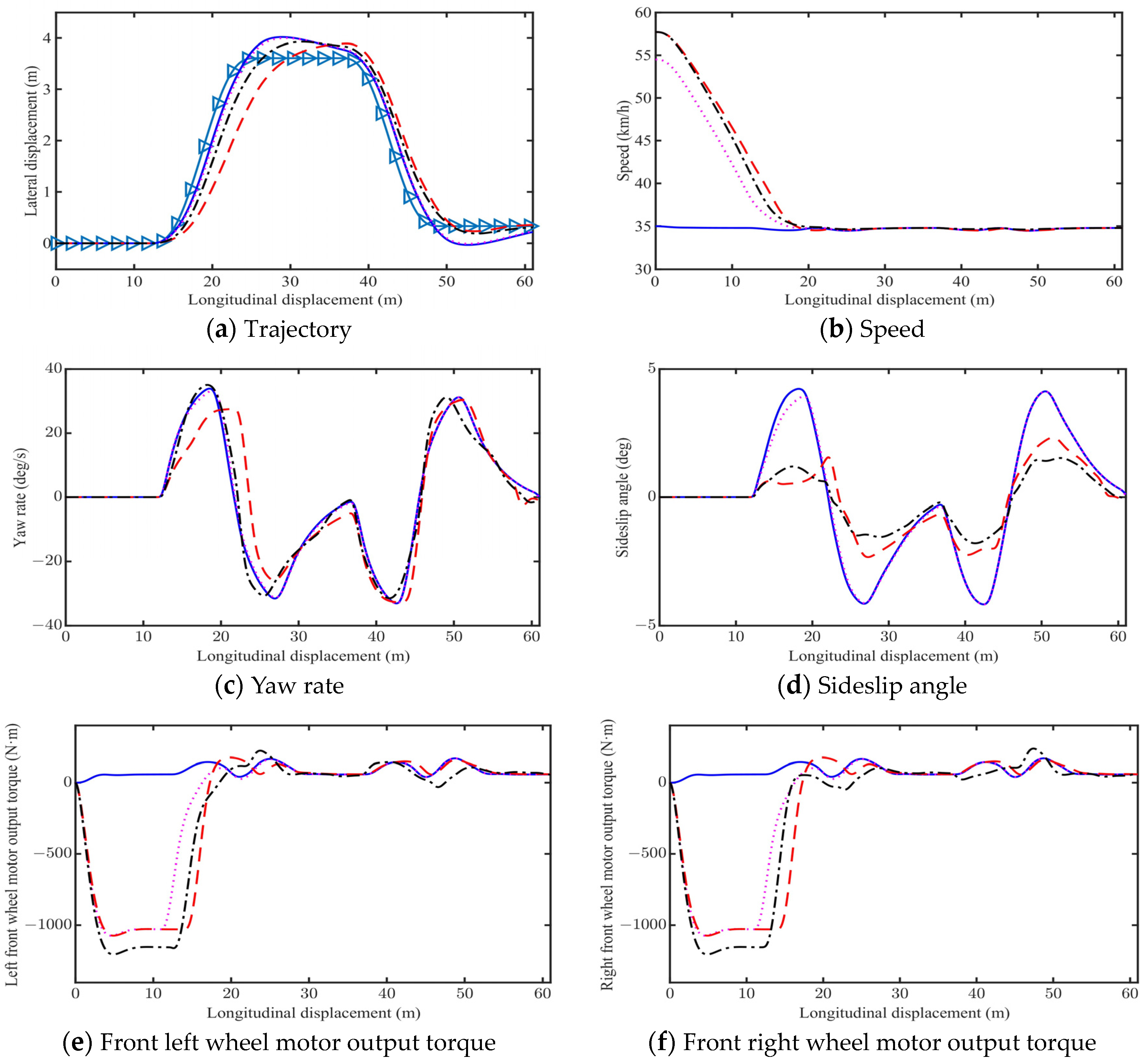
4.2. Medium Friction (µ = 0.6)
4.3. High Friction (µ = 1.0)
5. Conclusions
- (1)
- System ①, which adopts 2WS alone, exhibits poor vehicle stability during emergency collision avoidance.
- (2)
- Compared to System ①, the maximum stable vehicle speeds of System ② with PBC increase by 63.15%, 55.71%, and 48.67% on low, medium, and high friction road, respectively.
- (3)
- The maximum stable vehicle speeds of System ③ and System ④ are very close. Compared to System ①, the maximum stable vehicle speeds of System ③ and system ④ increase by 73.7%, 64.9%, and 56.9% on low, medium, and high friction road, respectively.
- (4)
- Compared to System ③, System ④ with DYC achieves a reduction in vehicle sideslip angle by 35.5%, 23.5%, and 22.0% on low, medium, and high friction road, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOF | Degrees of freedom |
| 2WS | Front-wheel steering |
| 4WS | Four-wheel steering |
| DYC | Direct yaw moment control |
| LMPC | Linear model predictive control |
| NMPC | Nonlinear model predictive control |
| PID | Proportional integral derivative controller |
| PBC | Pre-emptive braking control |
References
- Editorial Department of China Journal of Highway and Transport. Review on China’s automotive engineering research progress: 2017. China J. Highw. Transp. 2017, 30, 1–197. [Google Scholar]
- Zarkadis, K.; Velenis, E.; Siampis, E.; Longo, S. Predictive torque vectoring control with active trail-braking. In Proceedings of the 2018 European Control Conference, Limassol, Cyprus, 12–15 June 2018; pp. 569–574. [Google Scholar]
- Parra, A.; Tavernini, D.; Gruber, P.; Sorniotti, A.; Zubizarreta, A.; Pérez, J. On pre-emptive vehicle stability control. Veh. Syst. Dyn. 2022, 60, 2098–2123. [Google Scholar] [CrossRef]
- Abe, M.; Ohkubo, N.; Kano, Y. A direct yaw moment control for improving limit performance of vehicle handling-comparison and cooperation with 4WS. Veh. Syst. Dyn. 1996, 25, 3–23. [Google Scholar] [CrossRef]
- Yim, S. Comparison among active front, front independent, 4-wheel and 4-wheel independent steering systems for vehicle stability control. Electronics 2020, 9, 798. [Google Scholar] [CrossRef]
- Park, J.Y.; Na, S.; Cha, H.; Yi, K. Direct yaw moment control with 4WD torque-vectoring for vehicle handling stability and agility. Int. J. Automot. Technol. 2022, 23, 555–565. [Google Scholar] [CrossRef]
- Sun, P.; Trigell, A.S.; Drugge, L.; Jerrelind, J. Energy efficiency and stability of electric vehicles utilizing direct yaw moment control. Veh. Syst. Dyn. 2022, 60, 930–950. [Google Scholar] [CrossRef]
- Huang, C.; Lai, F. Pre-emptive braking control for stability improvement of autonomous vehicles on a curved road based on vehicle-to-everything technology. SAE Int. J. Commer. Veh. 2023, 16, 3–18. [Google Scholar] [CrossRef]
- Kojima, T.; Raksincharoensak, P. Environment-on-board predictive braking control functions for autonomous driving during sudden changes in the road friction coefficient on sharp curves. Int. J. Automot. Technol. 2022, 23, 451–460. [Google Scholar] [CrossRef]
- Guastadisegni, G.; So, K.M.; Parra, A.; Tavernini, D.; Montanaro, U.; Gruber, P.; Sorniotti, A. Vehicle stability control through pre-emptive braking. Int. J. Automot. Technol. 2023, 24, 347–365. [Google Scholar] [CrossRef]
- Zhou, H.; Gao, J.; Liu, H. Vehicle speed preview control with road curvature information for safety and comfort promotion. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 1527–1538. [Google Scholar] [CrossRef]
- Hiraoka, T.; Nishihara, Q.; Kumamoto, H. Automatic path-tracking controller of a four-wheel steering vehicle. Veh. Syst. Dyn. 2009, 47, 1205–1227. [Google Scholar] [CrossRef]
- Lai, F.; Huang, C. Comparative study on tracking control methods for automatic emergency steering and collision avoidance of intelligent vehicles. China J. Highw. Transp. 2021, 34, 250–264. [Google Scholar]
- Liu, Q.; Gordon, T.; Rahman, S. Model-free autonomous control of four-wheel steering using artificial flow guidance. Veh. Syst. Dyn. 2023, 2023, 2276761. [Google Scholar] [CrossRef]
- Chen, T.; Chen, L.; Xu, X.; Cai, Y.; Sun, X. Simultaneous path following and lateral stability control of 4WD-4WS autonomous electric vehicles with actuator saturation. Adv. Eng. Softw. 2019, 128, 46–54. [Google Scholar] [CrossRef]
- Xu, F.X.; Liu, X.H.; Chen, W.; Zhou, C.; Cao, B.W. Improving handling stability performance of four-wheel steering vehicle based on the H2/H∞ robust control. Appl. Sci. 2019, 9, 857. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Guo, H.Q.; Chen, Z.G.; Song, P. Longitudinal collision avoidance and lateral stability adaptive control system based on MPC of autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 2376–2385. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Yan, F.; Chen, N. Output constraint control on path following of four-wheel independently actuated autonomous ground vehicles. IEEE Trans. Veh. Technol. 2015, 65, 4033–4043. [Google Scholar] [CrossRef]
- Yim, S. Preview controller design for vehicle stability with V2V communication. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1497–1506. [Google Scholar] [CrossRef]
- Wang, Z.; Montanaro, U.; Fallah, S.; Sorniotti, A.; Lenzo, B. A gain scheduled robust linear quadratic regulator for vehicle direct yaw moment control. Mechatronics 2018, 51, 31–45. [Google Scholar] [CrossRef]
- Xie, X.; Jin, L.; Baicang, G.; Shi, J. Vehicle direct yaw moment control system based on the improved linear quadratic regulator. Ind. Robot Int. J. Robot. Res. Appl. 2021, 48, 378–387. [Google Scholar] [CrossRef]
- Tahami, F.; Farhangi, S.; Kazemi, R. A fuzzy logic direct yaw-moment control system for all-wheel-drive electric vehicles. Veh. Syst. Dyn. 2004, 41, 203–221. [Google Scholar] [CrossRef]
- Boada, B.L.; Boada, M.J.L.; Diaz, V. Fuzzy-logic applied to yaw moment control for vehicle stability. Veh. Syst. Dyn. 2005, 43, 753–770. [Google Scholar] [CrossRef]
- Li, H.M.; Wang, X.B.; Song, S.B.; Li, H. Vehicle control strategies analysis based on PID and fuzzy logic control. Procedia Eng. 2016, 137, 234–243. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Abunada, A.R. Vehicle yaw rate control based on fuzzy PID control technology. J. Adv. Res. Mech. Eng. Technol. 2018, 5, 17–23. [Google Scholar]
- Ding, S.; Liu, L.; Zheng, W.X. Sliding mode direct yaw-moment control design for in-wheel electric vehicles. IEEE Trans. Ind. Electron. 2017, 64, 6752–6762. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, J.; Jiang, H.; Cai, Y.; Xu, X. Stability research of distributed drive electric vehicle by adaptive direct yaw moment control. IEEE Access 2019, 7, 106225–106237. [Google Scholar] [CrossRef]
- Liu, D.; Huang, S.; Wu, S.; Fu, X. Direct yaw-moment control of electric vehicle with in-wheel motor drive system. Int. J. Automot. Technol. 2020, 21, 1013–1028. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Jomah, O.S. Vehicle yaw rate control for lane change maneuver using fuzzy PID controller and neural network controller. In Proceedings of the 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 2–3 December 2020; pp. 1–6. [Google Scholar]
- Liu, J. Sliding Mode Control Using MATLAB; Elsevier Inc.: Beijing, China, 2017. [Google Scholar]
- Chiliveri, V.R.; Kalpana, R.; Kishan, D. Composite control design for in-wheel drive electric vehicle with unknown disturbances and input delay. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022; pp. 1–6. [Google Scholar]
- Zhang, Y.; Hu, J.; Zhang, H.; Yi, X. Adaptive sliding mode control for uncertain nonlinear switched system under probabilistic replay attacks: The output feedback approach. Int. J. Adapt. Control Signal Process. 2023, 37, 2216–2232. [Google Scholar] [CrossRef]
- Tota, A.; Lenzo, B.; Lu, Q.; Sorniotti, A.; Gruber, P.; Fallah, S.; Velardocchia, M.; Galvagno, E.; Smet, J.D. On the experimental analysis of integral sliding modes for yaw rate and sideslip control of an electric vehicle with multiple motors. Int. J. Automot. Technol. 2018, 19, 811–823. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M. Adaptive sliding mode control for attitude stabilization with actuator saturation. IEEE Trans. Ind. Electron. 2011, 58, 4898–4907. [Google Scholar] [CrossRef]
- Han, J.; Kim, T.; Oh, T.; Lee, S.; Cho, D. Effective disturbance compensation method under control saturation in discrete-time sliding mode control. IEEE Trans. Ind. Electron. 2020, 67, 5696–5707. [Google Scholar] [CrossRef]
- Zhang, S.; Simkani, M.; Zadeh, M.H. Automatic vehicle parallel parking design using fifth degree polynomial path planning. In Proceedings of the 2011 IEEE Vehicular Technology Conference (VTC Fall), San Francisco, CA, USA, 5–8 September 2011; pp. 1–4. [Google Scholar]
- Tan, B.; Chen, Y.; Liao, Q.; Zhang, B.; Zhang, N.; Xie, Q. A condensed dynamic model of a heavy-duty truck for optimization of the powertrain mounting system considering the chassis frame flexibility. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 2602–2617. [Google Scholar] [CrossRef]
- Borase, R.P.; Maghade, D.K.; Sondkar, S.Y.; Pawar, S.N. A review of PID control, tuning methods and applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S. Effective adoption of vehicle models for autonomous vehicle path tracking: A switched MPC approach. Veh. Syst. Dyn. 2023, 61, 1236–1259. [Google Scholar] [CrossRef]
- Allgower, F.; Findeisen, R.; Nagy, Z.K. Nonlinear model predictive control: From theory to application. J.-Chin. Inst. Chem. Eng. 2004, 35, 299–316. [Google Scholar]
- Peicheng, S.; Li, L.; Ni, X.; Yang, A. Intelligent vehicle path tracking control based on improved MPC and hybrid PID. IEEE Access 2022, 10, 94133–94144. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, Y.; Li, F. Integrated control of differential braking and active aerodynamic control for improving high speed stability of vehicles. Int. J. Automot. Technol. 2020, 21, 61–70. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Bencherif, A.; Barambones, O. A novel robust adaptive sliding mode control using stochastic gradient descent for PEMFC power system. Int. J. Hydrogen Energy 2023, 48, 17277–17292. [Google Scholar] [CrossRef]
- Utkin, V. Discussion aspects of high-order sliding mode control. IEEE Trans. Autom. Control 2016, 61, 829–833. [Google Scholar] [CrossRef]
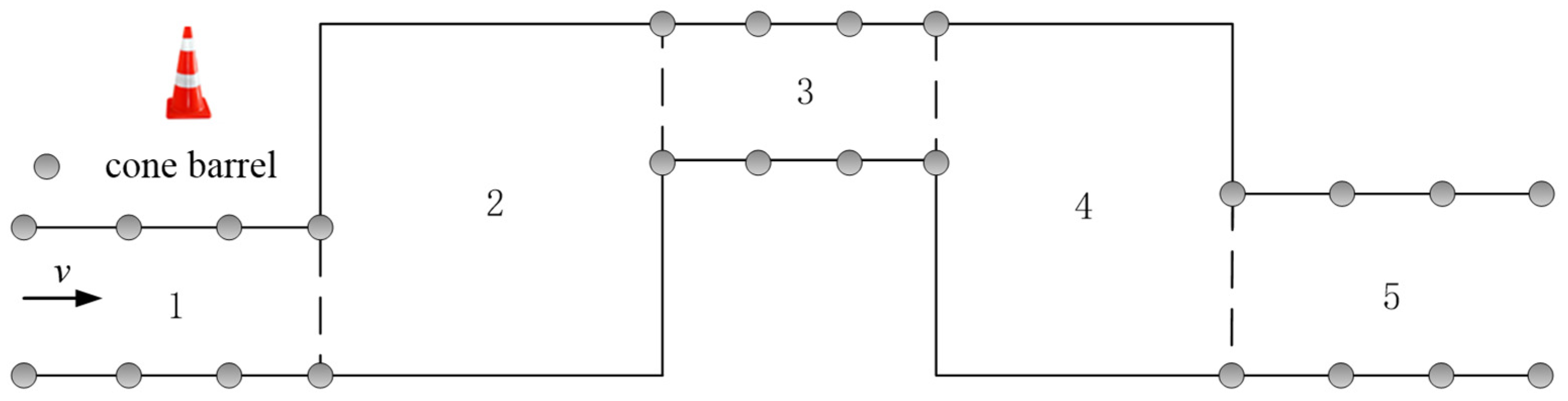

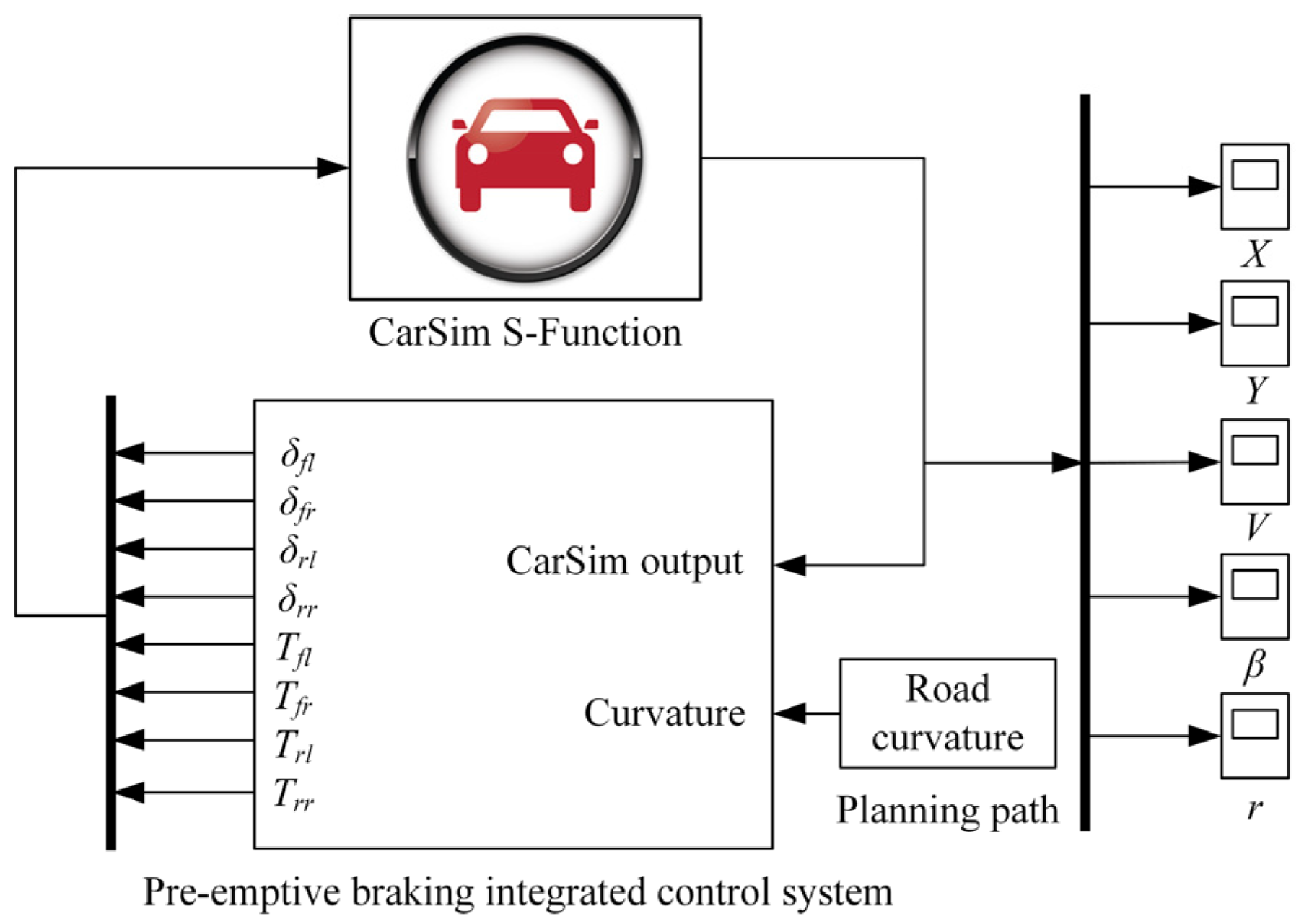



| Section | Length (m) | Width (m) |
|---|---|---|
| 1 | 12 | 2.329 |
| 2 | 13.5 | 6.219 |
| 3 | 11 | 2.89 |
| 4 | 12.5 | 6.219 |
| 5 | 12 | 3 |
| Symbol | Parameter Description | Value |
|---|---|---|
| m/(kg) | Vehicle mass | 1413 |
| lf/m | Distance from center of mass to front axle | 1.895 |
| lr/m | Distance from center of mass to rear axle | 1.015 |
| Iz/(kg·m2) | Moment of inertia about the Z axis | 1536.7 |
| Cf/(N·m−1) | Front axle lateral stiffness | 70,000 |
| Cr/(N·m−1) | Rear axle lateral stiffness | 35,000 |
| Np | Size of the prediction horizon | 20 |
| Nc | Size of the control horizon | 5 |
| T | Controller sample time | 0.05 |
| Q | State weighting matrix | Diag (24, 16.8, 1, 1) |
| R | Controls input weighting matrix | Diag (1, 1, 1) |
| ρ | Relaxation factor weight coefficient | 1000 |
| Control System | Description |
|---|---|
| ① | 2WS |
| ② | Pre-emptive braking control + 2WS |
| ③ | Pre-emptive braking control + 4WS |
| ④ | Pre-emptive braking control + 4WS + DYC |
| Evaluation Index | System ① | System ② | System ③ | System ④ |
|---|---|---|---|---|
| Vc (km/h) | 24.7 | 40.3 | 42.9 | 42.9 |
| Vf (km/h) | 24.7 | 24.7 | 24.7 | 24.7 |
| |βmax| (deg) | 5.09 | 5.13 | 3.38 | 2.18 |
| |r| (deg/s) | 22.02 | 22.48 | 33.46 | 29.65 |
| Evaluation Index | System ① | System ② | System ③ | System ④ |
|---|---|---|---|---|
| Vc (km/h) | 35 | 54.5 | 57.7 | 57.7 |
| Vf (km/h) | 35 | 35 | 35 | 35 |
| |βmax| (deg) | 3.99 | 3.91 | 2.34 | 1.79 |
| |r| (deg/s) | 33.84 | 33.32 | 32.39 | 35.01 |
| Evaluation Index | System ① | System ② | System ③ | System ④ |
|---|---|---|---|---|
| Vc (km/h) | 45 | 66.9 | 70.6 | 70.6 |
| Vf (km/h) | 45 | 45 | 45 | 45 |
| |βmax| (deg) | 3.15 | 3.11 | 2.23 | 1.74 |
| |r| (deg/s) | 45.11 | 46.06 | 48.35 | 50.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, F.; Wang, X. Enhancing Autonomous Vehicle Stability through Pre-Emptive Braking Control for Emergency Collision Avoidance. Appl. Sci. 2023, 13, 13219. https://doi.org/10.3390/app132413219
Lai F, Wang X. Enhancing Autonomous Vehicle Stability through Pre-Emptive Braking Control for Emergency Collision Avoidance. Applied Sciences. 2023; 13(24):13219. https://doi.org/10.3390/app132413219
Chicago/Turabian StyleLai, Fei, and Xiaoyu Wang. 2023. "Enhancing Autonomous Vehicle Stability through Pre-Emptive Braking Control for Emergency Collision Avoidance" Applied Sciences 13, no. 24: 13219. https://doi.org/10.3390/app132413219
APA StyleLai, F., & Wang, X. (2023). Enhancing Autonomous Vehicle Stability through Pre-Emptive Braking Control for Emergency Collision Avoidance. Applied Sciences, 13(24), 13219. https://doi.org/10.3390/app132413219







