Explainable AI for Machine Fault Diagnosis: Understanding Features’ Contribution in Machine Learning Models for Industrial Condition Monitoring
Abstract
:1. Introduction
- Filter-based methods: filters directly pre-process the collected features depending on the data intrinsic characteristics (correlation between features and class label), independent to the training of the algorithm. Typical importance indicators are Relief and Relief-F [35], information gain (IF) [36], Minimum Redundancy Maximum Relevance [37], Fischer score [38], and Distance Evaluation (DE) [39];
1.1. Literature Review
1.2. Scope of the Research and Outline
2. Theoretical Background
2.1. ML Models
2.1.1. Support Vector Machines (SVMs)
2.1.2. k-Nearest Neighbour (kNN)
2.2. Shapley Values
- Efficiency: the total gain is distributed ;
- Symmetry: if and are two players that contribute equally to all coalitions, then their Shapley value is the same ;
- Dummy player: if a player does not contribute to any coalitions, then his Shapley value is zero ;
- Monotonicity: if two games and and a player always makes a greater contribution to than to for all , then the gain for will be greater than that for ;
- Linearity: if two coalition games described by the gain functions and are combined, the distributed gain is the sum of the two gains is . This is valid also for a multiplication by a constant value , .
3. Dataset for Industrial Bearings
3.1. Test Rig Description
- Independent radial and axial loads of up to 200 kN on each tested bearing;
- Simultaneous testing of four bearings, which allows the self-balance of applied loads with minimal transmission to the platform;
- High modularity, which enables testing on different sized bearings up to 420 mm of the outer diameter;
- Direct measure of friction torque of tested bearings;
- Main bearings are immune to the loads acting on the test bearings.
3.2. Vibration Dataset
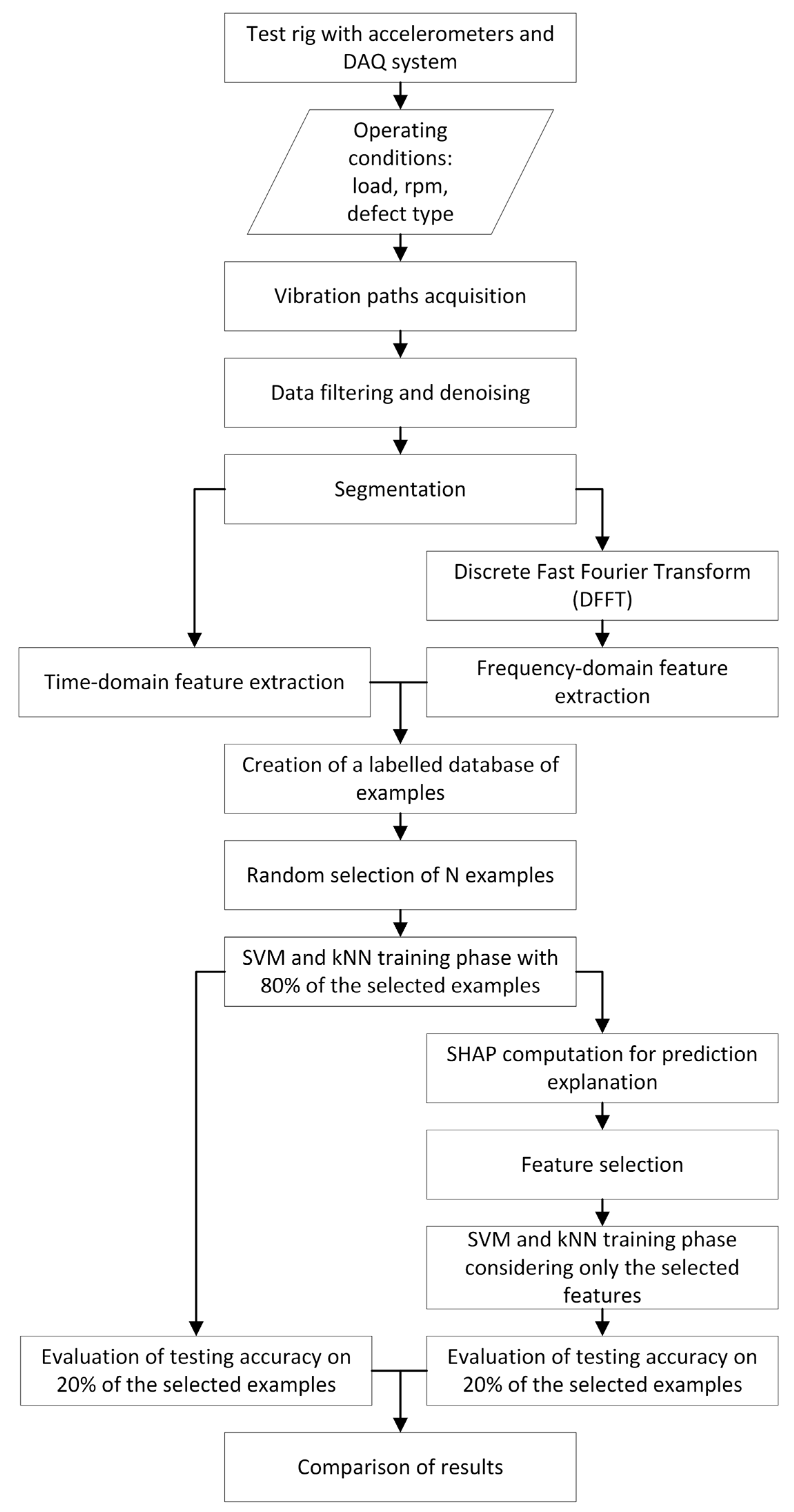
4. SHAP Analysis for Industrial Bearings
- Vibration database acquisition and data pre-processing;
- Feature extraction and creation of a database of the labelled samples;
- Training of AI algorithms;
- Shapley values computation and feature selection.
4.1. Features Extraction and Labelling of Vibration Samples
4.2. Training of AI Algortihms
- The kernel function that defines the function of the hyperplane used to separate data;
- C, called the regularisation term, which is the penalty parameter of the error term and controls the tradeoff between a smooth decision boundary and classifying the training points correctly;
- γ, which influences the number of nearby points used for the calculation of the separating hyperplane using the radial basis function (RBF) kernel.
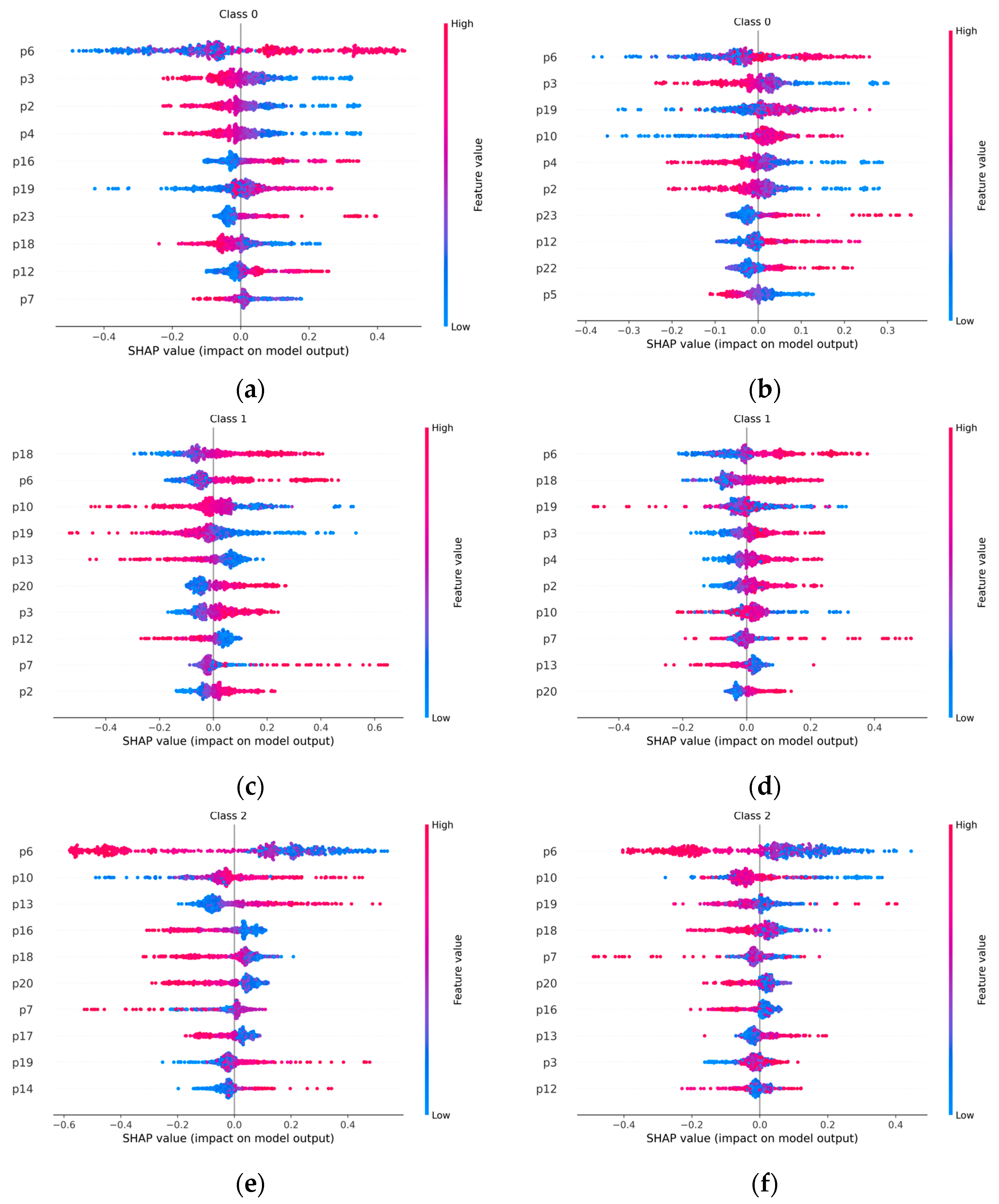
4.3. Shapley Values Computation and Features Selection
- Computation of Shapley values;
- Feature selection;
- Accuracy evaluation.
5. Results and Discussion
6. Conclusions
- The SVM and the kNN models are able to achieve diagnosis accuracies higher than 98.5% for medium-sized industrial bearings;
- The SHAP values are effective for interpreting machine learning models that are aimed at industrial condition monitoring;
- The SHAP analysis is employed to show that four features out of twenty-three are really important to achieve good diagnosis accuracies;
- The skewness and the shape factor of the vibration signals have the greatest impact on the outcomes of machine learning diagnosis models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, Y.; He, Z.; Zi, Y. A New Approach to Intelligent Fault Diagnosis of Rotating Machinery. Expert Syst. Appl. 2008, 35, 1593–1600. [Google Scholar] [CrossRef]
- Gupta, P.K. Advanced Dynamics of Rolling Elements; Springer: New York, NY, USA, 1984; ISBN 978-1-4612-9767-3. [Google Scholar]
- Singh, S.; Howard, C.Q.; Hansen, C.H. An Extensive Review of Vibration Modelling of Rolling Element Bearings with Localised and Extended Defects. J. Sound Vib. 2015, 357, 300–330. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. A Novel Optimized SVM Classification Algorithm with Multi-Domain Feature and Its Application to Fault Diagnosis of Rolling Bearing. Neurocomputing 2018, 313, 47–64. [Google Scholar] [CrossRef]
- Hasan, M.J.; Sohaib, M.; Kim, J.-M. A Multitask-Aided Transfer Learning-Based Diagnostic Framework for Bearings under Inconsistent Working Conditions. Sensors 2020, 20, 7205. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Huang, J.; Zhang, F. Quantitative and Localization Diagnosis of a Defective Ball Bearing Based on Vertical–Horizontal Synchronization Signal Analysis. IEEE Trans. Ind. Electron. 2017, 64, 8695–8706. [Google Scholar] [CrossRef]
- Tian, J.; Ai, Y.; Zhao, M.; Zhang, F.; Wang, Z.-J. Fault Diagnosis of Intershaft Bearings Using Fusion Information Exergy Distance Method. Shock. Vib. 2018, 2018, 7546128. [Google Scholar] [CrossRef]
- Rai, A.; Kim, J.-M. A Novel Health Indicator Based on the Lyapunov Exponent, a Probabilistic Self-Organizing Map, and the Gini-Simpson Index for Calculating the RUL of Bearings. Measurement 2020, 164, 108002. [Google Scholar] [CrossRef]
- Hasan, M.J.; Sohaib, M.; Kim, J.-M. An Explainable Ai-Based Fault Diagnosis Model for Bearings. Sensors 2021, 21, 4070. [Google Scholar] [CrossRef]
- Lacey, S.J. An Overview of Bearing Vibration Analysis. Maint. Asset Manag. 2008, 23, 32–42. [Google Scholar]
- Zheng, H.; Wang, R.; Yang, Y.; Li, Y.; Xu, M. Intelligent Fault Identification Based on Multisource Domain Generalization Towards Actual Diagnosis Scenario. IEEE Trans. Ind. Electron. 2020, 67, 1293–1304. [Google Scholar] [CrossRef]
- Oh, H.; Jung, J.H.; Jeon, B.C.; Youn, B.D. Scalable and Unsupervised Feature Engineering Using Vibration-Imaging and Deep Learning for Rotor System Diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 3539–3549. [Google Scholar] [CrossRef]
- Brusa, E.; Bruzzone, F.; Delprete, C.; Di Maggio, L.G.; Rosso, C. Health Indicators Construction for Damage Level Assessment in Bearing Diagnostics: A Proposal of an Energetic Approach Based on Envelope Analysis. Appl. Sci. 2020, 10, 8131. [Google Scholar] [CrossRef]
- Delprete, C.; Brusa, E.; Rosso, C.; Bruzzone, F. Bearing Health Monitoring Based on the Orthogonal Empirical Mode Decomposition. Shock. Vib. 2020, 2020, 8761278. [Google Scholar] [CrossRef]
- Delprete, C.; Milanesio, M.; Rosso, C. Rolling Bearings Monitoring and Damage Detection Methodology. Appl. Mech. Mater. 2006, 3–4, 293–302. [Google Scholar] [CrossRef]
- Brusa, E.; Delprete, C.; Giorio, L. Smart Manufacturing in Rolling Process Based on Thermal Safety Monitoring by Fiber Optics Sensors Equipping Mill Bearings. Appl. Sci. 2022, 12, 4186. [Google Scholar] [CrossRef]
- Li, Y.; Miao, B.; Zhang, W.; Chen, P.; Liu, J.; Jiang, X. Refined Composite Multiscale Fuzzy Entropy: Localized Defect Detection of Rolling Element Bearing. J. Mech. Sci. Technol. 2019, 33, 109–120. [Google Scholar] [CrossRef]
- Zhu, X.; Xiong, J.; Liang, Q. Fault Diagnosis of Rotation Machinery Based on Support Vector Machine Optimized by Quantum Genetic Algorithm. IEEE Access 2018, 6, 33583–33588. [Google Scholar] [CrossRef]
- Kang, M.; Kim, J.; Kim, J.-M.; Tan, A.C.C.; Kim, E.Y.; Choi, B.-K. Reliable Fault Diagnosis for Low-Speed Bearings Using Individually Trained Support Vector Machines With Kernel Discriminative Feature Analysis. IEEE Trans. Power Electron. 2015, 30, 2786–2797. [Google Scholar] [CrossRef]
- Widodo, A.; Kim, E.Y.; Son, J.-D.; Yang, B.-S.; Tan, A.C.C.; Gu, D.-S.; Choi, B.-K.; Mathew, J. Fault Diagnosis of Low Speed Bearing Based on Relevance Vector Machine and Support Vector Machine. Expert Syst. Appl. 2009, 36, 7252–7261. [Google Scholar] [CrossRef]
- Brusa, E.; Delprete, C.; Di Maggio, L.G. Eigen-Spectrograms: An Interpretable Feature Space for Bearing Fault Diagnosis Based on Artificial Intelligence and Image Processing. Mech. Adv. Mater. Struct. 2022, 1–13. [Google Scholar] [CrossRef]
- He, D.; Li, R.; Zhu, J. Plastic Bearing Fault Diagnosis Based on a Two-Step Data Mining Approach. IEEE Trans. Ind. Electron. 2013, 60, 3429–3440. [Google Scholar] [CrossRef]
- Safizadeh, M.S.; Latifi, S.K. Using Multi-Sensor Data Fusion for Vibration Fault Diagnosis of Rolling Element Bearings by Accelerometer and Load Cell. Inf. Fusion 2014, 18, 1–8. [Google Scholar] [CrossRef]
- Yang, D.-M.; Stronach, A.F.; Macconnell, P.; Penman, J. THIRD-ORDER SPECTRAL TECHNIQUES FOR THE DIAGNOSIS OF MOTOR BEARING CONDITION USING ARTIFICIAL NEURAL NETWORKS. Mech. Syst. Signal Process. 2002, 16, 391–411. [Google Scholar] [CrossRef]
- Zarei, J.; Tajeddini, M.A.; Karimi, H.R. Vibration Analysis for Bearing Fault Detection and Classification Using an Intelligent Filter. Mechatronics 2014, 24, 151–157. [Google Scholar] [CrossRef]
- He, X.; Wang, D.; Li, Y.; Zhou, C. A Novel Bearing Fault Diagnosis Method Based on Gaussian Restricted Boltzmann Machine. Math. Probl. Eng. 2016, 2016, 2957083. [Google Scholar] [CrossRef]
- Guo, S.; Yang, T.; Gao, W.; Zhang, C. A Novel Fault Diagnosis Method for Rotating Machinery Based on a Convolutional Neural Network. Sensors 2018, 18, 1429. [Google Scholar] [CrossRef]
- Brusa, E.; Delprete, C.; Di Maggio, L.G. Deep Transfer Learning for Machine Diagnosis: From Sound and Music Recognition to Bearing Fault Detection. Appl. Sci. 2021, 11, 11663. [Google Scholar] [CrossRef]
- Di Maggio, L.G. Intelligent Fault Diagnosis of Industrial Bearings Using Transfer Learning and CNNs Pre-Trained for Audio Classification. Sensors 2022, 23, 211. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of Machine Learning to Machine Fault Diagnosis: A Review and Roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Islam, M.R.; Islam, M.M.M.; Kim, J.-M. Feature Selection Techniques for Increasing Reliability of Fault Diagnosis of Bearings. In Proceedings of the 2016 9th International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 20–22 December 2016; pp. 396–399. [Google Scholar]
- Roelofs, R.; Shankar, V.; Recht, B.; Fridovich-Keil, S.; Hardt, M.; Miller, J.; Schmidt, L. A Meta-Analysis of Overfitting in Machine Learning. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc.: Vancouver, BC, Canada, 2019; Volume 32. [Google Scholar]
- Yassine, A.; Mohamed, C.; Zinedine, A. Feature Selection Based on Pairwise Evalution. In Proceedings of the 2017 Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 17–19 April 2017; pp. 1–6. [Google Scholar]
- Vega García, M.; Aznarte, J.L. Shapley Additive Explanations for NO2 Forecasting. Ecol. Inform. 2020, 56, 101039. [Google Scholar] [CrossRef]
- Kononenko, I. Estimating Attributes: Analysis and Extensions of RELIEF. In Proceedings of the Machine Learning: ECML-94; Bergadano, F., De Raedt, L., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 171–182. [Google Scholar]
- Hall, M.A.; Smith, L.A. Practical Feature Subset Selection for Machine Learning. In Proceedings of the 21st Australasian Computer Science Conference ACSC’98, Perth, Australia, 6 February 1998; Volume 20, pp. 181–191. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature Selection Based on Mutual Information Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Yang, B.S.; Han, T.; An, J.L. ART–KOHONEN Neural Network for Fault Diagnosis of Rotating Machinery. Mech. Syst. Signal Process. 2004, 18, 645–657. [Google Scholar] [CrossRef]
- Landau, S.; Leese, M.; Stahl, D.; Everitt, B.S. Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-0-470-97844-3. [Google Scholar]
- Hui, K.H.; Ooi, C.; Lim, M.; Leong, M.; Al-Obaidi, S. An Improved Wrapper-Based Feature Selection Method for Machinery Fault Diagnosis. PLoS ONE 2017, 12, e0189143. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and Smoothness via the Fused Lasso. J. R. Stat. Soc. Ser. B 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Springer: Dordrecht, The Netherlands, 1995; ISBN 978-90-481-4583-6. [Google Scholar]
- Qin, S.J. Survey on Data-Driven Industrial Process Monitoring and Diagnosis. Annu. Rev. Control. 2012, 36, 220–234. [Google Scholar] [CrossRef]
- Yadav, A.; Swetapadma, A. A Novel Transmission Line Relaying Scheme for Fault Detection and Classification Using Wavelet Transform and Linear Discriminant Analysis. Ain Shams Eng. J. 2015, 6, 199–209. [Google Scholar] [CrossRef]
- MacGregor, J.F.; Jaeckle, C.; Kiparissides, C.; Koutoudi, M. Process Monitoring and Diagnosis by Multiblock PLS Methods. AIChE J. 1994, 40, 826–838. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Long Beach, CA, USA, 2017; Volume 30. [Google Scholar]
- Choi, S.H.; Lee, J.M. Explainable Fault Diagnosis Model Using Stacked Autoencoder and Kernel SHAP. In Proceedings of the 2022 IEEE International Symposium on Advanced Control of Industrial Processes (AdCONIP), Vancouver, BC, Canada, 7–9 August 2022; pp. 182–187. [Google Scholar]
- Brito, L.C.; Susto, G.A.; Brito, J.N.; Duarte, M.A.V. An Explainable Artificial Intelligence Approach for Unsupervised Fault Detection and Diagnosis in Rotating Machinery. Mech. Syst. Signal Process. 2022, 163, 108105. [Google Scholar] [CrossRef]
- Adadi, A.; Berrada, M. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Doran, D.; Schulz, S.; Besold, T.R. What Does Explainable AI Really Mean? A New Conceptualization of Perspectives. arXiv 2017. [Google Scholar] [CrossRef]
- Song, E.; Nelson, B.L.; Staum, J. Shapley Effects for Global Sensitivity Analysis: Theory and Computation. SIAM/ASA J. Uncertain. Quantif. 2016, 4, 1060–1083. [Google Scholar] [CrossRef] [Green Version]
- Aas, K.; Jullum, M.; Løland, A. Explaining Individual Predictions When Features Are Dependent: More Accurate Approximations to Shapley Values. Artif. Intell. 2021, 298, 103502. [Google Scholar] [CrossRef]
- Lundberg, S.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. Explainable AI for Trees: From Local Explanations to Global Understanding. arXiv 2019, arXiv:1905.04610. [Google Scholar] [CrossRef] [PubMed]
- Štrumbelj, E.; Kononenko, I. Explaining Prediction Models and Individual Predictions with Feature Contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Redelmeier, A.; Jullum, M.; Aas, K. Explaining Predictive Models with Mixed Features Using Shapley Values and Conditional Inference Trees. In Machine Learning and Knowledge Extraction; Lecture Notes in Computer Science; Holzinger, A., Kieseberg, P., Tjoa, A.M., Weippl, E., Eds.; Springer International Publishing: Cham, Oslo, Norway, 2020; Volume 12279, pp. 117–137. ISBN 978-3-030-57320-1. [Google Scholar]
- Moehle, N.; Boyd, S.; Ang, A. Portfolio Performance Attribution via Shapley Value. arXiv 2021, arXiv:2102.05799. [Google Scholar]
- Fryer, D.; Strümke, I.; Nguyen, H. Shapley Values for Feature Selection: The Good, the Bad, and the Axioms. IEEE Access 2021, 9, 144352–144360. [Google Scholar] [CrossRef]
- Strumbelj, E.; Kononenko, I. An Efficient Explanation of Individual Classifications Using Game Theory. J. Mach. Learn. Res. 2010, 11, 1–18. [Google Scholar]
- Banerjee, T.; Paul, A.; Srikanth, V.; Strümke, I. Causal Connections between Socioeconomic Disparities and COVID-19 in the USA. Sci. Rep. 2022, 12, 15827. [Google Scholar] [CrossRef]
- Rohmer, J.; Thieblemont, R.; Le Cozannet, G.; Goelzer, H.; Durand, G. Improving Interpretation of Sea-Level Projections through a Machine-Learning-Based Local Explanation Approach. Cryosphere 2022, 16, 4637–4657. [Google Scholar] [CrossRef]
- Watson, D.S. Interpretable Machine Learning for Genomics. Hum. Genet. 2022, 141, 1499–1513. [Google Scholar] [CrossRef]
- Midtfjord, A.D.; Bin, R.D.; Huseby, A.B. A Decision Support System for Safer Airplane Landings: Predicting Runway Conditions Using XGBoost and Explainable AI. Cold Reg. Sci. Technol. 2022, 199, 103556. [Google Scholar] [CrossRef]
- Dong, H.; Sun, J.; Sun, X. A Multi-Objective Multi-Label Feature Selection Algorithm Based on Shapley Value. Entropy 2021, 23, 1094. [Google Scholar] [CrossRef]
- Goštautaitė, D.; Sakalauskas, L. Multi-Label Classification and Explanation Methods for Students’ Learning Style Prediction and Interpretation. Appl. Sci. 2022, 12, 5396. [Google Scholar] [CrossRef]
- Chen, Y.; Aleman, D.M.; Purdie, T.G.; McIntosh, C. Understanding Machine Learning Classifier Decisions in Automated Radiotherapy Quality Assurance. Phys. Med. Biol. 2022, 67, 025001. [Google Scholar] [CrossRef]
- Oh, A.R.; Park, J.; Lee, J.-H.; Kim, H.; Yang, K.; Choi, J.-H.; Ahn, J.; Sung, J.D.; Lee, S.-H. Association Between Perioperative Adverse Cardiac Events and Mortality During One-Year Follow-Up After Noncardiac Surgery. J. Am. Heart Assoc. 2022, 11, e024325. [Google Scholar] [CrossRef]
- Akimoto, S.; Lebreton, P.; Takahashi, S.; Yamagishi, K. Quantitative Causality Analysis of Viewing Abandonment Reasons Using Shapley Value. In Proceedings of the 2022 IEEE 24th International Workshop on Multimedia Signal Processing (MMSP), Shanghai, China, 26–28 September 2022; pp. 01–06. [Google Scholar]
- Li, L.; Wu, X.; Kong, M.; Zhou, D.; Tao, X. Towards the Quantitative Interpretability Analysis of Citizens Happiness Prediction. In Proceedings of the 39th International Joint Conference on Artificial Intelligence (IJCAI-ECAI 2022), Vienna, Austria, 23–29 July 2022; Volume 6, pp. 5094–5100. [Google Scholar]
- Sun, Q.; Sun, J.; Guo, K.; Liu, J. Investigation on Mechanical Properties and Energy Absorption Capabilities of AlSi10Mg Triply Periodic Minimal Surface Sheet Structures Fabricated via Selective Laser Melting. J. Mater. Eng. Perform. 2022, 31, 9110–9121. [Google Scholar] [CrossRef]
- Remman, S.B.; Strumke, I.; Lekkas, A.M. Causal versus Marginal Shapley Values for Robotic Lever Manipulation Controlled Using Deep Reinforcement Learning. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; Volume 2022, pp. 2683–2690. [Google Scholar]
- Cohen, S.; Ruppin, E.; Dror, G. Feature Selection Based on the Shapley Value. In Proceedings of the 19th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 19–27 August 2005; Cohen, S., Ruppin, E., Dror, G., Eds.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2005; pp. 665–670. [Google Scholar]
- Marcílio, W.E.; Eler, D.M. From Explanations to Feature Selection: Assessing SHAP Values as Feature Selection Mechanism. In Proceedings of the 2020 33rd SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Porto de Galinhas, Brazil, 7–10 November 2020; pp. 340–347. [Google Scholar]
- Zacharias, J.; von Zahn, M.; Chen, J.; Hinz, O. Designing a Feature Selection Method Based on Explainable Artificial Intelligence. Electron. Mark. 2022, 32, 2159–2184. [Google Scholar] [CrossRef]
- Guha, R.; Khan, A.H.; Singh, P.K.; Sarkar, R.; Bhattacharjee, D. CGA: A New Feature Selection Model for Visual Human Action Recognition. Neural Comput. Applic 2021, 33, 5267–5286. [Google Scholar] [CrossRef]
- Jothi, N.; Husain, W.; Rashid, N.A. Predicting Generalized Anxiety Disorder among Women Using Shapley Value. J. Infect. Public Health 2021, 14, 103–108. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, S.; Hemachandra, N.; Trivedi, P. Interpretable Feature Subset Selection: A Shapley Value Based Approach. In Proceedings of the 2020 IEEE International Conference on Big Data (Big Data), Atlanta, GA, USA, 10–13 December 2020; pp. 5463–5472. [Google Scholar]
- Mey, O.; Neufeld, D. Explainable AI Algorithms for Vibration Data-Based Fault Detection: Use Case-Adadpted Methods and Critical Evaluation. Sensors 2022, 22, 9037. [Google Scholar] [CrossRef]
- Yang, D.; Karimi, H.R.; Gelman, L. A Fuzzy Fusion Rotating Machinery Fault Diagnosis Framework Based on the Enhancement Deep Convolutional Neural Networks. Sensors 2022, 22, 671. [Google Scholar] [CrossRef] [PubMed]
- Brusa, E.; Delprete, C.; Giorio, L.; Di Maggio, L.G.; Zanella, V. Design of an Innovative Test Rig for Industrial Bearing Monitoring with Self-Balancing Layout. Machines 2022, 10, 54. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.-S. Support Vector Machine in Machine Condition Monitoring and Fault Diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Boser, B.; Guyon, I.; Vapnik, V. A Training Algorithm for Optimal Margin Classifier. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992. [Google Scholar] [CrossRef]
- Buchaiah, S.; Shakya, P. Bearing Fault Diagnosis and Prognosis Using Data Fusion Based Feature Extraction and Feature Selection. Measurement 2022, 188, 110506. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 1999; ISBN 978-0-387-98780-4. [Google Scholar]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms, 1st ed.; Cambridge University Press: New York, NY, USA, 2014; ISBN 978-1-107-05713-5. [Google Scholar]
- Fix, E. Discriminatory Analysis: Nonparametric Discrimination, Consistency Properties; USAF School of Aviation Medicine: Randolph Field, TX, USA, 1985. [Google Scholar]
- Hart, P.E.; Stork, D.G.; Duda, R.O. Pattern Classification; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Cover, T.; Hart, P. Nearest Neighbor Pattern Classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Wang, J.; Neskovic, P.; Cooper, L.N. Neighborhood Size Selection in the K-Nearest-Neighbor Rule Using Statistical Confidence. Pattern Recognit. 2006, 39, 417–423. [Google Scholar] [CrossRef]
- Hart, P. The Condensed Nearest Neighbor Rule (Corresp.). IEEE Trans. Inf. Theory 1968, 14, 515–516. [Google Scholar] [CrossRef]
- Shapley, L.S. A Value for N-Person Games. In Classics in Game Theory; The Rand Corporation: Santa Monica, CA, USA, 1997; Volume 69. [Google Scholar]
- Covert, I.; Lundberg, S.M.; Lee, S.-I. Understanding Global Feature Contributions with Additive Importance Measures. In Proceedings of the Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Seattle, WA, USA, 2020; Volume 33, pp. 17212–17223. [Google Scholar]
- Kumar, I.E.; Venkatasubramanian, S.; Scheidegger, C.; Friedler, S. Problems with Shapley-Value-Based Explanations as Feature Importance Measures. In Proceedings of the Proceedings of the 37th International Conference on Machine Learning; PMLR, Salt Lake City, UT, USA, 13 July 2020, Daumé, H., III, Singh, A., Eds.; Volume 119, pp. 5491–5500.
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An Intelligent Fault Diagnosis Method Using Unsupervised Feature Learning Towards Mechanical Big Data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Yousefi, S. A Data-Driven Approach for Fault Classification of a Manufacturing Process. Master’s Thesis, NTNU, Trondheim, Norway, 2022. [Google Scholar]
- Lei, Y.; Zuo, M.J.; He, Z.; Zi, Y. A Multidimensional Hybrid Intelligent Method for Gear Fault Diagnosis. Expert Syst. Appl. 2010, 37, 1419–1430. [Google Scholar] [CrossRef]
- Caesarendra, W.; Tjahjowidodo, T. A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
- Elliott, D.F.; Rao, K.R. Fast Transforms: Algorithms, Analyses, Applications; Academic Press: New York, NY, USA, 1982; ISBN 978-0-12-237080-9. [Google Scholar]
- Oppenheim, A.; Schafer, R. Discrete-Time Signal Processing, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2009; ISBN 978-0-13-198842-2. [Google Scholar]
- Lei, Y.; He, Z.; Zi, Y.; Hu, Q. Fault Diagnosis of Rotating Machinery Based on Multiple ANFIS Combination with GAs. Mech. Syst. Signal Process. 2007, 21, 2280–2294. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y.; Chen, X. New Clustering Algorithm-Based Fault Diagnosis Using Compensation Distance Evaluation Technique. Mech. Syst. Signal Process. 2008, 22, 419–435. [Google Scholar] [CrossRef]
- Dou, Z.; Sun, Y.; Wu, Z.; Wang, T.; Fan, S.; Zhang, Y. The Architecture of Mass Customization-Social Internet of Things System: Current Research Profile. ISPRS Int. J. Geo-Inf. 2021, 10, 653. [Google Scholar] [CrossRef]
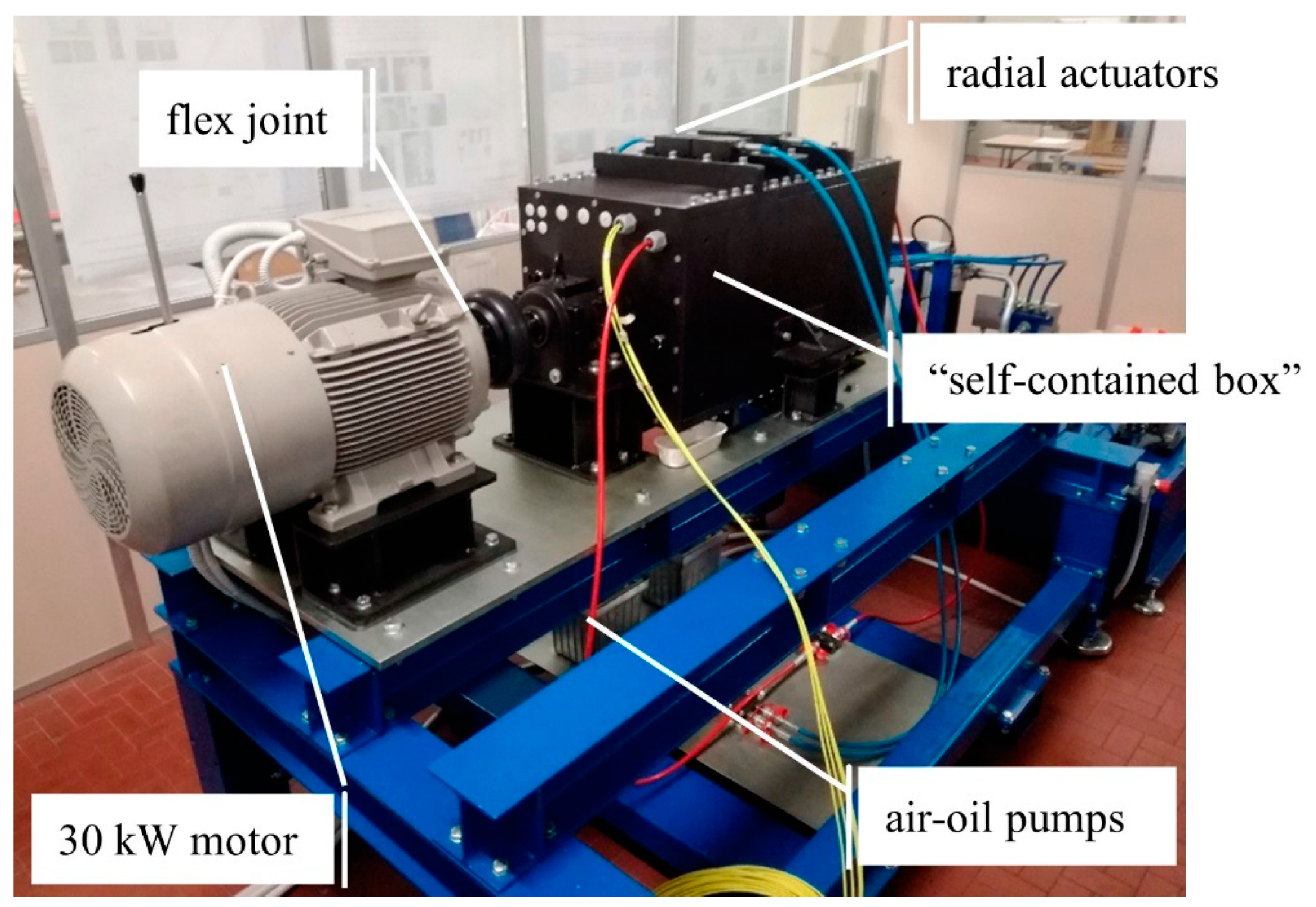





| Case 1 | Case 2 | Case 3 | |
|---|---|---|---|
| Radial load (kN) | 0 | 62.4 | 124.8 |
| Nominal speed (rpm) | 127, 227, 353, 457, 523, 607, 727, 877, 937, and 997 | ||
| Defect type | Non-defective (0), inner race defect (1), and outer race defect (2) | ||
| Time−Domain Features | Frequency−Domain Features |
|---|---|
| SVM | kNN | ||
|---|---|---|---|
| Kernel | Radial Basis Function (RBF) | Nearest neighbours | 1 |
| 43 | |||
| Distance metric | Euclidean | ||
| Decision function | one vs. one | ||
| Model | Selected Features |
|---|---|
| SVM | |
| kNN |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brusa, E.; Cibrario, L.; Delprete, C.; Di Maggio, L.G. Explainable AI for Machine Fault Diagnosis: Understanding Features’ Contribution in Machine Learning Models for Industrial Condition Monitoring. Appl. Sci. 2023, 13, 2038. https://doi.org/10.3390/app13042038
Brusa E, Cibrario L, Delprete C, Di Maggio LG. Explainable AI for Machine Fault Diagnosis: Understanding Features’ Contribution in Machine Learning Models for Industrial Condition Monitoring. Applied Sciences. 2023; 13(4):2038. https://doi.org/10.3390/app13042038
Chicago/Turabian StyleBrusa, Eugenio, Luca Cibrario, Cristiana Delprete, and Luigi Gianpio Di Maggio. 2023. "Explainable AI for Machine Fault Diagnosis: Understanding Features’ Contribution in Machine Learning Models for Industrial Condition Monitoring" Applied Sciences 13, no. 4: 2038. https://doi.org/10.3390/app13042038
APA StyleBrusa, E., Cibrario, L., Delprete, C., & Di Maggio, L. G. (2023). Explainable AI for Machine Fault Diagnosis: Understanding Features’ Contribution in Machine Learning Models for Industrial Condition Monitoring. Applied Sciences, 13(4), 2038. https://doi.org/10.3390/app13042038









