Investigation of Compressive Strength Characteristics of Hardfill Material and Seismic Stability of Hardfill Dams
Abstract
:1. Introduction
2. Materials and Methods
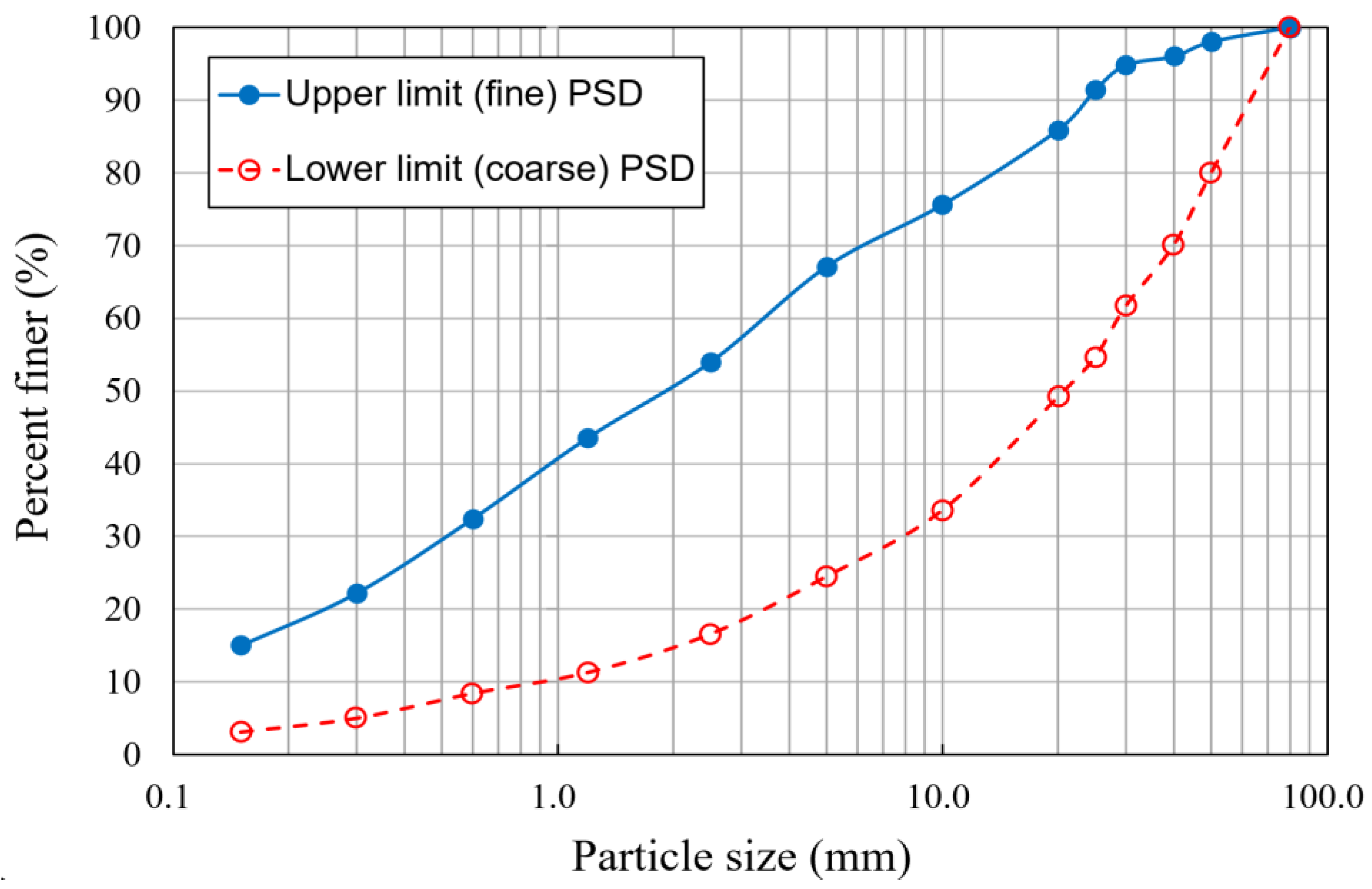
2.1. Materials
2.2. Laboratory Tests
2.3. Field Test Construction
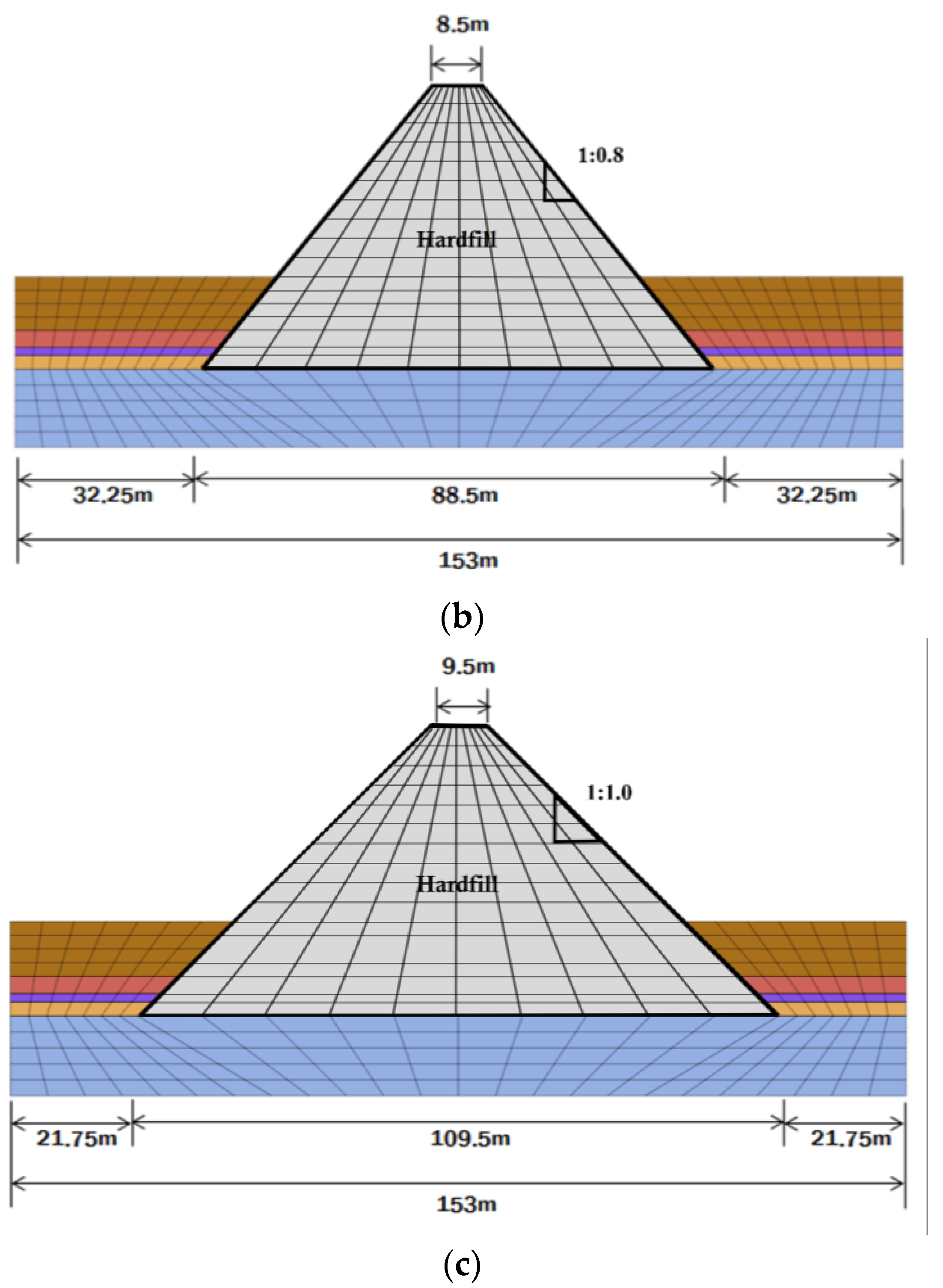
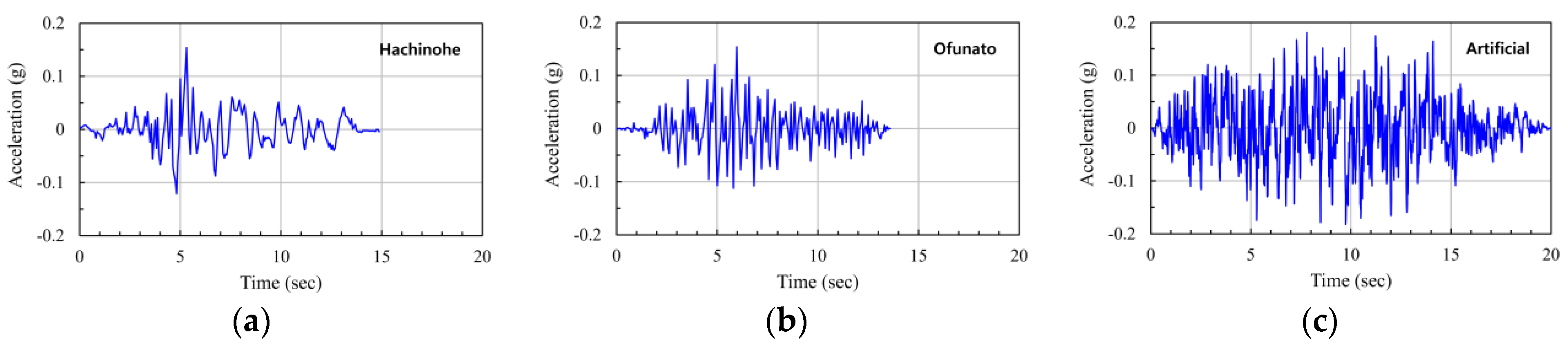
2.4. Numerical Investigation
3. Laboratory Test Results
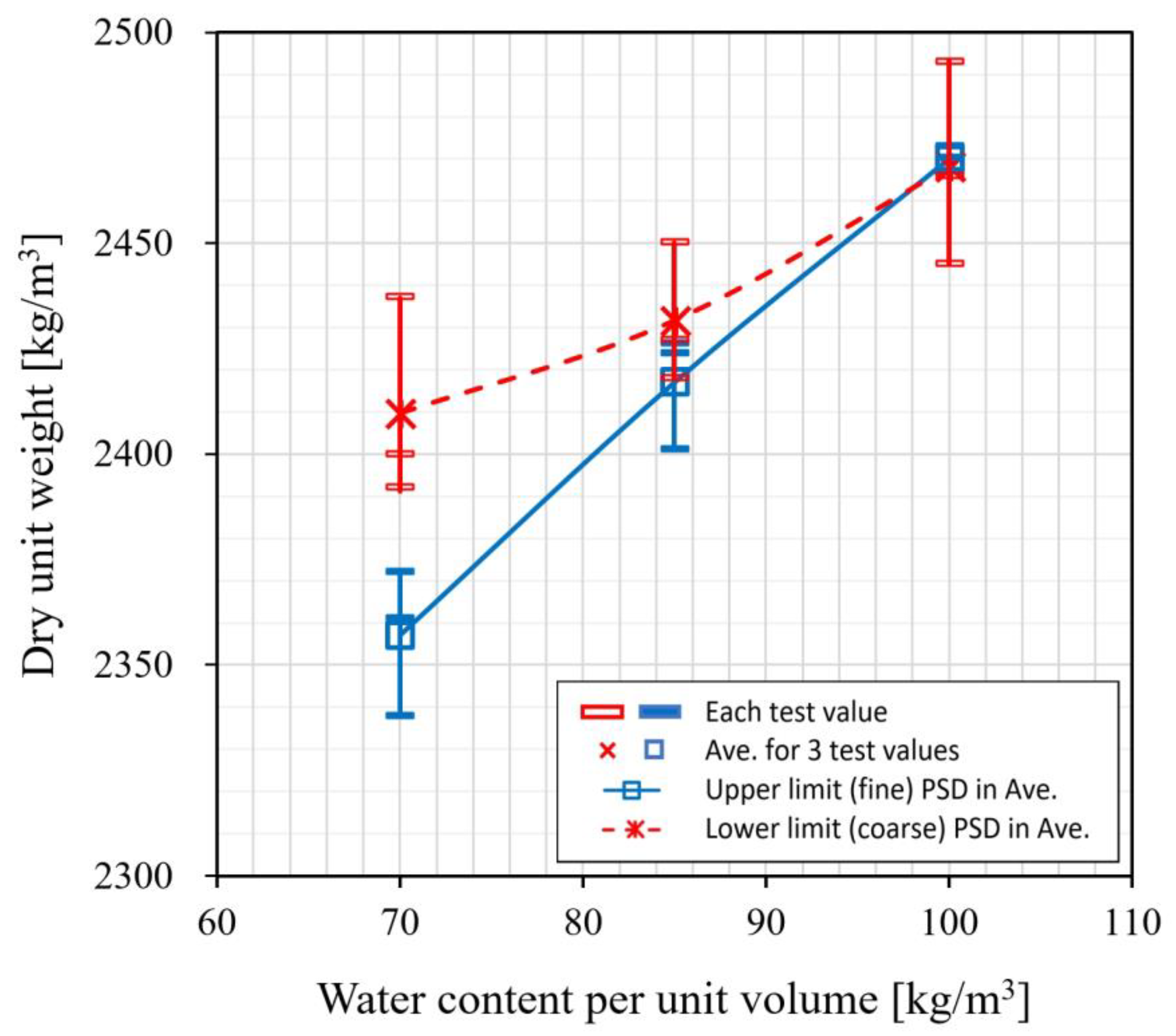
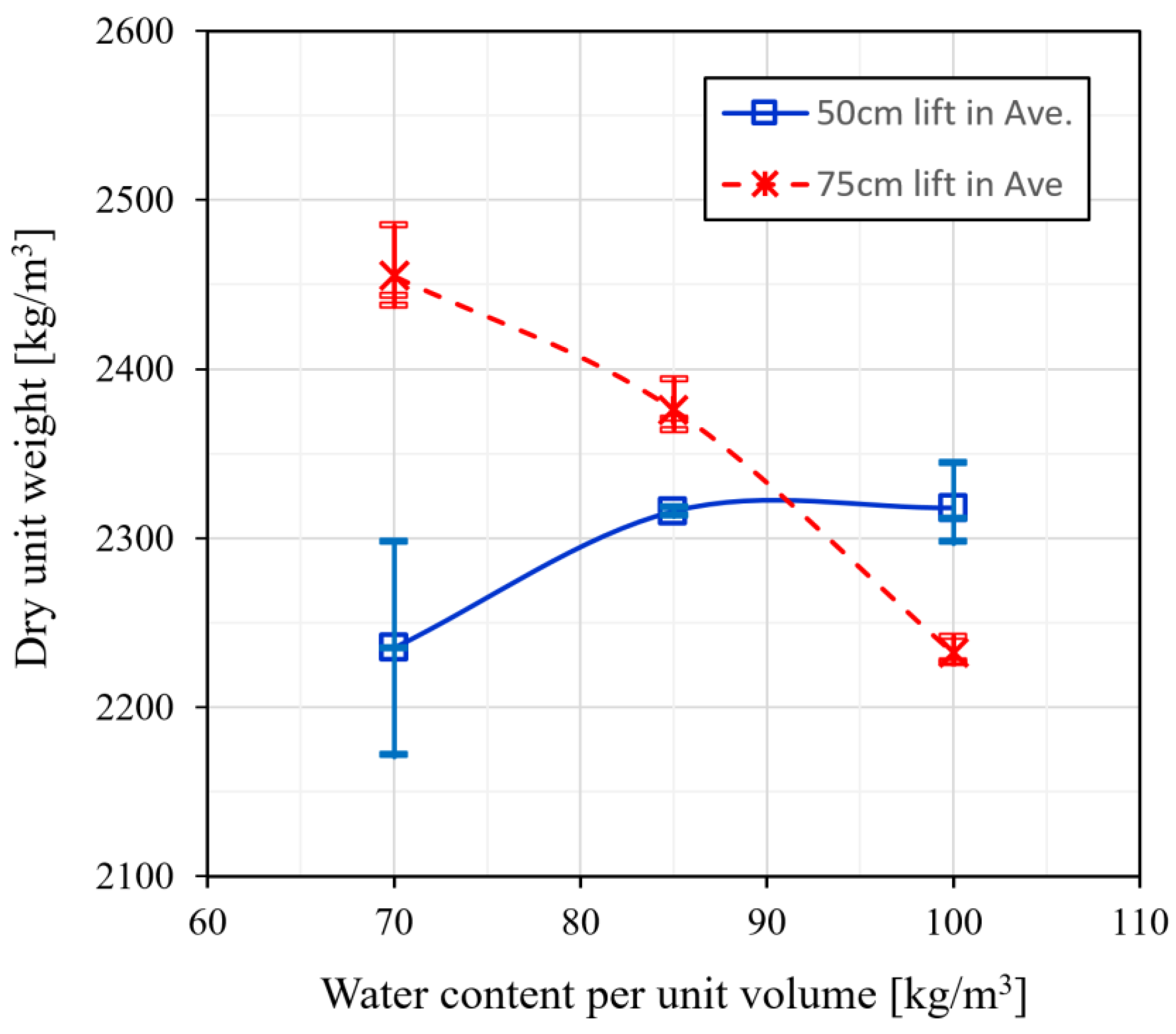
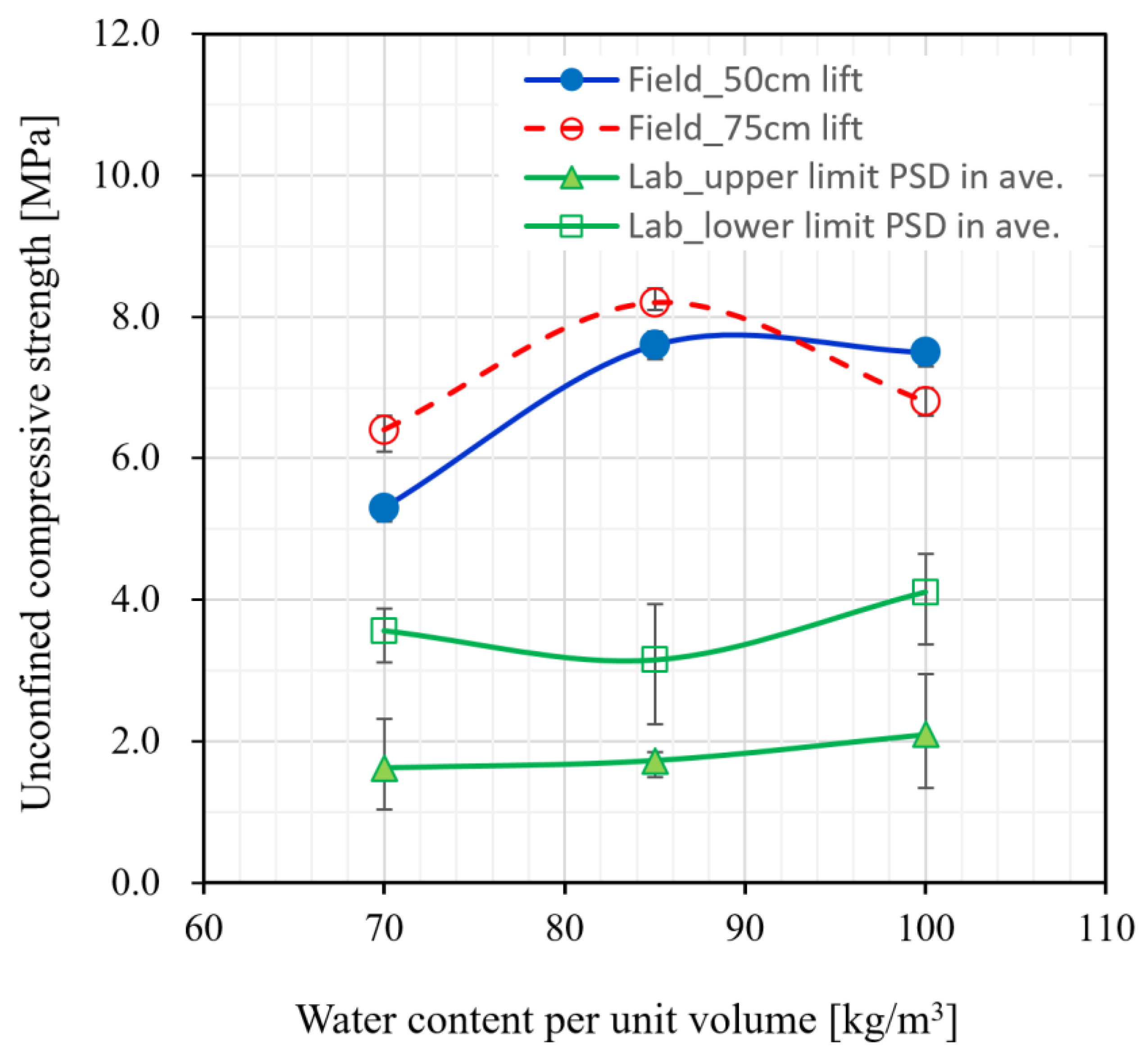
3.1. Variations in Dry Unit Weight and Uniaxial Compressive Strength for Hardfill Mix Conditions with Different Aggregate Size Distributions and Water Content per Unit Volume
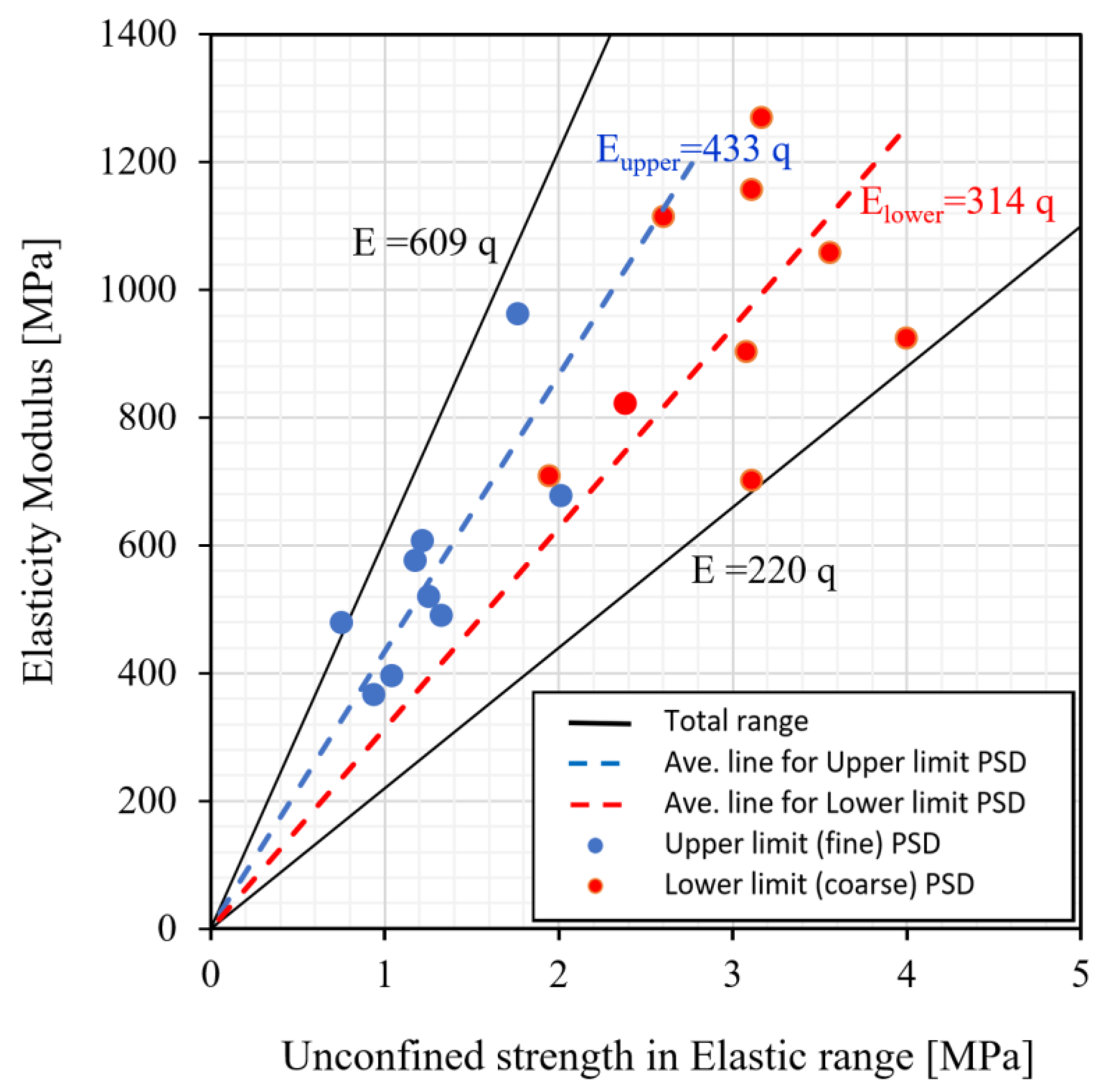
3.2. Elastic Properties of Hardfill
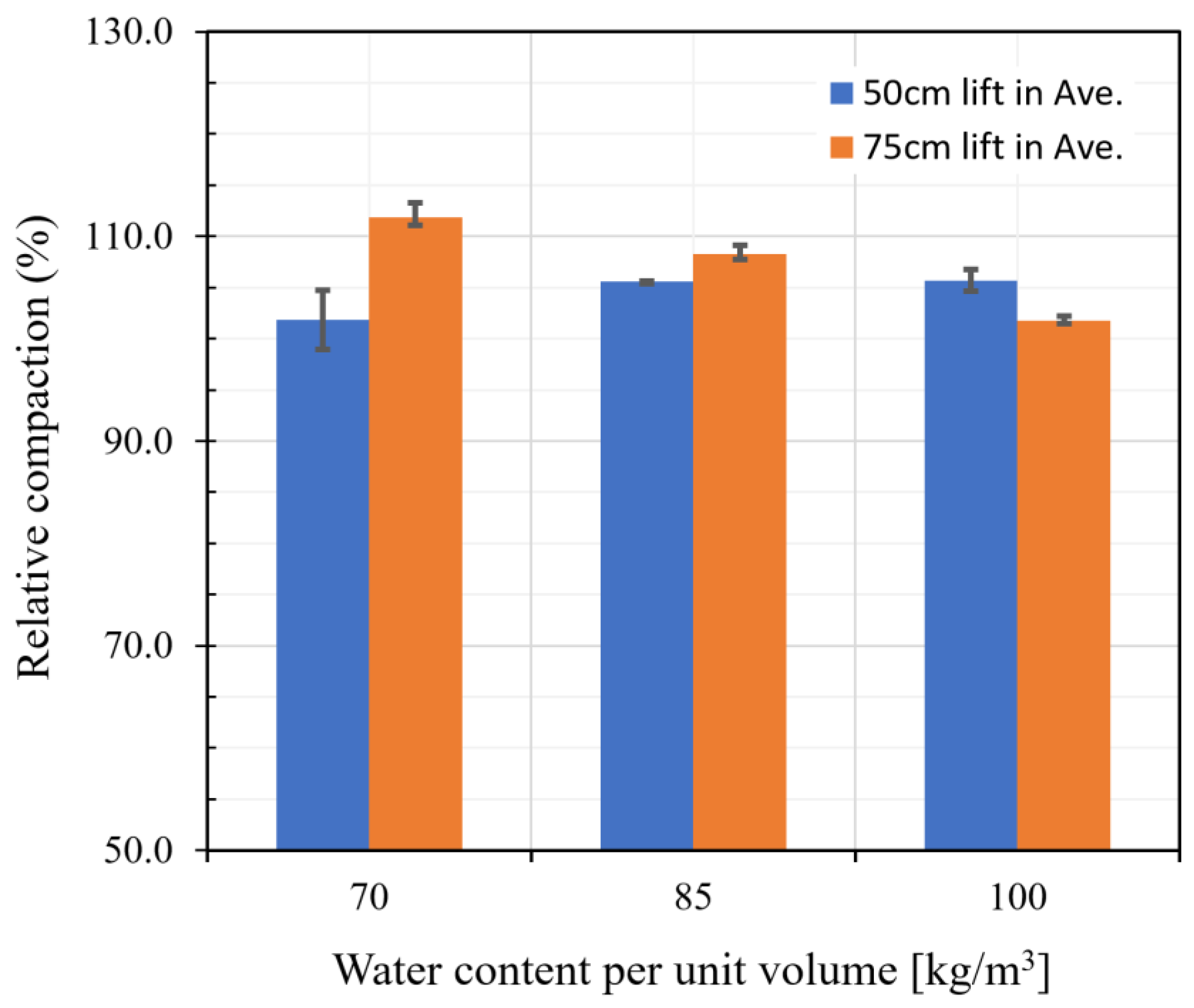
4. Field Test Construction Results
5. Numerical Analysis Results
6. Conclusions
- From the results of the uniaxial compressive strength test on the large indoor specimens, the compressive strength tended to increase very gently with the unit water content in general for both types of aggregate PSDs, i.e., the upper limit (fine) and lower limit (coarse), mixed with a unit cement content of 80 kg/m3 and three unit water contents of 70, 85, and 100 kg/m3, respectively. The strength range for the entire set of samples was 1.62–4.11 MPa, i.e., 3.15–4.11 MPa for the aggregate mix with the lower-limit PSD and 1.62–2.10 MPa for the aggregate mix with the upper-limit PSD. The uniaxial compressive strength of the aggregate mix with the lower limit PSD exceeded that of the aggregate mix with the upper limit PSD for the entire unit water content range. From the stress–strain relationship obtained from the uniaxial compressive strength test, the hardfill’s elastic modulus was found to be in the range of approximately 220 to 609 times the uniaxial compressive strength.
- Field compaction was performed with a vibration roller on the same type of aggregates as used in the indoor laboratory test by matching the PSD and mixing ratio to the laboratory test conditions. The results of the uniaxial compressive strength test on the cores collected from the field compacted hardfill after 28 d showed that the strength range for the entire core was 5.30–8.20 MPa, i.e., more than twice as large as the indoor test results, suggesting that the strength measurement of a hardfill through a laboratory test can conservatively evaluate the strength of a field compacted hardfill.
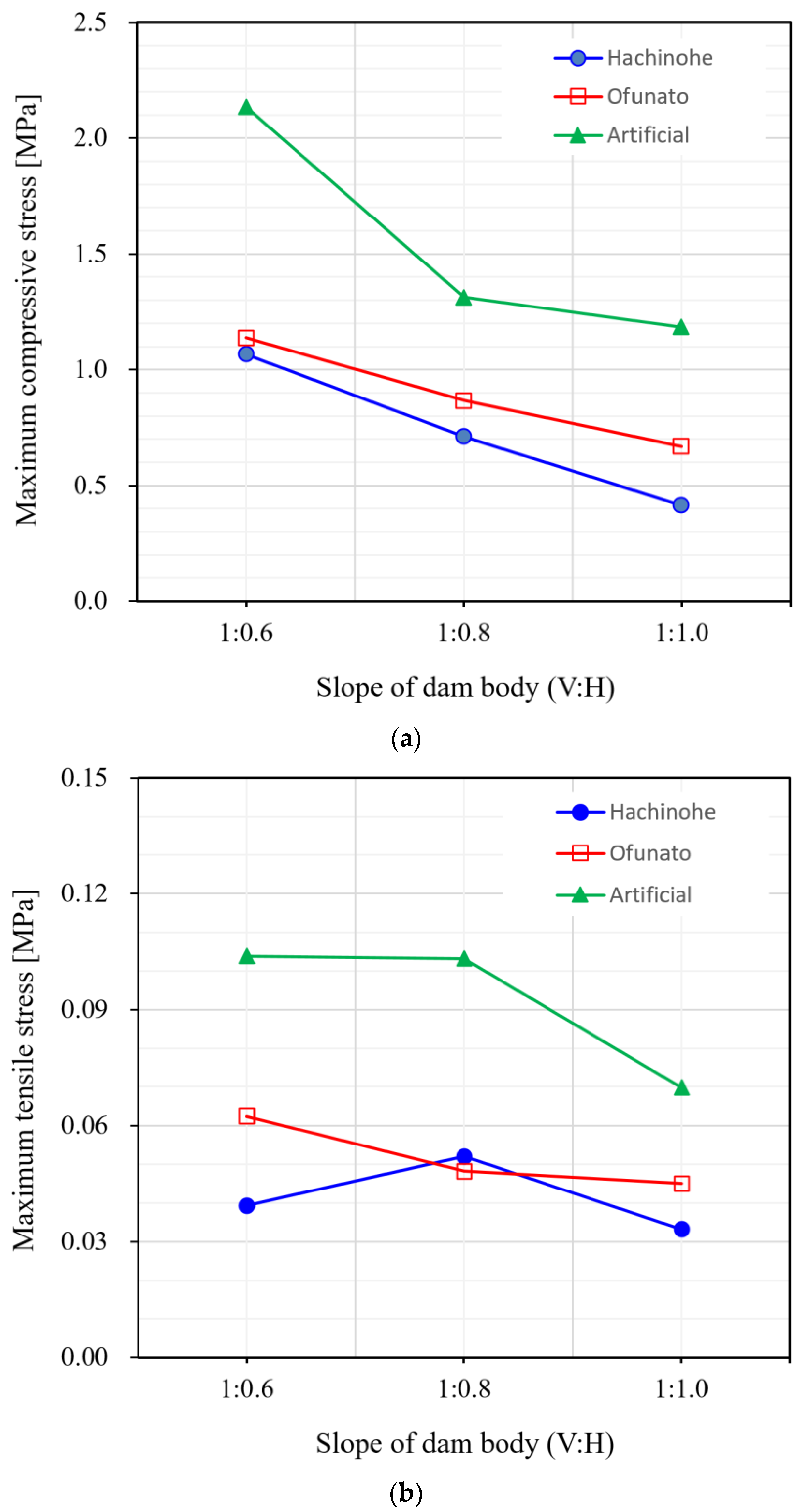
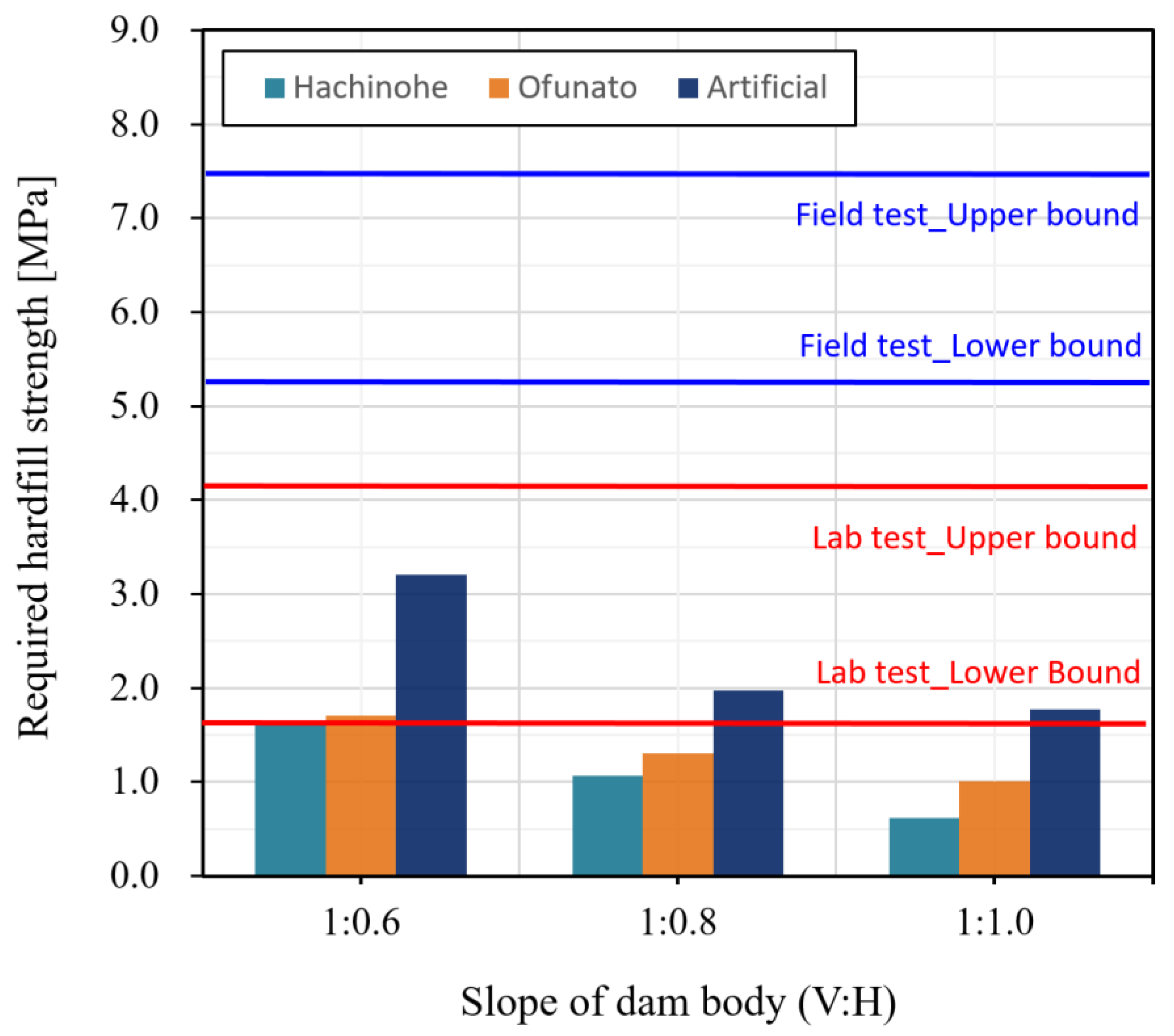
- The results of the finite element analysis on the hardfill dams modeled using the parameters determined based on the laboratory test results showed that the largest value of the maximum tensile stress of 0.1 MPa occurs in the hardfill dam body with a slope of 1:0.6 when the artificial wave is applied. The maximum tensile stress tended to decrease overall as the slope of the dam body was relaxed. Furthermore, it was shown that the overall strength range obtained for the indoor laboratory specimens and field compaction cores exceeded the required strength of the hardfill, thereby securing seismic stability (except for the hardfill dam with a 1:0.6 slope to which artificial wave was applied).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jia, J.; Lino, M.; Jin, F.; Zheng, C. The Cemented Material Dam: A New, Environmentally Friendly Type of Dam. Engineering 2016, 2, 490–497. [Google Scholar] [CrossRef]
- Kim, K.Y.; Park, H.G.; Jeon, J.S. Strength Characteristics of Cemented Sand and Gravel. J. Korean Geotech. Soc. 2005, 21, 61–71. (In Korean) [Google Scholar]
- Japan Dam Engineering Center. Engineering Manual for Design, Construction, and Quality Control of Trapezoidal CSG Dam; Japan Dam Engineering Center: Tokyo, Japan, 2012. (In Japan) [Google Scholar]
- Xia, B.; Ding, T.; Xiao, J. Life cycle assessment of concrete structures with reuse and recycling strategies: A novel framework and case study. Waste Manag. 2020, 105, 268–278. [Google Scholar] [CrossRef] [PubMed]
- Portland Cement Association. Guide for developing RCC Specifications and Commentary; Portland Cement Association: New York, NY, USA, 2000. [Google Scholar]
- U.S. Army Corps of Engineers. Engineering and Design Roller-Compacted Concrete; U.S. Army Corps of Engineers: Washington, DC, USA, 2006.
- Londe, P.; Lino, M. The faced symmetrical hardfill dam: A new concept for RCC. Int. Water Power Dam Constr. 1992, 44, 19–24. [Google Scholar]
- Toshio, H.; Tadahiko, F.; Hideaki, K.; Takashi, S. Design concept of trapezoid-shaped CSG dam. In Roller Compacted Concrete Dams; Routledge: London, UK, 2018; pp. 457–464. [Google Scholar]
- Cai, X.; Wu, Y.; Gui, X.; Ming, Y. Research review of the cement sand and gravel (CSG) dam. Front. Struct. Civ. Eng. 2012, 6, 19–24. [Google Scholar] [CrossRef]
- Chen, J.; Liu, P.; Xu, Q.; Li, J. Seismic analysis of hardfill dams considering spatial variability of material parameters. Eng. Struct. 2020, 211, 110439. [Google Scholar] [CrossRef]
- Yoon, J.S.; Park, W.Y.; Kim, K.T. Applicability analysis of Local Riverbed Aggregate for Hardfill Dam. Korean Soc. Civ. Eng. 2016, 10, 218–219. (In Korean) [Google Scholar]
- Guillemot, T.; Lino, M. Design and Construction Advantages of Hardfill Symmetrical Dams-Case Study: Safsaf Dam In Eastern Algeria. In Proceeding of the 6th International Symposium on Roller Compacted Concrete (RCC) Dams, Zaragoza, Algeria, 23–25 October 2012. [Google Scholar]
- Yuan, P.; He, Y.; Wang, Y. Study on seismic safety of Poshitougou flood intercepting dam. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 861, pp. 072–073. [Google Scholar] [CrossRef]
- Karimi, S.; Aghajani, H.F. A New Type of Cemented Sand-Gravel (CSG) Mixtures for Water-Tightening of Hardfill Dams. Res. Sq. Platf. LLC 2021. [Google Scholar] [CrossRef]
- Zheng, C. Progress on Cemented Material Dams in CHINA. In Proceedings of the International Symposium on the State-Of-The-Art Dam Construction Technology, Daejoen, Republic of Korea, 5–6 November 2015. [Google Scholar]
- Ayagh, A.G.; Mohammadian, A. Optimum characteristic compressive strength for cmds (case study: Dasht-e-palang dam). In Proceedings of the 2017 International Conference on Long-Term Behaviour and Environmentally Friendly Rehabilitation Technologies of Dams, Tehran, Iran, 17–19 October 2017; pp. 243–250. [Google Scholar] [CrossRef]
- Karimizad, N.; Teshnizi, E.S.; Mahdad, M.; Karimiazar, J. Investigating the design features of CSG dams. JOJ Sci. 2020, 3, 555588. [Google Scholar]
- Kim, K.Y. The Factors Affecting the Unconfined Compressive Strength of C.S.G Materials. J. Korean Geotech. Soc. 2006, 22, 33–45. (In Korean) [Google Scholar]
- Kim, K.Y.; Jeon, J.S.; Kim, Y.S. Laboratory Mix Design of C.S.G Method. J. Korean Geotech. Soc. 2006, 22, 27–37. (In Korean) [Google Scholar]
- Omae, S.; Sato, N.; Oomoto, I. Dynamic properties of CSG. In Proceedings of the International Symposium on Roller Compacted Concrete (RCC) Dams, Madrid, Spain, 17–19 November 2003; pp. 511–518. [Google Scholar]
- Liu, Z.; Jia, J.; Feng, W.; Ma, F.; Zheng, C. Shear Strength of Cemented Sand Gravel and Rock Materials. Sains Malays. 2017, 46, 2101–2108. [Google Scholar] [CrossRef]
- Fujisawa, T.; Nakamura, A.; Kawasaki, H.; Hirayama, D.; Yamaguchi, Y.; Sasaki, T. Material Properties of CSG for the Seismic Design of Trapezoid-Shaped CSG Dam. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; pp. 292–296. [Google Scholar]
- Peng, Y.; Yuan, Y. Analysis on the Dynamic Properties of Hardfill Materials. J. Appl. Sci. Eng. Innov. 2014, 1, 54–58. [Google Scholar]
- Ren, H.; Cai, X.; Wu, Y.; Jing, P.; Guo, W. A Study of Strength Parameter Evolution and a Statistical Damage Constitutive Model of Cemented Sand and Gravel. Materials 2023, 16, 542. [Google Scholar] [CrossRef] [PubMed]
- Farshbaf Aghajani, H.; Soltani-Jigheh, H.; Salimi, M.; Karimi, S.; Estekanchi, V.; Ahari, R.A. Investigating the strength, hydraulic conductivity, and durability of the CSG (cemented sand-gravel) check dams: A case study in Iran. SN Appl. Sci. 2022, 4, 169. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, J.; Guo, L.; Wang, J.; Shen, W. Research on profile design criteria of 100 m CSG dams. Case Stud. Constr. Mater. 2022, 16, e01137. [Google Scholar] [CrossRef]
- Peng, Y. Study on Structural Characteristics of CSG Dam. Int. J. Sci. 2014, 1, 70–74. [Google Scholar]
- Zafeiratos, E.; Psycharis, I.; Papanicolaou, P. Dynamic behavior of faced symmetrical hardfill dams. In Proceedings of the 11th ICOLD European Club Symposium, Crete, Greece, 2–4 October 2019. [Google Scholar]
- Standard No. ASTM D698-12:2021; Standard Test Method for Laboratory Compaction Characteristics of Soil Using Standard Effort (12,400 ft-lbf/ft3 (600 kN-m/m3)). American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2021.
- Standard No. ASTM D1557-12:2021; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Modified Effort (56,000 ft-lbf/ft3 (2700 kN-m/m3)). American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2021.
- Standard No. KS F 2314:2018; Standard Test Method for Unconfined Compression Test of Soils. Korean Standards Association: Seoul, South Korea, 2013. (In Korean)
- Standard No. KS F 2311:2016; Standard Test Method for Density of Soil in Place by the Sand Cone Method. Korean Standards Association: Seoul, South Korea, 2016. (In Korean)
- Standard No. ASTM C42/C42M:2020; Standard Test Method for Obtaining and Testing Drilled Cores and Sawed Beams of Concrete. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2020.
- Standard No. ASTM C39/C39M:2021; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2021.





| Specific Gravity | Fineness (cm2/g) | Setting Time (min) | Compressive Strength (MPa) | ||
|---|---|---|---|---|---|
| 3.17 | 3475 | Initial | Final | 7 d | 28 d |
| 205 | 295 | 44.4 | 59.3 | ||
| Aggregate | Cement Content per Unit Water Content (kg/m3) | Water Content per Unit Water Content (kg/m3) |
|---|---|---|
| Upper-limit (fine) PSD | 80 | 70, 85, 100 |
| Lower-limit (coarse) PSD | 80 | 70, 85, 100 |
| Compaction energy of vibration roller per unit time (E0p, J/min) | where, a: vibrating width (=0.00131 m), W: weight of vibration roller (=10.6 t), F: Average vibrating force (17,900 kgf) and f: Frequency (1920 Hz) |
| Compaction energy in field | where, n: number of roller passes (=6) and tp: average time per compaction (=0.06 min) |
| Compaction energy of hammer drill per unit time (E0l, J/min) | E0l = [single impact energy × number of impact per min] = 64,500 J/min |
| Compaction energy for large specimen | where, L: number of compaction layer (=4) and tl: average compaction time per layer |
| Compaction time per layer for large specimen | |
| Compaction energy of vibration roller per unit time (E0p, J/min) | where, a: vibrating width (=0.00131 m), W: weight of vibration roller (=10.6 t), F: Average vibrating force (17,900 kgf) and f: Frequency (1920 Hz) |
| Material (Mixing Ratio) | |
| Aggregate | PSD between upper- and lower-limit PSD with 80 mm max. particle size |
| Cement content per unit volume | 80 kg/m3 |
| Water content per unit volume | 70, 85, 100 (kg/m3) |
| Hardfill Test Construction | |
| Size | One fill lift with a floor area of 19 m width and 44 m length, which was partitioned into six parts for a total of six test cases |
| Lift thickness | 50, 75 (cm) |
| Compaction | Eight passes with a vibration roller (six vibrated passes and two non-vibrated passes) |
| Unit Weight (kN/m3) | Cohesion (kPa) | Friction Angle (°) | Elastic Modulus (MPa) | Poisson’s Ratio | P-Wave Velocity (m/s) | S-Wave Velocity (m/s) | Shear Modulus (MPa) | Dashpot Coefficient | ||
|---|---|---|---|---|---|---|---|---|---|---|
| CP (=ρVp) | CS (=ρVs) | |||||||||
| Soil | 18.0 | 5 | 25 | 20 | 0.38 | 450 | 63.2 | 7.2 | 810 | 114 |
| Soft rock | 24.0 | 200 | 34 | 1500 | 0.27 | 2000 | 496.1 | 590.6 | 4800 | 1191 |
| Moderate rock | 25.0 | 350 | 37 | 4000 | 0.24 | 2300 | 803.2 | 1612.9 | 5750 | 2008 |
| Hard rock | 26.0 | 2000 | 44 | 8000 | 0.20 | 3000 | 1132.3 | 3333.3 | 7800 | 2944 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Choi, W.; Kim, Y.; Shin, J.; Kim, B. Investigation of Compressive Strength Characteristics of Hardfill Material and Seismic Stability of Hardfill Dams. Appl. Sci. 2023, 13, 2492. https://doi.org/10.3390/app13042492
Kim S, Choi W, Kim Y, Shin J, Kim B. Investigation of Compressive Strength Characteristics of Hardfill Material and Seismic Stability of Hardfill Dams. Applied Sciences. 2023; 13(4):2492. https://doi.org/10.3390/app13042492
Chicago/Turabian StyleKim, Soogeun, Wonhyuk Choi, Yunhee Kim, Jaewoo Shin, and Bumjoo Kim. 2023. "Investigation of Compressive Strength Characteristics of Hardfill Material and Seismic Stability of Hardfill Dams" Applied Sciences 13, no. 4: 2492. https://doi.org/10.3390/app13042492
APA StyleKim, S., Choi, W., Kim, Y., Shin, J., & Kim, B. (2023). Investigation of Compressive Strength Characteristics of Hardfill Material and Seismic Stability of Hardfill Dams. Applied Sciences, 13(4), 2492. https://doi.org/10.3390/app13042492






