Consistency of Water Vapour Pressure and Specific Heat Capacity Values for Modelling Clay-Based Engineered Barriers
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Reference Information from the Literature
2.1.1. Saturated Water Vapour Pressure
2.1.2. Specific Heat Capacity of Water
2.2. Model Analysis and Selection for Saturated Water Vapour Pressure
2.3. Thermodynamic Basis for Analysing the Consistency of the Formulations
3. Results and Discussion
3.1. Saturated Water Vapour Pressure
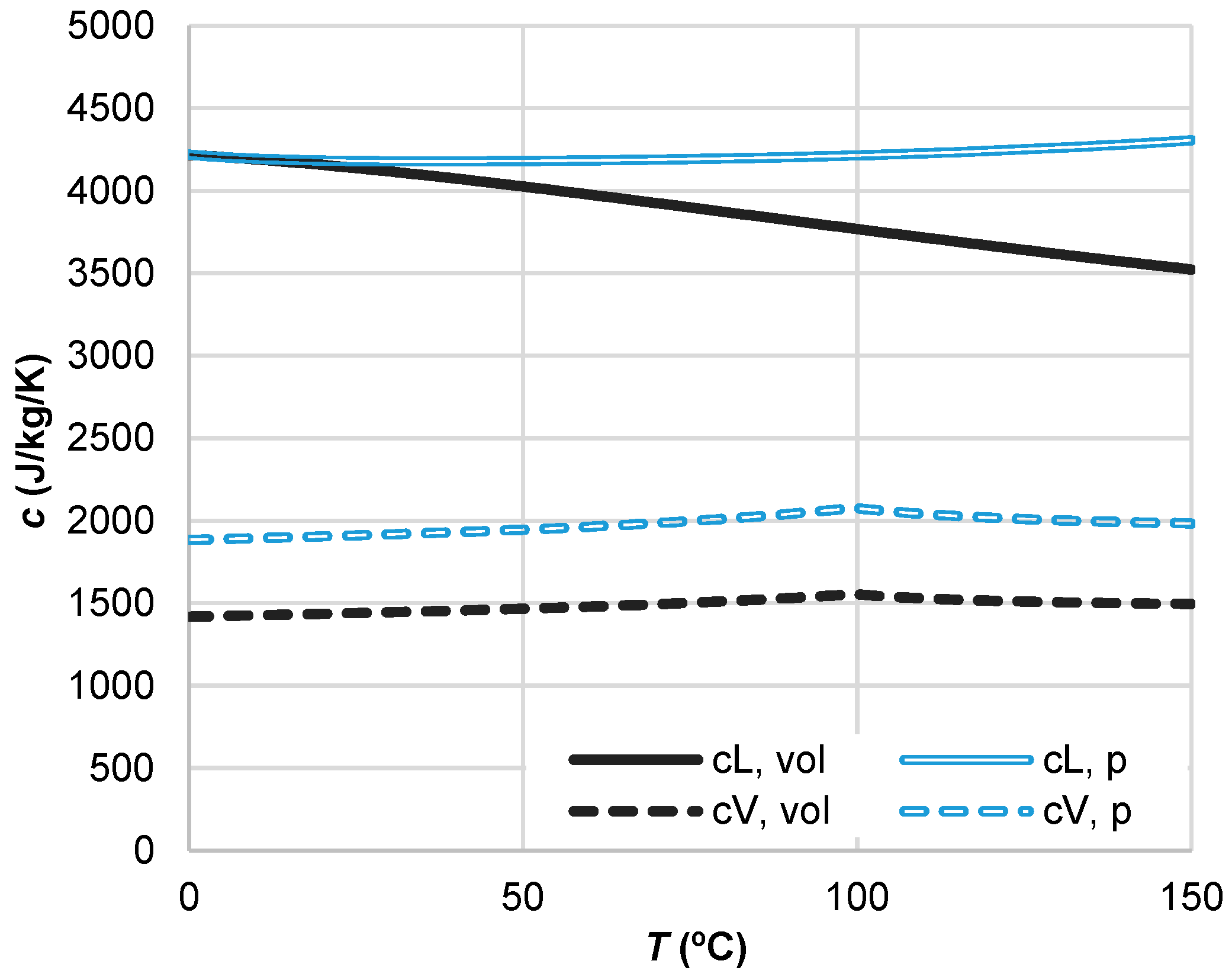
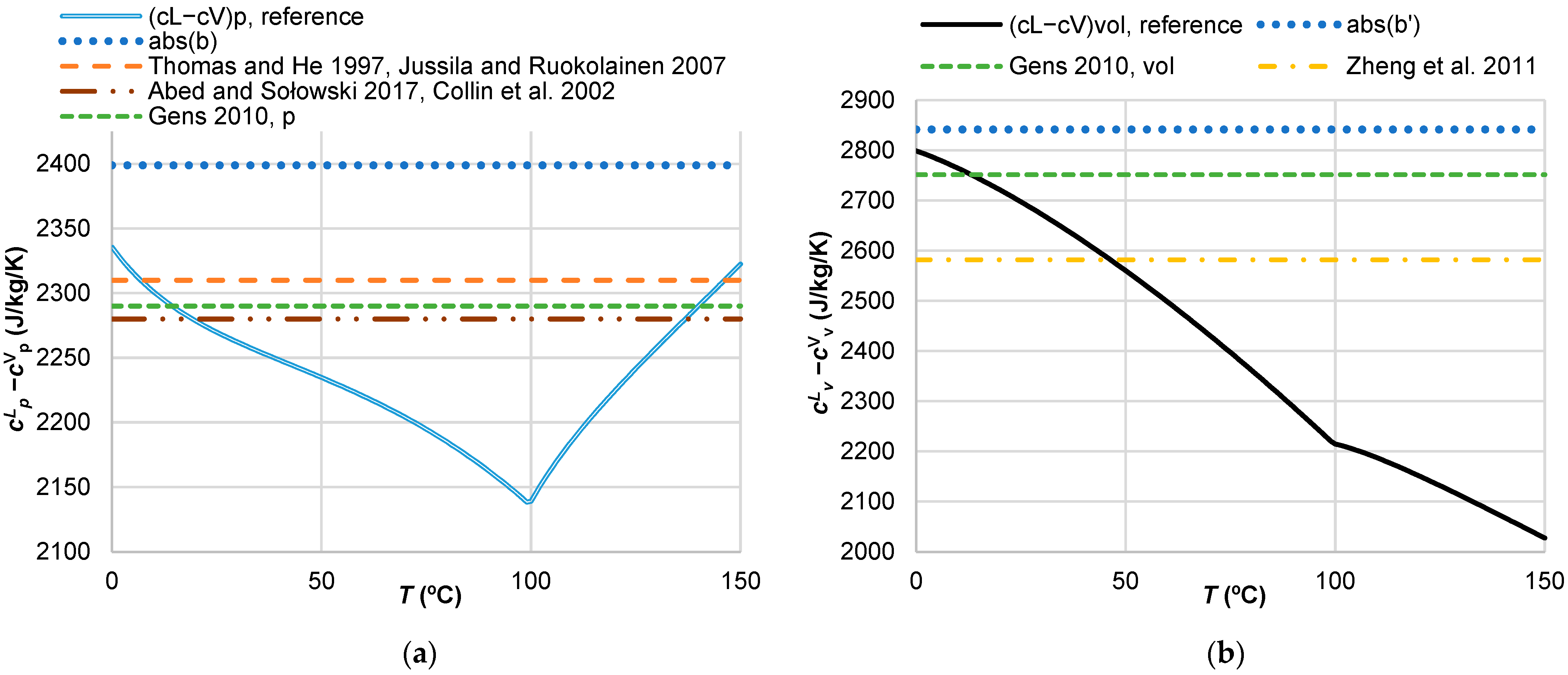
3.2. Vapour and Liquid Water Heat Capacities
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johnson, L.H.; Niemeyer, M.; Klubertanz, G.; Siegel, P.; Gribi, P. Calculations of the Temperature Evolution of a Repository for Spent Fuel, Vitrified High-Level Waste and Intermediate Level Waste in Opalinus Clay; Technical Report 01-04; Nagra: Wettingen, Switzerland, 2002. [Google Scholar]
- Wagner, W.; Pruss, A. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef] [Green Version]
- Lemmon, E.W. Vapor pressure and other saturation properties of water. In CRC Handbook of Chemistry and Physics, 97th ed.; Haynes, W.M., Ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wagner, W.; Pruss, A. International equations for the saturation properties of ordinary water substance—Revised according to the international temperature scale of 1990. J. Phys. Chem. Ref. Data 1993, 22, 783–787. [Google Scholar] [CrossRef] [Green Version]
- Buck, A.L. New Equations for Computing Vapor Pressure and Enhancement Factor. J. Appl. Meteorol. Climatol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Huang, J. A Simple Accurate Formula for Calculating Saturation Vapor Pressure of Water and Ice. J. Appl. Meteorol. Climatol. 2018, 57, 1265–1272. [Google Scholar] [CrossRef]
- Thomas, H.R.; He, Y. A coupled heat-moisture transfer theory for deformable unsaturated soil and its algorithmic implementation. Int. J. Numer. Methods Eng. 1997, 40, 3421–3441. [Google Scholar] [CrossRef]
- Gens, A.; Sanchez, M.; Guimaraes, L.D.N.; Alonso, E.E.; Lloret, A.; Olivella, S.; Villar, M.V.; Huertas, F. A full-scale in situ heating test for high-level nuclear waste disposal: Observations, analysis and interpretation. Geotechnique 2009, 59, 377–399. [Google Scholar] [CrossRef]
- Dupray, F.; François, B.; Laloui, L. Analysis of the FEBEX multi-barrier system including thermoplasticity of unsaturated bentonite. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 399–422. [Google Scholar] [CrossRef]
- Nowak, T.; Kunz, H.; Dixon, D.; Wang, W.; Görke, U.-J.; Kolditz, O. Coupled 3-D thermo-hydro-mechanical analysis of geotechnological in situ tests. Int. J. Rock Mech. Min. Sci. 2011, 48, 1–15. [Google Scholar] [CrossRef]
- Wang, X.; Shao, H.; Wang, W.; Hesser, J.; Kolditz, O. Numerical modeling of heating and hydration experiments on bentonite pellets. Eng. Geol. 2015, 198, 94–106. [Google Scholar] [CrossRef]
- Abed, A.A.; Sołowski, W.T. A study on how to couple thermo-hydro-mechanical behaviour of unsaturated soils: Physical equations, numerical implementation and examples. Comput. Geotech. 2017, 92, 132–155. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. Thermophysical Properties of Fluid Systems. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. [Google Scholar] [CrossRef]
- Collin, F.; Li, X.L.; Radu, J.P.; Charlier, R. Thermo-hydro-mechanical coupling in clay barriers. Eng. Geol. 2002, 64, 179–193. [Google Scholar] [CrossRef] [Green Version]
- Jussila, P.; Ruokolainen, J. Thermomechanics of porous media—II: Thermo-hydro-mechanical model for compacted bentonite. Transp. Porous Media 2007, 67, 275–296. [Google Scholar] [CrossRef]
- Gens, A. Soil-environment interactions in geotechnical engineering. Geotechnique 2010, 60, 3–74. [Google Scholar] [CrossRef]
- Zheng, L.; Samper, J.; Montenegro, L. A coupled THC model of the FEBEX in situ test with bentonite swelling and chemical and thermal osmosis. J. Contam. Hydrol. 2011, 126, 45–60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akaike, H. Information Theory as an Extension of the Maximum Likelihood Principle. In Second International Symposium on Information Theory; Petrov, B.N., Csaki, F., Eds.; Akademiai Kiado: Budapest, Hungary, 1973. [Google Scholar]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Çengel, Y.A.; Boles, M.A. Thermodynamics: An Engineering Approach; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Burnham, K.; Anderson, D.R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Pinder, G.F.; Shapiro, A. Physics of Flow in Geothermal Systems. Geol. Soc. Am. Spec. Pap. 1982, 189, 25–30. [Google Scholar] [CrossRef]
- Navarro Gámir, V. Modelo del Comportamiento Mecánico e Hidráulico de Suelos No Saturados en Condiciones No Isotermas. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 1998. [Google Scholar]
- Vestfálová, M.; Šafařík, P. Dependence of the isobaric specific heat capacity of water vapor on the pressure and temperature. EPJ Web Conf. 2016, 114, 02133. [Google Scholar] [CrossRef] [Green Version]
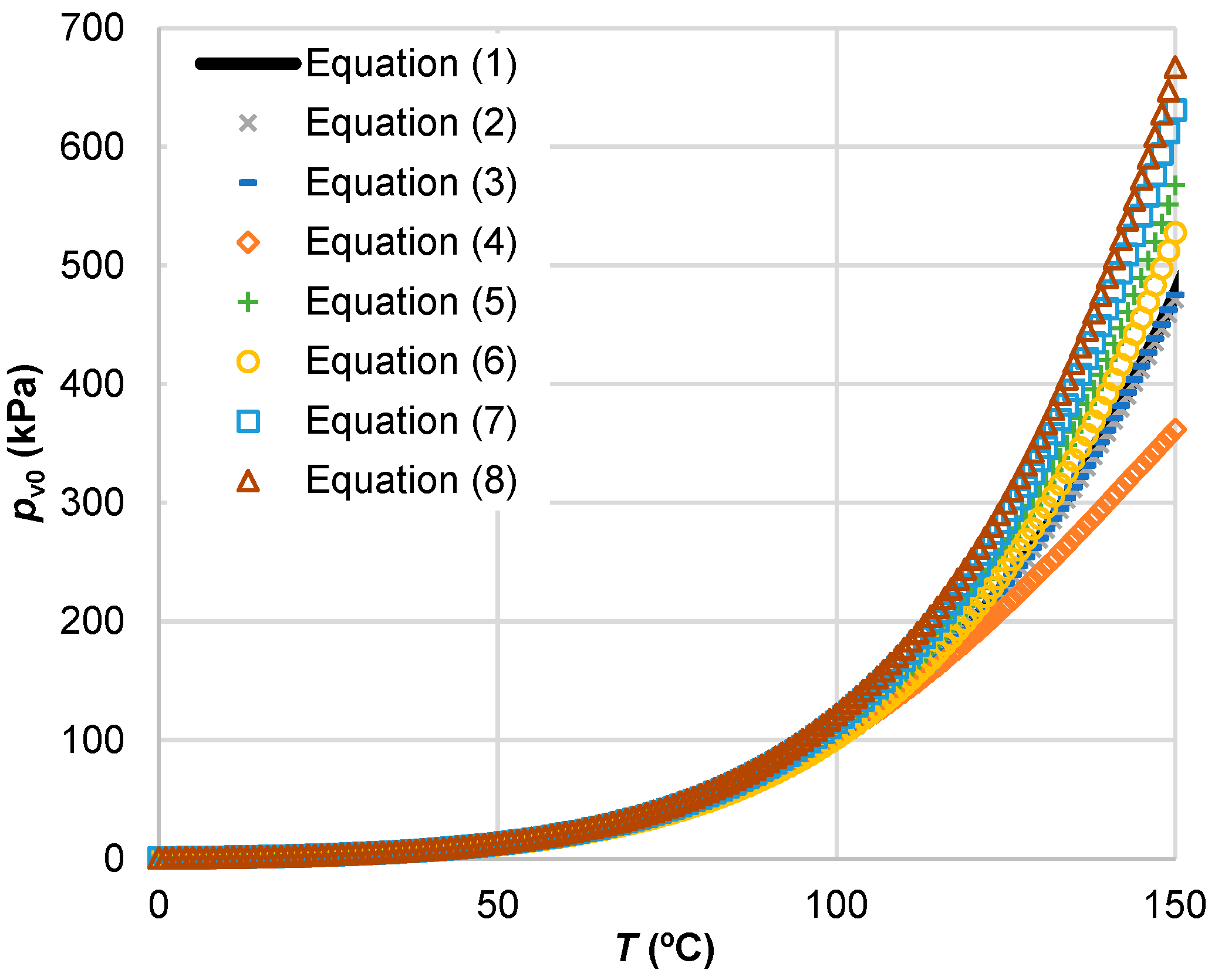





| Reference | Expression | Coefficients and Auxiliary Expressions | Equation No. |
|---|---|---|---|
| Wagner and Pruss [4] | , . | (1) | |
| Buck [5] | (2) | ||
| Huang [6] | , | (3) | |
| Thomas and He [7] | (4) | ||
| Gens et al. [8] | (5) | ||
| Dupray et al. [9] | (6) | ||
| Nowak et al. [10], Wang et al. [11] | (7) | ||
| Abed and Sołowski [12] | (8) |
| Reference | cL (J/kg/K) | cV (J/kg/K) |
|---|---|---|
| Thomas and He [7] | 4180 p | 1870 p |
| Collin et al. [14] | 4180 p | 1900 p |
| Jussila and Ruokolainen [15] | 4180 p | 1870 p |
| Gens [16] | 4180 p, vol | 1890 p, 1428 vol |
| Zheng et al. [17] | 4202 ns | 1620 ns |
| Abed and Sołowski [12] | 4180 ns | 1900 ns |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asensio, L.; Urraca, G.; Navarro, V. Consistency of Water Vapour Pressure and Specific Heat Capacity Values for Modelling Clay-Based Engineered Barriers. Appl. Sci. 2023, 13, 3361. https://doi.org/10.3390/app13053361
Asensio L, Urraca G, Navarro V. Consistency of Water Vapour Pressure and Specific Heat Capacity Values for Modelling Clay-Based Engineered Barriers. Applied Sciences. 2023; 13(5):3361. https://doi.org/10.3390/app13053361
Chicago/Turabian StyleAsensio, Laura, Gema Urraca, and Vicente Navarro. 2023. "Consistency of Water Vapour Pressure and Specific Heat Capacity Values for Modelling Clay-Based Engineered Barriers" Applied Sciences 13, no. 5: 3361. https://doi.org/10.3390/app13053361
APA StyleAsensio, L., Urraca, G., & Navarro, V. (2023). Consistency of Water Vapour Pressure and Specific Heat Capacity Values for Modelling Clay-Based Engineered Barriers. Applied Sciences, 13(5), 3361. https://doi.org/10.3390/app13053361







