Optimal Design and Experiment of Corn-Overlapped Strip Fertilizer Spreader
Abstract
:1. Introduction
2. Materials and Methods
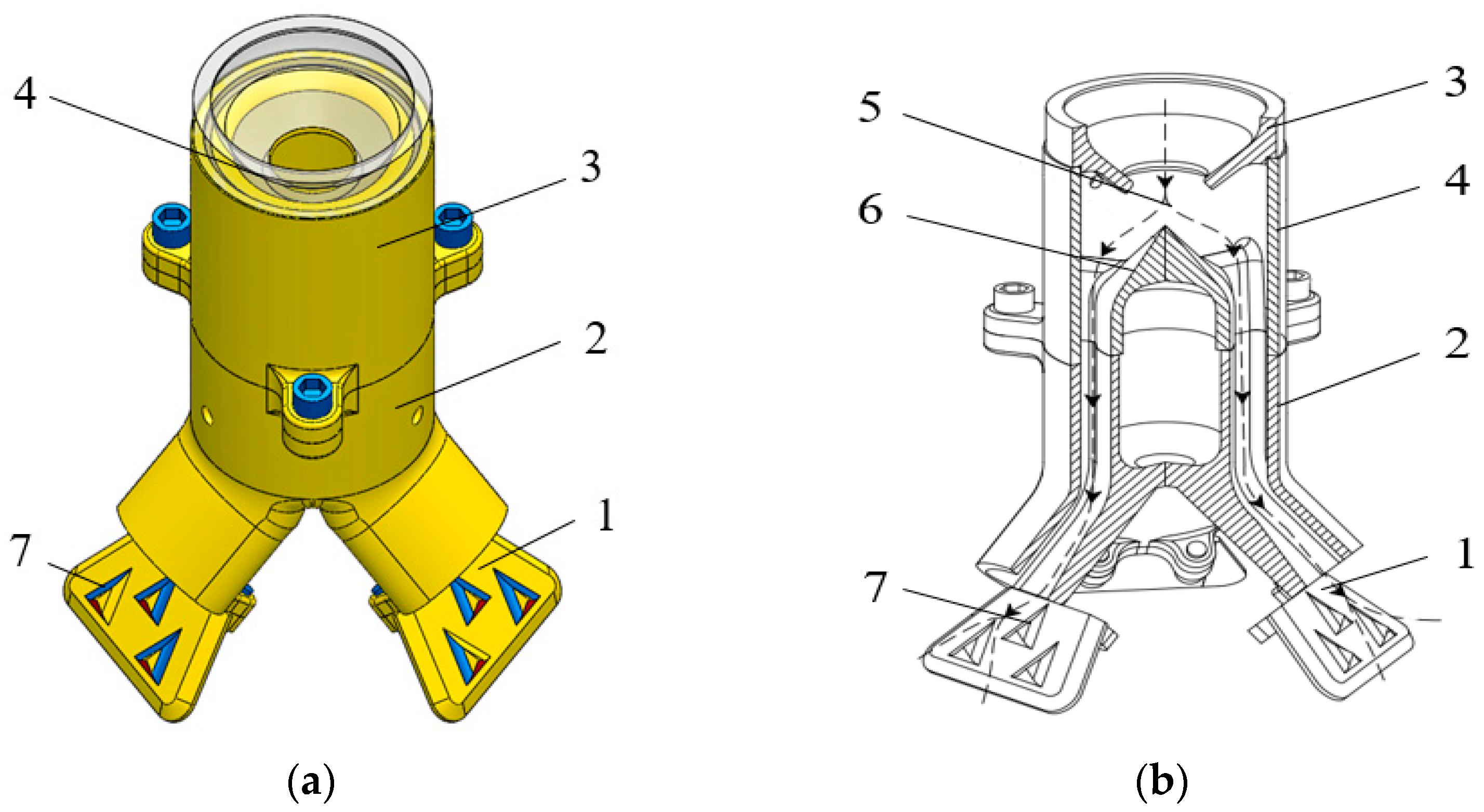
2.1. Operating Principle of the Corn-Overlapped Strip Fertilizer Spreader
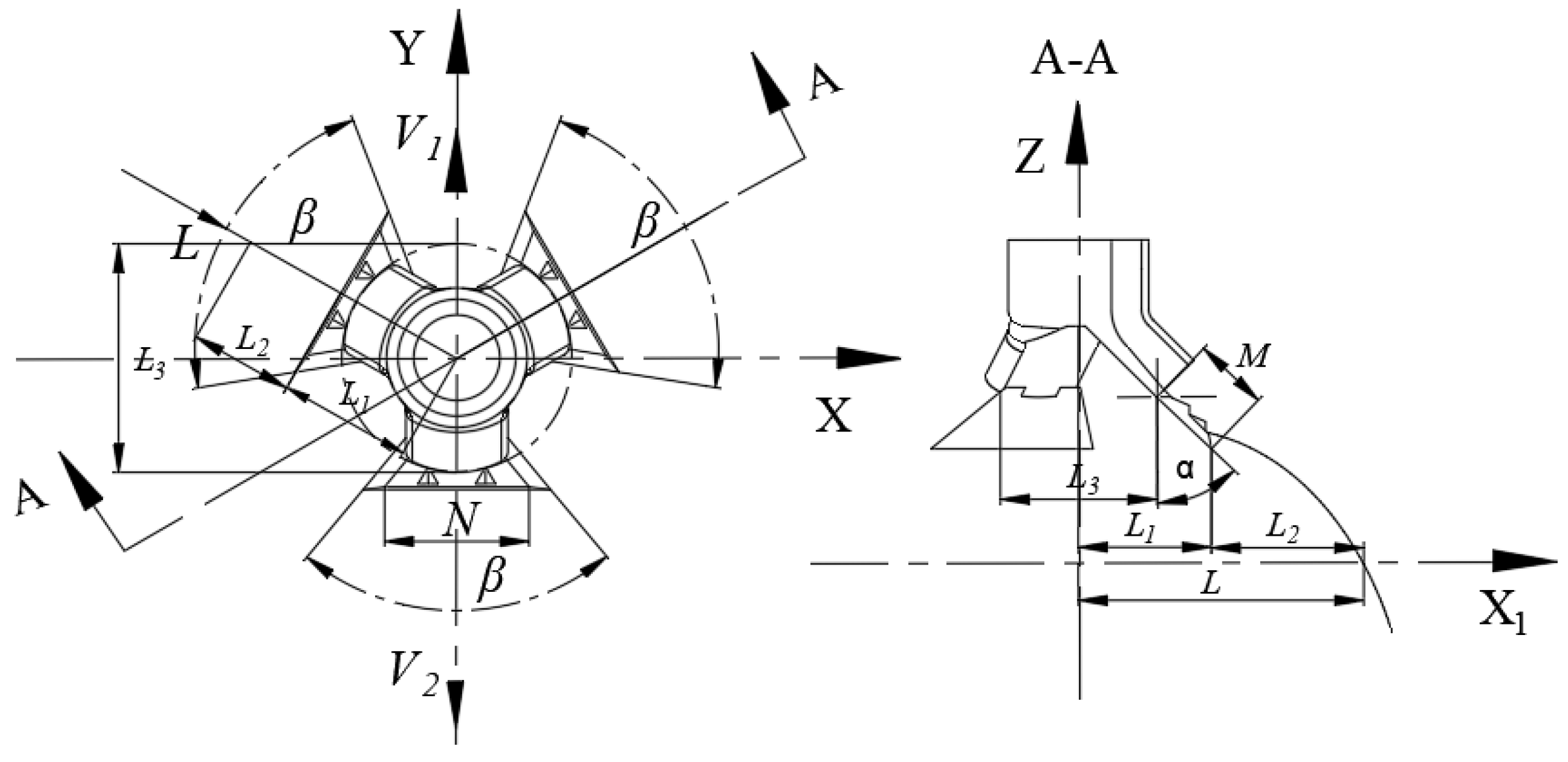
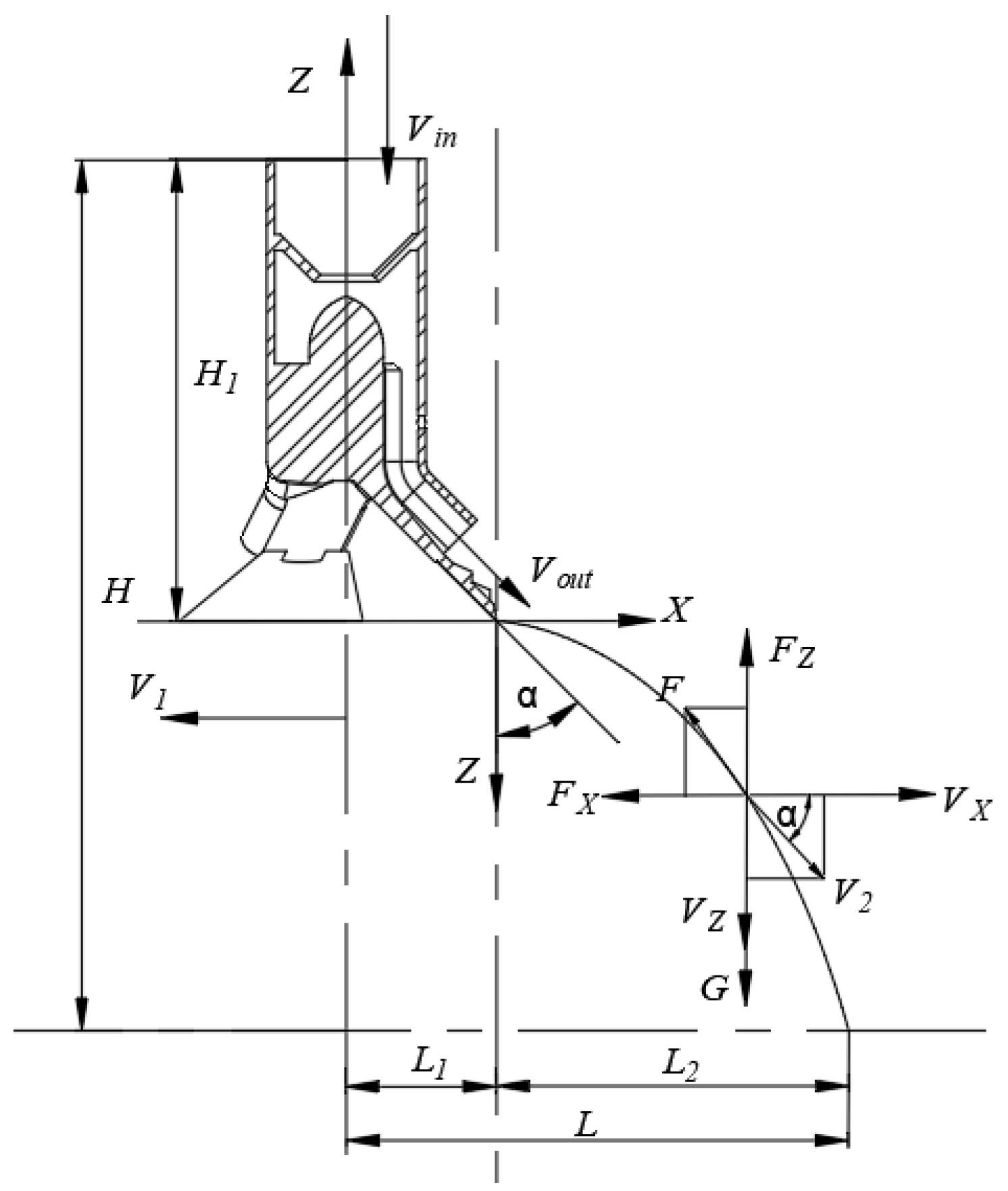
2.2. Analysis of Fertilizer Spreading Motion
2.2.1. Analysis of the Spatial Dispersion Motion of Fertilizer Particles
2.2.2. Analysis of the Vertical Throwing Motion of Fertilizer Particles
3. Simulation Test of Corn-Overlapped Strip Fertilizer Spreader
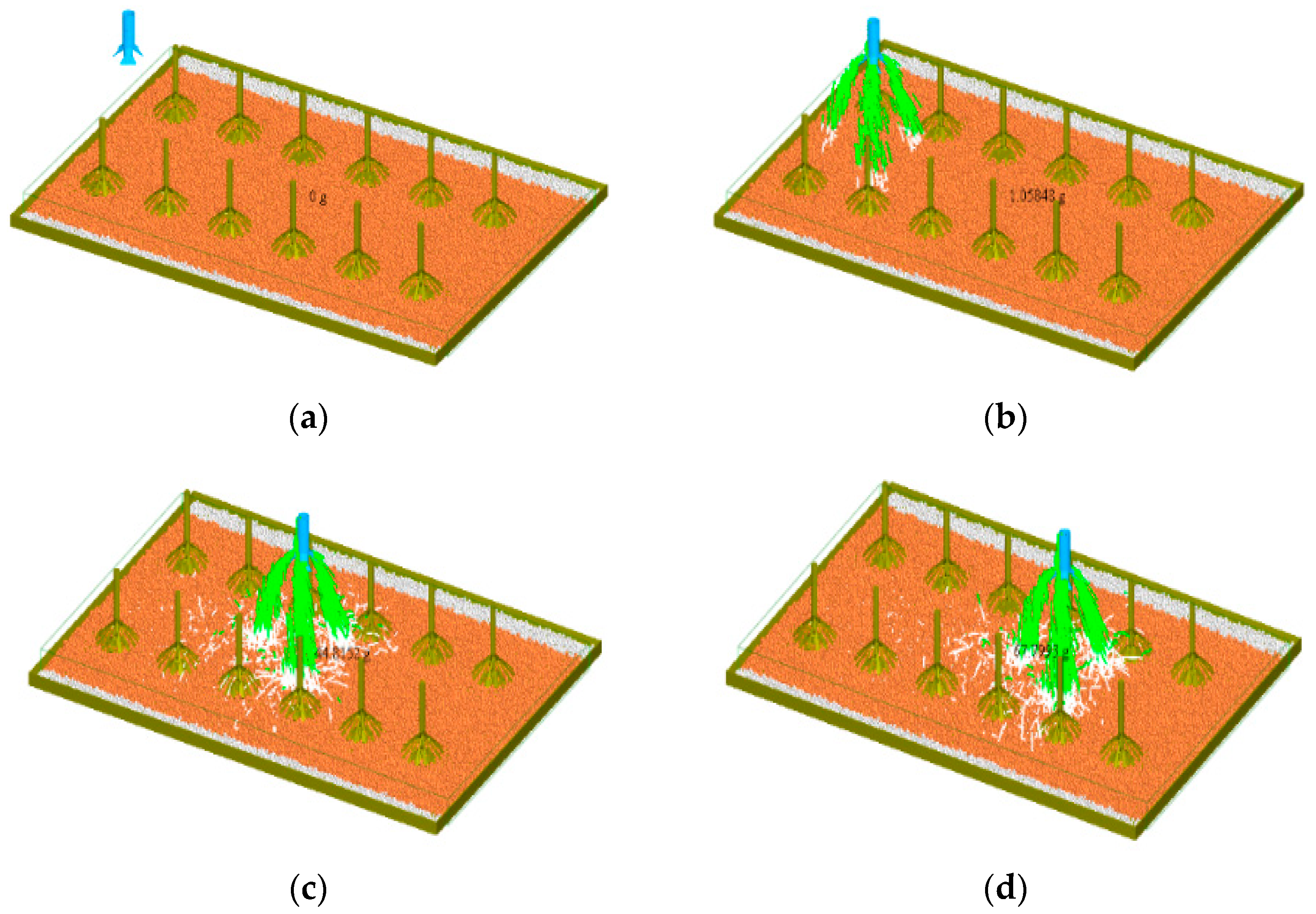
3.1. Simulation Test Model and Parameters
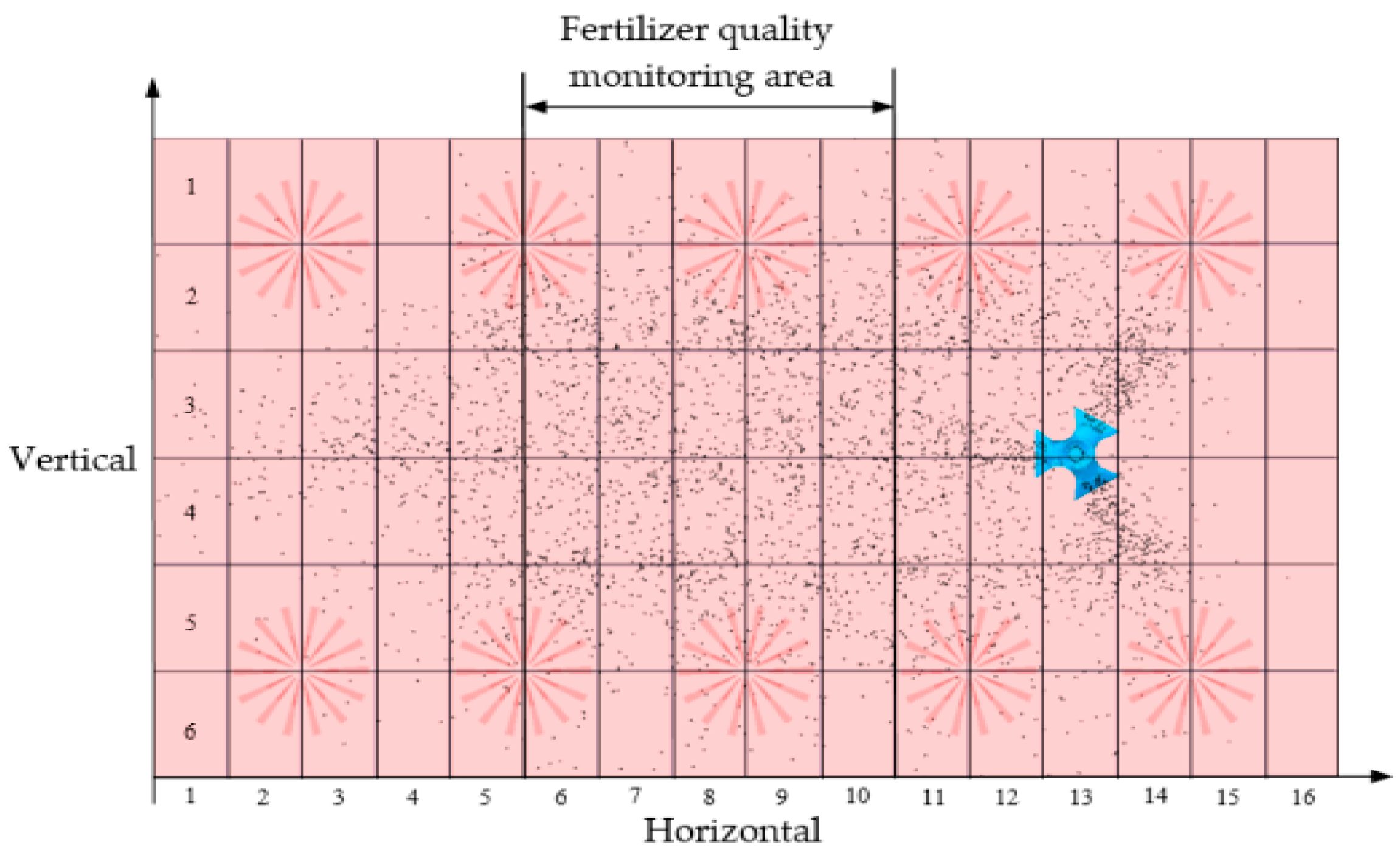
3.2. Simulation Test Model and Test Index
3.3. Parameter Optimization Test
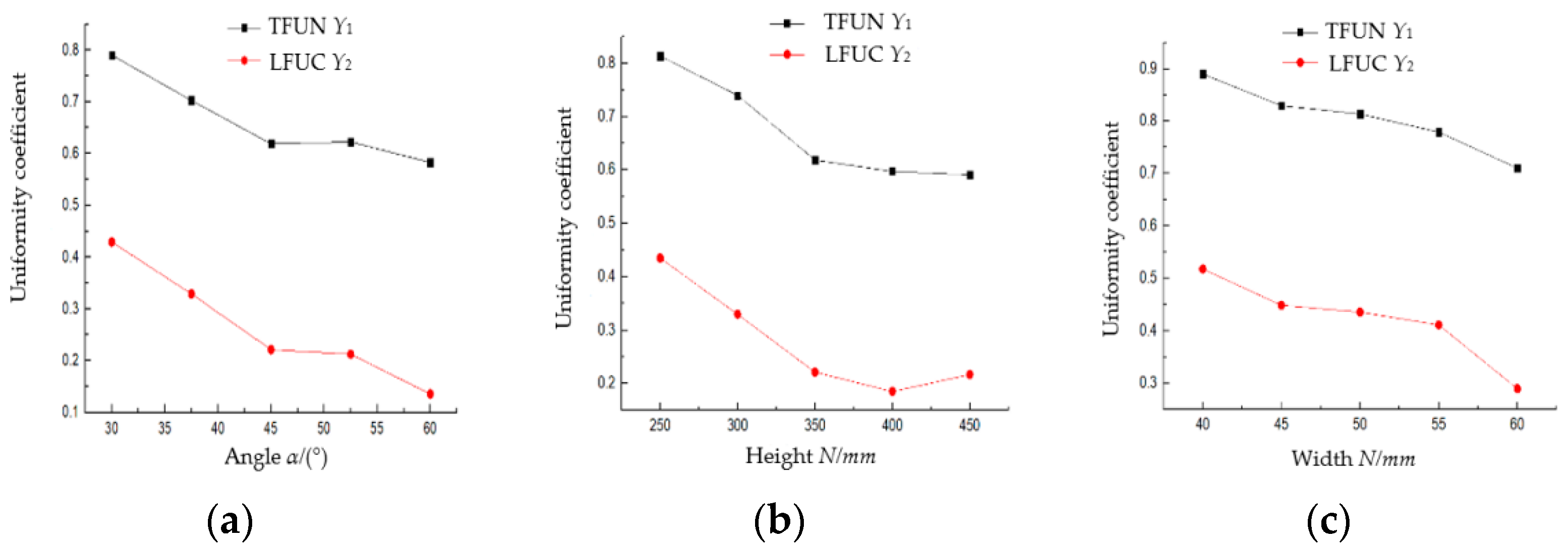
3.3.1. Single-Factor Simulation Test
3.3.2. Response Surface Simulation Test
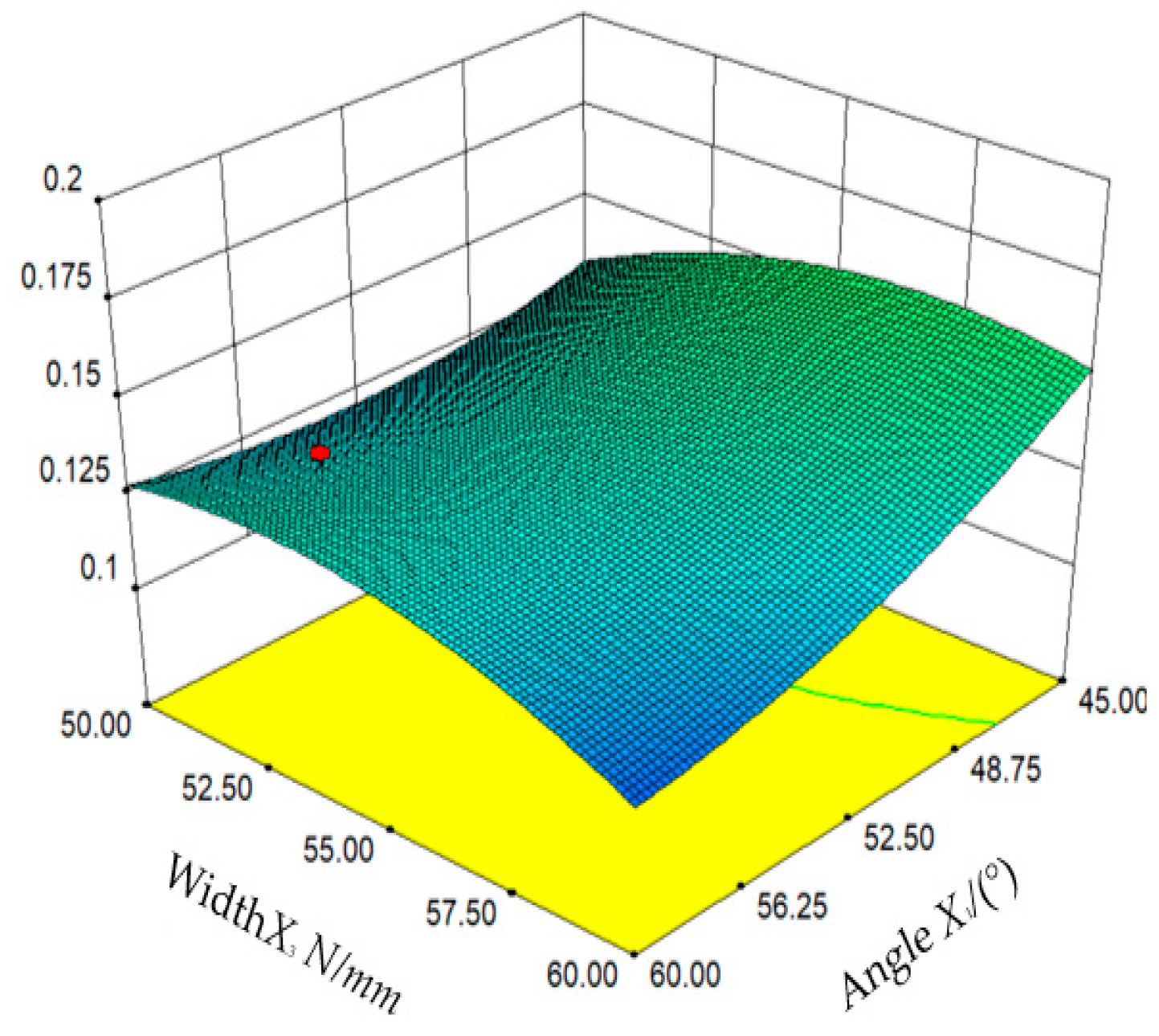
3.3.3. Response Surface Analysis
3.3.4. Parameter Optimization
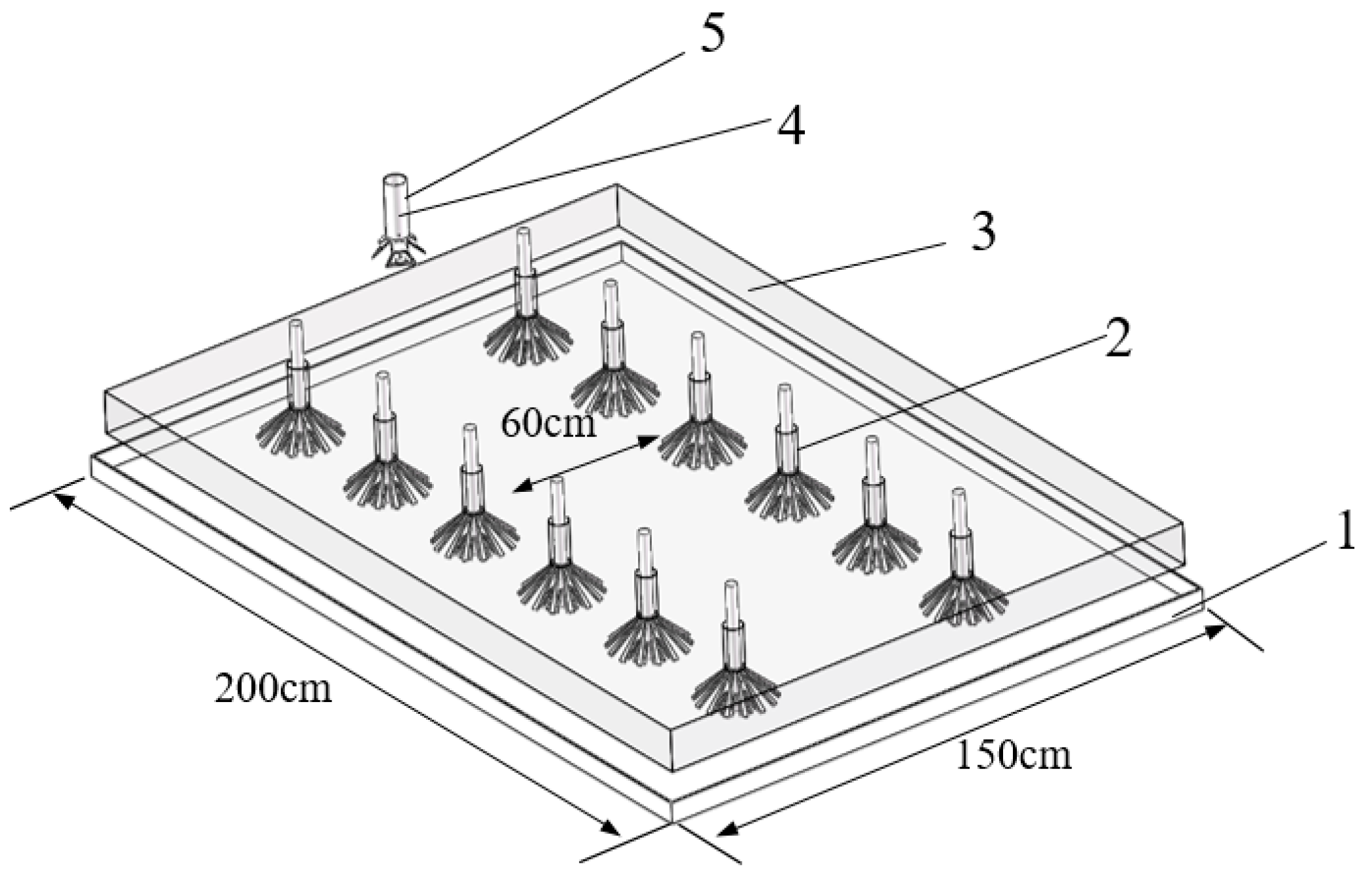
4. Validation Test
5. Conclusions
- (1)
- In this study, we designed a corn-overlapped strip fertilizer spreading device in without an external power source. By configuring a passive overlapping spreading method with a three-branch split chamber structure, uniform spreading of fertilizer in strips was achieved. Based on the theoretical analysis of the fertilizer particle motion model, the main factors affecting the distribution pattern of fertilizers were angle α, width N, and height H.
- (2)
- The single-factor ternary orthogonal rotational combination response surface simulation test was carried out with angle α, width N, and height H as test factors and the transversal fertilizer uniformity coefficient and longitudinal fertilizer uniformity coefficient as test indicators. The regression model was established using Design-expert8.0.6 software to derive the variation relationship of the test factors on the test indexes. The test results showed that the optimized transversal fertilizer uniformity coefficient and longitudinal fertilizer uniformity coefficient were less than 0.15% when the pendulum angle = 52°, height = 400 mm, and width = 50 mm, which were under the optimization criterion.
- (3)
- A verification test was carried out under the optimal combination of parameters for the simulation tests with the simulation conditions as the standard. The test results were consistent with the simulation results within the error range, and the deviation values of the transversal fertilizer uniformity coefficient and longitudinal fertilizer uniformity coefficient were 8.11% and 9.01%, respectively, which was in line with the ± 10% deviation range. The corn-overlapped strip fertilizer spreader was able to complete the fertilizer spreading operation smoothly.
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, Y.; Zhao, X.; Li, C.; Dou, H.; Li, S.; Wang, X. Research statusand analysis of corn topdressing mechan-ical fertilization technology. Agric. Mech. Res. 2021, 43, 1–9. [Google Scholar]
- Tan, S.; Xie, D.; Ni, J.; Chen, F.; Ni, C.; Shao, J.; Zhu, D.; Wang, S.; Lei, P.; Zhao, G.; et al. Characteristics and Influencing Factors of Chemical Fertilizer and Pesticide Applications by Farmers in Hilly and Mountainous Areas of Southwest, China. Ecol. Indic. 2022, 143, 109346. [Google Scholar] [CrossRef]
- Chen, A.; Tian, J.; Wu, H.; Zhang, H.; Li, B. Development status of organic fertilizers and their supporting fertiliza-tion machinery. Use Maint. Agric. Mach. 2022, 9, 1–5. [Google Scholar]
- Gao, J.; Peng, C.; Shi, Q. Study on the High Chemical Fertilizers Consumption and Fertilization Behavior of Small Rural Househo in China: Discovery from 1995~2016 National Fixed Point Survey Data. Manag. World 2019, 35, 120–132. [Google Scholar]
- Zhao, J.; Wang, X.; Tian, H.; Lu, Y.; Guo, C.; Liu, H. A Fertilizer Discharge Detection System Based on Point Cloud Data and an Efficient Volume Conversion Algorithm. Comput. Electron. Agric. 2021, 185, 106131. [Google Scholar] [CrossRef]
- Bu, H.; Yu, S.; Dong, W.; Zhang, L.; Xia, Y. Analysis of the Effect of Bivariate Fertilizer Discharger Control Sequence on Fertilizer Discharge Performance. Agriculture 2022, 12, 1927. [Google Scholar] [CrossRef]
- Zeng, Z.; Ma, X.; Cao, X.; Li, Z.; Wang, X. Application status and prospect of discrete element method in agricultural engineering research. J. Agric. Mach. 2021, 52, 1–20. [Google Scholar]
- Liu, H.; Du, C.; Yin, L.; Zhang, G. Study on the shape and control of the side-throwing jet of organic fertilizer on an inclined opposed disk. J. Agric. Mach. 2022, 53, 168–177. [Google Scholar]
- Liu, Z.; Wang, Q.; Li, H.; He, J.; Lu, C.; Yu, C. Analysis and test of fertilizer application path of pneumatic seed and fertilizer hole application device coupled with CFD-DEM. J. Agric. Eng. 2019, 35, 18–25. [Google Scholar]
- Song, C.; Zhou, Z.; Wang, G.; Wang, X.; Zang, Y. Optimization of the structural parameters of the sheaves of the fertiliser UAV sheaves. J. Agric. Eng. 2021, 37, 1–10. [Google Scholar]
- Liu, X.; Lü, Q.; Li, G.; Wang, J.; Yan, D.; Yang, L.; Liu, E. Design Optimization and Experimental Verification of Spiral Cone Centrifugal Fertilizer Apparatus Based on the Discrete Element Method. Processes 2023, 11, 199. [Google Scholar] [CrossRef]
- Ding, S.; Bai, L.; Yao, Y.; Yue, B.; Fu, Z.; Zheng, Z.; Huang, Y. Discrete Element Modelling (DEM) of Fertilizer Dual-Banding with Adjustable Rates. Comput. Electron. Agric. 2018, 152, 32–39. [Google Scholar] [CrossRef]
- Wang, J.; Qi, X.; Xu, C.; Wang, Z.; Jiang, Y.; Tang, H. Design Evaluation and Performance Analysis of the Inside-Filling Air-Assisted High-Speed Precision Maize Seed-Metering Device. Sustainability 2021, 13, 5483. [Google Scholar] [CrossRef]
- Shaikh, S.A.; Li, Y.; Ma, Z.; Chandio, F.A.; Tunio, M.H.; Liang, Z.; Solangi, K.A. Discrete Element Method (DEM) Simulation of Single Grouser Shoe-Soil Interaction at Varied Moisture Contents. Comput. Electron. Agric. 2021, 191, 106538. [Google Scholar] [CrossRef]
- Landry, H.; Laguë, C.; Roberge, M. Discrete Element Representation of Manure Products. Comput. Electron. Agric. 2006, 51, 17–34. [Google Scholar] [CrossRef]
- Lv, J.; Sun, Y.; Li, J.; Li, Z.; Liu, Z. Design and test of vertical organic fertilizer spiral spreading device. J. Agric. Eng. 2020, 36, 19–28. [Google Scholar]
- Zinkevičienė, R.; Jotautienė, E.; Jasinskas, A.; Kriaučiūnienė, Z.; Lekavičienė, K.; Naujokienė, V.; Šarauskis, E. Determination of Properties of Loose and Granulated Organic Fertilizers and Qualitative Assessment of Fertilizer Spreading. Sustainability 2022, 14, 4355. [Google Scholar] [CrossRef]
- Dang, Y.; Yang, G.; Wang, J.; Zhou, Z.; Xu, Z. A Decision-Making Capability Optimization Scheme of Control Combination and PID Controller Parameters for Bivariate Fertilizer Applicator Improved by Using EDEM. Agriculture 2022, 12, 2100. [Google Scholar] [CrossRef]
- Yang, L.; Chen, L.; Zhang, J.; Liu, H.; Sun, Z.; Sun, H.; Zheng, L. Fertilizer Sowing Simulation of a Variable-Rate Fertilizer Applicator Based on EDEM. IFAC PapersOnLine 2018, 51, 418–423. [Google Scholar] [CrossRef]
- Mudarisov, S.; Farkhutdinov, I.; Khamaletdinov, R.; Khasanov, E.; Mukhametdinov, A. Evaluation of the Significance of the Contact Model Particle Parameters in the Modelling of Wet Soils by the Discrete Element Method. Soil Tillage Res. 2022, 215, 105228. [Google Scholar] [CrossRef]
- Li, A.; Han, Y.; Jia, F.; Zhang, J.; Meng, X.; Chen, P.; Xiao, Y.; Zhao, H. Examination Milling Non-Uniformity in Friction Rice Mills Using by Discrete Element Method and Experiment. Biosyst. Eng. 2021, 211, 247–259. [Google Scholar] [CrossRef]
- Dun, G.; Chen, H.; Feng, Y.; Yang, J.; Li, A.; Cha, S. Parameter optimization and test of key components of fertilizer blending device based on EDEM software. J. Agric. Eng. 2016, 32, 36–42. [Google Scholar]
- Liu, J.-S.; Gao, C.-Q.; Nie, Y.-J.; Yang, B.; Ge, R.-Y.; Xu, Z.-H. Numerical Simulation of Fertilizer Shunt-Plate with Uniformity Based on EDEM Software. Comput. Electron. Agric. 2020, 178, 105737. [Google Scholar] [CrossRef]
- Pocius, A.; Jotautiene, E.; Pekarskas, J.; Mieldazys, R.; Jasinskas, A. Research of particle geometrical parameters and aerodynamic features of granular organic compost fertilizers. Eng. Rural. Dev. 2014, 13, 401–406. [Google Scholar]
- Zinkevičienė, R.; Jotautienė, E.; Juostas, A.; Comparetti, A.; Vaiciukevičius, E. Simulation of Granular Organic Fertilizer Application by Centrifugal Spreader. Agronomy 2021, 11, 247. [Google Scholar] [CrossRef]
- Lv, H.; Yu, J.; Fu, H. Simulation of the Operation of a Fertilizer Spreader Based on an Outer Groove Wheel Using a Discrete Element Method. Math. Comput. Model. 2013, 58, 842–851. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Siddique, M.A.A.; Kim, W.-S.; Kim, Y.-J.; Lee, S.-D.; Lee, D.-K.; Hwang, S.-J.; Nam, J.-S.; Park, S.-U.; Lim, R.-G. DEM Simulation for Draft Force Prediction of Moldboard Plow According to the Tillage Depth in Cohesive Soil. Comput. Electron. Agric. 2021, 189, 106368. [Google Scholar] [CrossRef]
- Van Liedekerke, P.; Tijskens, E.; Dintwa, E.; Rioual, F.; Vangeyte, J.; Ramon, H. DEM Simulations of the Particle Flow on a Centrifugal Fertilizer Spreader. Powder Technol. 2009, 190, 348–360. [Google Scholar] [CrossRef]
- Zhao, S.; Gao, L.; Yuan, Y.; Hou, L.; Zhang, X.; Yang, Y. The law of corn stalk movement in deep subsoiling operation based on discrete element method. J. Agric. Eng. 2021, 37, 53–62. [Google Scholar]
- Song, X.; Dai, F.; Zhang, F.; Wang, D.; Liu, Y. Calibration of DEM Models for Fertilizer Particles Based on Numerical Simulations and Granular Experiments. Comput. Electron. Agric. 2023, 204, 107507. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, Y.; Liu, H.; Ji, C.; Hou, Q.; Zhou, Y. Design and test of centrifugal side-throw lotus root fertilizer spreader. J. Agric. Eng. 2021, 37, 37–47. [Google Scholar]
- Yinyan, S.; Man, C.; Xiaochan, W.; Odhiambo, M.O.; Weimin, D. Numerical Simulation of Spreading Performance and Distribution Pattern of Centrifugal Variable-Rate Fertilizer Applicator Based on DEM Software. Comput. Electron. Agric. 2018, 144, 249–259. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, Y.; Zhang, H.; Lan, H.; Niu, H. Parameter Optimization of Spiral Fertilizer Applicator Based on Artificial Neural Network. Sustainability 2023, 15, 1744. [Google Scholar] [CrossRef]
- Barbosa, L.A.P. Modelling the Aggregate Structure of a Bulk Soil to Quantify Fragmentation Properties and Energy Demand of Soil Tillage Tools in the Formation of Seedbeds. Biosyst. Eng. 2020, 197, 203–2159. [Google Scholar] [CrossRef]
- Bai, J.; Hao, F.; Cheng, G.; Li, C. Machine Vision-Based Supplemental Seeding Device for Plug Seedling of Sweet Corn. Comput. Electron. Agric. 2021, 188, 106345. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, W.; Ma, Y.; Tong, J.; Liu, X.; Sun, J. DEM and Soil Bin Study on a Biomimetic Disc Furrow Opener. Comput. Electron. Agric. 2019, 156, 209–216. [Google Scholar] [CrossRef]
- Shi, Y.; Xin (Rex), S.; Wang, X.; Hu, Z.; Newman, D.; Ding, W. Numerical Simulation and Field Tests of Minimum-Tillage Planter with Straw Smashing and Strip Laying Based on EDEM Software. Comput. Electron. Agric. 2019, 166, 105021. [Google Scholar] [CrossRef]
- Jadhav, A.; Jadhav, V.S. A Review on 3D Printing: An Additive Manufacturing Technology. Mater. Today Proc. 2022, 62, 2094–2099. [Google Scholar] [CrossRef]
- Shahrubudin, N.; Lee, T.C.; Ramlan, R. An Overview on 3D Printing Technology: Technological, Materials, and Applications. Procedia Manuf. 2019, 35, 1286–1296. [Google Scholar] [CrossRef]




| Project | Property | Value |
|---|---|---|
| Poisson ratio | 0.25 | |
| Urea fertilizer granule | Shear modulus (Pa) | 1.04 × 107 |
| Density (kg·m3) | 1345 | |
| Poisson ratio | 0.25 | |
| Soil particles | Shear modulus (Pa) | 1 × 108 |
| Density (kg·m3) | 2000 | |
| Poisson ratio | 0.28 | |
| Fertilizer spreading device | Shear modulus (Pa) | 8.0 × 109 |
| Density (kg·m3) | 1240 | |
| Corn roots | Poisson ratio | 0.33 |
| Shear modulus (Pa) | 6.39 | |
| Density (kg·m3) | 107.64 | |
| Urea fertilizer granule–urea fertilizer granule | Restitution coefficient | 0.60 |
| Static friction coefficient | 0.40 | |
| Rolling friction coefficient | 0.01 | |
| Urea fertilizer granule–soil particles | Restitution coefficient | 0.60 |
| Static friction coefficient | 0.50 | |
| Rolling friction coefficient | 0.50 | |
| Urea fertilizer granule–corn roots | Restitution coefficient | 0.60 |
| Static friction coefficient | 0.60 | |
| Rolling friction coefficient | 0.20 | |
| Urea fertilizer granule–fertilizer spreading device | Restitution coefficient | 0.01 |
| Static friction coefficient | 0.02 | |
| Rolling friction coefficient | 0.01 | |
| Soil particles–corn roots | Restitution coefficient | 0.60 |
| Static friction coefficient | 0.60 | |
| Rolling friction coefficient | 0.02 |
| Test Factors | Range of Test Factors | Transversal Fertilizer Uniformity Coefficient Y1 | Longitudinal Fertilizer Uniformity Coefficient Y2 |
|---|---|---|---|
| Angle α | 30° | 0.7901 | 0.4293 |
| 37.5° | 0.7024 | 0.3290 | |
| 45° | 0.6190 | 0.2213 | |
| 52.5° | 0.6226 | 0.2127 | |
| 60° | 0.5828 | 0.1356 | |
| Width N | 250 mm | 0.8902 | 0.5160 |
| 300 mm | 0.8298 | 0.4489 | |
| 350 mm | 0.8139 | 0.4356 | |
| 400 mm | 0.7793 | 0.4112 | |
| 450 mm | 0.7105 | 0.28952 | |
| Height H | 40 | 0.8137 | 0.4351 |
| 45 | 0.7402 | 0.3296 | |
| 50 | 0.6190 | 0.2213 | |
| 55 | 0.597 | 0.1850 | |
| 60 | 0.5912 | 0.2168 |
| Code | Factor | ||
|---|---|---|---|
| Angle X1/(°) | Height X2/mm | Width X3/mm | |
| 1.682 | 60.00 | 450.00 | 60.00 |
| 1 | 56.96 | 429.73 | 57.97 |
| 0 | 52.50 | 400.00 | 55.00 |
| −1 | 48.04 | 370.27 | 52.03 |
| −1.682 | 45.00 | 350.00 | 50.00 |
| Code | Test Factor | Test Indexes | |||
|---|---|---|---|---|---|
| Angle X1/(°) | Height X2/mm | Width X3/mm | The Transversal Fertilizer Uniformity Coefficient Y1 | The Longitudinal Fertilizer Uniformity Coefficient Y2 | |
| 1 | 52.50 | 400.00 | 55.00 | 0.1763 | 0.1129 |
| 2 | 56.96 | 429.73 | 57.97 | 0.1700 | 0.1258 |
| 3 | 48.04 | 370.27 | 57.97 | 0.1101 | 0.1324 |
| 4 | 60.00 | 400.00 | 55.00 | 0.1354 | 0.1096 |
| 5 | 52.50 | 400.00 | 55.00 | 0.1445 | 0.1306 |
| 6 | 52.50 | 400.00 | 55.00 | 0.1275 | 0.1041 |
| 7 | 52.50 | 400.00 | 55.00 | 0.1458 | 0.1659 |
| 8 | 52.50 | 450.00 | 55.00 | 0.0975 | 0.1069 |
| 9 | 56.96 | 370.27 | 57.97 | 0.2110 | 0.1275 |
| 10 | 52.50 | 400.00 | 60.00 | 0.1361 | 0.0750 |
| 11 | 52.50 | 400.00 | 55.00 | 0.1559 | 0.1165 |
| 12 | 52.50 | 400.00 | 55.00 | 0.1404 | 0.1385 |
| 13 | 52.50 | 350.00 | 55.00 | 0.1302 | 0.1097 |
| 14 | 48.04 | 429.73 | 57.97 | 0.0997 | 0.2188 |
| 15 | 52.50 | 400.00 | 55.00 | 0.1488 | 0.2077 |
| 16 | 56.96 | 370.27 | 52.03 | 0.1468 | 0.2077 |
| 17 | 48.04 | 429.73 | 52.03 | 0.1428 | 0.1877 |
| 18 | 48.04 | 370.27 | 52.03 | 0.1718 | 0.2077 |
| 19 | 52.50 | 400.00 | 55.00 | 0.1458 | 0.2537 |
| 20 | 52.50 | 400.00 | 50.00 | 0.1218 | 0.2078 |
| 21 | 52.50 | 400.00 | 55.00 | 0.1448 | 0.2077 |
| 22 | 45.00 | 400.00 | 55.00 | 0.1478 | 0.2077 |
| 23 | 56.96 | 400.00 | 55.00 | 0.1763 | 0.1128 |
| Evaluation Indicators of the Transversal Fertilizer Uniformity Coefficient Y1 | ||||||
|---|---|---|---|---|---|---|
| Source of Variance | Square Sum | Degree of Freedom | Mean Square | F-Value | p-Value | Significance |
| Model | 0.010 | 9 | 1.137 × 10−3 | 4.44 | 0.0078 | *** |
| X1 | 2.170 × 10−3 | 1 | 2.170 × 10−3 | 8.48 | 0.0121 | ** |
| X2 | 1.774 × 10−3 | 1 | 1.774 × 10−3 | 6.93 | 0.0207 | ** |
| X3 | 1.196 × 10−3 | 1 | 1.196 × 10−3 | 4.68 | 0.0498 | ** |
| X1×2 | 1.347 × 10−8 | 1 | 1.347 × 10−8 | 5.264 × 10−5 | 0.9943 | |
| X1X3 | 8.920 × 10−4 | 1 | 8.920× 10−4 | 3.49 | 0.0846 | * |
| X2X3 | 6.478 × 10−4 | 1 | 6.478 × 10−4 | 2.53 | 0.1356 | |
| X12 | 1.125 × 10−3 | 1 | 1.125 × 10−3 | 4.40 | 0.0561 | * |
| X22 | 5.053 × 10−6 | 1 | 5.053 × 10−6 | 0.020 | 0.8904 | |
| X32 | 2.4 × 10−3 | 1 | 2.4 × 10−3 | 9.38 | 0.0091 | *** |
| Residual | 3.326 × 10−3 | 13 | 2.558 × 10−4 | 9.38 | 0.0091 | |
| Misfit term | 2.002 × 10−3 | 5 | 4.004 × 10−4 | 2.42 | 0.1279 | |
| Pure error | 1.324 × 10−3 | 8 | 1.655 × 10−4 | |||
| Total variation | 0.014 | 22 | ||||
| Evaluation Indicators of the Longitudinal Fertilizer Uniformity Coefficient Y2 | ||||||
|---|---|---|---|---|---|---|
| Source of Variance | Square Sum | Degree of Freedom | Mean Square | F-Value | p-Value | Significance |
| Model | 0.050 | 9 | 5.588 × 10−3 | 13.65 | <0.0001 | *** |
| X1 | 2.469 × 10−3 | 1 | 2.469 × 10−3 | 6.03 | 0.0289 | ** |
| X2 | 4.528 × 10−4 | 1 | 4.528 × 10−4 | 1.11 | 0.3120 | |
| X3 | 3.237 × 10−3 | 1 | 3.237 × 10−3 | 7.91 | 0.0147 | ** |
| X1X2 | 5.809 × 10−4 | 1 | 5.809 × 10−4 | 1.42 | 0.2548 | |
| X1X3 | 7.163 × 10−4 | 1 | 7.163 × 10−4 | 1.75 | 0.2086 | |
| X2X3 | 1.510 × 10−4 | 1 | 1.510× 10−4 | 0.37 | 0.5541 | |
| X12 | 0.024 | 1 | 0.024 | 59.63 | <0.0001 | *** |
| X22 | 0.014 | 1 | 0.014 | 34.78 | <0.0001 | *** |
| X32 | 4.552 × 10−3 | 1 | 4.552 × 10−3 | 11.12 | 0.0054 | *** |
| Residual | 5.32 × 10−3 | 13 | 4.092 × 10−4 | |||
| Misfit term | 2.879 × 10−3 | 5 | 5.758 × 10−4 | 1.89 | 0.2024 | |
| Pure error | 2.441 × 10−3 | 8 | 3.051 × 10−4 | |||
| Total variation | 0.056 | 22 | ||||
| Serial Number | The Transversal Fertilizer Uniformity Coefficient | The Longitudinal Fertilizer Uniformity Coefficient |
|---|---|---|
| 1 | 0.1451 | 0.1487 |
| 2 | 0.1567 | 0.1378 |
| 3 | 0.1354 | 0.1575 |
| 4 | 0.1289 | 0.1459 |
| 5 | 0.1476 | 0.1457 |
| Average value | 0.1427 | 0.1487 |
| Simulation value | 0.132 | 0.135 |
| Relative error | −8.11% | −9.01% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dun, G.; Mao, N.; Ji, X.; Zhang, F.; Ji, W. Optimal Design and Experiment of Corn-Overlapped Strip Fertilizer Spreader. Appl. Sci. 2023, 13, 2559. https://doi.org/10.3390/app13042559
Dun G, Mao N, Ji X, Zhang F, Ji W. Optimal Design and Experiment of Corn-Overlapped Strip Fertilizer Spreader. Applied Sciences. 2023; 13(4):2559. https://doi.org/10.3390/app13042559
Chicago/Turabian StyleDun, Guoqiang, Ning Mao, Xinxin Ji, Fuli Zhang, and Wenyi Ji. 2023. "Optimal Design and Experiment of Corn-Overlapped Strip Fertilizer Spreader" Applied Sciences 13, no. 4: 2559. https://doi.org/10.3390/app13042559




