Influence of Pile Foundation Stiffness on Column Design in One-Story Reinforced Concrete Frames
Abstract
:1. Introduction
2. Consideration of Subsoil Stiffness in the Design of Reinforced Concrete Hall Columns
- IF—moment of inertia of the foundation base field;
- Cz—coefficient of elasticity of the subsoil.

3. Method for Calculating Pile Foundation Settlement
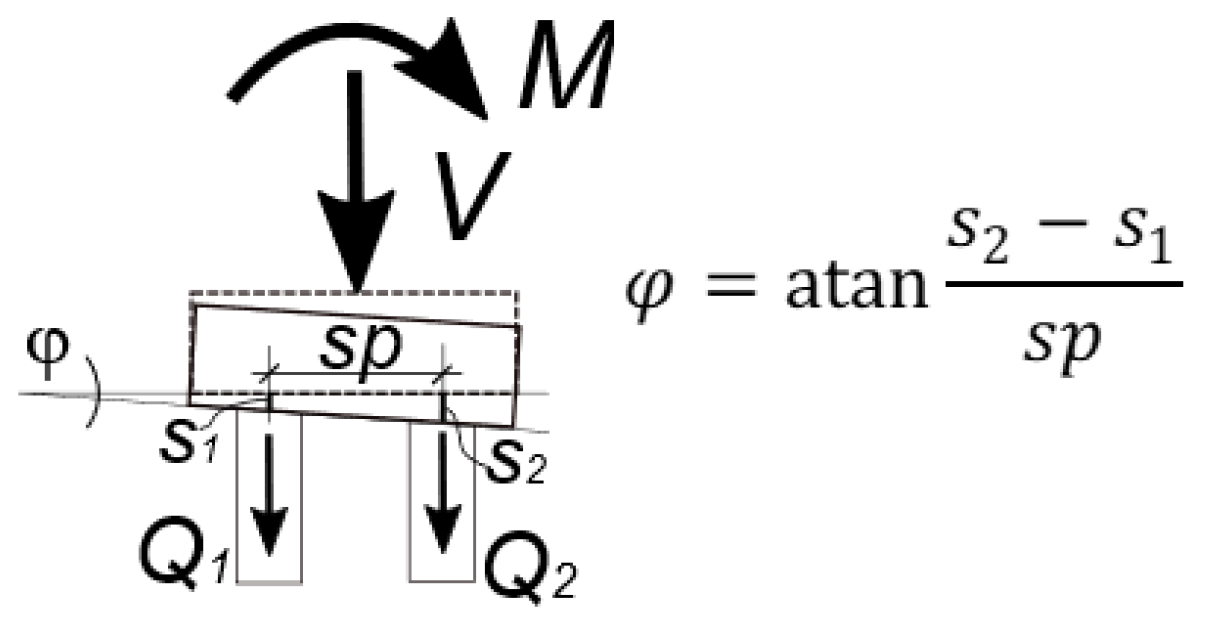
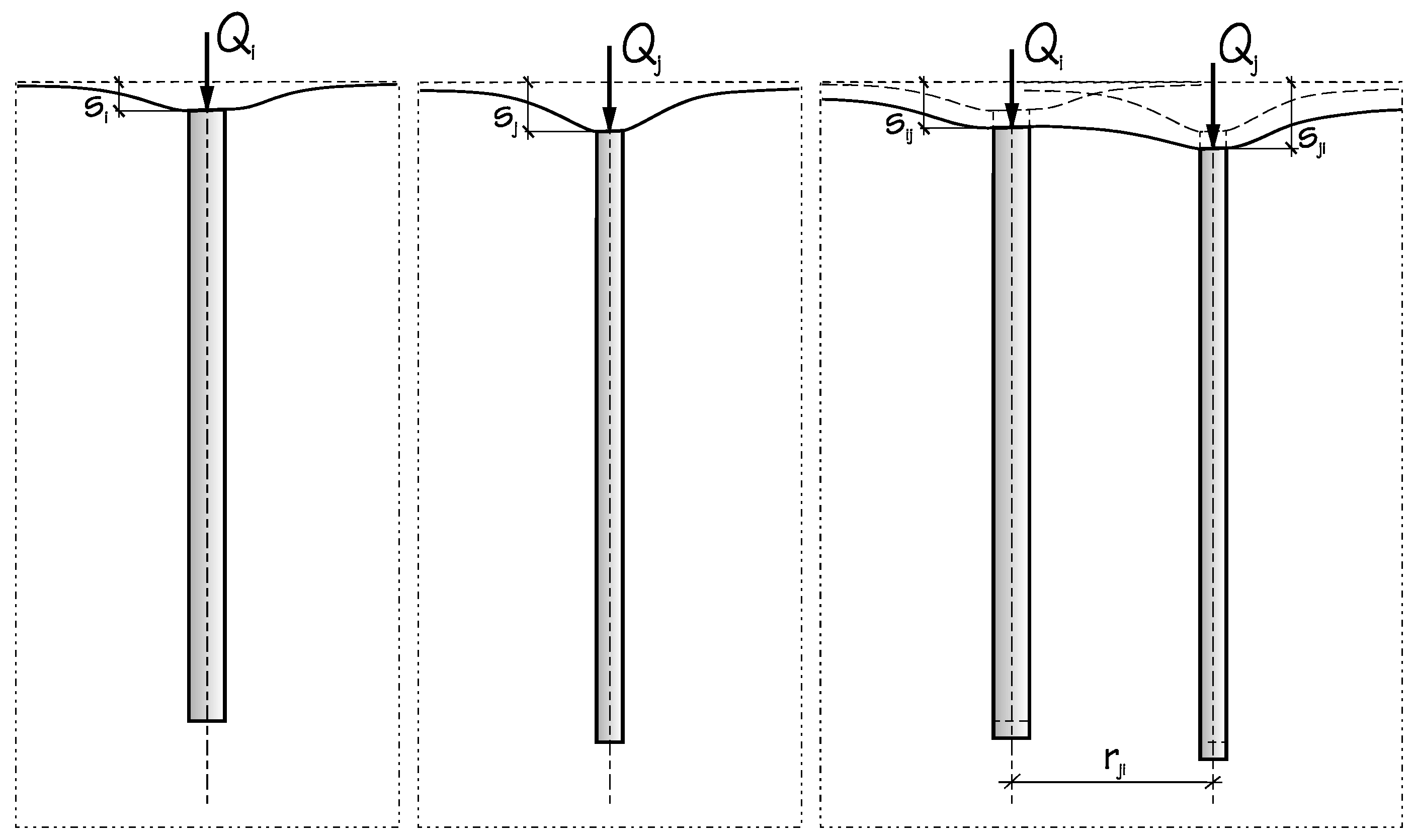
- si—settlement of the single pile i under the load Qi;
- sij—settlement of the pile pair i and j loaded with the forces Qi and Qj.
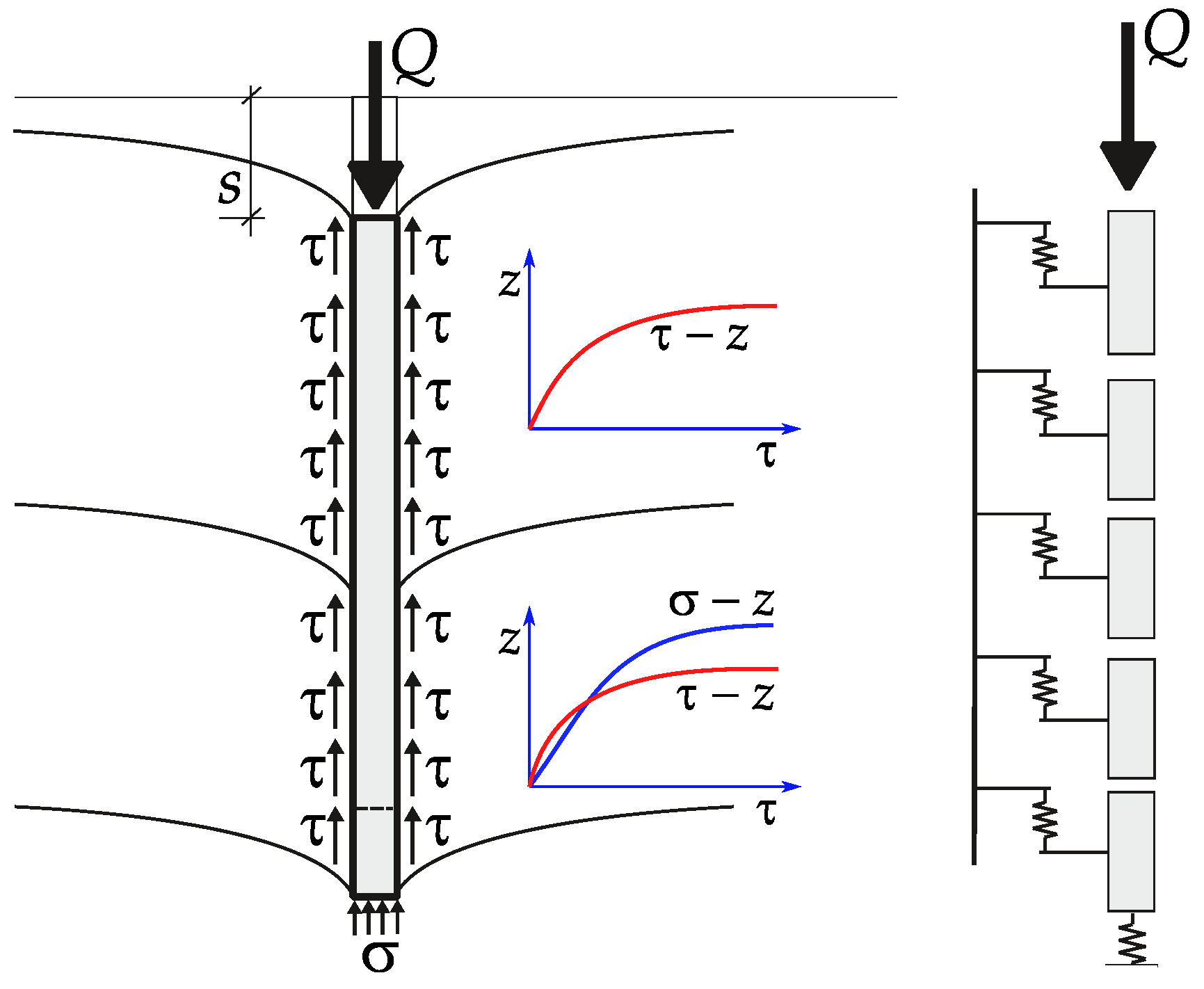
- ss—displacement of the nodal point of the pile sidewall;
- τ0—tangent stress on the side of the pile;
- R0—radius of the pile shaft;
- Rmax—range of influence of the pile;
- Gs—shear modulus of the soil in the vicinity of the pile shaft.
- Lp—length of the pile in the subsoil;
- z—depth below ground level;
- ν—Poisson’s ratio.
- Rb—pile base radius;
- Gb—shear modulus of the soil under the base of the pile;
- νb—Poisson’s ratio;
- µd—impact factor of base depth, µd = 0.5.
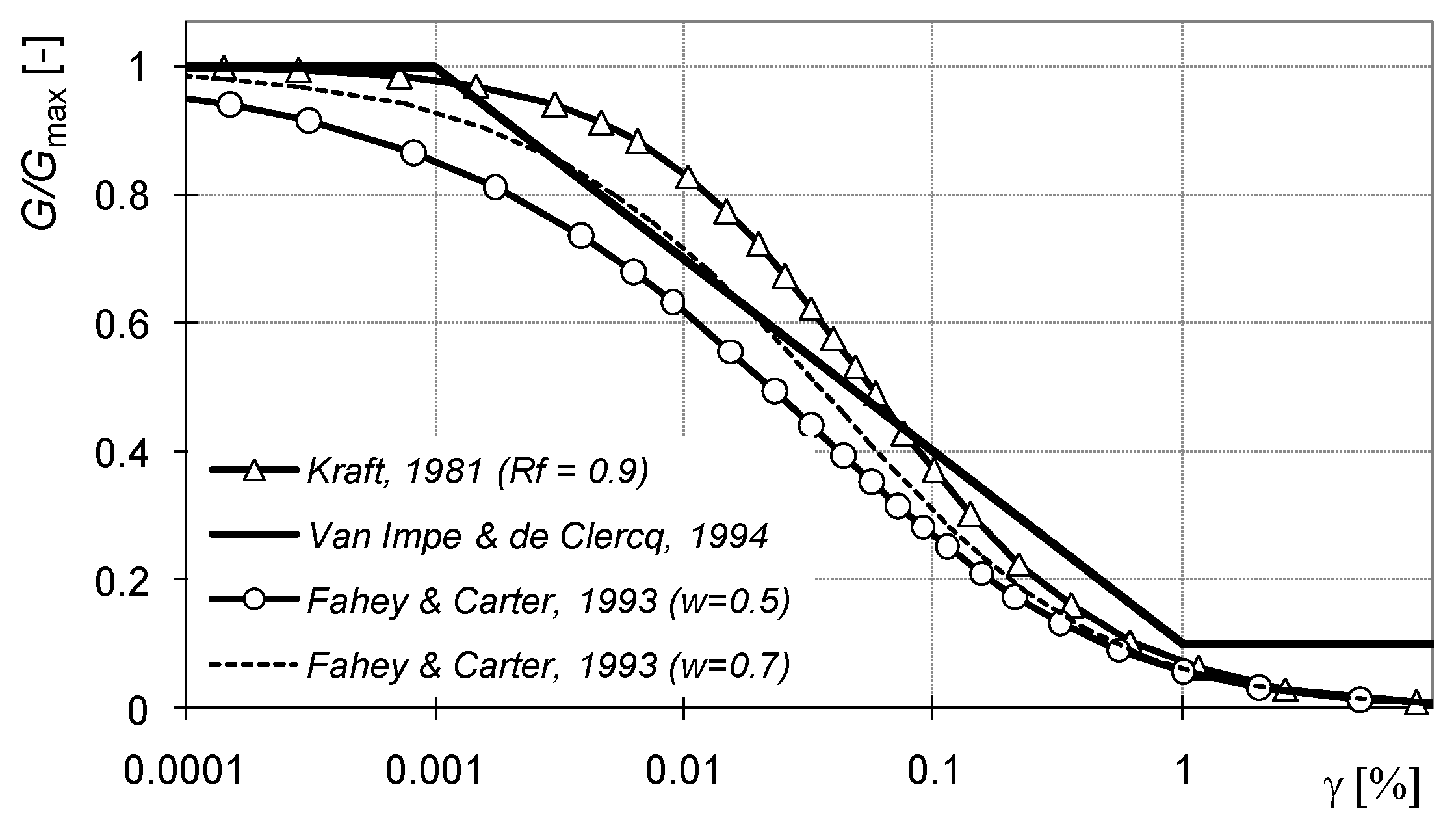
- Gmax—initial shear modulus;
- τ—current, mobilized soil resistance;
- τf—limit soil resistance (at failure);
- Rf—hyperbolic curve constant, Rf = 0.5 ÷ 0.9.
- according to Van Impe and De Clercq [33]:
- according to Fahey and Carter [34]:
- Gmax—initial shear modulus;
- w—equation parameter.
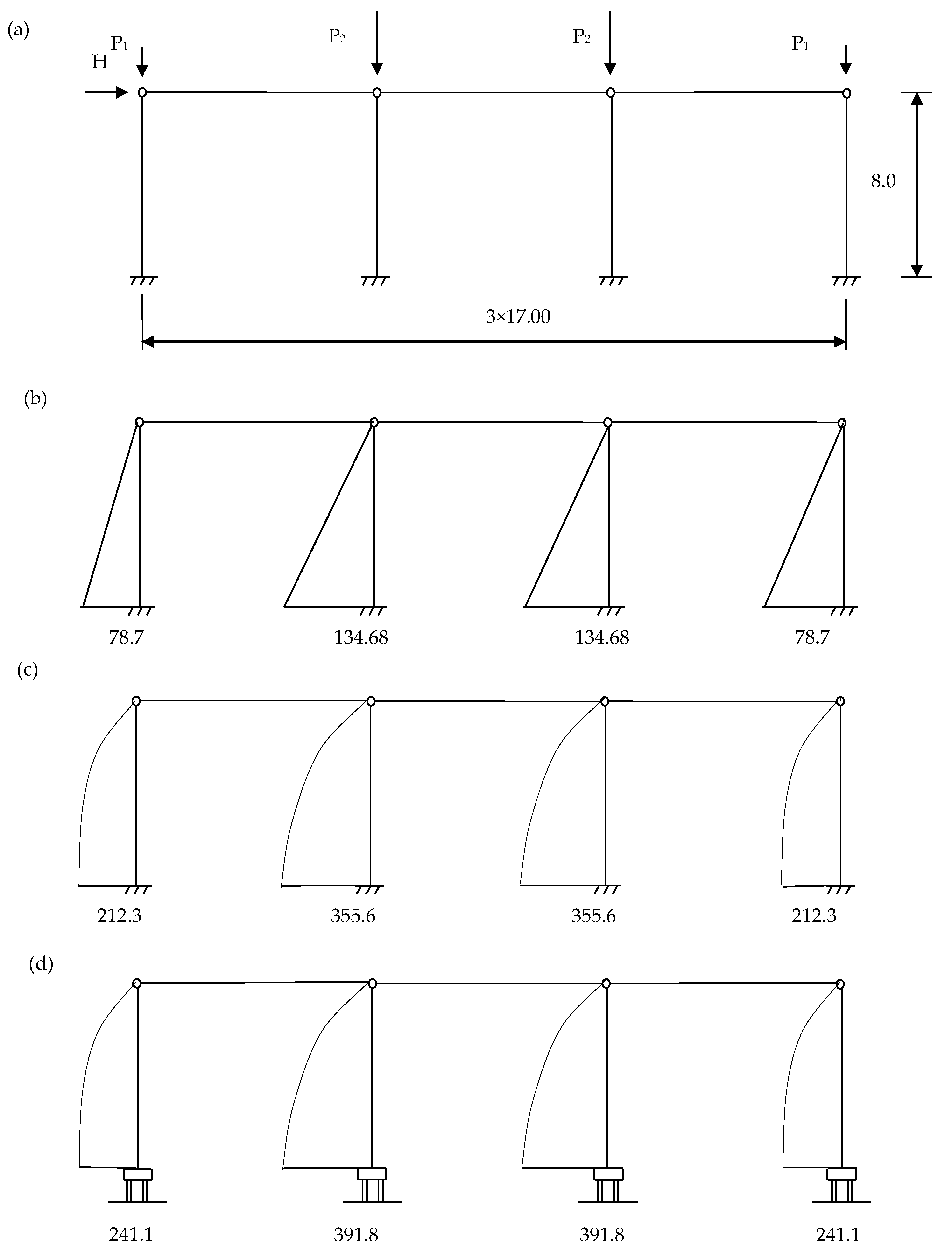
4. Examples
- (I)
- Static calculation of the hall’s structural system, assuming that the columns are restrained at their supports and obtaining nodal forces;
- (II)
- Determination of the pile loads Qi, verification of the ultimate limit state of the pile, calculation of the pile settlement and foundation rotation (Figure 9);
- (III)
- Making a static calculation of the hall’s structural system according to the second-order theory, taking into account the rotational stiffness of the pile supports and obtaining new values for the nodal forces;
- (IV)
- Determination of new loads on the pile Qi, verification of the ultimate limit state of the pile, calculation of pile settlement and foundation rotation as in step (II).
4.1. Example 1
4.2. Example 2
5. Discussion
6. Conclusions
- The paper presents a method for modeling the support of a column fixed in a pile-founded footing. The originality of the method is to take into account the non-linear behavior of piles through the use of the degradation function of the stiffness modulus of the soil in the application to the calculation of bending moments in columns.
- Example frame calculations were carried out with the rigorous method of the second-order analysis with nominal stiffnesses, modeling the column support conditions as described in the paper. Rotation of the foundation leads to increased ultimate moments in the columns, which can be important in some cases of slender column foundations.
- In the case of pile foundations, the effect of the increase in the moments is smaller than for shallow foundations [15] and should not be omitted from the calculations. In more complex cases, accurate calculations, as in the presented examples, should be used for the dimensioning of the reinforcement in the columns rather than the simplified methods used for separated columns, according to Eurocode [1].
- The proposal allows for a more rational design of similar structures compared to standard simplified methods. The example presented should be considered strictly in relation to the conditions adopted in it. The adopted structural system, the loading, type, number and spacing of the piles and the geotechnical conditions will all affect the results obtained.
- Piles should be designed for the ultimate forces obtained according to the second-order theory, especially for the design of slender columns.
- Piles should be designed for both ultimate limit state conditions and displacement limitation conditions. Knowledge of the predicted mechanical characteristics (Q–s settlement curves) of pile supports enables more rational static calculations of the entire structural system of the structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- in the end columns ;
- in the center columns .
Appendix B
- in the end columns ;
- in the center columns .
References
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures. Part 1-1. General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Zucca, M.; Crespi, P.G.; Longarini, N.; Scamardo, M.A. The new foundation system of the Basilica di Collemaggio’s transept. Int. J. Mason. Res. Innov. 2020, 5, 67–84. [Google Scholar] [CrossRef]
- Gonzáleza, F.; Carbonarib, S.; Padróna, L.A.; Moricic, M.; Aznáreza, J.J.; Dezid, F.; Maesoa, O.; Leonic, G. Benefits of inclined pile foundations in earthquake resistant design of bridges. Eng. Struct. 2020, 203, 109873. [Google Scholar] [CrossRef]
- Klempka, K.; Knauff, M. Design of slender RC columns according to Eurocode and polish code compared with the improved numerical model. Arch. Civ. Eng. 2005, 51, 23–42. [Google Scholar]
- Hamed, E.; Lai, C. Geometrically and materially nonlinear creep behaviour of reinforced concrete columns. Structures 2016, 5, 1–12. [Google Scholar] [CrossRef]
- Gilbert, R.I.; Ranzi, G. In-service deformations of reinforced concrete columns in biaxial bending. In Proceedings of the Twelfth East Asia-Pacific Conference on Structural Engineering and Construction, Hong Kong, China, 26–28 January 2011. [Google Scholar]
- Kim, C.S.; Gong, Y.; Zhang, X.; Hwang, H.J. Experimental study on long-term behavior of RC columns subjected to sustained eccentric load. Adv. Concr. Constr. 2020, 9, 289–299. [Google Scholar]
- Strauss, A.; Hauser, M.; Täubling, B.; Ivanković, A.M.; Skokandić, D.; Matos, J.; Galvão, N.; Benko, V.; Dobrý, J.; Wan-Wendner, R.; et al. Probabilistic and semi-probabilistic analysis of slender columns frequently used in structural engineering. Appl. Sci. 2021, 11, 8009. [Google Scholar] [CrossRef]
- Dwaikat, M.; Dwaikat, M.M.S. Slenderness lower limit for sway-inhibited reinforced high strength concrete beam-columns. ACI Struct. J. 2018, 115, 1243–1252. [Google Scholar] [CrossRef]
- Mari, A.R.; Helleslan, J. Lower slenderness limits for rectangular reinforced concrete columns. J. Struct. Eng. 2005, 131, 85–95. [Google Scholar] [CrossRef]
- Knauff, M.; Klempka, K. Effective lengths of reinforced concrete columns in single-storey frame structures in the light of the Eurocode. Tech. Sci. 2009, 12, 71–82. [Google Scholar] [CrossRef]
- Fischer, K. Beispiele zur Bodenmechanik; Ernst und Sohn: Berlin, Germany, 1965. [Google Scholar]
- Kany, M. Berechnung von Flächengründingen; Ernst und Sohn: Berlin, Germany, 1974. [Google Scholar]
- Knauff, M.; Klempka, K. Projektowanie smukłych słupów żelbetowych według Eurokodu 2. Inżynieria I Bud. 2009, 12, 663–665. [Google Scholar]
- Klempka, K.; Knauff, M. Taking subsoil susceptibility into account in designing columns in reinforced single-storey structures. Tech. Sci. 2010, 13, 80–89. [Google Scholar] [CrossRef] [Green Version]
- Gorbunow-Posadow, M.T. Obliczanie Konstrukcji na Podłożu Sprężystym; Budownictwo i Architektura: Warszawa, Poland, 1956. [Google Scholar]
- Lewiński, P. Analiza Współpracy Żelbetowych Zbiorników Cylindycznych z Podłóżem; ITB: Warszawa, Poland, 2007. [Google Scholar]
- Coyle, H.M.; Reese, L.C. Load transfer for axially loaded piles in clay. J. Soil Mech. Found. Div. 1966, 92, 1–26. [Google Scholar] [CrossRef]
- Vijayvergiya, V.N.; Focht, J.A. A new way to predict the capacity of piles in clay. In Proceedings of the 4-th Annual Offshore Technology Conference, Houston, TX, USA, 2–5 May 1977. [Google Scholar]
- Randolph, M.F.; Wroth, C.P. Analysis of deformation of vertically loaded piles. J. Geotech. Eng. Div. 1978, 104, 1465–1488. [Google Scholar] [CrossRef]
- Kraft, L.M.; Ray, R.P.; Kagawa, T. Theoretical t-z curves. J. Geotech. Eng. Div. 1981, 107, 1543–1561. [Google Scholar] [CrossRef]
- Guo, W.D.; Randolph, M.F. Rationality of load transfer approach for pile analysis. Comput. Geotech. 1998, 23, 85–112. [Google Scholar] [CrossRef]
- Zhu, H.; Chang, M.F. Load transfer curves along bored piles considering modulus degradation. J. Geotech. Geoenviron. Eng. 2002, 128, 764–774. [Google Scholar] [CrossRef]
- Lu, Q.; Luo, Q.A. Load transfer approach for studying the load-deformation response of vertically loaded single pile. In Proceedings of the 2nd International Symposium on Asia Urban GeoEngineering, Changsha, China, 24–27 November 2017. [Google Scholar]
- Bateman, A.H.; Crispin, J.J.; Vardanega, P.J.; Mylonakis, G.E. Theoretical t -z Curves for Axially Loaded Piles. J. Geotech. Geoenviron. Eng. 2022, 148, 04022052. [Google Scholar] [CrossRef]
- Dyka, I. The Analysis and the Calculation Method of Pile Group Settlement. Ph.D. Thesis, Technical University of Gdansk, Gdansk, Poland, 2001. (In Polish). [Google Scholar]
- Gwizdała, K.; Dyka, I. Estimation of settlements of piles in group. In Proceedings of the 9th Conference on Piling and Deep Foundations, Nice, France, 3–5 June 2002. [Google Scholar]
- Randolph, M.F. Science and empiricism in pile foundation design. Geotechnique 2003, 53, 847–875. [Google Scholar] [CrossRef]
- Poulos, H.G. Pile group settlement estimation—Research to practice. In Proceedings of the Sessions of the GeoShanghai Conference -Foundation Analysis and Design: Innovative Methods, Shanghai, China, 6–8 June 2006. [Google Scholar]
- Mandolini, A.; Russo, G.; Viggiani, C. Pile foundations: Experimental investigations, analysis and design. In Proceedings of the 16th international Conference of Soil Mechanics & Geotechnical Engineering, Osaka, Japan, 12–16 September 2005. [Google Scholar]
- Liu, H.; Xiao, Z.; Lee, K. Load-settlement behaviour analysis based on the characteristics of the vertical loads under a pile group. Appl. Sci. 2022, 12, 6282. [Google Scholar] [CrossRef]
- Chow, Y.K. Analysis of vertically loaded pile groups. Int. J. Numer. Anal. Methods Geomech. 1986, 10, 59–72. [Google Scholar] [CrossRef]
- Van Impe, W.F.; De Clercq, Y. A piled raft interaction model. In Proceedings of the 5-th International Conference and Exhibition on Piling and Deep Foundations-DFI’94, Bruges, Belgium, 13–15 June 1994. [Google Scholar]
- Fahey, M.; Carter, J.P. A finite element study of the pressuremeter test in sand using nonlinear elastic plastic model. Can. Geotech. J. 1993, 30, 348–362. [Google Scholar] [CrossRef]
- Bustamante, M.; Gianaselli, L. Pile bearing capacity prediction by means of static penetrometer CPT. In Proceedings of the 2nd European Symposium on Penetration Testing: ESOPT–II, Amsterdam, The Netherland, 24–27 May 1982. [Google Scholar]
- Mayne, P.W.; Rix, G.J. Gmax-qc relationships for clays. Geotech. Test. J. 1993, 16, 54–60. [Google Scholar]
- Dyka, I. Use of the laboratory tests of soil modulus in modelling pile behaviour. Stud. Geotech. Et Mech. 2012, 34, 53–61. [Google Scholar] [CrossRef] [Green Version]
- Srokosz, P.; Dyka, I.; Bujko, M. Interpretation of shear modulus degradation tests. Stud. Geotech. Et Mech. 2018, 40, 125–132. [Google Scholar] [CrossRef] [Green Version]


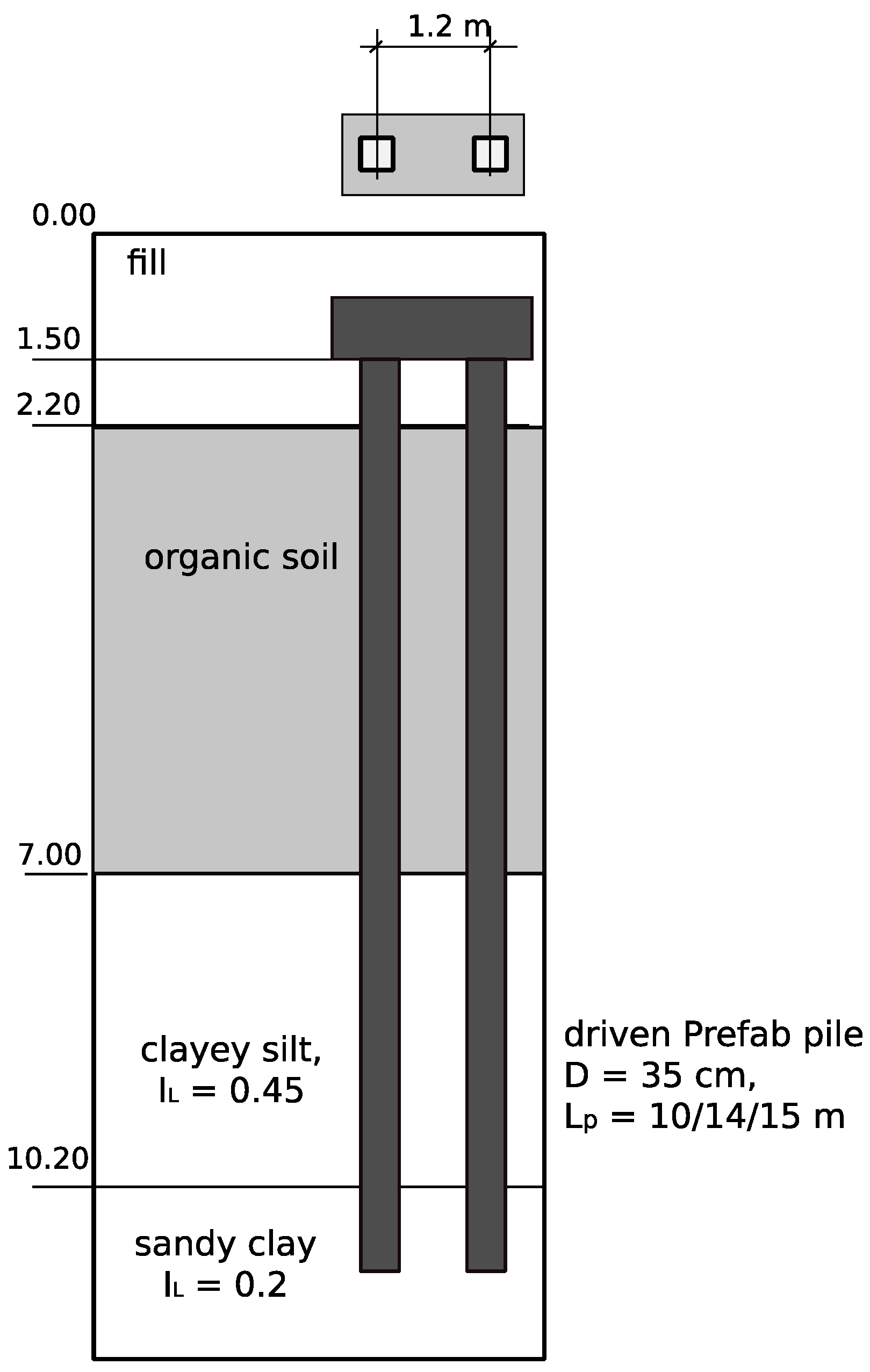
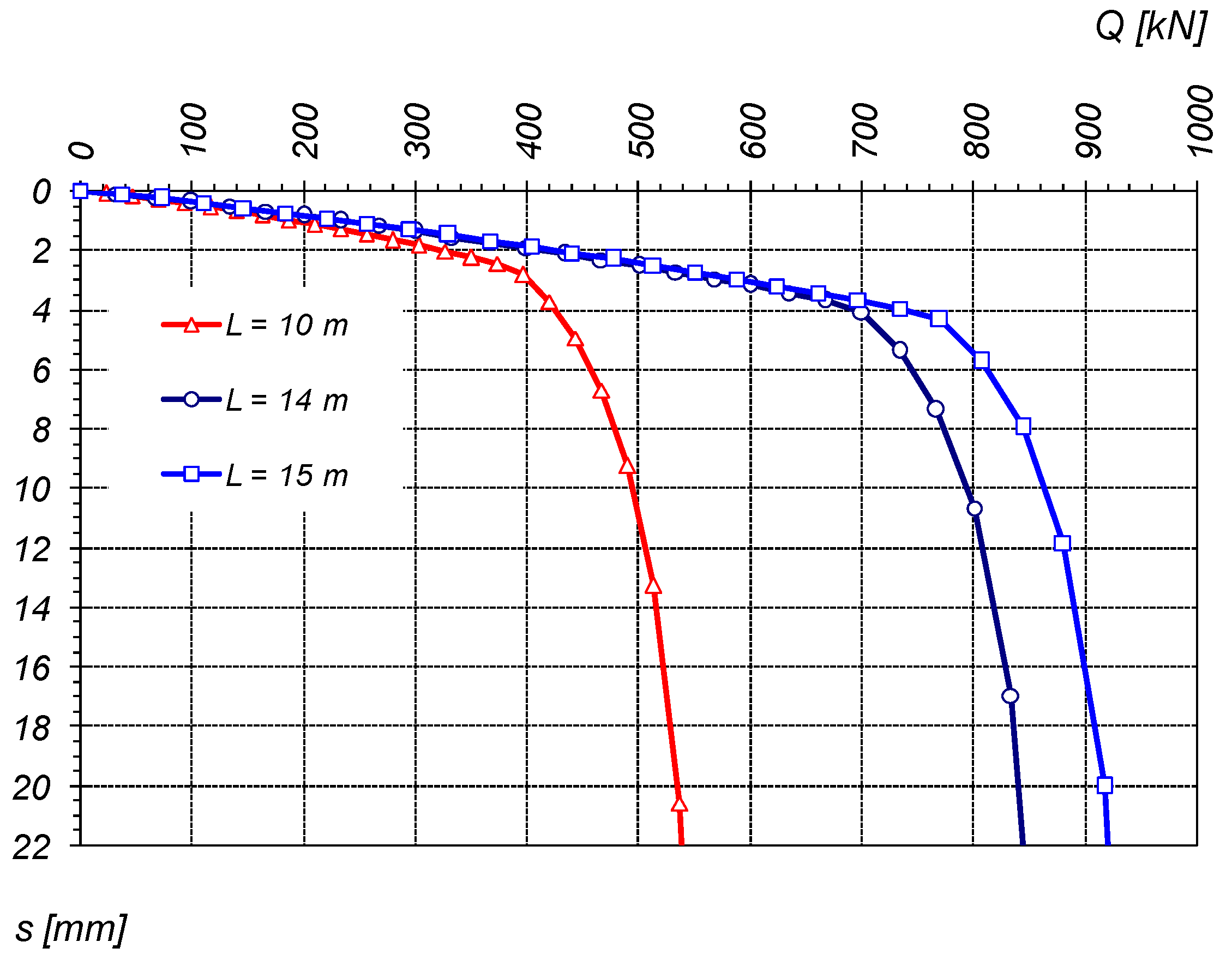

| No. of Layer | Soil | Unit Weight (Effective Value) [kN/m3] | τf [kPa] | qf [kPa] | Gmax [MPa] |
|---|---|---|---|---|---|
| 1 | fill | 16.0 | 5 | - | 24 |
| 2 | organic soil | 5.0 | 5 | - | 7 |
| 3 | clayey silt | 11.5 | 40 | - | 40 |
| 4 | sandy clay | 11.0 | 53 | 1800 | 54 |
| Outer Columns Lp = 10.0 m V = P1 = 500 kN | Internal Columns Lp = 14.0 m V = P2 = 1000 kN | |||
|---|---|---|---|---|
| Iteration 1 | Iteration 3 | Iteration 1 | Iteration 3 | |
| M [kNm] | 212.3 | 241.1 | 355.6 | 391.8 |
| Q1 [kN] | 210 | 198 | 400 | 385 |
| Q2 [kN] | 387 | 399 | 696 | 711 |
| s1 [mm] | 1.49 | 1.43 | 2.44 | 2.36 |
| s2 [mm] | 2.89 | 3.09 | 4.67 | 5.26 |
| angle φ [rad] | 0.00117 | 0.00138 | 0.00186 | 0.00242 |
| M/φ [MNm] | 182 | 174 | 191 | 162 |
| Outer-Left Columns Lp = 10.0 m V = P1 = 400 kN | Internal Columns Lp = 15.0 m V = P2 = 1000 kN | Outer-Right Columns Lp = 10.0 m V = P1 = 400 kN | ||||
|---|---|---|---|---|---|---|
| Iteration 1 | Iteration 3 | Iteration 1 | Iteration 3 | Iteration 1 | Iteration 3 | |
| M [kNm] | 212.3 | 241.1 | 399.1 | 416.5 | 355.6 | 391.8 |
| Q1 [kN] | 210 | 198 | 382 | 375 | 400 | 385 |
| Q2 [kN] | 387 | 399 | 714 | 722 | 696 | 711 |
| s1 [mm] | 1.49 | 1.43 | 2.28 | 2.25 | 2.44 | 2.36 |
| s2 [mm] | 2.89 | 3.09 | 4.24 | 4.29 | 4.67 | 5.26 |
| angle φ [rad] | 0.00117 | 0.00138 | 0.00163 | 0.00170 | 0.00186 | 0.00242 |
| M/φ [MNm] | 182 | 174 | 244 | 245 | 191 | 162 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dyka, I.; Klempka, K. Influence of Pile Foundation Stiffness on Column Design in One-Story Reinforced Concrete Frames. Appl. Sci. 2023, 13, 2915. https://doi.org/10.3390/app13052915
Dyka I, Klempka K. Influence of Pile Foundation Stiffness on Column Design in One-Story Reinforced Concrete Frames. Applied Sciences. 2023; 13(5):2915. https://doi.org/10.3390/app13052915
Chicago/Turabian StyleDyka, Ireneusz, and Krzysztof Klempka. 2023. "Influence of Pile Foundation Stiffness on Column Design in One-Story Reinforced Concrete Frames" Applied Sciences 13, no. 5: 2915. https://doi.org/10.3390/app13052915
APA StyleDyka, I., & Klempka, K. (2023). Influence of Pile Foundation Stiffness on Column Design in One-Story Reinforced Concrete Frames. Applied Sciences, 13(5), 2915. https://doi.org/10.3390/app13052915