A Method to Determine the Torque Ripple Harmonic Reduction in Skewed Synchronous Reluctance Machines
Abstract
:1. Introduction
2. Selected Machines
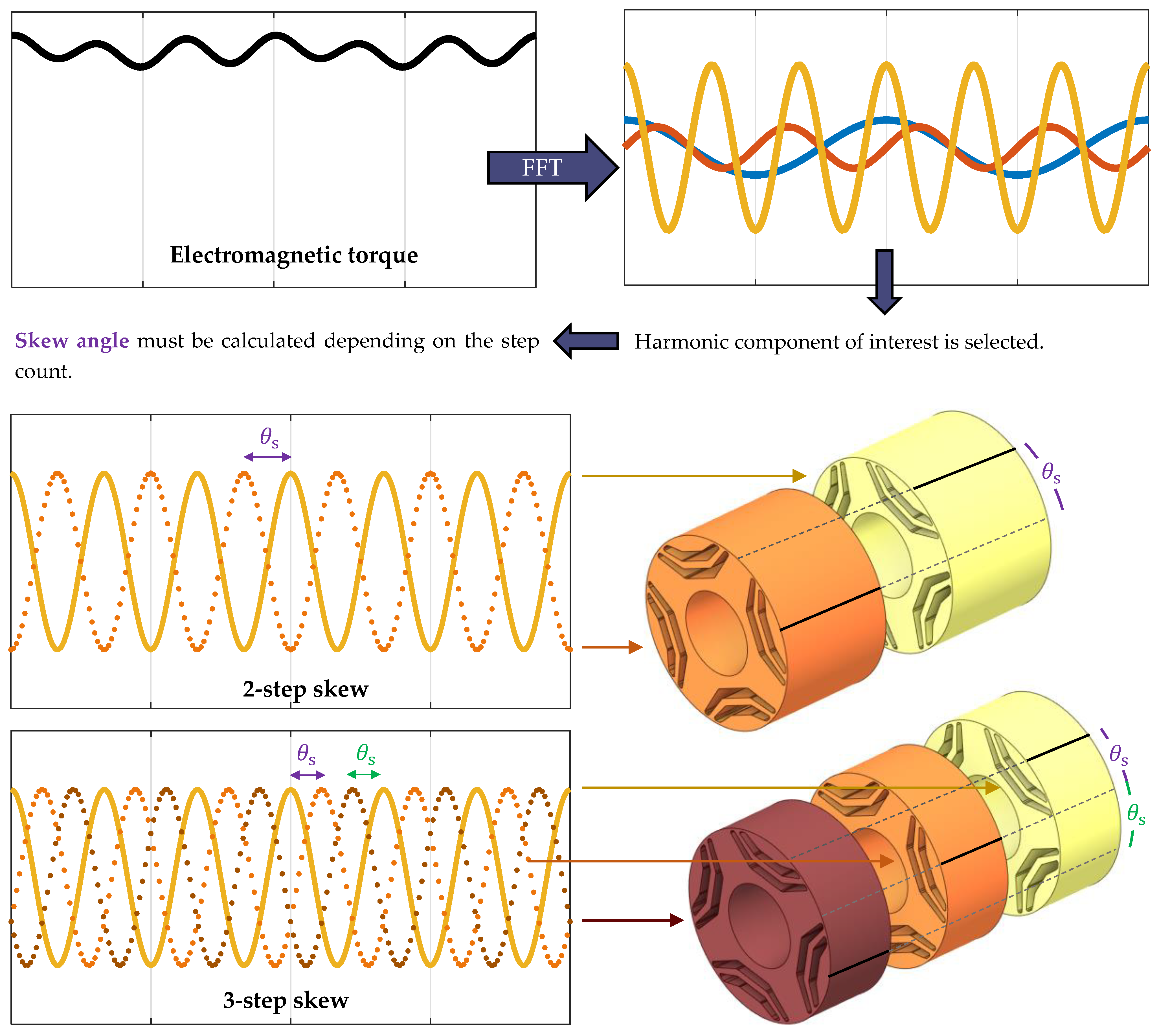
3. Analytical Method Derivation for Discrete Skewing
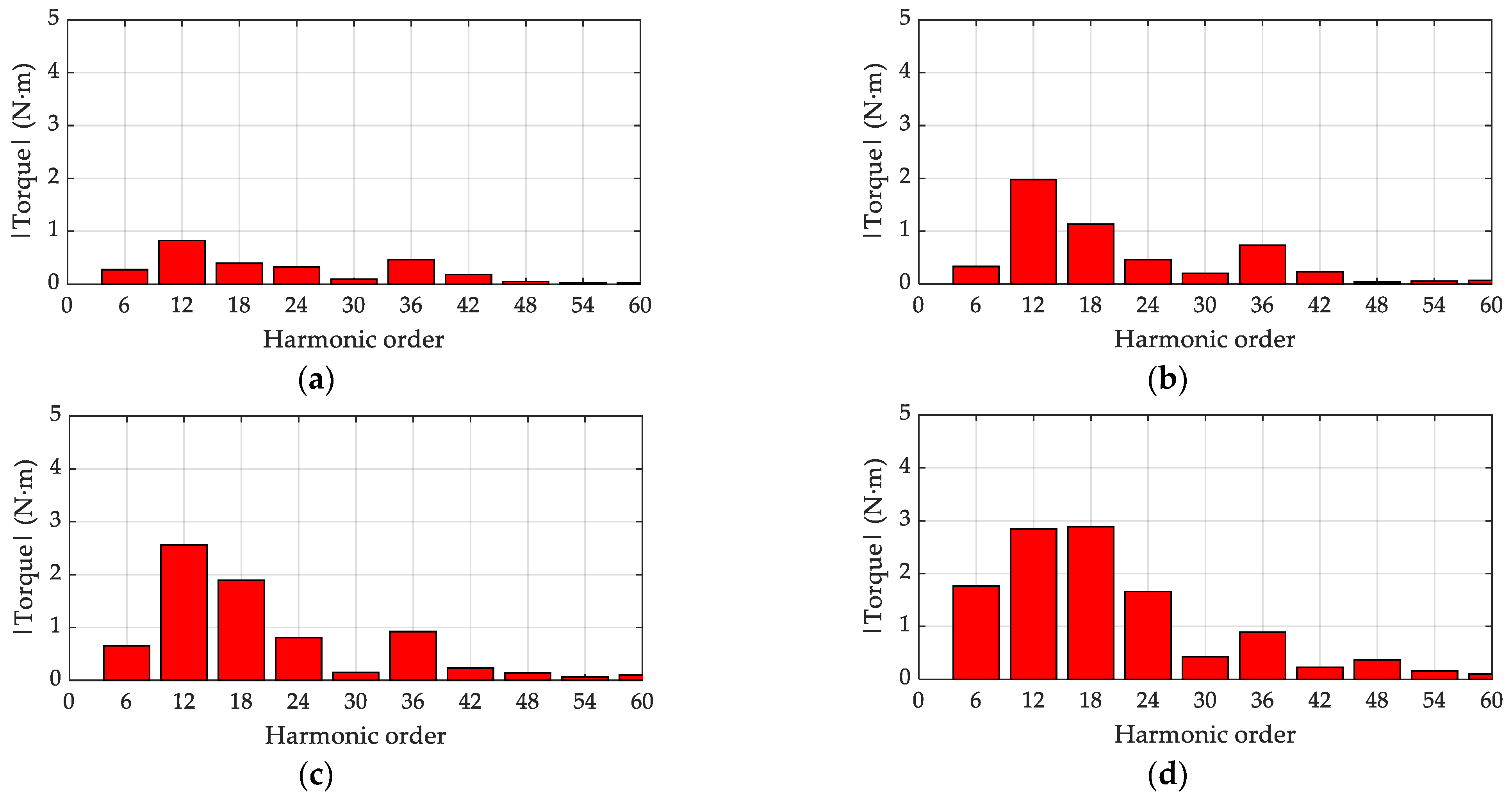
4. Results and Discussion: Finite Element Validation
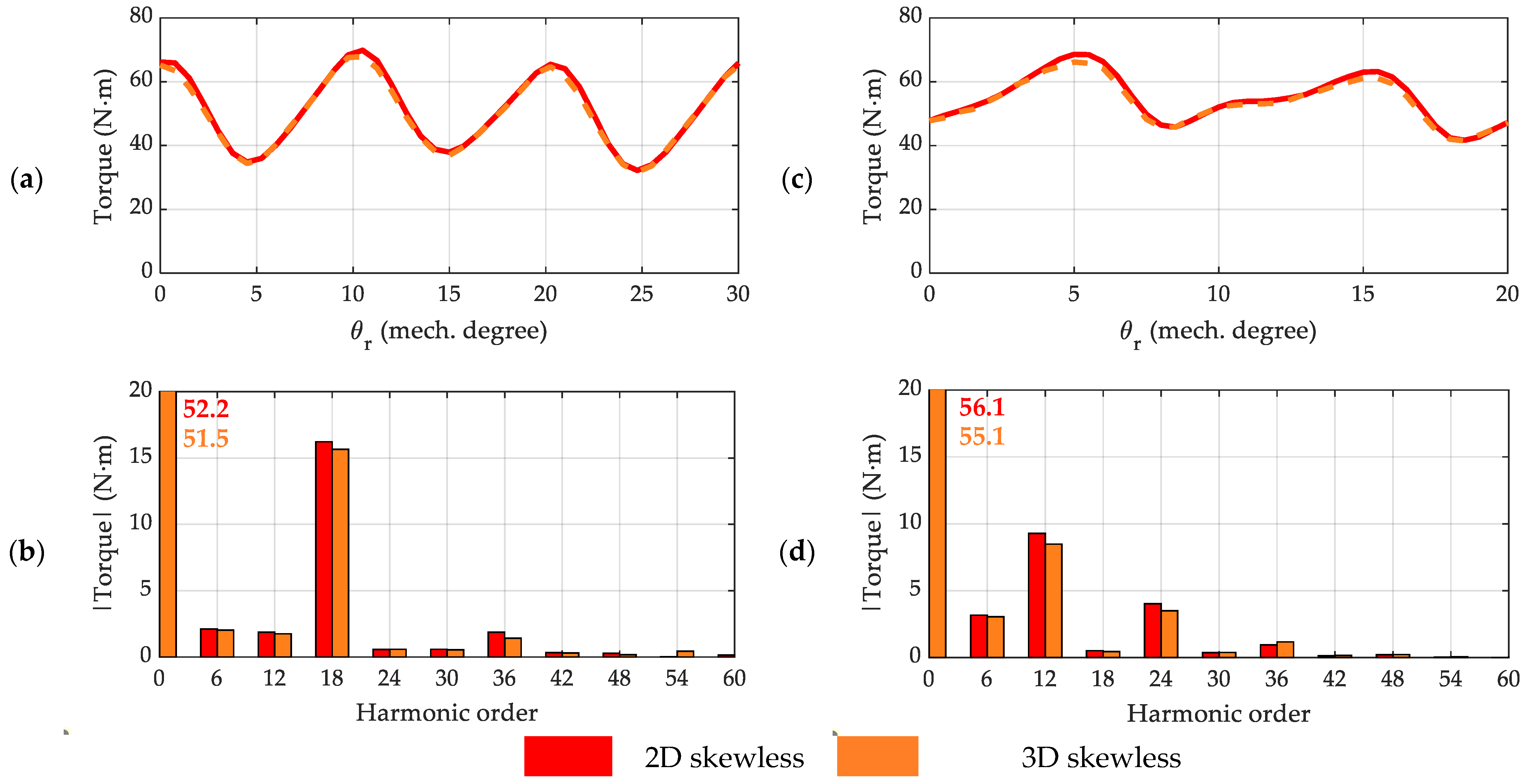
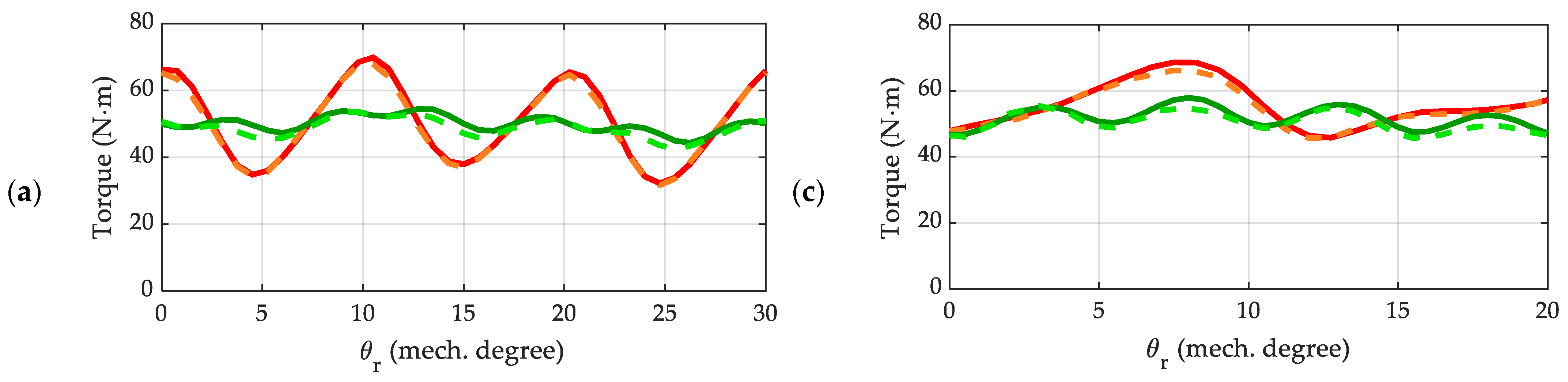
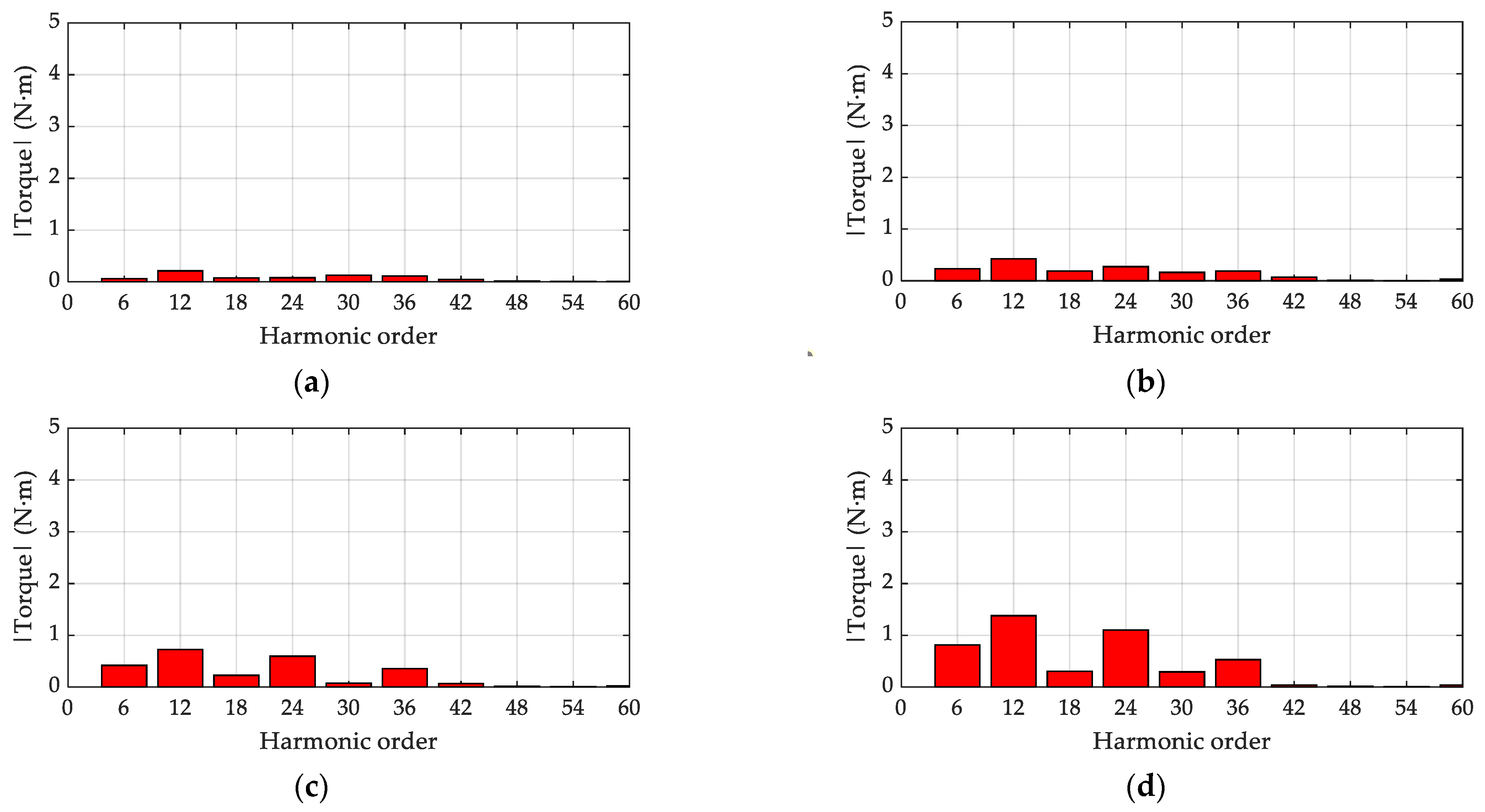
4.1. FEA Evaluation Original Designs (Skewless Machines)
4.2. Evaluation of Torque Ripple Reduction by Means of Two-Step Discrete Skew
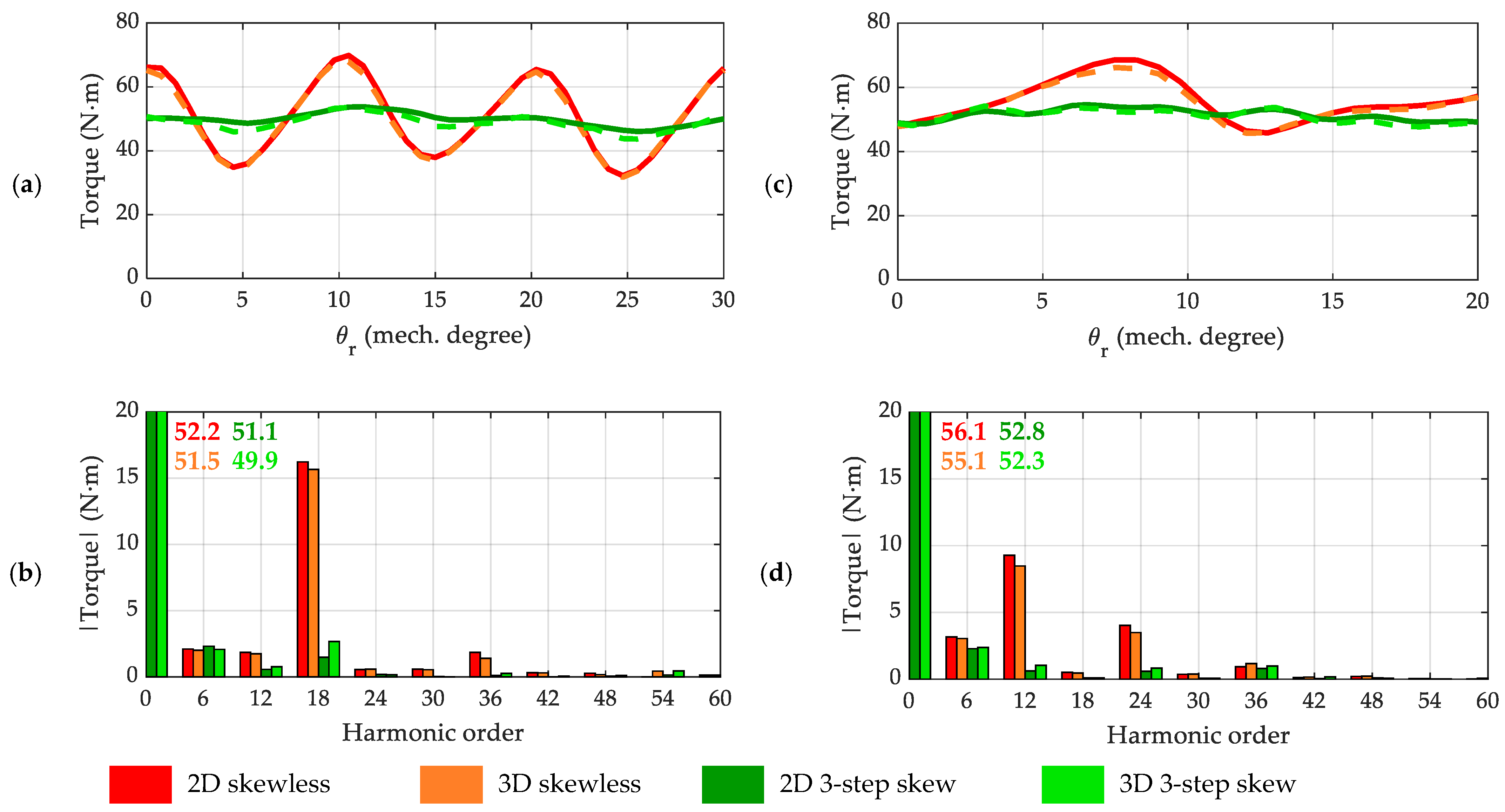
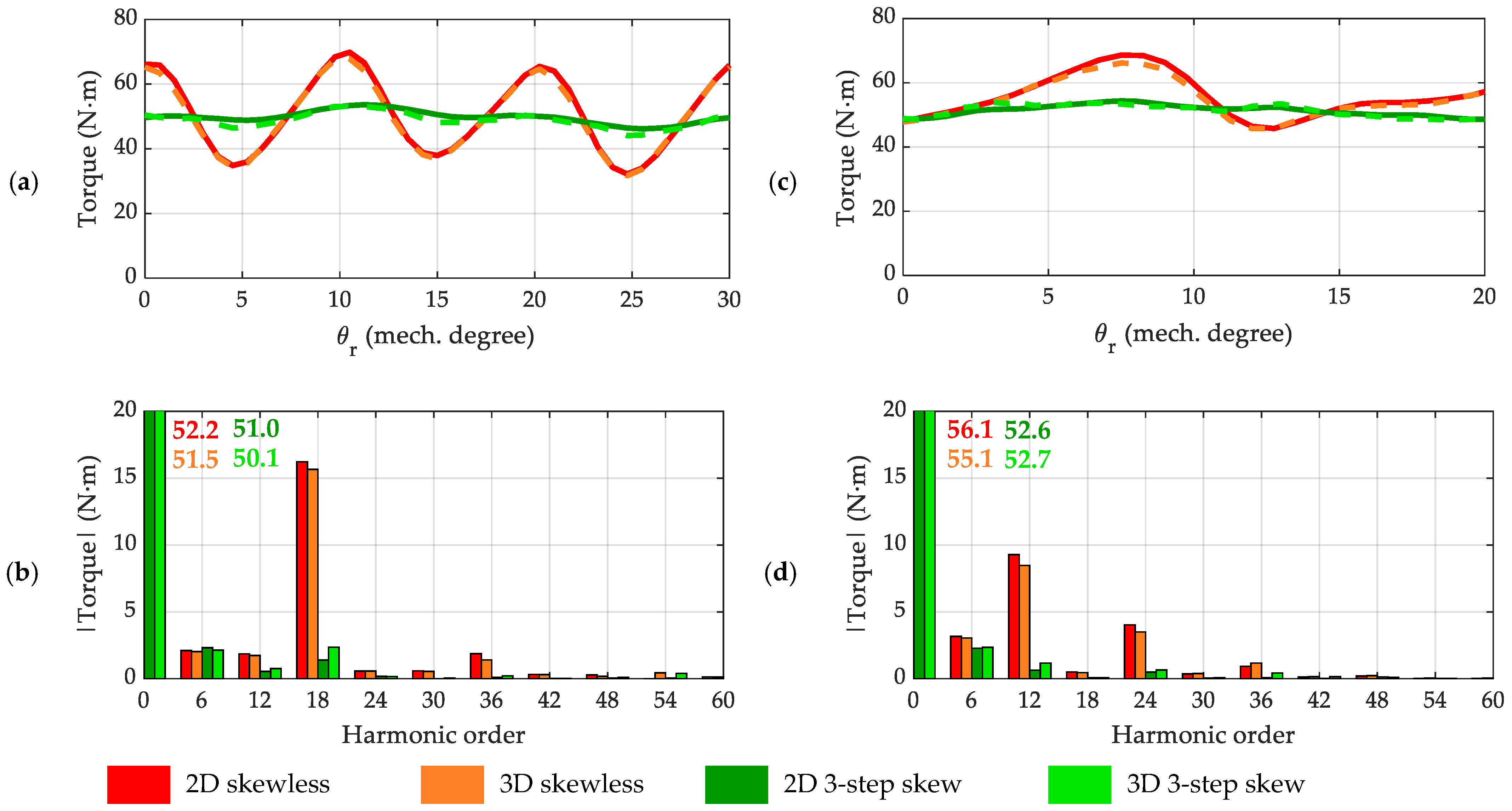
4.3. Evaluation of Torque Ripple Reduction by Means of Three-Step Discrete Skew
4.4. Evaluation of Torque Ripple Reduction by Means of Four-Step Discrete Skew
5. Study Case: Optimized SynRM for Minimum Ripple Torque
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Naseer, M.U.; Kallaste, A.; Asad, B.; Vaimann, T.; Rassõlkin, A. Analytical modelling of synchronous reluctance motor including non-linear magnetic condition. IET Electr. Power Appl. 2022, 16, 511–524. [Google Scholar] [CrossRef]
- Ibrahim, M.N.F.; Abdel-Khalik, A.S.; Rashad, E.M.; Sergeant, P. An Improved Torque Density Synchronous Reluctance Machine With a Combined Star–Delta Winding Layout. IEEE Trans. Energy Convers. 2018, 33, 1015–1024. [Google Scholar] [CrossRef]
- Tawfiq, K.B.; Ibrahim, M.N.; El-Kholy, E.E.; Sergeant, P. Performance Improvement of Synchronous Reluctance Machines—A Review Research. IEEE Trans. Magn. 2021, 57, 1–11. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Sen, B.; Griffo, A.; Sun, Z.; Chong, E. A Fault-Tolerant Machine Drive Based on Permanent Magnet-Assisted Synchronous Reluctance Machine. IEEE Trans. Ind. Appl. 2018, 54, 1349–1359. [Google Scholar] [CrossRef]
- Villani, M.; Fabri, G.; Credo, A.; Di Leonardo, L.; Collazzo, F.P. Line-Start Synchronous Reluctance Motor: A Reduced Manufacturing Cost Avenue to Achieve IE4 Efficiency Class. IEEE Access 2022, 10, 100094–100103. [Google Scholar] [CrossRef]
- Ozcelik, N.G.; Dogru, U.E.; Imeryuz, M.; Ergene, L.T. Synchronous Reluctance Motor vs. Induction Motor at Low-Power Industrial Applications: Design and Comparison. Energies 2019, 12, 2190. [Google Scholar] [CrossRef] [Green Version]
- Fratta, A.; Toglia, G.P.; Vagati, A.; Villata, F. Ripple evaluation of high-performance synchronous reluctance machines. IEEE Ind. Appl. Mag. 1995, 1, 14–22. [Google Scholar] [CrossRef]
- Zhao, W.; Sun, Y.; Ji, J.; Ren, Z.; Song, X. Phase Shift Technique to Improve Torque of Synchronous Reluctance Machines With Dual M-Phase Windings. IEEE Trans. Ind. Electron. 2021, 69, 5–17. [Google Scholar] [CrossRef]
- Liang, J.; Dong, Y.; Sun, H.; Liu, R.; Zhu, G. Flux-Barrier Design and Torque Performance Analysis of Synchronous Reluctance Motor with Low Torque Ripple. Appl. Sci. 2022, 12, 3958. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Griffo, A.; Sen, B. Experimental assessments of a triple redundant nine-phase fault-tolerant PMA SynRM drive. IEEE Trans. Ind. Electron. 2017, 66, 772–783. [Google Scholar] [CrossRef] [Green Version]
- Sanada, M.; Hiramoto, K.; Morimoto, S.; Takeda, Y. Torque ripple improvement for synchronous reluctance motor using an asymmetric flux barrier arrangement. IEEE Trans. Ind. Appl. 2004, 40, 1076–1082. [Google Scholar] [CrossRef]
- Credo, A.; Villani, M.; Popescu, M.; Riviere, N. Application of Epoxy Resin in Synchronous Reluctance motors with fluid-shaped barriers for e mobility. IEEE Trans. Ind. Appl. 2021, 57, 6440–6452. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Bon, D.; Pre, M.D. Rotor flux-barrier design for torque ripple reduction in synchronous reluctance motors. In Proceedings of the Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, USA, 8–12 October 2006; pp. 1193–1200. [Google Scholar]
- Gallardo, C.; Tapia, J.A.; Degano, M.; Mahmoud, H.; Hoffer, A.E. Rotor Asymmetry Impact on Synchronous Reluctance Machines Performance. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 848–854. [Google Scholar]
- Ferrari, S.; Armando, E.; Pellegrino, G. Torque Ripple Minimization of PM-assisted Synchronous Reluctance Machines via Asymmetric Rotor Poles. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–03 October 2019; pp. 4895–4902. [Google Scholar]
- Ban, B.; Stipetic, S. Systematic Metamodel-Based Optimization Study of Synchronous Reluctance Machine Rotor Barrier Topologies. Machines 2022, 10, 712. [Google Scholar] [CrossRef]
- Ocak, O.; Aydin, M. An Innovative Semi-FEA Based, Variable Magnet-Step-Skew to Minimize Cogging Torque and Torque Pulsations in Permanent Magnet Synchronous Motors. IEEE Access 2020, 8, 210775–210783. [Google Scholar] [CrossRef]
- Xu, M.; Liu, G.; Chen, Q.; Ji, J.; Zhao, W. Design and optimization of a fault tolerant modular permanent magnet assisted synchronous reluctance motor with torque ripple minimization. IEEE Trans. Ind. Electron. 2020, 68, 8519–8530. [Google Scholar] [CrossRef]
- Vagati, A.; Canova, A.; Chiampi, M.; Pastorelli, M.; Repetto, M. Design refinement of synchronous reluctance motors through finite-element analysis. IEEE Trans. Ind. Appl. 2000, 36, 1094–1102. [Google Scholar] [CrossRef]
- Bomela, X.B.; Kamper, M.J. Effect of stator chording and rotor skewing on performance of reluctance synchronous machine. IEEE Trans. Ind. Appl. 2002, 38, 91–100. [Google Scholar] [CrossRef]
- Hamiti, T.; Lubin, T.; Rezzoug, A. A Simple and Efficient Tool for Design Analysis of Synchronous Reluctance Motor. IEEE Trans. Magn. 2008, 44, 4648–4652. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ionel, D.M.; Rallabandi, V.; Jiang, M.; Stretz, S.J. Large-Scale Optimization of Synchronous Reluctance Machines Using CE-FEA and Differential Evolution. IEEE Trans. Ind. Appl. 2016, 52, 4699–4709. [Google Scholar] [CrossRef]
- Juergens, J.; Fricassè, A.; Marengo, L.; Gragger, J.; De Gennaro, M.; Ponick, B. Innovative design of an air cooled ferrite permanent magnet assisted synchronous reluctance machine for automotive traction application. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 803–810. [Google Scholar]
- Ban, B.; Stipetic, S.; Jercic, T. Minimum Set of Rotor Parameters for Synchronous Reluctance Machine and Improved Optimization Convergence via Forced Rotor Barrier Feasibility. Energies 2021, 14, 2744. [Google Scholar] [CrossRef]
- Bernard, N.; Dang, L.; Moreau, L.; Bourguet, S. A Pre-Sizing Method for Salient Pole Synchronous Reluctance Machines with Loss Minimization Control for a Small Urban Electrical Vehicle Considering the Driving Cycle. Energies 2022, 15, 9110. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Bon, D.; Pre, M.D. Rotor Flux-Barrier Design for Torque Ripple Reduction in Synchronous Reluctance and PM-Assisted Synchronous Reluctance Motors. IEEE Trans. Ind. Appl. 2009, 45, 921–928. [Google Scholar] [CrossRef]
- Bianchi, N.; Fornasiero, E.; Carraro, E.; Bolognani, S.; Castiello, M. Electric vehicle traction based on a PM assisted synchronous reluctance motor. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014. [Google Scholar]
- Lazari, P.; Wang, J.; Sen, B. 3-D Effects of Rotor Step-Skews in Permanent Magnet-Assisted Synchronous Reluctance Machines. IEEE Trans. Magn. 2015, 51, 8112704. [Google Scholar] [CrossRef]
- Hofer, M.; Schroedl, M. Comparison of a flux barrier and a salient pole synchronous reluctance machine for high rotational speeds in electric traction applications. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar]
- Lee, T.-H.; Lee, J.-H.; Yi, K.-P.; Lim, D.-K. Optimal Design of a Synchronous Reluctance Motor Using a Genetic Topology Algorithm. Processes 2021, 9, 1778. [Google Scholar] [CrossRef]
- Lee, T.-H.; Lim, D.-K.; Moon, K.-Y.; Jeon, K.-W. Topology Optimization Combined with a Parametric Algorithm for Industrial Synchronous Reluctance Motor Design. Processes 2022, 10, 746. [Google Scholar] [CrossRef]
- Baziruwiha, J.-C.; Kamper, M.J.; Botha, S. High Pole Number Epoxy-Casted Rotor Reluctance Synchronous Wind Generator. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–8. [Google Scholar]
- Howard, E.; Kamper, M.J.; Gerber, S. Asymmetric Flux Barrier and Skew Design Optimization of Reluctance Synchronous Machines. IEEE Trans. Ind. Appl. 2015, 51, 3751–3760. [Google Scholar] [CrossRef]
- Hubert, T.; Reinlein, M.; Kremser, A.; Herzog, H.-G. Torque ripple minimization of reluctance synchronous machines by continuous and discrete rotor skewing. In Proceedings of the 2015 5th International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 15–16 September 2015; pp. 1–7. [Google Scholar]
- Korman, O.; Nardo, M.D.; Degano, M.; Gerada, C. A Novel Flux Barrier Parametrization for Synchronous Reluctance Machines. IEEE Trans. Energy Convers. 2022, 37, 675–684. [Google Scholar] [CrossRef]
- Islam, M.S.; Shrestha, A.; Islam, M. Effect of Step Skew in Synchronous Reluctance Machines for High Performance Applications. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–6. [Google Scholar]
- Cai, S.; Hao, H.; Jin, M.-J.; Shen, J.-X. A simplified method to analyze synchronous reluctance machine. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016; pp. 1–6. [Google Scholar]
- Ibrahim, M.N.F.; Sergeant, P.; Rashad, E. Simple design approach for low torque ripple and high output torque synchronous reluctance motors. Energies 2016, 9, 942. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, N.; Degano, M.; Fornasiero, E. Sensitivity Analysis of Torque Ripple Reduction of Synchronous Reluctance and Interior PM Motors. IEEE Trans. Ind. Appl. 2015, 51, 187–195. [Google Scholar] [CrossRef]
- Fitouri, M.; Bensalem, Y.; Abdelkrim, M.N. Comparison Between 2D and 3D Modeling of Permanent Magnet Synchronous Motor Using FEM Simulations. In Proceedings of the 2020 17th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 20–23 July 2020; pp. 681–685. [Google Scholar]
- Cupertino, F.; Pellegrino, G.; Gerada, C. Design of synchronous reluctance motors with multiobjective optimization algorithms. IEEE Trans. Ind. Appl. 2014, 50, 3617–3627. [Google Scholar] [CrossRef]
- Degano, M.; Murataliyev, M.; Shuo, W.; Barater, D.; Buticchi, G.; Jara, W.; Bianchi, N.; Galea, M.; Gerada, C. Optimised Design of Permanent Magnet Assisted Synchronous Reluctance Machines for Household Appliances. IEEE Trans. Energy Convers. 2021, 4, 3084–3095. [Google Scholar] [CrossRef]
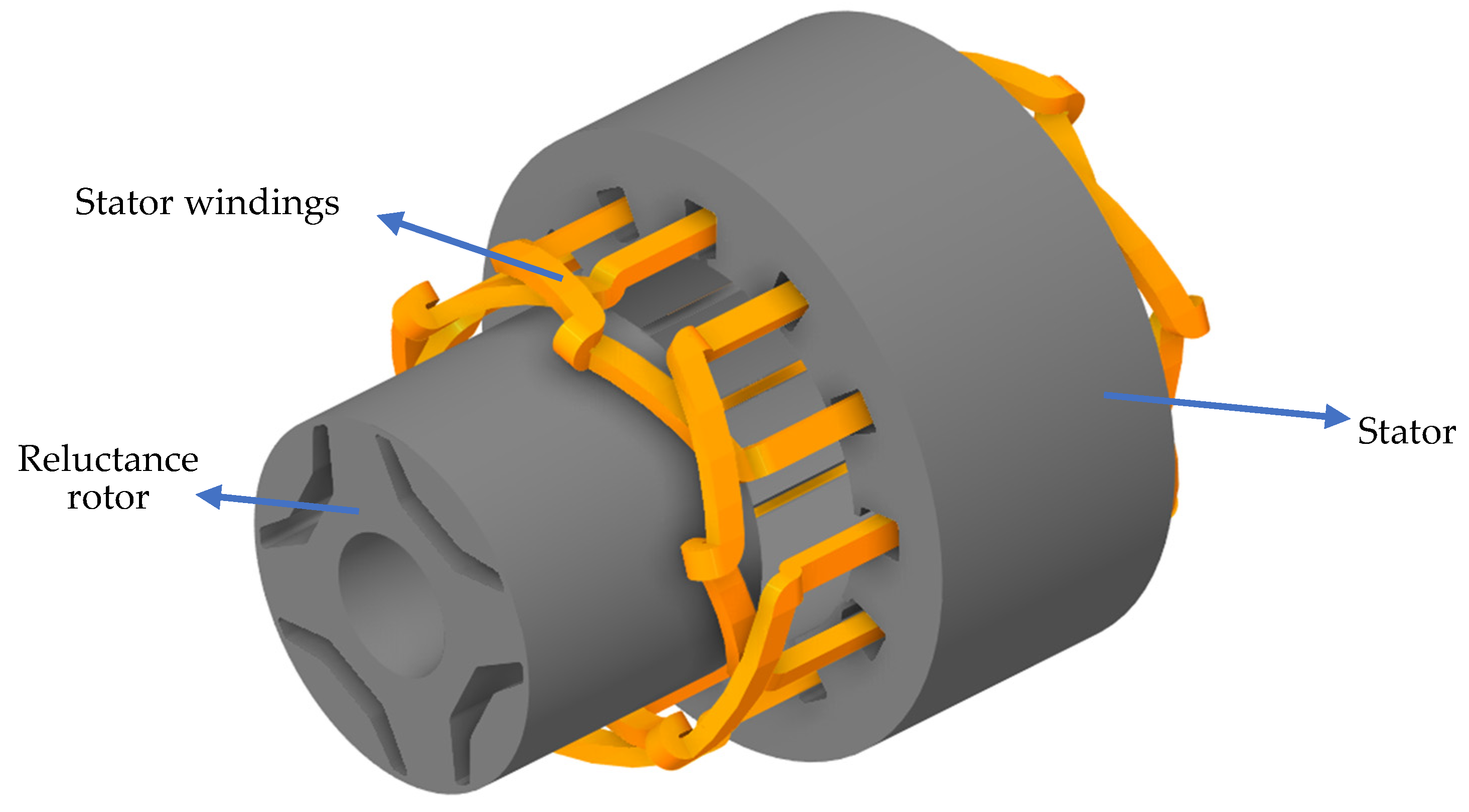
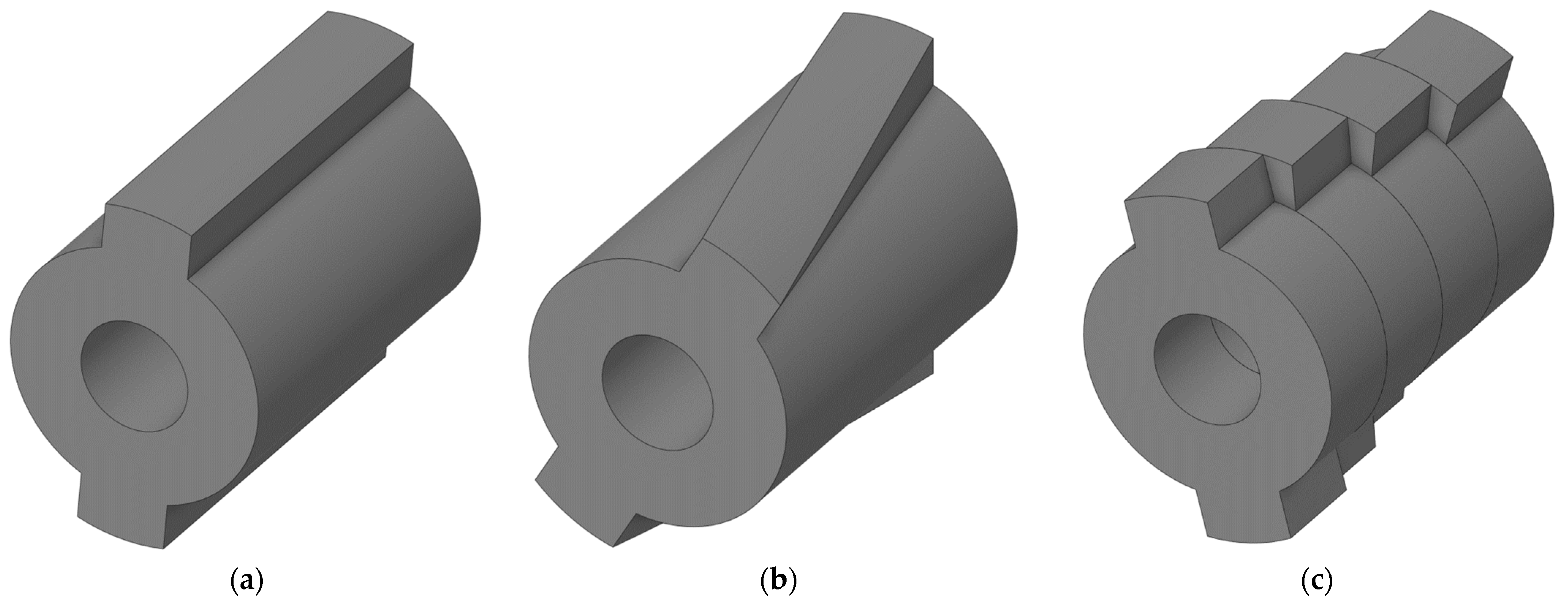



| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Stator outer diameter | 245 | mm | |
| Stator inner diameter | 161.4 | mm | |
| Rotor outer diameter | 160.4 | mm | |
| Rotor inner diameter | 70 | mm | |
| Tooth height | 22.8 | mm | |
| Tooth width | 9 | mm | |
| Air-gap length | 0.5 | mm | |
| Stack length | 120 | mm | |
| Turns per slot | 20 | - | |
| Number of slots | 36 | - | |
| Speed | 3000 | rpm | |
| Current Density | 10 | ||
| Current angle | 60 | electric degrees |
| Harmonic Order | Mechanical Angle for Two-Step Skew | Mechanical Angle for Three-Step Skew | Mechanical Angle for Four-Step Skew | |
|---|---|---|---|---|
| 2p2b | 18th | 5° | 3.33° | 2.5° |
| 3p2b | 12nd | 5° | 3.33° | 2.5° |
| Harmonic Order | Four-Pole SynRM | Six-Pole SynRM | ||
|---|---|---|---|---|
(Analytical) | (FEA) | (Analytical) | (FEA) | |
| 0.87 | 0.95 | 0.71 | 0.77 | |
| 0.50 | 0.45 | 0.00 | 0.06 | |
| 0.00 | 0.10 | - | - | |
| - | - | 1.00 | 0.87 | |
| - | - | - | - | |
| 1.00 | 1.02 | 0.00 | 0.14 | |
| Skewless 2D | Skewless 3D | Two-Step Skew 2D | Two-Step Skew 3D | ||
|---|---|---|---|---|---|
| Four-pole SynRM | 51.0 Nm | 50.2 Nm | 50.0 Nm | 48.7 Nm | |
| 73.9% | 72.1% | 20.2% | 22.6% | ||
| Six-pole SynRM | 54.7 Nm | 53.8 Nm | 51.9 Nm | 50.5 Nm | |
| 49.2% | 45.9% | 21.4% | 19.2% |
| Harmonic Order | Four-Pole SynRM | Six-Pole SynRM | ||
|---|---|---|---|---|
(Analytical) | (FEA) | (Analytical) | (FEA) | |
| 0.84 | 0.95 | 0.67 | 0.70 | |
| 0.45 | 0.45 | 0.00 | 0.06 | |
| 0.00 | 0.09 | - | - | |
| - | - | 0.00 | 0.12 | |
| - | - | - | - | |
| 0.00 | 0.06 | 1.00 | 0.90 | |
| Skewless 2D | Skewless 3D | Three-Step Skew 2D | Three-Step Skew 3D | ||
|---|---|---|---|---|---|
| Four-pole SynRM | 51.0 Nm | 50.2 Nm | 49.9 Nm | 48.7 Nm | |
| 73.9% | 72.1% | 15.6% | 18.3% | ||
| Six-pole SynRM | 54.7 Nm | 53.8 Nm | 51.5 Nm | 51.0 Nm | |
| 49.2% | 45.9% | 11.8% | 12.7% |
| Harmonic Order | Four-Pole SynRM | Six-Pole SynRM | ||
|---|---|---|---|---|
(Analytical) | (FEA) | (Analytical) | (FEA) | |
| 0.84 | 1.01 | 0.65 | 0.74 | |
| 0.43 | 0.35 | 0.00 | 0.06 | |
| 0.00 | 0.08 | - | - | |
| - | - | 0.00 | 0.12 | |
| - | - | - | - | |
| 0.00 | 0.05 | 0.00 | 0.06 | |
| Skewless 2D | Skewless 3D | Four-Step Skew 2D | Four-Step Skew 3D | ||
|---|---|---|---|---|---|
| Four-pole SynRM | 51.0 Nm | 50.2 Nm | 49.8 Nm | 48.7 Nm | |
| 73.9% | 72.1% | 15.0% | 18.3% | ||
| Six-pole SynRM | 54.7 Nm | 53.8 Nm | 51.4 Nm | 51.0 Nm | |
| 49.2% | 45.9% | 11.2% | 12.7% |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Stator outer diameter | 246 | mm | |
| Stator inner diameter | 161.4 | mm | |
| Rotor outer diameter | 160.4 | mm | |
| Rotor inner diameter | 70 | mm | |
| Tooth height | 22.8 | mm | |
| Toot width | 9 | mm | |
| Air-gap length | 0.5 | mm | |
| Stack length | 120 | mm | |
| Number of slots | 36 | - | |
| Number of turns | 20 | - | |
| Number of pole pairs | 3 | ||
| Synchronous speed | 5000 | rpm | |
| Rated current density | 7.5 | ||
| Stacking factor | 0.95 | mm | |
| Lamination thickness | 0.5 | mm |
| Harmonic Order | Mechanical Angle for Two-Step Skew | Mechanical Angle for Three-Step Skew | Mechanical Angle for Four-Step Skew | Mechanical Angle for Five-Step Skew |
|---|---|---|---|---|
| 6th | 10° | 6.66° | 5° | 4° |
| 12th | 5° | 3.33° | 2.5° | 2° |
| 18th | 3.33° | 2.22° | 1.66° | 1.33° |
| Harmonic Order | Mechanical Angle for Two-Step Skew | Mechanical Angle for Three-Step Skew | Mechanical Angle for Four-Step Skew | Mechanical Angle for Five-Step Skew |
|---|---|---|---|---|
| 6th | 0 | 0 | 0 | 0 |
| 12th | 1 | 0 | 0 | 0 |
| 18th | 0 | 1 | 0 | 0 |
| 24th | 1 | 0 | 1 | 0 |
| Harmonic Order | Mechanical Angle for Two-Step Skew | Mechanical Angle for Three-Step Skew | Mechanical Angle for Four-Step Skew | Mechanical Angle for Five-Step Skew |
|---|---|---|---|---|
| 6th | 0.7 | 0.6 | 0.6 | 0.6 |
| 12th | 0 | 0 | 0 | 0 |
| 18th | 0.7 | 0.3 | 0.3 | 0.2 |
| 24th | 1 | 0 | 0 | 0 |
| Harmonic Order | Mechanical Angle for Two-Step Skew | Mechanical Angle for Three-Step Skew | Mechanical Angle for Four-Step Skew | Mechanical Angle for Five-Step Skew |
|---|---|---|---|---|
| 6th | 0.8 | 0.8 | 0.8 | 0.8 |
| 12th | 0.5 | 0.4 | 0.4 | 0.4 |
| 18th | 0 | 0 | 0 | 0 |
| 24th | 0.5 | 0.3 | 0.2 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallardo, C.; Madariaga, C.; Tapia, J.A.; Degano, M. A Method to Determine the Torque Ripple Harmonic Reduction in Skewed Synchronous Reluctance Machines. Appl. Sci. 2023, 13, 2949. https://doi.org/10.3390/app13052949
Gallardo C, Madariaga C, Tapia JA, Degano M. A Method to Determine the Torque Ripple Harmonic Reduction in Skewed Synchronous Reluctance Machines. Applied Sciences. 2023; 13(5):2949. https://doi.org/10.3390/app13052949
Chicago/Turabian StyleGallardo, César, Carlos Madariaga, Juan A. Tapia, and Michele Degano. 2023. "A Method to Determine the Torque Ripple Harmonic Reduction in Skewed Synchronous Reluctance Machines" Applied Sciences 13, no. 5: 2949. https://doi.org/10.3390/app13052949
APA StyleGallardo, C., Madariaga, C., Tapia, J. A., & Degano, M. (2023). A Method to Determine the Torque Ripple Harmonic Reduction in Skewed Synchronous Reluctance Machines. Applied Sciences, 13(5), 2949. https://doi.org/10.3390/app13052949










