Simplified Calculation of Shear Rotations for First-Order Shear Deformation Theory in Deep Bridge Beams
Abstract
1. Introduction
2. Materials and Methods
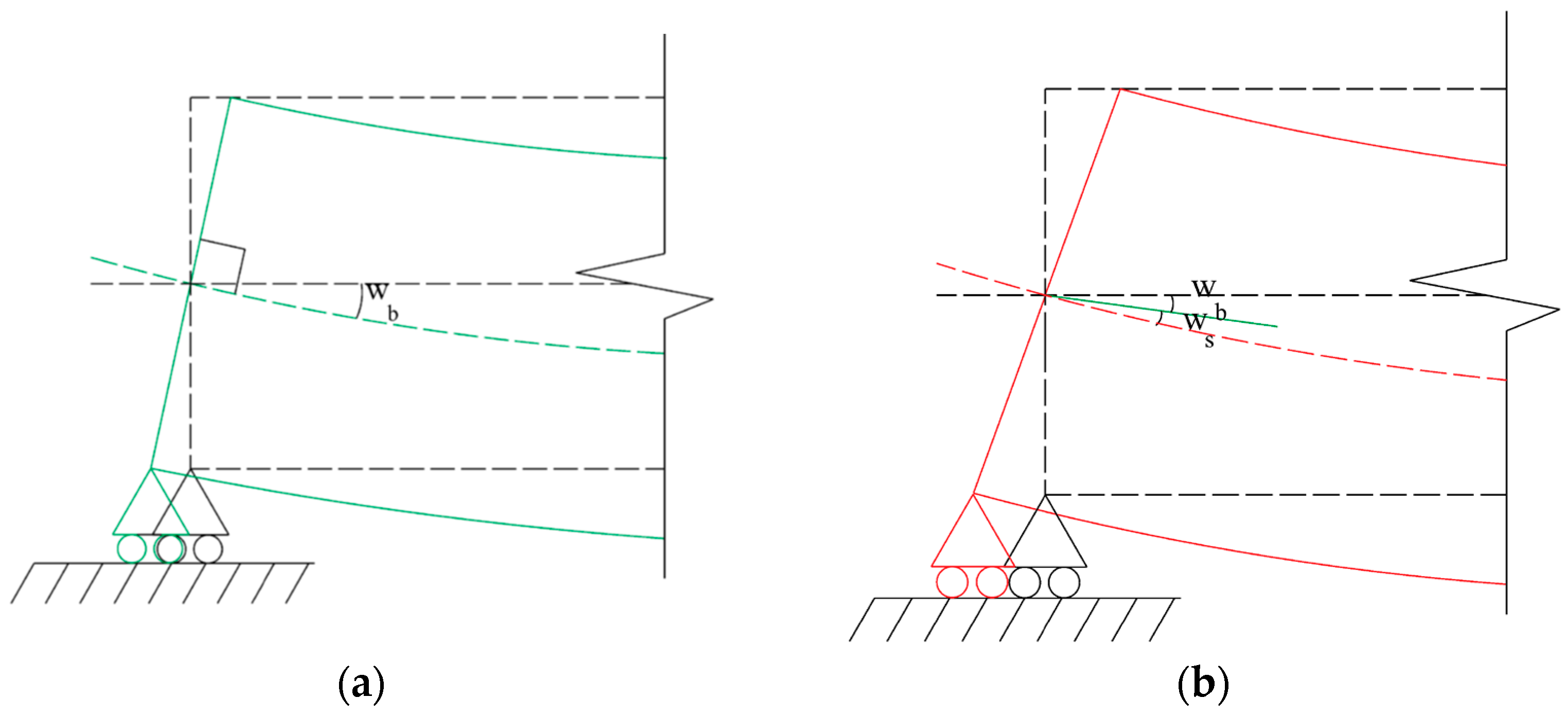
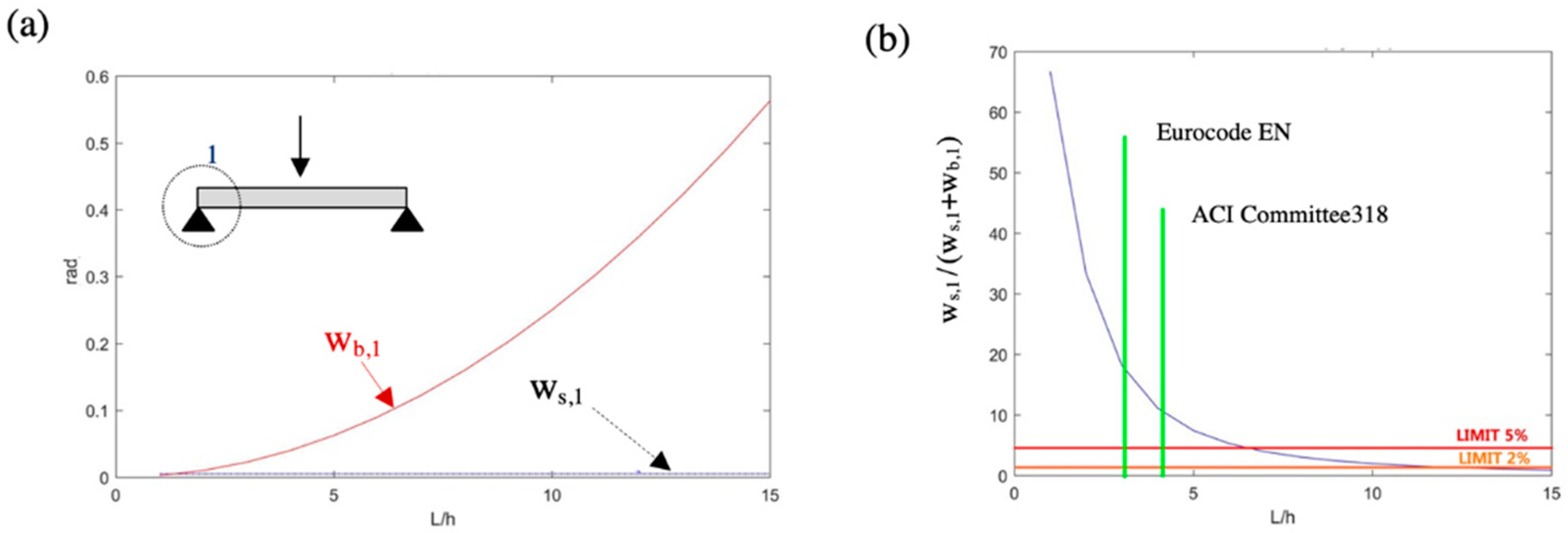
2.1. Example 1: Simply Supported Beam with a Concentrated Load
2.2. Calculation of Total Rotations with Structural Software
- -
- Step 1: calculate the bending rotations (wb,i,j) and the shear forces (Si,j) at each node (i) for each element (j) with the simulation software.
- -
- Step 2: apply Timoshenko’s beam theory to calculate the shear rotations (ws,i,j) at each node (i) for each element (j). According to this theory, the shear rotations can be calculated from G, Av and Si,j. The former two terms can be directly obtained from the mechanical properties of the structure, while Si,j corresponds with the shear forces calculated in step 1.
- -
- Step 3: obtain the real rotations at the ith node at element j by summing up the bending (wb,i) and the shear (ws,i,j) rotations calculated in steps 1 and 2, respectively.
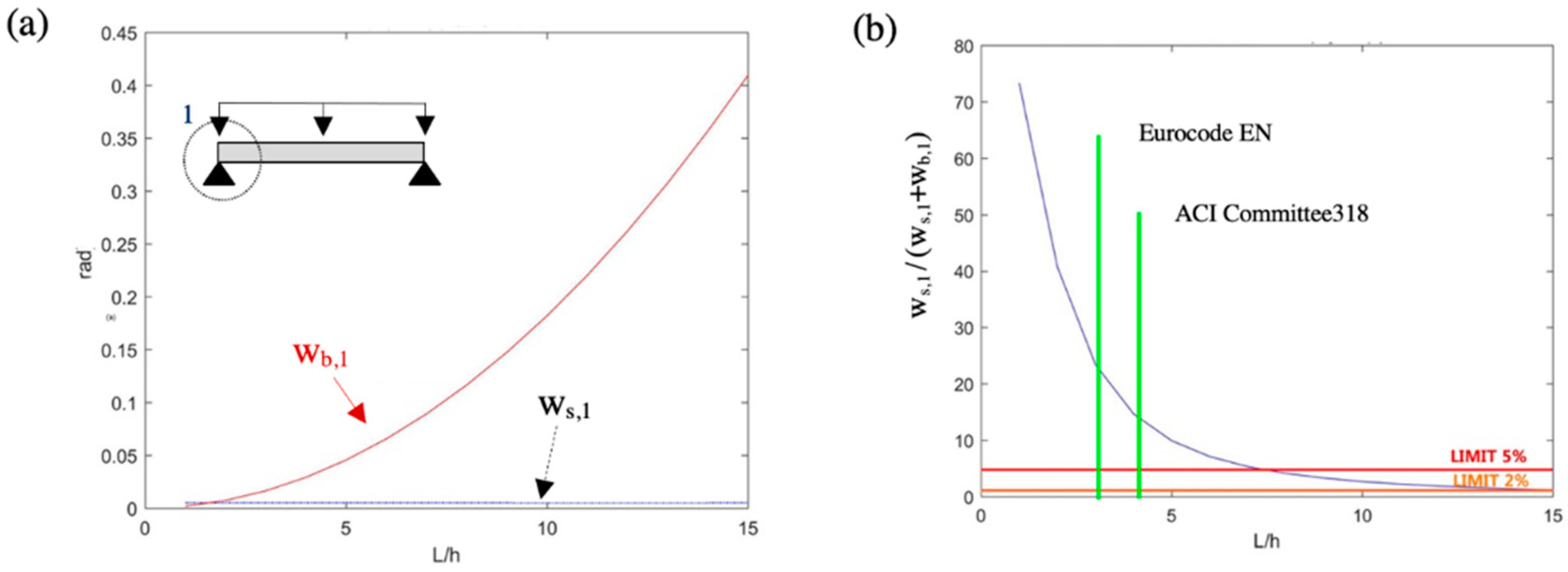
2.3. Example 2: Continuous Beam with a Concentrated Load
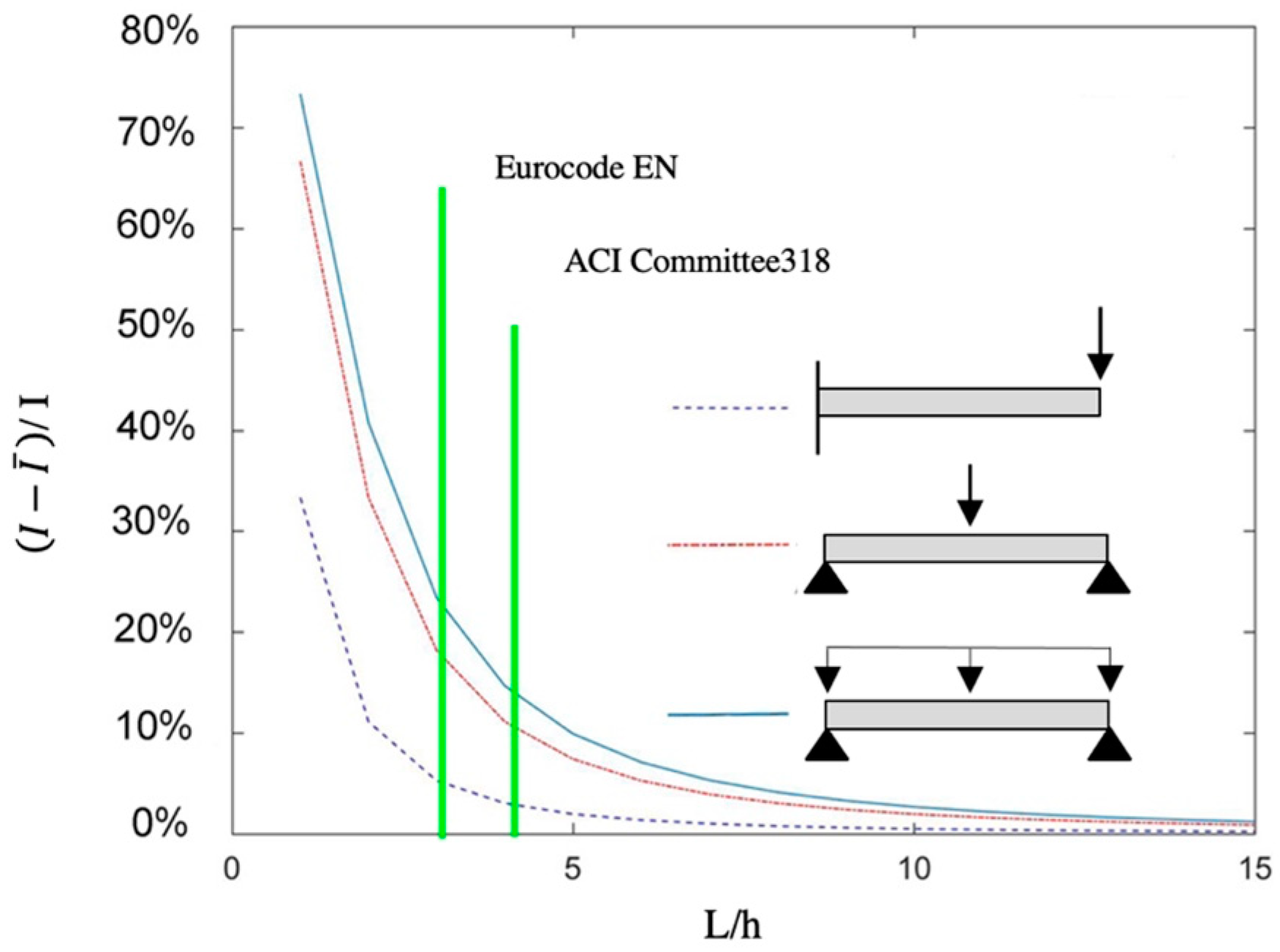
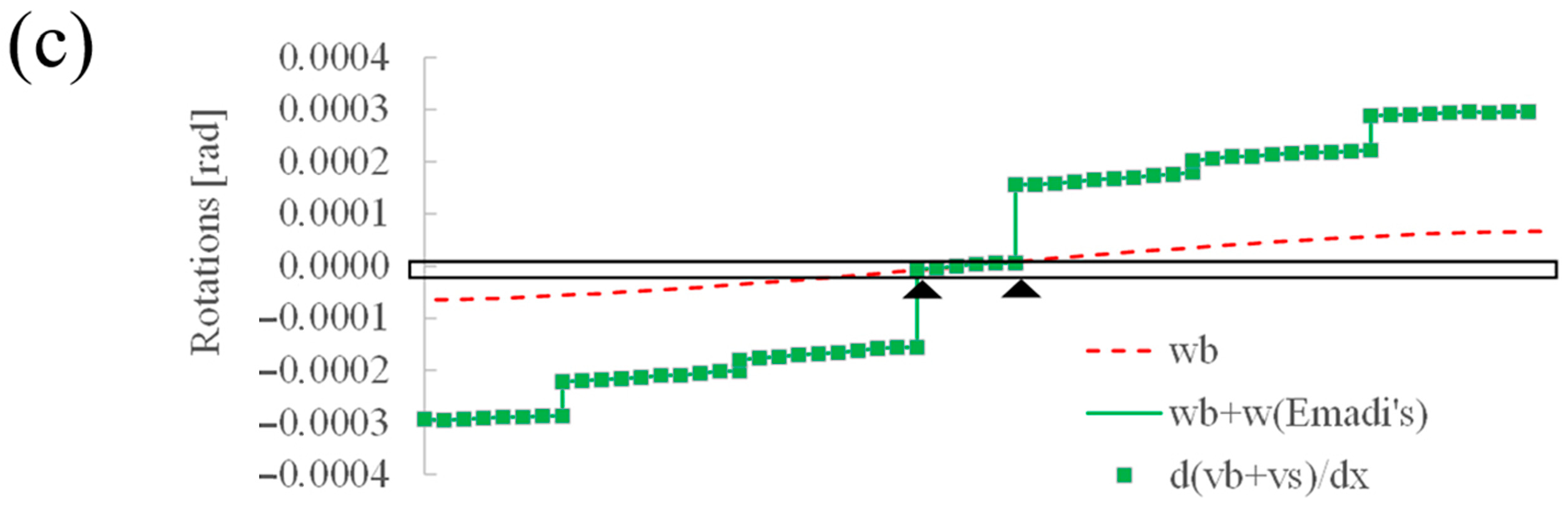
3. Results
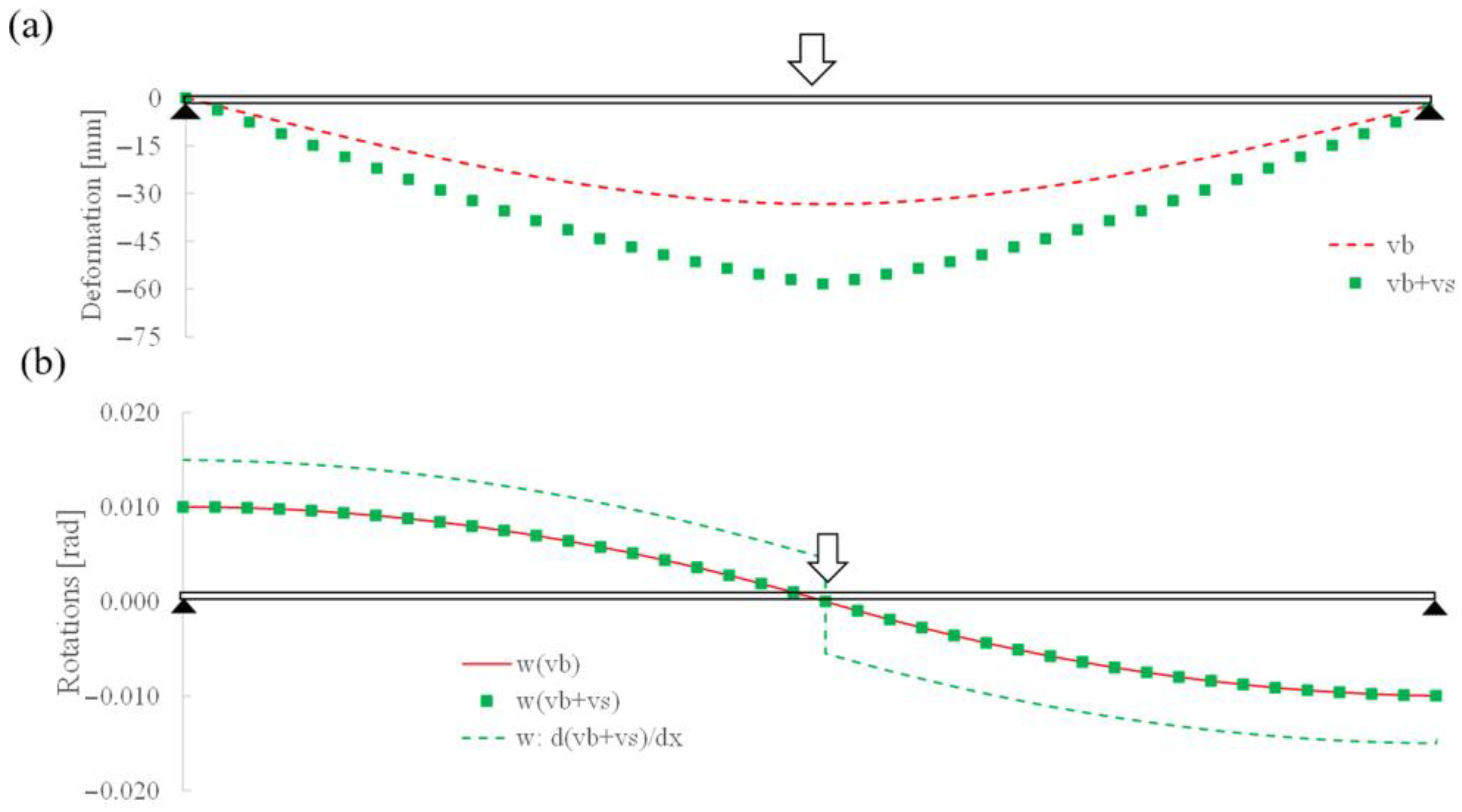
3.1. Direct Analysis
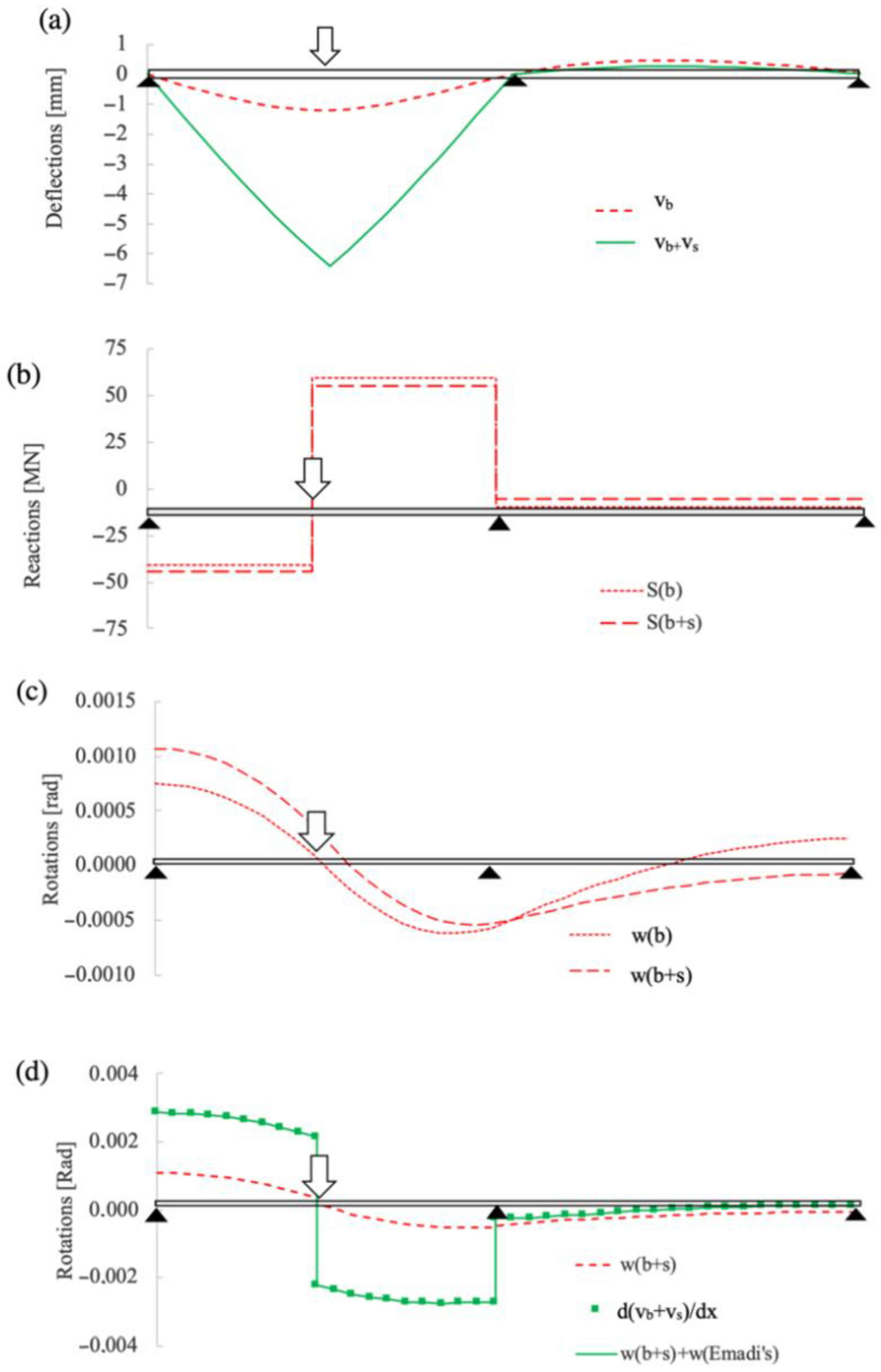
3.2. Inverse Analysis
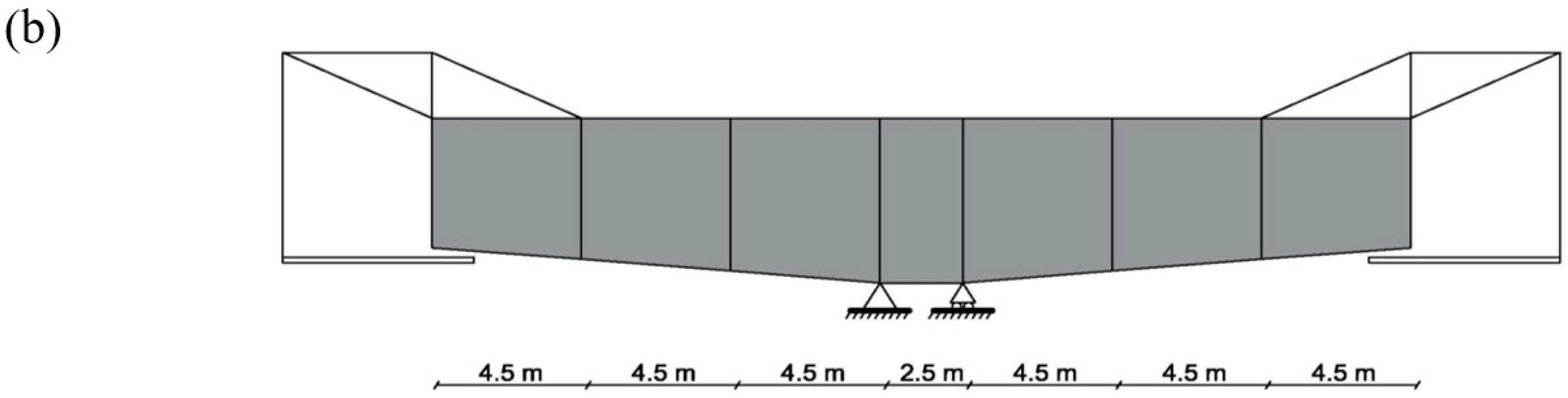
3.3. Application on the Real Bridge
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Vadlamani, S.; Arun, C.O. A stochastic B-spline wavelet on the interval finite element method for beams. Comput. Struct. 2020, 233, 106246. [Google Scholar] [CrossRef]
- Yang, T.; Dabbaghi, F.; Tanhadoust, A.; Emadi, S.; Dehestani, M.; Yousefpour, H. Experimental and numerical investigation on post-fire seismic performance of light weight aggregate reinforced concrete beams. Eng. Struct. 2022, 266, 114791. [Google Scholar] [CrossRef]
- Doğruoğlu, A.N.; Kömürcü, S. Nonlinear mixed finite element formulations for the analysis of planar curved beams. Comput. Struct. 2019, 222, 63–81. [Google Scholar] [CrossRef]
- Chai, H.K.; Tanhadoust, A.; Dabbaghi, F.; Dehestani, M.; Emadi, S.; Yousefpour, H. Predicting compression behavior of lightweight aggregate concrete exposed to high temperature using Long Short-Term Memory (LSTM) neural network approach. Constr. Build. Mater. 2023, 362, 129703. [Google Scholar] [CrossRef]
- Turmo, J.; Lozano-Galant, J.A.; Mirambell, E.; Xu, D. Modeling composite beams with partial interaction. J. Constr. Steel Res. 2015, 114, 380–393. [Google Scholar] [CrossRef]
- Turmo, J.; Banthia, N.; Gettu, R.; Barragán, B. Study of the shear behaviour of fibre reinforced concrete beams. Mater. Construct. 2008, 58, 292. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Kong, L.; Wang, J.; Shen, H. Strain gradient differential quadrature beam finite elements. Comput. Struct. 2019, 218, 170–189. [Google Scholar] [CrossRef]
- Dahake, A.; Ghugal, Y.; Uttam, B.; Kalwane, U.B. Displacements in thick beams using refined shear deformation theory. In Proceedings of 3rd International Conference on Recent Trends in Engineering & Technology; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Dym, C.L.; Williams, H.E. Estimating Fundamental Frequencies of Tall Buildings. J. Struct. Eng. 2007, 133, 1479–1483. [Google Scholar] [CrossRef]
- Timoshenko, S.P. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Philos. Mag. 1921, 41, 742–746. [Google Scholar] [CrossRef]
- Timoshenko, S.P. On the transverse vibrations of bars of uniform cross-section. Philos. Mag. 1922, 43, 125–131. [Google Scholar] [CrossRef]
- Zhou, T.; Chazot, J.-D.; Perrey-Debain, E.; Cheng, L. Performance of the Partition of Unity Finite Element Method for the modeling of Timoshenko beams. Comput. Struct. 2019, 222, 148–154. [Google Scholar] [CrossRef]
- Long, G.; Zhou, R.; Ma, H.; Xin, G.; Emadi, S.; Shi, X. Experimental and Numerical Study on UHPC–RC Decks within Hogging Moment Region. Appl. Sci. 2022, 12, 11446. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, Z.; Ma, H.; Emadi, S.; Cao, Z. Failure mechanism and design method for box girder bridge with interior hinged supports under eccentrically vertical loads. Structures 2023, 48, 438–449. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of Rotatory Inertia and Shear on Flexural Motions of Isotropic, Elastic Plates. ASME J. Appl. Mech. 1951, 18, 31–38. [Google Scholar] [CrossRef]
- Cowper, G.R. The Shear Coefficient in Timoshenko’s Beam Theory. J. Appl. Mech. 1966, 33, 335–340. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method; McGraw-Hill Education: New York, NY, USA, 2006; ISBN 9780072466850. [Google Scholar]
- Bacciocchi, M.; Fantuzzi, N.; Ferreira, A.J.M. Conforming and nonconforming laminated finite element Kirchhoff nanoplates in bending using strain gradient theory. Comput. Struct. 2020, 239, 106322. [Google Scholar] [CrossRef]
- Thomas, D.L.; Wilson, J.M.; Wilson, R.R. Timoshenko beam finite element. J. Sound Vib. 1973, 31, 315–330. [Google Scholar] [CrossRef]
- McCalley, R.B. Rotary Inertia Ccrrectior: For Mass Matrices; Report DIG/SA; General Electric Knolls Atomic Power Laboratory, Schenectady: New York, NY, USA, 1963; pp. 68–73. [Google Scholar]
- Archer, J.S. Consistent matrix formulations for structural analysis using finite-element techniques. Am. Inst. Aeronaut. Astronaut. J. 1965, 3, 1910–1918. [Google Scholar] [CrossRef]
- Kapur, K.K. Vibrations of a Timoshenko beam, using finite element approach. J. Acoust. Soc. Am. 1966, 40, 1058–1063. [Google Scholar] [CrossRef]
- Augarde, C.E. Numerical Modelling of Tunneling Processes for Assessment of Damage to Buildings. Ph.D. Thesis, University of Oxford, Oxford, UK, 1997. [Google Scholar]
- Astley, R.J. Finite Elements in Solids and Structures: An Introduction; Chapman and Hall: London, UK, 1992. [Google Scholar]
- Pickhaver, J.A. Numerical Modelling of Building Response to Tunneling. Ph.D. Thesis, University of Oxford, Oxford, UK, 2006. [Google Scholar]
- Banerjee, J.; Ananthapuvirajah, A. Coupled axial-bending dynamic stiffness matrix for beam elements. Comput. Struct. 2019, 215, 1–9. [Google Scholar] [CrossRef]
- Caliò, I.; D’Urso, D.; Greco, A. The influence of damage on the eigen-properties of Timoshenko spatial arches. Comput. Struct. 2017, 190, 13–24. [Google Scholar] [CrossRef]
- Lozano-Galant, J.A.; Nogal, M.; Paya-Zaforteza, I.; Turmo, J. Structural system identification of cable-stayed bridges with observability techniques. Struct. Infrastruct. Eng. 2014, 10, 1331–1344. [Google Scholar] [CrossRef]
- Lozano-Galant, J.A.; Nogal, M.; Castillo, E.; Turmo, J. Application of Observability Techniques to Structural System Identification. Comput. Civ. Infrastruct. Eng. 2013, 28, 434–450. [Google Scholar] [CrossRef]
- Heyliger, P.R.; Reddy, J.N. A higher order beam finite element for bending and vibration problems. J. Sound Vib. 1988, 126, 309–326. [Google Scholar] [CrossRef]
- Nickel, R.E.; Secor, G.A. Convergence of consistently derived Timoshenko beam finite elements. Int. J. Numer. Methods Eng. 1972, 5, 243–252. [Google Scholar] [CrossRef]
- Prathap, G.; Bhashyam, G.R. Reduced integration and the shear-flexible beam element. Int. J. Numer. Methods Eng. 1982, 18, 195–210. [Google Scholar] [CrossRef]
- Tessler, A.; Dong, S.B. On a hierarchy of conforming timoshenko beam elements. Comput. Struct. 1981, 14, 335–344. [Google Scholar] [CrossRef]
- Przemieniecki, J.S. Theory of Matrix Structural Analysis. Libr. Congr. Cat. Card Number 1968, 67, 19151. [Google Scholar]
- Davis, R.; Henshell, R.D.; Warburton, G.B. A Timoshenko beam element. J. Sound Vib. 1972, 22, 475–487. [Google Scholar] [CrossRef]
- Severn, R.T. Inclusion of shear deformation in the stiffness matrix for a beam element. J. Strain Anal. 1970, 5, 239–241. [Google Scholar] [CrossRef]
- Carnegie, W.; Thomas, J.; Dokumaci, E. An Improved Method of Matrix Displacement Analysis in Vibration Problems. Aeronaut. Q. 1969, 20, 321–332. [Google Scholar] [CrossRef]
- Ali, R.; Hedges, J.L.; Mills, B. The Application of Finite Element Techniques to the Analysis of an Automobile Structure: First Paper: Static Analysis of an Automobile Chassis Frame. Automob. Div. 1971, 185, 665–674. [Google Scholar] [CrossRef]
- Midas Civil [Computer Software] Midas Information Technology Co., Ltd. 2015. Available online: http://en.midasuser.com/product/civil_overview.asp (accessed on 14 February 2019).
- Lei, J.; Xu, D.; Turmo, J. Static structural system identification for beam-like structures using compatibility conditions. Struct. Control Health Monit. 2017, 25, e2062. [Google Scholar] [CrossRef]
- Castillo, E.; Lozano-Galant, J.A.; Nogal, M.; Turmo, J. New tool to help decision making in civil engineering. J. Civ. Eng. Manag. 2015, 21, 689–697. [Google Scholar] [CrossRef]
- Nogal, M.; Lozano-Galant, J.A.; Turmo, J.; Castillo, E. Numerical damage identification of structures by observability techniques based on static loading tests. Struct. Infrastruct. Eng. 2015, 12, 1216–1227. [Google Scholar] [CrossRef]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. CEN: Brussels, Belgium, 2002.
- American Concrete Institute. ACI Committee 318 Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Detroit, MI, USA, 2000. [Google Scholar]
- Tomàs, D.; Lozano-Galant, J.A.; Ramos, G.; Turmo, J. Structural system identification of thin web bridges by observability techniques considering shear deformation. Thin-Walled Struct. 2018, 123, 282–293. [Google Scholar] [CrossRef]
- Lei, J.; Lozano-Galant, J.A.; Nogal, M.; Xu, D.; Turmo, J. Analysis of measurement and simulation errors in structural system identification by observability techniques. Struct. Control Health Monit. 2016, 24, e1923. [Google Scholar] [CrossRef]
- Emadi, S.; Lozano-Galant, J.A.; Xia, Y.; Turmo, J. Structural System Identification including shear deformation of composite bridges from vertical deflections. Steel Compos. Struct. 2019, 32, 731–741. [Google Scholar]
- Lozano-Galant, J.A.; Nogal, M.; Turmo, J.; Castillo, E. Selection of measurement sets in static structural identification of bridges using observability trees. Comput. Concr. 2015, 15, 771–794. [Google Scholar] [CrossRef]
- Chen, H.-L.; Guadalupe, L. Direct Determination of Dynamic Elastic Modulus and Poisson’s Ratio of Rectangular Timoshenko Prisms. J. Eng. Mech. 2019, 145, 04019071. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.-C.; Lin, T.-K.; Tullini, N. Influence of prestressing on the behavior of uncracked concrete beams with a parabolic bonded tendon. Struct. Eng. Mechan. 2021, 77, 1–17. [Google Scholar] [CrossRef]
- Valerio, P.; Ibell, T.J.; Darby, A.P. Shear assessment of prestressed concrete bridges. Proc. Inst. Civ. Eng. Bridg. Eng. 2011, 164, 195–210. [Google Scholar] [CrossRef]
- Dong, X.; Zhao, L.; Xu, Z.; Du, S.; Wang, S.; Wang, X.; Jin, W. Construction of the Yunbao Bridge over the yellow river. In Proceedings of the EASEC-15, Xi’an, China, 11–13 October 2017. [Google Scholar]
- He, J.; Li, X.; Li, C.; Correia, J.A.; Xin, H.; Zhou, M. A novel asynchronous-pouring-construction technology for prestressed concrete box girder bridges with corrugated steel webs. Structures 2020, 27, 1940–1950. [Google Scholar] [CrossRef]
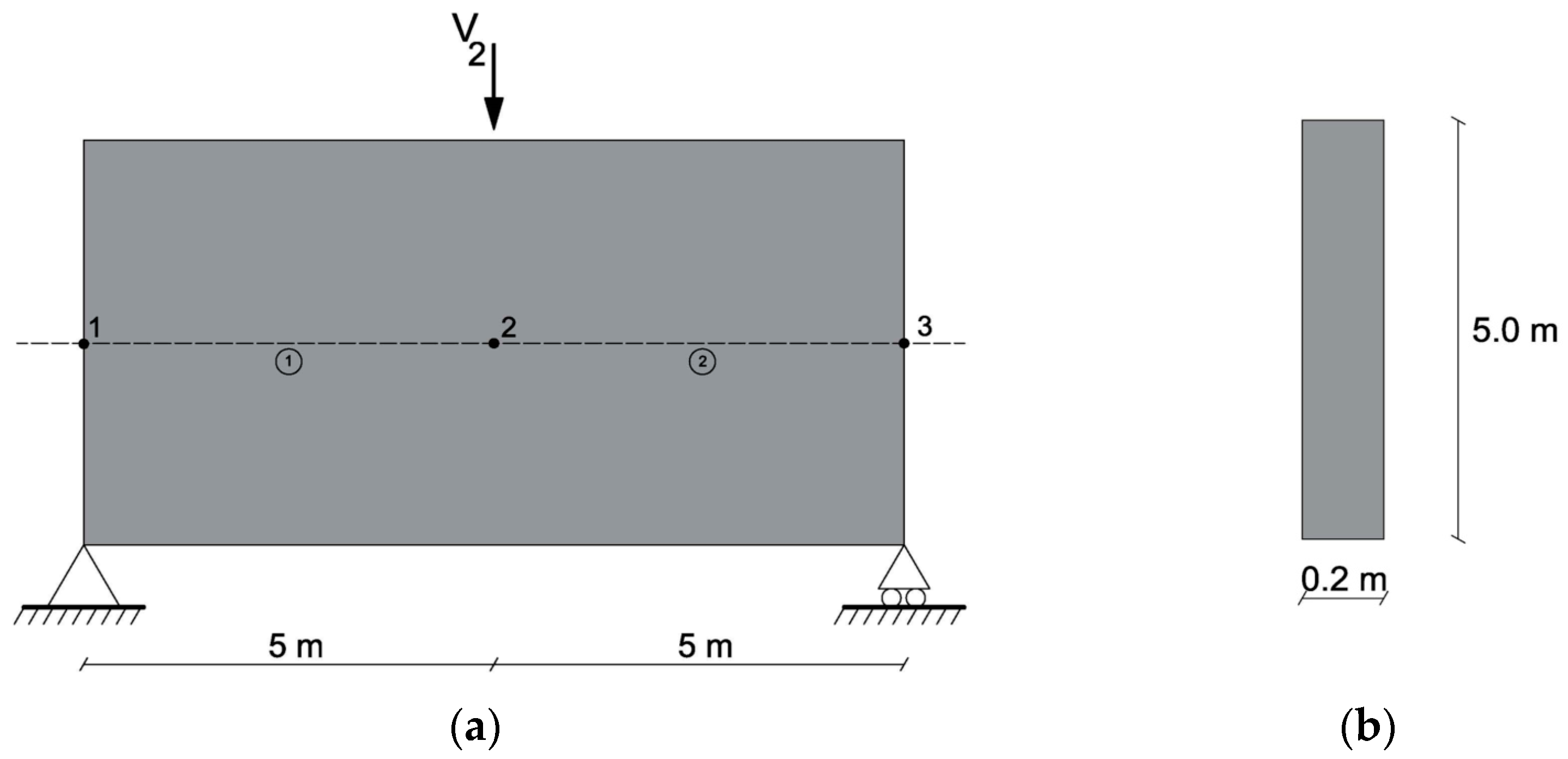




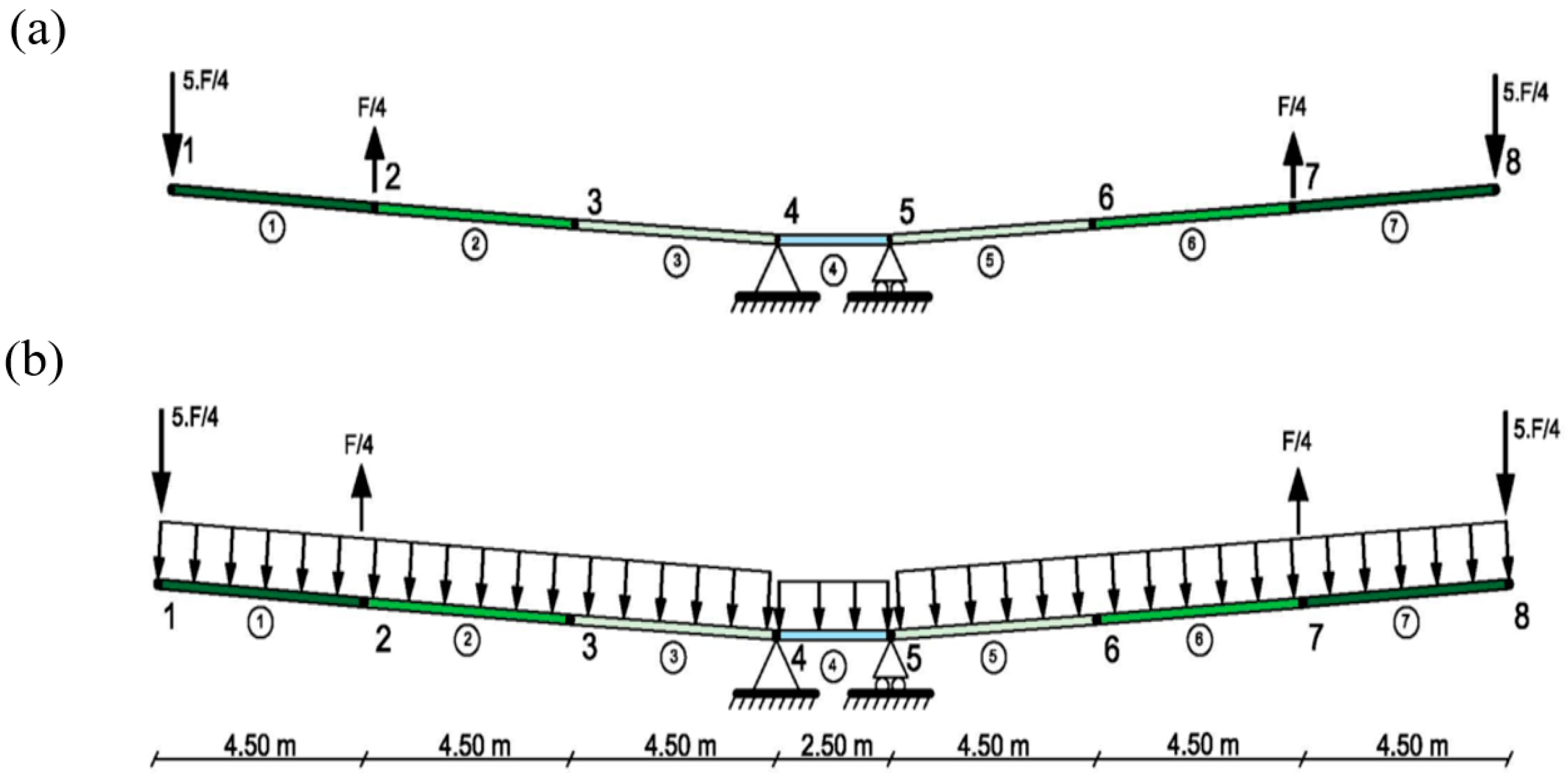

| Properties (Unit) | Value |
|---|---|
| Area (m2) | 1.000 |
| Shear area (m2) | 0.833 |
| Inertia (m4) | 2.083 |
| Young’s modulus (GPa) | 30.000 |
| Poisson’s ratio | 0.250 |
| Method | vb,2 (mm) | vs,2 (mm) | wb,1 (rad) | ws,1 (rad) |
|---|---|---|---|---|
| Timoshenko’s beam theory | 33.34 | 20.00 | 0.010 | 0.005 |
| Midas/Civil without shear | 33.34 | 0.00 | 0.010 | 0.000 |
| Midas/Civil with shear | 33.34 | 20.00 | 0.010 | 0.000 |
| Parameters | Elements 1 and 7 | Elements 2 and 6 | Elements 3 and 5 | Element 4 |
|---|---|---|---|---|
| EA (N) | 4.33 × 1011 | 4.38 × 1011 | 4.43 × 1011 | 4.46 × 1011 |
| GAv (N) | 1.10 × 1010 | 1.25 × 1011 | 1.43 × 1011 | 1.53 × 1011 |
| EI (N·m2) | 1.34 × 1012 | 1.69 × 1012 | 2.13 × 1012 | 2.38 × 1012 |
| Rotation | wb (rad) | ws (rad) | ws/(wb + ws) |
|---|---|---|---|
| w1,1 | −6.6 × 10−5 | −2.3 × 10−4 | 77.7% |
| w2,2 | −5.6 × 10−5 | −1.7 × 10−4 | 74.8% |
| w3,3 | −3.5 × 10−5 | −1.7 × 10−4 | 82.7% |
| w4,4 | −0.8 × 10−5 | −1.5 × 10−4 | 94.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emadi, S.; Ma, H.; Lozano-Galant, J.A.; Turmo, J. Simplified Calculation of Shear Rotations for First-Order Shear Deformation Theory in Deep Bridge Beams. Appl. Sci. 2023, 13, 3362. https://doi.org/10.3390/app13053362
Emadi S, Ma H, Lozano-Galant JA, Turmo J. Simplified Calculation of Shear Rotations for First-Order Shear Deformation Theory in Deep Bridge Beams. Applied Sciences. 2023; 13(5):3362. https://doi.org/10.3390/app13053362
Chicago/Turabian StyleEmadi, Seyyedbehrad, Haiying Ma, Jose Antonio Lozano-Galant, and Jose Turmo. 2023. "Simplified Calculation of Shear Rotations for First-Order Shear Deformation Theory in Deep Bridge Beams" Applied Sciences 13, no. 5: 3362. https://doi.org/10.3390/app13053362
APA StyleEmadi, S., Ma, H., Lozano-Galant, J. A., & Turmo, J. (2023). Simplified Calculation of Shear Rotations for First-Order Shear Deformation Theory in Deep Bridge Beams. Applied Sciences, 13(5), 3362. https://doi.org/10.3390/app13053362









