Behavior of Barrier Wall under Hydrogen Storage Tank Explosion with Simulation and TNT Equivalent Weight Method
Abstract
:1. Introduction
1.1. Objectives
1.2. Composite Structure
1.3. Importance of Study
2. TNT Equivalent Method
2.1. Composite Structure TNT Equivalent Method for Hydrogen Gas in Liquid Form
- MH2 is mass of the hydrogen gas = 300 kg
- QH2 is Explosion energy of Hydrogen gas = 142.5 MJ/kg
- QTNT is explosive energy of TNT = 4.6 MJ/kg
- η is Explosion efficiency (this value is from 0.01 to 0.1) but for this study 0.01 was taken.
2.2. Blast Wave Process
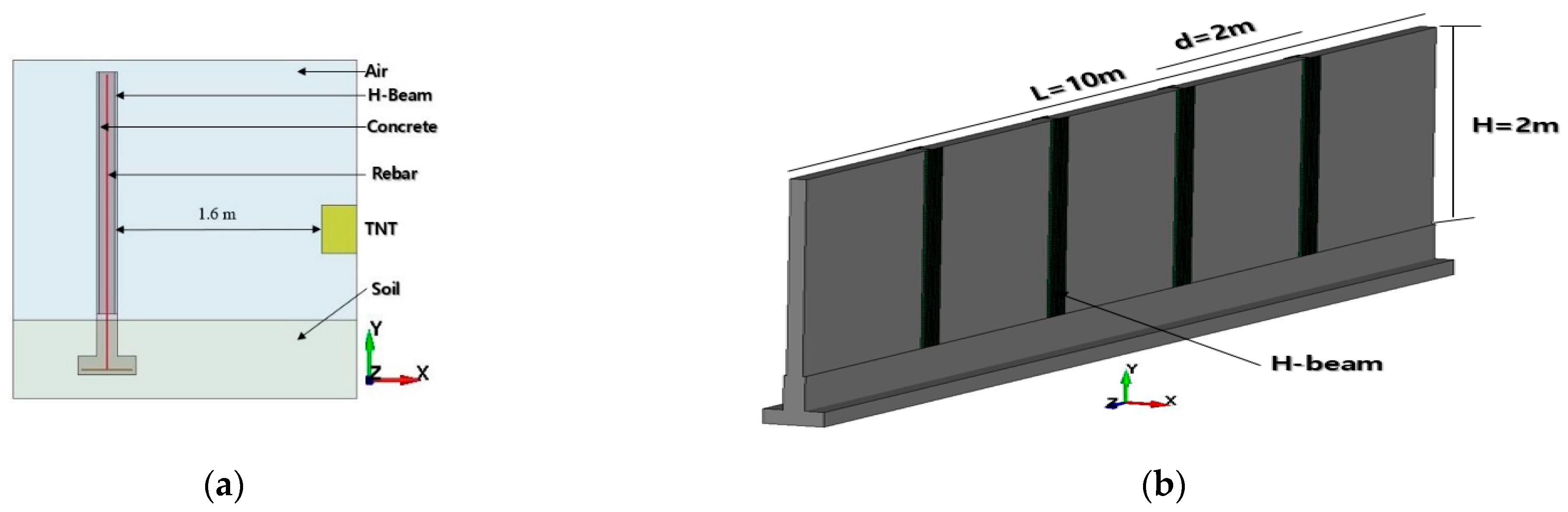
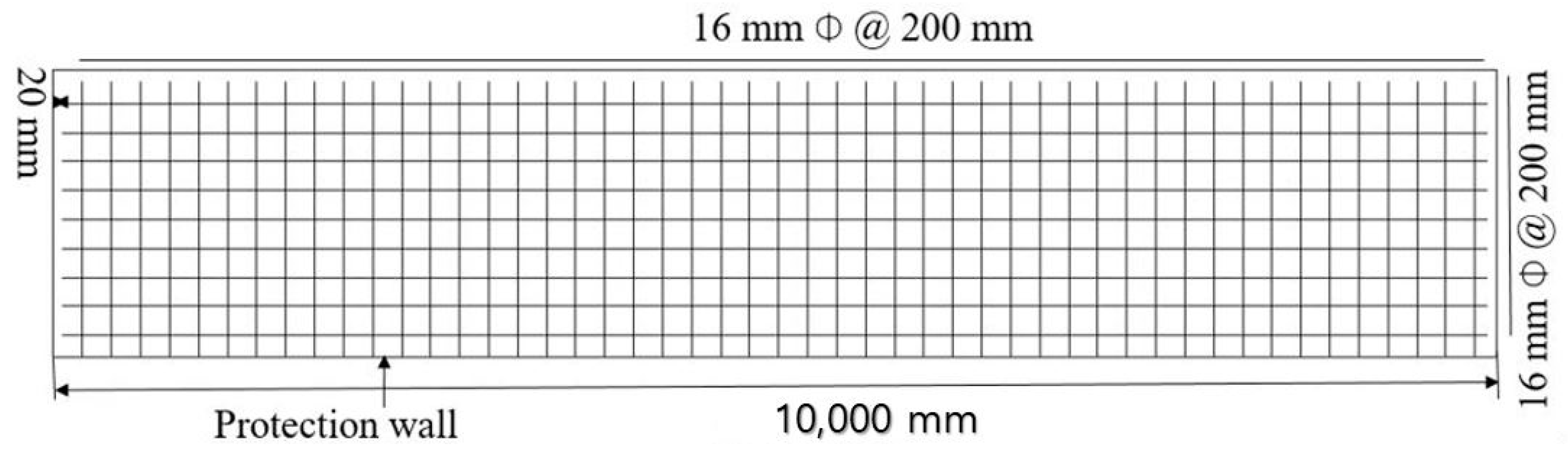
3. Finite Element Modeling
3.1. Modelling of Protection Barrier Wall
3.2. Material Model from LS-DYNA
3.2.1. Concrete Model
3.2.2. Reinforcement and H-Beam
3.2.3. TNT, Air and Soil
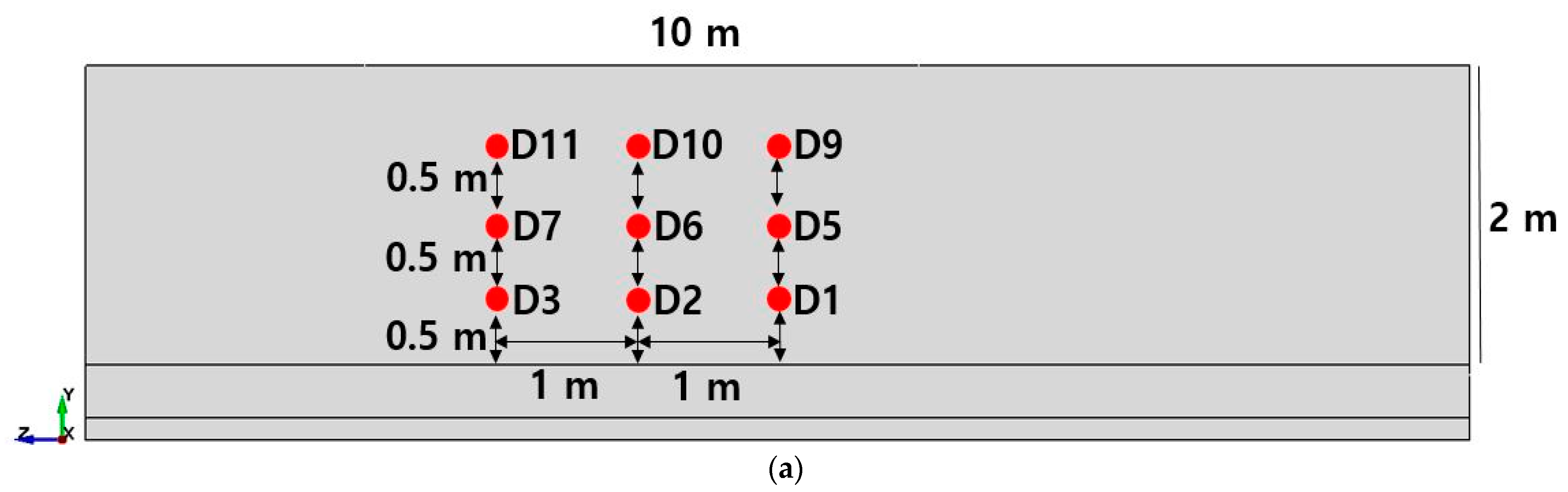
3.2.4. Boundary Condition and Mesh
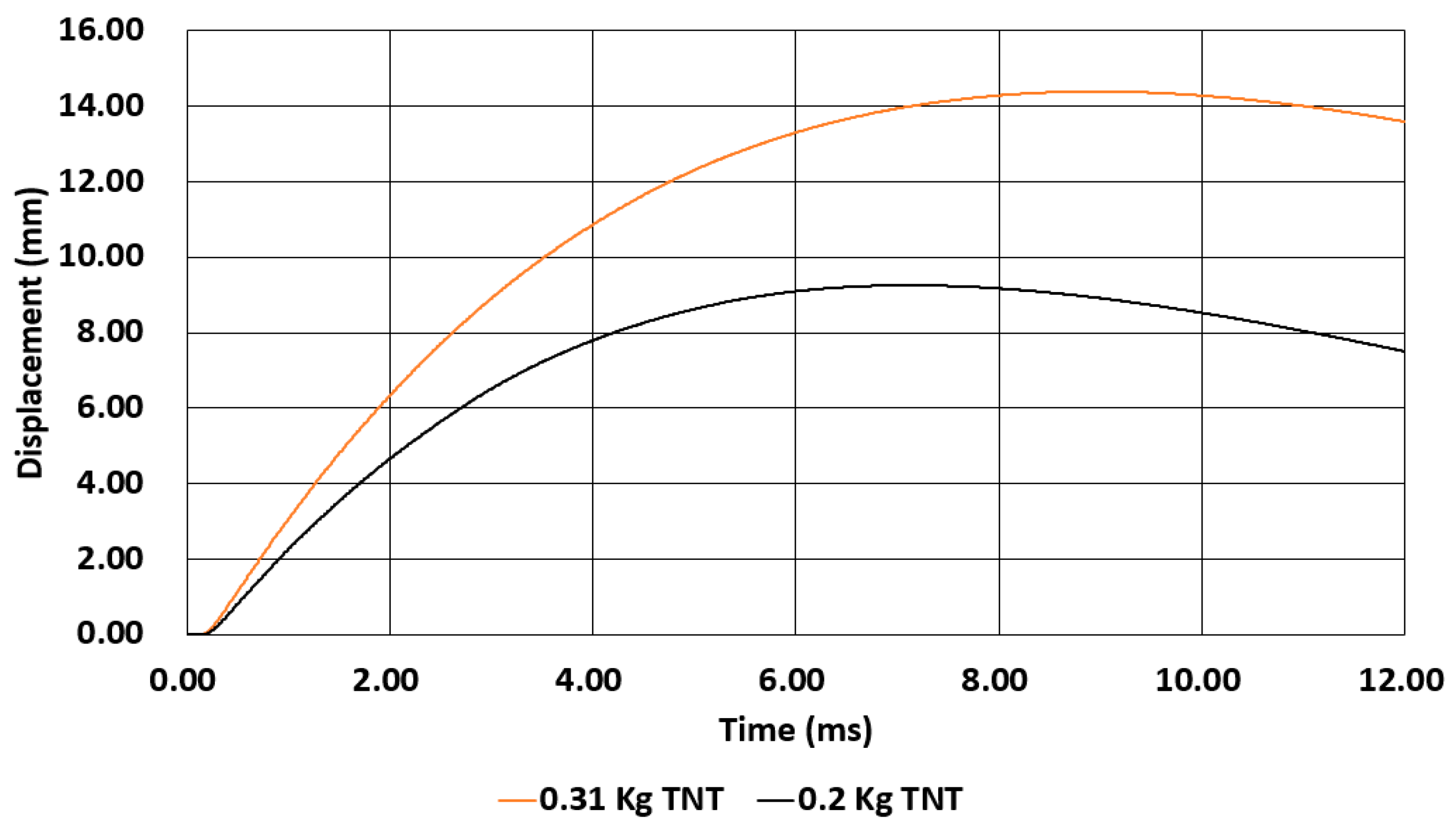
3.2.5. Simulation Analysis of Previous Study [39]
4. Results
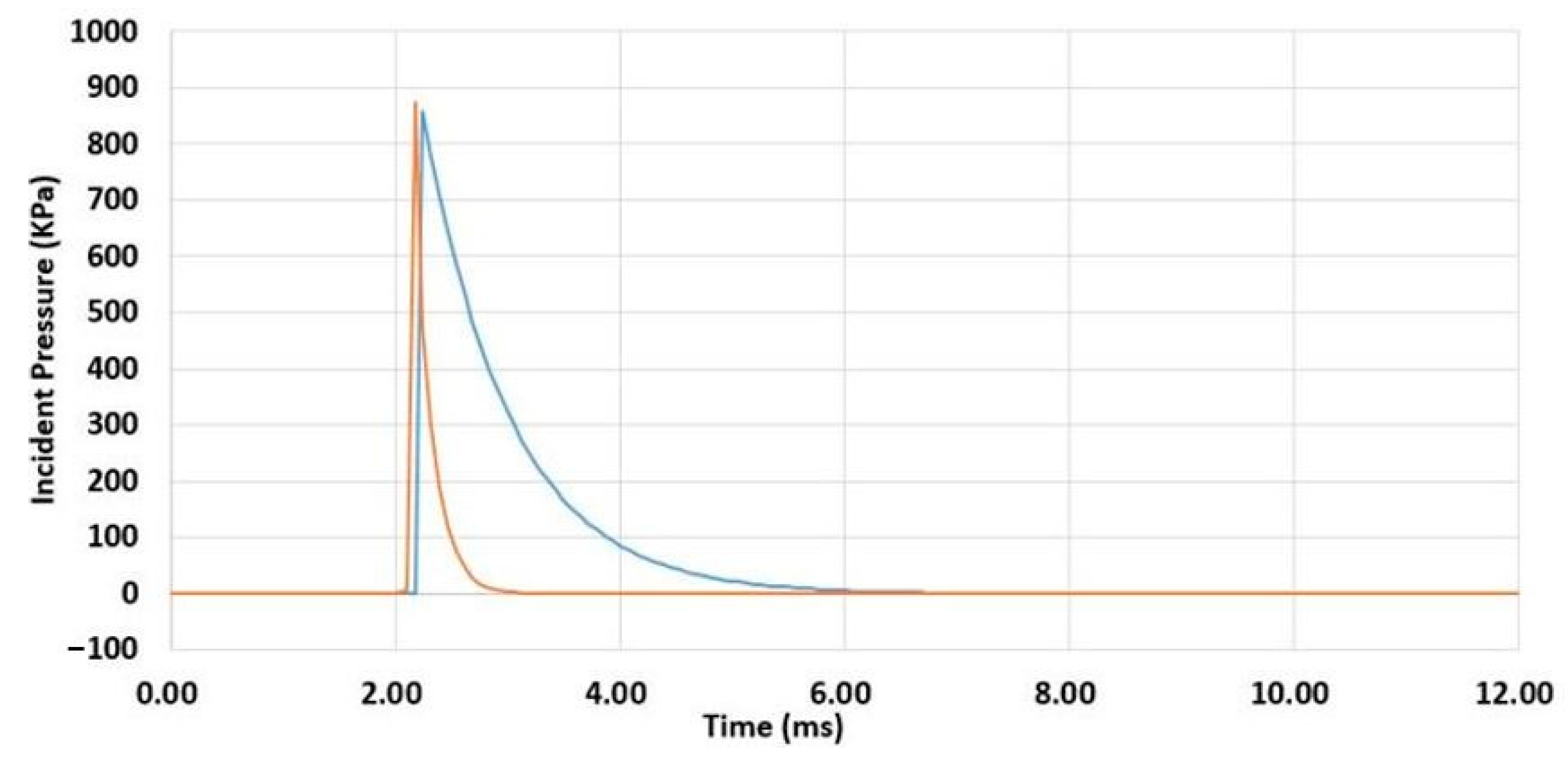
4.1. Compare between ConWep and ALE Incident Pressure
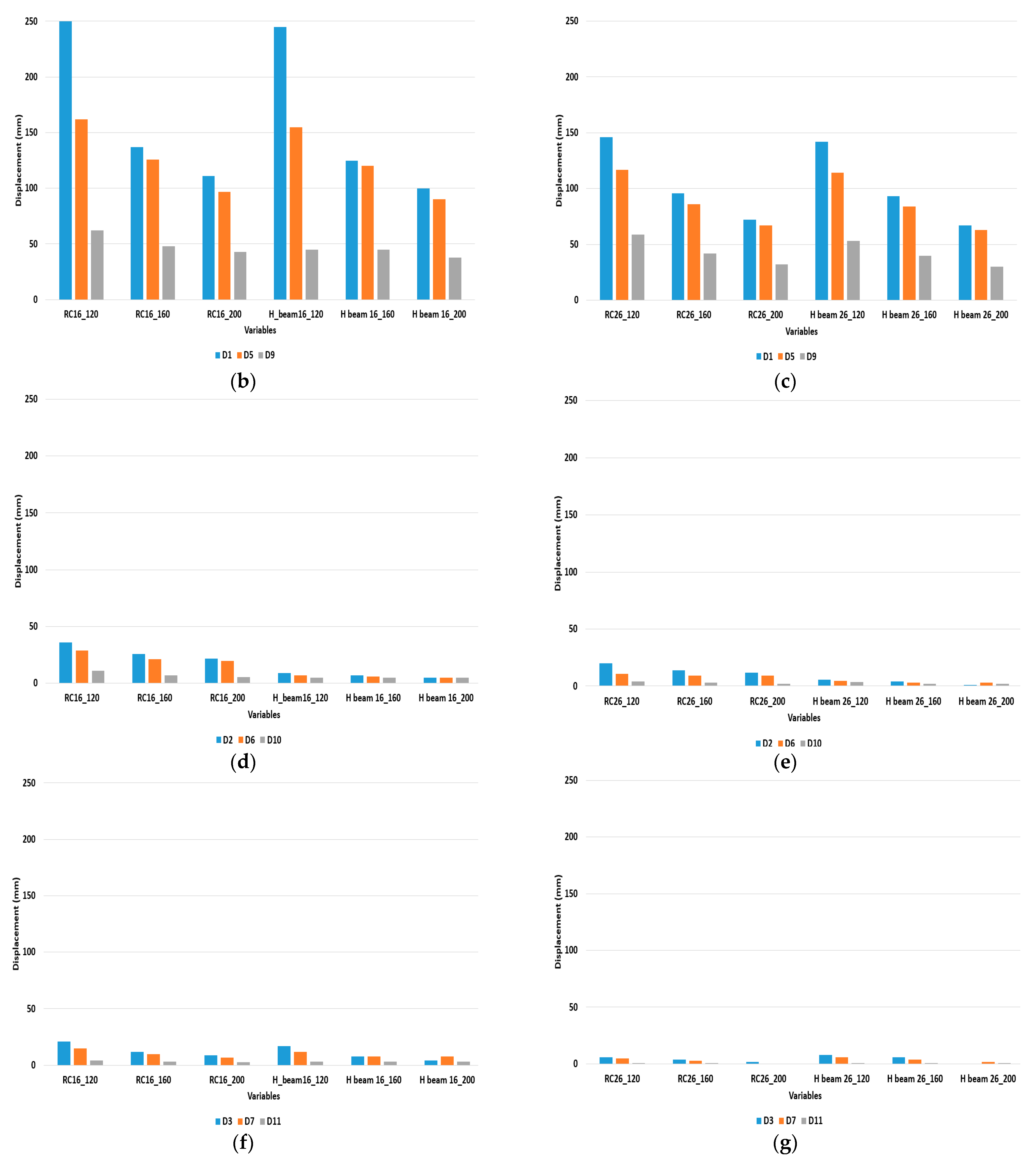
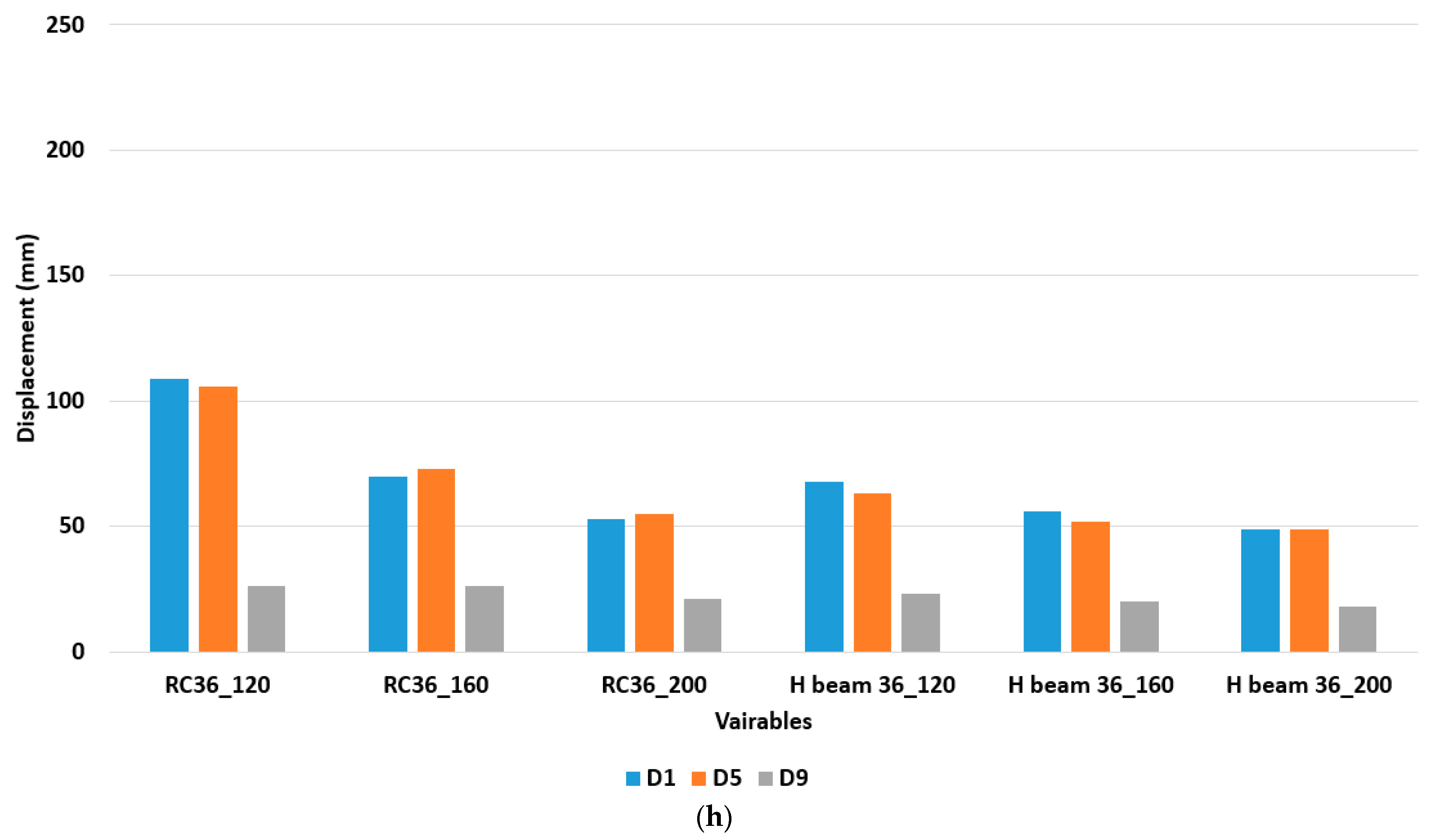
4.2. Displacement Results from Simulation
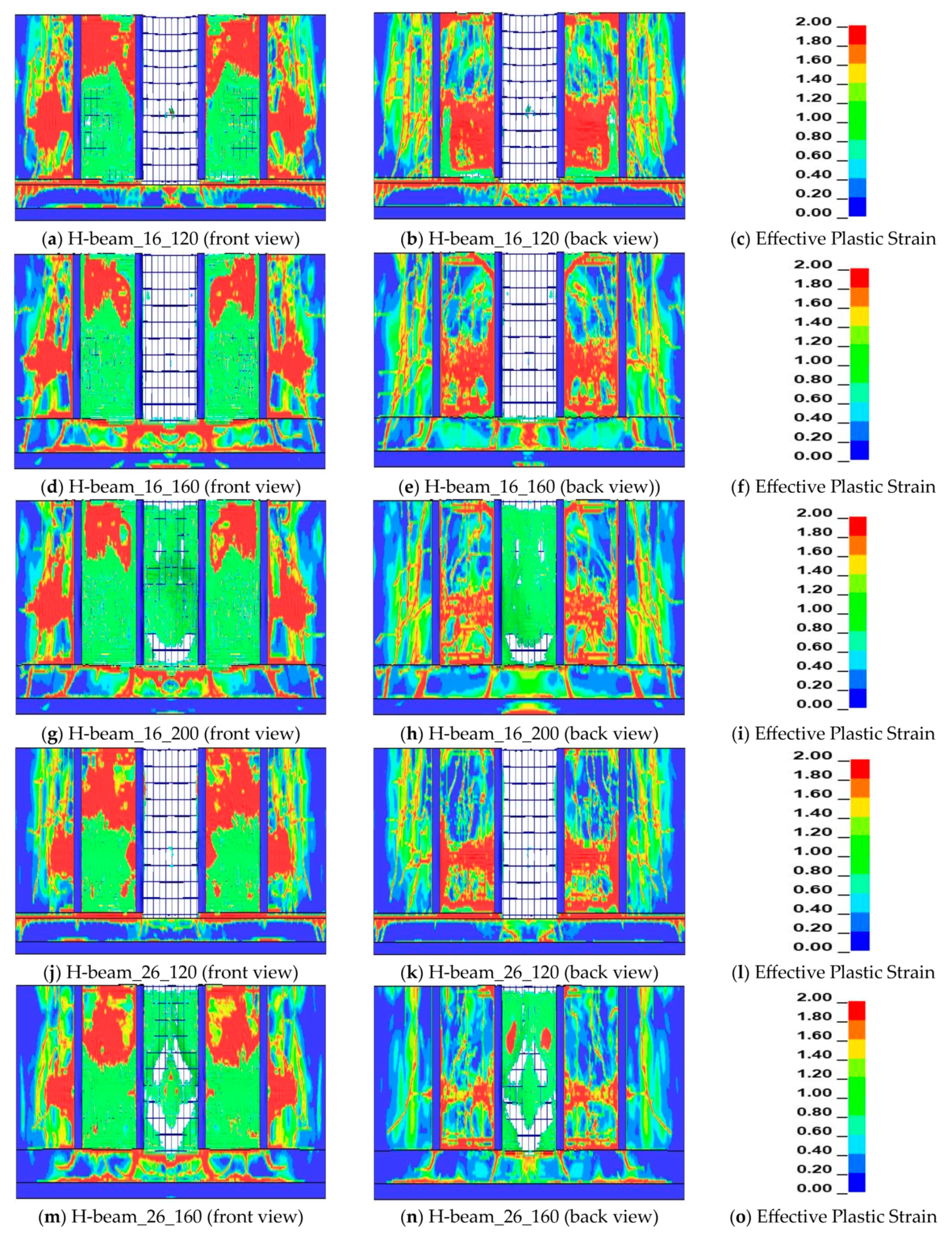
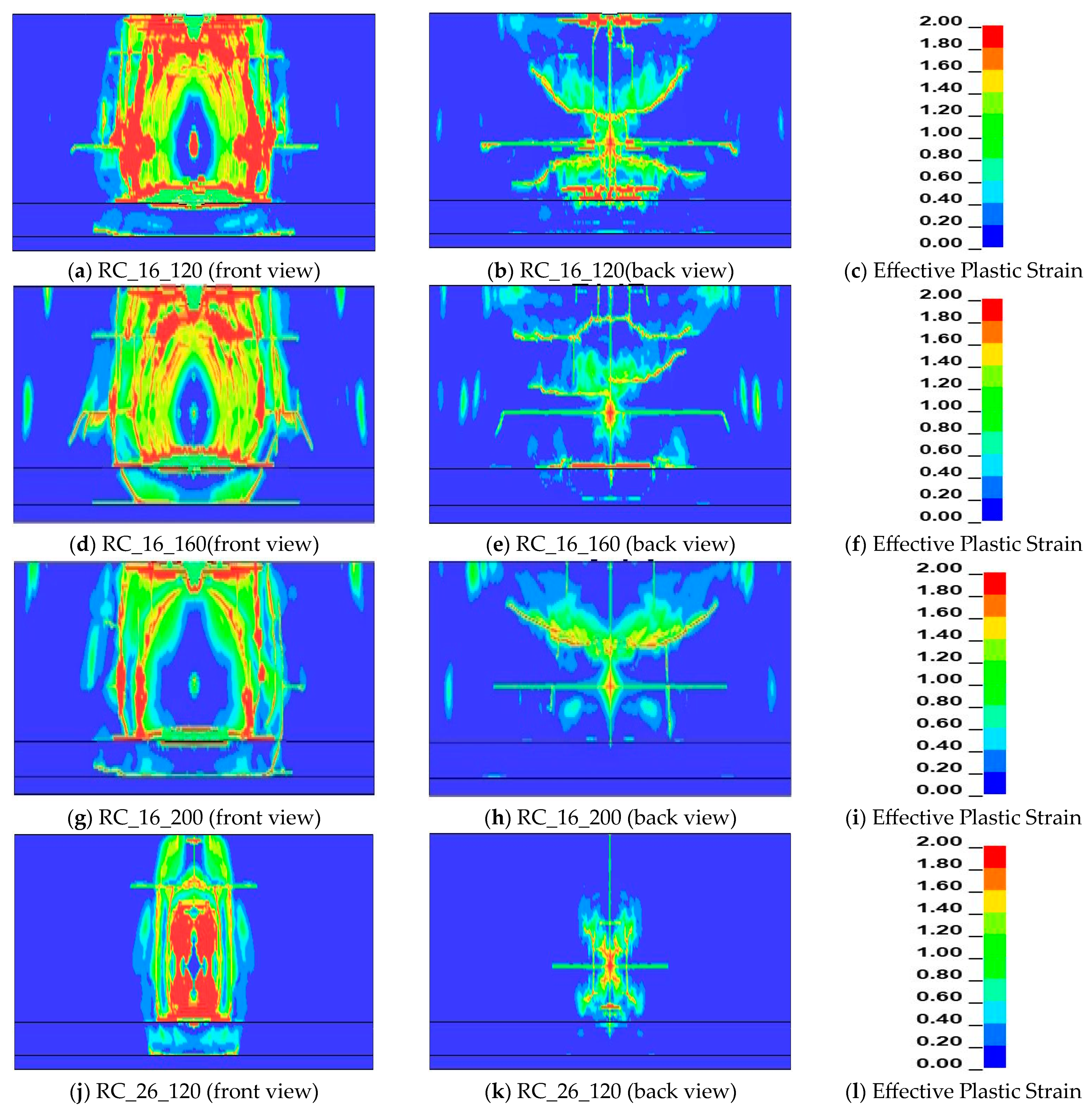
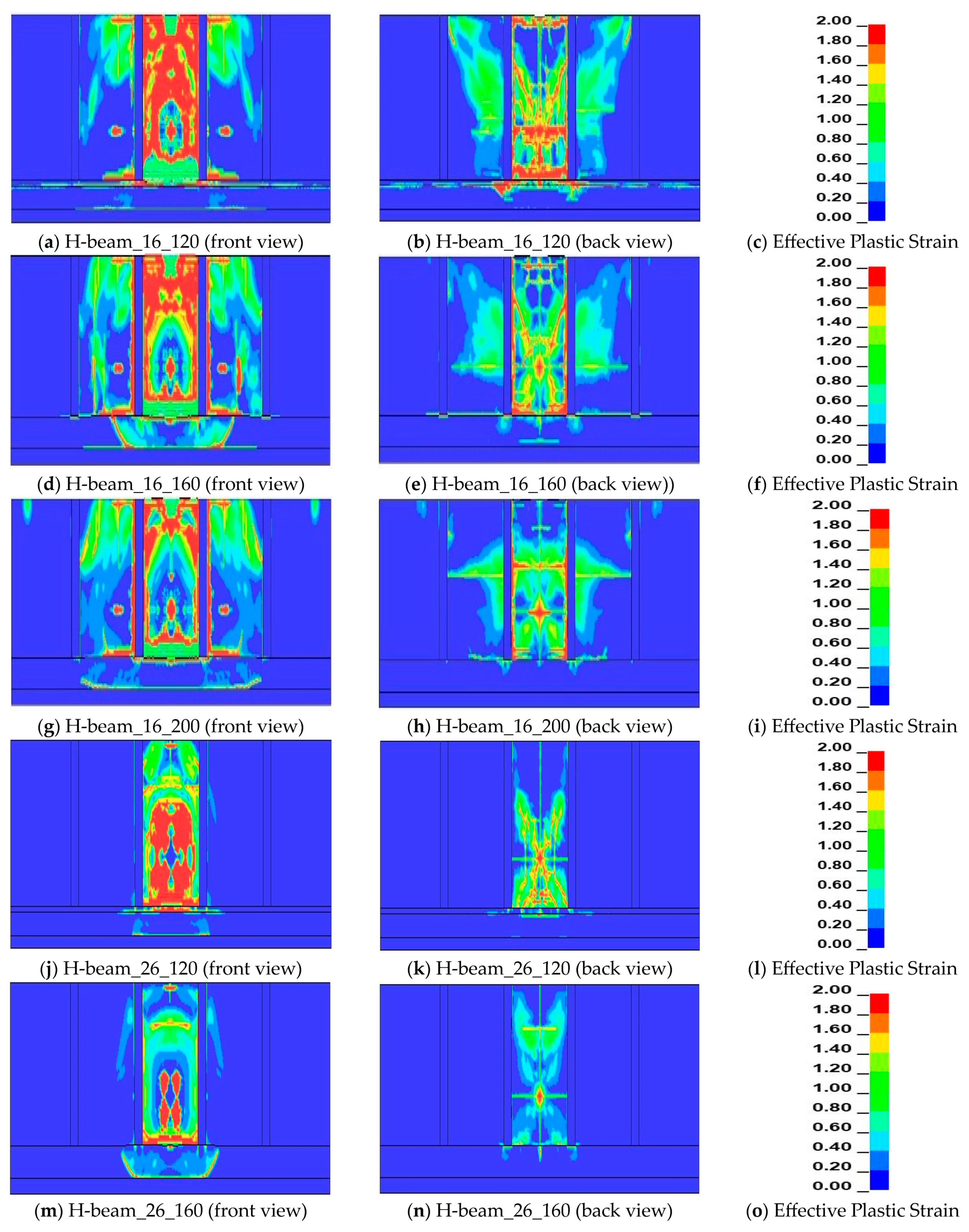
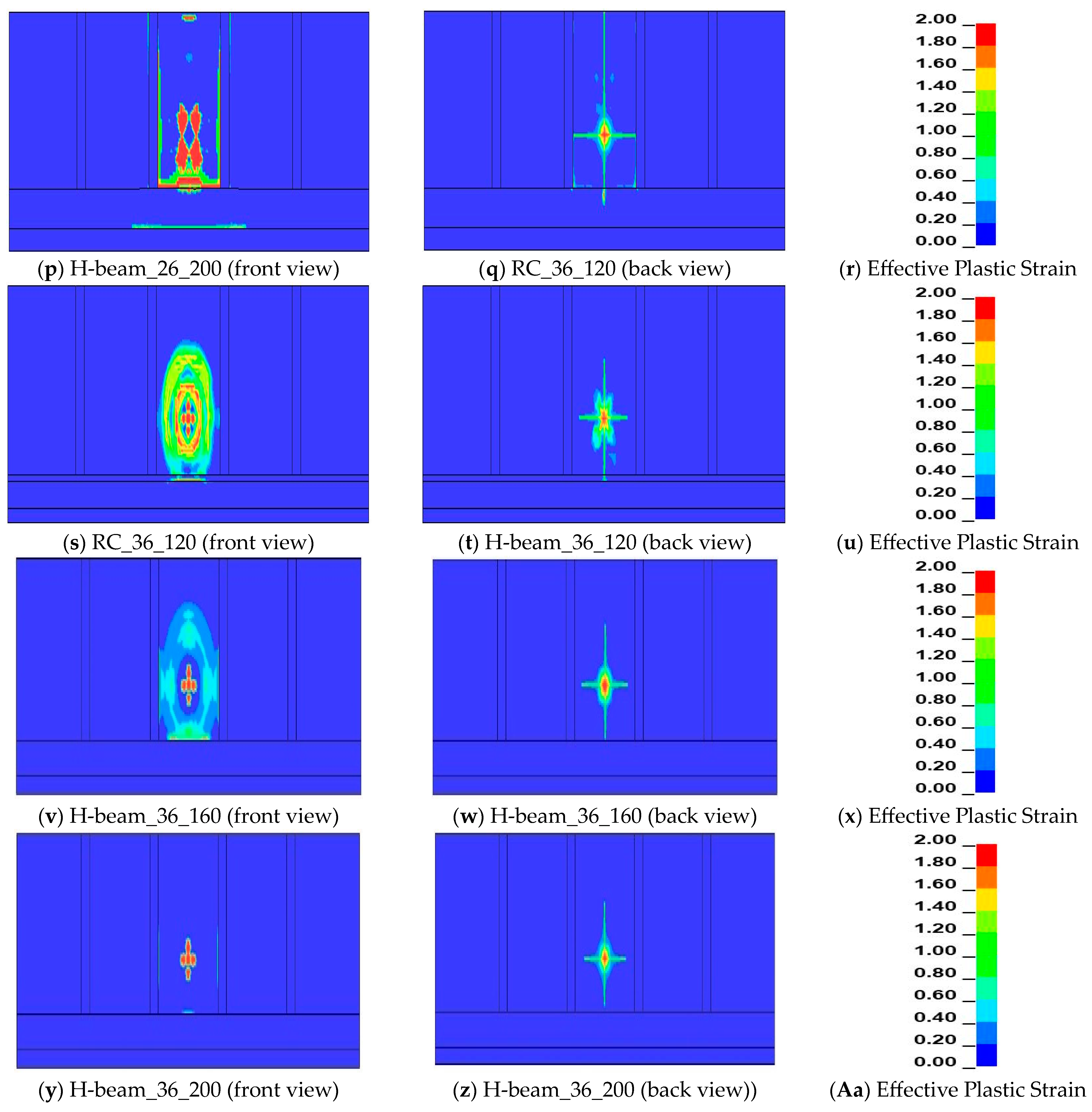
4.3. Failure on Reinforced Concrete and Composite Protection Wall during Worse Case Scenario of Hydrogen Gas Explosion
4.4. Failure on Reinforced Concrete and Composite Protection Wall during 30 kg of Hydrogen Gas Explosion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Balat, M. Potential Importance of Hydrogen as a Future Solution to Environmental and Transportation Problems. Int. J. Hydrogen Energy 2008, 33, 4013–4029. [Google Scholar] [CrossRef]
- South Korea’s Hydrogen Industrial Strategy. Available online: https://www.csis.org/analysis/south-koreas-hydrogen-industrial-strategy (accessed on 2 February 2023).
- Eckhoff, R.K. Explosion Hazards in the Process Industries; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 9780128032732. [Google Scholar]
- Hydrogen Safety—Wikipedia. Available online: https://en.wikipedia.org/wiki/Hydrogen_safety (accessed on 2 February 2023).
- Pasman, H.J.; Rogers, W.J. Safety Challenges in View of the Upcoming Hydrogen Economy: An Overview. J. Loss Prev. Process Ind. 2010, 23, 697–704. [Google Scholar] [CrossRef]
- Khan, R.; Farooq, S.H.; Usman, M. Blast Loading Response of Reinforced Concrete Panels Externally Reinforced with Steel Strips. Infrastructures 2019, 4, 54. [Google Scholar] [CrossRef] [Green Version]
- Yao, S.; Zhang, D.; Chen, X.; Lu, F.; Wang, W. Experimental and Numerical Study on the Dynamic Response of RC Slabs under Blast Loading. Eng. Fail. Anal. 2016, 66, 120–129. [Google Scholar] [CrossRef]
- Nozu, T.; Tanaka, R.; Ogawa, T.; Hibi, K.; Sakai, Y. Numerical Simulation of Hydrogen Explosion Tests with a Barrier Wall for Blast Mitigation. In Proceedings of the 1st International Conference on Hydrogen Safety, Pisa, Italy, 8–10 September 2005. [Google Scholar]
- Liu, Y.; Yan, J.B.; Huang, F.L. Behavior of Reinforced Concrete Beams and Columns Subjected to Blast Loading. Def. Technol. 2018, 14, 550–559. [Google Scholar] [CrossRef]
- Nassr, A.A.; Razaqpur, A.G.; Tait, M.J.; Campidelli, M.; Foo, S. Experimental Performance of Steel Beams under Blast Loading. J. Perform. Constr. Facil. 2012, 26, 600–619. [Google Scholar] [CrossRef]
- Anandavalli, N.; Lakshmanan, N.; Iyer, N.R.; Samuel Knight, G.M.; Rajasankar, J. A Novel Modelling Technique for Blast Analysis of Steel-Concrete Composite Panels. Procedia Eng. 2011, 14, 2429–2437. [Google Scholar] [CrossRef] [Green Version]
- Bruhl, J.C.; Varma, A.H.; Kim, J.M. Static Resistance Function for Steel-Plate Composite (SC) Walls Subject to Impactive Loading. Nucl. Eng. Des. 2015, 295, 843–859. [Google Scholar] [CrossRef] [Green Version]
- Lan, S.; Lok, T.S.; Heng, L. Composite Structural Panels Subjected to Explosive Loading. Constr. Build. Mater. 2005, 19, 387–395. [Google Scholar] [CrossRef]
- Richard Liew, J.Y.; Wang, T.Y. Novel Steel-Concrete-Steel Sandwich Composite Plates Subject to Impact and Blast Load. Adv. Struct. Eng. 2011, 14, 673–688. [Google Scholar] [CrossRef]
- Zheng, Z.; Yu, J.; Wei, F.; Wu, J. Numerical Study of Blast Performance of Concrete Filled Double-Steel-Plate Composite Walls. Int. J. Prot. Struct. 2020, 11, 23–40. [Google Scholar] [CrossRef]
- KGS Code Gas Technical Standard Information System. Available online: https://cyber.kgs.or.kr/kgscode.Index.do (accessed on 2 March 2021).
- Center for Hydrogen Safety (CHS). Review: Hydrogen Tank Explosion in Gangneung, South Korea. Available online: https://www.aiche.org/chs/conferences/international-center-hydrogen-safety-conference/2019/proceeding/paper/review-hydrogen-tank-explosion-gangneung-south-korea (accessed on 5 January 2023).
- International Fire Code (IFC). Available online: https://codes.iccsafe.org/content/IFC2018 (accessed on 2 January 2023).
- Air, K. Comparison of Regulations Codes and Standards for Hydrogen Refueling Stations in Japan and France. In Proceedings of the International Conference on Hydrogen Safety, Adelaide, Australia, 25 September 2019. [Google Scholar]
- Center for Strategic and International Studies. China Unveils Its First Long-Term Hydrogen Plan. Available online: https://www.csis.org/analysis/china-unveils-its-first-long-term-hydrogen-plan (accessed on 5 January 2023).
- Focus on Hydrogen: Japan’s Energy Strategy for Hydrogen and Ammonia. Available online: https://www.cliffordchance.com/content/dam/cliffordchance/briefings/2022/08/focus-on-hydrogen-in-japan.pdf (accessed on 2 January 2023).
- Statista. Number of Hydrogen Fuel Stations by Country. 2022. Available online: https://www.statista.com/statistics/1026719/number-of-hydrogen-fuel-stations-by-country/?fbclid=IwAR3eFnTx9d8wkLUCIr3aVHsbm4Tmb8xBaPshE1nBmSt74jz-0QH9pa6OGaQ (accessed on 5 January 2023).
- Statista. South Korea: Hydrogen Fueling Stations Cumulative Number 2018–2030. Available online: https://www.statista.com/statistics/957810/south-korea-hydrogen-fueling-stations-cumulative-number/ (accessed on 5 January 2023).
- Statista. Hydrogen Demand Worldwide. Available online: https://www.statista.com/statistics/1121206/global-hydrogen-demand/ (accessed on 5 January 2023).
- Casal, J. Evaluation of the Effects and Consequences of Major Accidents in Industrial Plants, 2nd ed.; Fedor, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780128127667. [Google Scholar]
- Kwon, S.; Park, J. A Review of TNT Equivalent Method for Evaluating Explosion Energy Due to Gas Explosion. Korean Soc. Explos. Blasting Eng. 2015, 33, 1–13. [Google Scholar]
- Training Program Analysis for Hydrogen Releted Emergencies. Available online: https://academic.naver.com/article.naver?doc_id=939895533 (accessed on 20 December 2022).
- López, E.; Rengel, R.; Mair, G.W.; Isorna, F. Analysis of High-Pressure Hydrogen and Natural Gas Cylinders Explosions through TNT Equivalent Method. In Proceedings of the 5th Iberian Symposium on Hydrogen, Fuel Cells and Advanced Batteries, Tenerife, Spain, 5–8 July 2015. [Google Scholar] [CrossRef]
- Lopes, K.B.; Melo, P.F.F.F. Analysis of the Effects of Explosion of a Hydrogen Cylinder on the Transfer of Radioactive Liquid Wastes at Nuclear Power Stations. In Proceedings of the 2011 International Nuclear Atlantic Conference, Belo Horizonte, Brazil, 24–18 October 2011. [Google Scholar]
- Malvar, L.J.; Crawford, J.E.; Wesevich, J.W.; Simons, D. A Plasticity Concrete Material Model for DYNA3D. Int. J. Impact Eng. 1997, 19, 847–873. [Google Scholar] [CrossRef]
- Yin, X.; Li, Q.; Chen, B.; Xu, S. An Improved Calibration of Karagozian & Case Concrete/Cementitious Model for Strain-Hardening Fibre-Reinforced Cementitious Composites under Explosion and Penetration Loadings. Cem. Concr. Compos. 2023, 137, 104911. [Google Scholar] [CrossRef]
- Wu, Y.; Crawford, J.E. Numerical Modeling of Concrete Using a Partially Associative Plasticity Model. J. Eng. Mech. 2015, 141, 04015051. [Google Scholar] [CrossRef]
- Murray, Y. Users Manual for LS-DYNA Concrete Material Model 159; Federal Highway Administration: Washington, DC, USA, 2007; Volume 77. [Google Scholar]
- Yin, X.; Li, Q.; Xu, X.; Chen, B.; Guo, K.; Xu, S. Investigation of Continuous Surface Cap Model (CSCM) for Numerical Simulation of Strain-Hardening Fibre-Reinforced Cementitious Composites against Low-Velocity Impacts. Compos. Struct. 2023, 304, 116424. [Google Scholar] [CrossRef]
- Manual, K.U.S.; Ii, V. Ls-Dyna Manual Volume Ii R6.10; LSTC: Driffield, UK, 2012; Volume 2. [Google Scholar]
- Rashed, A.; Yazdani, M.; Babaluo, A.A.; Hajizadeh Parvin, P. Investigation on High-Velocity Impact Performance of Multi-Layered Alumina Ceramic Armors with Polymeric Interlayers. J. Compos. Mater. 2016, 50, 3561–3576. [Google Scholar] [CrossRef]
- Gomah, M.; Demiral, M. An Experimental and Numerical Investigation of an Improved Shearing Process with Different Punch Characteristics. Stroj. Vestn. J. Mech. Eng. 2020, 66, 375–384. [Google Scholar] [CrossRef]
- Wang, I.T. 1440. Simulation and Experimental Validation of the Dynamic Pressure of Shock Wave under Free-Field Blast Loading. J. Vibroeng. 2014, 16, 3547–3556. [Google Scholar]
- Wang, W.; Zhang, D.; Lu, F.; Wang, S.C.; Tang, F. Experimental Study and Numerical Simulation of the Damage Mode of a Square Reinforced Concrete Slab under Close-in Explosion. Eng. Fail. Anal. 2013, 27, 41–51. [Google Scholar] [CrossRef]
- Zhao, C.F.; Chen, J.Y. Damage Mechanism and Mode of Square Reinforced Concrete Slab Subjected to Blast Loading. Theor. Appl. Fract. Mech. 2013, 63–64, 54–62. [Google Scholar] [CrossRef]
- Sadique, M.R.; Zaid, M.; Alam, M.M. Rock Tunnel Performance Under Blast Loading Through Finite Element Analysis. Geotech. Geol. Eng. 2022, 40, 35–56. [Google Scholar] [CrossRef]
- Protective, F.O.F.; Weapons, F.O.R.C. {TM} 5-855-1: Fundamentals of Protective Design for Conventional Weapons; US Department of the Army: Washington, DC, USA, 1986. [Google Scholar]


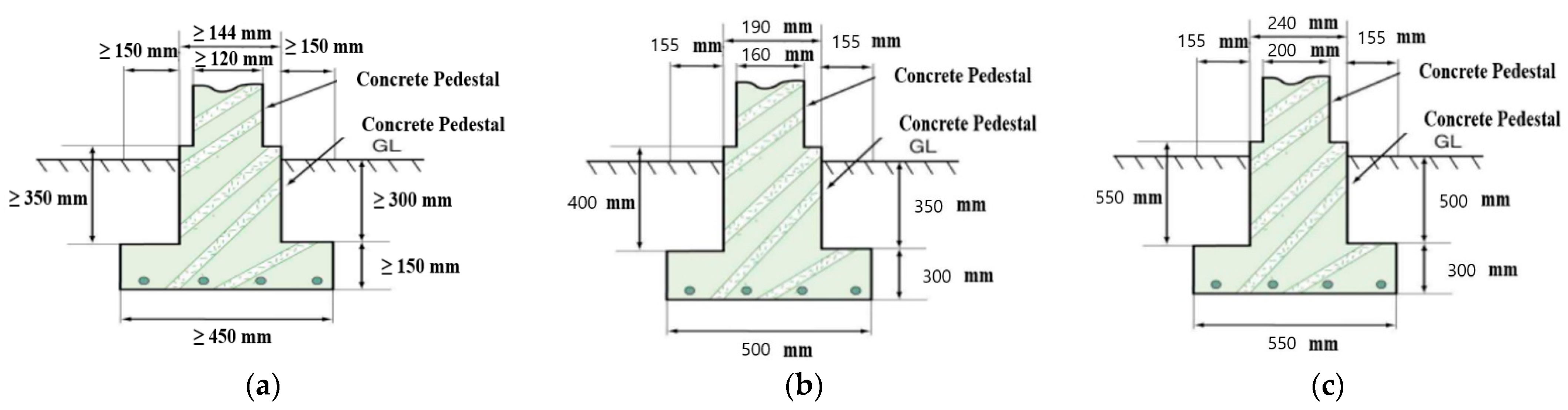



| Country | Minimum Requirement of Barrier Wall |
|---|---|
| South Korea | 120 mm |
| Japan | 120 mm |
| France | Simple wall satisfying REI120 of European fire resistance class |
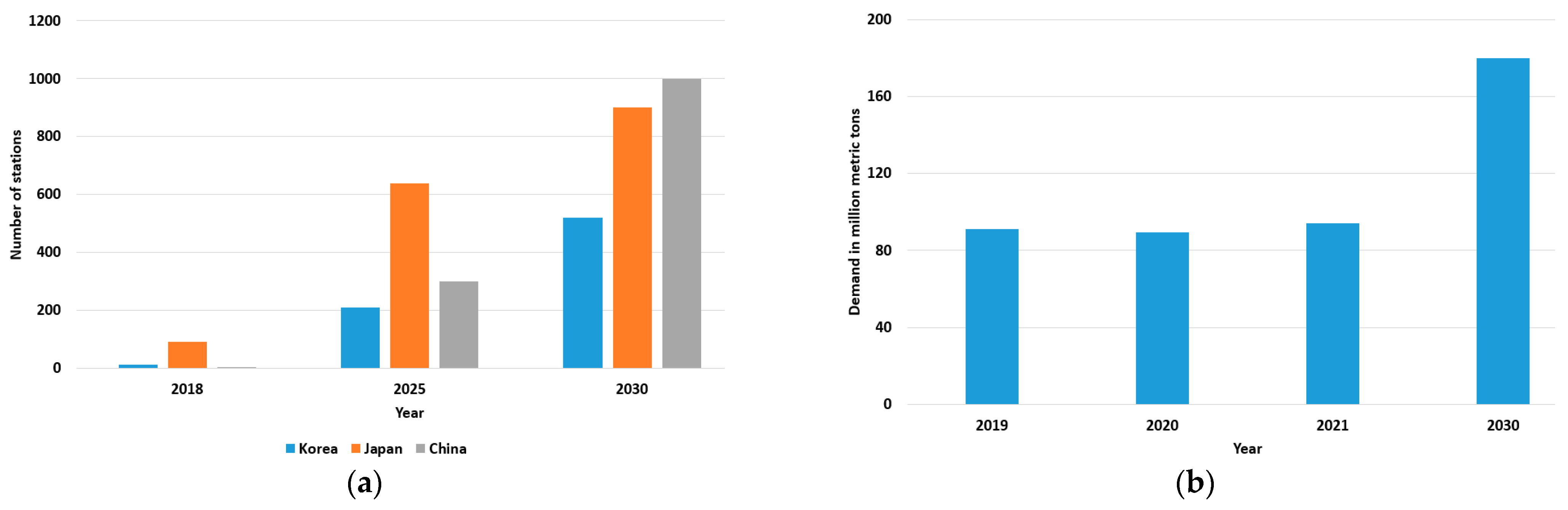
| Country | Number of Hydrogen Fueling Stations (2022) |
|---|---|
| China | 250 |
| Japan | 161 |
| South Korea | 141 |
| Germany | 93 |
| France | 21 |
| Netherlands | 11 |
| Canada | 9 |
| Parameter | Value |
|---|---|
| Density | 2.4 × 10−6 kg/mm3 |
| Compressive Strength | 0.035 GPa |
| Parameters | MAT_JHONSON_COOK (H-Beam) | MAT_PLASTIC_KINEMATIC (Steel Rebar) |
|---|---|---|
| Density | 7.85 × 10−6 kg/mm3 | 7.85 × 10−6 kg/mm3 |
| Young’s modulus | 200 GPa | 205 GPa |
| Poison ratio | 0.26 | 0.3 |
| Shear Modulus | 88 GPa | |
| Yield stress | 0.42 GPa | |
| Strain rate parameter (SRC) | 40.4 | |
| Strain rate parameter (SRP) | 5 | |
| Failure strain (FS) | 0.25 | |
| A | 0.28 GPa | |
| B | 0.5 GPa | |
| N | 0.26 | |
| C | 0.22 | |
| M | 0.91 | |
| Damage (D1) | 0.40 | |
| Damage (D2) | 1.10 | |
| Damage (D3) | 0.1 | |
| Damage (D4) | 0.009 | |
| Damage (D5) | 0 |
| Component | Unit (Kg, mm, ms) | ||||||
|---|---|---|---|---|---|---|---|
| Air | MAT_NULL | ||||||
| RO | PC | MU | TEROD | CEROD | TM | PR | |
| 1.293 × 10−9 | 0 | 0 | 0 | 0 | 0 | 0 | |
| *EOS_LINEAR_POLYNOMIAL | |||||||
| C0 | C1 | C2 | C3 | C4 | C5 | C6 | |
| 0 | 0 | 0 | 0 | 0.4 | 0.4 | 0 | |
| E0 | Vo | ||||||
| 2.50E−04 | 1 | ||||||
| TNT | *MAT_HIGH_EPLOSIVE_BURN | ||||||
| RO | D | PCJ | BETA | K | G | SIGY | |
| 1.630 × 10−6 | 8193 | 28 | 0 | 0 | 0 | 0 | |
| *EOS_JWL | |||||||
| A | B | R1 | R2 | OMEG | E0 | Vo | |
| 609.772 | 12.95 | 4.5 | 1.4 | 0.25 | 9 | 1 | |
| Soil | |||||||
| RO | NPLOT | SPGRAV | RHOWAT | VN | GAMMAR | ITERMAX | |
| 2.35E−06 | 3 | 2.79 | 1.0 × 10−6 | 1.1 | 0 | 10 | |
| K | G | PHIMAX | AHYP | COH | ECCEN | AN | |
| 0.00325 | 0.0013 | 1.1 | 1.0 × 10−7 | 6.2 × 10−6 | 0.7 | 0.0 | |
| Variable | TNT Weight (kg) | Central Displacement form Experiment [39] (mm) | Central Displacement from Simulation [39] (mm) | Central Displacement from Simulation [40] (mm) | Central Displacement from Simulation [41] (mm) | Central Displacement from This Study (mm) | Error (%) |
|---|---|---|---|---|---|---|---|
| 1 | 0.2 | 10 | 8 | 8.8 | 8.15 | 9.25 | 8.1 |
| 2 | 0.31 | 15 | 13 | 12.7 | 12.25 | 14.39 | 4.23 |
| Distance (mm) | Peak Pressure (kPa) | Error (%) | |
|---|---|---|---|
| ConWep | LS-DYNA | ||
| 1600 | 3433 | 3234.83 | 5.77 |
| 2600 | 1564 | 1588.02 | 1.54 |
| 3600 | 857 | 872.74 | 1.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Jang, T.; Oli, T.; Park, C. Behavior of Barrier Wall under Hydrogen Storage Tank Explosion with Simulation and TNT Equivalent Weight Method. Appl. Sci. 2023, 13, 3744. https://doi.org/10.3390/app13063744
Kim S, Jang T, Oli T, Park C. Behavior of Barrier Wall under Hydrogen Storage Tank Explosion with Simulation and TNT Equivalent Weight Method. Applied Sciences. 2023; 13(6):3744. https://doi.org/10.3390/app13063744
Chicago/Turabian StyleKim, Seungwon, Taejin Jang, Topendra Oli, and Cheolwoo Park. 2023. "Behavior of Barrier Wall under Hydrogen Storage Tank Explosion with Simulation and TNT Equivalent Weight Method" Applied Sciences 13, no. 6: 3744. https://doi.org/10.3390/app13063744
APA StyleKim, S., Jang, T., Oli, T., & Park, C. (2023). Behavior of Barrier Wall under Hydrogen Storage Tank Explosion with Simulation and TNT Equivalent Weight Method. Applied Sciences, 13(6), 3744. https://doi.org/10.3390/app13063744







