Optimal Interplanetary Transfer of Solar Wind Ion Focusing Thruster-Based Spacecraft
Abstract
1. Introduction
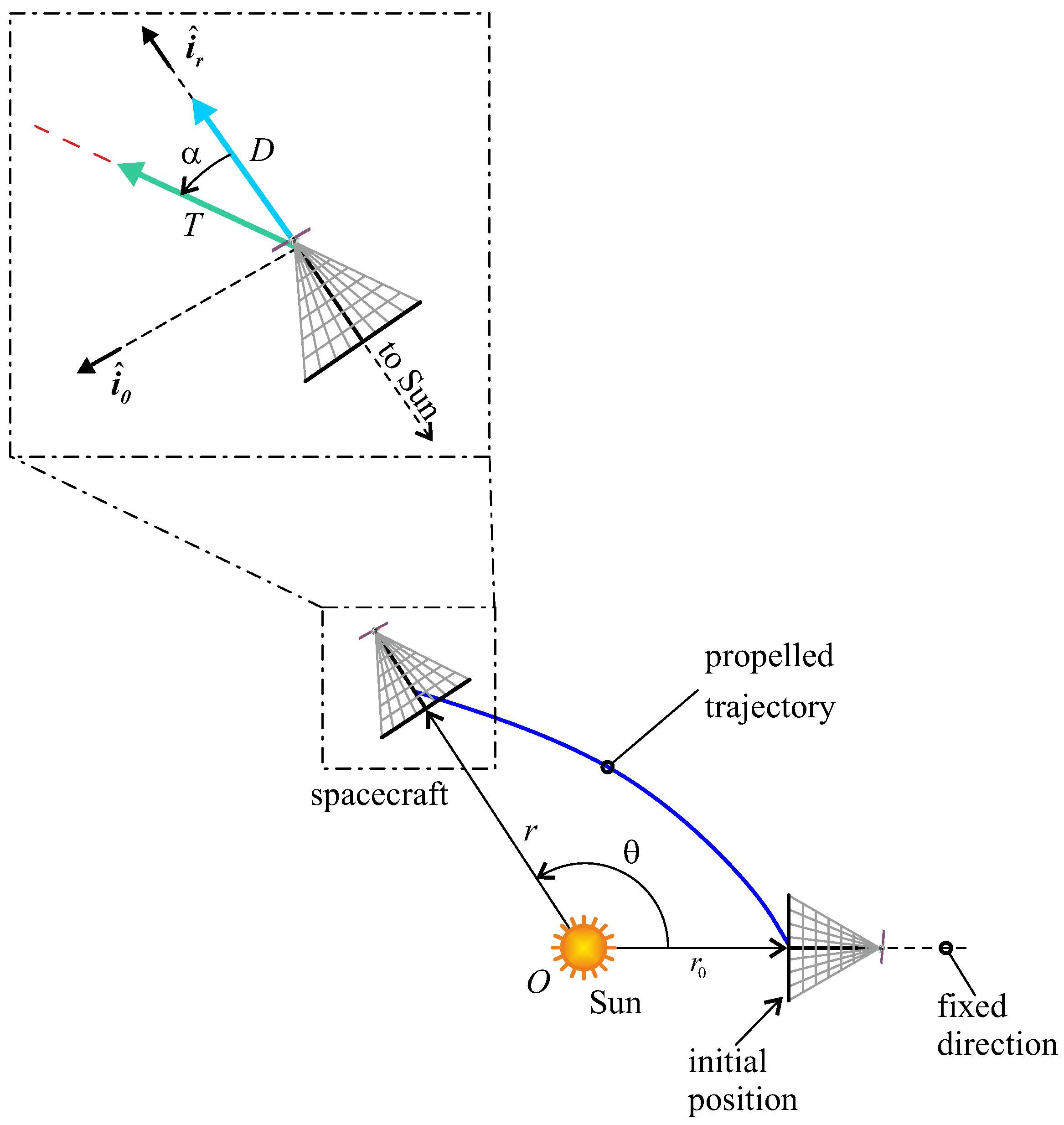
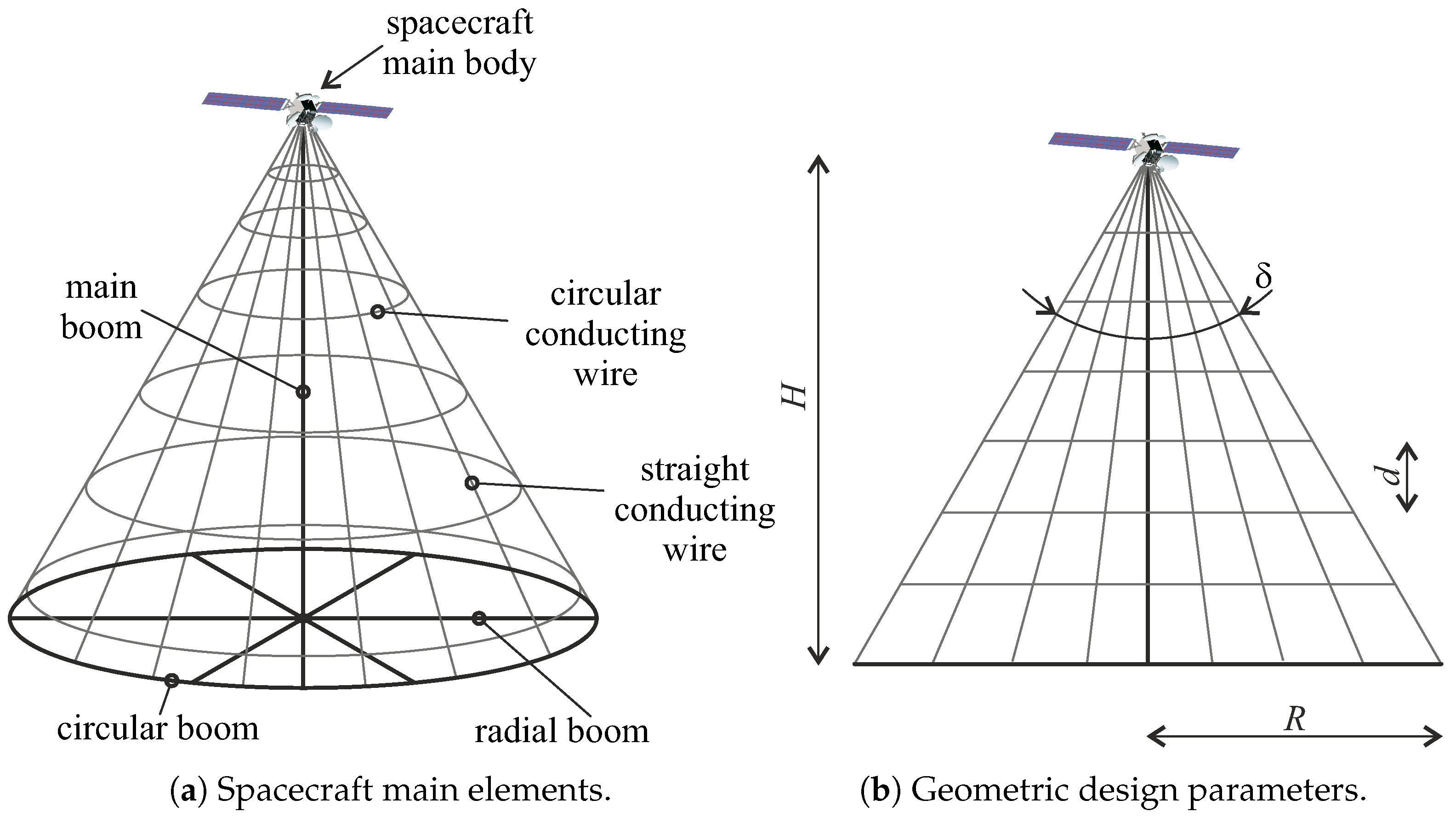
2. Mathematical Model
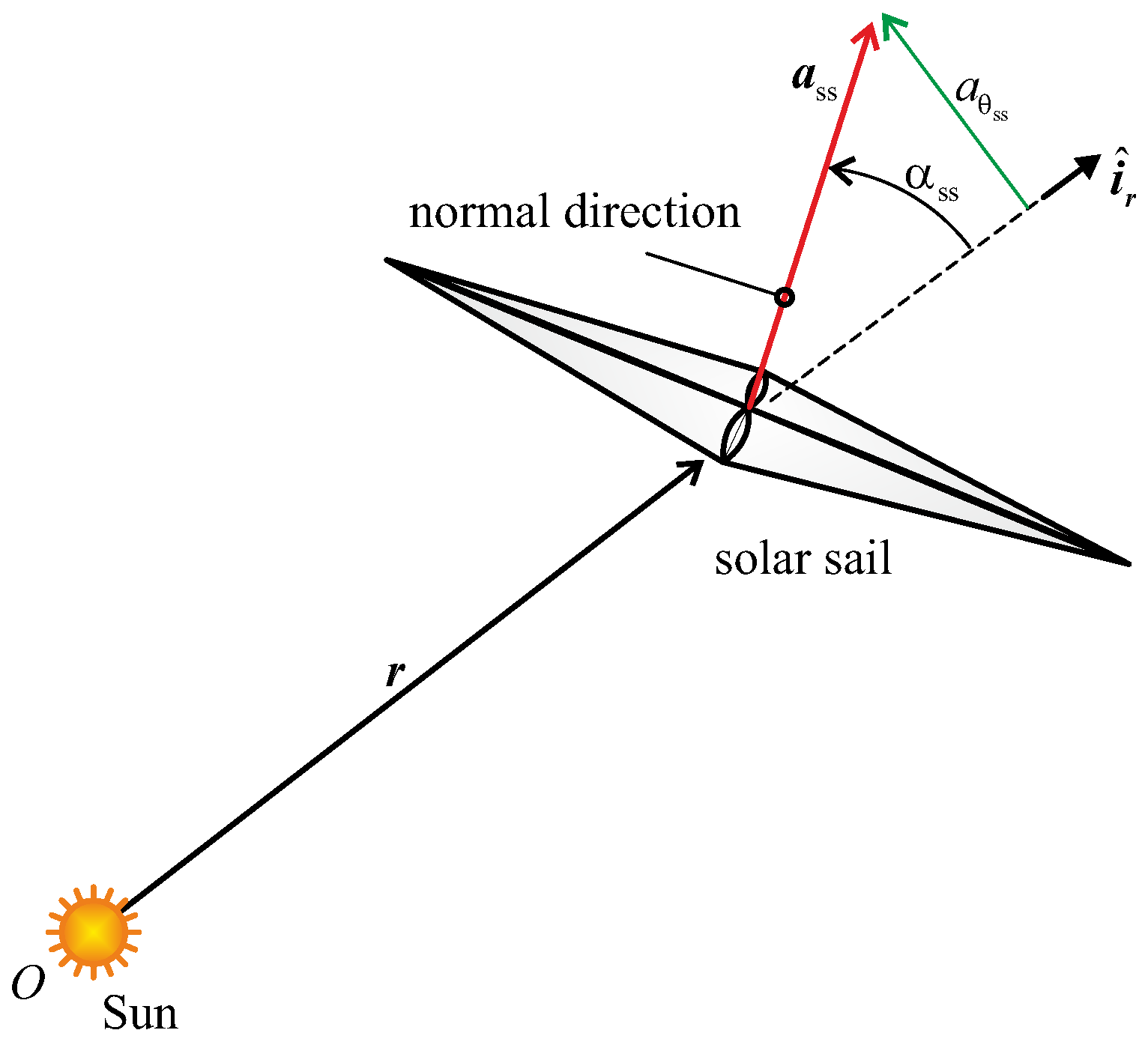
Thrust Vector Description
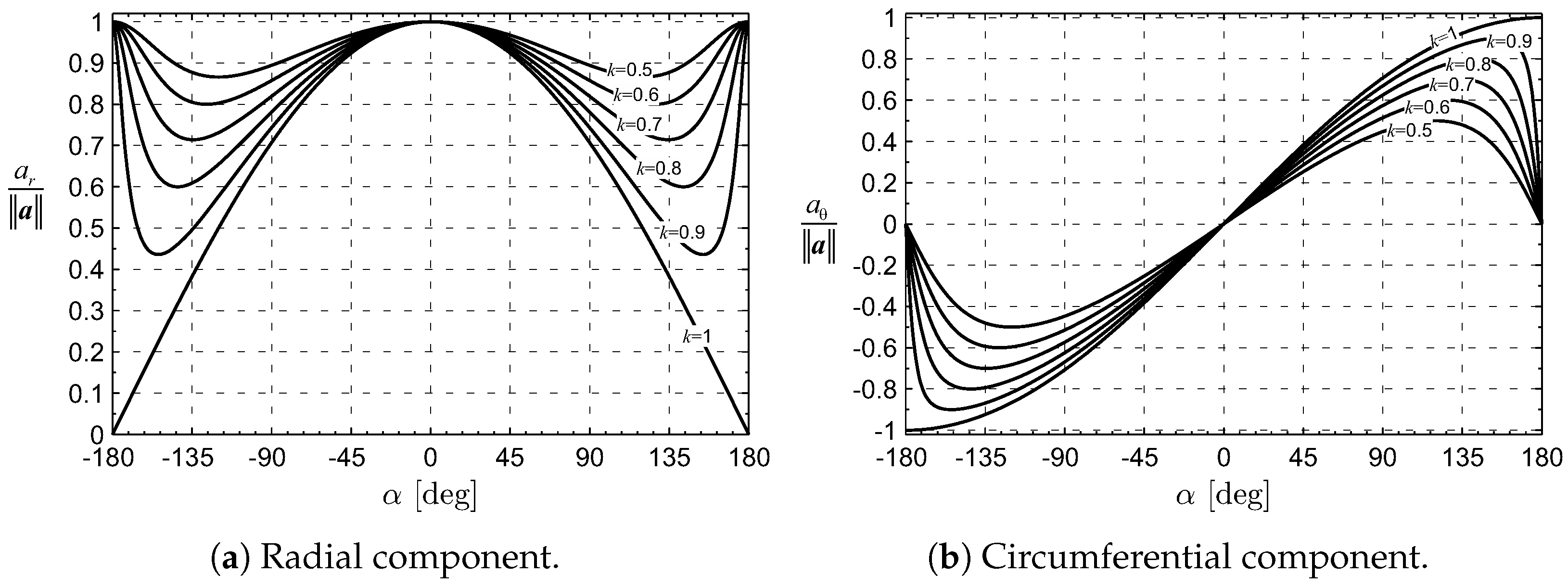
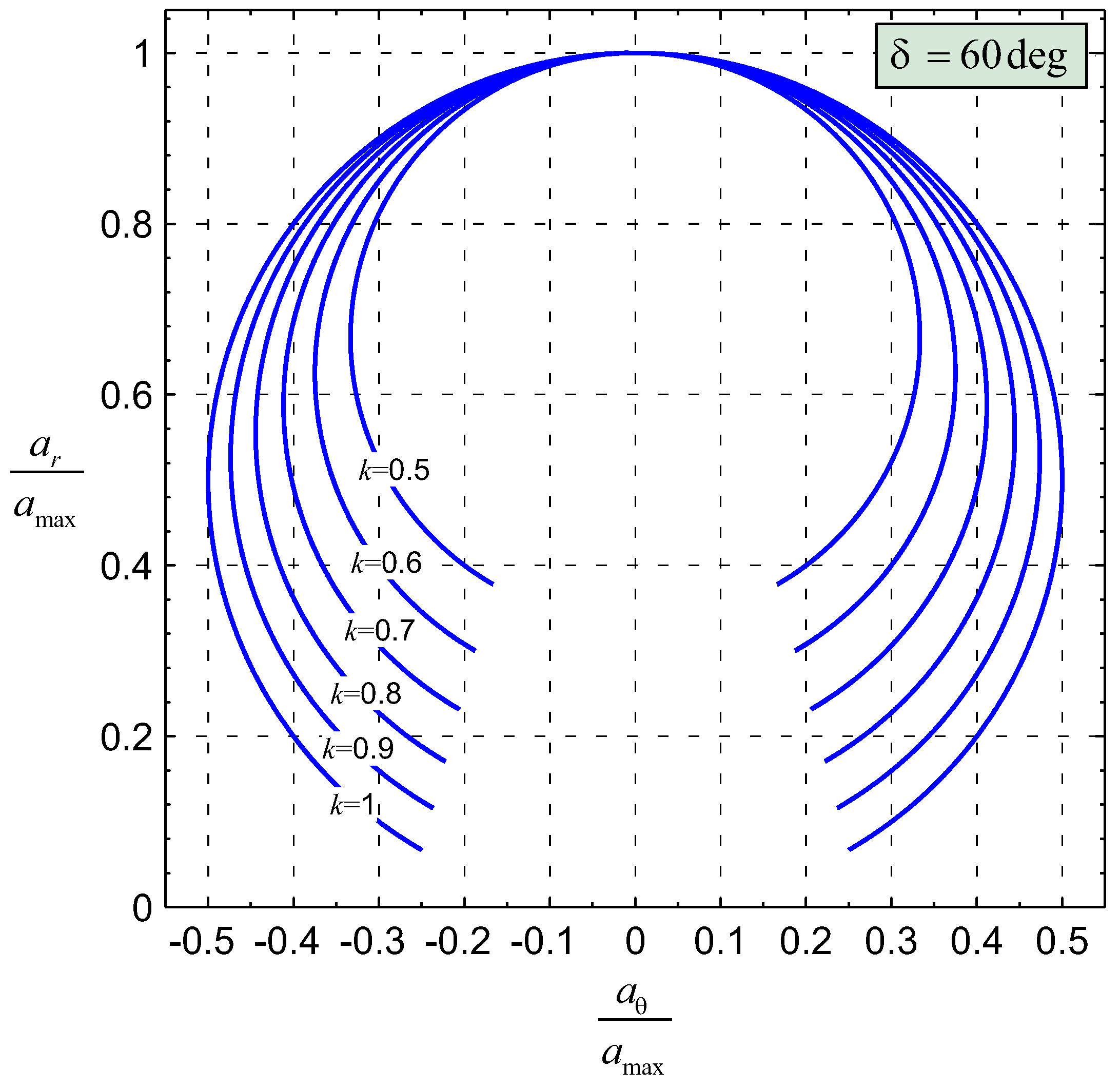
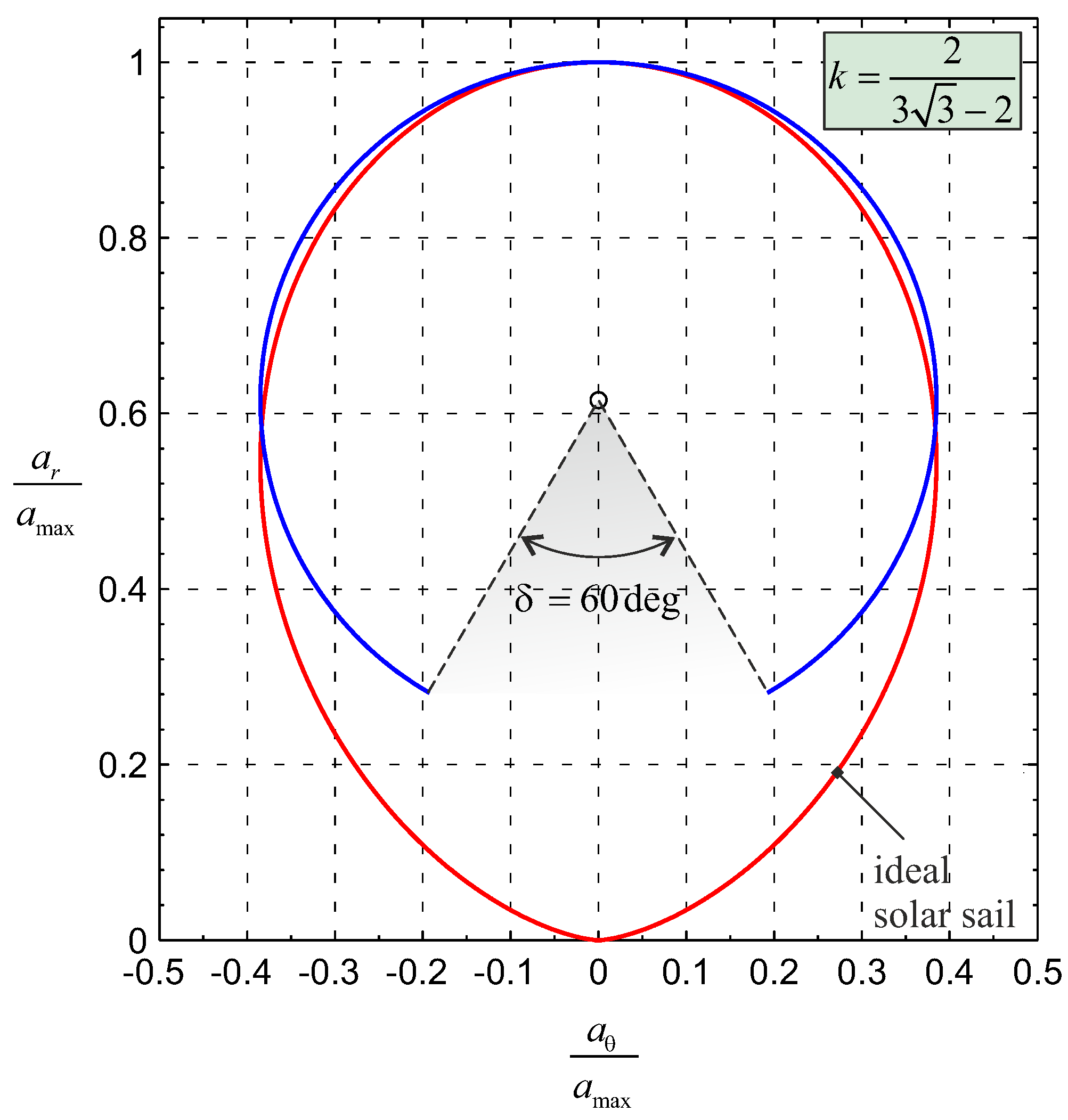
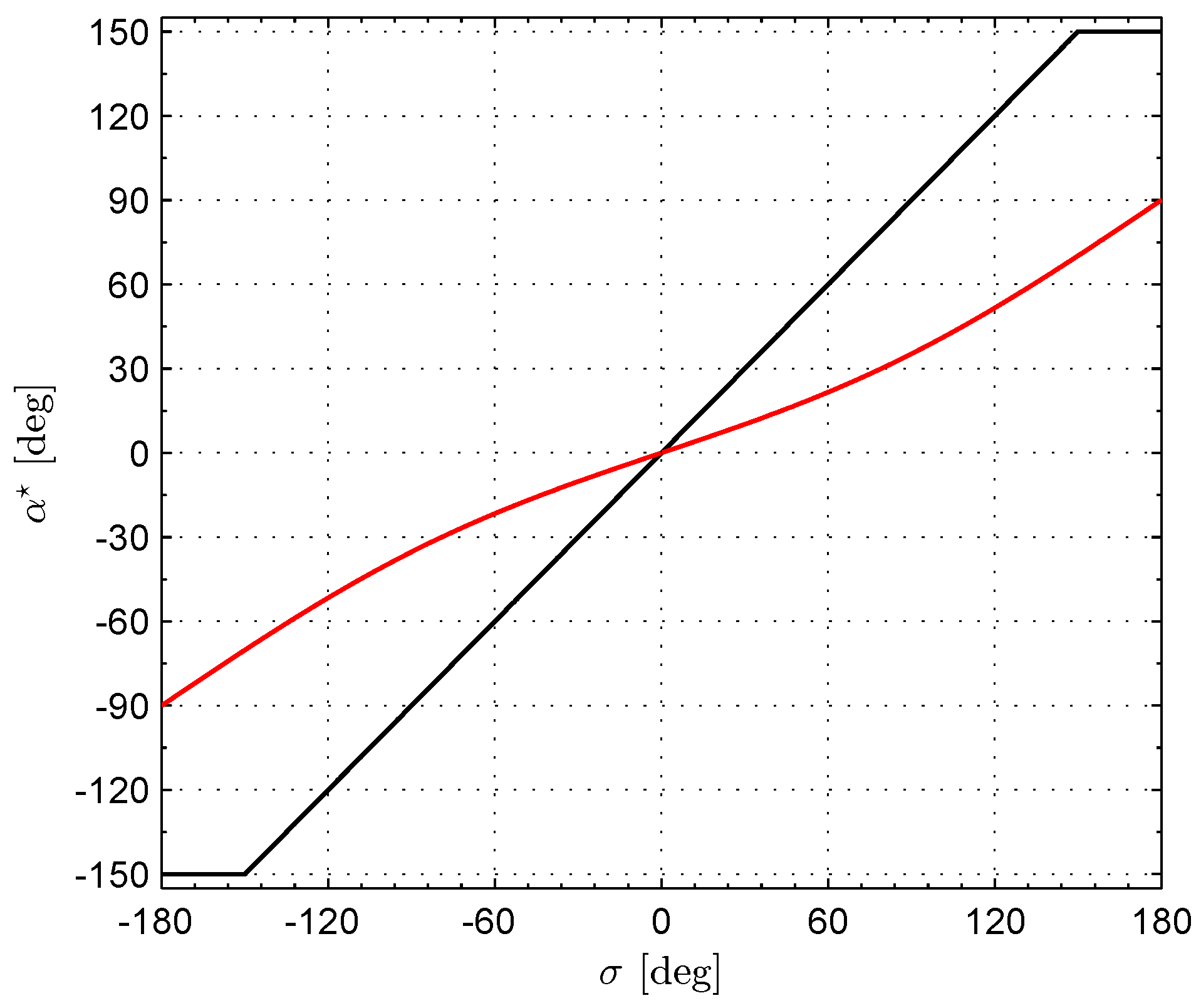
3. Trajectory Optimization
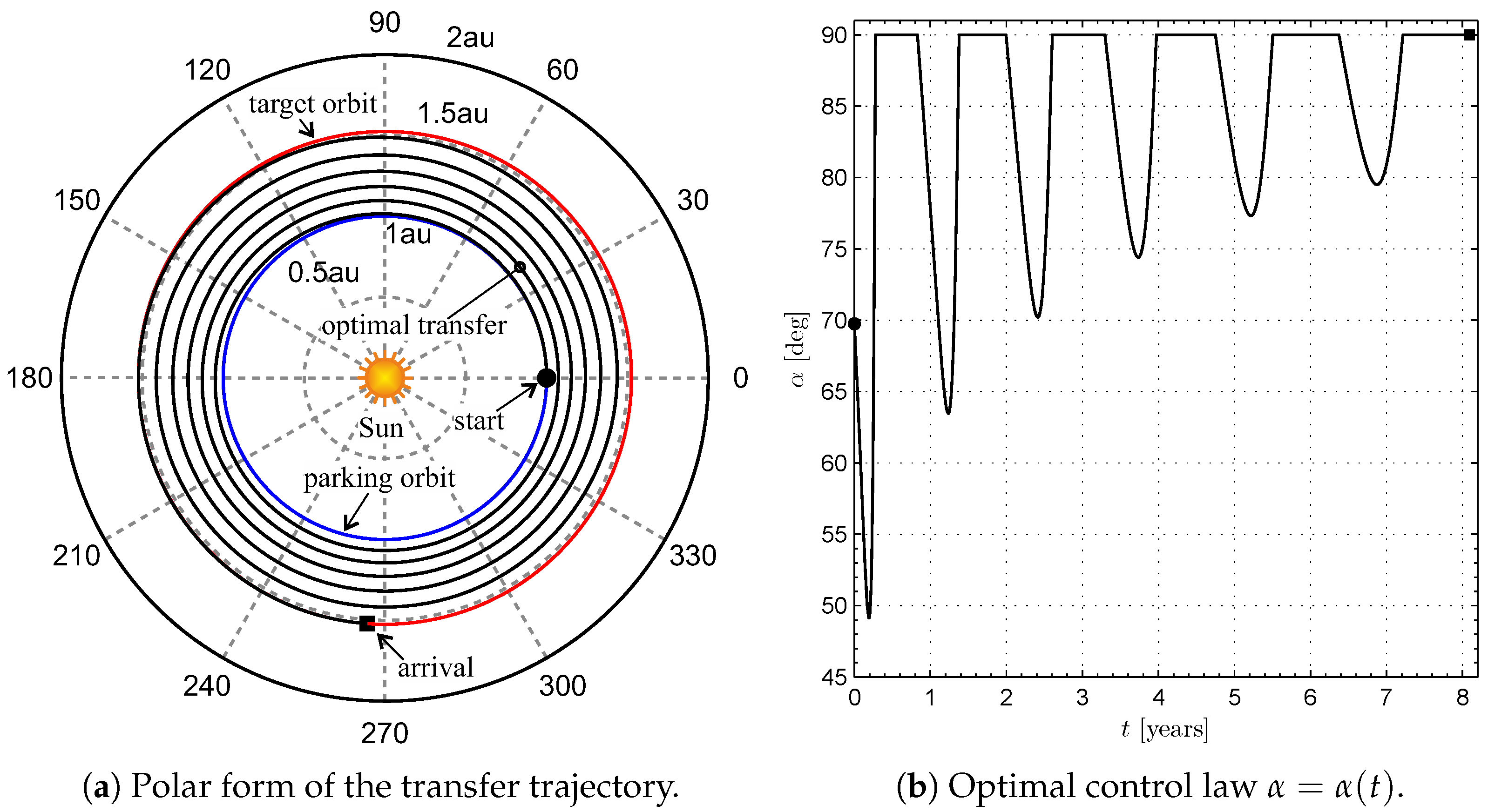
4. Numerical Simulations and Mission Applications
Case Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Notation | |
| A | SWIFT cone base area [m] |
| design parameter; see Equation (16) [mm/s] | |
| propulsive acceleration vector [mm/s] | |
| maximum propulsive acceleration magnitude [mm/s] | |
| radial component of [mm/s] | |
| transverse component of [mm/s] | |
| D | radial thrust (“drag”) [N] |
| d | spacing between circular conducting wires [m] |
| e | elementary charge [C] |
| H | SWIFT cone height [m] |
| Hamiltonian | |
| k | dimensionless design parameter; see Equation (11) |
| critical value of k; see Equation (37) | |
| radial unit vector | |
| circumferential unit vector | |
| J | performance index |
| total length of structural elements [m] | |
| total length of conducting wires [m] | |
| m | total spacecraft mass [kg] |
| spacecraft main body mass [kg] | |
| electron mass [kg] | |
| proton mass [kg] | |
| SWIFT power generation system mass [kg] | |
| SWIFT structure mass [kg] | |
| SWIFT wires total mass [kg] | |
| number of circular conducting wires | |
| number of straight conducting wires | |
| number of radial support booms | |
| solar wind density [particles/m] | |
| value of at from the Sun | |
| O | Sun’s center of mass |
| P | total power required by the SWIFT [W] |
| power required by ion acceleration [W] | |
| power required by wire grid [W] | |
| R | SWIFT cone base radius [m] |
| r | Sun-spacecraft radial distance [au] |
| spacecraft position vector [au] | |
| conducting wire radius [m] | |
| reference distance [] | |
| T | steerable thrust [N] |
| t | time [days] |
| polar reference frame | |
| spacecraft velocity vector [km/s] | |
| radial component of the spacecraft velocity [km/s] | |
| solar wind velocity [km/s] | |
| exhaust velocity [km/s] | |
| transverse component of the spacecraft velocity [km/s] | |
| thrust angle [deg] | |
| optimal thrust angle [deg] | |
| contingency value [deg] | |
| power system specific mass [kg/W] | |
| SWIFT cone aperture [deg] | |
| conducting wire electric potential [V] | |
| variable adjoint to r | |
| variable adjoint to | |
| variable adjoint to | |
| variable adjoint to | |
| Sun’s gravitational parameter [km/s] | |
| support boom linear density [kg/m] | |
| conducting wire density [kg/m] | |
| spacecraft polar angle [deg] | |
| Subscripts | |
| 0 | initial, parking orbit |
| f | final, target orbit |
| ♂ | Mars |
| ♀ | Venus |
| ss | ideal flat solar sail |
References
- Jacobson, R.A.; Thornton, C.L. Elements of solar sail navigation with application to a Halley’s comet rendezvous. J. Guid. Control Dyn. 1978, 1, 365–371. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Janhunen, P. Electric sail option for cometary rendezvous. Acta Astronaut. 2016, 127, 684–692. [Google Scholar] [CrossRef]
- Hughes, G.W.; McInnes, C.R. Small-body encounters using solar sail propulsion. J. Spacecr. Rocket. 2004, 41, 140–150. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Janhunen, P. Electric sail for a near-Earth asteroid sample return mission: Case 1998 KY26. J. Aerosp. Eng. 2014, 27, 4014031. [Google Scholar] [CrossRef]
- Slavinskis, A.; Janhunen, P.; Toivanen, P.; Muinonen, K.; Penttilä, A.; Granvik, M.; Kohout, T.; Gritsevich, M.; Pajusalu, M.; Sunter, I.; et al. Nanospacecraft fleet for multi-asteroid touring with electric solar wind sails. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–20. [Google Scholar] [CrossRef]
- Dandouras, I.; Pirard, B.; Prado, J.Y. High performance solar sails for linear trajectories and heliostationary missions. Adv. Space Res. 2004, 34, 198–203. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G. Optimal solar sail transfer to linear trajectories. Acta Astronaut. 2013, 82, 189–196. [Google Scholar] [CrossRef]
- Gong, S.; Li, J. Solar sail heliocentric elliptic displaced orbits. J. Guid. Control Dyn. 2014, 37, 2021–2025. [Google Scholar] [CrossRef]
- Niccolai, L.; Quarta, A.A.; Mengali, G. Electric sail elliptic displaced orbits with advanced thrust model. Acta Astronaut. 2017, 138, 503–511. [Google Scholar] [CrossRef]
- Niccolai, L.; Anderlini, A.; Mengali, G.; Quarta, A.A. Electric sail displaced orbit control with solar wind uncertainties. Acta Astronaut. 2019, 162, 563–573. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Mengali, G. Magnetic sail-based displaced non-Keplerian orbits. Aerosp. Sci. Technol. 2019, 92, 363–372. [Google Scholar] [CrossRef]
- Aliasi, G.; Mengali, G.; Quarta, A.A. Artificial equilibrium points for a generalized sail in the circular restricted three-body problem. Celest. Mech. Dyn. Astron. 2011, 110, 343–368. [Google Scholar] [CrossRef]
- Niccolai, L.; Caruso, A.; Quarta, A.A.; Mengali, G. Artificial collinear Lagrangian point maintenance with electric solar wind sail. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4467–4477. [Google Scholar] [CrossRef]
- Bianchi, C.; Niccolai, L.; Mengali, G.; Quarta, A.A. Collinear artificial equilibrium point maintenance with a wrinkled solar sail. Aerosp. Sci. Technol. 2021, 119, 1–14. [Google Scholar] [CrossRef]
- Zeng, X.; Gong, S.; Li, J.; Alfriend, K.T. Solar sail body-fixed hovering over elongated asteroids. J. Guid. Control Dyn. 2016, 39, 1223–1231. [Google Scholar] [CrossRef]
- McInnes, C.R. Solar Sailing: Technology, Dynamics and Mission Applications; Springer: Berlin, Germany, 1999; pp. 171–196. [Google Scholar] [CrossRef]
- Fu, B.; Sperber, E.; Eke, F. Solar sail technology—A state of the art review. Prog. Aerosp. Sci. 2016, 86, 1–19. [Google Scholar] [CrossRef]
- Bovesecchi, G.; Corasaniti, S.; Costanza, G.; Tata, M.E. A novel self-deployable solar sail system activated by shape memory alloys. Aerospace 2019, 6, 78. [Google Scholar] [CrossRef]
- Zhang, F.; Gong, S.; Baoyin, H. Three-axes attitude control of solar sail based on shape variation of booms. Aerospace 2021, 8, 198. [Google Scholar] [CrossRef]
- Zou, J.; Li, D.; Wang, J.; Yu, Y. Experimental study of measuring the wrinkle of solar sails. Aerospace 2022, 9, 289. [Google Scholar] [CrossRef]
- Janhunen, P. Electric sail for spacecraft propulsion. J. Propuls. Power 2004, 20, 763–764. [Google Scholar] [CrossRef]
- Bassetto, M.; Niccolai, L.; Quarta, A.A.; Mengali, G. A comprehensive review of Electric Solar Wind Sail concept and its applications. Prog. Aerosp. Sci. 2022, 128, 100768. [Google Scholar] [CrossRef]
- Huo, M.Y.; Mengali, G.; Quarta, A.A. Electric sail thrust model from a geometrical perspective. J. Guid. Control Dyn. 2018, 41, 735–741. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Mengali, G.; Cipolla, V. Spiral trajectories induced by radial thrust with applications to generalized sails. Astrodynamics 2020, 5, 121–137. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Bassetto, M.; Niccolai, L. Optimal circle-to-ellipse orbit transfer for Sun-facing E-sail. Aerospace 2022, 9, 671. [Google Scholar] [CrossRef]
- Forward, R.L. Solar Photon Thrustor. J. Spacecr. Rocket. 1990, 27, 411–416. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Earth escape by ideal sail and solar-photon thrustor spacecraft. J. Guid. Control Dyn. 2004, 27, 1105–1108. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Time-optimal three-dimensional trajectories for solar photon thruster spacecraft. J. Spacecr. Rocket. 2005, 42, 379–381. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Compound solar sail with optical properties: Models and performance. J. Spacecr. Rocket. 2006, 43, 239–245. [Google Scholar] [CrossRef]
- Fieseler, P.; Anderson, K.R.; Cable, V. Critical look at the solar photon thruster concept. J. Spacecr. Rocket. 2015, 52, 1152–1162. [Google Scholar] [CrossRef]
- Gemmer, T.R.; Mazzoleni, A.P. Introduction and Performance Analysis of the Solar Wind Ion Focusing Thruster (SWIFT). In Proceedings of the 65th International Astronautical Congress, Toronto, ON, Canada, 29 September–3 October 2014. Paper IAC-14,C4,8,1,x24646. [Google Scholar]
- Gemmer, T.R.; Mazzoleni, A.P. Solar wind ion focusing thruster (SWIFT) Orbital Performance Analysis. In Proceedings of the 66th International Astronautical Congress, Jerusalem, Israel, 12–16 October 2015. [Google Scholar]
- Gemmer, T.R.; Mazzoleni, A.P. Comparative orbital performance study of a solar wind ion focusing thruster (SWIFT). In Proceedings of the 67th International Astronautical Congress, Guadalajara, Mexico, 26–30 September 2016. Paper IAC-16,C4,8,8,x33664. [Google Scholar]
- Gemmer, T.R.; Yoder, C.D.; Mazzoleni, A.P. Performance Analysis and Parametric Studies of the Solar Wind Ion Focusing Thruster (SWIFT) for Interplanetary Travel. J. Br. Interplanet. Soc. 2021, 74, 30–40. [Google Scholar]
- Ross, I.M. A Primer on Pontryagin’s Principle in Optimal Control; Collegiate Publishers: San Francisco, CA, USA, 2015; Chapter 2; pp. 127–129. ISBN 9780984357116. [Google Scholar]
- Lawden, D.F. Optimal Trajectories for Space Navigation; Butterworths & Co.: London, UK, 1963; pp. 54–60. [Google Scholar]
- Sauer, C.G., Jr. Optimum Solar-Sail Interplanetary Trajectories. In Proceedings of the AIAA/AAS Astrodynamics Conference, San Francisco, CA, USA, 18–20 August 1976. [Google Scholar] [CrossRef]
- Gallana, L.; Fraternale, F.; Fosson, S.M.; Magli, E.; Opher, M.; Richardson, J.D.; Tordella, D. Voyager 2 solar plasma and magnetic field spectral analysis for intermediate data sparsity. J. Geophys. Res. A Space Phys. 2016, 121, 3905–3919. [Google Scholar] [CrossRef]
- Phillips, J.L.; Bame, S.J.; Barnes, A.; Barraclough, B.M.; Feldman, W.C.; Goldstein, B.E. Ulysses solar wind plasma observations from pole to pole. Geophys. Res. Lett. 1995, 22, 3301–3304. [Google Scholar] [CrossRef]
- Stone, E.C.; Frandsen, A.M.; Mewaldt, R.A.; Christian, E.R.; Margolies, D.; Ormes, J.F. The Advanced Composition Explorer. Space Sci. Rev. 1998, 86, 1–22. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A.; Circi, C.; Dachwald, B. Refined solar sail force model with mission application. J. Guid. Control Dyn. 2007, 30, 512–520. [Google Scholar] [CrossRef]
- Wright, J.L. Space Sailing; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Bassetto, M.; Quarta, A.A.; Mengali, G.; Cipolla, V. Trajectory analysis of a Sun-facing solar sail with optical degradation. J. Guid. Control Dyn. 2020, 43, 1727–1732. [Google Scholar] [CrossRef]
- Antonakis, A.; Nikolaidis, T.; Pilidis, P. Multi-objective climb path optimization for aircraft/engine integration using particle swarm optimization. Appl. Sci. 2017, 7, 469. [Google Scholar] [CrossRef]
- Morante, D.; Sanjurjo Rivo, M.; Soler, M. A Survey on Low-Thrust Trajectory Optimization Approaches. Aerospace 2021, 8, 88. [Google Scholar] [CrossRef]
- Jia, F.; Peng, Q.; Zhou, W.; Li, X. Integrated design of Moon-to-Earth transfer trajectory considering re-entry constraints. Appl. Sci. 2022, 12, 8716. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere Publishing Corporation: New York, NY, USA, 1975; Chapter 2; pp. 71–89. ISBN 0-891-16228-3. [Google Scholar]
- Stengel, R.F. Optimal Control and Estimation; Dover Publications, Inc.: New York, NY, USA, 1994; pp. 222–254. [Google Scholar]
- Mengali, G.; Quarta, A.A. Optimal three-dimensional interplanetary rendezvous using nonideal solar sail. J. Guid. Control Dyn. 2005, 28, 173–177. [Google Scholar] [CrossRef]
- Shiu, K.T.; Zimmerman, J.; Wang, H.; Forrest, S.R. Ultrathin film, high specific power InP solar cells on flexible plastic substrates. Appl. Phys. Lett. 2009, 95, 223503. [Google Scholar] [CrossRef]
- Brophy, J.R.; Polk, J.E.; Goebel, D.M. Development of a 50,000-s, Lithium-fueled, Gridded Ion Thruster. In Proceedings of the 35th International Electric Propulsion Conference, Atlanta, GA, USA, 8–15 October 2017. Paper IEPC-2017-042. [Google Scholar]
- Caruso, A.; Quarta, A.A.; Mengali, G. Comparison Between Direct and Indirect Approach to Solar Sail Circle-to-circle Orbit Raising Optimization. Astrodynamics 2019, 3, 273–284. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G. Approximate Solutions to Circle-to-Circle Solar Sail Orbit Transfer. J. Guid. Control Dyn. 2013, 36, 1866–1890. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G. Semi-Analytical Method for the Analysis of Solar Sail Heliocentric Orbit Raising. J. Guid. Control Dyn. 2012, 35, 330–335. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Caruso, A.; Mengali, G. Optimal heliocentric transfers of a Sun-facing heliogyro. Aerosp. Sci. Technol. 2021, 119, 107094. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Trajectory design with hybrid low-thrust propulsion system. J. Guid. Control Dyn. 2007, 30, 419–426. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Optimal trade studies of interplanetary electric propulsion missions. Acta Astronaut. 2008, 62, 657–667. [Google Scholar] [CrossRef]


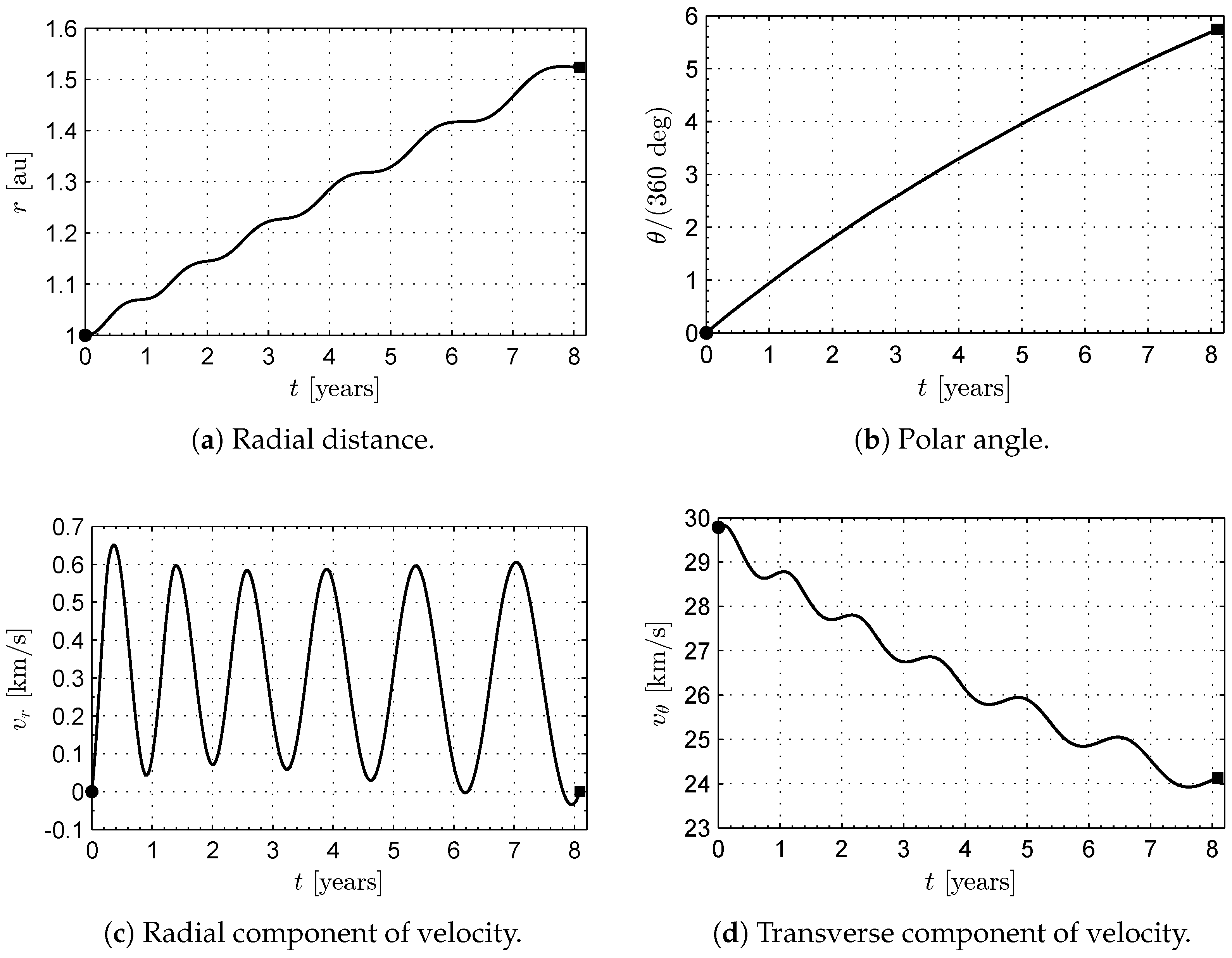
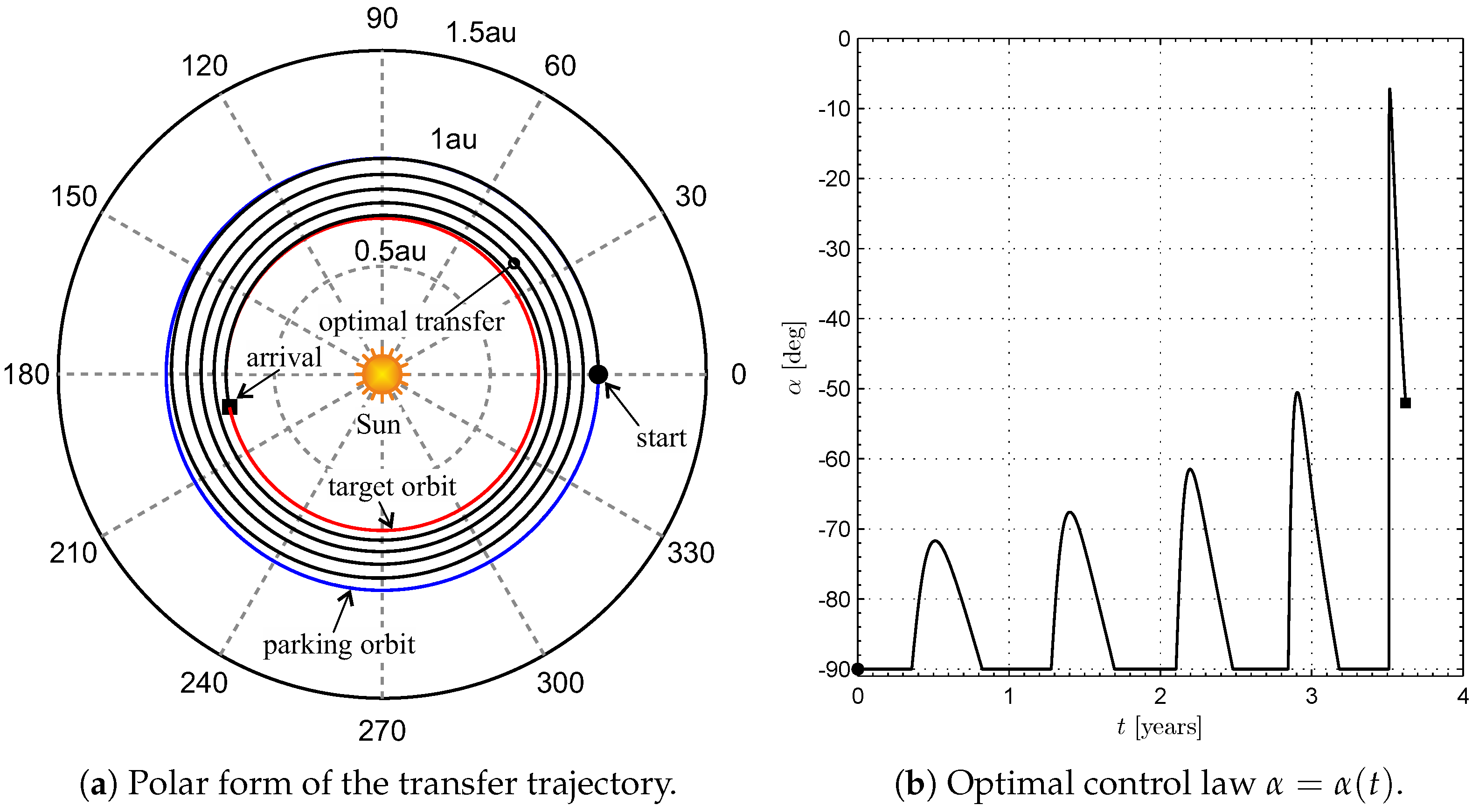
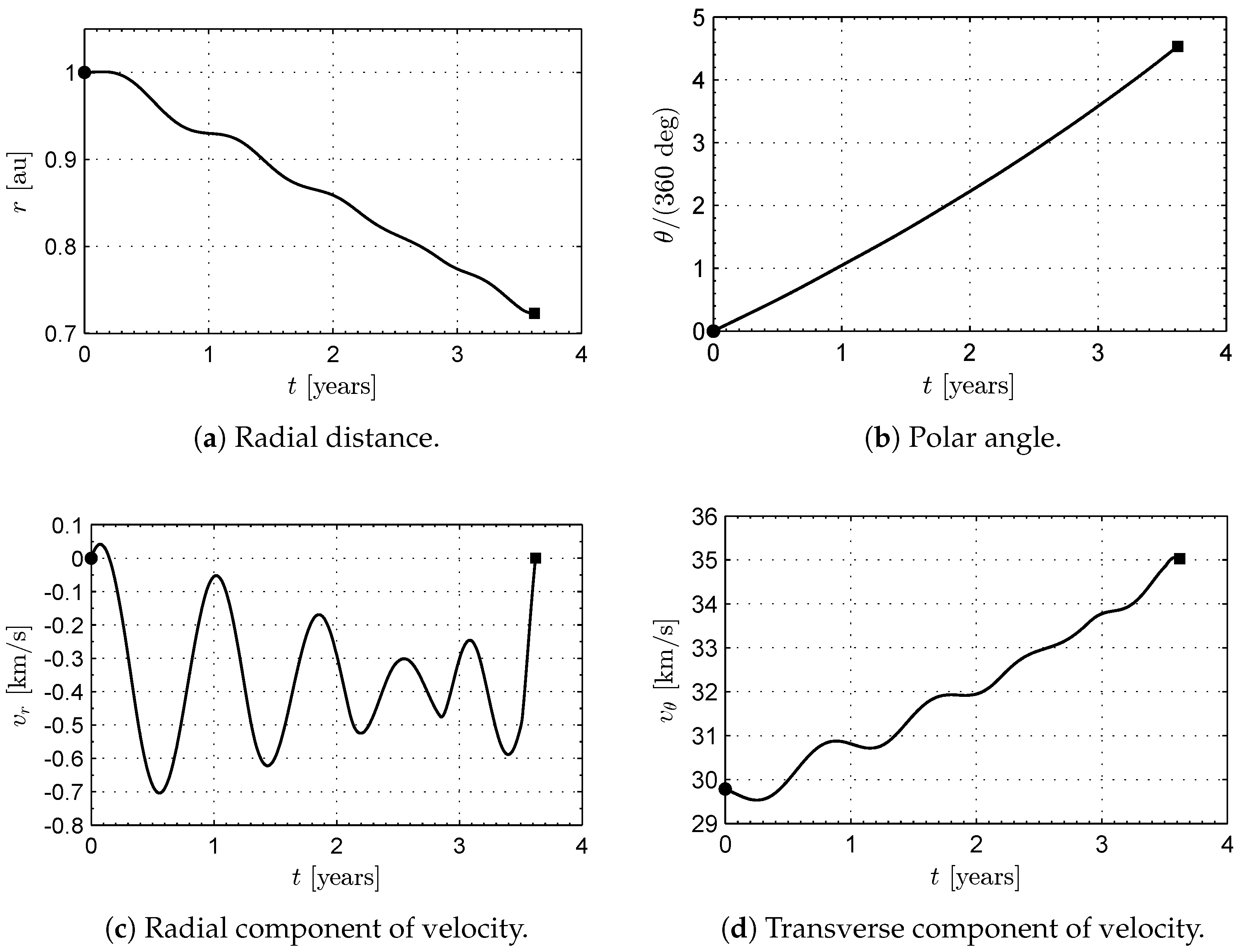
| Parameter | Value | Units |
|---|---|---|
| e | ||
| 1 | ||
| 400 | ||
| 132,712,439,935.5 | ||
| 2700 |
| Parameter | Value | Units |
|---|---|---|
| d | 10 | |
| 250 | ||
| 100 | − | |
| 4 | − | |
| R | 3 | |
| 400 | ||
| 120 | ||
| 30 | ||
| 10 | ||
| Parameter | Value | Units |
|---|---|---|
| m | ||
| P | ||
| k | 1 | − |
| 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quarta, A.A.; Niccolai, L.; Mengali, G.; Bassetto, M. Optimal Interplanetary Transfer of Solar Wind Ion Focusing Thruster-Based Spacecraft. Appl. Sci. 2023, 13, 3820. https://doi.org/10.3390/app13063820
Quarta AA, Niccolai L, Mengali G, Bassetto M. Optimal Interplanetary Transfer of Solar Wind Ion Focusing Thruster-Based Spacecraft. Applied Sciences. 2023; 13(6):3820. https://doi.org/10.3390/app13063820
Chicago/Turabian StyleQuarta, Alessandro A., Lorenzo Niccolai, Giovanni Mengali, and Marco Bassetto. 2023. "Optimal Interplanetary Transfer of Solar Wind Ion Focusing Thruster-Based Spacecraft" Applied Sciences 13, no. 6: 3820. https://doi.org/10.3390/app13063820
APA StyleQuarta, A. A., Niccolai, L., Mengali, G., & Bassetto, M. (2023). Optimal Interplanetary Transfer of Solar Wind Ion Focusing Thruster-Based Spacecraft. Applied Sciences, 13(6), 3820. https://doi.org/10.3390/app13063820






