Design and Feasibility Study of Novel Flying Wing Carrier for Launching Small Satellites in Low Earth Orbit
Abstract
:1. Introduction
2. The Flying Wing Carrier-Launcher System
2.1. Historical Data Analysis
2.2. Comparison of Ground and Air Launch Systems: Velocity Budgets Estimation
2.3. Description of Geometry and Mass Properties of the Carrier-Launcher System
3. The Carrier-Launcher System Performance: Preliminary Analyses and Results
3.1. Aerodynamic and Aeromechanical Analyses of the Carrier-Launcher System
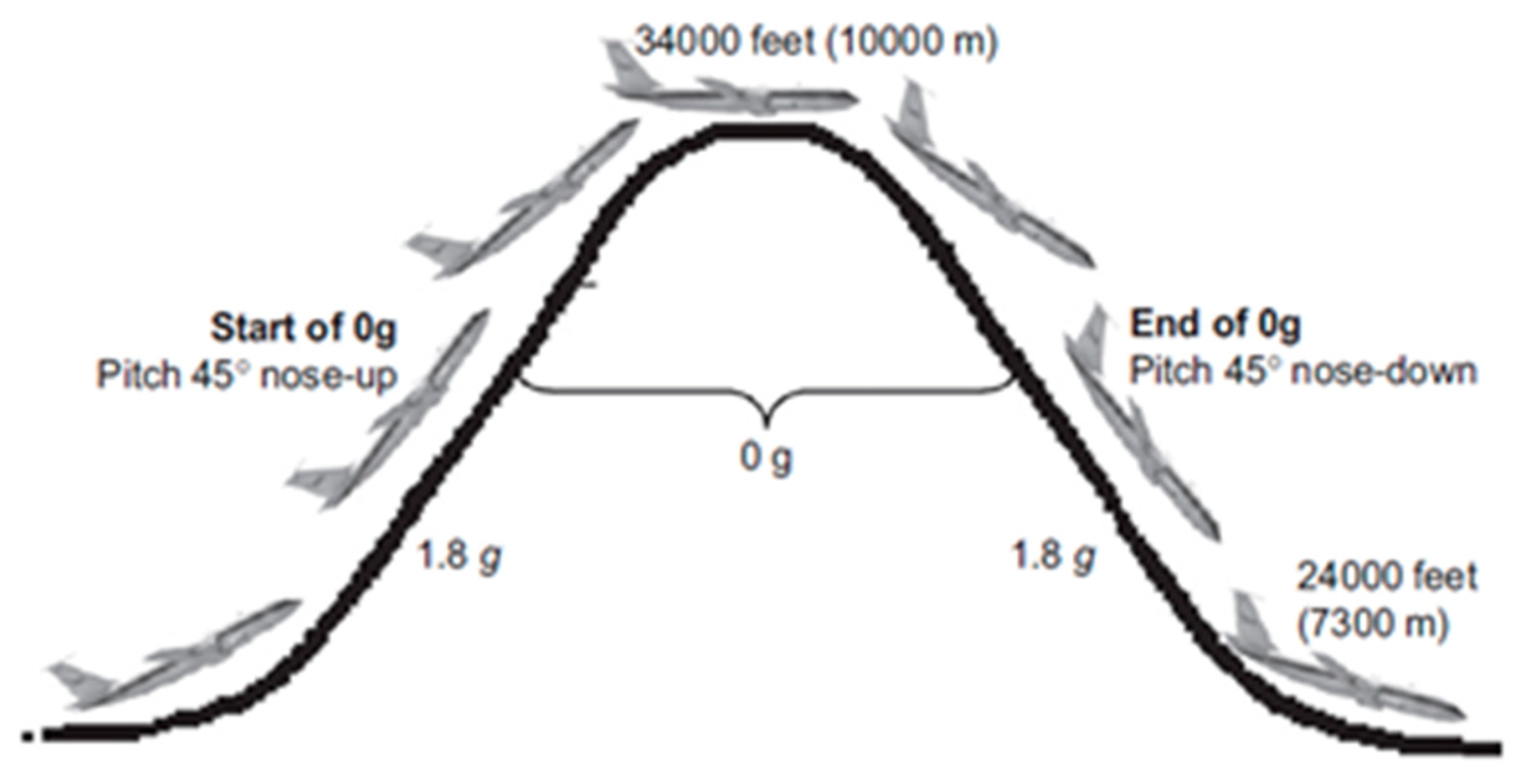
3.2. Choice of Engines Needed to Perform the Parabolic Manoeuvre
3.3. Modal Analyses and Aeroelastic Analyses of the Carrier-Launcher System
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sippel, M.; Stappert, S.; Koch, A. Assessment of multiple mission reusable launch vehicles. J. Space Saf. Eng. 2019, 6, 165–180. [Google Scholar] [CrossRef] [Green Version]
- Dresia, K.; Jentzsch, S.; Waxenegger-Wilfing, G.; Hahn, R.D.S.; Deeken, J.; Oschwald, M.; Mota, F. Multidisciplinary Design Optimization of Reusable Launch Vehicles for Different Propellants and Objectives. J. Spacecr. Rocket. 2021, 58, 1017–1029. [Google Scholar] [CrossRef]
- Brevault, L.; Balesdent, M.; Hebbal, A. Multi-Objective Multidisciplinary Design Optimization Approach for Partially Reusable Launch Vehicle Design. J. Spacecr. Rocket. 2020, 57, 373–390. [Google Scholar] [CrossRef]
- Ansgar, M.; Josef, K.; Johannes, R.; Daniel, K.; Sebastian, K.; Davide, B.; Vos, J.; Matthew, J.; Anett, K.; João, C. Retro propulsion assisted landing technologies (retalt): Current Status and Outlook of the EU Funded Project on Reusable Launch Vehicles. In Proceedings of the 70th International Astronautical Congress, Washington DC, USA, 21–25 October 2019; Available online: https://elib.dlr.de/132566/ (accessed on 1 April 2023).
- Cheng, G.; Jing, W.; Gao, C. Recovery trajectory planning for the reusable launch vehicle. Aerosp. Sci. Technol. 2021, 117, 106965. [Google Scholar] [CrossRef]
- Burton, R.L.; Brown, K.; Jacobi, A. Low-Cost Launch of Payloads to Low Earth Orbit. J. Spacecr. Rocket. 2006, 43, 696–698. [Google Scholar] [CrossRef]
- Crisp, N.; Roberts, P.; Livadiotti, S.; Oiko, V.; Edmondson, S.; Haigh, S.; Huyton, C.; Sinpetru, L.; Smith, K.; Worrall, S.; et al. The benefits of very low earth orbit for earth observation missions. Prog. Aerosp. Sci. 2020, 117, 100619. [Google Scholar] [CrossRef]
- del Portillo, I.; Cameron, B.G.; Crawley, E.F. A technical comparison of three low earth orbit satellite constellation systems to provide global broadband. Acta Astronaut. 2019, 159, 123–135. [Google Scholar] [CrossRef]
- Curzi, G.; Modenini, D.; Tortora, P. Large Constellations of Small Satellites: A Survey of Near Future Challenges and Missions. Aerospace 2020, 7, 133. [Google Scholar] [CrossRef]
- Karmali, F.; Shelhamer, M. The dynamics of parabolic flight: Flight characteristics and passenger percepts. Acta Astronaut. 2008, 63, 594–602. [Google Scholar] [CrossRef] [Green Version]
- Pletser, V. Aircraft Parabolic Flights: A Gateway to Orbital Microgravity and Extra-Terrestrial Planetary Gravities. 2020. Available online: https://www.intechopen.com/chapters/72224 (accessed on 29 May 2020).
- Goetzendorf-Grabowski, T. Flight dynamics of unconventional configurations. Prog. Aerosp. Sci. 2023, 137, 100885. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Xing, Y.; Yang, Z. Investigation of wing structure layout of aerospace plane based on the finite element method. Adv. Mech. Eng. 2017, 9, 1687814017713701. [Google Scholar] [CrossRef] [Green Version]
- Pan, Y.; Huang, J. Influences of airfoil profile on lateral-directional stability of aircraft with flying wing layout. Aircr. Eng. Aerosp. Technol. 2019, 91, 1011–1017. [Google Scholar] [CrossRef]
- Keidel, D.; Molinari, G.; Ermanni, P. Aero-structural optimization and analysis of a camber-morphing flying wing: Structural and wind tunnel testing. J. Intell. Mater. Syst. Struct. 2019, 30, 908–923. [Google Scholar] [CrossRef]
- Sarigul-Klijn, M.; Sarigul-Klijn, N.; Hudson, G.; McKinney, B.; Voss, J.; Chapman, P.; Morgan, B.; Tighe, J.; Kramb, J.; Doyle, K. Selection of a Carrier Aircraft and a Launch Method for Air Launching Space Vehicles. In Proceedings of the AIAA SPACE 2008 Conference & Exposition, San Diego, CA, USA, 9–11 September 2008. [Google Scholar] [CrossRef] [Green Version]
- Sarigul-Klijn, M.; Sarigul-Klijn, N.; Morgan, B.; Tighe, J.; Leon, A.; Hudson, G.; McKinney, B.; Gump, D. Flight Testing of a New Earth-to-Orbit Air Launch Method. J. Aircr. 2006, 43, 577–583. [Google Scholar] [CrossRef]
- Sarigul-Klijn, N.; Sarigul-Klijn, M.; Noel, C. Air Launching Earth-to-Orbit Vehicles: Delta V gains from Launch Conditions and Vehicle Aerodynamics. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar] [CrossRef]
- Sarigul-Klijn, N.; Sarigul-Klijn, M.; Noel, C. Air-Launching Earth to Orbit: Effects of Launch Conditions and Vehicle Aerodynamics. J. Spacecr. Rocket. 2005, 42, 569–575. [Google Scholar] [CrossRef]
- Dagur, R.; Singh, V.; Grover, S.; Sethi, N.; Arora, B.B. Design of Flying Wing UAV and Effect of Winglets on its Performance. Int. J. Emer. Tech. Adv. Eng. 2018, 8, 414–428. [Google Scholar]
- Rajendran, S. Design of Parametric Winglets and Wing Tip Devices—A Conceptual Design Approach. Master’s Thesis, Linkoping University, Institute of Technology, Linkoping, Sweden, 2012. Available online: https://liu.diva-portal.org/smash/get/diva2:547954/FULLTEXT01.pdf (accessed on 1 April 2023).
- Anderson, J.D., Jr. Introduction to Flight, 7th ed.; McGraw-Hill Education: New York, NY, USA, 2011. [Google Scholar]
- Kundu, A.K. Aircraft Design; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Hoerner, F.S. Fluid-Dynamic Drag; Hoerner Fluid Dynamics: Bakersfield, CA, USA, 1992. [Google Scholar]
- Tulapurkara, E.G. Flight Dynamics–II (Stability and Control), Department of Aerospace Engineering, I.I.T. Madras, Chennai-600036, India. 2008. Available online: https://cnj.atu.edu.iq/wp-content/uploads/2020/03/3b.pdf (accessed on 1 April 2023).
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 6th ed.; AIAA: Reston, VA, USA, 2018. [Google Scholar]
- Lan, C.E.; Roskam, J. Airplane Aerodynamics and Performance, 5th ed.; DARcorporation: Lawrence, KS, USA, 2016. [Google Scholar]
- Niţă, M.; Scholz, D. Estimating the Oswald Factor from Basic Aircraft Geometrical Parameters; Deutscher Luft- und Raumfahrtkongress: Berlin, Germany, 2012; Available online: https://www.dglr.de/publikationen/2012/281424.pdf (accessed on 1 April 2023).
- Mardanpour, P.; Hodges, D.H.; Neuhart, R.; Graybeal, N. Engine Placement Effect on Nonlinear Trim and Stability of Flying Wing Aircraft. J. Aircr. 2013, 50, 1716–1725. [Google Scholar] [CrossRef]
- Borrometi, F.B. The Flying Wing “R6” as a First Stage Carrier of a Small Launcher for the Deployment of Satellites in LEO. Master’s Thesis, University of Pisa, Pisa, Italy, 2022. Available online: https://etd.adm.unipi.it/t/etd-05172022-160106/ (accessed on 1 April 2023).
- AVL. Available online: https://web.mit.edu/drela/Public/web/avl/ (accessed on 1 April 2023).
- Chiarelli, M.R.; Cagnoni, M.; Ciabattari, M.; De Biasio, M.; Massai, A. High Aspect Ratio Wing with Curved Planform: CFD and FE Analyses. In Proceedings of the 27th Congress of the International Council of the Aeronautical Sciences (ICAS ‘10), Nice, France, 19–24 September 2010. [Google Scholar]
- Chiarelli, M.R.; Bonomo, S. Aeroelastic analysis of wings in the transonic regime: Planform’s influence on the dynamic instability. Int. J. Aer. Eng. 2016, 2016, 3563684. Available online: https://www.hindawi.com/journals/ijae/2016/3563684/ (accessed on 1 April 2023).
- Chiarelli, M.R.; Bonomo, S. Numerical Investigation into Flutter and Flutter-Buffet Phenomena for a Swept Wing and a Curved Planform Wing. Int. J. Aerosp. Eng. 2019, 2019, 8210235. Available online: https://www.hindawi.com/journals/ijae/2019/8210235/ (accessed on 1 April 2023). [CrossRef] [Green Version]
- Schmidt, D.K.; Danowsky, B.P.; Seiler, P.J.; Kapania, R.K. Flight-Dynamics and Flutter Analysis and Control of an MDAO-Designed Flying-Wing Research Drone. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 1816. [Google Scholar] [CrossRef]
- Syed, A.A.; Moshtaghzadeh, M.; Hodges, D.H.; Mardanpour, P. Aeroelasticity of Flying-Wing Aircraft Subject to Morphing: A Stability Study. AIAA J. 2022, 60, 5372–5385. [Google Scholar] [CrossRef]
- Moshtaghzadeh, M.; Izadpanahi, E.; Bejan, A.; Mardanpour, P. Evolutionary Aeroelastic Design of Flying-Wing Cross Section. AIAA J. 2022, 60, 913–924. [Google Scholar] [CrossRef]
- Shi, P.; Liu, F.; Gu, Y.; Yang, Z. The Development of a Flight Test Platform to Study the Body Freedom Flutter of BWB Flying Wings. Aerospace 2021, 8, 390. [Google Scholar] [CrossRef]
- Richards, P.W.; Yao, Y.; Herd, R.A.; Hodges, D.H.; Mardanpour, P. Effect of Inertial and Constitutive Properties on Body-Freedom Flutter for Flying Wings. J. Aircr. 2016, 53, 756–767. [Google Scholar] [CrossRef]
- Izadpanahi, E.; Rastkar, S.; Mardanpour, P. Constructal Design of Flying Wing Aircraft: Curved and Swept Configurations. AIAA J. 2019, 57, 5527–5542. [Google Scholar] [CrossRef]
- PW4000-112 Engine. Available online: https://prattwhitney.com/products-and-services/products/commercial-engines/pw4000-112 (accessed on 1 April 2023).
- COSMIC GIRL 747. Available online: https://www.virgin.com/branson-family/richard-branson-blog/virgin-orbits-launcherone-meets-cosmic-girl-747 (accessed on 1 April 2023).
- Northrop Grumman. Available online: https://www.northropgrumman.com/what-we-do/air/b-2-stealth-bomber/10-cool-facts-about-the-b-2/ (accessed on 1 April 2023).
- Military Factory. Northrop XB-35/YB-35. Available online: https://www.militaryfactory.com/aircraft/detail.php?aircraft_id=976 (accessed on 1 April 2023).
- Military Factory. Northrop YB-49. Available online: https://www.militaryfactory.com/aircraft/detail.php?aircraft_id=977 (accessed on 1 April 2023).
- Military Factory. McDonnell Douglas/General Dynamics A-12 Avenger II. Available online: https://www.militaryfactory.com/aircraft/detail.php?aircraft_id=723 (accessed on 1 April 2023).
- Military Factory. Horten Ho XVIII (Amerika Bomber). Available online: https://www.militaryfactory.com/aircraft/detail.php?aircraft_id=1351 (accessed on 1 April 2023).
- Naval Technology. X-47B Unmanned Combat Air System (UCAS). Available online: https://www.naval-technology.com/projects/x-47b-unmanned-combat-air-system-carrier-ucas/ (accessed on 1 April 2023).
- Cole, W. X-45A Makes HISTORY—Successful First Flight at Dryden Paves the Way for More Tests, More UCAVs; Boeing Frontiers Online: Arlington, VA, USA, 2022. [Google Scholar]
- Military Factory. Lockheed Martin/Boeing RQ-3 DarkStar. Available online: https://www.militaryfactory.com/aircraft/detail.php?aircraft_id=1152#:~:text=Overall%20dimensions%20of%20the%20aircraft,loaded%20weight%20of%208%2C500lbs (accessed on 1 April 2023).
- Tsagarakis, M. Project Solaris—Analysis of Airfoil for Solar Powered Flying Wing UAV. Bachelor’s Thesis, Aeronautical Engineering, Mälardalen University, Västerås, Sweden, 2011. Available online: https://www.diva-portal.org/smash/get/diva2:450812/fulltext01 (accessed on 1 April 2023).
- Airfoil Tools. Available online: http://airfoiltools.com/airfoil/details?airfoil=bacxxx-il (accessed on 1 April 2023).
- Jones, T.; Rustenburg, J.W.; Skinn, D.A.; Tipps, D.O.; DeFiore, T. Statistical Data for the Boeing-747-400 Aircraft in Commercial Operations; Federal Aviation Administration: Springfield, VA, USA, 2005. [Google Scholar]
- Boeing BACXXX Airfoil. Available online: https://m-selig.ae.illinois.edu/ads/afplots/bacxxx.gif (accessed on 1 April 2023).
- Humble, R.W.; Henry, G.N.; Larson, W.J. Space Propulsion Analysis and Design; McGraw Hill: New York, NY, USA, 1995. [Google Scholar]
- Rolls-Royce UltraFan Engine. Available online: https://www.rolls-royce.com/innovation/ultrafan.aspx (accessed on 1 April 2023).
- MSC NASTRAN. Available online: https://hexagon.com/it/products/product-groups/computer-aided-engineering-software/msc-nastran (accessed on 1 April 2023).
- PATRAN. Available online: https://hexagon.com/it/products/patran (accessed on 1 April 2023).
- Sarigul-Klijn, N.; Sarigul-Klijn, M. A comparative analysis of methods for air-launching vehicles from earth to sub-orbit or orbit. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2006, 220, 439–452. [Google Scholar] [CrossRef]

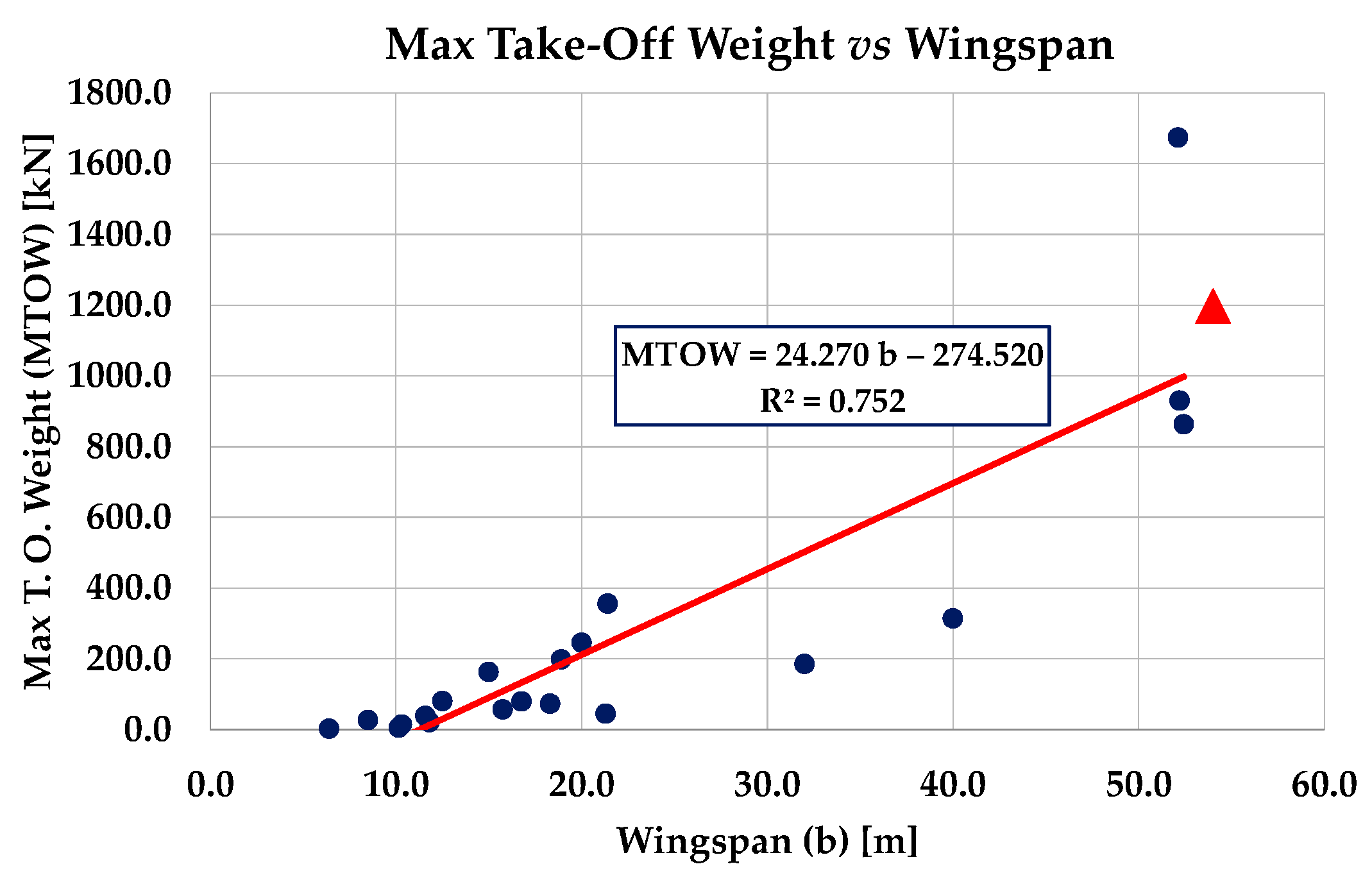
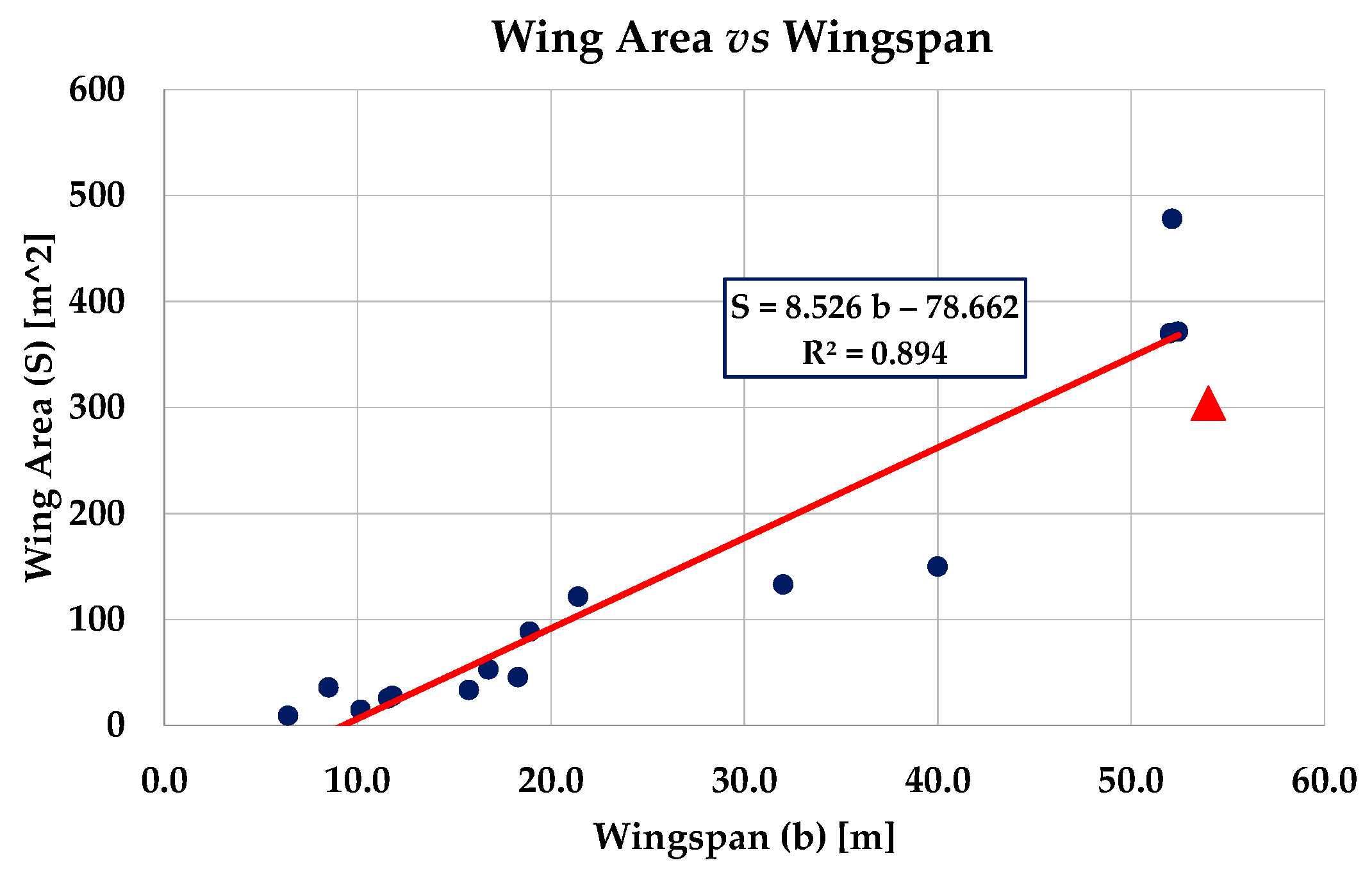
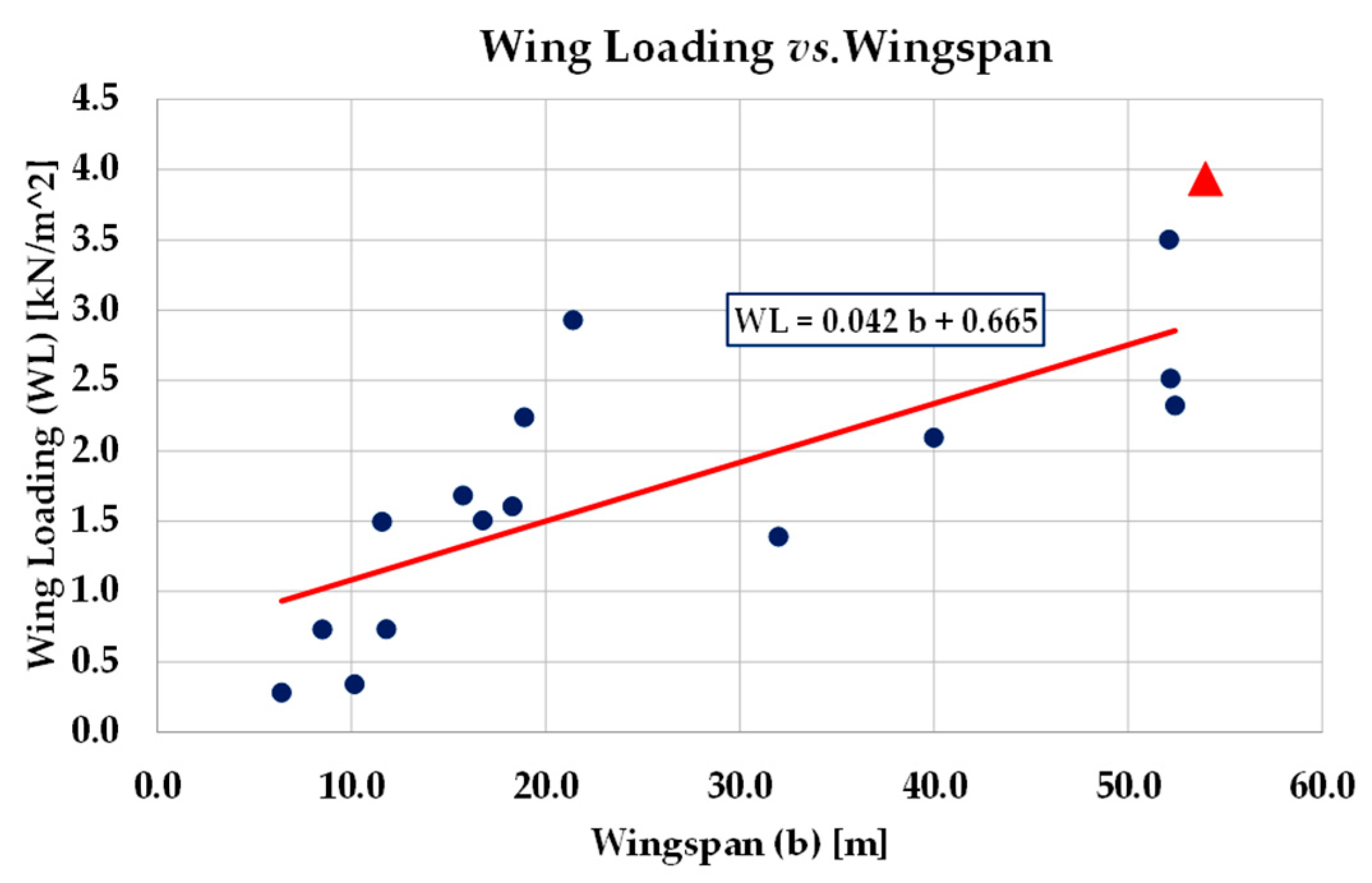
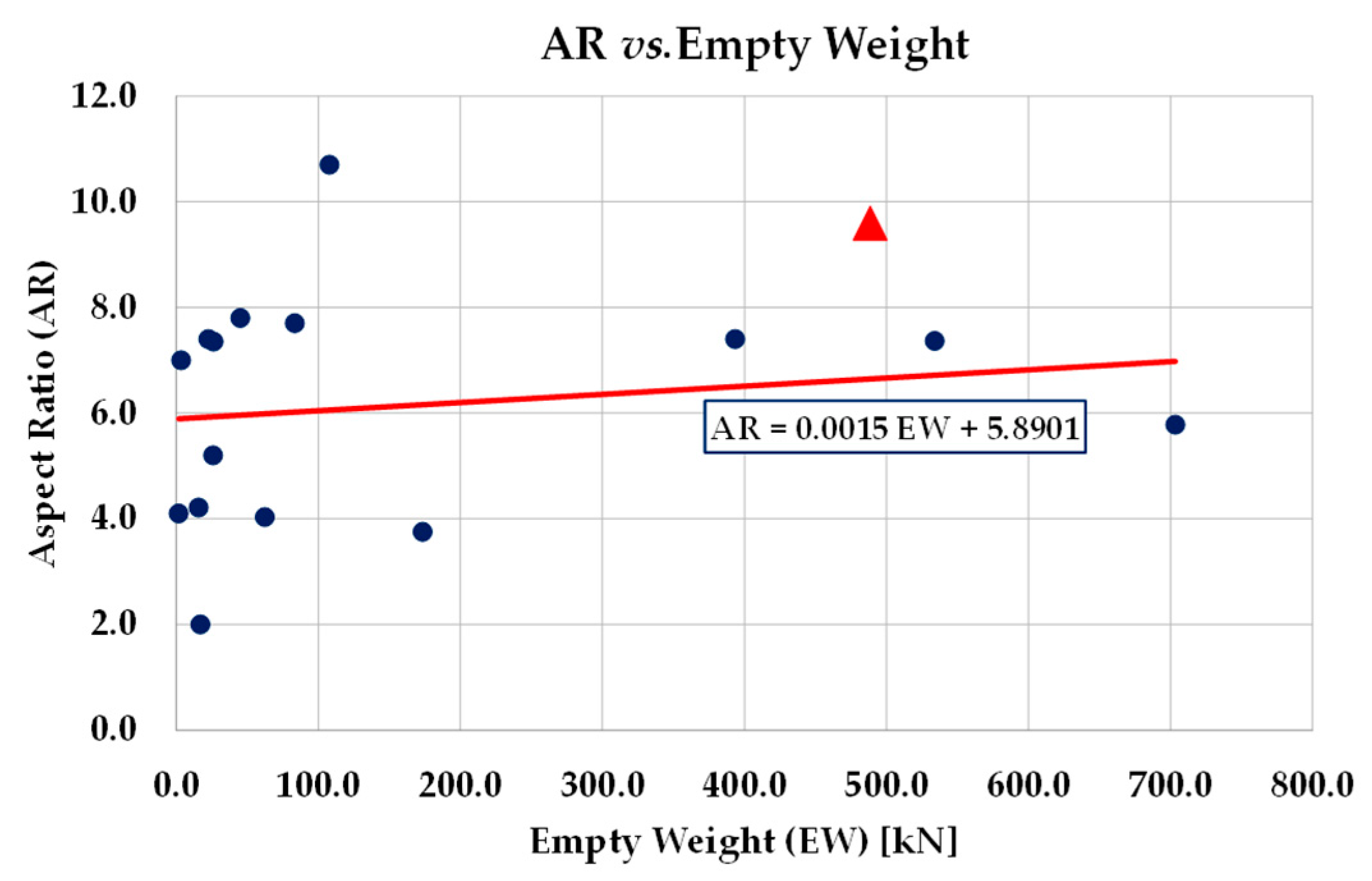



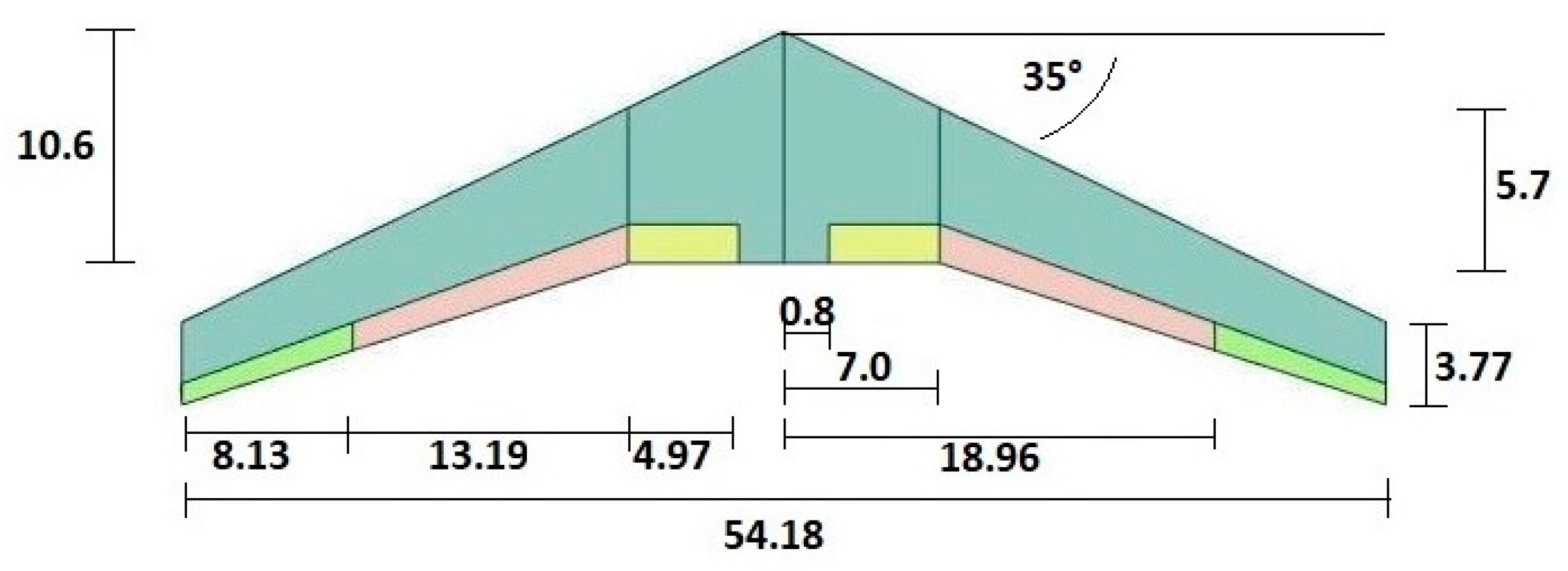
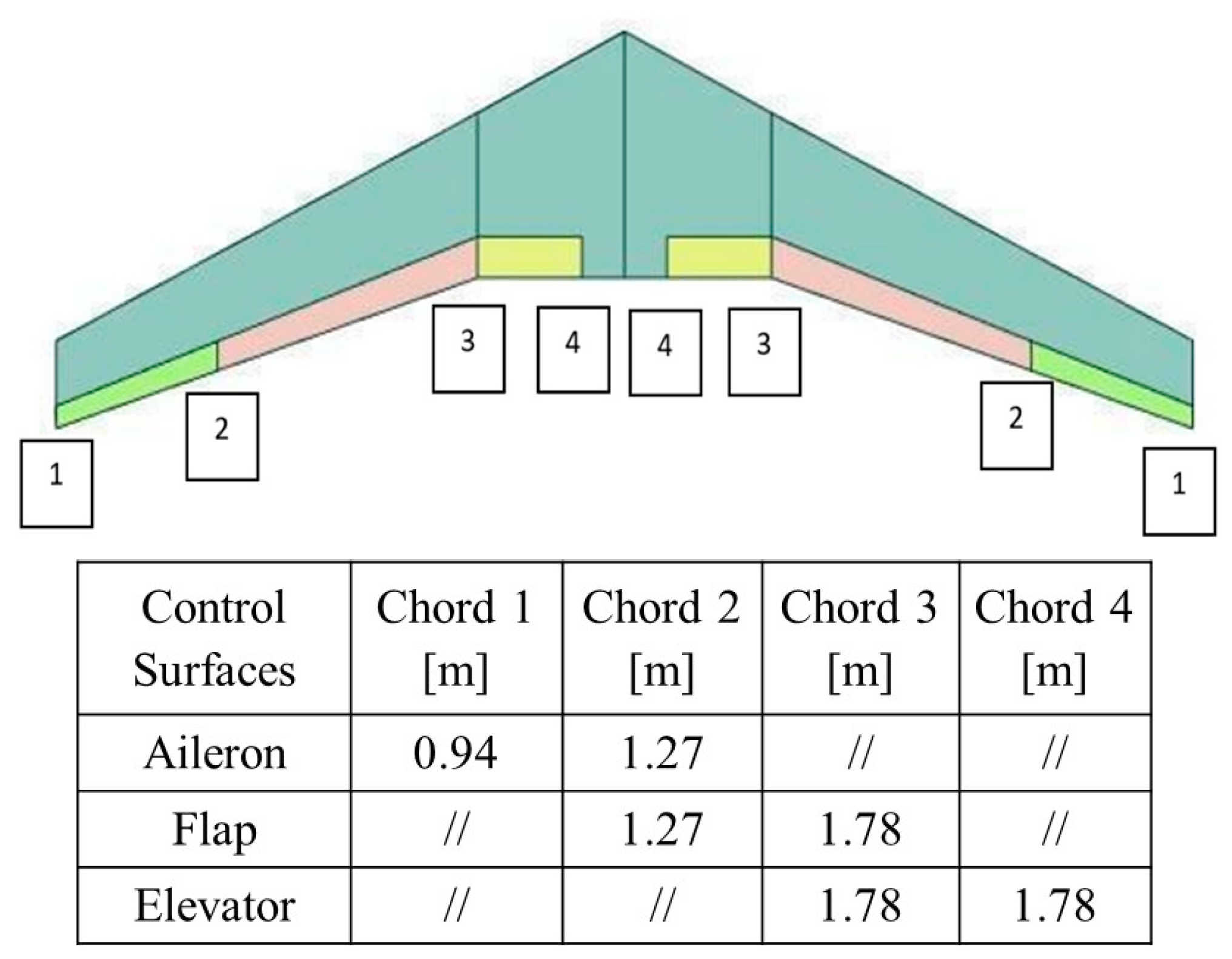
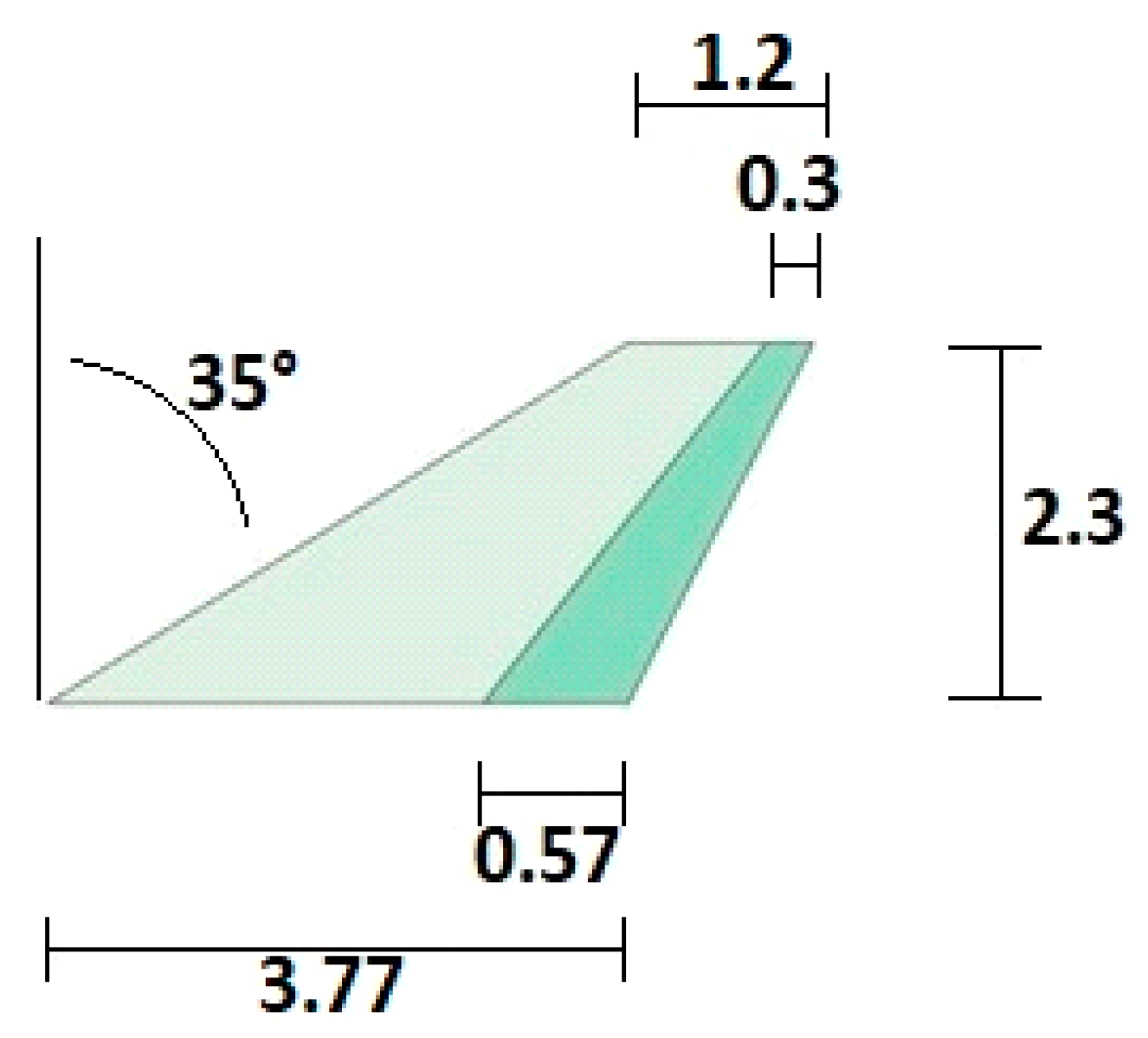
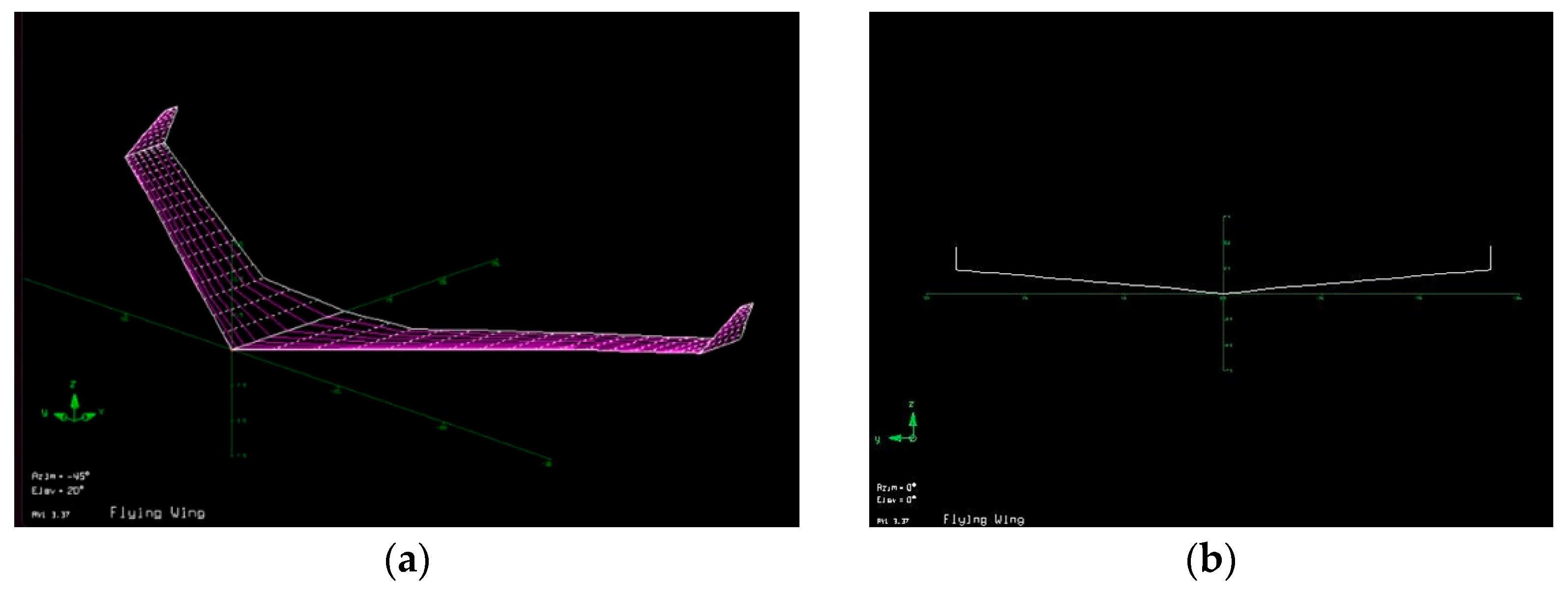

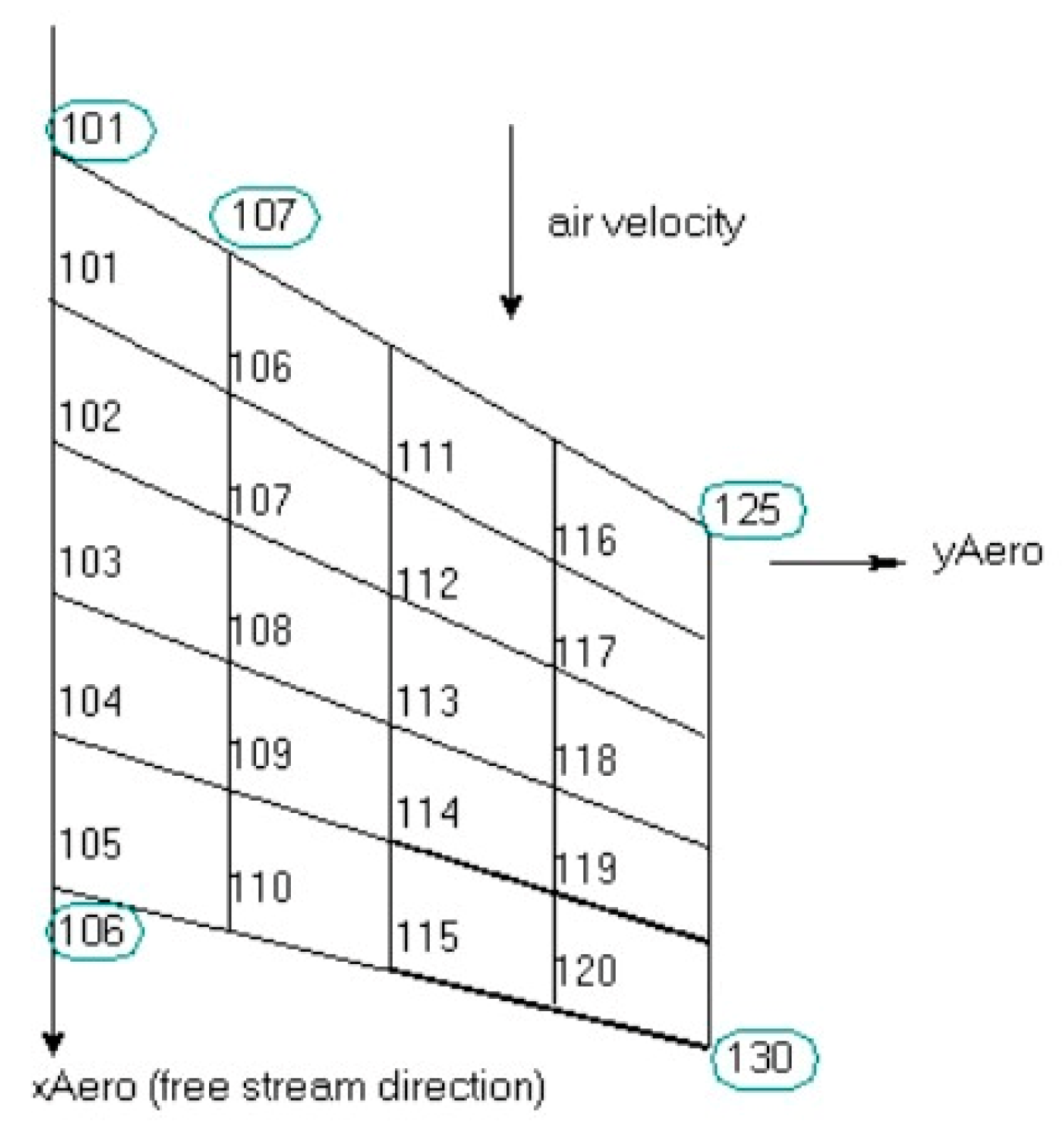





| Note | Flying Wing Model | Wingspan [m] | Aspect Ratio | Wing Area [m2] | Empty Weight [kN] | Max T.O. Weight [kN] | Wing Loading [kN/m2] | Airfoil |
|---|---|---|---|---|---|---|---|---|
| Northrop B-2 Spirit [43] | 52.12 | 5.78 | 478.00 | 703.38 | 1673.59 | 3.501 | NACA 0018 | |
| Northrop YB-35 [44] | 52.00 | 7.40 | 370.00 | 533.98 | 929.99 | 2.513 | tip: NACA 653-018 | |
| root: NACA 653-019 | ||||||||
| Northrop YB-49 [45] | 52.43 | 7.20 | 370.00 | 393.54 | 862.98 | 2.322 | tip: NACA 653-018 | |
| root: NACA 653-019 | ||||||||
| Northrop XP-79B | 11.58 | 5.19 | n.a. * | 26.00 | 38.57 | 1.495 | NACA 662-018 | |
| Blended | Northrop X-47B [48] | 18.90 | 4.03 | 88.59 | 62.29 | 198.31 | 2.239 | n.a. * |
| Northrop N-1M | 11.79 | 4.21 | 33.00 | 15.70 | 20.42 | 0.732 | n.a. * | |
| Northrop N-9M | 18.30 | 7.35 | 45.50 | 26.22 | 73.01 | 1.605 | NACA 65-019 | |
| Blended/UAV | Northrop Grumman X-47A Pegasus | 8.50 | 2.00 | 35.98 | 17.07 | 26.27 | 0.730 | n.a. * |
| McDonnell Douglas/General Dynamics A-12 Avenger II [46] | 21.41 | 3.75 | 121.50 | 173.54 | 355.98 | 2.930 | n.a. * | |
| Horten Ho 229A | 16.76 | 7.80 | 52.80 | 45.13 | 79.46 | 1.505 | 13% thickness | |
| Horten H.XVIIIA [47] | 40.00 | 10.70 | 150.00 | 107.91 | 313.92 | 2.093 | 16% thickness | |
| Interstate XBDR-1 | 15.75 | 7.40 | 33.60 | 22.62 | 56.54 | 1.683 | n.a. * | |
| DINFIA IA 38 | 32.00 | 7.70 | 133.00 | 83.39 | 184.66 | 1.388 | n.a. * | |
| Baynes Bat | 10.16 | 7.00 | 14.86 | 3.40 | 5.04 | 0.339 | n.a. * | |
| Blended | Boeing X-48B | 6.40 | 4.10 | 9.34 | 1.75 | 2.62 | 0.280 | n.a. * |
| Blended/UAV | Boeing X-45A [49] | 10.30 | n.a. * | n.a. * | 35.60 | 14.24 | n.a. * | n.a. * |
| Boeing Phantom Ray | 15.00 | n.a. * | n.a. * | 64.97 | 162.41 | n.a. * | n.a. * | |
| Blended | Lockheed Martin RQ-3 DarkStar [50] | 21.00 | n.a. * | n.a. * | 19.42 | 44.55 | n.a. * | n.a. * |
| Dassault nEUROn | 12.50 | n.a. * | n.a. * | 48.07 | 80.79 | n.a. * | n.a. * | |
| Supersonic | Sukhoi S-70 Okhotnik | 20.00 | n.a. * | n.a. * | 147.15 | 245.25 | n.a. * | n.a. * |
| Launch System | [m/s] | [m/s] | [m/s] | [m/s] | [m/s] | [m/s] | [m/s] |
|---|---|---|---|---|---|---|---|
| Ariane A-44L | 7802 | 1576 | 135 | 38 | 9551 | −413 | 9138 |
| Atlas I | 7946 | 1395 | 110 | 167 | 9618 | −375 | 9243 |
| Delta 7925 | 7842 | 1150 | 136 | 33 | 9161 | −347 | 8814 |
| Space Shuttle | 7794 | 1222 | 107 | 358 | 9481 | −395 | 9086 |
| Saturn V | 7798 | 1534 | 40 | 243 | 9615 | −348 | 9267 |
| Titan IV/Centaur | 7896 | 1442 | 156 | 65 | 9559 | −352 | 9207 |
| Mean Values | 7846 | 1387 | 114 | 151 | 9498 | −372 | 9126 |
| Launch System | [m/s] | [m/s] | [m/s] | [m/s] | [m/s] | [m/s] | [m/s] |
|---|---|---|---|---|---|---|---|
| Flying Wing | 9498 | −284.27 | −22.23 | −29.38 | −100 | −260 | 8802 |
| Launcher Mass | Structural Mass | Mass of Systems |
|---|---|---|
| 10,000 | 300 | 300 |
| Launch System | [m/s] | Propellant Mass | Payload Mass |
|---|---|---|---|
| Ground Launch to Orbit | 9126 | 9023 | 377 |
| Air Launch to Orbit (FW) | 8802 | 8939 | 461 |
| Geometry Parameter | Component | Mass/Weight | |
|---|---|---|---|
| Surface Area [m2] | 304.00 | Structure [kg] | 23,535 |
| Root chord [m] | 10.60 | Engines [kg] | 18,300 |
| Kink chord [m] | 5.70 | Landing gears [kg] | 3660 |
| Tip chord [m] | 3.77 | On-board systems [kg] | 3520 |
| Kink section position [m] | 7.00 | Control surfaces [kg] | 495 |
| Half wingspan [m] | 27.09 | Batteries [kg] | 200 |
| Aspect Ratio | 9.64 | APU [kg] | 80 |
| Angle of Sweep at L.E. [deg] | 35.00 | Fuel [kg] | 62,190 |
| Max t/c [%] | 11.30 | Launcher (payload) [kg] | 10,000 |
| Dihedral angle [deg] | 7.00 | Carrier’s Structural Mass [kg] | 49,790 |
| Winglet cant angle [deg] | 35.00 | Carrier’s Take-Off Mass [kg] | 121,980 |
| Empty Weight [kN] | 488 | ||
| Max Take-Off Weight (MTOW) [kN] | 1196 | ||
| Wing loading [kN/m2] | 3.936 |
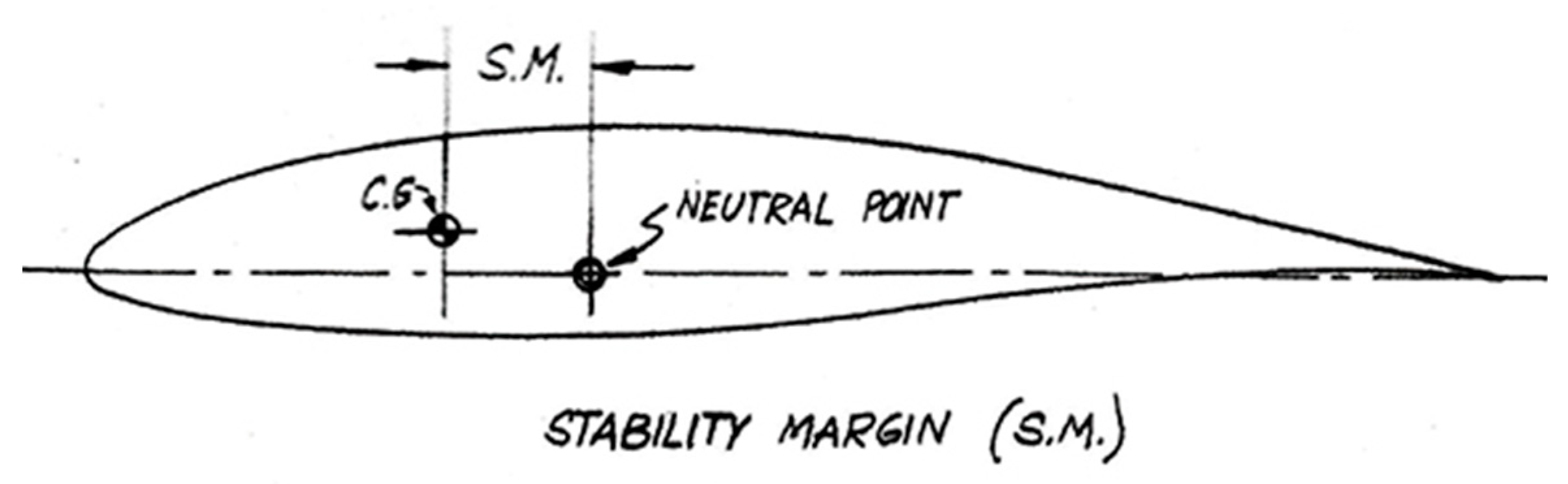
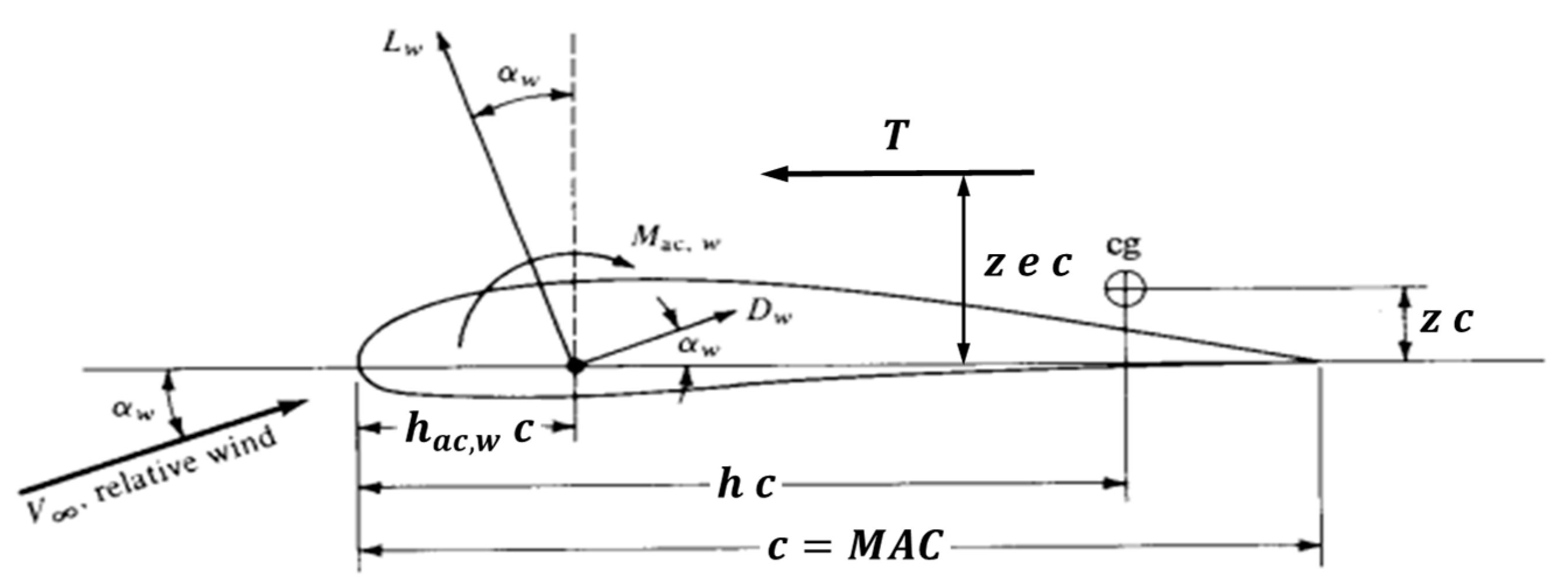
| Reference Point | x-Coordinate [m] | Source |
|---|---|---|
| Aerodynamic Centre/Neutral Point | AVL model | |
| C. G.—Flying Wing/Carrier (empty) | 9.00 | CAD model |
| C. G.—Fuel (full) | 7.20 | Geometry of the tanks |
| C. G.—Launcher | 3.61 | Launcher geometry |
| C. G.—Carrier-Launcher system | Calculation result |
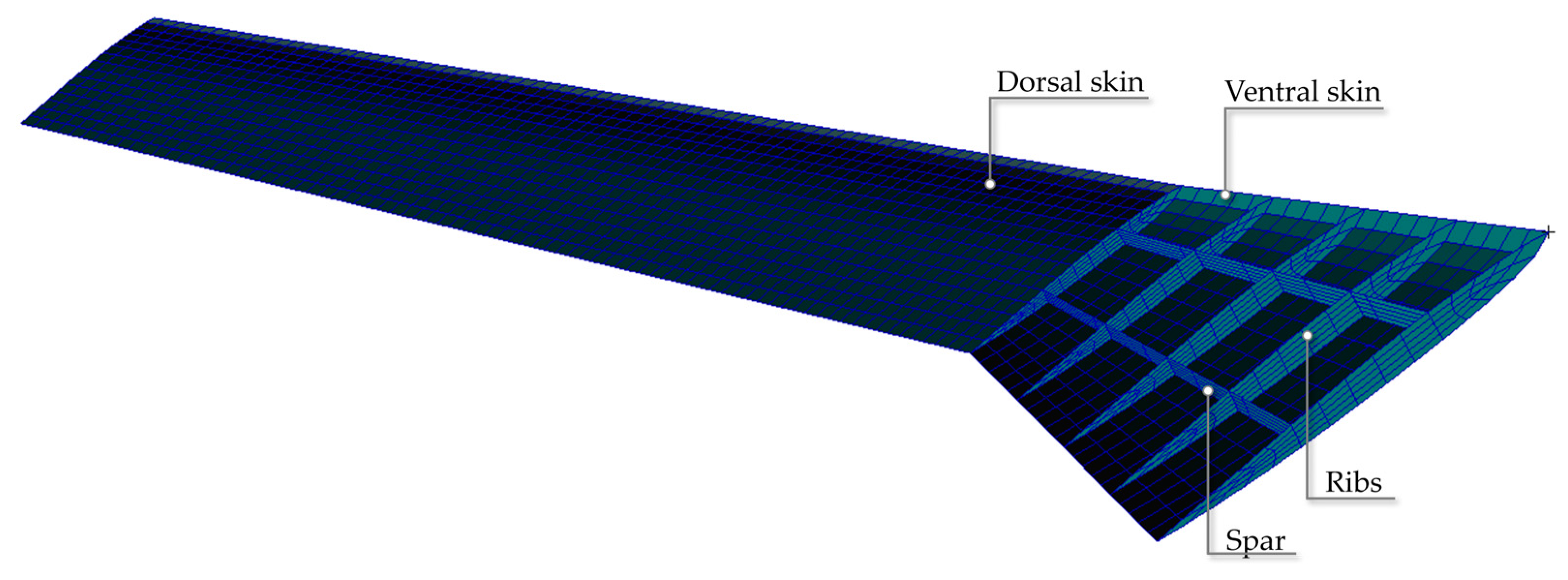
| Component | Thickness [mm] | Size of Parts [mm] |
|---|---|---|
| Skin | 2.5 | --- |
| Stringers—Z section | 2.0 | Flange: 16 |
| 2.0 | Web: 15 | |
| Spar—I section | 30.0 | Flange Width: 300 |
| 30.0 | Web—Root: 840 | |
| 30.0 | Web—tip: 300 | |
| Ribs | 3.0 | --- |
| Component | C.G. Location | ||
|---|---|---|---|
| Engine | 4273 | 16,750 | 3.4 m (from local leading edge) |
| Landing Gear 1 | 732 | --- | --- |
| Landing Gear 2 | 1464 | --- | --- |
| Launcher | 10,000 | 14,000 | 3.61 (from the wing nose) |
| Component | Distance from the Wing Root [m] | Distance from the Wing Nose [m] |
|---|---|---|
| Engine 1 | 7.0 | --- |
| Engine 2 | 17.0 | --- |
| Landing Gear 1 | 0.0 | 2.0 |
| Landing Gear 2 | 3.0 | 9.0 |
| Free Half-Wing Model | Clamped Half-Wing Model | ||
|---|---|---|---|
| Mode 1 | 0 Hz | ||
| Mode 2 | 0 Hz | ||
| Mode 3 | 0.40 Hz | Mode 1 | 0.35 Hz |
| Mode 4 | 0.60 Hz | Mode 2 | 0.57 Hz |
| Mode 5 | 0.70 Hz | Mode 3 | 0.62 Hz |
| Mode 6 | 1.15 Hz | Mode 4 | 1.13 Hz |
| Mode 7 | 1.49 Hz | Mode 5 | 1.48 Hz |
| Mode 8 | 1.74 Hz | Mode 6 | 1.50 Hz |
| Mode 9 | 2.00 Hz | Mode 7 | 2.00 Hz |
| Mode 10 | 3.52 Hz | Mode 8 | 3.40 Hz |
| Mode 11 | 3.54 Hz | Mode 9 | 3.54 Hz |
| Mode 12 | 3.95 Hz | Mode 10 | 3.95 Hz |
| Free Model | Clamped Model | Mode Type | ||
|---|---|---|---|---|
| Mode 3 | 0.40 Hz | Mode 1 | 0.35 Hz | Bending |
| Mode 8 | 1.74 Hz | Mode 6 | 1.50 Hz | Bending—Torsion |
| Mode 9 | 2.00 Hz | Mode 7 | 2.00 Hz | In Plane Bending |
| Mode 12 | 3.95 Hz | Mode 10 | 3.95 Hz | Torsion |
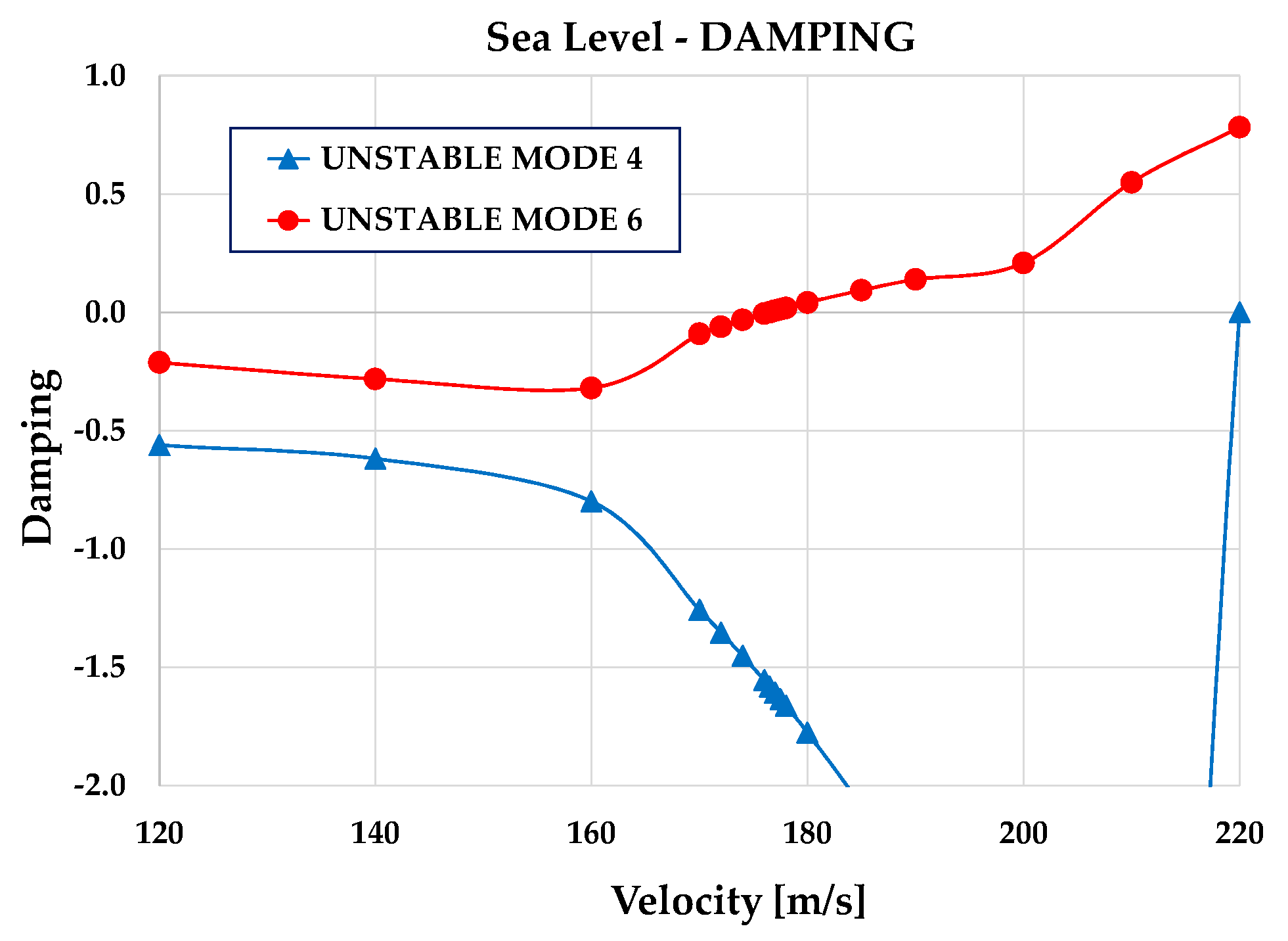
| Unstable Mode | Speed [m/s] | Mach | Frequency [Hz] | Instability |
|---|---|---|---|---|
| Mode 6 (sea level) | 176.5 | 0.52 | 1.4 | Flutter |
| Mode 4 (sea level) | 220.0 | 0.64 | 0.0 | Divergence |
| Mode 8 (cruise) | 281.5 | 0.954 | 1.9 | Flutter |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiarelli, M.R.; Borrometi, F.B.; Cipolla, V.; Binante, V.; Abu Salem, K.; Palaia, G. Design and Feasibility Study of Novel Flying Wing Carrier for Launching Small Satellites in Low Earth Orbit. Appl. Sci. 2023, 13, 4712. https://doi.org/10.3390/app13084712
Chiarelli MR, Borrometi FB, Cipolla V, Binante V, Abu Salem K, Palaia G. Design and Feasibility Study of Novel Flying Wing Carrier for Launching Small Satellites in Low Earth Orbit. Applied Sciences. 2023; 13(8):4712. https://doi.org/10.3390/app13084712
Chicago/Turabian StyleChiarelli, Mario R., Fabiano B. Borrometi, Vittorio Cipolla, Vincenzo Binante, Karim Abu Salem, and Giuseppe Palaia. 2023. "Design and Feasibility Study of Novel Flying Wing Carrier for Launching Small Satellites in Low Earth Orbit" Applied Sciences 13, no. 8: 4712. https://doi.org/10.3390/app13084712







