A Method Based on Blackbody to Estimate Actual Radiation of Measured Cooperative Target Using an Infrared Thermal Imager
Abstract
1. Introduction
2. Materials and Methods
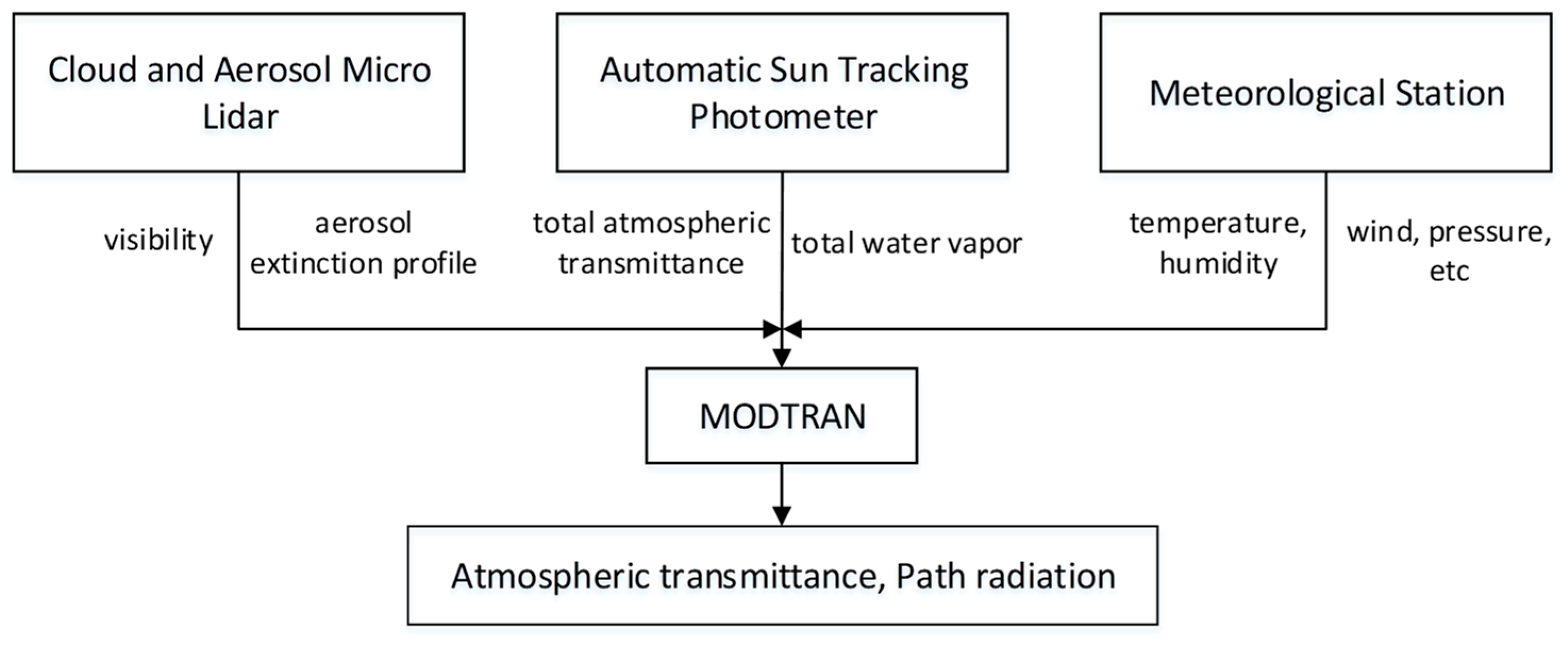
2.1. MODTRAN
2.2. Theory of Infrared Radiation
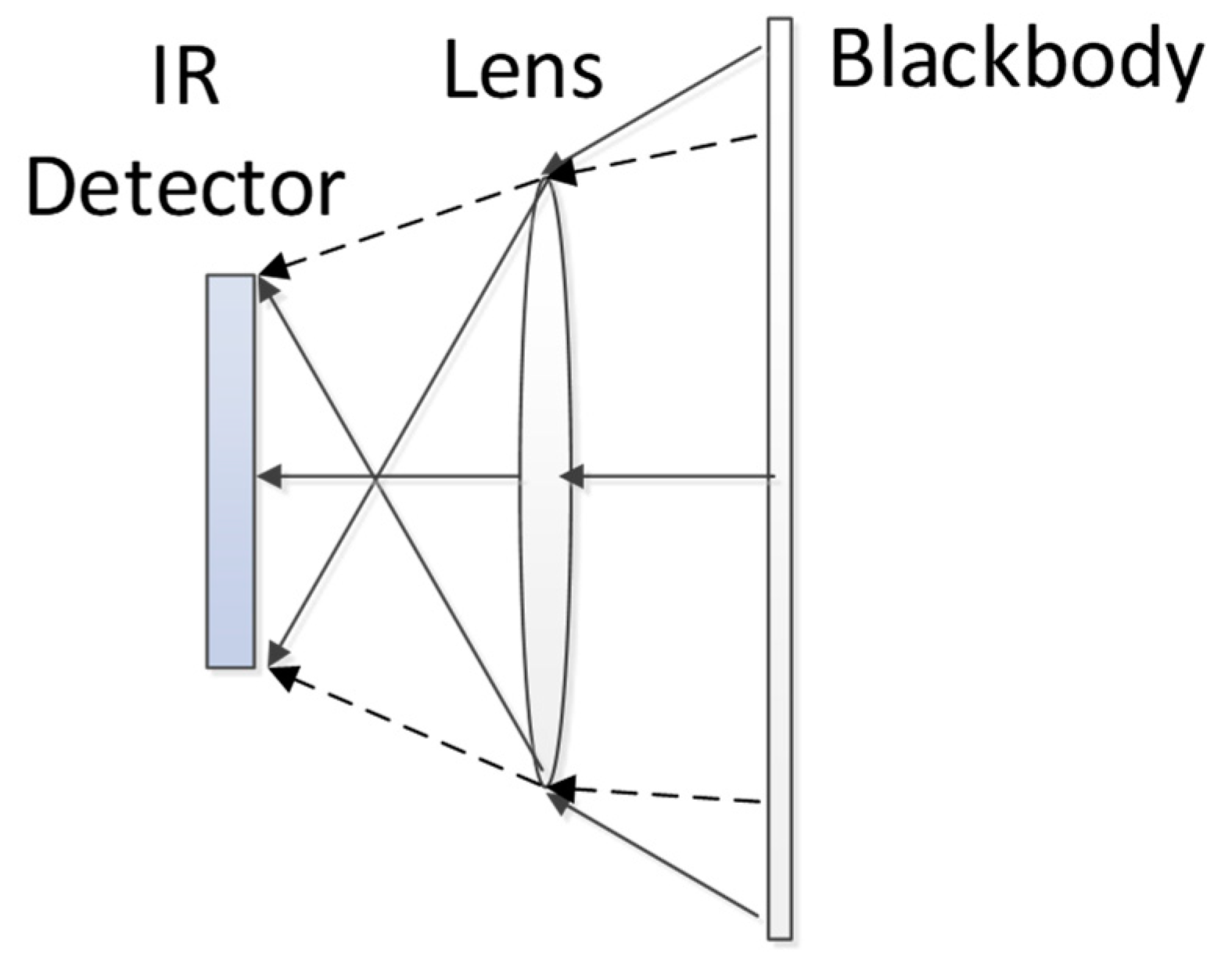
2.3. Model of Radiometric Calibration and Infrared Thermal Imager
- Turn off the auto gain function of the infrared thermal imager, and set focus to infinity;
- Apply NUC to the blackbody source;
- Save frames of image when the temperature of blackbody source is completely stable, then average the saved images to reduce random noises;
- Collect DN value for the averaged images of different temperatures;
- Calculate the radiance according to Equation (14);
- Change the temperature of the blackbody and repeat the steps 3–5 until all temperatures are measured;
- Fit DN value and the radiance in Equation (13) by the least square method.
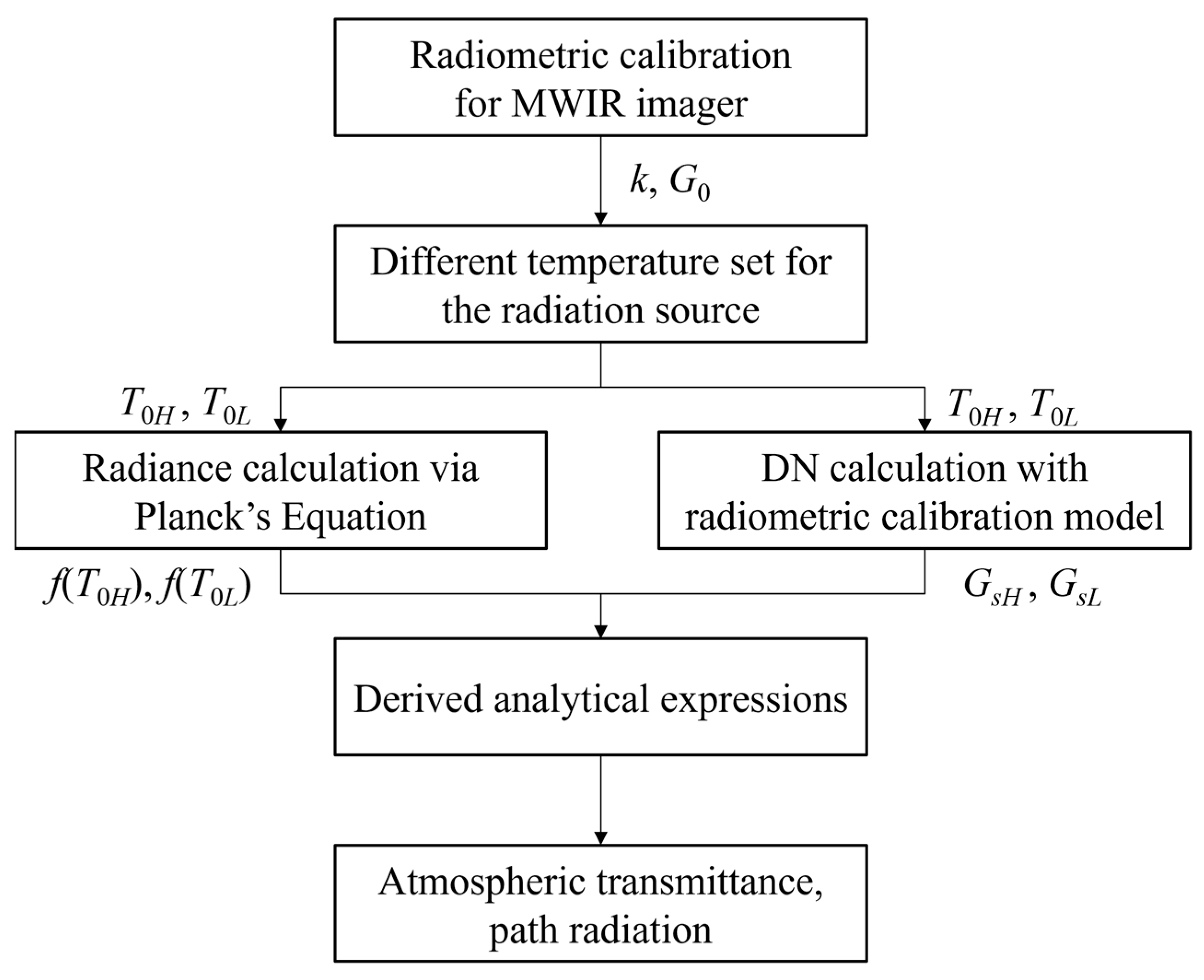
2.4. The Proposed Blackbody-Based Method
3. Results
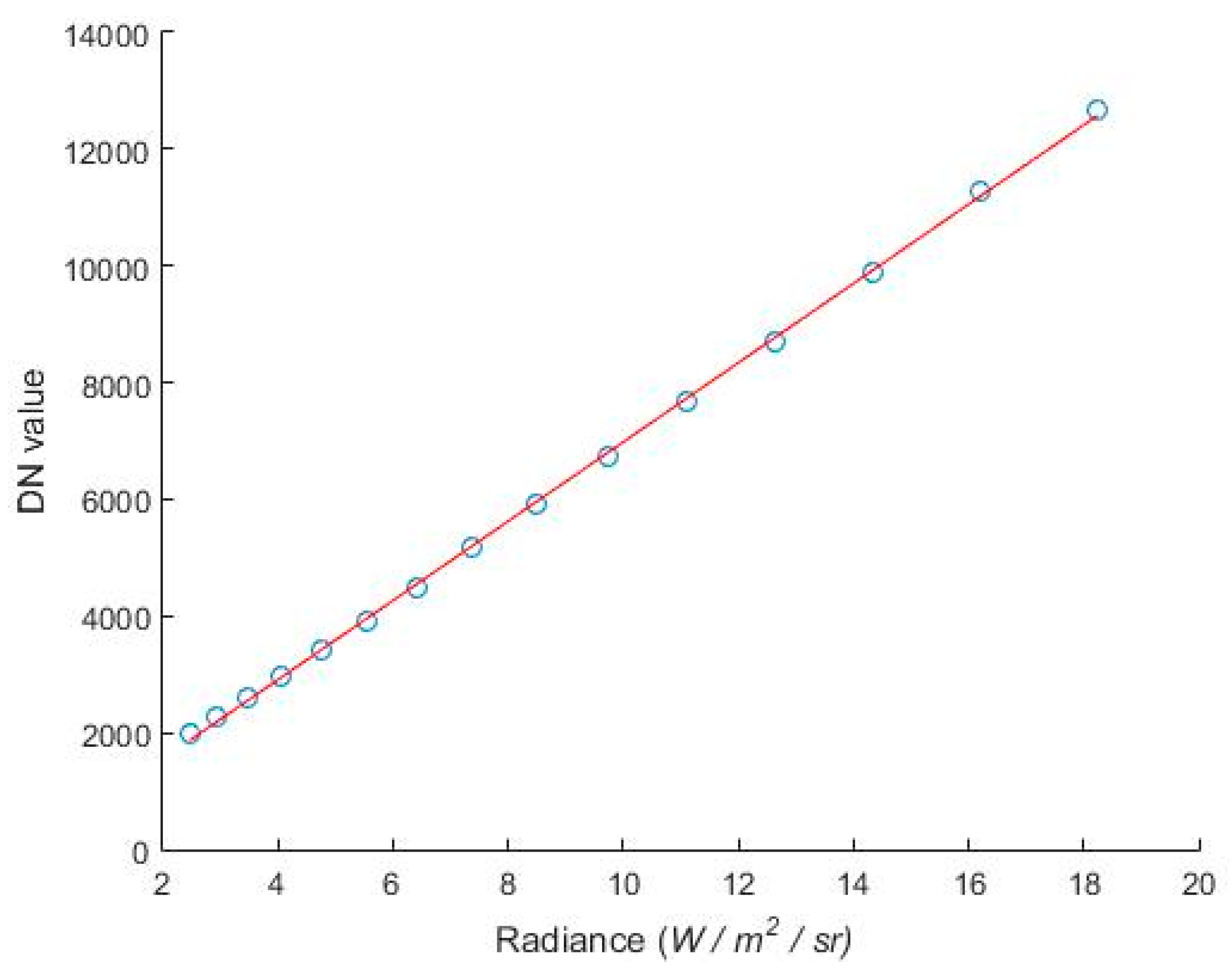
3.1. Radiometric Calibration for the Infrared Thermal Imager
3.2. Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jacobs, A. Thermal Infrared Characterization of Ground Targets and Backgrounds; SPIE Optical Engineering Press: Washington, DC, USA, 1996; pp. 140–149. [Google Scholar]
- Mahulikar, P.; Sonawane, R.; Arvind Rao, G. Infrared signature studies of aerospace vehicles. Prog. Aerosp. Sci. 2007, 43, 218–245. [Google Scholar] [CrossRef]
- Zhao, B.; Xiao, S.; Lu, H.; Wu, D. Modeling and simulation of infrared signature of remote aerial targets. In Proceedings of the 2017 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Shanghai, China, 14–16 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.-C.; Chen, Y.-M.; Fu, X.-B.; Luo, C. The research on the effect of atmospheric transmittance for the measuring accuracy of infrared thermal imager. Infrared Phys. Technol. 2016, 77, 375–381. [Google Scholar] [CrossRef]
- Leslie, P.; Furxhi, O.; Short, R.; Grimming, R.; Driggers, R. Mid-Wave and Long-Wave Infrared Signature Model and Measurements of Power Lines Against Atmospheric Path Radiance. In Proceedings of the 2021 IEEE Research and Applications of Photonics in Defense Conference (RAPID), Miramar Beach, FL, USA, 2–4 August 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Talghader, J.J.; Gawarikar, A.S.; Shea, R.P. Spectral selectivity in infrared thermal detection. Light. Sci. Appl. 2012, 1, 6–16. [Google Scholar] [CrossRef]
- Qiu, H.; Hu, L.; Zhang, Y.; Lu, D.; Qi, J. Absolute Radiometric Calibration of Earth Radiation Measurement on FY-3B and Its Comparison With CERES/Aqua Data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4965–4974. [Google Scholar] [CrossRef]
- Poline, M.; Rebrov, O.; Larsson, M.; Zhaunerchyk, V. Theoretical studies of infrared signatures of proton-bound amino acid dimers with homochiral and heterochiral moieties. Chirality 2020, 32, 359–369. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Yue, H.; Lin, J.; Zhang, Y. A Simulation Method of Aircraft Infrared Signature Measurement with Subscale Models. Procedia Comput. Sci. 2019, 147, 2–16. [Google Scholar] [CrossRef]
- Knežević, D.M.; Matavulj, P.S.; Nikolić, Z.M. Modeling of aircraft infrared signature based on comparative tracking. Optik 2021, 225, 165782. [Google Scholar] [CrossRef]
- Zhang, D.; Bai, L.; Wang, Y.; Lv, Q.; Zhang, T. An improved SHDOM coupled with CFD for simulating infrared radiation signatures of rocket plumes. Infrared Phys. Technol. 2022, 122, 104054. [Google Scholar] [CrossRef]
- Xu, M.; Bu, X.; Yu, J.; He, Z. Spinning projectile’s attitude measurement with LW infrared radiation under sea-sky background. Infrared Phys. Technol. 2018, 90, 214–220. [Google Scholar] [CrossRef]
- Haq, F.; Huang, J. Parametric design and IR signature study of exhaust plume from elliptical-shaped exhaust nozzles of a low flying UAV using CFD approach. Results Eng. 2022, 13, 100320. [Google Scholar] [CrossRef]
- Cheng, W.; Wang, Z.; Zhou, L.; Shi, J.; Sun, X. Infrared signature of serpentine nozzle with engine swirl. Aerosp. Sci. Technol. 2019, 86, 794–804. [Google Scholar] [CrossRef]
- Ata, Y.; Nakiboğlu, K.C. IR signature estimation of an object or a target by taking into account atmospheric effects. Opt. Commun. 2010, 283, 3901–3910. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Bernstein, L.S.; Acharya, P.K.; Dothe, H.; Matthew, M.W.; Adler-Golden, S.M.; Chetwynd, J.H., Jr.; Richtsmeier, S.C.; Pukall, B.; et al. MODTRAN4 radiative transfer modeling for atmospheric correction. In Proceedings of the SPIE’s International Symposium on Optical Science, Engineering, and Instrumentation, Denver, CO, USA, 18–23 July 1999; pp. 348–353. [Google Scholar] [CrossRef]
- Ni, N.; Zhang, K.; Hu, J.; Li, L.; Mi, S.; Zhang, Y.; Zhang, Y. Combined Use of Blackbody and Infrared Radiation for Accurate Measurement of Temperature Field of Aluminum Alloys. Optik 2022, 268, 169763. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, Y.; Xing, T. The study on the measurement accuracy of non-steady state temperature field under different emissivity using infrared thermal image. Infrared Phys. Technol. 2018, 94, 207–213. [Google Scholar] [CrossRef]
- Zhang, Y.-C.; Chen, Y.-M.; Luo, C. A method for improving temperature measurement precision on the uncooled infrared thermal imager. Measurement 2015, 74, 64–69. [Google Scholar] [CrossRef]
- Yang, G.; Yu, Y.; Sun, Z.; Li, Z.; Pang, X.; Zhang, T. Radiometric calibration algorithm for high dynamic range infrared imaging system. Infrared Phys. Technol. 2023, 130, 104607. [Google Scholar] [CrossRef]
- Lin, D.; Cui, X.; Wang, Y.; Yang, B.; Tian, P. Pixel-wise radiometric calibration approach for infrared focal plane arrays using mul-tivariate polynomial correction. Infrared Phys. Technol. 2022, 123, 104110. [Google Scholar] [CrossRef]
- Li, Z.; Yu, Y.; Tian, Q.-J.; Chang, S.-T.; He, F.-Y.; Yin, Y.-H.; Qiao, Y.-F. High-efficiency non-uniformity correction for wide dynamic linear infrared radiometry system. Infrared Phys. Technol. 2017, 85, 395–402. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Manufacturer | FLIR Systems |
| Model | MINICORE-600Z |
| Band Range | 3.7–4.8 μm |
| Resolution | 640 × 512 pixel |
| Pixel Size | 15 μm × 15 μm |
| Output Bit | 14 bit |
| F# | F4 |
| Focus | 30–600 mm continuous zooming |
| Cooling Type | Stirling cooling |
| Parameter | Value |
|---|---|
| Manufacturer | CI Systems |
| Model | SR800-12LT |
| Size | 305 mm × 305 mm |
| Temperature range | −40–150 °C |
| Emissivity | 0.97 ± 0.02 |
| Uniformity | ±0.03 °C |
| Temperature/°C | Radiance/W·m−2·str−1 | DN Value |
|---|---|---|
| 35 | 2.4764 | 1986 |
| 40 | 2.9356 | 2257 |
| 45 | 3.4627 | 2584 |
| 50 | 4.0649 | 2979 |
| 55 | 4.7501 | 3399 |
| 60 | 5.5267 | 3900 |
| 65 | 6.4034 | 4491 |
| 70 | 7.3896 | 5162 |
| 75 | 8.4950 | 5904 |
| 80 | 9.7299 | 6722 |
| 85 | 11.1051 | 7668 |
| 90 | 12.6318 | 8717 |
| 95 | 14.3216 | 9880 |
| 100 | 16.1866 | 11,295 |
| 105 | 18.2395 | 12,658 |
| 110 | 20.4933 | 15,106 |
| 115 | 22.9614 | 15,114 |
| Temperature/°C | Radiance/W·m−2·str−1 | DN Value |
|---|---|---|
| 65 | 6.4034 | 4072 |
| 75 | 8.4950 | 5298 |
| 85 | 11.1051 | 6764 |
| 95 | 14.3216 | 8605 |
| 105 | 18.2395 | 11,207 |
| Atmospheric Parameters | Value |
|---|---|
| Atmospheric profile | Mid-latitude summer |
| Altitude of observer (km) | 0.216 |
| Visibility (km) | 13 |
| Humidity (%) | 54 |
| Temperature (°C) | 20 |
| Atmospheric path | horizontal |
| Distance from observer to target (m) | 30 |
| CO2 mixing ratio (ppmv) | 370 |
| Temp (°C) | DN Value | Actual Radiance (W/m2/sr) | Radiance with MODTRAN (W/m2/sr) | Error with MODTRAN (%) | Radiance with Derivation (W/m2/sr) | Error with Derivation (%) |
|---|---|---|---|---|---|---|
| 65 | 4072 | 6.4034 | 6.7654 | 5.6 | 6.4348 | 0.48 |
| 75 | 5298 | 8.4950 | 8.9174 | 4.9 | 8.4696 | 0.29 |
| 85 | 6764 | 11.1051 | 11.4908 | 3.4 | 10.9010 | 1.83 |
| 95 | 8605 | 14.3216 | 14.7224 | 2.7 | 13.9552 | 2.55 |
| 105 | 11,207 | 18.2395 | 19.2899 | 5.7 | 18.2731 | 0.18 |
| Atmospheric Parameters | Value |
|---|---|
| Atmospheric profile | Mid-latitude summer |
| Altitude of observer (km) | 0.22 |
| Visibility (km) | 13 |
| Humidity (%) | 45 |
| Temperature (°C) | 28 |
| atmospheric path | slant |
| distance from observer to target (m) | 1560 |
| CO2 mixing ratio (ppmv) | 370 |
| Temp (°C) | DN Value | Actual Radiance (W/m2/sr) | Radiance with MODTRAN (W/m2/sr) | Error with MODTRAN (%) | Radiance with Derivation (W/m2/sr) | Error with Derivation (%) |
|---|---|---|---|---|---|---|
| 35 | 1630 | 2.4764 | 2.0611 | −16.7 | 2.4789 | 0.10 |
| 38 | 1701 | 2.7442 | 2.3392 | −14.8 | 2.7532 | 0.33 |
| 41 | 1823 | 3.0354 | 2.8171 | −7.2 | 3.2246 | 6.2 |
| 44 | 1944 | 3.3515 | 3.2911 | −1.8 | 3.6922 | 10.2 |
| 47 | 1978 | 3.6941 | 3.4243 | −7.3 | 3.8235 | 3.5 |
| 50 | 2041 | 4.0649 | 3.6711 | −9.7 | 4.0669 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Xu, L.; Tan, X.; Shen, H. A Method Based on Blackbody to Estimate Actual Radiation of Measured Cooperative Target Using an Infrared Thermal Imager. Appl. Sci. 2023, 13, 4832. https://doi.org/10.3390/app13084832
Yang M, Xu L, Tan X, Shen H. A Method Based on Blackbody to Estimate Actual Radiation of Measured Cooperative Target Using an Infrared Thermal Imager. Applied Sciences. 2023; 13(8):4832. https://doi.org/10.3390/app13084832
Chicago/Turabian StyleYang, Mingyu, Liang Xu, Xin Tan, and Honghai Shen. 2023. "A Method Based on Blackbody to Estimate Actual Radiation of Measured Cooperative Target Using an Infrared Thermal Imager" Applied Sciences 13, no. 8: 4832. https://doi.org/10.3390/app13084832
APA StyleYang, M., Xu, L., Tan, X., & Shen, H. (2023). A Method Based on Blackbody to Estimate Actual Radiation of Measured Cooperative Target Using an Infrared Thermal Imager. Applied Sciences, 13(8), 4832. https://doi.org/10.3390/app13084832





