Examination of the Effects of Different Frequencies on Rock Fracturing via Laboratory-Scale Variable Amplitude Fatigue Loading Experiments

Abstract

In this study, the characteristics of the fracture evolution of argillaceous shale under increasing-amplitude loading were investigated. The GCTS RTR-2000 test system and in-situ acoustic emission (AE) monitoring were employed to execute the tests. The following results were observed. (1) The strength, deformation, and fatigue life increased with the frequency, and the morphology of the hysteresis curve changed regularly with time. (2) The cumulative damage of the rock at the location in which the stress amplitude suddenly increased exceeded that at the fatigue loading stage. The AE count and AE energy were affected by the loading frequency. (3) The secant modulus exhibited different values for different loading frequencies; the smaller the loading frequency, the fewer loading stages the samples experienced, and the faster the secant modulus decreased. The change in Poisson’s ratio over the entire process was composed of a steady growth stage and a rapid growth stage. (4) The rock exhibited two stages of damage evolution, with rapid damage accumulation occurring at the beginning of the loading and relatively smooth damage occurring thereafter. This study developed a cumulative fatigue damage model that can adequately fit the accumulated damage during the fracturing process. The experiments revealed that variable amplitude fatigue loading at different frequencies significantly influences the damage deterioration and the failure law of the rock. The results are expected to improve the understanding of the frequency effect on the fracture behavior and help predict the lifespan of rock structures. This is of great significance to the promotion of slope management, landslide disaster prevention, and mine reuse at the West Open-pit Mine.

1. Introduction

In many slope engineering situations, the rock is in a state of continuous load, which adversely affects the slope stability, resulting in slope failure accidents and disasters such as landslides [1,2,3,4]. Therefore, investigating the geomechanical properties of rocks that are under cyclic loading is important to ensure the rock structure reliability.

To date, many studies have tried to determine the fatigue behavior of soft rock on a laboratory scale. In mining and geotechnical engineering, the surrounding rock is affected by cyclic blasting vibration, rock drilling disturbance, etc., and the stability of the surrounding rock is related to the safety of the underground structure. Therefore, the mechanical characteristics of the rock under a non-static load should be considered completely. The rocks affected by the mechanics in different environments exhibit varied properties. The main research directions of cyclic loading involve the stress and strain, and a large number of laws have been summarized in uniaxial and triaxial cyclic loading [5,6,7]. The main conclusions are as follows. The strength of rock is usually enhanced under the fatigue load without a confining pressure, but the opposite occurs under the condition of a confining pressure. Several mechanical tests [8,9,10] showed that the deformation characteristics of rock, concrete, soil, and other materials were mainly reflected in the relationship between the stress and strain, and extended toward the direction of thermodynamics, such as the input and the consumption of energy, regardless of the stress mode of the creep or cyclic load. However, changing the stress mode directly leads to changes in the strain rate. For example, different loading frequencies, stress waveforms, and loading sequences significantly impact the deformation and mechanical behavior of the test material. Cyclic load tests on sandstone, marble, coal rock, rock salt, and other rocks [11,12,13] have shown that the loading frequency and stress amplitude significantly affect the mechanical stress of the rock. The strain accumulation of the first and last cycles in the static loading exceeds the cumulative deformation at the intermediate stages. In the uniaxial test, the energy dissipation increases with the increase in the loading frequency. Bagde and Petro [14] tested the properties of coal mine samples of intact sandstone under a fatigue load and demonstrated that the frequency and stress amplitude significantly affect the behavior of the rocks. Miao et al. [15] conducted fatigue tests on argillaceous quartz siltstone to study the laws describing the deformation and strength changes, the mechanical parameter evolutions, and the microstructure characteristics, revealing the response characteristics of argillaceous quartz siltstone under a cyclic load. Ashid Geranmayeh Vaneghi et al. [16] studied the influence of the maximum stress level, frequency, and amplitude of the constant amplitude cyclic loading and focused on the fatigue damage response of typical crystal and granular rock.

The abovementioned studies focused on the static loading conditions. However, in actual engineering situations, rocks are usually disturbed by variable stress amplitudes and frequencies, and there is minimal research on the fatigue damage characteristics of soft rocks subjected to increasing-amplitude loading [17,18,19,20,21]. Therefore, the evolution of the failure mechanism of argillaceous shale samples was determined based on the stress–strain curves in this study. Additionally, the evolution of the failure process was studied via real-time acoustic emission (AE) monitoring, which allowed for examinations of the structural deterioration and fracture evolution that occurred under multi-stage cyclic loading and unloading. This loading mode is closer to the actual loading mode of the slope, which can provide basic data support for slope stability engineering.

2. Materials and Methods

The test materials were selected based on the application of the test results in engineering. The mined rock was disturbed by blasting, shoveling, and other disturbances, and its internal properties were observed to have changed. Therefore, it was of test value to select an in-situ rock core for the mechanical testing.

2.1. Rock Materials and Sample Preparation

For this study, the test material was taken from a large open-pit coal mine located in the Liaoning Province, China, and the core was taken from the north slope of the Fushun West Open pit Mine in the west section of the Fushun Coalfield (Figure 1a,b). This mine was first exploited in 1901 and then converted to an open-pit mine in 1914 [22]. (Figure 1d,e). The West Open-pit Mine area is located in the Sino-Korean paraplatform Jiaoliao upthrust. It belongs to the Hunhe fault control area in the southwest section of the “Dunhua–Mishan” fault, which is the main branch fault of the northeast extension of the Tanlu fault [22]. Recently, the frequency, scale, and spatial location of landslides occurring in the mining area have changed significantly, and these landslides primarily occur on the northern slope (Figure 1c). The eastern section of the southern slope features a typical argillaceous shale interbedded geological structure and is composed of soft rock on a steep slope. Owing to the long-term cyclic loads exerted by coal transport trains and cars, the slope instability is extremely likely. For the laboratory experiment performed in this study, drilling and sampling were performed at the following coordinates: 123°53′02″ E 41°51′08″ N, as shown in Figure 1c by the position of the five-pointed star.

Figure 1d,e show the results obtained after drilling. By compiling and comparing the quality of the drilled cores, the possible depth of the slope failure and sliding surfaces were determined. The rock samples with a good quality and integrity in this section were selected and sealed for experimentation.

For identifying the rock meso-structural characteristics, X-ray powder diffraction (XRD) tests were employed to reveal the main mineral composition. These results are presented in Figure 2a. The rock was primarily composed of quartz (7.6%), potassium feldspar (2.1%), plagioclase (2.1%), siderite (3.5%), analcite (10.5%), iron dolomite (39.8%), and clay minerals (33.9%). The scanning electron microscopy (SEM) results revealed a differential mesoscopic structure in the matrix, as shown in Figure 2b. The interior was not smooth and complete but was composed of different mineral components, and the junctions between the mineral crystals were filled with cemented material. Microcracks and holes of various lengths and widths were noted in the sample, and the sizes and positions of the holes were distributed irregularly, which reflected the heterogeneity and anisotropy of the sample.

2.2. Rock Sample Preparation

In this study, the samples were cut into cylinders. The rock sample preparation primarily included coring and rock sample cutting and grinding. Considering the precision and accuracy of the tests, the rock samples were finely processed using high-precision cutting and grinding, and the flatness, parallelism, and verticality were strictly controlled so that the deviation was within a certain range. This ensured that the shapes and sizes met the accuracy requirements of the international rock mechanics. The core was drilled using an RCD-250 controllable pressure coring machine (Figure 3a), and the rock samples were cut and ground by a YMT-8 grinder (Figure 3b). The typical morphologies of the processed argillaceous shale samples are shown in Figure 3c.

2.3. Testing System

Multi-stage cyclic loading tests were performed using a servo-hydraulic rock mechanics test apparatus, which is shown in Figure 4a. The system was used to test the mechanical properties of the rocks under different temperatures and pressures, which were controlled by a wide range of highly accurate test functions. This system was an advanced three-axis instrument that can be used to measure the dynamic and static properties, and it can reach a maximum frequency of 10 Hz. Axial and circumferential strain linear variable differential transformer (LVDT) devices were installed on the samples throughout the deformation process (Figure 4b). For a given loading frequency, the deformation and strength parameters were recorded by a computer.

During the deformation or fracture of the materials, a certain amount of strain energy was released in the form of elastic waves, resulting in an AE. The AE signals were recorded using a Physical Acoustics (PAC) monitoring system with an MSPS sampling rate of one and an 18-bit resolution. The frequency range of the sampling filter of the system was 125–750 kHz. The AE sensor was the PAC Nano 30, which had a resonant frequency of 300 kHz and a diameter of 6 mm × 6 mm. The fracturing event was recorded using two AE sensors installed on the sample surfaces, with a sampling interval of 50 μs, a threshold of 42 dB, and a frequency of 10²–10⁴ Hz.

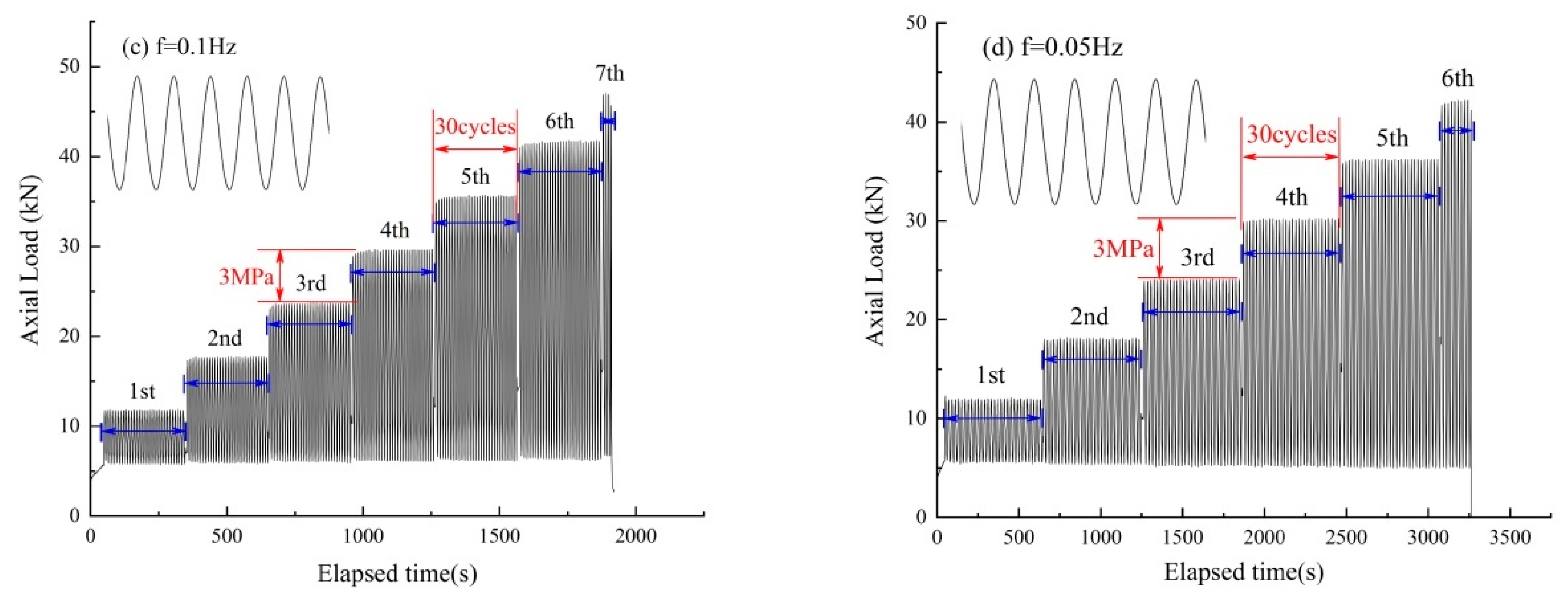
2.4. Testing Scheme

The loading tests performed on the argillaceous shale samples were executed in two stages.

(1)

Conventional uniaxial static compression stage. A constant strain rate of 0.06 mm/min was applied to the argillaceous shale samples. The samples were loaded under a stress of 3 MPa at a constant strain rate.

(2)

Increasing-amplitude stress-cycling stage. According to the field data for the blast vibrations and vehicle loading, four different frequency values were applied to the samples: 0.04, 0.1, 0.5, and 1.0 Hz. During the loading process, the stress amplitude of each cyclic loading stage was increased by 3 MPa. For each loading stage, 30 stress cycles were applied to the argillaceous shale samples. The stress cycling was continued in this manner until each sample failed. Two groups of samples were tested, as listed in

Table 1. Testing scheme for the argillaceous shale samples.

Group	Sample ID	L × d (mm × mm)	Mass (g)	Peak Strength (MPa)	Loading Cycles	Loading Frequency (Hz)	Lower Limit Stress (MPa)	Loading and Unloading Conditions
I	UC-1	100.25 × 49.45	399.8	24.5	/	/	/	Uniaxial, monotonous compression, 0.06 mm/min
	UC-2	100.03 × 49.94	401.4	27.1	/	/	/
II	UF-1	99.58 × 49.88	401.8	27.6	228	0.5	3	Increasing-amplitude stress of 3 MPa, 30 cycles were performed for each fatigue loading stage
	UF-2	100.01 × 49.61	402.5	27.1	219	0.5	3
	UF-3	99.66 × 49.77	399.9	26.1	214	0.2	3
	UF-4	100.05 × 49.95	402.3	25.8	211	0.2	3
	UF-5	99.73 × 49.98	398.5	24.1	184	0.1	3
	UF-6	100.72 × 49.82	400.3	23.5	175	0.1	3
	UF-7	100.02 × 50.01	397.1	21.3	159	0.05	3
	UF-8	100.08 × 49.91	401.2	22.1	146	0.05	3

.

3. Experimental Results and Analyses

The cylindrical shale standard sample was subjected to fatigue load tests under four loading frequencies. These tests focused on the analysis of the impact of the frequency changes on the direction of the rock deformation and the stiffness deterioration, and the acoustic emission characteristics of the shale internal structure after the stress damage.

3.1. Rock Fatigue Life Analysis

Owing to the different loading frequencies, the time–axial load curves behaved differently, as shown in Figure 5. The loading path curve indicated that the samples subjected to different loading frequencies went through different fatigue loading stages, including failure. For the frequencies of 0.5, 0.2, 0.1, and 0.05 Hz, failure occurred at the fifth, sixth, sixth, and seventh stages, respectively. The curve also shows that the loading cycle number varied owing to the differences in the loading frequencies. The total number of loading cycles for the four tested frequencies were 228, 214, 184, and 159, respectively. The fatigue life of the rock decreased accordingly. As the loading frequency increased, the loading cycle number showed an increasing trend. The peak stress of the failure for the four samples were 21.3, 23.9, 26.1, and 27.6 MPa, respectively, indicating that the peak stress increased with the frequency.

Further analyses showed that the increase in the fatigue life occurred for two reasons. First, the changes in the strain and stress were not synchronized, which usually indicated that the changes in the strain damage lagged behind the changes in the stress, (i.e., the so-called elastic after-effect). For the different loading frequency disturbances, the stress loading stage led to an accumulation of the damage strain. However, for the higher loading frequencies, the strain accumulation in the loading stage was incomplete, and the stress change entered the unloading stage, which caused the plastic strain to decrease with the increase in the frequency under a single cycle load. However, the maximum plastic strain generated when the rock sample was damaged remained similar. Therefore, the sample underwent additional cyclic loads after it was damaged (i.e., it had a longer fatigue life). Second, in the test frequency range, especially when f = 0.5 Hz, the average strain rate was 10⁻³. At this rate, the dynamic strength was higher than the static strength. However, the fatigue test involved the incremental variable amplitude loading to destroy the sample without considering the improvement in the strength, and the strain rate for the uniaxial compressive strength (10⁻⁶) was still used as a reference for the comparison. This confirmed that the fatigue life increased with the loading frequency.

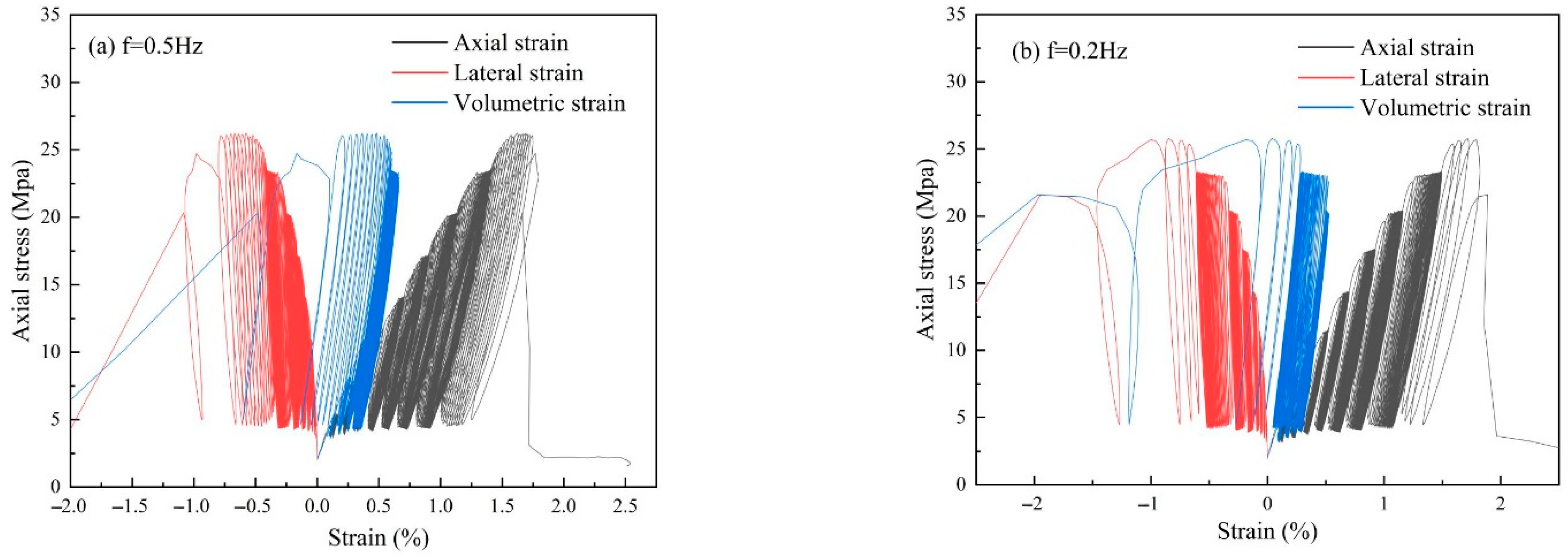
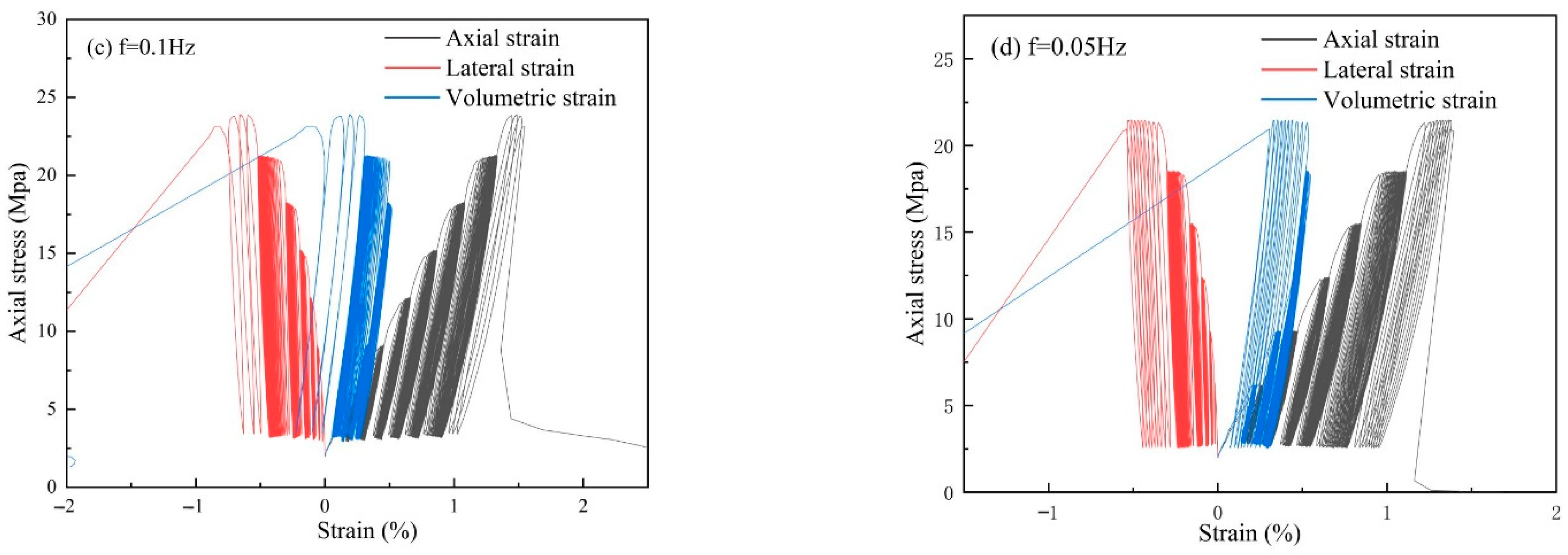
3.2. Representative Stress–Strain Curves

To further explore the effect of the different frequencies on the properties of the rocks, the stress–strain curves were plotted, as shown in Figure 6.

Based on the full stress–strain curve diagrams, under the fatigue loading, a sharp leaf-shaped blank area existed between the loading and unloading curves. When the loading stage curve was above the unloading stage curve, the stress and strain were not synchronized. The morphology of the hysteresis curve varied with the loading time and then changed from sparse to dense before the samples were destroyed. The sparse form indicated a large plastic deformation owing to the increase in the stress amplitude, after which the formed cracks steadily closed. Subsequently, the hysteresis curve became dense, and the rock fatigue damage caused by each additional unloading cycle was significantly reduced. However, the final loading stage was different from the previous stage. The hysteresis curve was very sparse because the sample was in the destruction stage, which accelerated the deformation rate, resulting in a large deformation over a small number of cycles. This demonstrated that the variations in the internal structure of the rock could be reflected in the morphological characteristics of the hysteresis curve.

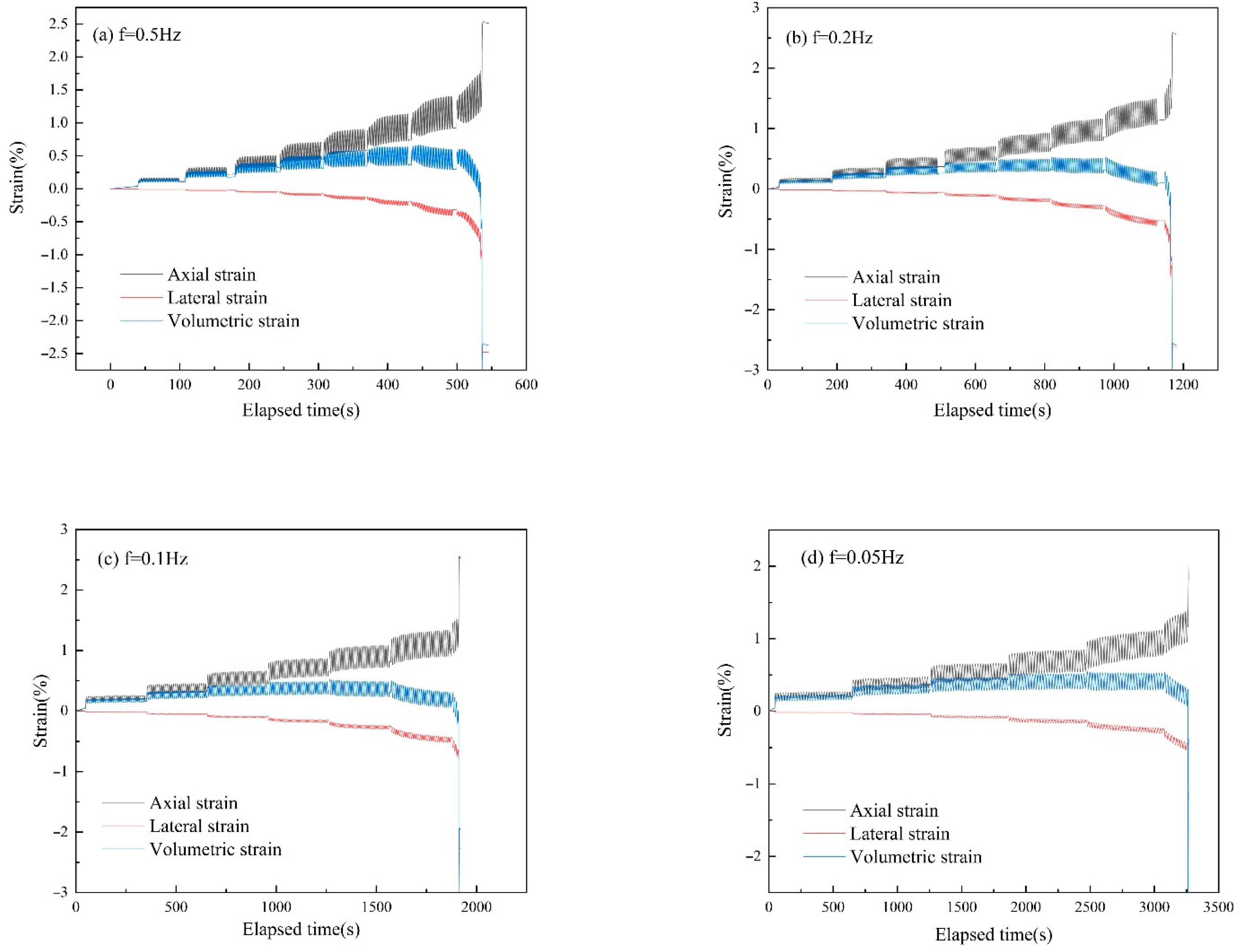
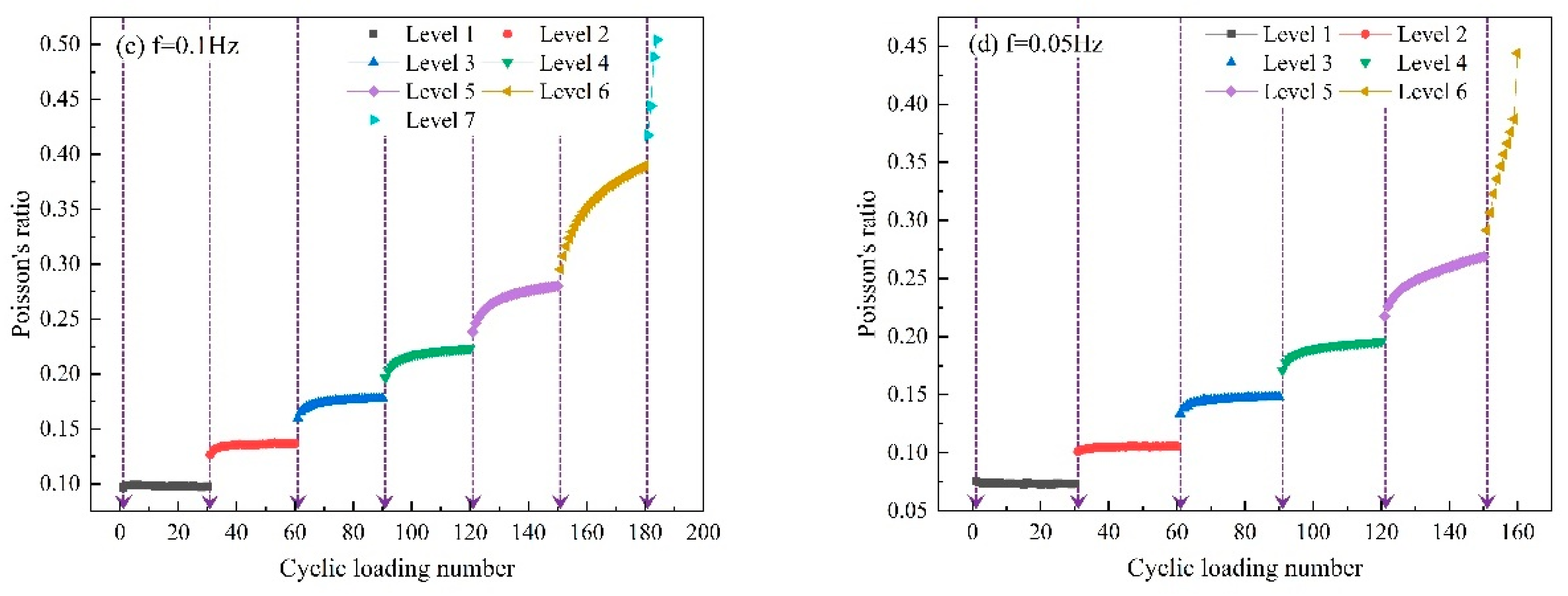
3.3. Sample Deformation Characteristics

3.3.1. Relationship between Deformation and the Number of Cycles

Under the disturbance of the cyclic loads, the internal cracks in the rocks went through different stages of development, and the fatigue damage could be quantified by the axial and radial deformation measurements. Thus, the process by which the rocks were damaged could be characterized by the “deformation” parameter. The deformation increased as the loading period increased, and the rate was affected by the loading stage and frequency. The axial and radial relationships to the test time are shown in Figure 7. When the number of loading cycles was small, the axial, lateral, and volumetric strains were low. However, after a while, the growth of the axial, lateral, and volumetric strains accelerated until failure. The deformation increased steadily in several stages before failure, but it increased significantly when the amplitude changed (i.e., when the loading stage changed). In the last loading stage, the deformation growth rate was the largest, and the deformation of the sample increased until it was destroyed. From the perspective of the entire failure process, the deformation gradually became larger and the deformation rate gradually increased.

By plotting the curve describing the relationship between the deformation and the number of fatigue cycles, the deformation characteristics of the sample could be described more intuitively. For example, the axial deformation is shown in Figure 8, where it can be seen that the growth rate of the axial strain increased with the number of fatigue cycles. In the last stage of the fatigue loading, the axial strain increased sharply. In the time required to change the loading stage, the deformation increased substantially as the stress suddenly increased. The rapid growth of the sample deformation led to a sudden increase in the stress, which caused greater damage to the rock. At the same stage of the initial loading, the deformation tended to be stable because both the loading stress and the change in amplitude were small. The corresponding stress adjustment was implemented for each material part of the rock, and the sample was in the adaptive adjustment state. In the failure stage, the internal cracks were connected to each other, the strength dropped sharply, and the deformation of the sample was large. The deformation and failure responses of the rocks under the different frequencies were characterized by the curves shown in Figure 8.

To study the effect of the axial deformation (ε₁) and radial deformation (ε₂) on the variation in the argillaceous shale volume (ε_v), the volume strain (ε_v) of each sample was calculated via ε_v = ε₁ − 2ε₂. The volume strain reflected the joint effect of the axial and radial deformation on the deformation of the sample. The changes in the volume strain were consistent and uniform (i.e., it changed regularly) as the axial and radial strains changed.

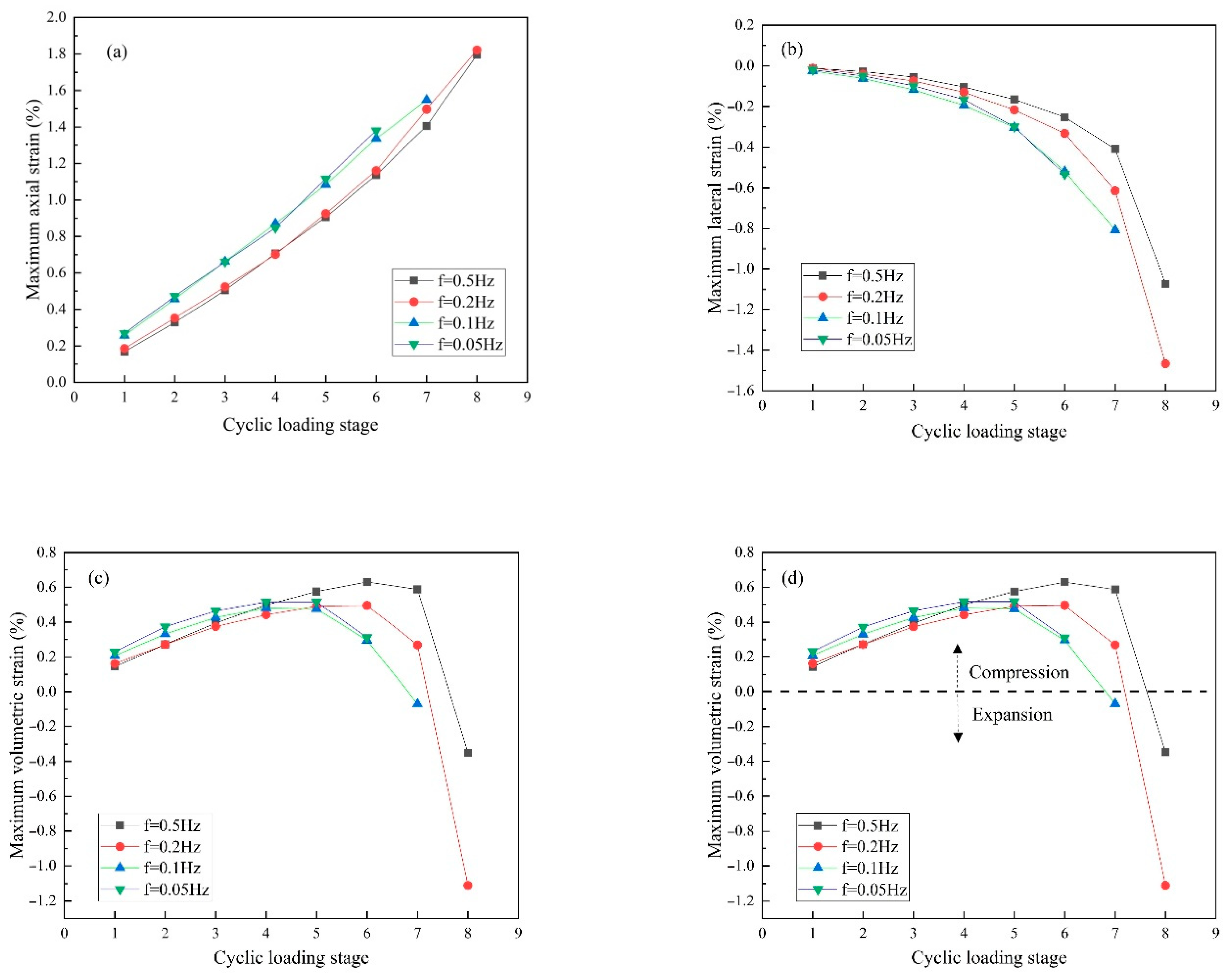
3.3.2. Relationship between the Deformation and Loading Stage

The relationship between the loading stage and the strain, as shown in Figure 9, demonstrated that the axial strain varied approximately linearly with the fatigue loading stage for a given loading frequency. In addition, the rate of change of the axial cumulative strain in each stage of the loading process remained nearly constant (this was relevant to the sample loading conditions), whereas the rate of change of the radial cumulative strain gradually became larger. The change in the volumetric strain was divided into three stages: (1) a steady increase, (2) a steady decrease, and (3) a sharp decrease toward negative values. This trend also indicated that, as the stress increased, cracks were generated and expanded within the sample, causing the volume of the sample to change from initially compressed to expanded. The sample went through a shear expansion process before it was damaged. The location of the expansion point appeared to vary owing to the different loading stages. For the different loading frequencies, the cumulative strain occurring at the point of final damage also varied. Overall, this showed that the higher the frequency, the higher the accumulated strain at the final deformation. This result corresponded well with the influence of the frequency on the fatigue life, indicating a consistency between the before and after results.

3.4. Analysis of Rock Fatigue Stiffness Degradation

The secant modulus and Poisson’s ratio are two important parameters in rock mechanics, and they are normally employed to describe the stress–strain characteristics of the rocks that incur dynamic loading damage [23,24,25]. The secant modulus is defined as the slope of the line connecting the upper stress point and the cycle start point for each stage, and Poisson’s ratio is defined as the ratio of the radial strain to the axial strain for each cycle in the loading stage. Figure 10 shows that the secant modulus decreased continuously as the number of cycles increased, and the rate increased more clearly in the last few cycles. Thus, the stiffness of the sample changed continuously during the deformation process. This occurred because the internal fracture holes expanded and penetrated each other during the loading process, the rock structure deteriorated continuously, and the stiffness decreased until the stability was lost. In addition, the change in the secant modulus was different for each loading frequency; the smaller the loading frequency, the fewer loading stages were experienced, and the faster the secant modulus decreased.

Figure 11 shows the evolution of Poisson’s ratio for the increasing levels of the fatigue loading. Poisson’s ratio increased rapidly at the beginning of each stage, and the whole process was composed of two stages: (1) steady growth and (2) rapid growth. Poisson’s ratio can reflect the change in radial strain, and the increase in the radial strain was larger in the stage that occurred close to the time when the rock is damaged. For the rock samples subjected to the different loading frequencies, Poisson’s ratio went through the different stages to reach the maximum value, but the overall trend was consistent, and it tended to reach 0.5 at the time the damage occurred.

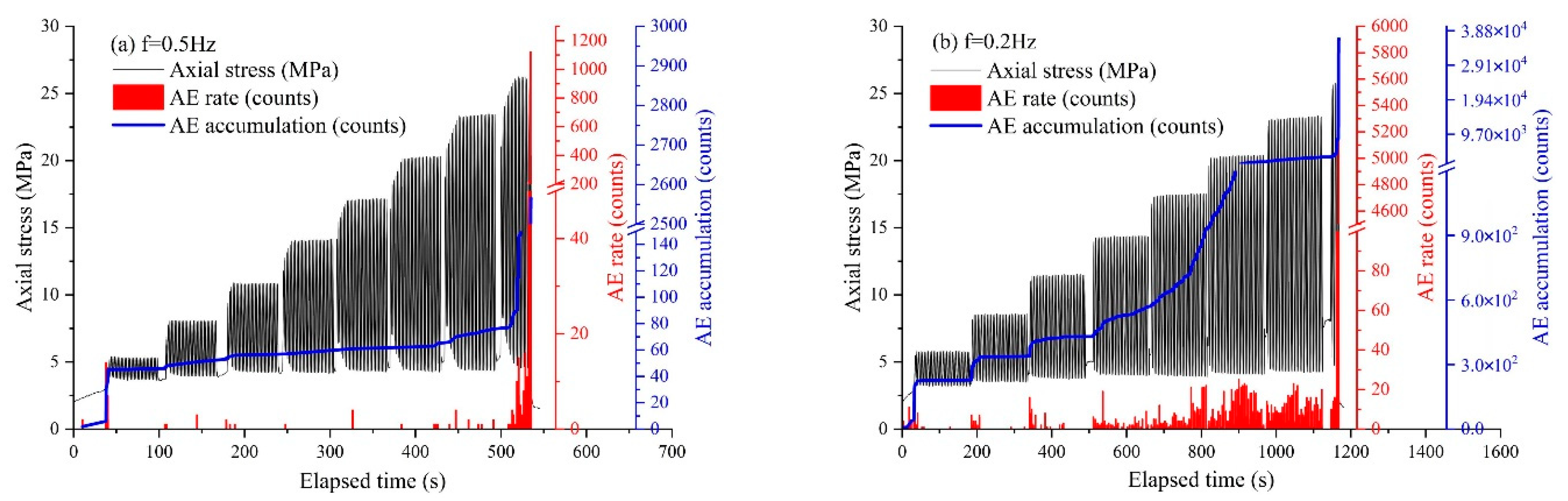
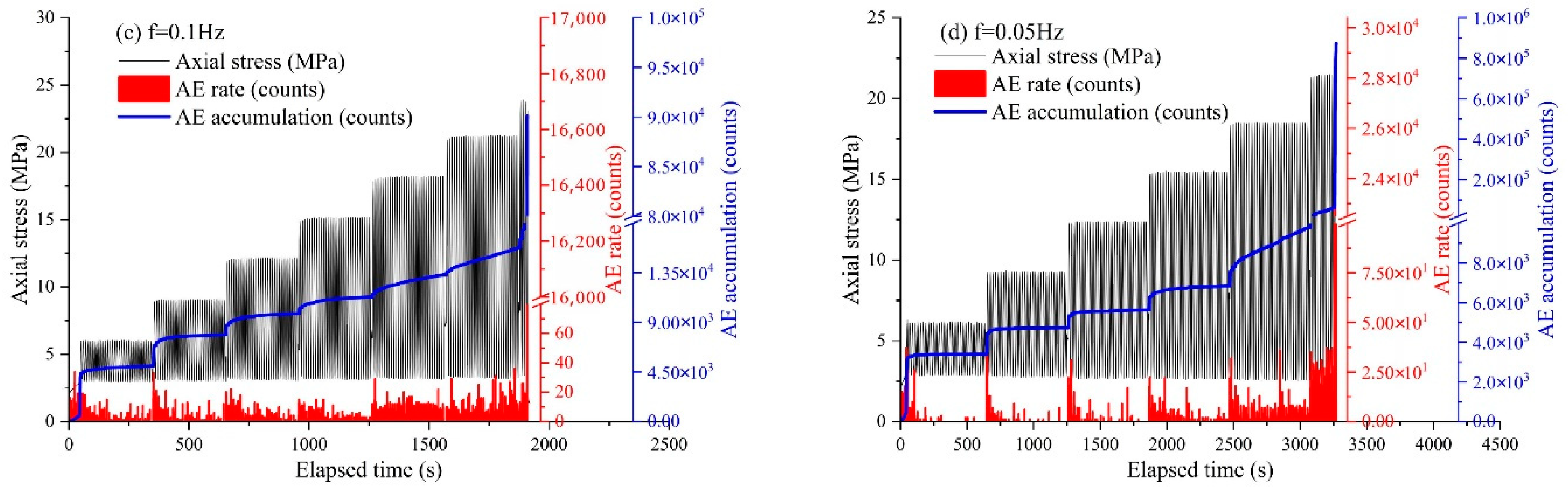
3.5. AE Count/Energy Characteristics

The aforementioned experiments described the evolution of the macroscopic fracturing of the argillaceous shale, but they could not characterize the internal structural changes or crack extensions that occurred during the process of the rock loading. The AE characteristics effectively monitored the rock deformation, crack extension, and rock damage processes, and provided information for understanding the fracture processes undertaken by the rocks [26,27,28,29,30,31].

3.5.1. AE Count Characteristics during Sample Deformation

The curve describing the relationship between the AE parameters and the time is shown in Figure 12. The variation in the AE rate count reflects the evolutionary characteristics of the cracks. The AE counts increased significantly at the beginning of each stage. This occurred owing to the sudden increase in the axial stress, which led to a further expansion of the internal cracks and produced a large deformation. In the fatigue loading stage, the AE counts grew relatively fast in the first few loading cycles, which produced a jump in their growth rate, and then they increased steadily after this stage. From the perspective of the entire damage process, the AE counts grew steadily in the first few loading stages. However, in the failure stages, numerous AE counts were generated until each sample was damaged. The cumulative AE count curve increased steeply in the damage stage, and when the frequency was 0.2 Hz, the curve increased more and more from stage 5. The stepped shape of the cumulative AE count curve also indicated that there were sudden increases in the AE counts. The increasing value of the cumulative AE count curve showed that the cumulative damage, crack initiation, expansion, and penetration behavior of the rock sample occurred throughout the loading process.

A comparison between the AE count curves at four different frequencies showed that the cumulative AE counts decreased as the loading frequency increased. In particular, for f = 0.5 Hz, the loading frequency was relatively high, and the AE count was significantly lower than those at the other frequencies. This is because the energy stored inside the cracks was not released on time when the crack formed or expanded.

3.5.2. AE Energy Characteristics during Sample Deformation

To better detect the effect of the loading frequency, the connections between the AE energy/cumulative energy and the loading stage were plotted, as shown in Figure 13. In the AE nondestructive detection, the AE energy signal was a parameter related to the amplitude of the signal (i.e., the energy defined for the signal waveform) and not the actual physical energy released by the AE source. However, the AE energy was still of great significance for measuring and evaluating the degree to which the materials were damaged. The figure indicates that, at the start of each stage, the AE energy suddenly increased, and the AE cumulative energy exhibited a periodic jump in which the energy significantly increased. This was due to the sudden increase in the stress during the stage transitions and the structural damage (e.g., the small-scale slips and other internal damage), which released a large number of stress waves, resulting in the rapid growth of the cumulative curve of the AE energy (producing a step function). Throughout the sample destruction process, the AE energy increased as the loading stage increased. The AE cumulative energy changed roughly in two stages, exhibiting a steady increase followed by a rapid surge. In the stability stage, the internal structure was steadily damaged, and the cracks gradually expanded. In the surge stage, the sample experienced deformation damage and cracks throughout the process, the rocks lost bearing energy, and the energy accumulated inside the sample was released. Therefore, at this moment in the AE count peak, the energy surged. In addition, a comparison between the AE cumulative energy curves at the different frequencies revealed that the samples with low loading frequencies produce more AE energy than the samples with relatively high loading frequencies. The effect of the frequency on the AE energy reflects the response of the material characteristics to the loading rate (strain rate).

Figure 12 and Figure 13 indicate that the AE energy and AE count corresponded well to the trends observed in the cumulative count, especially considering the spikes in the AE rate. The AE accumulation energy also exhibited jumps in growth throughout the damage process. Thus, the AE count and energy were proportional to each other.

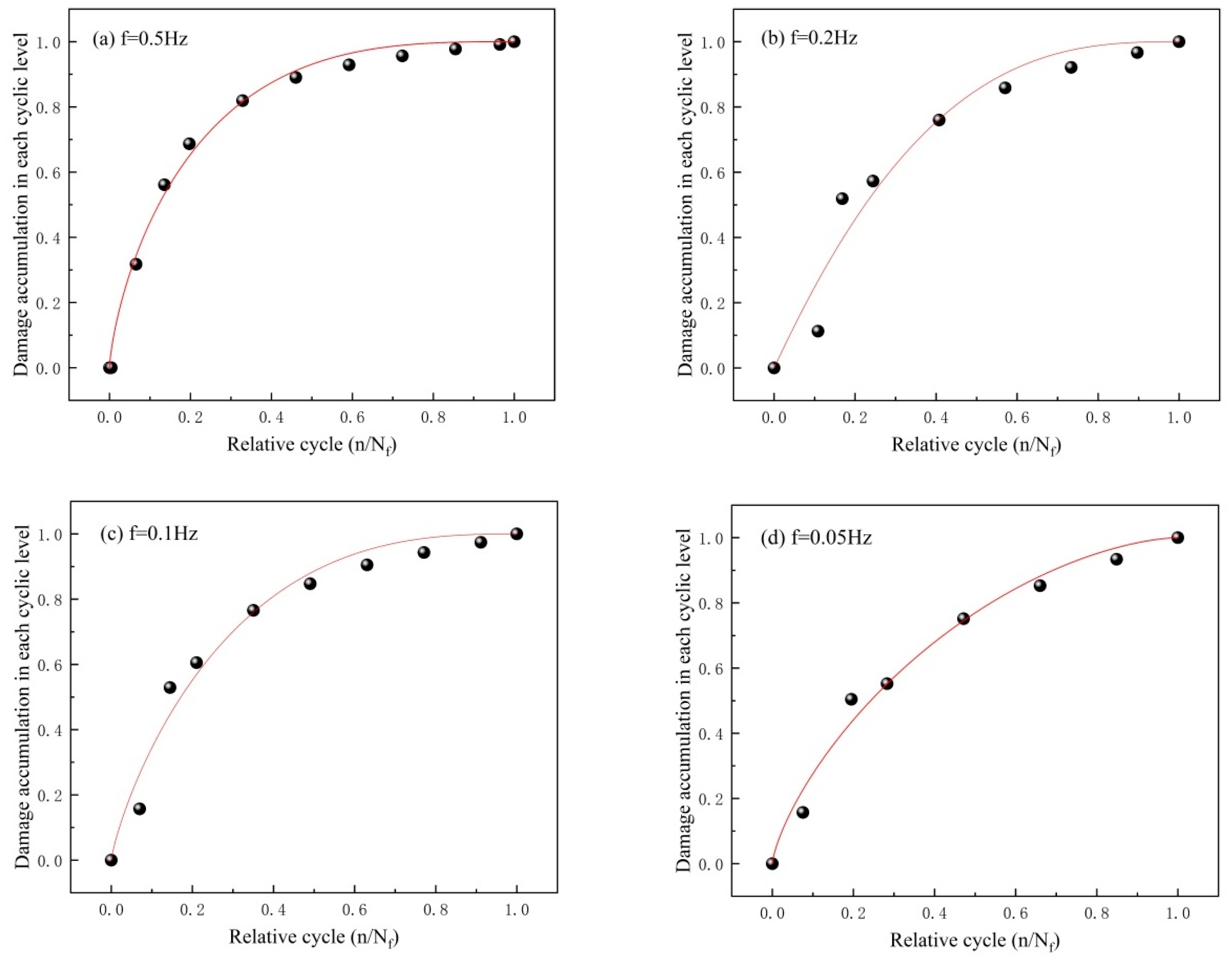
3.6. Analysis of Fatigue Damage Evolution

Under the fatigue loading, the cracks in the rocks underwent three stages, namely, sprouting, extension, and penetration, and the damage inflicted upon them was a progressive process. There were various ways to represent the fatigue damage variables, and it was more common to characterize the evolution of the damage that occurred during the rock fracture via the axial deformation. The plastic deformation led to the generation of hysteresis loops, and the plastic deformation was irreversible. Quantifying the accumulated damage deformation of the sample by analyzing the irreversible axial strain was a reliable process. Therefore, the concept of using damage mechanics to determine the law describing the evolution of the rock damage can now be introduced.

The equation describing the damage caused by the uniaxial compression of the rock based on the elastic strain method is

$$1-D=\frac{\sigma }{E\epsilon }$$

(1)

where $\sigma$, $\epsilon$, and $E$ are the stress, strain, and elastic modulus of the rock sample, respectively, and D reflects the degree of the damage within the material (if D = 0, the rock is intact and undamaged; if D = 1, the rock is fully damaged).

For each loading stage, the amplitude of each stress cycle in Equation (1) was considered to be constant, which allowed for the relationship between the value of the cumulative damage variable D and the cumulative strain to be analyzed. The derivative of both sides of Equation (1) is

$$dD=\frac{\sigma }{E{\epsilon }^2}d\epsilon$$

(2)

Let ${\epsilon }_0$ and ${\epsilon }_d$ be the axial strain at the beginning and end of the cycle. Integrating Equation (2) from ${\epsilon }_0$ to ${\epsilon }_d$,

$${\displaystyle {\int }_0^{D}dD}=\frac{\sigma }{E}{\displaystyle {\int }_{{\epsilon }_0}^{{\epsilon }_d}\frac{1}{{\epsilon }^2}}d\epsilon ,$$

(3)

allows the damage index D to be obtained as

$$D=\frac{\sigma }{E}\left(\frac{1}{{\epsilon }_0}-\frac{1}{{\epsilon }_d}\right)+C$$

(4)

when D = 0, $\epsilon ={\epsilon }_0$ and C = 0, and when D = 1,$\epsilon ={\epsilon }_d$. Substituting D = 1 into Equation (4) results in

$$\frac{\sigma }{E}=\frac{{\epsilon }_0{\epsilon }_d}{{\epsilon }_d-{\epsilon }_0}$$

(5)

Combining Equations (4) and (5), the damage index D of the argillaceous shale can be expressed as

$$\frac{\sigma }{E}=\frac{{\epsilon }_0{\epsilon }_d}{{\epsilon }_d-{\epsilon }_0}$$

(6)

The loading frequency had an important impact on the damage evolution. The damage variable jumped, reaching 0.5 or slightly higher for the different frequencies in the second loading stage. Subsequently, the growth rate changed, and the rock samples subjected to higher frequencies became damaged more quickly, with the damage occurring after fewer loading stages. Overall, the variation in the damage variable in the later stages was gradually reduced and became more continuous, indicating that the rock samples experienced the greatest damage during the first several loading stages.

In the cycle loading mechanical tests, the damage exhibited two stages: (1) rapid growth and (2) stabilization. This was different from the results of the equal amplitude cycle loading test. The previous “S”-type damage evolution model was not suitable for this situation. The relationship between the cumulative damage factors and the loading stage (according to the damage factors defined in Equation (1)) is shown in Figure 14. The sample damage exhibited two stages. The damage accumulated quickly at the beginning, and after that, it became relatively more stable.

3.7. Evolution of Accumulative Fatigue Damage of the Argillaceous Shale Samples

To further predict the fatigue life, the correlation between the damage accumulation and the relative cycle was examined, as shown in Figure 15. The rock damage exhibited a quickly rising trend and then stabilized. Combined with the two-stage damage accumulation shown in Figure 15a–d, a new damage evolution model was proposed. It is expressed as

$$D=1-{\left(1-{\left(n/N_f\right)}^a\right)}^b$$

(7)

where D is the damage variable caused by irreversible plastic deformation. N is the number of loading cycles. N_f is the fatigue life, and a and b are related to the material parameters. Before loading, the rock damage was defined as 0 (N = 0), and when the sample was completely damaged, it was defined as 1 (N = N_f).

The fitted results for the rock samples subjected to the different frequencies are shown in

Table 2. Fitted relationship between the accumulative damage and the relative cycle during the sample deformation for the different loading frequencies.

Loading Frequency (Hz)	$\mathit{y}=1-{(1-{\mathit{x}}^{\mathit{A}})}^{\mathit{B}}$		R2
	A	B
0.5	0.73574	2.90574	0.99319
0.2	1.01348	2.78921	0.95081
0.1	0.82709	2.61645	0.97423
0.05	0.74002	1.62622	0.98501

. The correlation coefficients of the fitted equations for 0.5 Hz, 0.2 Hz, 0.1 Hz, and 0.05 Hz were 0.993, 0.951, 0.974, and 0.985, respectively. These correlation coefficients were high, which demonstrated how well the damage evolution equations fit the data.

4. Discussion

At present, many scholars focus on the constant stress amplitude load conditions in the study of rock mechanical behaviors under cyclic loading. In addition, the rock samples used in these experiments were mostly hard rocks. However, in field research, the amplitudes of the rock mass stress disturbances in the project were often not constant [31]. This situation does not only exist in mining projects such as the Three Gorges Project. With fluctuations in water storage levels, the rock mass and the dam body on both sides of a river are continuously disturbed by variable stresses. The mechanical response of the argillaceous shale was revealed using indoor fatigue loading tests at different frequencies. The effect of the loading frequency was essentially caused by the differences in the loading rates. It was found that the rock strength, fatigue life, mechanical properties, AE, and damage evolution characteristics all changed regularly at the different loading frequencies.

Under a constant stress amplitude loading, the deformation and destruction law can be summarized in three forms, as shown in Figure 16a. Among the three forms, the b-class curve rule was more universal, and the axial irreversible deformation of the rock can be divided into an initial stage, an equal speed stage, and an acceleration stage. These stages can be observed in most rock fatigue tests performed on rocks such as marble, red sandstone, and granite [32,33,34]. However, the mechanical behavior of rocks under increasing fatigue loading conditions was different from that of fixed amplitude fatigue loading, and the cumulative damage destruction was composed of multiple stages. The sample damage occurred in the last stage, which was defined as the failure stage. Each fatigue stage before the failure stage lasted a long time, and there was no sign of a peak strain acceleration. The deformation pattern in each stage was similar to the “c”-type shown in the curve in Figure 16a. However, during the destruction phase, the deformation increased sharply, showing a rapid upward trend, and the sample failed in a short time, which was shown by a small phase similar to the “a”-type curve shown in Figure 16a. Therefore, the damage deformation of the rocks under increasing fatigue loading conditions was more complex, and the damage accumulation trend was more similar to that of the “b”-type curve shown in Figure 16a. Compared to the fixed amplitude loading condition, the acceleration stage was significantly shorter, as shown in Figure 16b.

Many similar studies have been conducted; however, all these previous studies had limitations [35,36]. In this study, using a fine damage variable calculation method, the damage variable was first defined using the axial deformation, and a multi-stage cyclic load comprehensive injury model was then established by our calculations. The model was highly consistent with the test results, and it can be used to predict the fatigue life of the rocks under the increasing-amplitude fatigue loading conditions, which has a considerable engineering significance.

5. Conclusions

To reveal the characteristics of the evolution of the fatigue damage of the argillaceous shale found in the Fushun West Open-pit Mine, multi-stage cyclic loading tests were applied to the samples. The fatigue mechanical properties of the rocks were analyzed, and a cumulative fatigue damage model describing the evolution of the damage accumulation was proposed. The main conclusions are as follows.

(1)

As the loading frequency increased, the number of loading cycles and the fatigue life gradually increased. The morphology of the hysteresis curve changed with the loading time. In addition, the hysteresis curve changed from sparse to dense at each fatigue loading stage before failure, while the final failure stage was sparse.

(2)

For a given loading frequency, the axial, radial, and volumetric strains showed different trends. The cumulative strains in the argillaceous shale at the different loading frequencies were also different. Overall, the higher the frequency, the higher the cumulative strain during the final deformation. The damage process was divided into three stages based on the results of the deformation characteristics of the fatigue test.

(3)

The AE count and AE energy exhibited during the rupture of the rock were affected by the loading frequency, and the accumulated damage of the rock that occurred when the stress amplitude suddenly increased was greater than that at the fatigue loading stage. The entire process of the accumulative AE energy corresponded well to the accumulative AE count.

(4)

The rock exhibited two stages of damage evolution under incremental variable amplitude fatigue loads: (1) rapid damage accumulation at the beginning of the loading and (2) relatively smooth damage evolution thereafter. The proposed cumulative fatigue damage model can fit the damage accumulated throughout the rock fracturing process.

These experiments were closer to the actual loading mode of the slope, which can provide basic data support for slope stability engineering. This study had certain limitations. Specifically, the experiments only considered the rock subjected to variable frequency loading and increased amplitudes. In future studies, the fatigue deterioration mechanisms of the rocks subjected to environments with complex stress disturbances, such as dry–wet cycles, freeze–thaw cycles, and temperature cycles, will be investigated.