A Theory of Slope Shear Scouring and the Failure Mechanism of PFC3D on a Gangue Slope
Abstract
:1. Introduction
2. Materials and Methods
2.1. Formula Improvement and Model Establishment
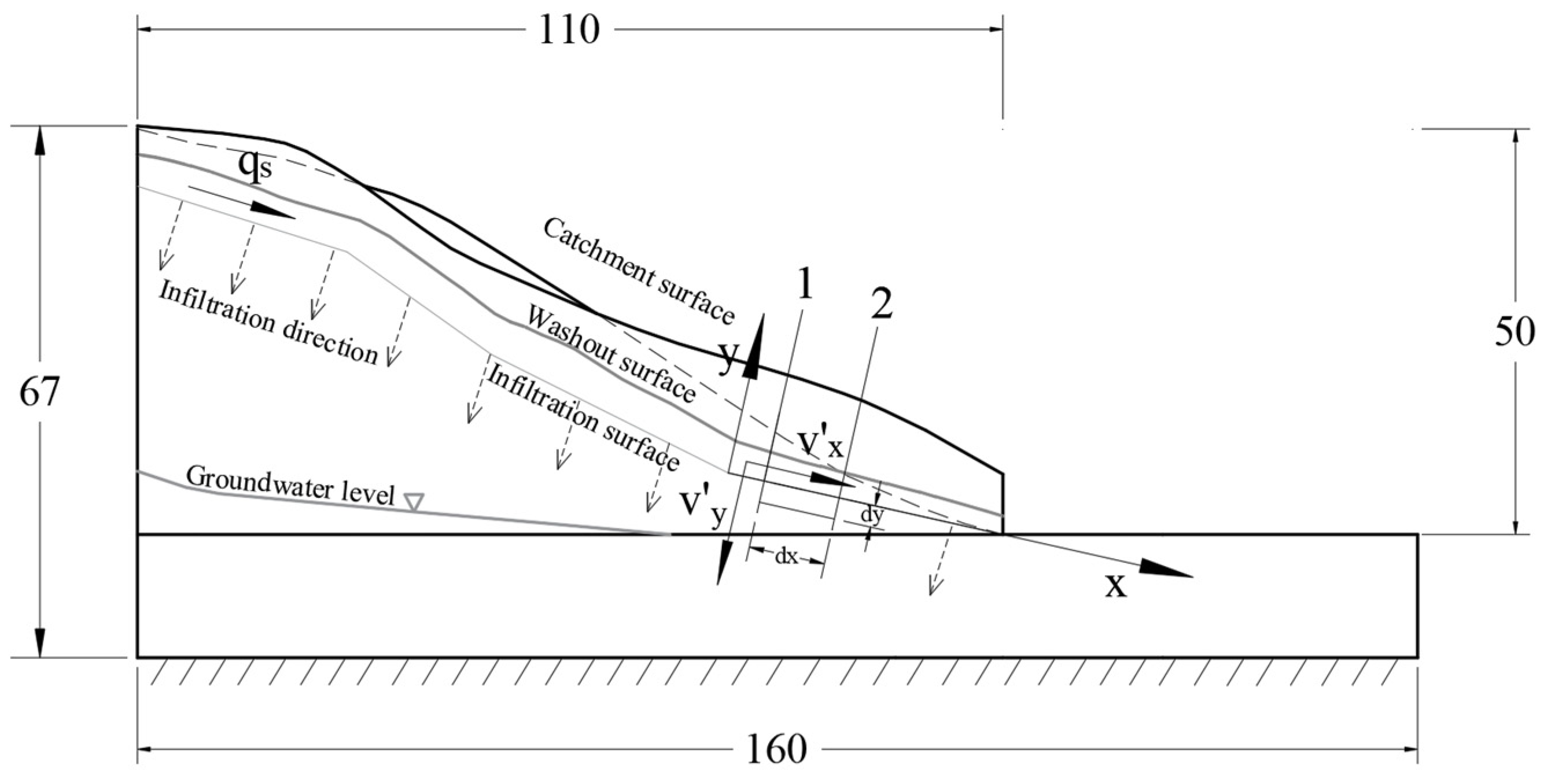
2.1.1. Improvement of the Rainfall Scouring Theory
2.1.2. Case Data
2.1.3. PFC Principle
2.2. Clump Model of Gangue and Analysis of Its Meso-Parameters
2.2.1. Simplified Model of Gangue Clump
2.2.2. Comparative Analysis of Triaxial Tests
2.2.3. Calibration of the Meso-Parameters of Gangue
2.2.4. Clump Model of Gangue Slopes
3. Results
3.1. Failure Mode
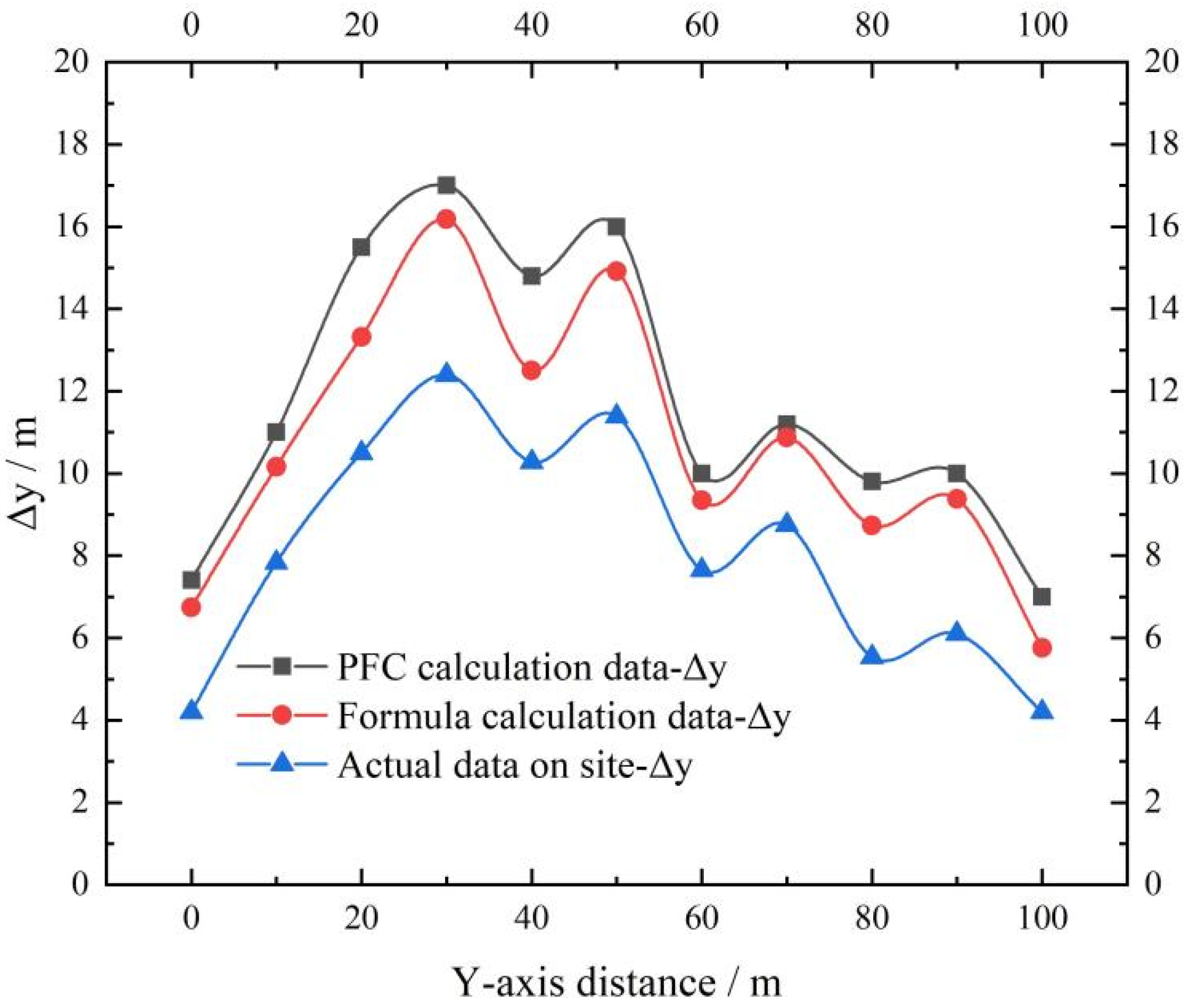
3.2. Comparison between Theory and Simulation
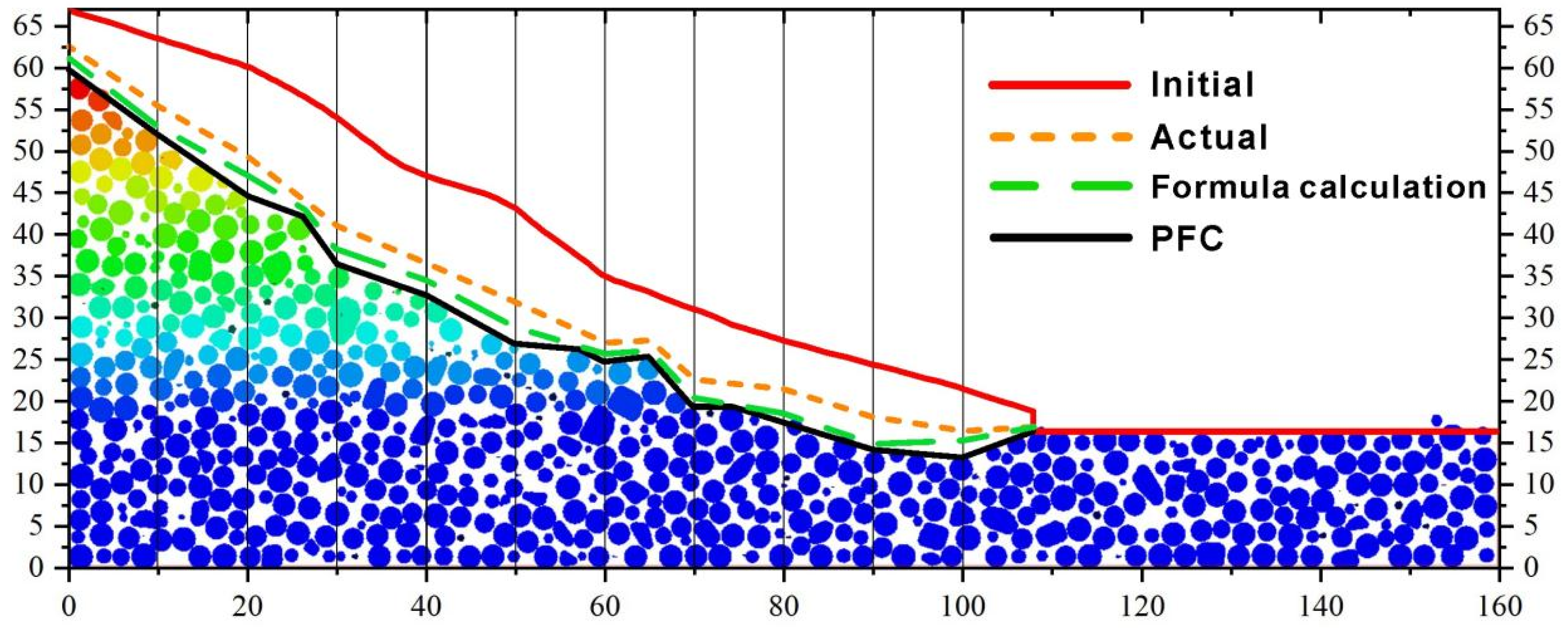
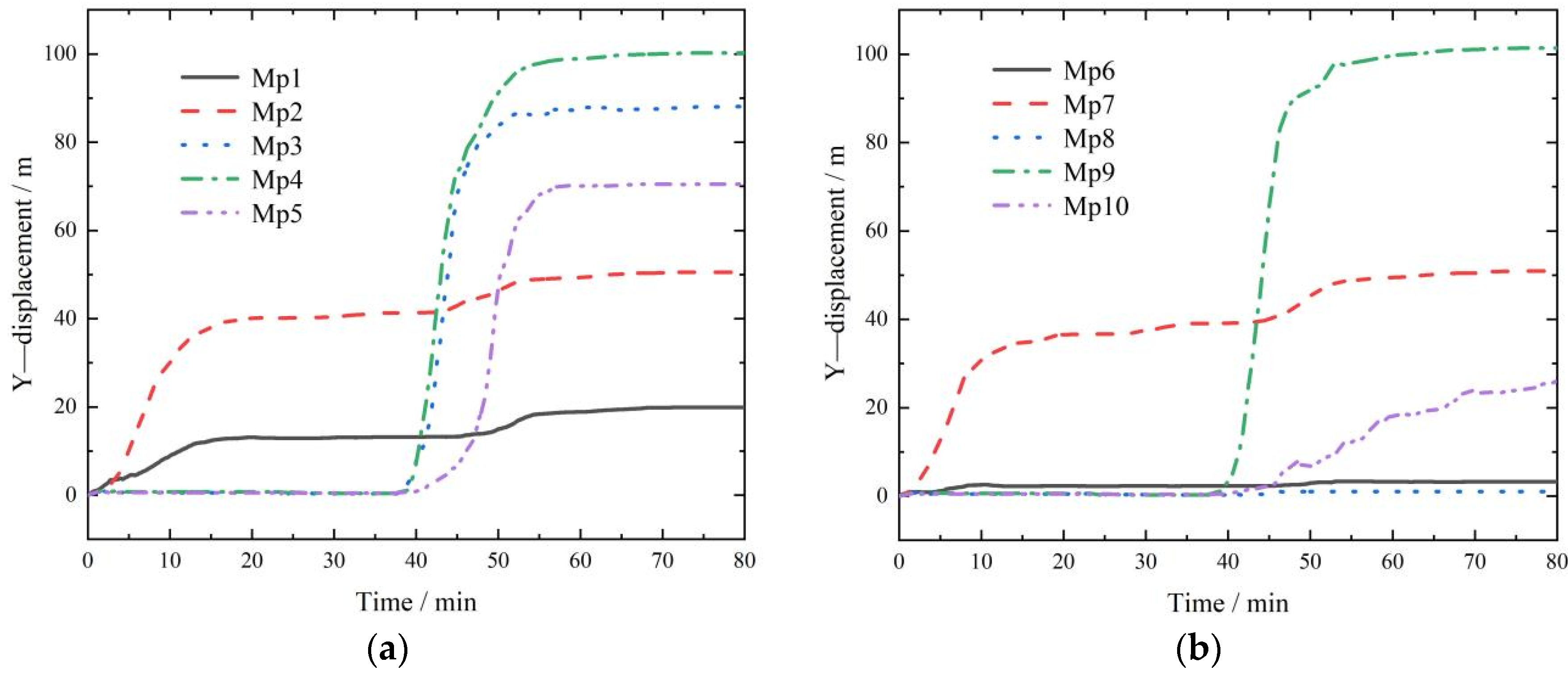
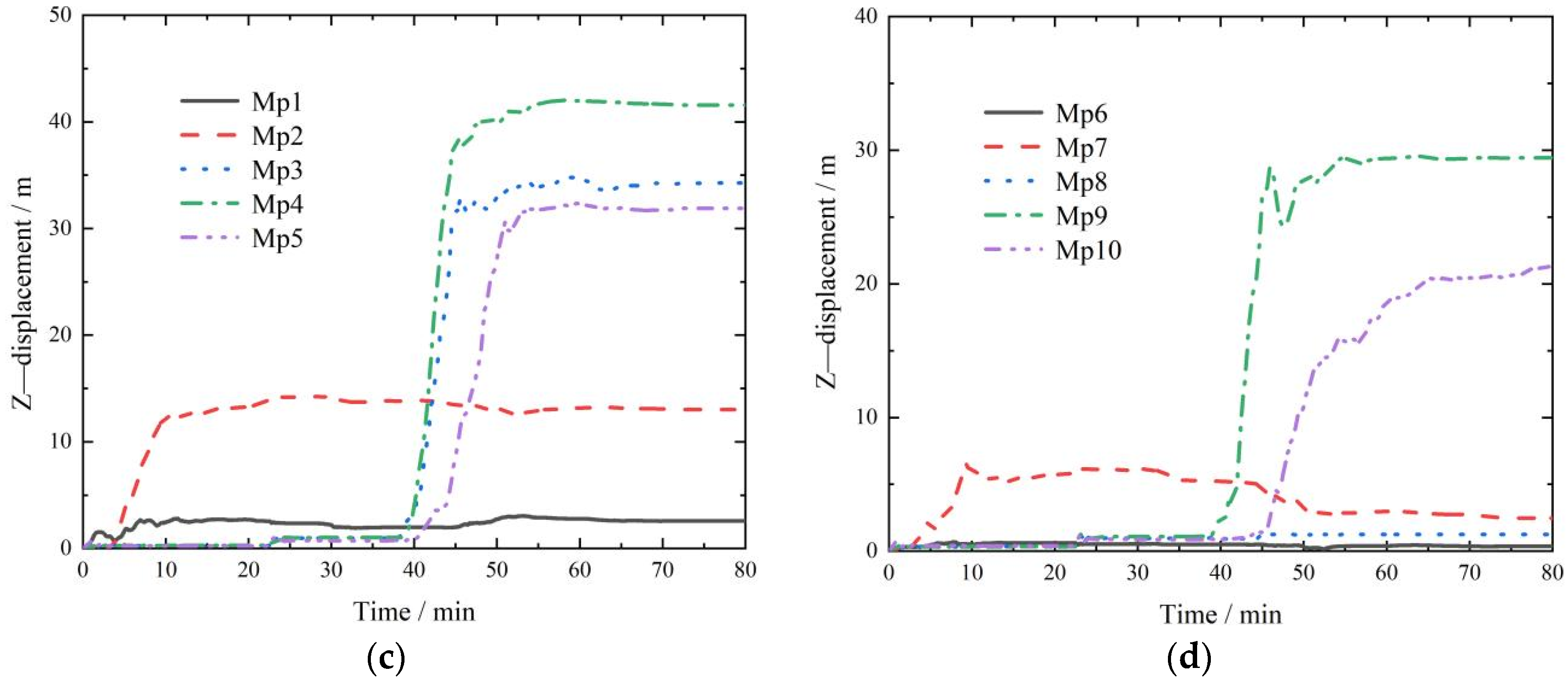
3.3. Displacement Analysis
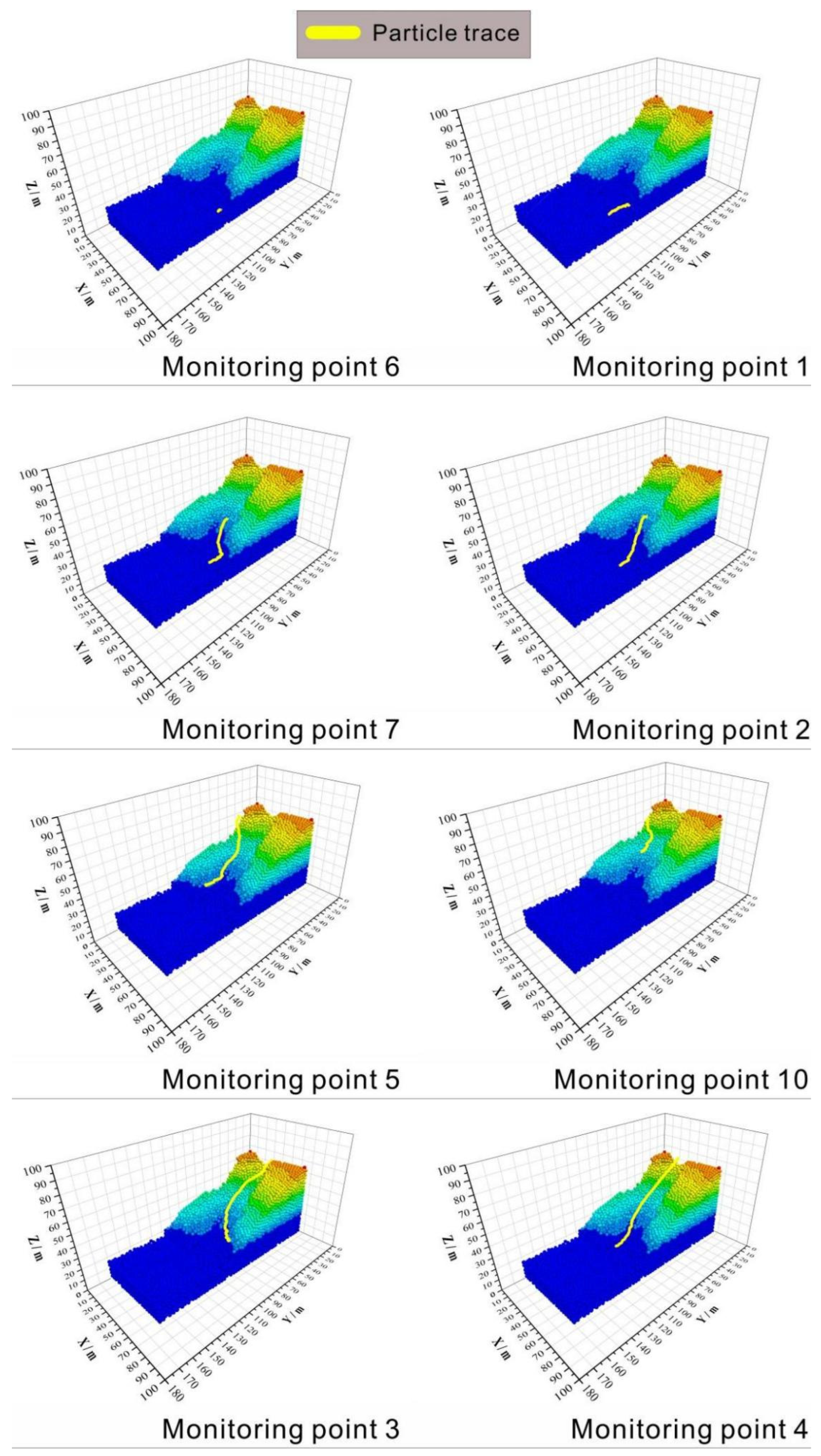
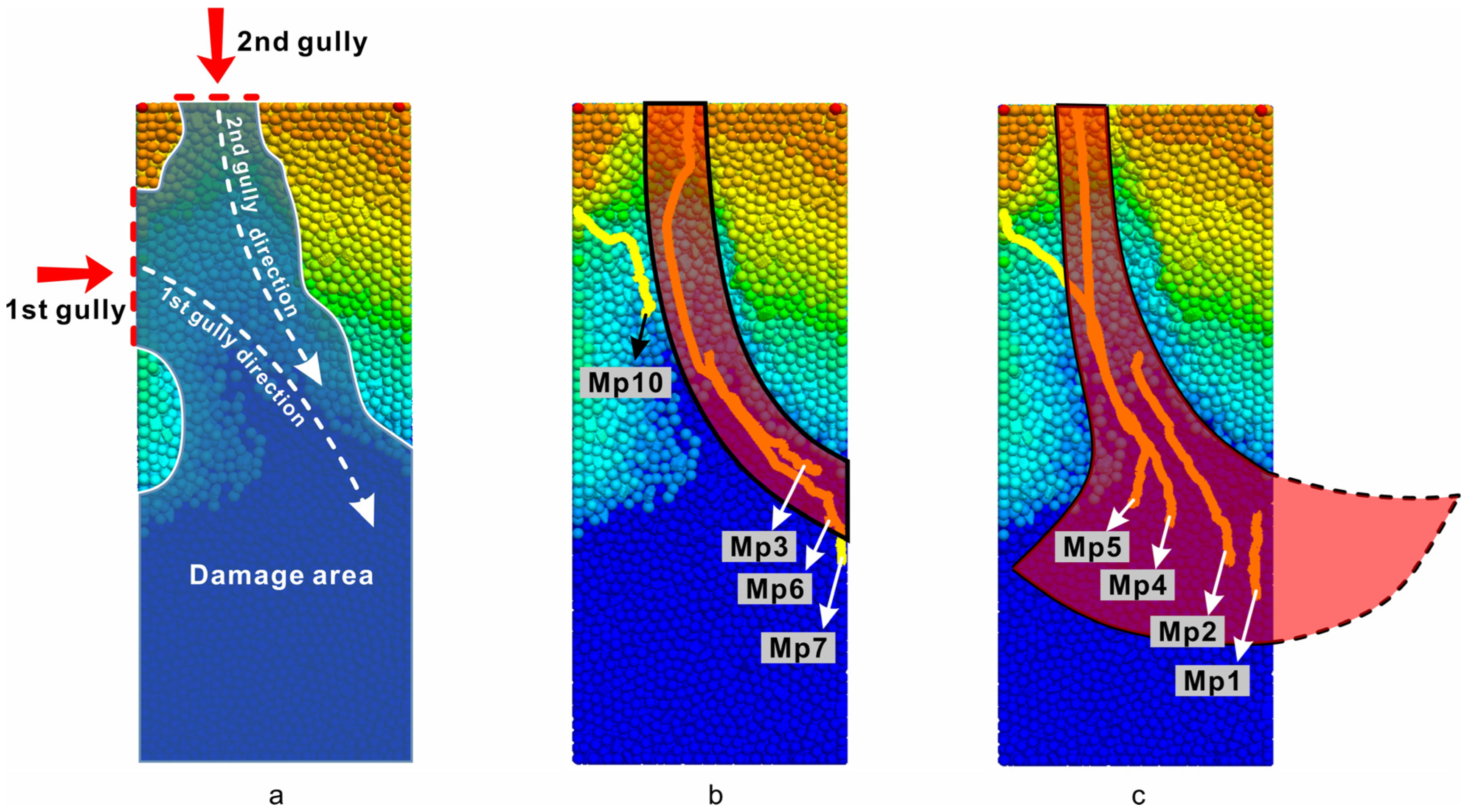
3.4. Scour Tracking and Accumulation
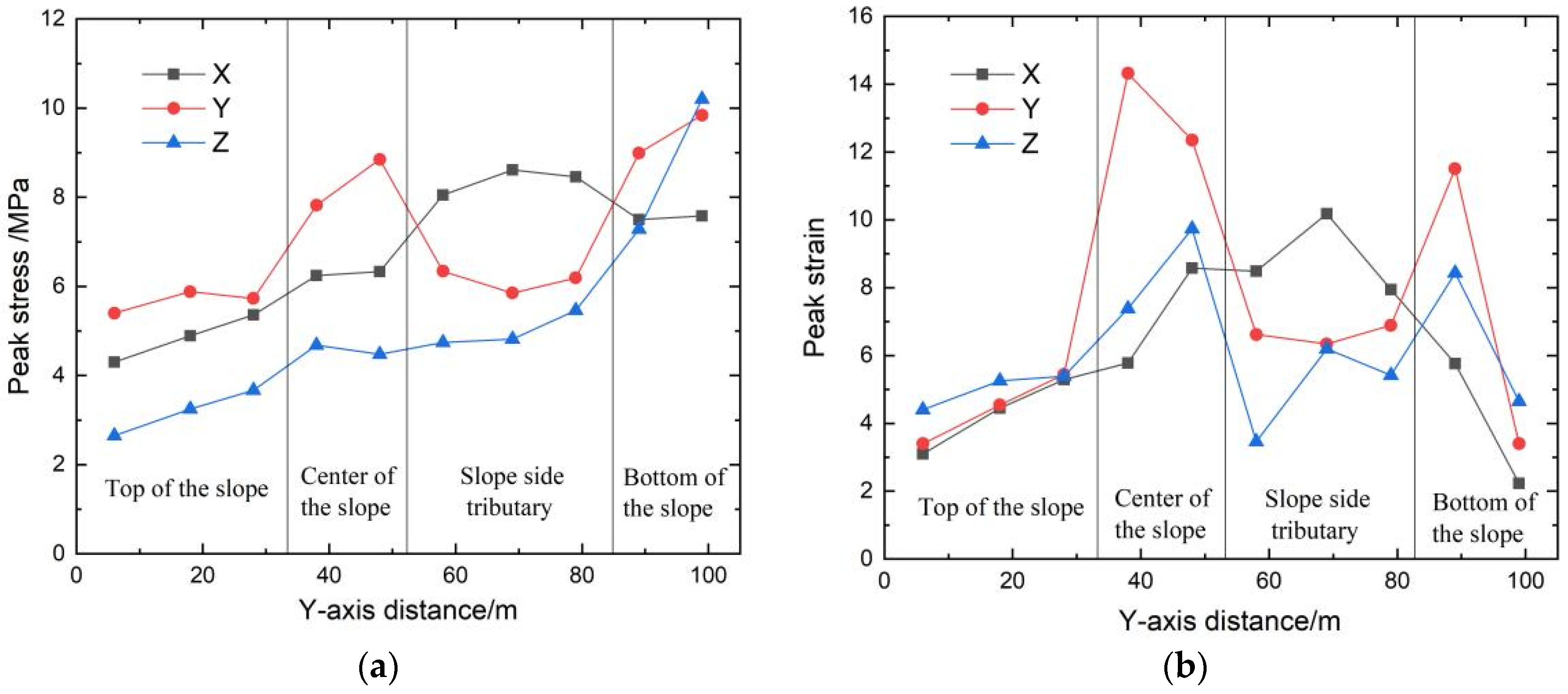
3.5. Stress–Strain Analysis
4. Discussion
5. Conclusions
- (1)
- Based on the previously derived rainfall scouring shear failure theory, a scouring depth optimization theory was further developed by taking into account the two types of scouring intensity factors (c and φ) and combining the characteristics of the PFC time effect calculation. Verification shows that the curve trends of the PFC calculation, the optimization theory calculation, and the actual slope depth data are consistent. The combination of these methods provides a valuable reference for early warnings of coal gangue slope engineering disasters and for the hydrodynamic theory.
- (2)
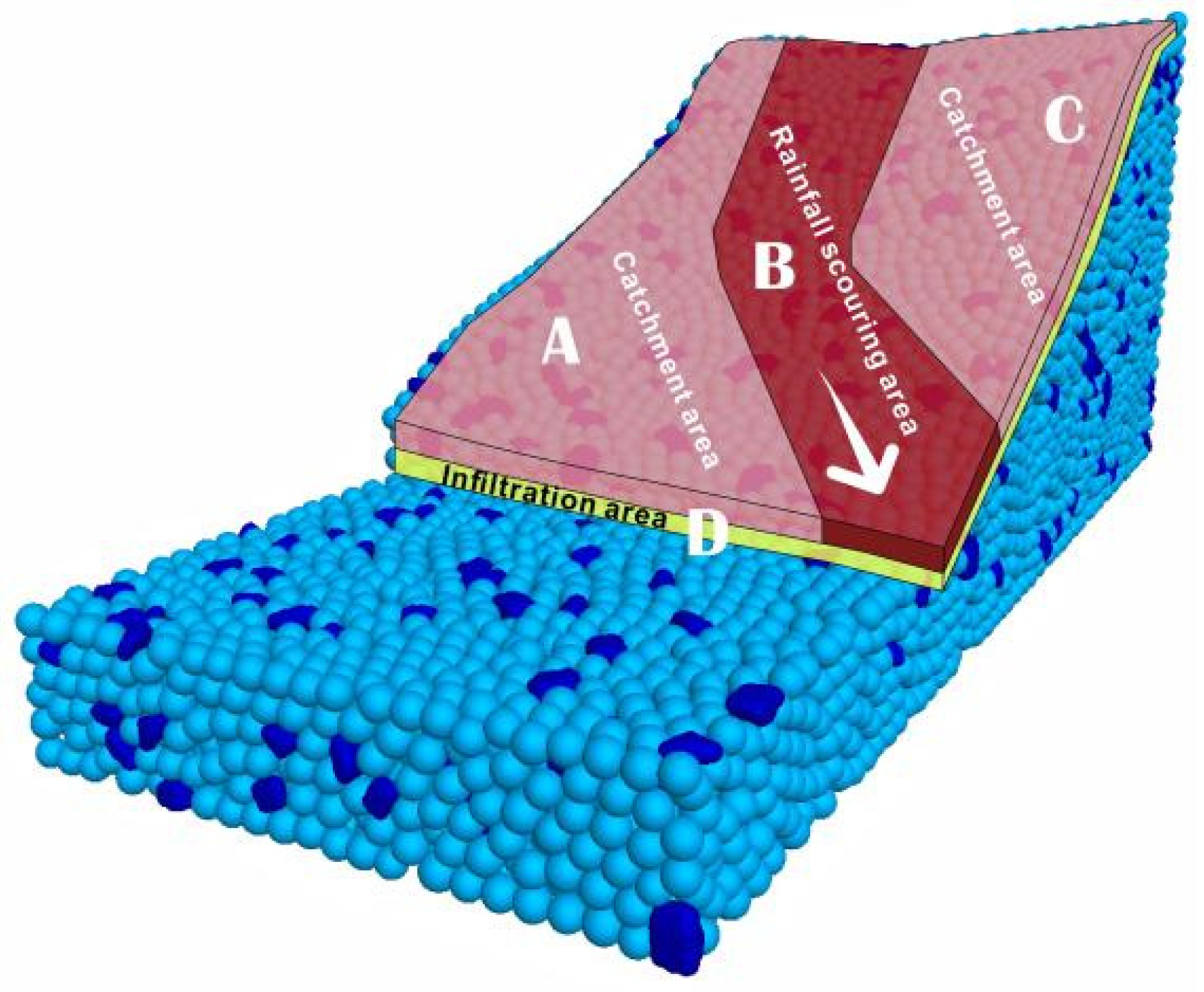
- The rain erosion failure of the coal gangue slope can be divided into four stages: (1) overall splash erosion and local schist erosion at the bottom of the slope; (2) erosion diversion and sheeting in the middle of the slope; (3) the tributary–slope crest extension and etching stage; and (4) the integral gully erosion and landslide stage. The scouring failure process has the characteristics of a discontinuous failure. Moreover, the failure sequence is as follows: slope bottom–slope middle–lateral tributary–slope top. The tributary gully in area A on the slope is determined by the water flow trend in the early catchment stage. The process of coal gangue scouring and destruction forms a three-stage ladder effect, which is concentrated at the top of the slope, the middle of the slope, and the bottom of the slope (0~25 m, 25~65 m, and 65~110 m). This step effect fully verifies the intermittent characteristics of the erosion failure of the coal gangue slope.
- (3)
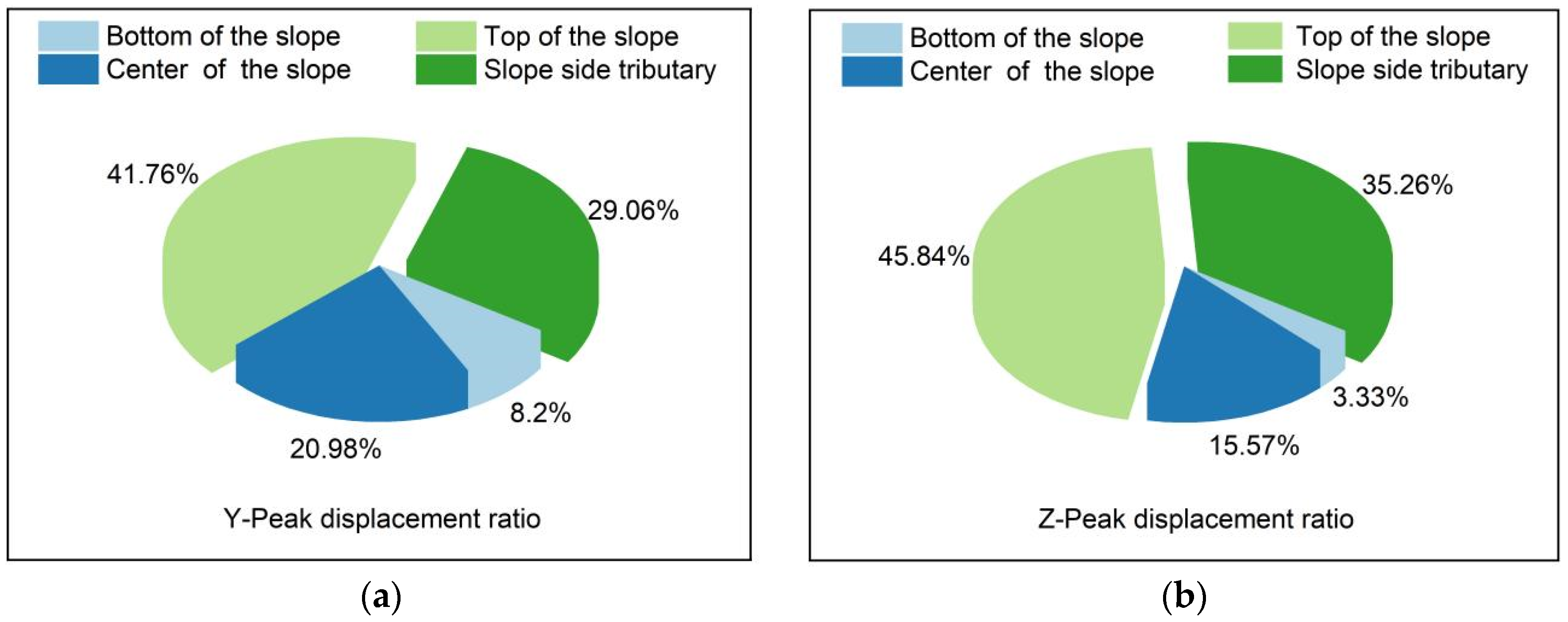
- During the whole process, the maximum displacement is concentrated at the top of the slope, according to the following proportions: top of the slope > tributaries > middle of the slope > bottom of the slope. The peak displacement of the slope top in the horizontal Y-direction accounts for 41.76%, and that in the Z-direction accounts for 45.84%. In efforts to prevent and control rainfall-induced landslides, priority should be given to the protection of the sliding soil mass at the bottom of the slope, and the focus should be on reducing the soil mass in the middle of the slope to prevent the maximum energy fluctuation caused by scouring, so as to prevent extensive displacement damage at the top of the slope. The latter part of the second stage of scouring is the incubation period for the tributary gully. During the whole scouring process, the strain fluctuation caused by scouring in the middle of the slope is the largest; this is the hub area for the development of scouring damage. The peak stress is up to 8.9 MPa, the peak strain is up to 14.3, and the damage caused by scouring is the strongest. The larger peak stress and strain values of coal gangue slope scouring failure are distributed in the horizontal Y-direction of the middle of the slope, the horizontal X-direction for the tributary, and the vertical Z-direction for the slope bottom. The generation of the branch notch is mainly determined by the X-direction stress, and 8.6 MPa is the critical stress.
- (4)
- There are two modes of erosion accumulation integration, namely, the arc erosion accumulation mode and the fan erosion accumulation mode. Arc-shaped erosion and accumulation are mainly controlled by deep particles, and fan-shaped erosion and accumulation are mainly affected by shallow particles. In the actual process of rainfall erosion, most of the slope erosion and failure modes show the effect of multi-ditch collection. The main stream gully mainly controls arc-shaped or linear erosion and accumulation. Due to their complex roles in the slope, the interaction between laminar flow and turbulent flow is intense, providing conditions for the development of tributaries and further forming the fan erosion and accumulation model. This provides favorable conditions for a more effective study of the internal mechanisms of coal gangue scouring and accumulation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J. Reflection on lowcarbon development of coal energy in china. J. China Univ. Min. Technol. Soc. Sci. 2011, 13, 5–12. [Google Scholar]
- Zhou, H.C. The comprehensive utilization of coal gangue should pay attention to demand orientation. Environ. Life 2020, 12, 78–81. [Google Scholar]
- Jia, M. The current situation research on comprehensive utilization of coal gangue. Conserv. Util. Miner. Resour. 2019, 39, 46–52. [Google Scholar]
- Dong, Q.; Liu, D. Nonlinear plasticity limit analysis upper bound method of gangue hill stability. J. China Coal Soc. 2007, 32, 131–135. [Google Scholar]
- Li, D.; Liu, D.; Wang, Y. Plastic upper bound theory reliability analysis of coal gangue hills. J. Chongqing Univ. 2008, 31, 1441–1445. [Google Scholar]
- Ju, N.; He, X. Study on coal gangue stability and disaster prevention measures. Geol. Explor. 2010, 46, 142–146. [Google Scholar]
- Zang, Y.; Liu, D.; Jiang, K. Characteristics of rainfall infiltration and stability of gangue hills in Chongqing mountainous area. China Civ. Eng. J. 2009, 42, 85–89. [Google Scholar]
- Yang, M.; Wu, M.; Li, J.; Wu, R.; He, Y. Calibration of mechanical parameters of granular gangue and stability analysis of gangue dump slope. Saf. Coal Mines 2021, 52, 232–236. [Google Scholar]
- Hurly, D.G.; Pantelis, G. Unsaturated and saturated flow through a thin porous layer on a hillslope. Water Resour. Res. 1985, 21, 821–824. [Google Scholar] [CrossRef]
- Li, N.; Xu, J.; Qin, Y. Research on calculation model for stability evaluation of rainfall- -induced shallow landslides. Rock Soil Mech. 2012, 33, 1485–1490. [Google Scholar]
- Chen, X. Analysis Methods for Slope Stability and Prediction for Landslide Intensity. Ph.D. Thesis, Tsinghua University, Bejjing, China, 2007. [Google Scholar]
- Li, L.; Zhao, R.; Wang, T.; Zhao, H.; Wang, M. Simulation study on grain flow of soil slope deformation and failure under rainfall. Sci. Technol. Eng. 2020, 20, 8496–8502. [Google Scholar]
- Li, S.; Liu, T.; Liu, X. Analysis method for land-slide stability. Chin. J. Rock Mech. Eng. 2009, 28, 3309–3324. [Google Scholar]
- Tingwen, H.; Jun, L.; Xiaopeng, K. Stability analysis of high slope of jointed open-pit mine under rainfall conditions. Sci. Technol. Eng. 2019, 19, 75–80. [Google Scholar]
- Wang, R.B.; Xia, R.; Qi, J. Numerical analysis of seep-age stability of hydrodynamic-induced landslide deposits. J. China Three Gorges Univ. Nat. Sci. 2019, 41, 50–54. [Google Scholar]
- Dongfang, T.; Hong, Z.; Defu, L. 2D FEM numerical simulation of rainfall infiltration for landslide with considering runoff effect and its application. Rock Soil Mech. 2016, 37, 1179–1186. [Google Scholar]
- Xin, T.; Ran, F.; Hong, L. Effects analysis of rainfall on landslide stability and drainage measures suggestion. Geotech. Eng. Tech. 2021, 35, 52–55, 59. [Google Scholar]
- Tangjin, Y.; Yiyuan, L.; Zewen, W.; Junjie, L.; Yan, L. Study on instability mechanism of rolling slope under rainfall condition. Sci. Eng. 2021, 21, 3513–3519. [Google Scholar]
- Chenghua, W.; Zhengyi, W.; Chenglin, Z. Tests and numerical simulations of non-orthogonal rainfall infiltration on surfaces of unsaturated sand slopes. Chin. J. Geotech-Nical. Eng. 2015, 37, 1357–1364. [Google Scholar]
- Zeng, L.; Shi, Z.N.; Fu, H.Y.; Bian, H.B. Influence of rain-fall infiltration on distribution characteristics of slope transient saturated zone. China J. Highw. Transp. 2017, 30, 25–34. [Google Scholar]
- Shiau, J.; Lai, V.Q.; Keawsawasvong, S. Multivariate adaptive regression splines analysis for 3D slope stability in anisotropic and heterogenous clay. J. Rock Mech. Geotech. Eng. 2022, in press. [Google Scholar] [CrossRef]
- Yodsomjai, W.; Keawsawasvong, S.; Thongchom, C.; Lawongkerd, J. Undrained stability of unsupported conical slopes in two-layered clays. Innov. Infrastruct. Solut. 2020, 6, 15. [Google Scholar] [CrossRef]
- Chen, H.-W.; Chen, C.-Y. Warning Models for Landslide and Channelized Debris Flow under Climate Change Conditions in Taiwan. Water 2022, 14, 695. [Google Scholar] [CrossRef]
- Hai, W.; Qian, J.; Weijun, W.; Nong, Z.; Yiming, Z. Experimental Test on Nonuniform Deformation in the Tilted Strata of a Deep Coal Mine. Sustainability 2021, 13, 13280. [Google Scholar]
- Weijian, Y.; Ke, L.; Ze, L.; Baifu, A.; Ping, W.; Hai, W. Mechanical characteristics and deformation control of surrounding rock in weakly cemented siltstone. Environ. Earth Sci. 2021, 80, 337. [Google Scholar]
- Yanlin, Z.; Chunshun, Z.; Yixian, W.; Hang, L. Shear-related roughness classification and strength model of natural rock joint based on fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. Sci. 2021, 137, 104550. [Google Scholar]
- Zhao, Y.; Wang, Y.; Wang, W.; Tang, L.; Liu, Q.; Cheng, G. Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mech. 2019, 101, 59–66. [Google Scholar] [CrossRef]
- Hu, M.J.; Wang, R.; Meng, Q.S.; Liu, G.S. Gravelly soil slope surface shape and criticality under rainfall conditions. Rock Soil Mech. 2006, 27, 1550–1553. [Google Scholar] [CrossRef]
- Liu, B.Y.; Nearing, M.A.; Risse, L. Slope gradient effects on soil loss for slopes. Trans. ASCE 1994, 37, 34–39. [Google Scholar]
- Luo, B.; Wang, B.G.; Wang, X.C. Basic theory of side slope surface scouring. J. Highw. Transp. Res. Dev. 2002, 19, 27–29. [Google Scholar]
- Khan, K.U.J.; Wang, C.-M.; Khan, M.W.J.; Liang, Z.; Li, S.; Li, B.-L. Influence of rainfall infiltration on the stability of unsaturated coal gangue accumulated slope. J. Mt. Sci. 2021, 18, 1696–1709. [Google Scholar] [CrossRef]
- Wu, G.Y.; Zhu, Z.H.; Cheng, J.; Wu, R.N.; Zhang, Y.S.; Wu, F.Q. Preliminary study on rainfall erosivity in the southern loess plateau. J. Soil Water Conserv. 2011, 25, 33–38. [Google Scholar] [CrossRef]
- Tang, D.; Li, D.Q.; Cao, Z.J. Slope stability analysis in the Three Gorges Reservoir area considering effect of antecedent rainfall. Georisk: Assess. Manag. Risk Eng. Syst. Geohazards 2017, 11, 161–172. [Google Scholar] [CrossRef]
- Shruti NaiduNaidu, S.; Sajinkumar, K.; Oommen, T.; Anuja, V.; Samuel, R.A.; Muraleedharan, C. Early warning system for shallow landslides using rainfall threshold and slope stability analysis. Geosci. Front. 2018, 9, 1871–1882. [Google Scholar] [CrossRef]
- Suradi, M.; Fourie, A.B.; Saynor, M.J. An experimental and numerical study of a landslide triggered by an extreme rainfall event in northern Australia. Landslides 2015, 13, 1125–1138. [Google Scholar] [CrossRef]
- Yun, T.; Yong, W.; Jiangyu, L.; Xueling, L.; Dafu, X.; Futao, Z.; Qi, F. Characterization of the Erosion Damage Mechanism of Coal Gangue Slopes through Rainwater Using a 3D Discrete Element Method: A Case Study of the Guizhou Coal Gangue Slope (Southwestern China). Appl. Sci. 2022, 12, 8548. [Google Scholar]
- Lin, J.Z.; Ruan, X.D.; Chen, B.G.; Wang, J.P.; Zhou, J.; Ren, A.L. Fluid Mechanics, 2nd ed.; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- Shen, S.J.; Sun, H.Y.; Shang, Y.Q.; Zhong, J.; Huang, J. Scouring-Penetration Coupling Analysis Of Embankment Slope Under Rainfall Action. Chin. J. Rock Mech. Eng. 2011, 30, 2456–2462. [Google Scholar]
- Wu, C.G. Hydraulics; Higher Education Press: Beijing, China, 2003; pp. 268–281. (In Chinese) [Google Scholar]
- Li, J.M. 3D Fabric Spatiotemporal Evolution Characteristics and Transparent Characterization of Gangue Solid Waste Backfilling Material during Compression; China University of Mining and Technology: Xuzhou, China, 2020. [Google Scholar]
- Yong, R.; Qin, J.-B.; Huang, M.; Du, S.-G.; Liu, J.; Hu, G.-J. An Innovative Sampling Method for Determining the Scale Effect of Rock Joints. Rock Mech. Rock Eng. 2019, 52, 935–946. [Google Scholar] [CrossRef]
- Jun, P.; Guan, R.; Ming, C.; Kun, P. Determination of residual strength of rocks by abrittle index. Rock Soil Mech. 2015, 36, 403–408. [Google Scholar]
- Wu, Q.; Wang, C.M.; Song, P.R.; Zhu, H.B.; Ma, D.H. Rainfall erosion experiment for steep loess slope and fluid-soil coupling simulation with PFC3D. Rock Soil Mech. 2014, 35, 977–984. [Google Scholar] [CrossRef]



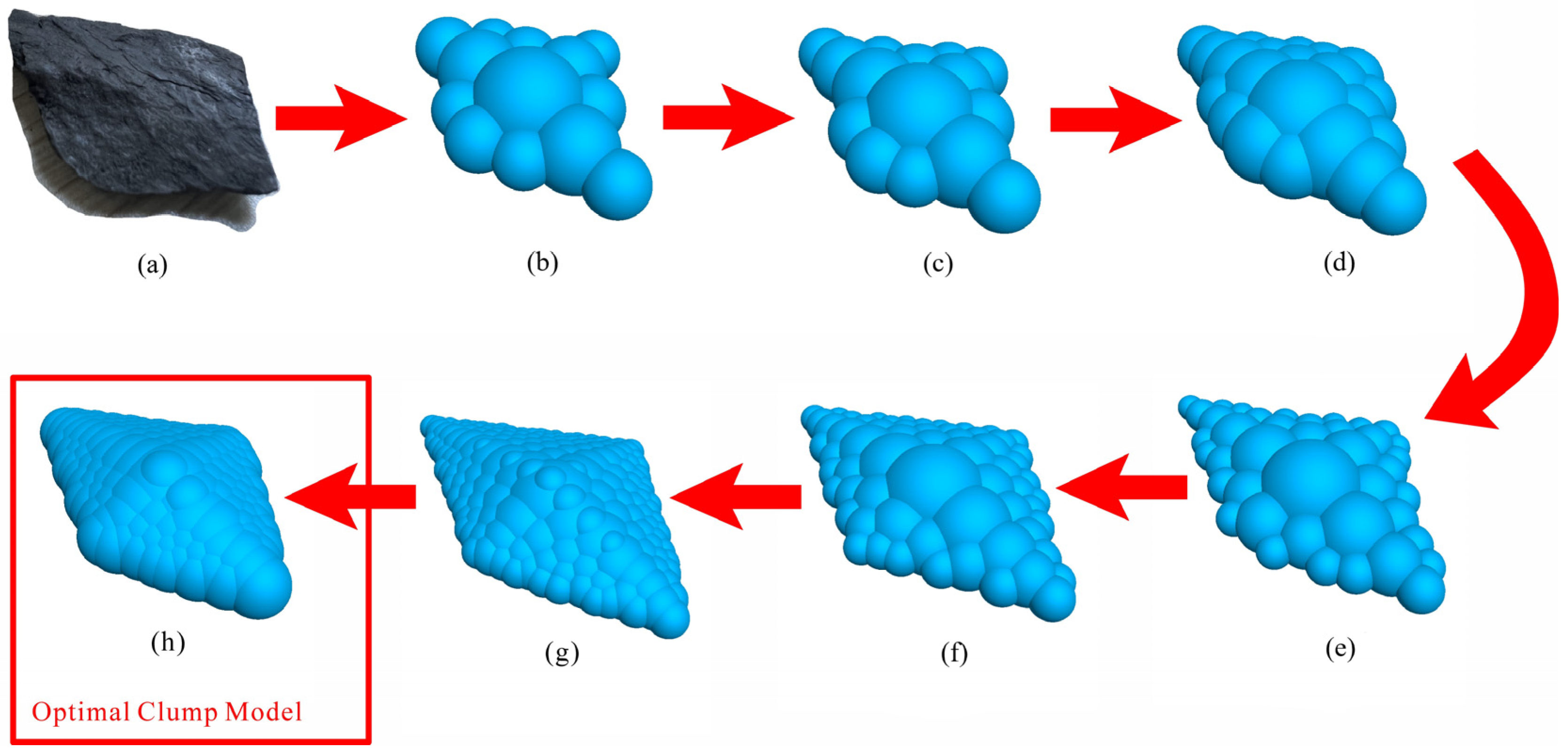




| Granule Group | Coarse Particles | Medium Particles | Fine Particles | Clump 1 | Clump 2 |
|---|---|---|---|---|---|
| Particle size (m) | 2.0–2.5 | 1.5–2.0 | 1.0–1.5 | 2.0–3.0 | 2.0–3.0 |
| Content (%) | 10 | 50 | 10 | 15 | 15 |
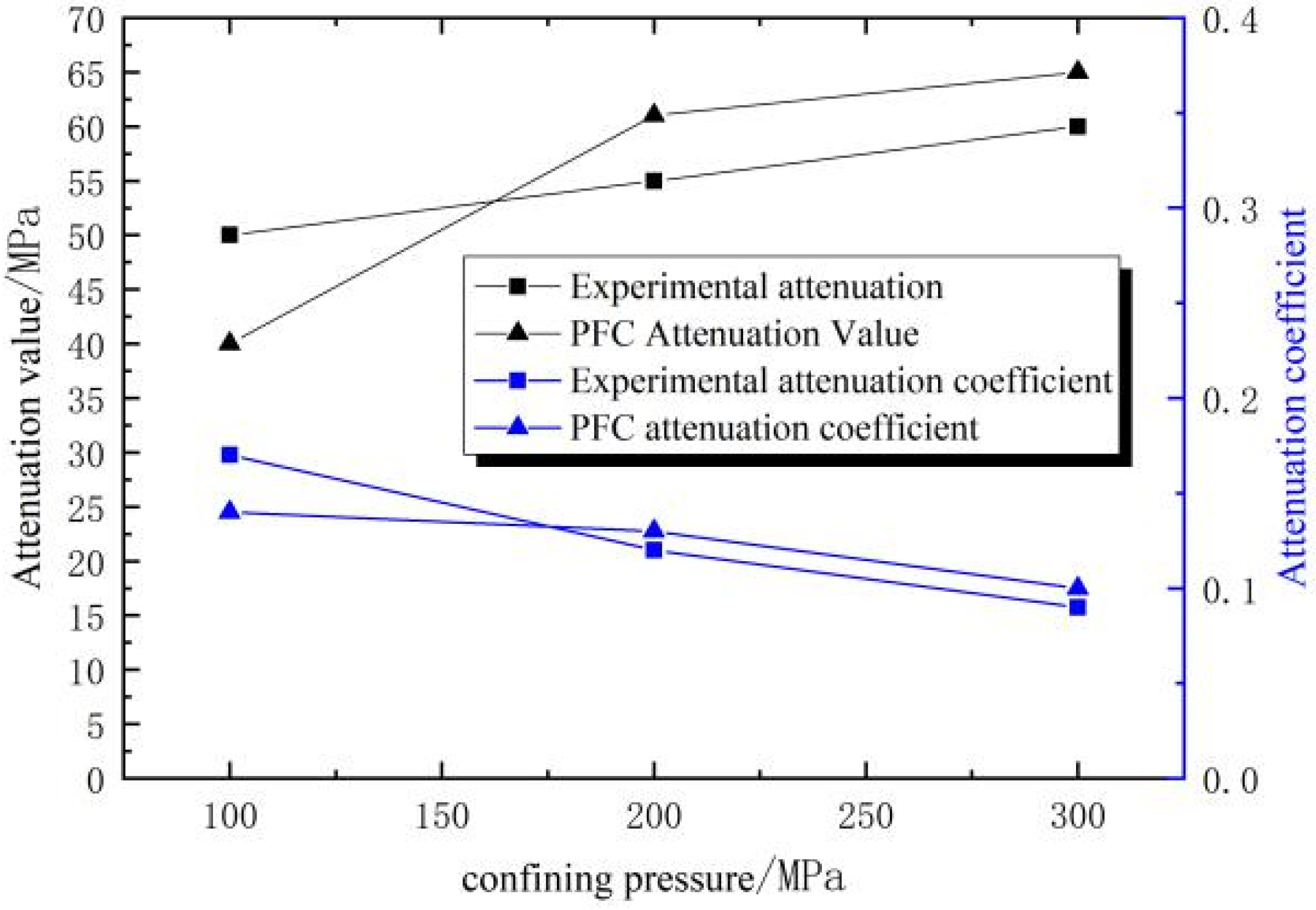
| Test Method | Confining Pressure (Kpa) | Peak Stress Difference (KPa) | Peak Stress (Kpa) | Residual Stress (Kpa) | Attenuation Value (Kpa) | Attenuation Coefficient | Cohesion (Kpa) |
|---|---|---|---|---|---|---|---|
| Real | 100 | 300 | 400 | 250 | 50 | 0.17 | 33.17 |
| 200 | 455 | 650 | 400 | 55 | 0.12 | ||
| 300 | 660 | 960 | 600 | 60 | 0.09 | ||
| PFC | 100 | 280 | 380 | 240 | 40 | 0.14 | 30.18 |
| 200 | 456 | 670 | 395 | 61 | 0.13 | ||
| 300 | 660 | 960 | 595 | 65 | 0.10 |
| D /kg·m−3 | E * /Gpa | K * | μ | λ | Kc * | Ec * /Gpa | /Mpa | /Mpa | /° | dw /kg·m−3 | vs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3000 | 1.2 | 1.0 | 0.75 | 1.00 | 1.0 | 10 | 8.6 | 11 | 26 | 1.0 | 2.5 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Wu, Y.; Wang, H.; Li, H.; He, L.; Zhao, H. A Theory of Slope Shear Scouring and the Failure Mechanism of PFC3D on a Gangue Slope. Appl. Sci. 2023, 13, 5066. https://doi.org/10.3390/app13085066
Tian Y, Wu Y, Wang H, Li H, He L, Zhao H. A Theory of Slope Shear Scouring and the Failure Mechanism of PFC3D on a Gangue Slope. Applied Sciences. 2023; 13(8):5066. https://doi.org/10.3390/app13085066
Chicago/Turabian StyleTian, Yun, Yong Wu, Hao Wang, Hongtao Li, Lindong He, and Hong Zhao. 2023. "A Theory of Slope Shear Scouring and the Failure Mechanism of PFC3D on a Gangue Slope" Applied Sciences 13, no. 8: 5066. https://doi.org/10.3390/app13085066
APA StyleTian, Y., Wu, Y., Wang, H., Li, H., He, L., & Zhao, H. (2023). A Theory of Slope Shear Scouring and the Failure Mechanism of PFC3D on a Gangue Slope. Applied Sciences, 13(8), 5066. https://doi.org/10.3390/app13085066










