Deep Learning-Assisted Transmit Antenna Classifiers for Fully Generalized Spatial Modulation: Online Efficiency Replaces Offline Complexity
Abstract
:1. Introduction
2. Related Works
- There are no repositories that have the TAS dataset for FGSM. In total, two datasets of size 25,000 are created by applying the EDAS algorithm repeatedly. These datasets include information about channel setups and antenna counts for various MIMO configurations, as well as basic performance metrics such as ED.
- Three distinct supervised DL methods are incorporated to demonstrate the improvements of DL over ML algorithms, including feed-forward neural networks (FNN), recurrent neural networks (RNN), and 1D convolutional neural networks (CNN).
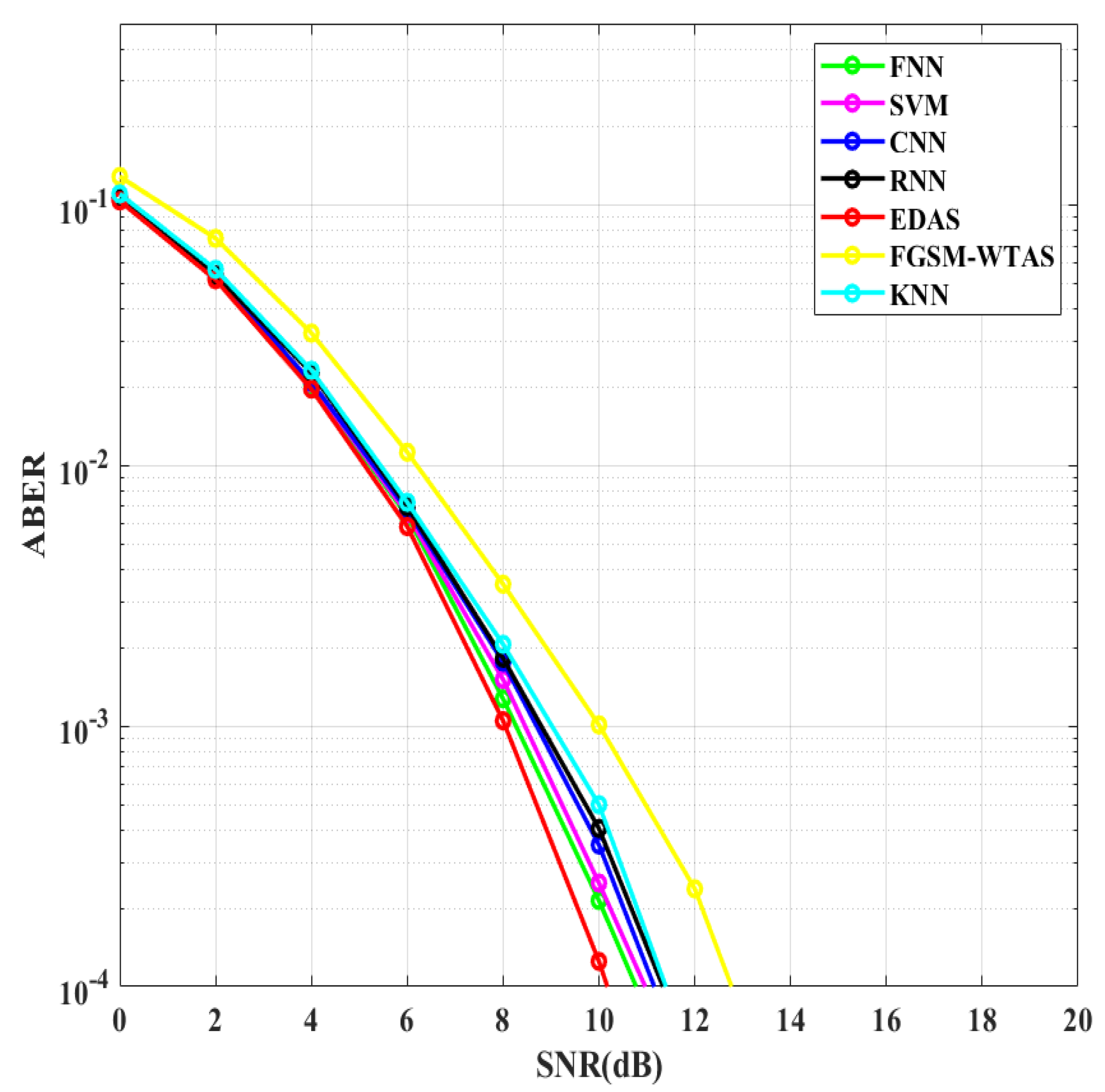
- ML- and DL-based TAS methods are compared to WTAS and EDAS in terms of ABER and computational complexity.
3. System Model of FGSM and Traditional EDAS
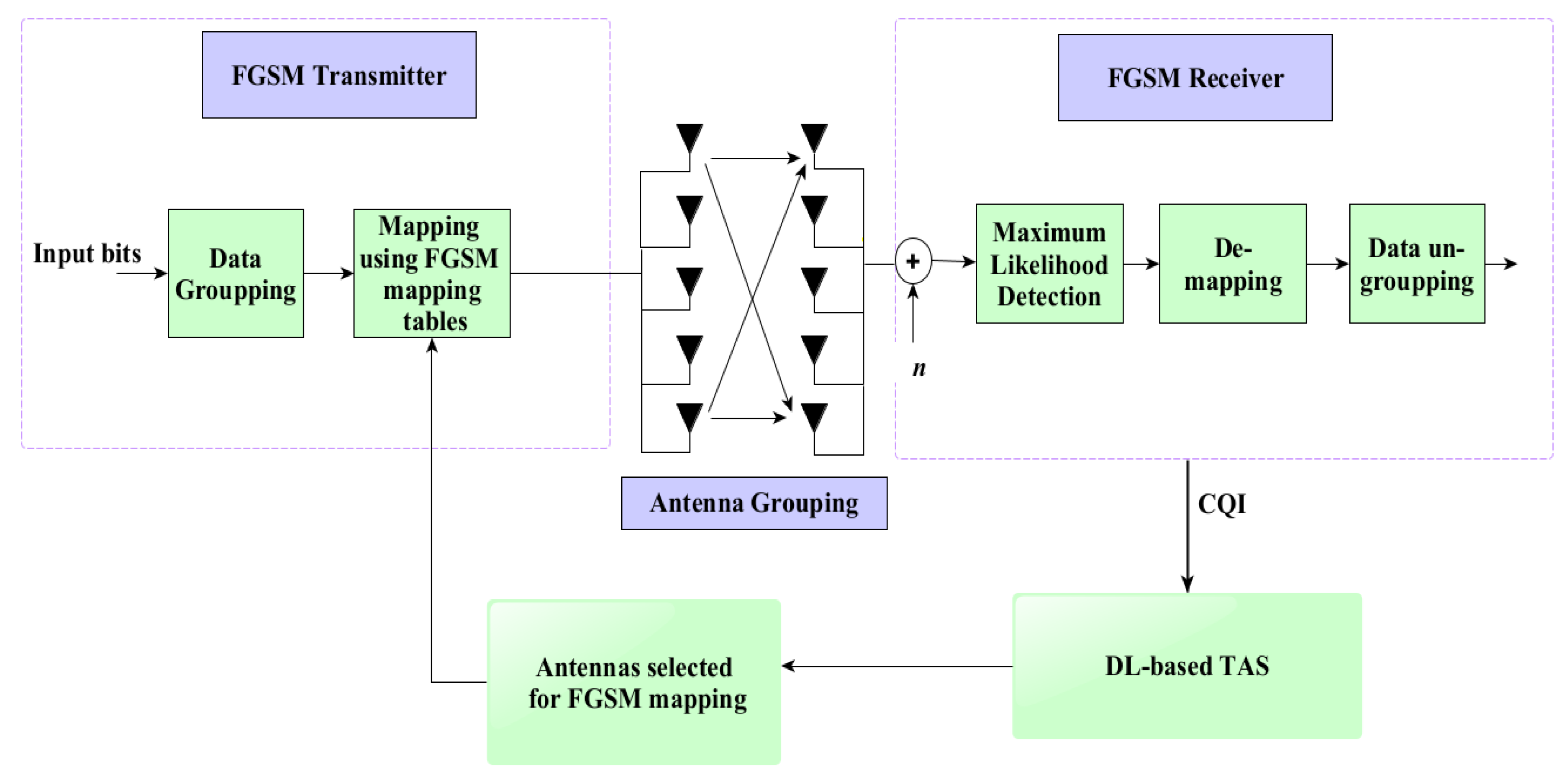
3.1. FGSM
3.2. EDAS
- (1)
- Determine the total number of distinct feasible subsets = .
- (2)
- Find all of the possible transmit vectors for each antenna subset.
- (3)
- For each antenna subset, calculate their least possible ED using:
- (4)
- Determine the subset of antennas with the maximum ED.here .
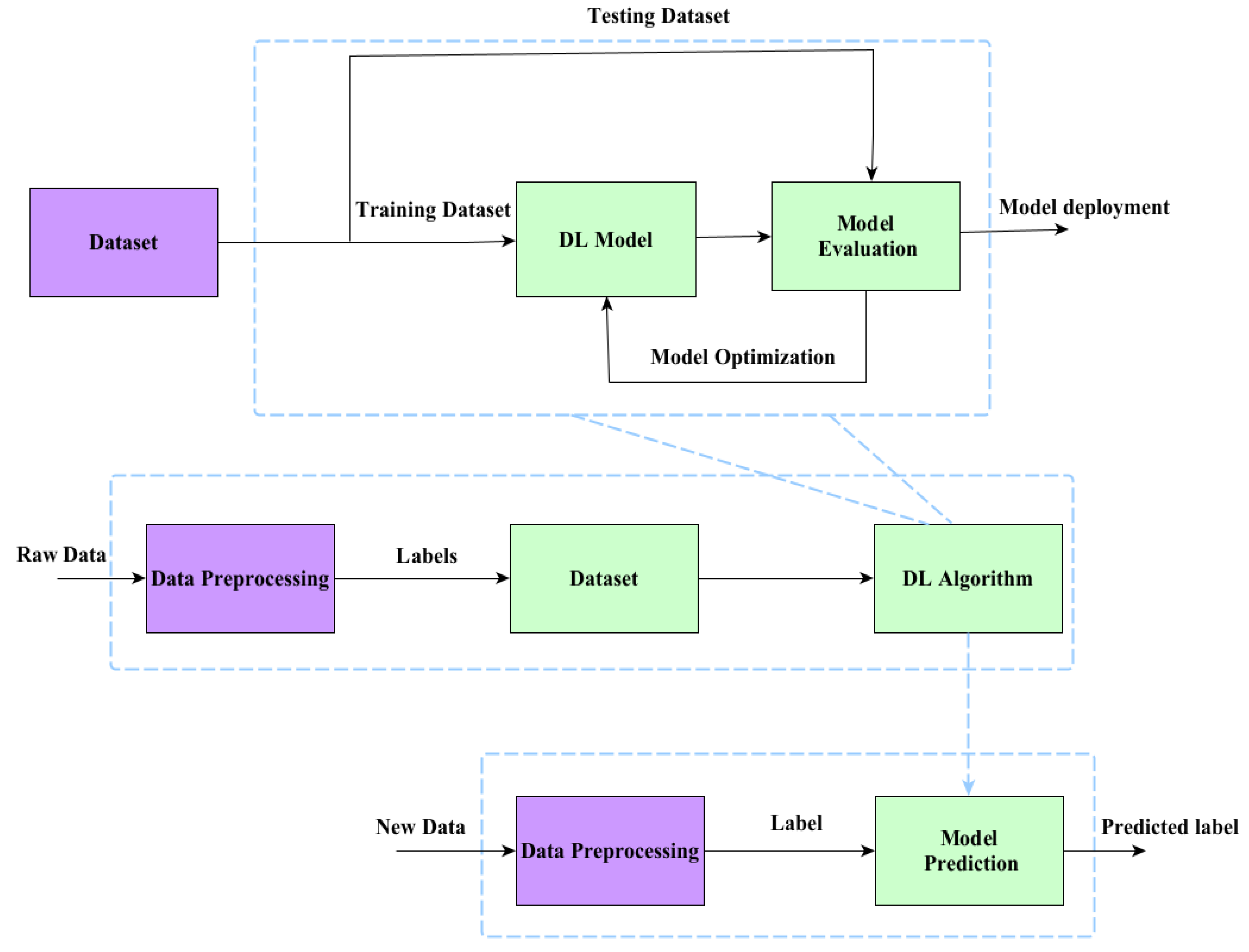
4. Design and Complexity of Proposed DL Architectures
4.1. DL-Based TAS Schemes for FGSM
- i.
- Dataset generation: random channel matrices , are generated to create the dataset.consists of all these records or channel matrices.
- ii.
- Feature vector extraction: This work utilized the absolute values of every element of the channel matrix as an input feature with size . The resulting feature vector is given by:here is the (j, k)th element of , its absolute value is given as:The mean normalization is performed to avoid the effect of bias [21].
- iii.
- Calculation of KPI: (3) is used to evaluate ED, which is considered the key performance indicator (KPI) in this study. The KPI is utilized to label the dataset.
- iv.
- Class labeling: There is a unique label associated with every antenna subset. Antenna subset and class label mapping examples for the configurations , 3, and is given in Table 2.
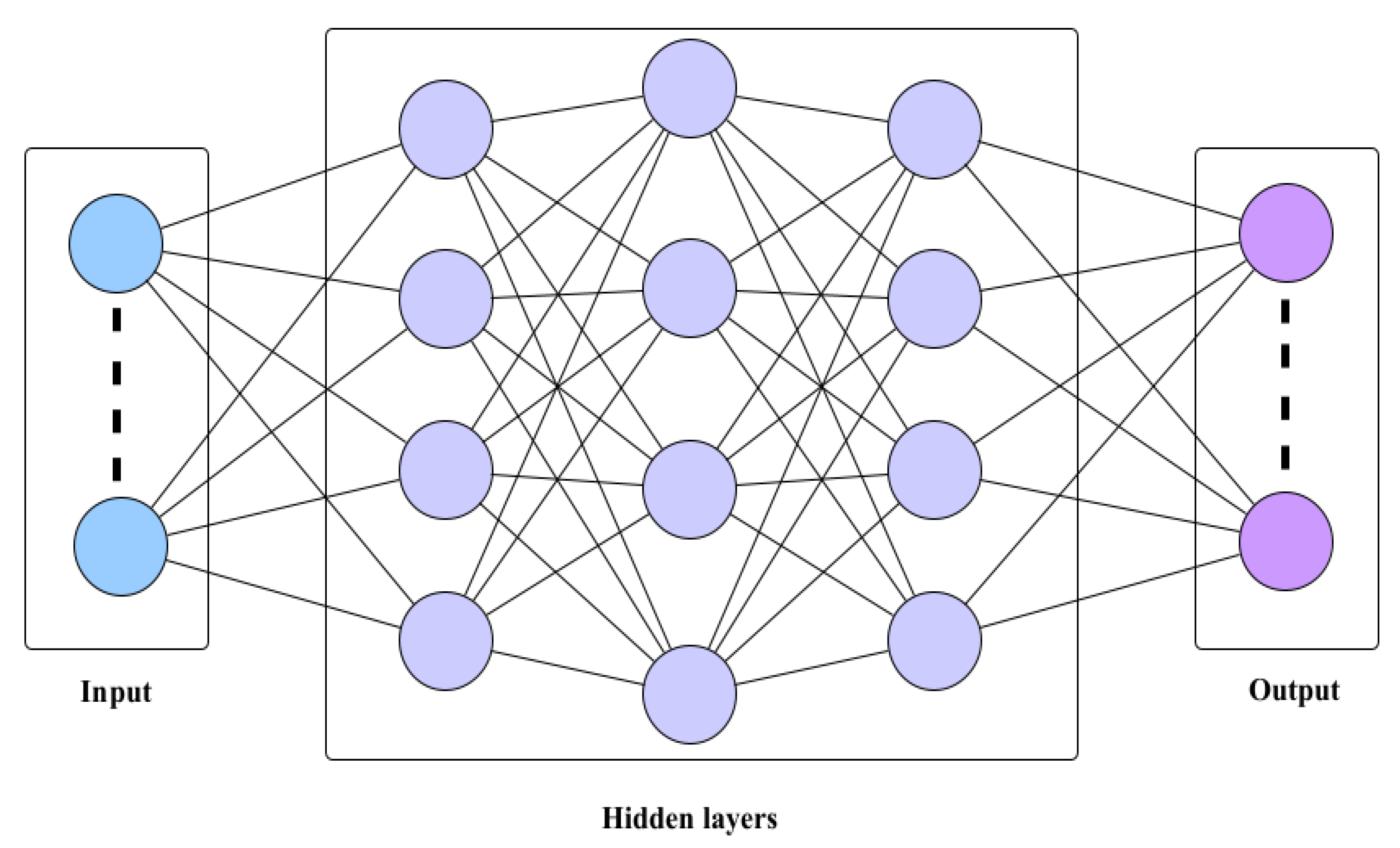
4.2. DL Architecture
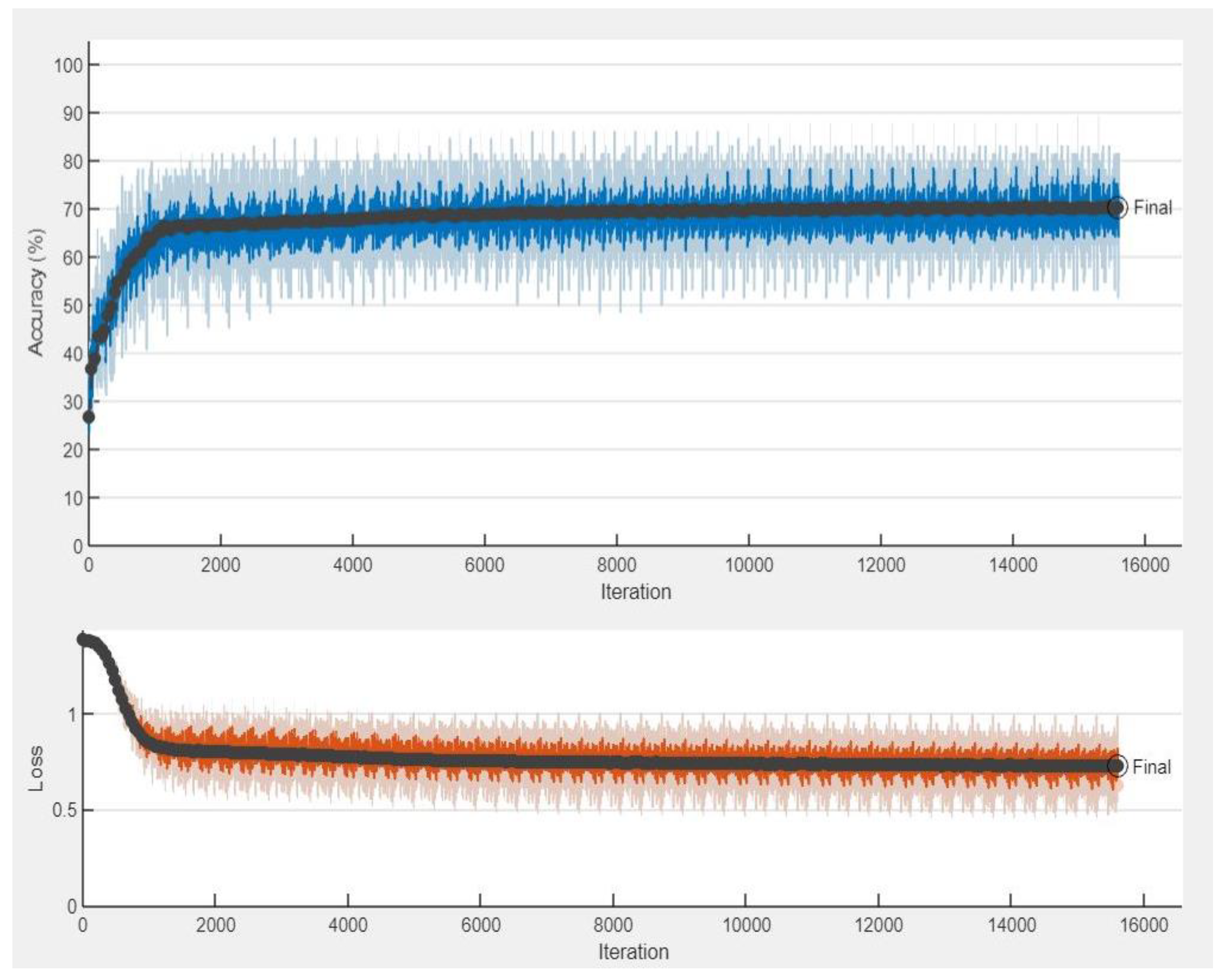
4.3. Complexity of Proposed DL-Based TAS Schemes
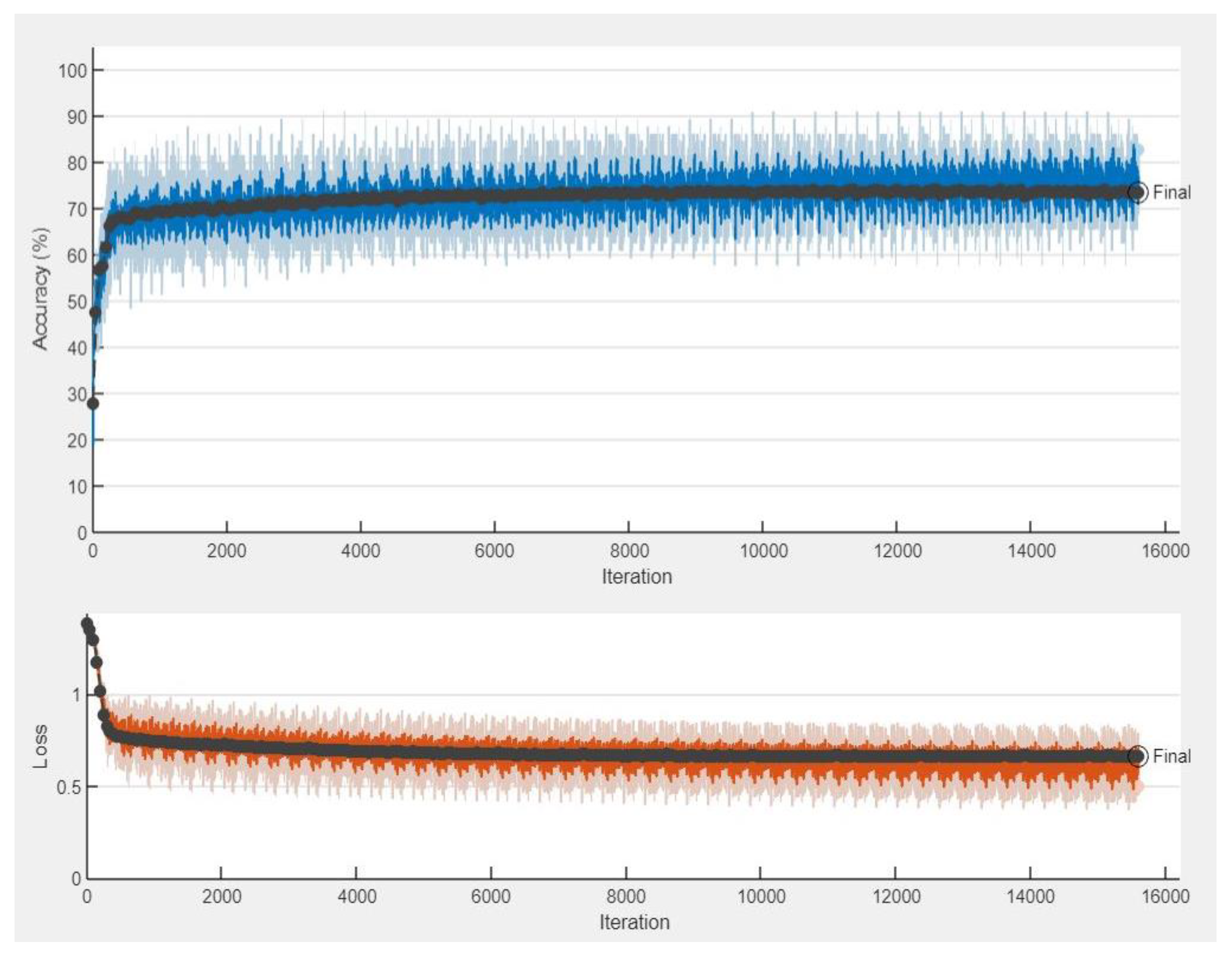
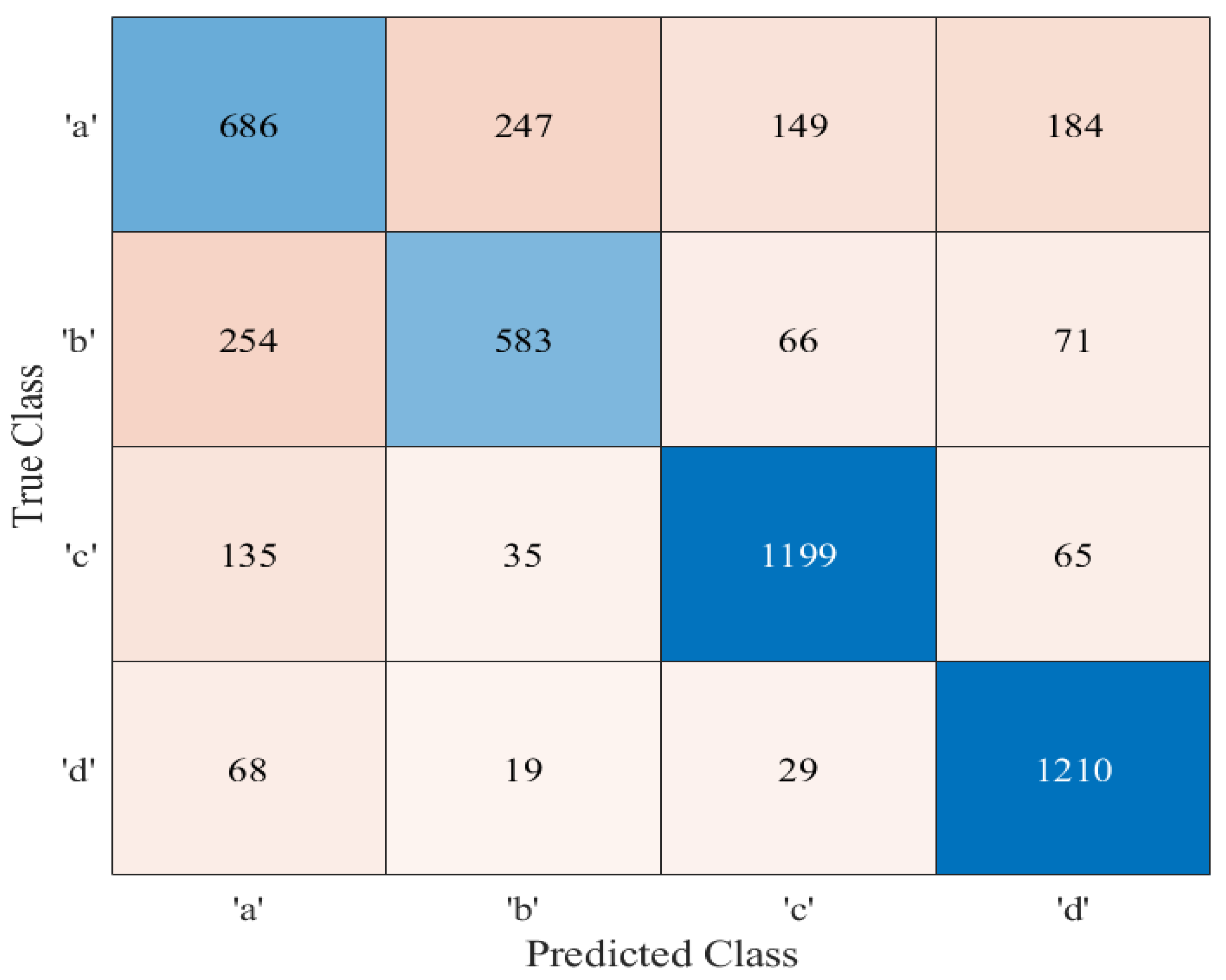
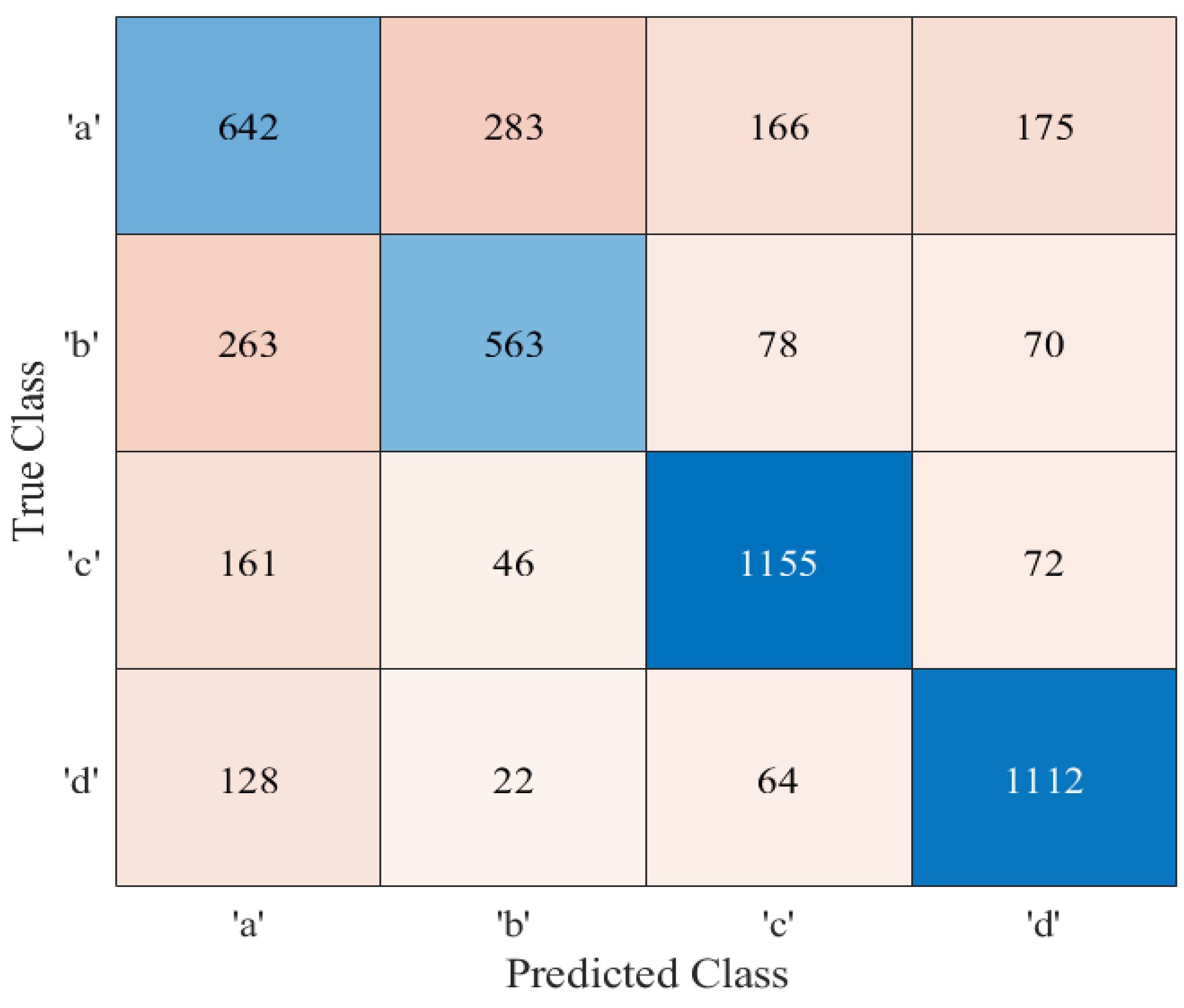
5. Discussion on Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hong, E.-K.; Lee, I.; Shim, B.; Ko, Y.-C.; Kim, S.-H.; Pack, S.; Lee, K.; Kim, S.; Kim, J.-H.; Shin, Y.; et al. 6G R&D vision: Requirements and candidate technologies. J. Commun. Netw. 2022, 24, 232–245. [Google Scholar]
- Dang, S.; Amin, O.; Shihada, B.; Alouini, M.-S. What should 6G be? Nat. Electron. 2020, 3, 20–29. [Google Scholar] [CrossRef]
- Rekkas, V.P.; Sotiroudis, S.; Sarigiannidis, P.; Wan, S.; Karagiannidis, G.K.; Goudos, S.K. Machine learning in beyond 5G/6G networks—State-of-the-art and future trends. Electronics 2021, 10, 2786. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Mu, X.; Ding, Z.; Schober, R.; Al-Dhahir, N.; Hossain, E.; Shen, X. Evolution of NOMA toward next generation multiple access (NGMA) for 6G. IEEE J. Sel. Areas Commun. 2022, 40, 1037–1071. [Google Scholar] [CrossRef]
- Guan, G.; Liu, M.; Tang, F.; Kato, N.; Adachi, F. 6G: Opening new horizons for integration of comfort, security, and intelligence. IEEE Wirel. Commun. 2020, 27, 126–132. [Google Scholar]
- Basar, E. Transmission through large intelligent surfaces: A new frontier in wireless communications. In Proceedings of the 2019 European Conference on Networks and Communications (EuCNC), Valencia, Spain, 18–21 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 112–117. [Google Scholar]
- Ertugrul, B.; Wen, M.; Mesleh, R.; Di Renzo, M.; Xiao, Y.; Haas, H. Index modulation techniques for next-generation wireless networks. IEEE Access 2017, 5, 16693–16746. [Google Scholar]
- Chien-Chun, C.; Sari, H.; Sezginer, S.; Su, T.Y. Enhanced spatial modulation with multiple signal constellations. IEEE Trans. Commun. 2015, 63, 2237–2248. [Google Scholar]
- Abdelhamid, Y.; Mesleh, R.; Di Renzo, M.; Haas, H. Generalised spatial modulation for large-scale MIMO. In Proceedings of the 2014 22nd European Signal Processing Conference (EUSIPCO), Lisbon, Portugal, 1–5 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 346–350. [Google Scholar]
- Gaurav, J.; Gudla, V.V.; Kumaravelu, V.B.; Reddy, G.R.; Murugadass, A. Modified spatial modulation and low complexity signal vector based minimum mean square error detection for MIMO systems under spatially correlated channels. Wirel. Pers. Commun. 2020, 110, 999–1020. [Google Scholar]
- Raed, M.; Ikki, S.S.; Aggoune, H.M. Quadrature spatial modulation. IEEE Trans. Veh. Technol. 2014, 64, 2738–2742. [Google Scholar]
- Vardhan, G.V.; Kumaravelu, V.B.; Murugadass, A. Transmit antenna selection strategies for spectrally efficient spatial modulation techniques. Int. J. Commun. Syst. 2022, 35, e5099. [Google Scholar]
- Rakshith, R.; Hari, K.V.S.; Hanzo, L. Antenna selection in spatial modulation systems. IEEE Commun. Lett. 2013, 17, 521–524. [Google Scholar]
- Narushan, P.; Xu, H. “Comments on” antenna selection in spatial modulation systems. IEEE Commun. Lett. 2013, 17, 1681–1683. [Google Scholar]
- Hindavi, J.; Kumaravelu, V.B. Transmit Antenna Selection Assisted Spatial Modulation for Energy Efficient Communication. In Proceedings of the 2021 Innovations in Power and Advanced Computing Technologies (i-PACT), Kuala Lumpur, Malaysia, 27–29 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Bo, L.; Gao, F.; Zhang, S.; Zhou, T.; Alkhateeb, A. Deep learning-based antenna selection and CSI extrapolation in massive MIMO systems. IEEE Trans. Wirel. Commun. 2021, 20, 7669–7681. [Google Scholar]
- Narushan, P.; Xu, H. Low-complexity transmit antenna selection schemes for spatial modulation. IET Commun. 2015, 9, 239–248. [Google Scholar]
- Ping, Y.; Xiao, Y.; Li, L.; Tang, Q.; Yu, Y.; Li, S. Link adaptation for spatial modulation with limited feedback. IEEE Trans. Veh. Technol. 2012, 61, 3808–3813. [Google Scholar]
- Ping, Y.; Zhu, J.; Xiao, Y.; Chen, Z. Antenna selection for MIMO system based on pattern recognition. Digit. Commun. Netw. 2019, 5, 34–39. [Google Scholar]
- Ping, Y.; Xiao, Y.; Xiao, M.; Guan, Y.L.; Li, S.; Xiang, W. Adaptive spatial modulation MIMO based on machine learning. IEEE J. Sel. Areas Commun. 2019, 37, 2117–2131. [Google Scholar]
- Kishor, J.H.; Kumaravelu, V.B. Transmit antenna selection for spatial modulation based on machine learning. Phys. Commun. 2022, 55, 101904. [Google Scholar]
- Meenu, K. Deep learning based low complexity joint antenna selection scheme for MIMO vehicular adhoc networks. Expert Syst. Appl. 2023, 219, 119637. [Google Scholar]
- Gökhan, A.; Arslan, İ.A. Joint transmit and receive antenna selection for spatial modulation systems using deep learning. IEEE Commun. Lett. 2022, 26, 2077–2080. [Google Scholar]
- Ahmet, A.İ.; Altin, G. A novel deep neural network based antenna selection architecture for spatial modulation systems. In Proceedings of the 2021 56th International Scientific Conference on Information, Communication and Energy Systems and Technologies (ICEST), Sozopol, Bulgaria, 16–18 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 141–144. [Google Scholar]
- Shilian, Z.; Chen, S.; Yang, X. DeepReceiver: A deep learning-based intelligent receiver for wireless communications in the physical layer. IEEE Trans. Cogn. Commun. Netw. 2020, 7, 5–20. [Google Scholar]
- Abeer, M.; Bai, Z.; Oloruntomilayo, F.-P.; Pang, K.; Yang, Y.; Zhou, D.; Kwak, K.S. Low complexity deep neural network based transmit antenna selection and signal detection in SM-MIMO system. Digit. Signal Process. 2022, 130, 103708. [Google Scholar]
- Jianfeng, Z.; Mao, X.; Chen, L. Speech emotion recognition using deep 1D & 2D CNN LSTM networks. Biomed. Signal Process. Control. 2019, 47, 312–323. [Google Scholar]
- Serkan, K.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar]
- Yanzhao, W.; Liu, L.; Pu, C.; Cao, W.; Sahin, S.; Wei, W.; Zhang, Q. A comparative measurement study of deep learning as a service framework. IEEE Trans. Serv. Comput. 2019, 15, 551–566. [Google Scholar]
- Synho, D.; Song, K.D.; Chung, J.W. Basics of deep learning: A radiologist's guide to understanding published radiology articles on deep learning. Korean J. Radiol. 2020, 21, 33–41. [Google Scholar]





| Sr. No. | Input Bits | Antenna Set | Symbols | Transmit Vector |
|---|---|---|---|---|
| 1 | 0000 | 1, 2 | −1 | 𝟆 = [−1, −1, 0, 0] |
| 2 | 0001 | 1, 2 | +1 | 𝟆 = [1, 1, 0, 0] |
| 3 | 0010 | 1, 3 | −1 | 𝟆 = [−1, 0, −1, 0] |
| 4 | 0011 | 1, 3 | +1 | 𝟆 = [1, 0, 1, 0] |
| 5 | 0100 | 1, 4 | −1 | 𝟆 = [−1, 0, 0, −1] |
| 6 | 0101 | 1, 4 | +1 | 𝟆 = [1, 0, 0, 1] |
| 7 | 0110 | 2, 3 | −1 | 𝟆 = [0, −1, −1, 0] |
| 8 | 0111 | 2, 3 | +1 | 𝟆 = [0, 1, 1, 0] |
| 9 | 1000 | 2, 4 | −1 | 𝟆 = [0, −1, 0, −1] |
| 10 | 1001 | 2, 4 | +1 | 𝟆 = [0, 1, 0, 1] |
| 11 | 1010 | 3, 4 | −1 | 𝟆 = [0, 0, −1, −1] |
| 12 | 1011 | 3, 4 | +1 | 𝟆 = [0, 0, 1, 1] |
| 13 | 1100 | 1, 2, 3 | −1 | 𝟆 = [−1, −1, −1, 0] |
| 14 | 1101 | 1, 2, 3 | +1 | 𝟆 = [1, 1, 1, 0] |
| 15 | 1110 | 2, 3, 4 | −1 | 𝟆 = [0, −1, −1, −1] |
| 16 | 1111 | 2, 3, 4 | +1 | 𝟆 = [0, 1, 1, 1] |
| Labels | Antenna Subsets |
|---|---|
| a | 1, 2, 3] |
| b | 1, 2, 4] |
| c | |
| d |
| Parameters | Values |
|---|---|
| Number of hidden layers | 3 |
| 1D convolution layer 1 | Filter Size = 3/Number of filters = 32 |
| 1D convolution layer 2 | Filter Size = 6/Number of filters = 32 |
| 1D convolution layer 3 | Filter Size = 9/Number of filters = 32 |
| Activation function | ReLU |
| Optimizer | Adam |
| DL-Based TAS Scheme | Order of Complexity | Configuration 1 , , | Configuration 2 , , |
|---|---|---|---|
| Traditional EDAS | [12] | O(0.753 × 109) | O(12.07 × 109) |
| FNN-based TAS | [23] | O(4.194 × 106) | O(4.194 × 106) |
| RNN-based TAS | [23] | O(4.194 × 106) | O(4.194 × 106) |
| 1D CNN-based TAS | ) [23] | O(5.308 × 106) | O(5.308 × 106) |
| Parameters | Values |
|---|---|
| Dataset Size () | 25,000 |
| Holdout ratio | 80–20% |
| Mini batch size | 64 |
| Maximum epochs | 50 |
| Initial learning rate | 0.00012 |
| Optimizer | Adam |
| Learning drop rate factor | 0.15 |
| Target ABER |
| Dataset | Configurations | Size |
|---|---|---|
| Dataset 1 | = 4, = 3, 4, M = 4 | 25,000 |
| Dataset 2 | = 4, = 3, 4, M = 16 | 25,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jadhav, H.K.; Kumaravelu, V.B. Deep Learning-Assisted Transmit Antenna Classifiers for Fully Generalized Spatial Modulation: Online Efficiency Replaces Offline Complexity. Appl. Sci. 2023, 13, 5134. https://doi.org/10.3390/app13085134
Jadhav HK, Kumaravelu VB. Deep Learning-Assisted Transmit Antenna Classifiers for Fully Generalized Spatial Modulation: Online Efficiency Replaces Offline Complexity. Applied Sciences. 2023; 13(8):5134. https://doi.org/10.3390/app13085134
Chicago/Turabian StyleJadhav, Hindavi Kishor, and Vinoth Babu Kumaravelu. 2023. "Deep Learning-Assisted Transmit Antenna Classifiers for Fully Generalized Spatial Modulation: Online Efficiency Replaces Offline Complexity" Applied Sciences 13, no. 8: 5134. https://doi.org/10.3390/app13085134
APA StyleJadhav, H. K., & Kumaravelu, V. B. (2023). Deep Learning-Assisted Transmit Antenna Classifiers for Fully Generalized Spatial Modulation: Online Efficiency Replaces Offline Complexity. Applied Sciences, 13(8), 5134. https://doi.org/10.3390/app13085134







