Dynamic Path-Planning and Charging Optimization for Autonomous Electric Vehicles in Transportation Networks
Abstract
:1. Introduction
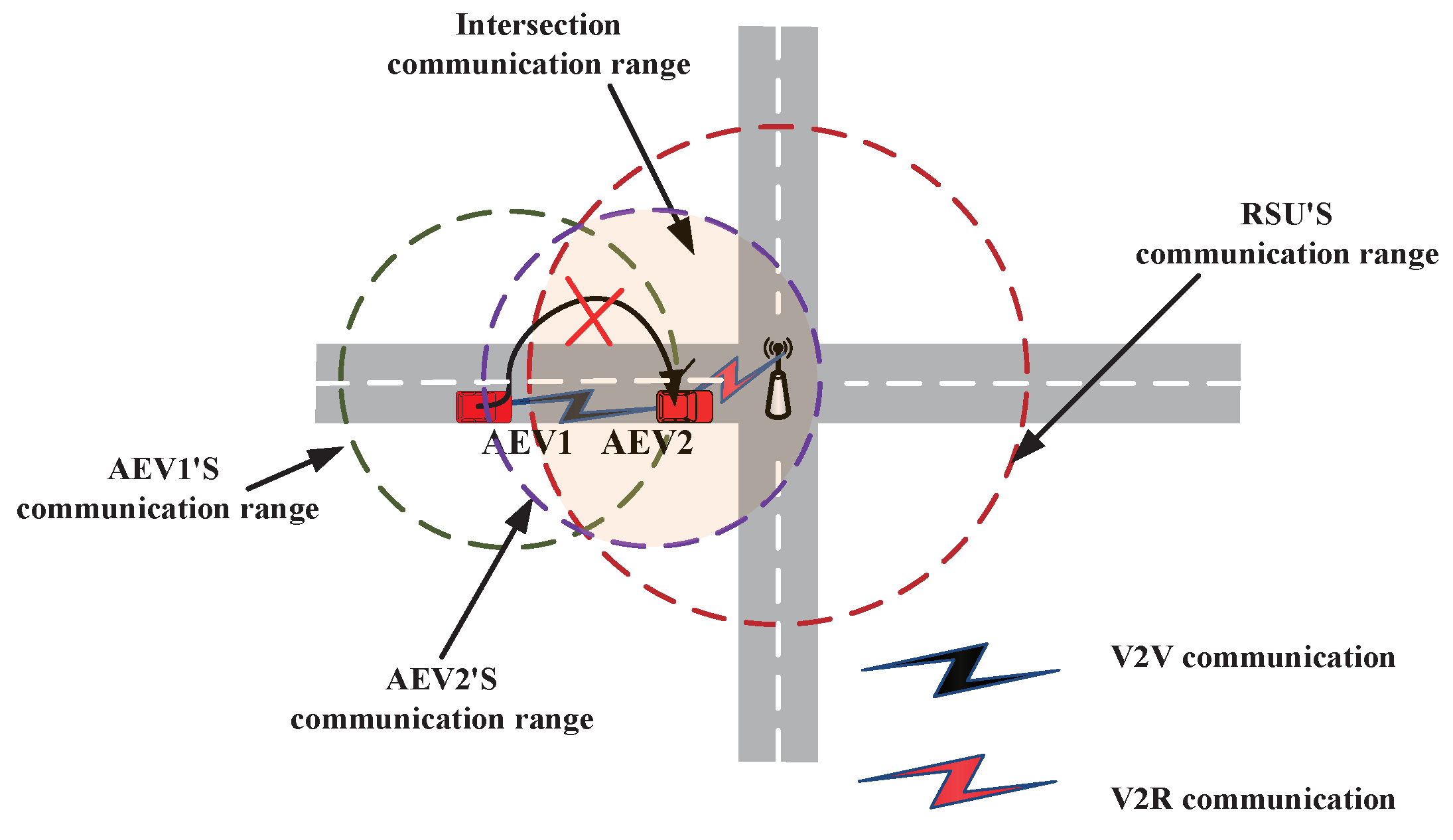
- A joint push–pull communication mode is proposed to obtain real-time traffic conditions and charging infrastructure service status information. Moreover, the paper discusses the selection of relay vehicles based on link stability, vehicle distance, and service satisfaction in multi-hop communication routing.
- A dynamic optimization problem is formulated based on the mode of real-time communication to solve the dynamic path optimization with charging selection. This problem considers several factors, such as travel time, queuing time, charging time, and consumption of charge, while also including both CSs and ESs as energy providers.
- A novel approach for addressing dynamic optimization problems in transportation networks is proposed. The proposed method involves transforming the original problem into a series of single optimization problems and simplifying the road network through preprocessing. After that, a dynamic real-time A* (DRT-A*) algorithm is proposed to efficiently solve the path-optimization problem. Furthermore, a dynamic real-time charging selection (DRT-CS) algorithm based on dynamic path optimization to solve the charging selection problem is proposed.
2. Related Work
3. System Model
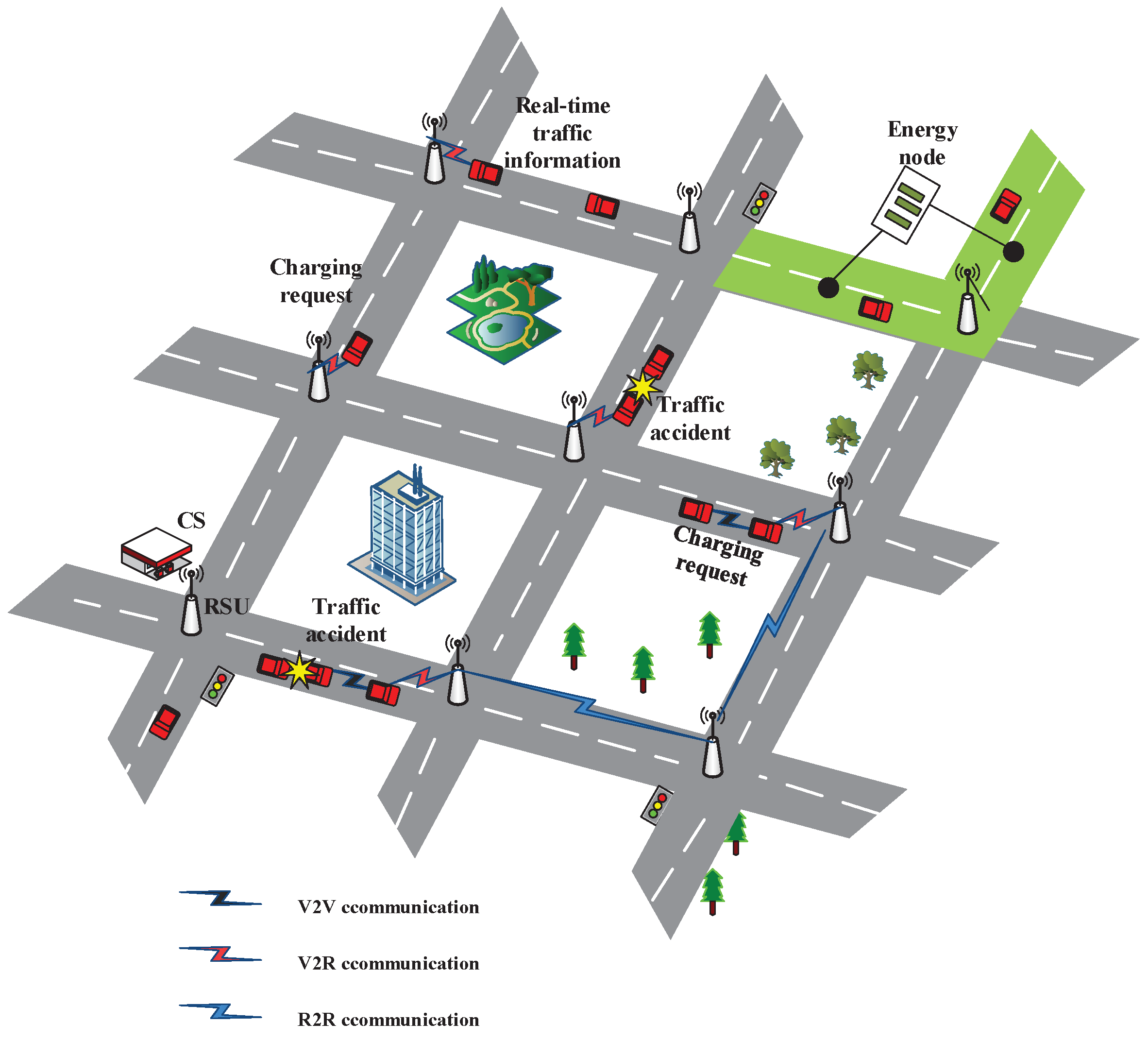
3.1. Transportation Network Architecture
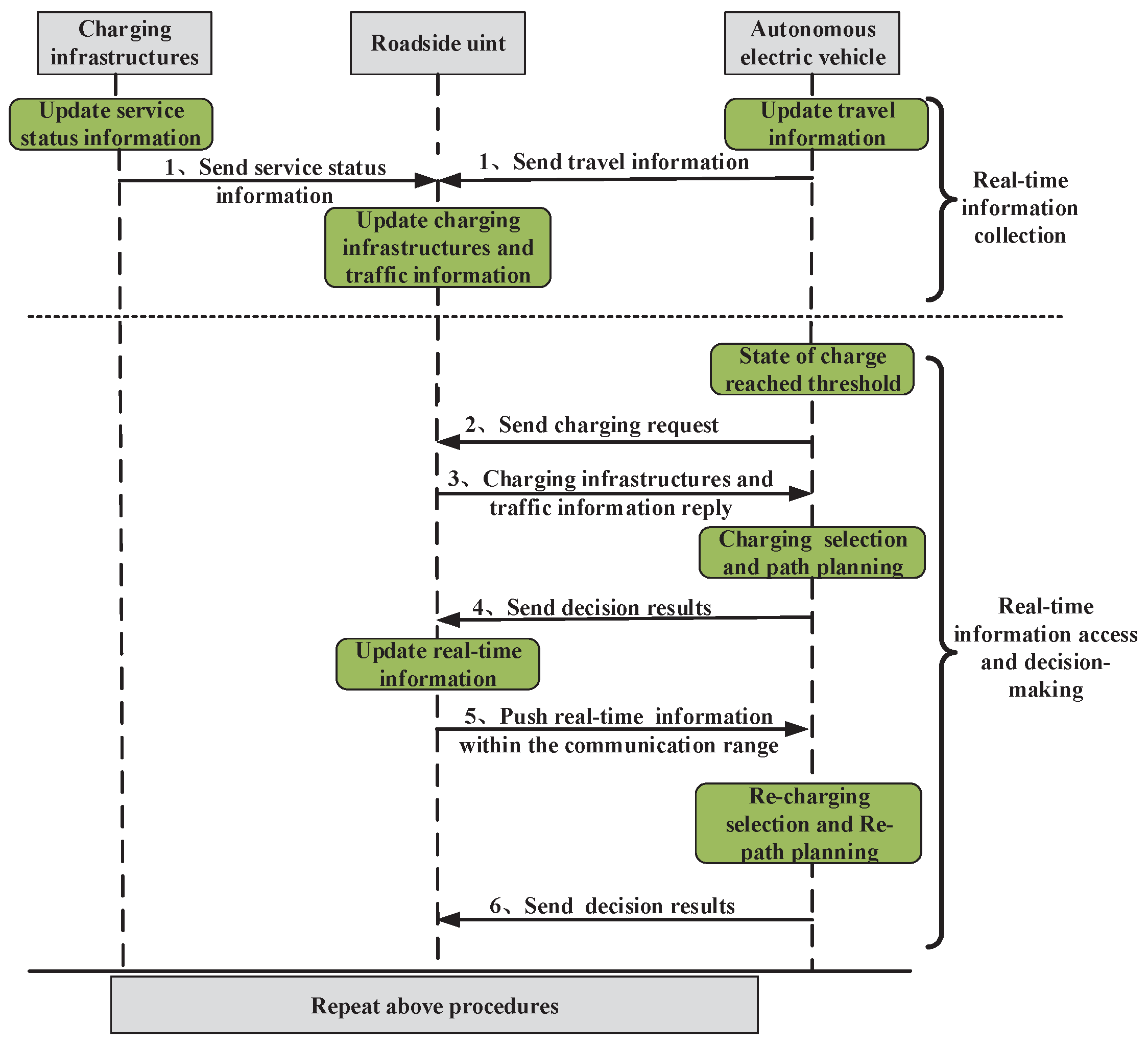
3.2. Dynamic Path and Charging System Process
4. Joint Push–Pull Communication Mode
| Algorithm 1: Relay Vehicle Selection Algorithm. |
|
5. Mathematical Formulations for Vehicle Travel and Charging
5.1. Time Cost
5.1.1. Travel Time
5.1.2. Queuing Time
5.1.3. Charging Time
5.2. Charge Consumption
6. Dynamic Path Optimization with Charging Selection
6.1. Problem Formulation
6.2. Optimization Model
7. Simplified Model and Algorithm
7.1. Travel Problem Model
- SoC-based road segment elimination
- TFD-based road segment elimination
| Algorithm 2: DRT-A* algorithm. |
|
7.2. Charging Problem Model
| Algorithm 3: DRT-CS algorithm. |
|
8. Performance Analysis
8.1. Simulation Setup
8.2. The TFD Thresholds Parameter Analysis
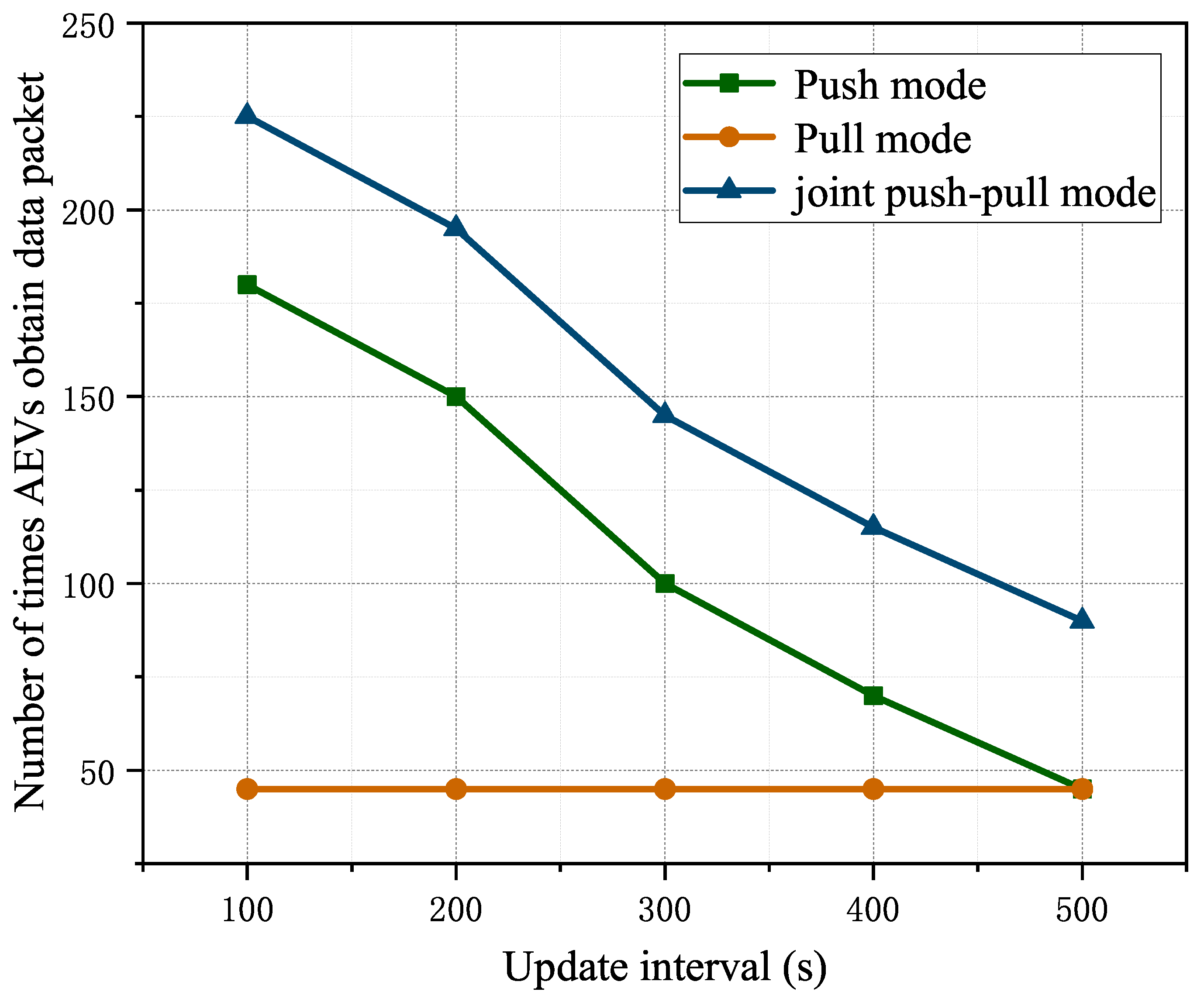
8.3. The Evaluation of Communication Mode
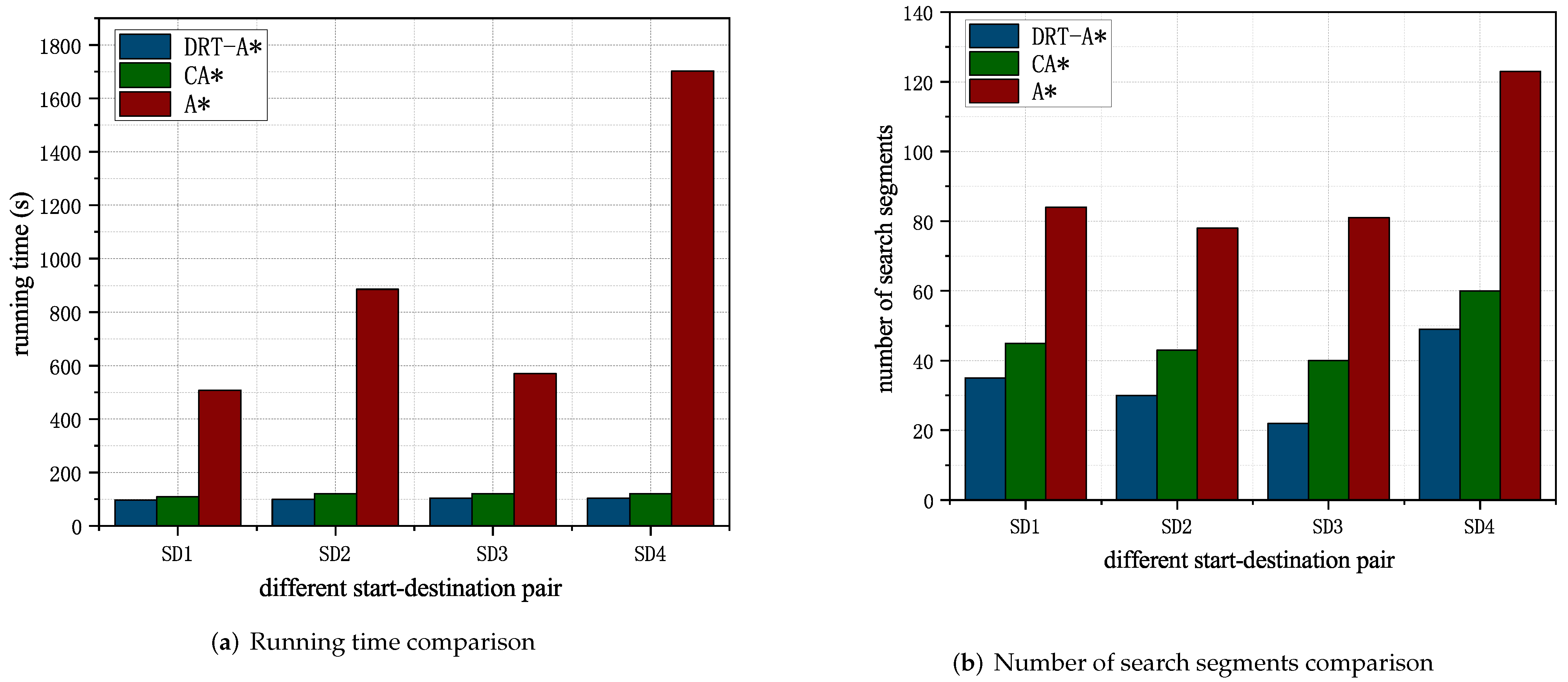
8.4. The Evaluation of Running Time
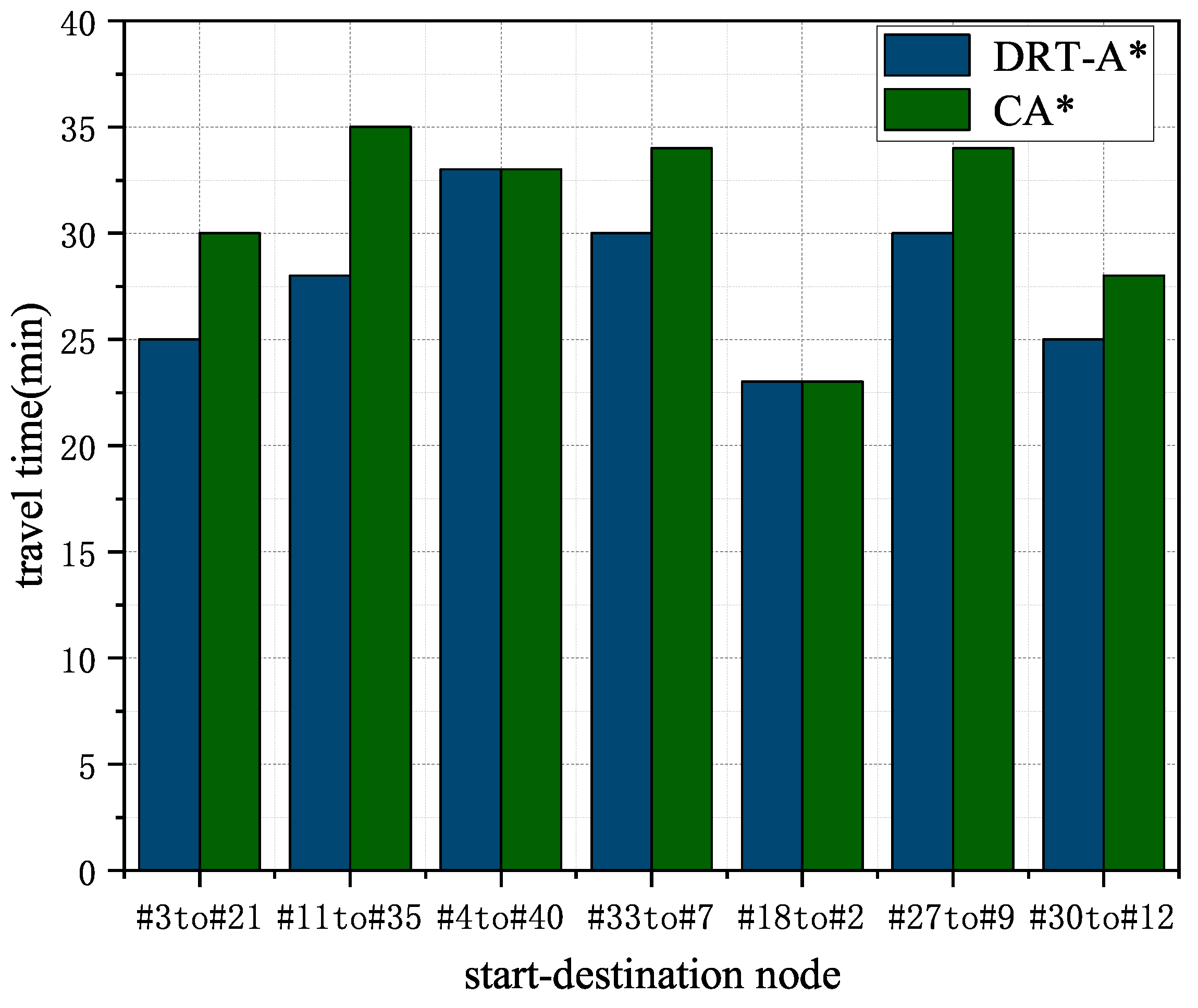
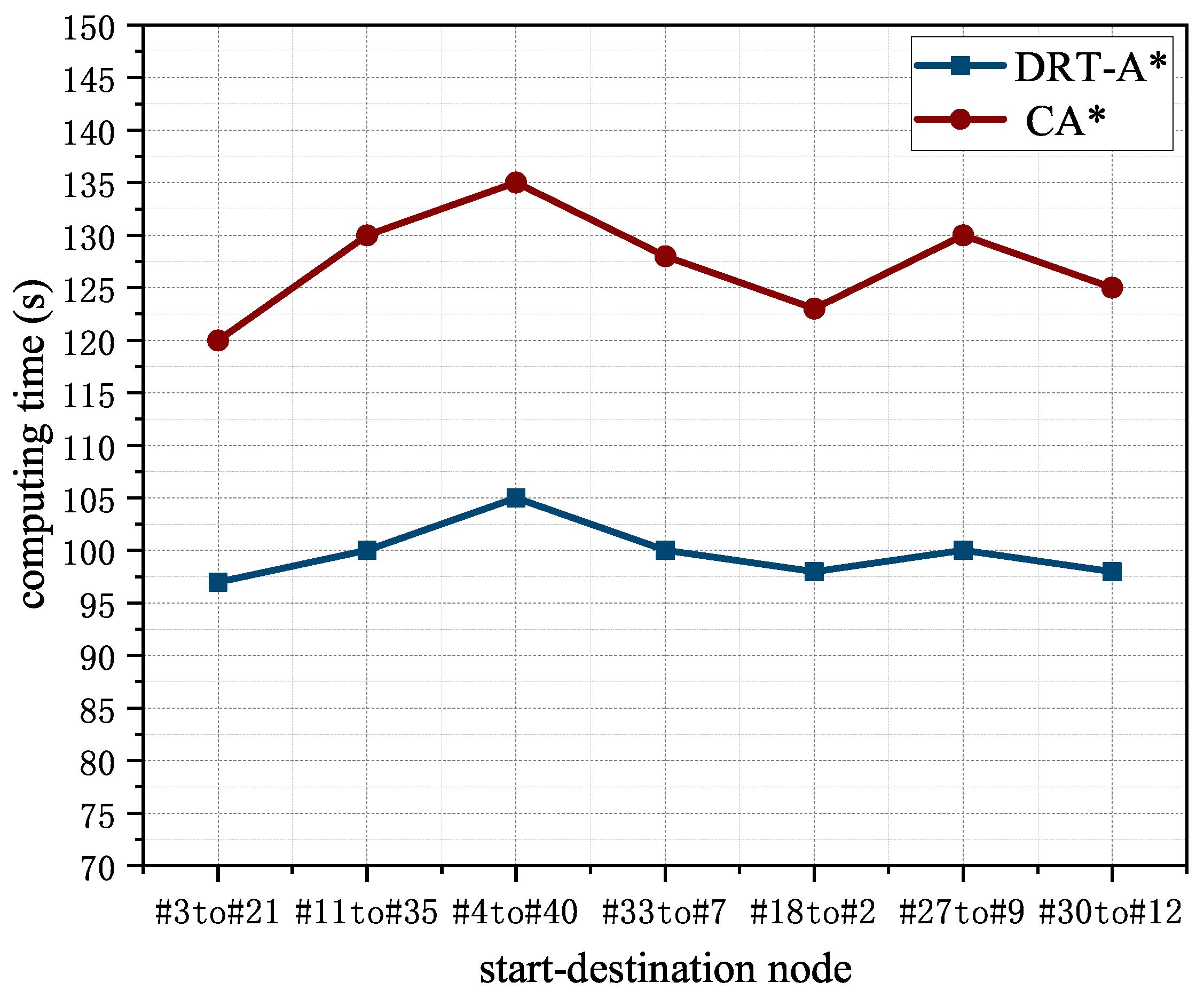
8.5. The Evaluation of Different Travel Start–Destination Time Cost
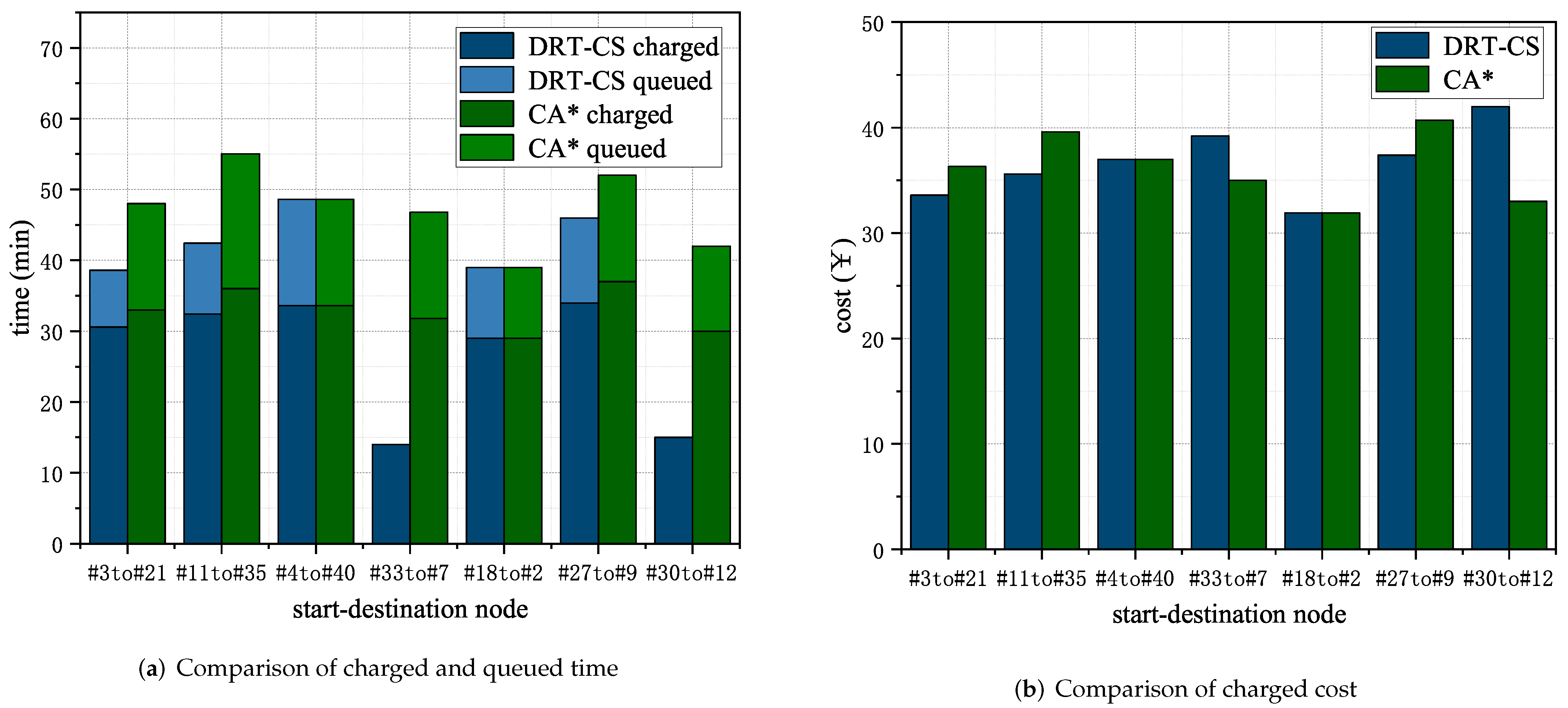
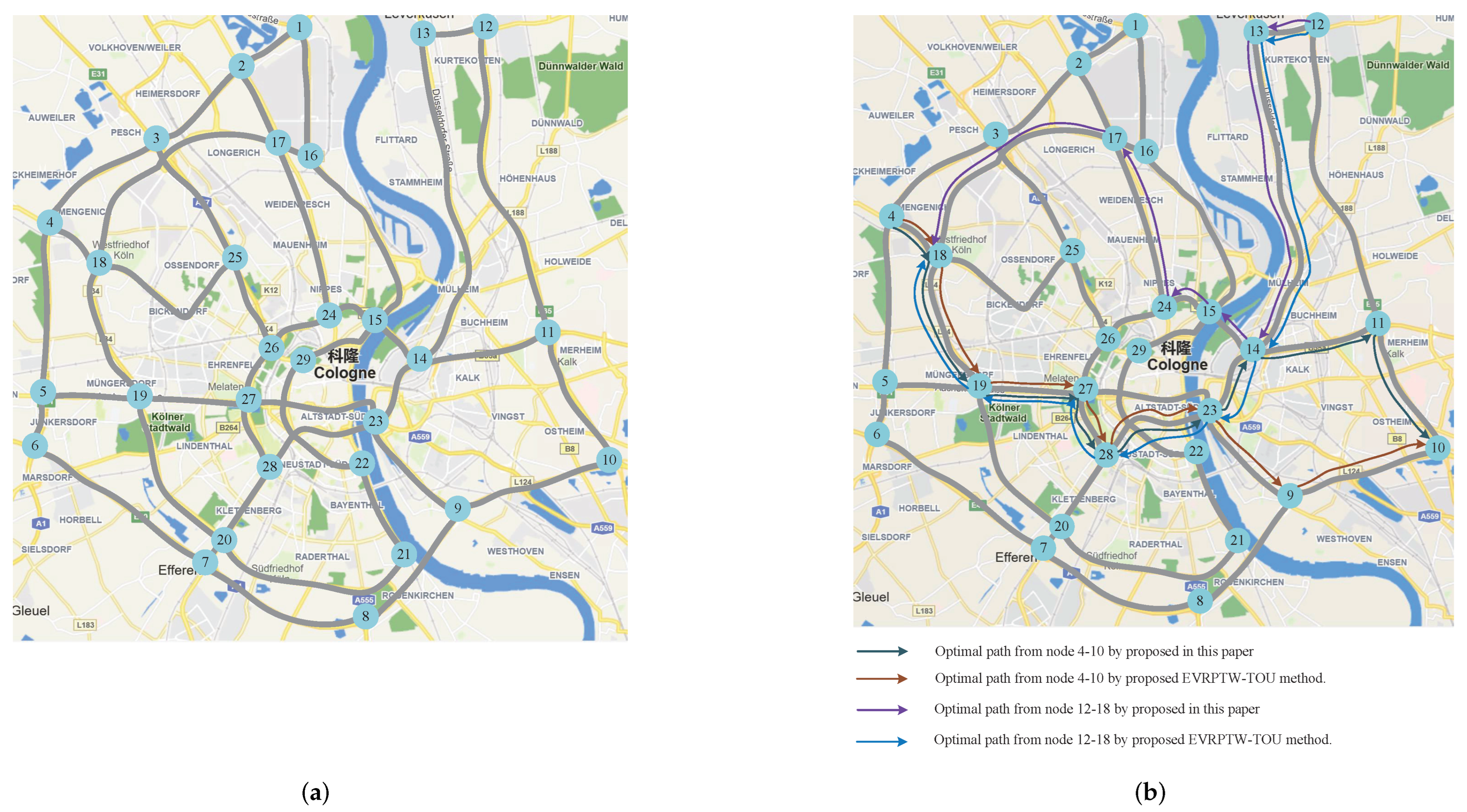
8.6. The Evaluation of Path-Planning and Charging Selection
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Iacobucci, R.; McLellan, B.; Tezuka, T. Modeling shared autonomous electric vehicles: Potential for transport and power grid integration. Energy 2018, 158, 148–163. [Google Scholar] [CrossRef]
- Wu, J.; Liao, H.; Wang, J.W.; Chen, T. The role of environmental concern in the public acceptance of autonomous electric vehicles: A survey from China. Transp. Res. Part F Traffic Psychol. Behav. 2019, 60, 37–46. [Google Scholar] [CrossRef]
- Huang, T.; Pan, H.; Sun, W.; Gao, H. Sine resistance network-based motion planning approach for autonomous electric vehicles in dynamic environments. IEEE Trans. Transp. Electrif. 2022, 8, 2862–2873. [Google Scholar] [CrossRef]
- Hwang, M.H.; Lee, G.S.; Kim, E.; Kim, H.W.; Yoon, S.; Talluri, T.; Cha, H.R. Regenerative Braking Control Strategy Based on AI Algorithm to Improve Driving Comfort of Autonomous Vehicles. Appl. Sci. 2023, 13, 946. [Google Scholar] [CrossRef]
- Ercan, T.; Onat, N.C.; Keya, N.; Tatari, O.; Eluru, N.; Kucukvar, M. Autonomous electric vehicles can reduce carbon emissions and air pollution in cities. Transp. Res. Part D Transp. Environ. 2022, 112, 103472. [Google Scholar] [CrossRef]
- Vdovic, H.; Babic, J.; Podobnik, V. Automotive software in connected and autonomous electric vehicles: A review. IEEE Access 2019, 7, 166365–166379. [Google Scholar] [CrossRef]
- Cao, Y.; Li, D.; Zhang, Y.; Chen, X. Joint optimization of delay-tolerant autonomous electric vehicles charge scheduling and station battery degradation. IEEE Internet Things J. 2020, 7, 8590–8599. [Google Scholar] [CrossRef]
- Yao, C.; Chen, S.; Yang, Z. Joint routing and charging problem of multiple electric vehicles: A fast optimization algorithm. IEEE Trans. Intell. Transp. Syst. 2021, 23, 8184–8193. [Google Scholar] [CrossRef]
- Liu, H.; Yin, W.; Yuan, X.; Niu, M. Reserving charging decision-making model and route plan for electric vehicles considering information of traffic and charging station. Sustainability 2018, 10, 1324. [Google Scholar] [CrossRef]
- Li, M.; Deng, Y.; Yang, H.; Lai, M.; Dong, Z. Electric Vehicle Route Selection and Charging Navigation Strategy Considering Time-of-Use Pric. South. Power Syst. Technol 2016, 10, 61–66. [Google Scholar]
- Xing, Q.; Chen, Z.; Leng, Z.; Lu, Y.; Liu, Y. Route Planning and Charging Navigation Strategy for Electric Vehicles Based on Real-time Traffic Information. Proc. CSEE 2020, 40, 534–550. [Google Scholar]
- Luo, Y.; Zhu, T.; Wan, S.; Zhang, S.; Li, K. Optimal charging scheduling for large-scale EV (electric vehicle) deployment based on the interaction of the smart-grid and intelligent-transport systems. Energy 2016, 97, 359–368. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Feng, H. Research on dynamic energy saving path planning algorithm based on real-time traffic information. In Proceedings of the 2016 4th International Conference on Advanced Materials and Information Technology Processing (AMITP 2016), Guilin, China, 24–25 September 2016; Atlantis Press: Amsterdam, The Netherlands, 2016; pp. 314–319. [Google Scholar]
- Li, G.; Sun, Q.; Boukhatem, L.; Wu, J.; Yang, J. Intelligent vehicle-to-vehicle charging navigation for mobile electric vehicles via VANET-based communication. IEEE Access 2019, 7, 170888–170906. [Google Scholar] [CrossRef]
- Wang, M.; Liang, H.; Deng, R.; Zhang, R.; Shen, X.S. VANET based online charging strategy for electric vehicles. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 4804–4809. [Google Scholar]
- Bi, X.; Gao, D.; Yang, M. A reinforcement learning-based routing protocol for clustered EV-VANET. In Proceedings of the 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; pp. 1769–1773. [Google Scholar]
- Liu, C.; Zhou, M.; Wu, J.; Long, C.; Wang, Y. Electric vehicles en-route charging navigation systems: Joint charging and routing optimization. IEEE Trans. Control Syst. Technol. 2017, 27, 906–914. [Google Scholar] [CrossRef]
- Liu, P.; Wang, C.; Hu, J.; Fu, T.; Cheng, N.; Zhang, N.; Shen, X. Joint Route Selection and Charging Discharging Scheduling of EVs in V2G Energy Network. IEEE Trans. Veh. Technol. 2020, 69, 10630–10641. [Google Scholar] [CrossRef]
- Liu, J.; Lin, G.; Huang, S.; Zhou, Y.; Rehtanz, C.; Li, Y. Collaborative EV routing and charging scheduling with power distribution and traffic networks interaction. IEEE Trans. Power Syst. 2022, 37, 3923–3936. [Google Scholar] [CrossRef]
- Lam, A.Y.; Leung, K.C.; Li, V.O. Vehicular energy network. IEEE Trans. Transp. Electrif. 2017, 3, 392–404. [Google Scholar] [CrossRef]
- Fu, T.; Wang, C.; Cheng, N. Deep-learning-based joint optimization of renewable energy storage and routing in vehicular energy network. IEEE Internet Things J. 2020, 7, 6229–6241. [Google Scholar] [CrossRef]
- Manshadi, S.D.; Khodayar, M.E.; Abdelghany, K.; Üster, H. Wireless charging of electric vehicles in electricity and transportation networks. IEEE Trans. Smart Grid 2017, 9, 4503–4512. [Google Scholar] [CrossRef]
- Duell, M.; Gardner, L.M.; Waller, S.T. Policy implications of incorporating distance constrained electric vehicles into the traffic network design problem. Transp. Lett. 2018, 10, 144–158. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, J.; Mu, T. Context-aware and energy-driven route optimization for fully electric vehicles via crowdsourcing. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1331–1345. [Google Scholar] [CrossRef]
- Yang, H.; Deng, Y.; Qiu, J.; Li, M.; Lai, M.; Dong, Z.Y. Electric vehicle route selection and charging navigation strategy based on crowd sensing. IEEE Trans. Ind. Inform. 2017, 13, 2214–2226. [Google Scholar] [CrossRef]
- Ding, D.; Li, J.; Tu, P.; Wang, H.; Cao, T.; Zhang, F. Electric vehicle charging warning and path planning method based on spark. IEEE Access 2020, 8, 8543–8553. [Google Scholar] [CrossRef]
- Schoenberg, S.; Dressler, F. Reducing waiting times at charging stations with adaptive electric vehicle route planning. IEEE Trans. Intell. Veh. 2022, 8, 95–107. [Google Scholar] [CrossRef]
- Del Razo, V.; Jacobsen, H.A. Smart charging schedules for highway travel with electric vehicles. IEEE Trans. Transp. Electrif. 2016, 2, 160–173. [Google Scholar] [CrossRef]
- Ferro, G.; Paolucci, M.; Robba, M. Optimal charging and routing of electric vehicles with power constraints and time-of-use energy prices. IEEE Trans. Veh. Technol. 2020, 69, 14436–14447. [Google Scholar] [CrossRef]
- Gusrialdi, A.; Qu, Z.; Simaan, M.A. Distributed scheduling and cooperative control for charging of electric vehicles at highway service stations. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2713–2727. [Google Scholar] [CrossRef]
- Weist, M. A Transport Simulation-Based Analysis of Optimal Long-Distance Route Planning for Battery Electric Vehicles in Germany. Ph.D Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2021. [Google Scholar]
- Embleton, N.D.; Munteanu, A.; Ho, E. Northumbria Research Link. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 8–19. [Google Scholar]
- Alqahtani, M.; Hu, M. Dynamic energy scheduling and routing of multiple electric vehicles using deep reinforcement learning. Energy 2022, 244, 122626. [Google Scholar] [CrossRef]
- Subramanian, V.; Feijoo, F.; Sankaranarayanan, S.; Melendez, K.; Das, T.K. A bilevel conic optimization model for routing and charging of EV fleets serving long distance delivery networks. Energy 2022, 251, 123808. [Google Scholar] [CrossRef]
- Guo, C.; Li, D.; Zhang, G.; Zhai, M. Real-time path planning in urban area via vanet-assisted traffic information sharing. IEEE Trans. Veh. Technol. 2018, 67, 5635–5649. [Google Scholar] [CrossRef]
- Umoren, I.A.; Shakir, M.Z.; Tabassum, H. Resource efficient vehicle-to-grid (V2G) communication systems for electric vehicle enabled microgrids. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4171–4180. [Google Scholar] [CrossRef]
- Juvva, K.; Rajkumar, R. A Real-Time Push-Pull Communications Model for Distributed Real-Time and Multimedia Systems; Technical Report; Carnegie-Mellon Univ Pittsburgh Pa Dept of Computer Science: Pittsburgh, PA, USA, 1999. [Google Scholar]
- Naderi, M.; Zargari, F.; Sadatpour, V.; Ghanbari, M. A 3-parameter routing cost function for improving opportunistic routing performance in VANETs. Wirel. Pers. Commun. 2017, 97, 109–123. [Google Scholar] [CrossRef]
- Patel, A.; Jinwala, D. A reputation-based RPL protocol to detect selective forwarding attack in Internet of Things. Int. J. Commun. Syst. 2022, 35, e5007. [Google Scholar] [CrossRef]
- Skabardonis, A.; Dowling, R. Improved speed-flow relationships for planning applications. Transp. Res. Rec. 1997, 1572, 18–23. [Google Scholar] [CrossRef]
- Zadobrischi, E.; Cosovanu, L.M.; Dimian, M. Traffic flow density model and dynamic traffic congestion model simulation based on practice case with vehicle network and system traffic intelligent communication. Symmetry 2020, 12, 1172. [Google Scholar] [CrossRef]
- Zhang, Y.; You, P.; Cai, L. Optimal charging scheduling by pricing for EV charging station with dual charging modes. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3386–3396. [Google Scholar] [CrossRef]
- Wang, H.; Cai, X.; Zhang, Y.; Liu, A.; Huang, P.; Li, C. Driving on GWB: Energy-efficiency-driven route optimisation for EVs. IET Intell. Transp. Syst. 2019, 14, 25–35. [Google Scholar] [CrossRef]
- Arnott, R.; Rave, T.; Schöb, R. Alleviating Urban Traffic Congestion; MIT Press Books: Cambridge, MA, USA, 2005; Volume 1. [Google Scholar]
- Zeng, W.; Church, R.L. Finding shortest paths on real road networks: The case for A. Int. J. Geogr. Inf. Sci. 2009, 23, 531–543. [Google Scholar] [CrossRef]
- Huber, S.; Rust, C. Calculate travel time and distance with OpenStreetMap data using the Open Source Routing Machine (OSRM). Stata J. 2016, 16, 416–423. [Google Scholar] [CrossRef]
- Mortimer, B.J.; Hecht, C.; Goldbeck, R.; Sauer, D.U.; De Doncker, R.W. Electric Vehicle Public Charging Infrastructure Planning Using Real-World Charging Data. World Electr. Veh. J. 2022, 13, 94. [Google Scholar] [CrossRef]
- Sumo. Traffic Data. 2015. Available online: https://sourceforge.net/projects/sumo/files/traffic_data/scenarios/TAPASCologne/ (accessed on 26 October 2022).
- Ruilin, Q. Vehicle Configuration Information. 2022. Available online: https://www.tyncar.com/Q/qirui_rq_185.html (accessed on 25 October 2022).


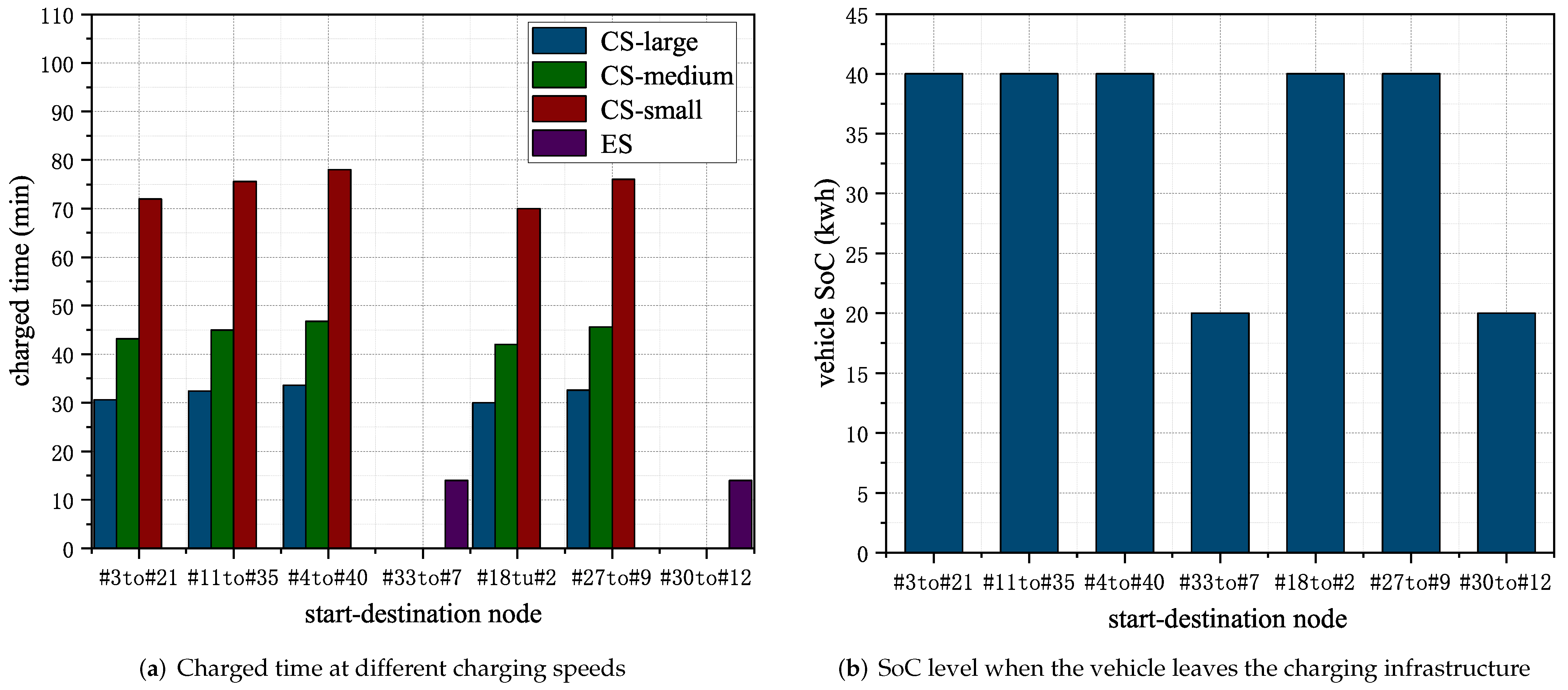
| Article Reference | Energy Cost | Travel Time | Waiting Time | Charging Location | Battery Capacity | Dynamic Optimization | Distributed Decision |
|---|---|---|---|---|---|---|---|
| Liu et al. [17] | × | × | × | × | × | × | |
| Liu et al. [18] | × | × | × | × | |||
| Liu et al. [19] | × | × | × | ||||
| Manshadi et al. [22] | × | × | × | ||||
| Liu et al. [23] | × | × | × | ||||
| Wang et al. [24] | × | × | × | × | |||
| Yang et al. [25] | × | × | × | ||||
| Ding et al. [26] | × | × | × | × | × | × | |
| Schoenberg et al. [27] | × | × | × | × | × | ||
| Del Razo et al. [28] | × | × | × | × | × | × | |
| Ferro et al. [29] | × | × | × | × | × | ||
| Gusrialdi et al. [30] | × | × | × | ||||
| Weist et al. [31] | × | × | × | × | × | × | |
| Embleton et al. [32] | × | ||||||
| Alqahtani et al. [33] | × | × | × | ||||
| Subramanian et al. [34] | × | × | × | × | |||
| our work in this paper | × | × | × | × | × | × | × |
| Notation | Description |
|---|---|
| Road node set in graph G. | |
| Set of charging stations. | |
| Charging station at road node i. | |
| Road section set in graph G. | |
| ES set in graph G. | |
| Time for AEV k to reach node i. | |
| Time for AEV k to leave node i. | |
| AEV k charging time at . | |
| AEV k queuing time at . | |
| AEV k travel time on segment . | |
| AEV k energy consumption on segment . | |
| AEV k SoC at road node i. | |
| The SoC that AEV needs to charge. | |
| Traffic flow density on segment . | |
| Length of road segment . | |
| Maximum number of AEVs on segment . | |
| The number of AEVs on segment at t. | |
| The variation in the position between two vehicles k and h. | |
| The distance difference between the vehicle k and h to the R. | |
| The total number of data packets sent from vehicle k to vehicle h. | |
| The total number of data packets forwarded by vehicle k to vehicle h. | |
| The total number of packets lost by vehicle k to vehicle h. |
| Abbreviation | Description |
|---|---|
| AEV | autonomous electric vehicle |
| VANETs | vehicular ad hoc networks |
| RSU | roadside unit |
| V2V | vehicle-to-vehicle |
| V2R | vehicle to roadside unit |
| V2G | vehicle to gird (charging infrastructure) |
| CS | charging station |
| ES | energy segment |
| TFD | traffic flow density |
| SoC | state of charge |
| DRT-A* | dynamic real-time A* |
| DRT-CS | dynamic real-time charging selection |
| Simulation Parameters | Value |
|---|---|
| Network area | 20 (km) |
| AEV speed(V) | 25–60 (km/h) |
| AEV mass (M) | 1200 kg |
| Acceleration of gravity (g) | 9.8 m/s |
| Rolling friction coefficient () | 0.009 |
| Air density () | 1.2 kg/m |
| Coefficient of air resistance () | 0.335 |
| Frontal area (A) | 2 m |
| Road slope () | 0 deg |
| Weight parameters | , |
| , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Q.; Li, D.; Zhang, Y.; Chen, X. Dynamic Path-Planning and Charging Optimization for Autonomous Electric Vehicles in Transportation Networks. Appl. Sci. 2023, 13, 5476. https://doi.org/10.3390/app13095476
Tang Q, Li D, Zhang Y, Chen X. Dynamic Path-Planning and Charging Optimization for Autonomous Electric Vehicles in Transportation Networks. Applied Sciences. 2023; 13(9):5476. https://doi.org/10.3390/app13095476
Chicago/Turabian StyleTang, Qinghua, Demin Li, Yihong Zhang, and Xuemin Chen. 2023. "Dynamic Path-Planning and Charging Optimization for Autonomous Electric Vehicles in Transportation Networks" Applied Sciences 13, no. 9: 5476. https://doi.org/10.3390/app13095476
APA StyleTang, Q., Li, D., Zhang, Y., & Chen, X. (2023). Dynamic Path-Planning and Charging Optimization for Autonomous Electric Vehicles in Transportation Networks. Applied Sciences, 13(9), 5476. https://doi.org/10.3390/app13095476






